Addressing Uncertainty by Designing an Intelligent Fuzzy System to Help Decision Support Systems for Winter Road Maintenance
Abstract
1. Introduction
1.1. Motivation
1.2. Significance of the Topic
1.3. State-of-the-Art Method
1.4. Contributions
1.5. Outline of the Paper
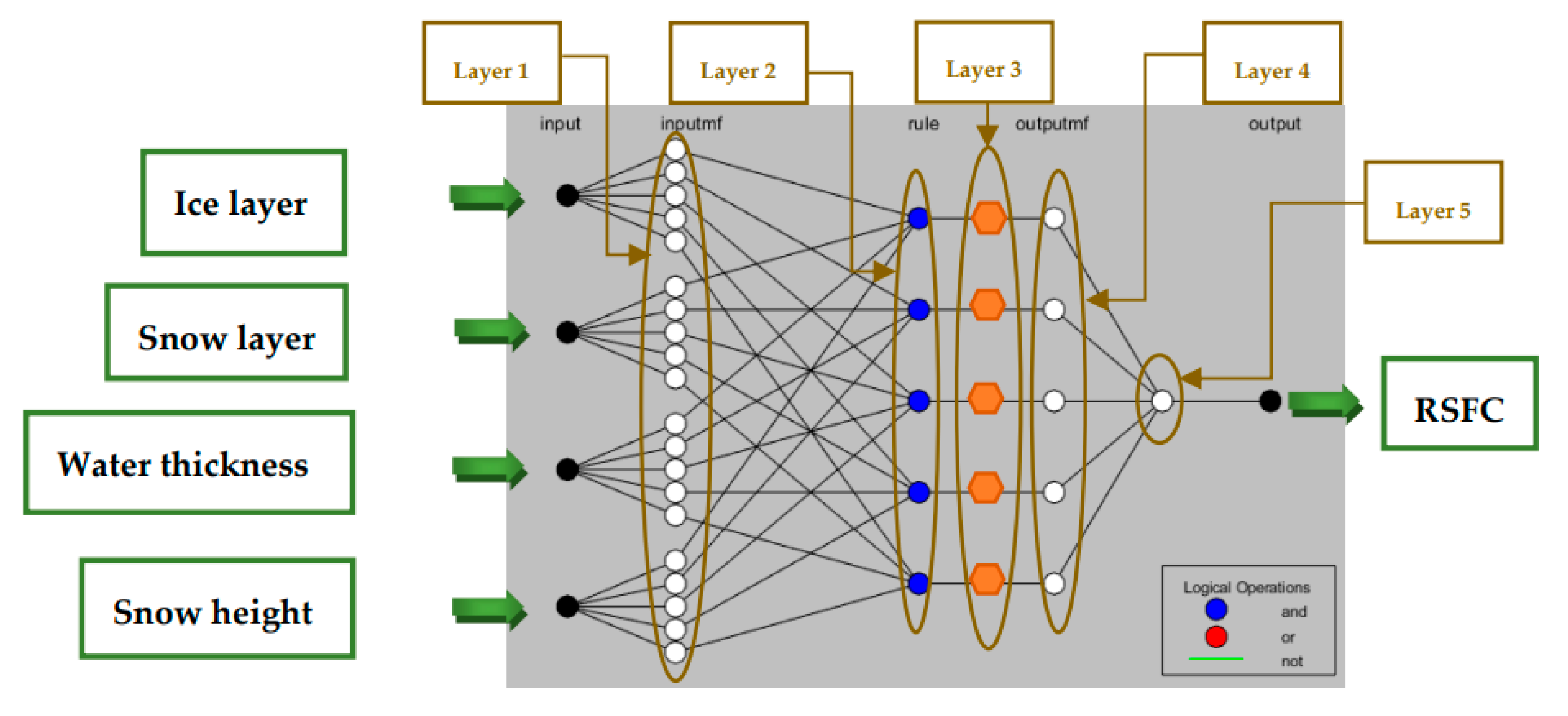
2. Adaptive Neuro-Fuzzy Inference System (ANFIS)
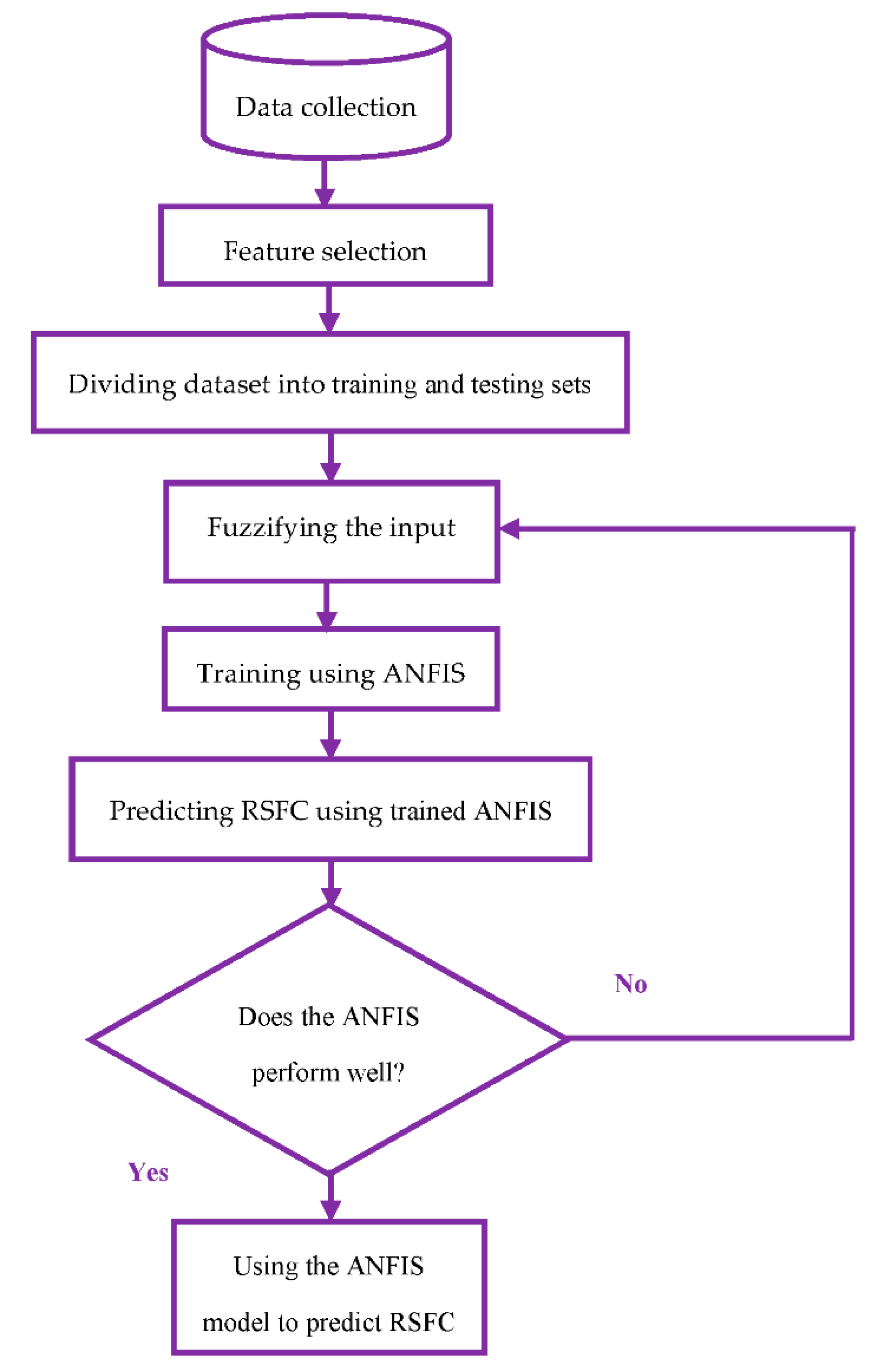
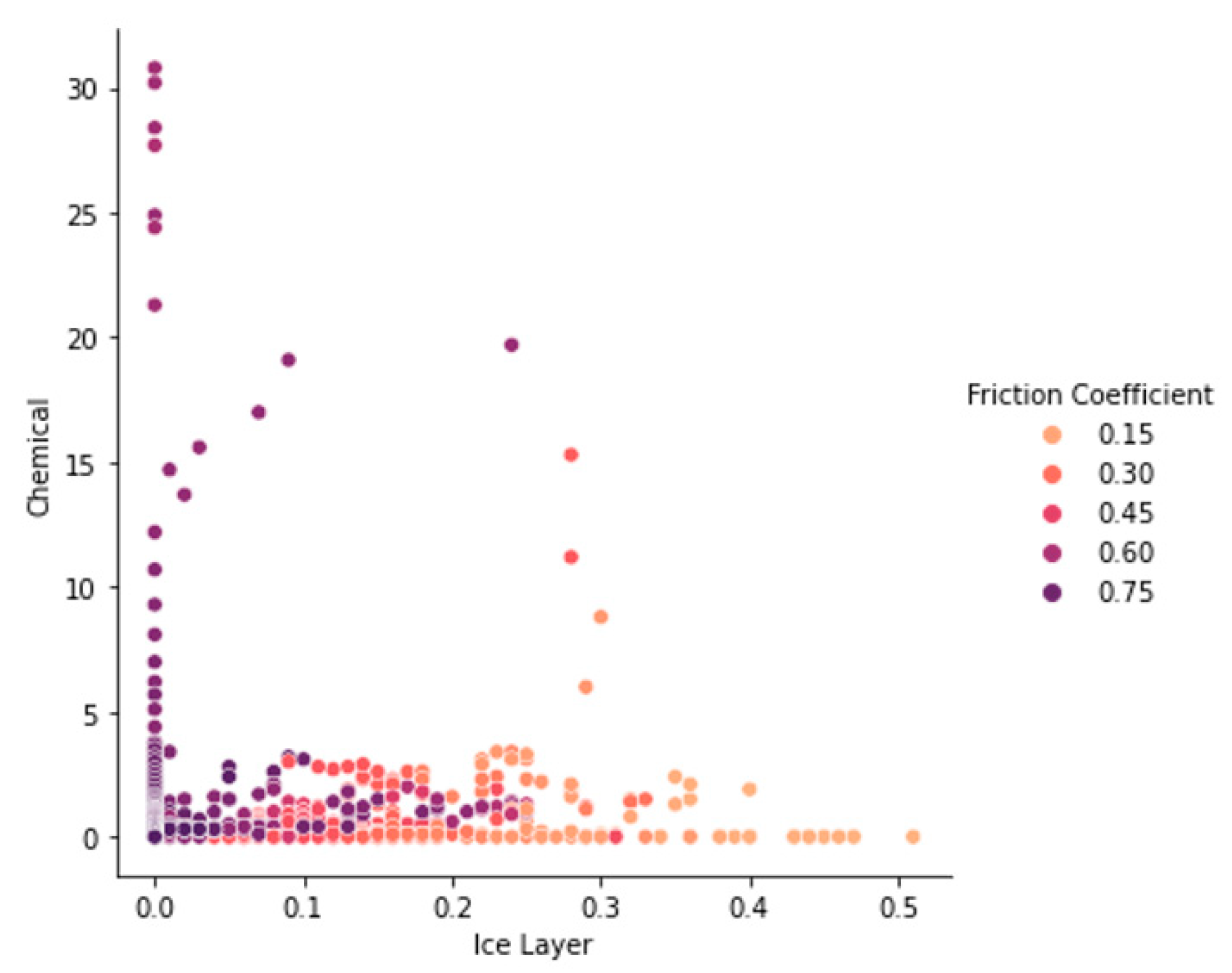
3. Data and Methods
3.1. Data Collection
3.2. Feature Selection
3.3. Dividing the Dataset into Training and Testing Sets
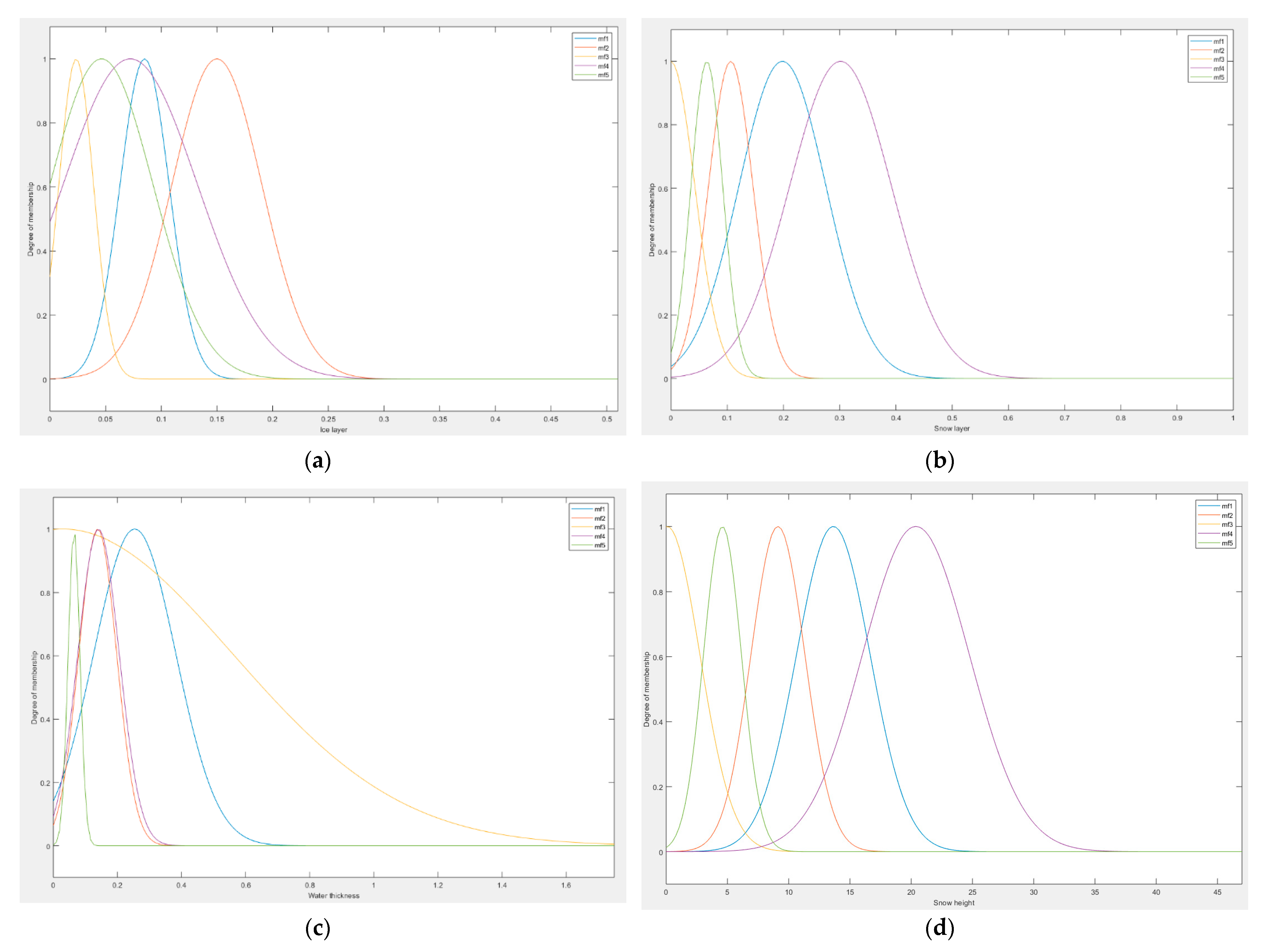
3.4. Generating Basic Fuzzy Inference System
3.5. Training Using ANFIS
3.6. Evaluating Performance of ANFIS
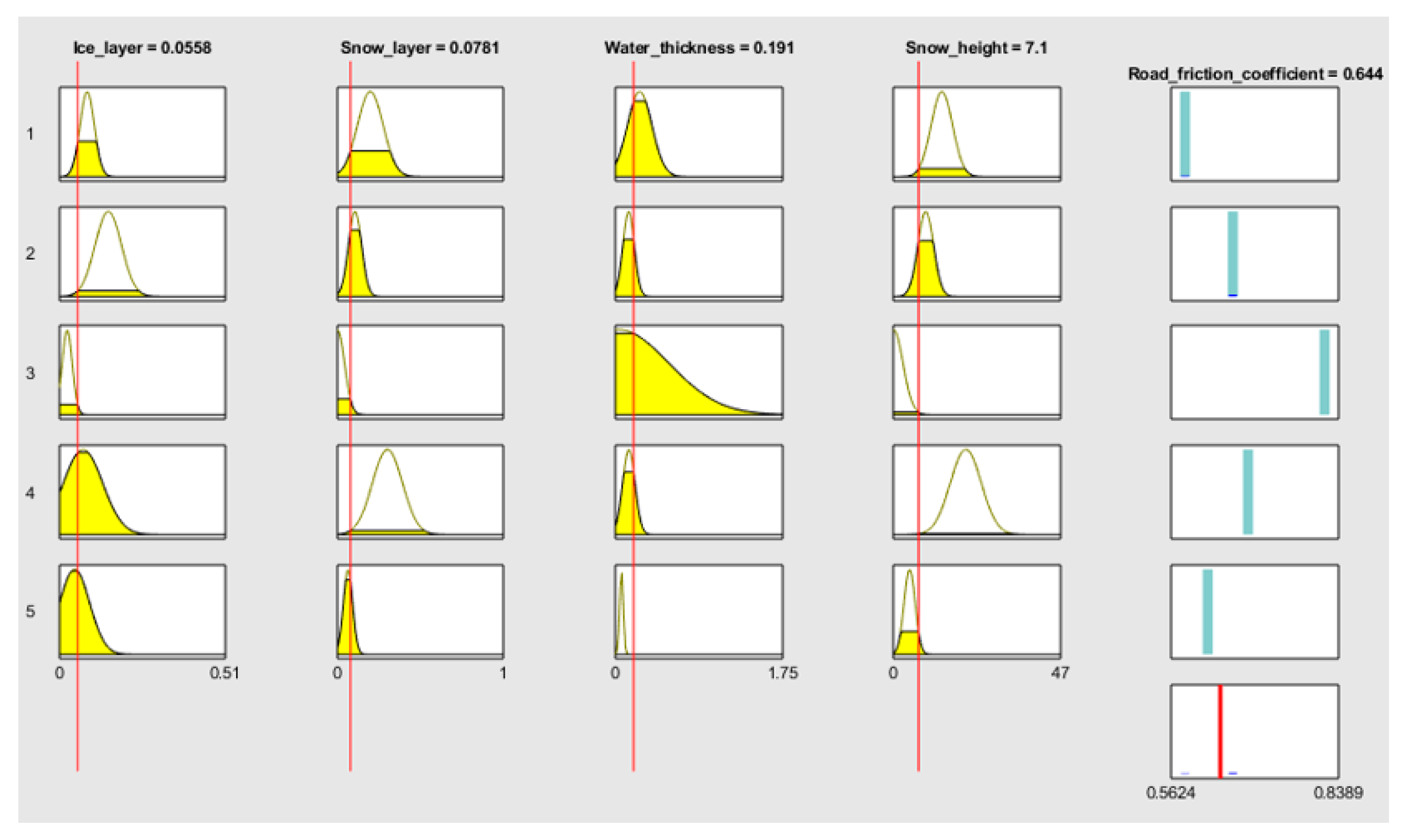
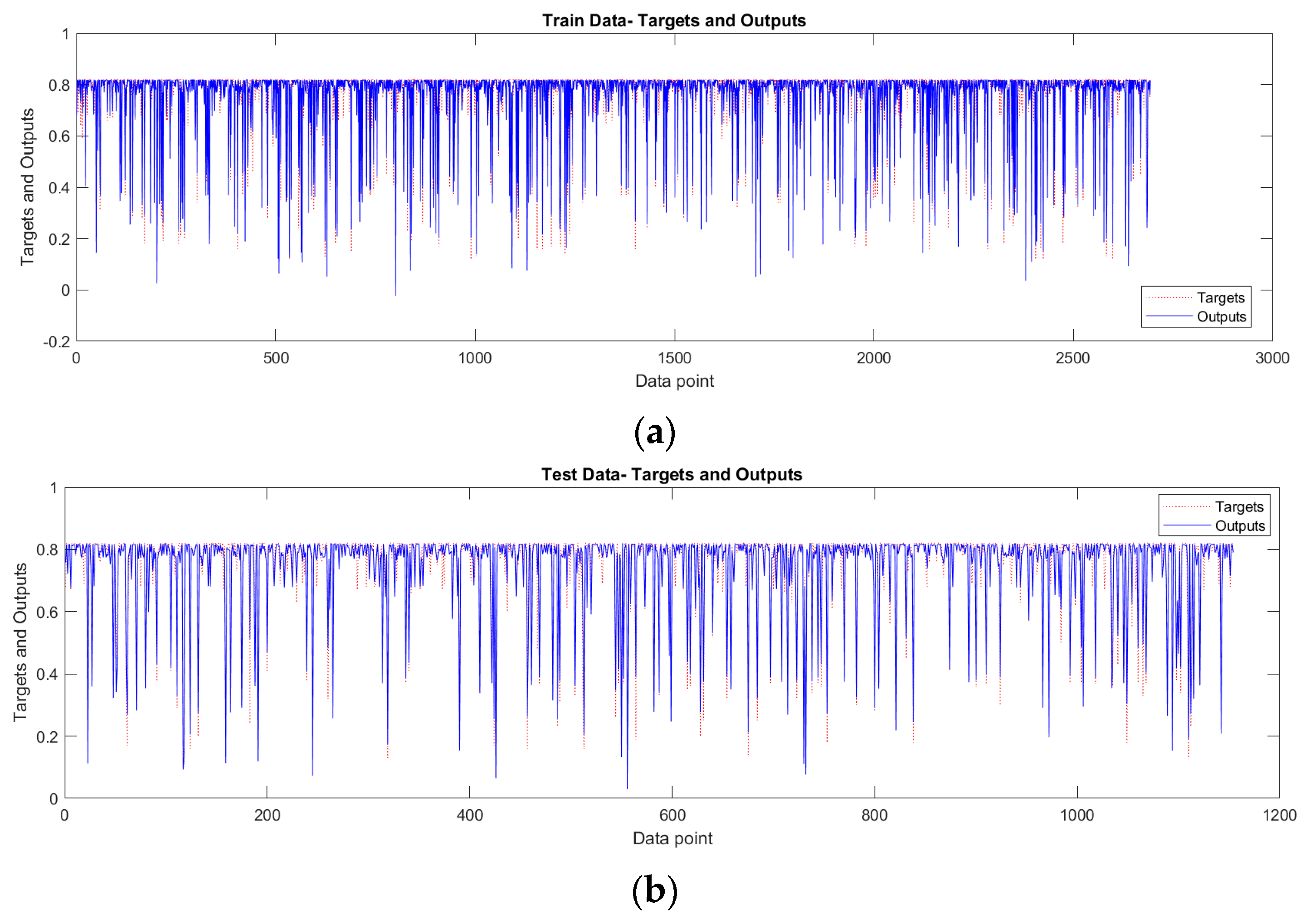
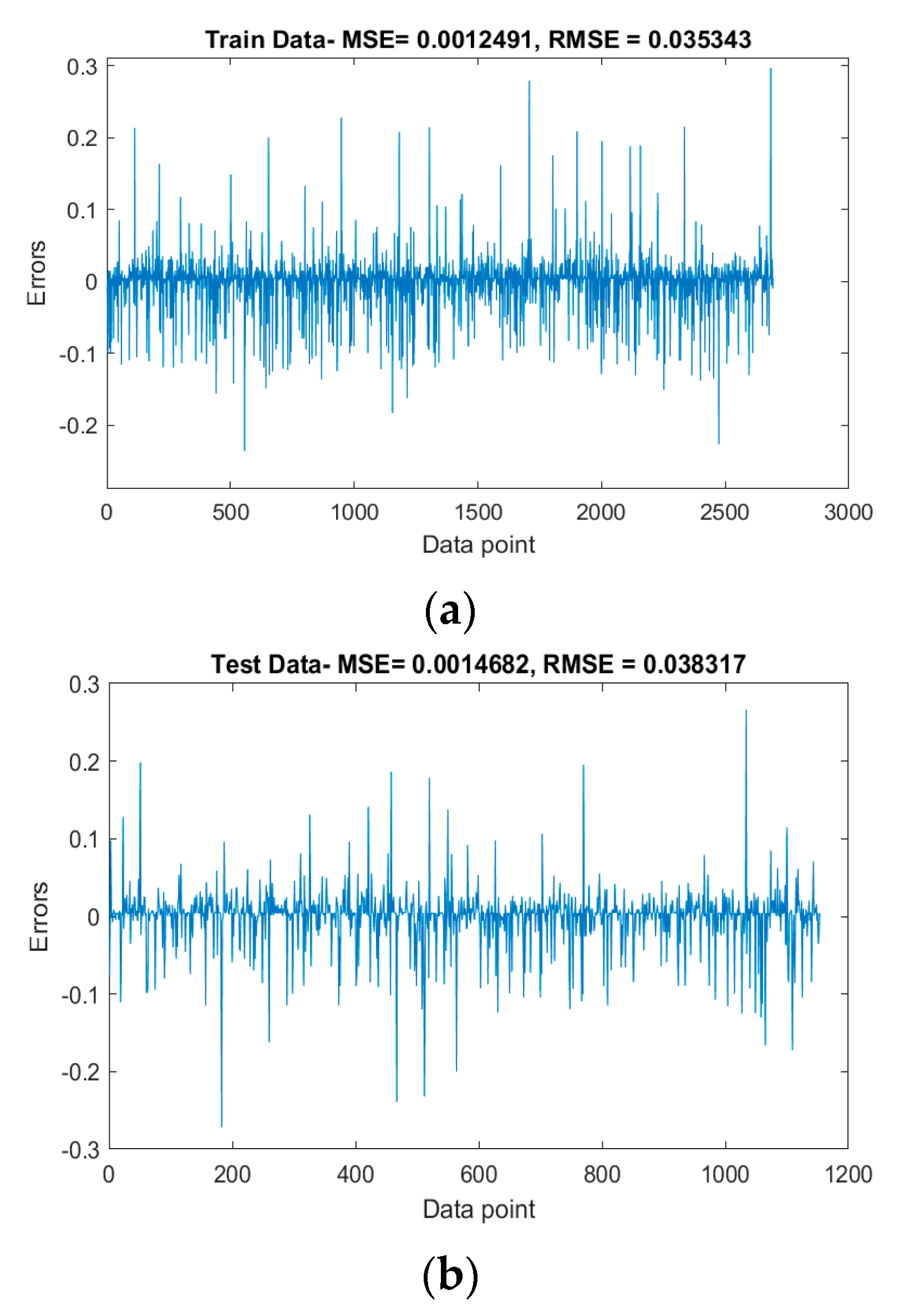
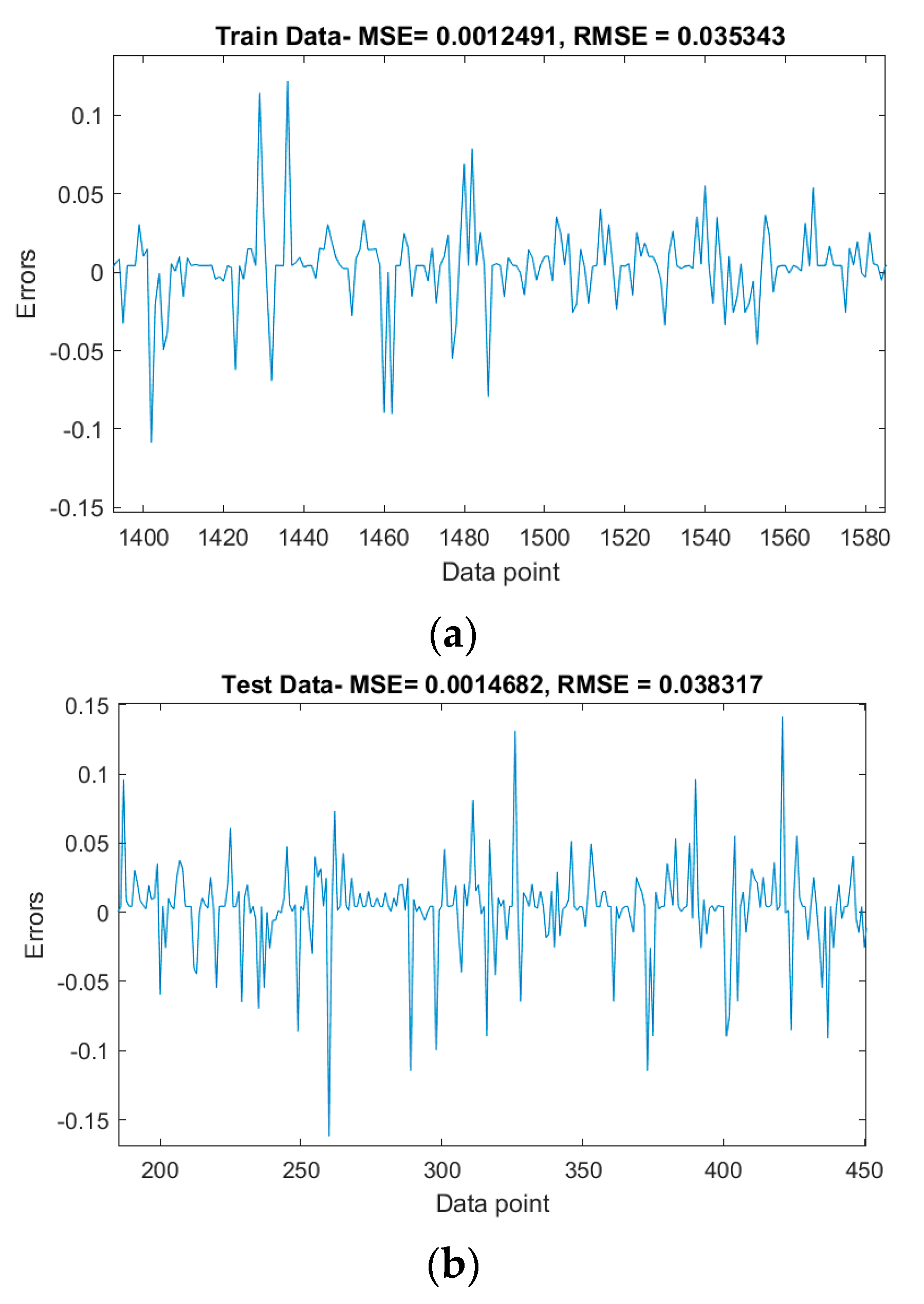
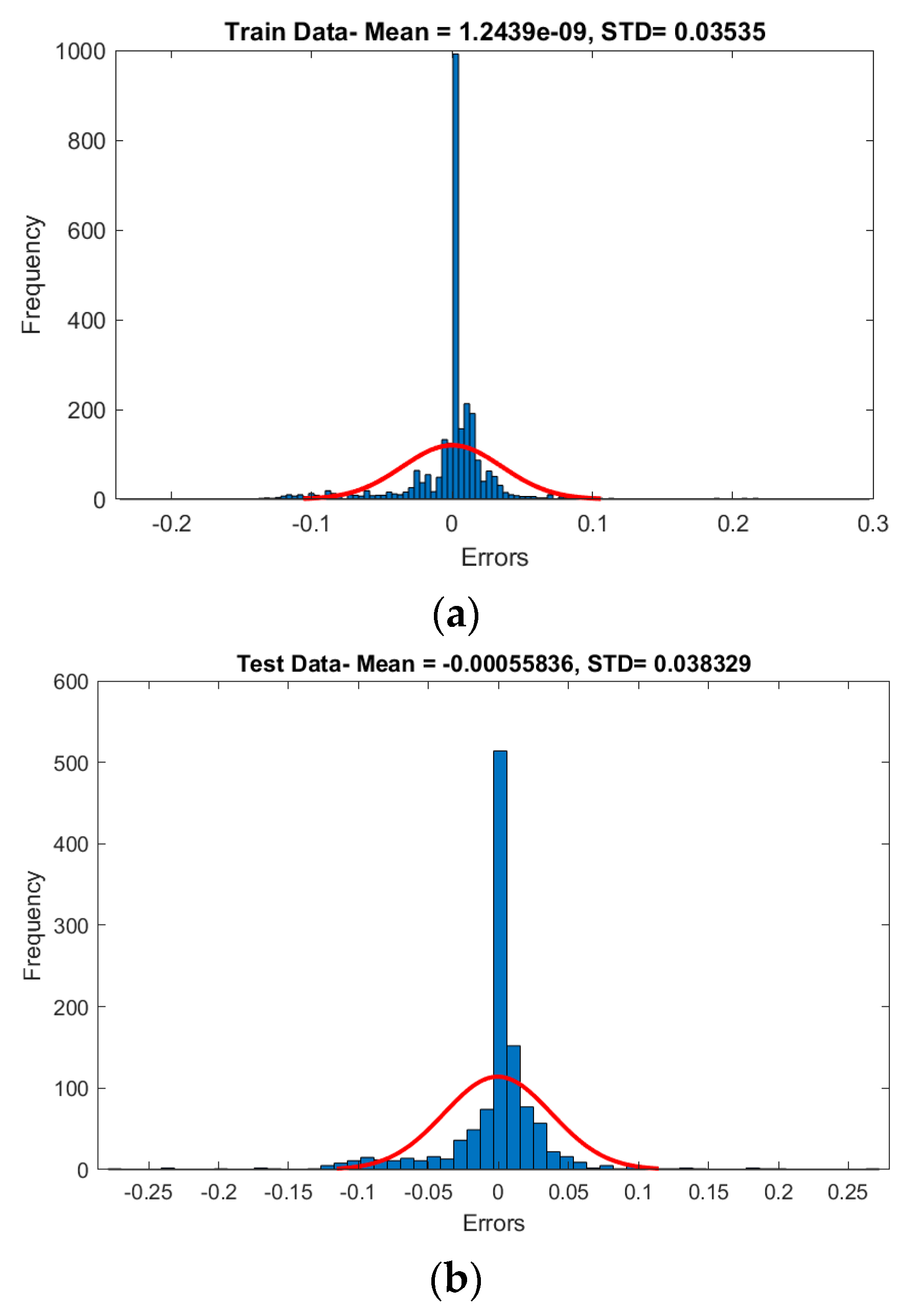
4. Analytic Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Feng, F.; Fu, L. Winter Road surface condition forecasting. J. Infrastruct. Syst. 2014, 21, 04014049. [Google Scholar] [CrossRef]
- Strong, C.; Shi, X. Benefit-cost analysis of weather information for winter maintenance: A case study. Transp. Res. Rec. 2008, 2055, 119–127. [Google Scholar] [CrossRef]
- Shao, J.; Lister, P.J. An automated nowcasting model of road surface temperature and state for winter road maintenance. J. Appl. Meteorol. Climatol. 1996, 35, 1352–1361. [Google Scholar] [CrossRef]
- Mohseni, A. LTPP Data Analysis: Improved Low Pavement Temperature Prediction. FHWA Contract 1998, 73, 285–2730. [Google Scholar]
- Kangas, M.; Heikinheimo, M.; Hippi, M. RoadSurf: A modelling system for predicting road weather and road surface conditions. Meteorol. Appl. 2015, 22, 544–553. [Google Scholar] [CrossRef]
- Ye, Z.; Shi, X.; Strong, C.; Larson, R. Vehicle-based sensor technologies for winter highway operations. IET Intell. Transp. Syst. 2012, 6, 336–345. [Google Scholar] [CrossRef]
- Ewan, L.; Al-Kaisy, A.; Veneziano, D. Remote Sensing of Weather and Road Surface Conditions: Is technology mature for reliable intelligent transportation systems applications? Transp. Res. Rec. 2013, 2329, 8–16. [Google Scholar] [CrossRef]
- Feng, F.; Fu, L. Evaluation of Two New Vaisala Sensors for Road Surface Conditions Monitoring; HIIFP-054; Department of Civil & Environmental Engineering, University of Waterloo: Toronto, ON, Canada, 2008. [Google Scholar]
- Ahabchane, C.; Trépanier, M.; Langevin, A. Street-segment-based salt and abrasive prediction for winter maintenance using machine learning and GIS. Willey Trans. GIS 2018, 23, 48–69. [Google Scholar] [CrossRef]
- Pan, G.; Fu, L.; Yu, R.; Muresan, M.L. Winter Road surface condition recognition using a pre-trained deep convolutional neural network. In Proceedings of the Transportation Research Board 97th Annual Meeting, Washington, DC, USA, 7–11 January 2018; pp. 838–855. [Google Scholar]
- Liu, B.; Yan, S.; You, H.; Dong, Y.; Li, Y.; Lang, J.; Gu, R. Road surface temperature prediction based on gradient extreme learning machine boosting. Comput. Ind. 2018, 99, 294–302. [Google Scholar] [CrossRef]
- Roychowdhury, S.; Zhao, M.; Wallin, A.; Ohlsson, N.; Jonasson, M. Machine Learning Models for Road Surface and Friction Estimation using Front-Camera Images. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Panahandeh, G.; Ek, E.; Mohammadiha, N. Road friction estimation for connected vehicles using supervised machine learning. In Proceedings of the Intelligent Vehicles Symposium (IV), Los Angeles, CA, USA, 31 July 2017; pp. 1262–1267. [Google Scholar] [CrossRef]
- Pu, Z.; Liu, C.; Shi, X.; Cui, Z.; Wang, Y. Road surface friction prediction using long short-term memory neural network based on historical data. J. Intell. Transp. Syst. 2020, 26, 34–45. [Google Scholar] [CrossRef]
- Song, S.; Min, K.; Park, J.; Kim, H.; Huh, K. Estimating the maximum road friction coefficient with uncertainty using deep learning. In Proceedings of the 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 10 December 2018; pp. 3156–3161. [Google Scholar] [CrossRef]
- Matuško, J.; Petrović, I.; Perić, N. Neural network based tire/road friction force estimation. Eng. Appl. Artif. Intell. 2008, 21, 442–456. [Google Scholar] [CrossRef]
- Kim, H.M.; Park, S.H.; Han, S.I. Precise friction control for the nonlinear friction system using the friction state observer and sliding mode control with recurrent fuzzy neural networks. Mechatronics 2009, 19, 805–815. [Google Scholar] [CrossRef]
- Ross, T.J. Fuzzy Logic with Engineering Applications; JWS: Hoboken, NJ, USA, 2005. [Google Scholar]
- Jang, J.S.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Pourdaryaei, A.; Mokhlis, H.; Illias, H.A.; Kaboli, S.H.A.; Ahmad, S. Short-Term Electricity Price Forecasting via Hybrid Backtracking Search Algorithm and ANFIS Approach. IEEE Access 2019, 7, 77674–77691. [Google Scholar] [CrossRef]
- Elbaz, K.; Shen, S.; Sun, W.; Yin, Z.; Zhou, A. Prediction Model of Shield Performance During Tunneling via Incorporating Improved Particle Swarm Optimization Into ANFIS. IEEE Access 2020, 8, 39659–39671. [Google Scholar] [CrossRef]
- Shekarian, E.; Gholizadeh, A.A. Application of adaptive network based fuzzy inference system method in economic welfare. Knowl. Based Syst. 2013, 39, 151–158. [Google Scholar] [CrossRef]
- Yousefi, M.; Hajizadeh, A.; Soltani, M.N. A comparison study on stochastic modeling methods for home energy management systems. IEEE Trans. Industr. Inform. 2019, 15, 4799–4808. [Google Scholar] [CrossRef]
- Trafikverket. Available online: https://www.trafikverket.se/trafikinformation/vag/?TrafficType=personalTraffic&map=3%2F50315918%2F6763671.79%2F&Layers=RoadCondition%2BRoadWeather%2B (accessed on 12 December 2019).
- MATLAB. Version 9.6.0.1072779 (R2019a); The MathWorks Inc.: Natick, MA, USA, 2019; Available online: https://www.mathworks.com/help/fuzzy/neuro-adaptive-learning-and-anfis.html (accessed on 1 April 2019).
- Khan, A.; Pahwa, V. Design and Implementation of ANFIS Based Controller on Variable Speed Isolated Wind-Diesel Hybrid System for Better Performance. Am. J. Electr. Electron. 2017, 5, 172–178. [Google Scholar] [CrossRef][Green Version]
- Wallman, C.G.; Åström, H. Friction Measurement Methods and the Correlation between Road Friction and Traffic Safety: A Literature Review; Swedish National Road and Transport Research Institute: Linköping, Sweden, 2001. [Google Scholar]


| Variables | Count | Mean | Std | Min | 25% | 50% | 75% | Max |
|---|---|---|---|---|---|---|---|---|
| Ice layer | 3847 | 0.019 | 0.059 | 0.000 | 0.000 | 0.000 | 0.000 | 0.510 |
| Snow layer | 3847 | 0.037 | 0.146 | 0.000 | 0.000 | 0.000 | 0.000 | 1.040 |
| Water thickness | 3847 | 0.060 | 0.135 | 0.000 | 0.000 | 0.030 | 0.060 | 1.880 |
| Snow height | 3847 | 2.562 | 5.341 | 0.000 | 0.000 | 0.000 | 2.000 | 47.000 |
| Surface temperature | 3847 | 0.607 | 4.627 | −14.600 | −1.500 | 1.100 | 3.300 | 14.200 |
| Air temperature | 3847 | 0.813 | 4.978 | −20.000 | −0.900 | 1.900 | 3.800 | 10.400 |
| RSFC (output) | 3847 | 0.750 | 0.149 | 0.110 | 0.780 | 0.810 | 0.820 | 0.820 |
| Input | Absolute Value of Correlation between Input and RSFC |
|---|---|
| Ice layer | 0.88 |
| Snow layer | 0.69 |
| Water thickness | 0.65 |
| Snow height | 0.61 |
| Surface temperature | 0.29 |
| Air temperature | 0.27 |
| Variables | Mean | Std | Min | Max |
|---|---|---|---|---|
| Ice layer | 0.016 | 0.047 | 0.000 | 0.380 |
| Snow layer | 0.015 | 0.053 | 0.000 | 0.830 |
| Water thickness | 0.045 | 0.135 | 0.000 | 1.880 |
| Snow height | 0.067 | 0.099 | 0.000 | 1.890 |
| RSFC (output) | 0.756 | 0.133 | 0.120 | 0.820 |
| Network Information | Number |
|---|---|
| Number of nodes | 57 |
| Number of linear parameters | 25 |
| Number of nonlinear parameters | 40 |
| Total number of parameters | 65 |
| Number of training data pairs | 2693 |
| Number of testing data pairs | 1154 |
| Number of fuzzy rules | 5 |
| Variable | Range | Number of mf |
|---|---|---|
| Ice layer | [0, 0.51] | 5 |
| Snow layer | [0, 1] | 5 |
| Water thickness | [0, 1.75] | 5 |
| Snow height | [0, 47] | 5 |
| RSFC (output) | [0.11, 0.82] | 5 |
| mf | Ice Layer | Snow Layer | Water Thickness | Snow Height | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | |
| mf 1 | 0.085 | 0.022 | 0.198 | 0.077 | 0.254 | 0.128 | 13.643 | 3.005 |
| mf 2 | 0.150 | 0.040 | 0.106 | 0.040 | 0.139 | 0.059 | 9.121 | 2.202 |
| mf 3 | 0.024 | 0.016 | −0.001 | 0.043 | 0.030 | 0.530 | 0.087 | 2.666 |
| mf 4 | 0.072 | 0.060 | 0.301 | 0.091 | 0.141 | 0.065 | 20.379 | 4.365 |
| mf 5 | 0.046 | 0.046 | 0.064 | 0.028 | 0.065 | 0.018 | 4.593 | 1.551 |
| mf | Coeff1 | Coeff2 | Coeff3 | Coeff4 | Constant |
|---|---|---|---|---|---|
| mf 1 | −1.737 | −0.284 | −0.022 | 0.017 | 0.585 |
| mf 2 | 0.598 | −4.210 | 0.599 | 0.009 | 0.664 |
| mf 3 | −2.547 | 3.370 | 0.510 | 0 | 0.816 |
| mf 4 | −1.216 | −0.237 | −0.038 | −0.001 | 0.689 |
| mf 5 | 2.680 | −0.026 | −2.737 | 0.025 | 0.623 |
| Evaluation Metric | Training Set | Testing Set |
|---|---|---|
| MSE | 0.0012 | 0.0015 |
| RMSE | 0.0350 | 0.0380 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hatamzad, M.; Polanco Pinerez, G.; Casselgren, J. Addressing Uncertainty by Designing an Intelligent Fuzzy System to Help Decision Support Systems for Winter Road Maintenance. Safety 2022, 8, 14. https://doi.org/10.3390/safety8010014
Hatamzad M, Polanco Pinerez G, Casselgren J. Addressing Uncertainty by Designing an Intelligent Fuzzy System to Help Decision Support Systems for Winter Road Maintenance. Safety. 2022; 8(1):14. https://doi.org/10.3390/safety8010014
Chicago/Turabian StyleHatamzad, Mahshid, Geanette Polanco Pinerez, and Johan Casselgren. 2022. "Addressing Uncertainty by Designing an Intelligent Fuzzy System to Help Decision Support Systems for Winter Road Maintenance" Safety 8, no. 1: 14. https://doi.org/10.3390/safety8010014
APA StyleHatamzad, M., Polanco Pinerez, G., & Casselgren, J. (2022). Addressing Uncertainty by Designing an Intelligent Fuzzy System to Help Decision Support Systems for Winter Road Maintenance. Safety, 8(1), 14. https://doi.org/10.3390/safety8010014







