On the Adequacy of API 521 Relief-Valve Sizing Method for Gas-Filled Pressure Vessels Exposed to Fire
Abstract
:1. Introduction
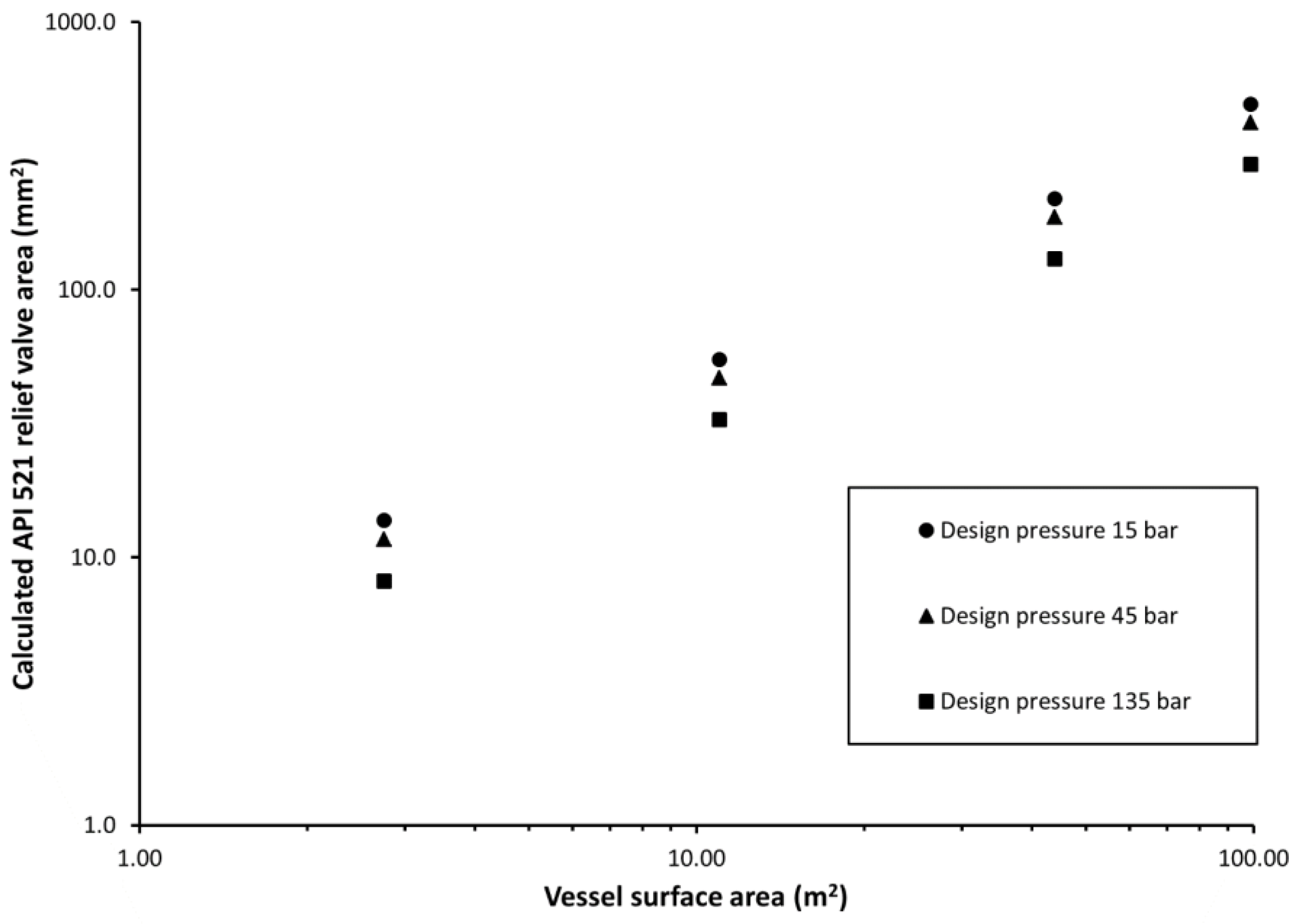
- Is the API 521 sizing too conservative leading to too large PRVs? Thus, increasing installation costs due to larger piping and valves—but even more importantly an overly large valve—may lead to chatter, jeopardizing the integrity of the valve due to vibrations, ultimately leading to failure of the PRV.
- Does the PRV really offer protection of the vessel or is it just a false sense of security? This question could also be posed as; in which situations does the PRV actually offer real protection of the vessel?
2. Methods
2.1. API 521 Relief Valve Sizing
- A′: Fire exposed area of vessel (in2)
- : Vessel pressure at relieving conditions including allowed overpressure (psi)
- M′: Relative molecular mass of gas
- TW: Maximum vessel wall temperature (°R). For carbon steel plates, this is normally set to 1100 °F (593 °C)
- T1: Vessel inventory temperature at relieving conditions (°R)
- Tn: Normal operating temperature (°R)
- : Normal operating pressure (psi)
- A: Required relief valve area (in2)
- Kb: Back pressure correction factor. Assumed equal to 1
- Kd: Effective discharge coefficient. Assumed to be 0.975
- Kc: Combination correction factor. Assumed to be 1 (no rupture disc installed)
- Z: Compressibility of the gas
- M: Molecular mass of gas (lbm/lb-mole)
- Ideal gas law. The assumption that an ideal gas inside the vessel is used several times during the derivation of the relief rate equation. The relieving temperature calculation assumes ideal gas behaviour, and the density of the gas is assumed to be that of an ideal gas. However, at elevated temperatures, the deviation between ideal gas and real gas decreases, and this assumption may not be severe.
- Gas similar to air. The assumption that gas viscosity is similar to that of air can give relief rates of up to a factor of two for other gases compiled in [15].
- The gas properties relevant to the heat transfer from the hot vessel wall to the gas used in the derivation should in reality be evaluated at the film temperature, (Twall − Tgas)/2 [17]. However, thermal conductivity, heat capacity, viscosity and gas expansion factors, which all appear in the applied relation for the heat transfer coefficient for natural convection, are either evaluated at the gas temperature, or at 20 °C.
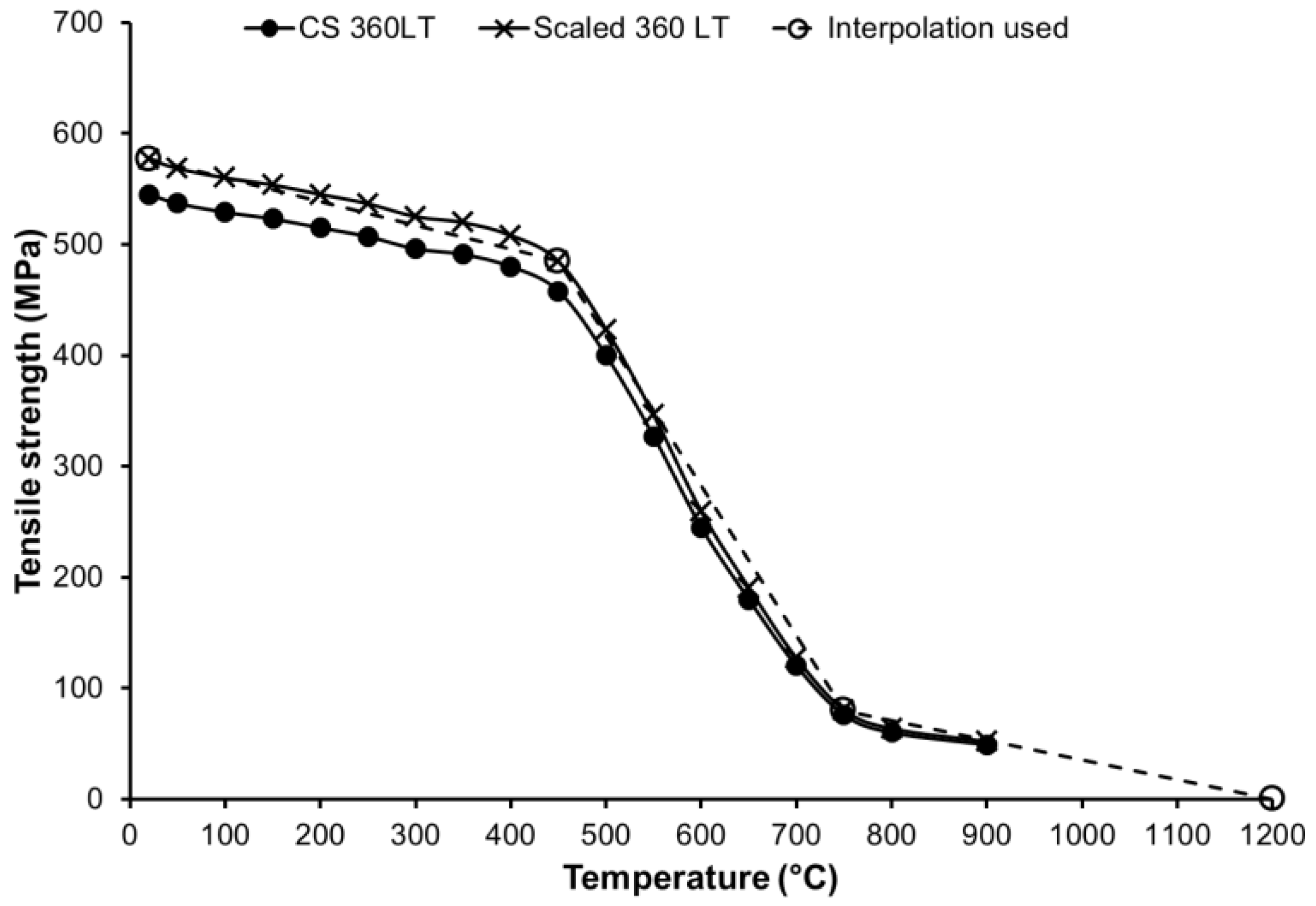
- Assumed Twall. The assumption of a maximum wall temperature of 1100 °F (593 °C) may not be justified. Depending on the steel grade, the vessel may fail at temperatures below 1100 °F [5], and in that case the sizing becomes conservative. Furthermore, many relief devices are limited to 1000 °F (538 °C) [5,6], thus the assumptions in the capacity calculation exceeds that of the relief valve design.
- Steady state. It is assumed that the relief process is a steady-state process in the derivation of the formulae. This is far from reality. Before the relieving pressure is reached, the temperature of the vessel material and the gas inventory increases steadily, and pressure builds up. When the relief valve opens, the vessel material continues to heat up, and the temperature difference between the wall and the gas is reduced.
- Vessel insulation is not taken into account.
2.2. Fire Heat Flux Modelling
- : heat absorbed by a segment (W/m2)
- σ: Stefan–Boltzmann constant, 5.67 × 10−8 (W/m2 K4)
- Tf: flame temperature (K)
- Tamb: ambient temperature (K)
- hf: flame convective heat transfer coefficient (W/m2 K)
- αs: surface absorptivity
- εs: surface emissivity
- εf: flame emissivity
- Ts: segment temperature (K) (time dependent)
2.3. Vessel Rupture Criteria
- σa: Longitudinal stress due to the external force. Assumed to be 30 MPa [9]
- D: Outside diameter
- d: Inside diameter
- p: Gas pressure (MPa)
2.4. Simulation Software and Post-Processing
- Nu: Nusselt number
- Gr: Grashof number
- Pr: Prandtl number
- k: Thermal conductivity of the gas (W/m K)
- L: Characteristic length (m) (defined internally by simulation software)
- a: Empirical coefficient, selected by simulation software
- m: Empirical exponent, selected by simulation software
- Qnet: The net heat load to an element of the vessel wall (W/m2)
- Qconv: The heat loss from a vessel wall element to the gas inventory by convection (W/m2)
- Tg: Temperature of the gas inventory (K)
- h: Inside gas convective heat transfer coefficient (W/m2 K)
- g: Gravitational acceleration (m/s2)
- β: Gas thermal expansion coefficient
- Ts: Internal surface temperature (K)
- Tg: Gas inventory temperature (K)
- ν: Gas kinematic viscosity (m2/s)
- Cp: Gas specific heat capacity (J/kg K)
- μ: Dynamic viscosity (kg/m s)
- L: Characteristic length set equal to the vertical vessel tan-to-tan height (m)
2.5. Calculation Workflow
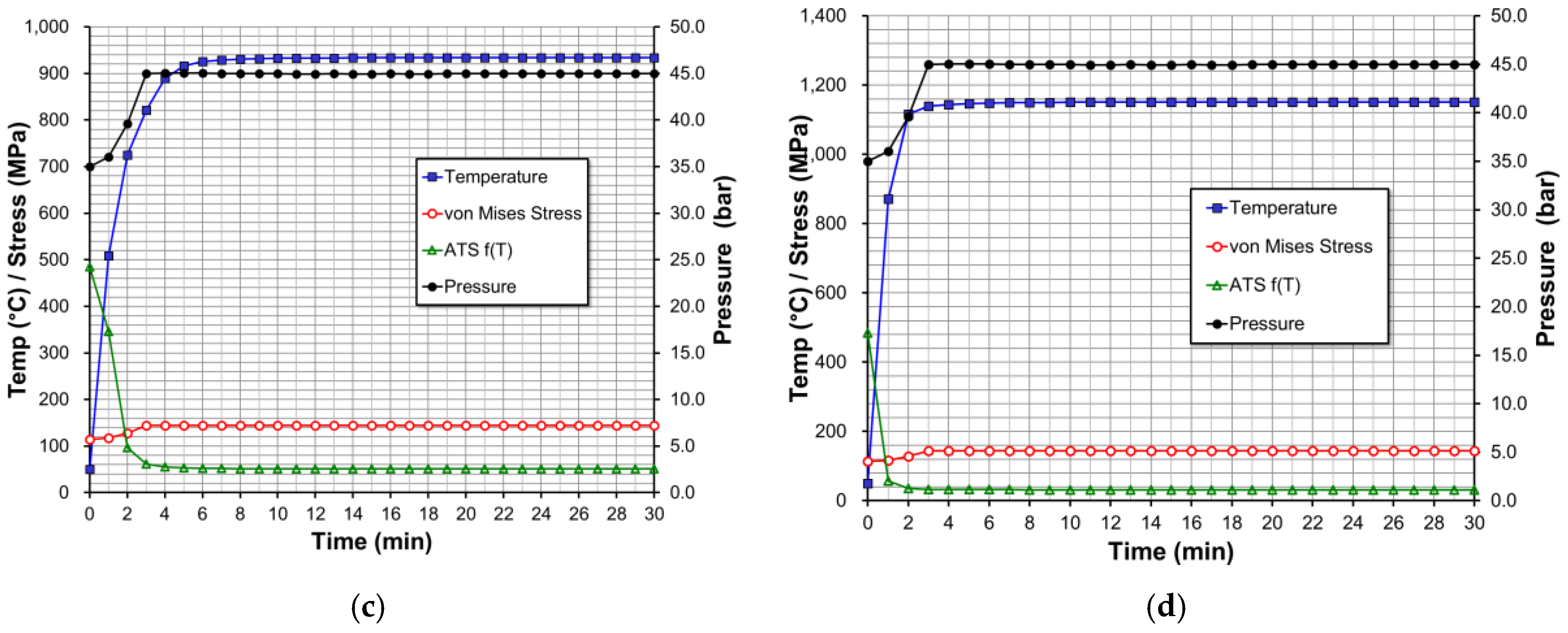
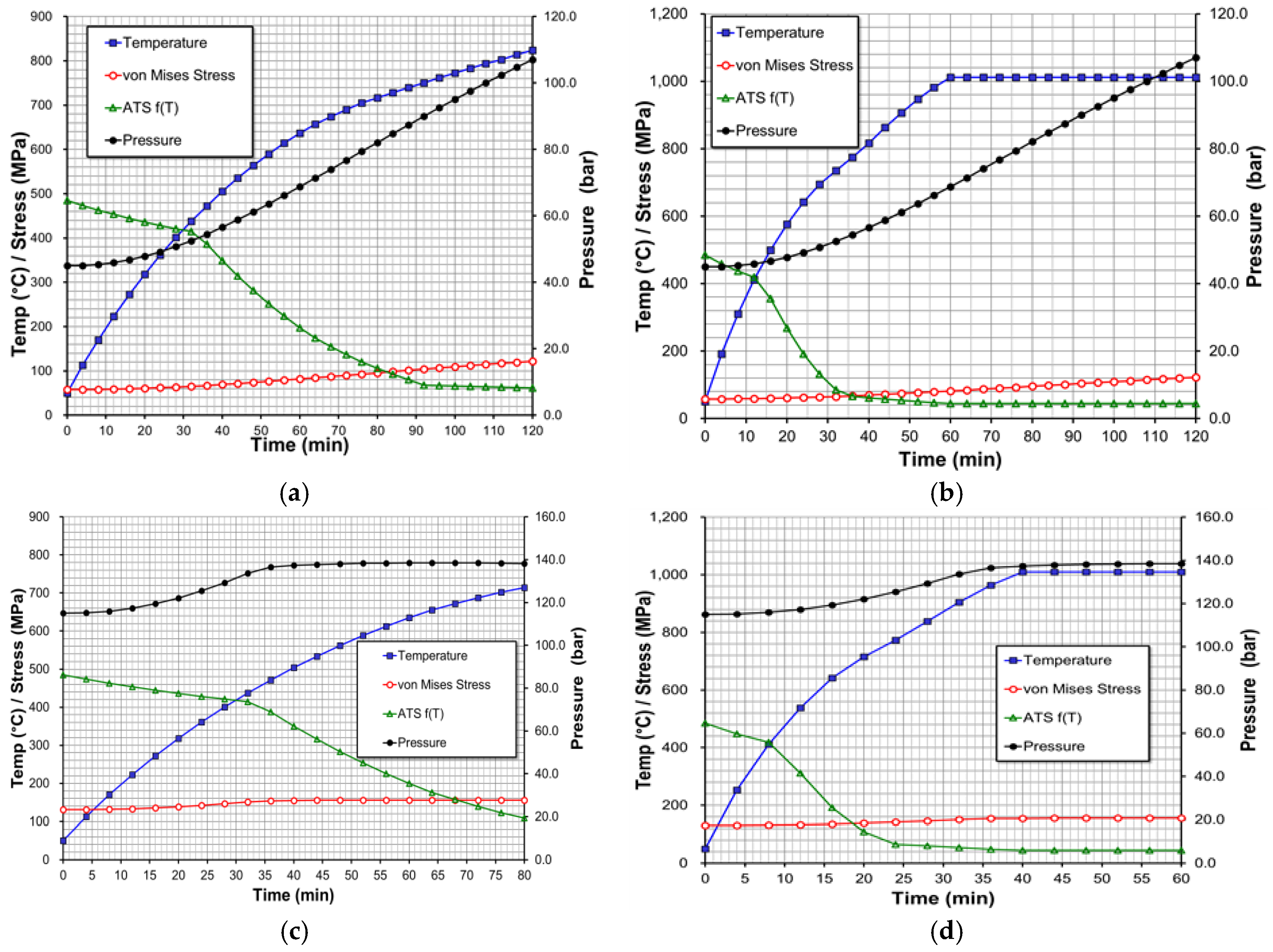
- The calculation workflow begins by calculating the pressure response due to the global heat flux from the S–B equation. This is done by integration of the vessel energy and mass balances using the chosen simulation software. The calculations are performed for a sufficient period in order for the relief valve to be activated. It is verified that the selected relief valve has sufficient capacity to keep the pressure below 121% of the set pressure/assumed design pressure.
- The local vessel wall temperature is performed by a local heat balance employing a simple approach using the flame temperature calibrated for the local heat loads. Both pool fire and jet fire temperature responses are calculated.
- : Density of steel (kg/m3)
- : Vessel wall thickness (m)
- : specific heat capacity of steel (J/kg K)
3. Results and Discussion
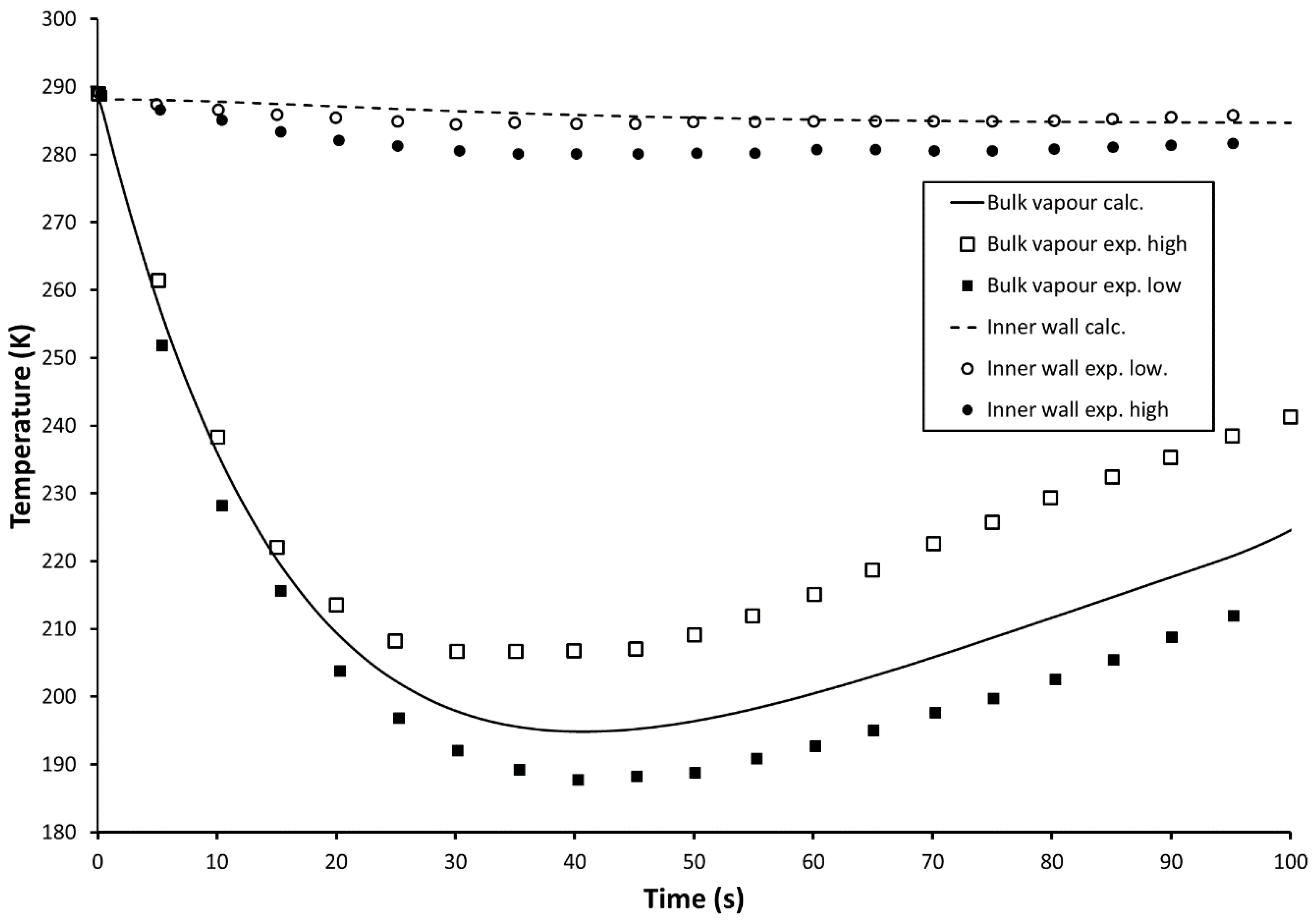
3.1. Validation
3.2. Calculation and Simulation Matrix
- P: Design pressure (MPa gauge)
- D: Diameter of vessel (m)
- S: Maximum allowable stress (MPa)
- E: Joint efficiency (assumed 1.0 in this study)
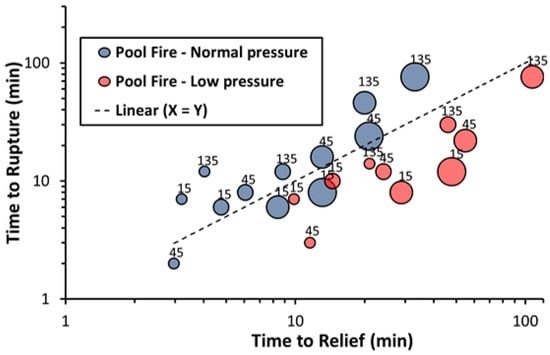
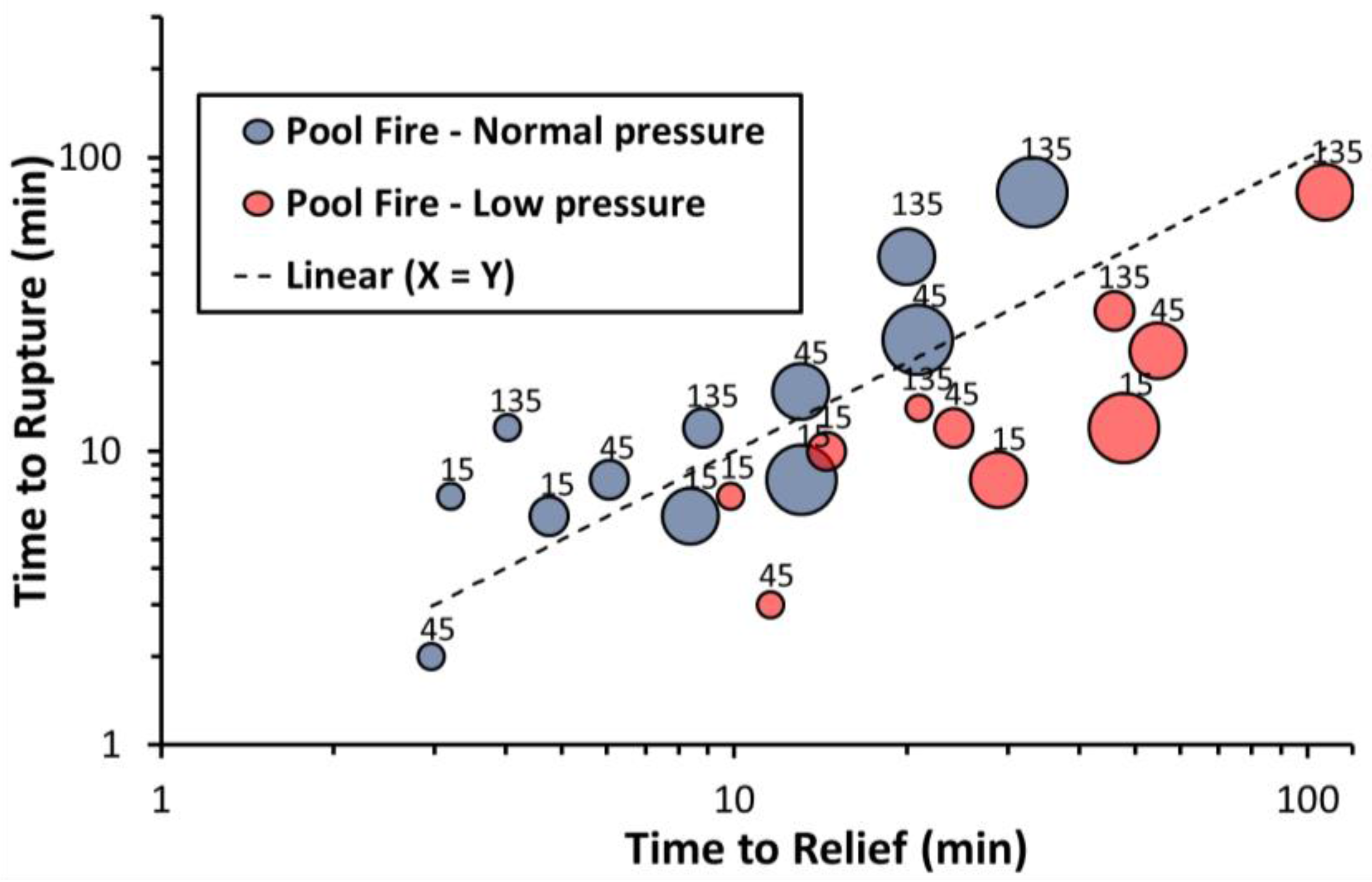
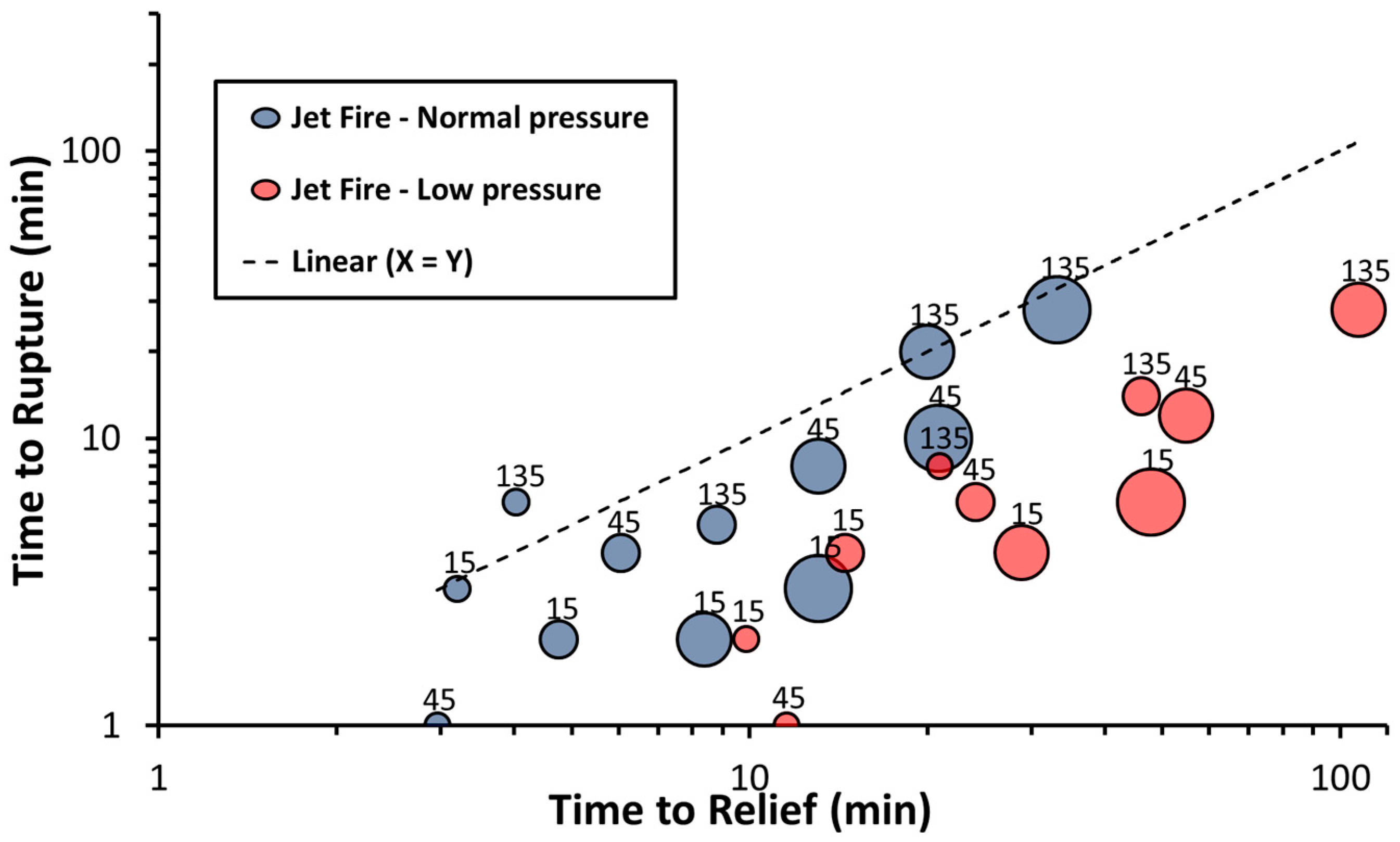
3.3. Dynamic Thermomechanical Vessel Response and Rupture
4. Conclusions
- Never base relief valve sizing for gas-filled vessels on API 521 equations—except maybe for early phase studies for cost estimation purposes. For detailed design and actual installation purposes, always base relief valve sizing on dynamic simulations with rigorous modelling of the heat transfer process in order to avoid grossly oversized PRVs.
- Carefully consider if the vessel survival time actually benefits from an installed PRV by performing thermomechanical calculations of the vessel rupture time and taking the chosen material properties into account.
- If the vessel rupture time is not significantly prolonged by the presence of a PRV, consider alternative means for protecting the vessel, such as e.g., insulation, or even better, blowdown activated by fusible plugs.
- In case of protection against jet fire, never rely on a PRV; always consider alternative means of protection.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- ASME. Asme International Boiler and Pressure Vessel Code Section 8: Rules for Construction of Pressure Vessels Division 1; American Society of Mechanical Engineers: New York, NY, USA, 2013. [Google Scholar]
- American Petroleum Institute. Recommened Practise for Analysis, Design, Installation, and Testing of Basic Surface Safety Systems for Offshore Production Platforms; American Petroleum Institute: Washington, DC, USA, 2001; ISBN 5925731107. [Google Scholar]
- American Petroluem Institute. Pressure-Relieving and Depressuring Systems, API Standard 521; American Petroleum Institute: Washington, DC, USA, 2014. [Google Scholar]
- Nylund, J. Fire Survival of Process Vessels Containing Gas. I. Chem. E. Symp. Ser. 1984, 85, 137–148. [Google Scholar]
- Heitner, I.; Trautmanis, T.; Morissey, M. Relieving requirements for gas-filled vessels exposed to fire. In Proceedings of the API Refining Department 48th Midyear Meeting, Los Angeles, CA, USA, 9–12 May 1983. [Google Scholar]
- Wong, W.Y. Improve the Fire Protection of Pressure Vessels. Chem. Eng. 1999, 106, 193–196. [Google Scholar]
- Bjerre, M.; Eriksen, J.G.I.; Andreasen, A.; Stegelmann, C.; Mandø, M. Analysis of pressure safety valves for fire protection on offshore oil and gas installations. Process Saf. Environ. Prot. 2017, 105, 60–68. [Google Scholar] [CrossRef]
- Dalzell, G.; Chesterman, A. Nothing, Is Safety Critical. Process Saf. Environ. Prot. 1997, 75, 152–156. [Google Scholar] [CrossRef]
- Hekkelstrand, B.; Skulstad, P. Guidelines for the Protection of Pressurised Systems Exposed to Fire; Scandpower Risk Management AS: Kjeller, Norway, 2004. [Google Scholar]
- NORSOK. Technical Safety, NORSOK Standard S-001; NORSOK: Lysaker, Norway, 2008. [Google Scholar]
- Roberts, T.A.; Buckland, I.; Shirvill, L.C.; Lowesmith, B.J.; Salater, P. Design and Protection of Pressure Systems to Withstand Severe Fires. Process Saf. Environ. Prot. 2004, 82, 89–96. [Google Scholar] [CrossRef]
- Energy Institute. Guidelines for the Design and Protection of Pressure Systems to Withstand Severe Fires; Energy Institute: London, UK, 2003. [Google Scholar]
- Zamejc, E. API Standard 521 new alternative method to evaluate fire relief for pressure relief device sizing and depressuring system design. J. Loss Prev. Process Ind. 2014, 27, 21–31. [Google Scholar] [CrossRef]
- American Petroluem Institute. Sizing, Selection and Installation of Pressure Relieving Devices in Refineries, Part I—Sizing and Selection. API Standard 520; American Petroleum Institute: Washington, DC, USA, 2008. [Google Scholar]
- Duggan, J.J.; Gilmour, C.H.; Fisher, P.F. Requirements for relief of pressure vessels. Trans. ASME 1944, 66, 1–53. [Google Scholar]
- Rahimi, S. The Basis of API Correlation for Fire Relief of Unwetted Vessels. Available online: https://www.scribd.com/document/246359787/The-Basis-of-API-Corrolation-for-Fire-Relief-of-Unwetted-Vessels (accessed on 13 April 2016).
- Geankoplis, C.J. Transport Processes and Unit Operations, 3rd ed.; Chemical Engineering; PTR Prentice Hall: Upper Saddle River, NJ, USA, 1993; ISBN 9780139304392. [Google Scholar]
- Salater, P.; Overaa, S.J.; Kjensjord, E. Size Depressurization and Relief Devices for Pressurized Segments Exposed to Fire. CEP Mag. 2002, 98, 38–45. [Google Scholar]
- Biswas, S.; Fischer, B.J. Application and validation of the API analytical fire method in pressure-relieving and depressuring systems. J. Loss Prev. Process Ind. 2017, 50, 154–164. [Google Scholar] [CrossRef]
- Peng, D.-Y.; Robinson, D.B. A New Two-Constant Equation of State. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Ely, J.F.; Hanley, H.J.M. A Computer Program for the Prediction of Viscosity and Thermal Conductivity in Hydrocarbon Mixtures—NBS Technical Note 1039; National Bureau of Standards: Boulder, CO, USA, 1981.
- D’Aulisa, A.; Simone, D.; Landucci, G.; Tugnoli, A.; Cozzani, V.; Birk, M. Numerical simulation of tanks containing pressurized gas exposed to accidental fires: Evaluation of the transient heat up. Chem. Eng. Trans. 2014, 36, 241–246. [Google Scholar] [CrossRef]
- Birk, A.M.; Poirier, D.; Davison, C. On the response of 500 gal propane tanks to a 25% engulfing fire. J. Loss Prev. Process Ind. 2006, 19, 527–541. [Google Scholar] [CrossRef]
- Moodie, K.; Cowley, L.T.; Denny, R.B.; Small, L.M.; Williams, I. Fire engulfment tests on a 5 tonne LPG tank. J. Hazard. Mater. 1988, 20, 55–71. [Google Scholar] [CrossRef]
- Droste, B.; Schoen, W. Full scale fire tests with unprotected and thermal insulated LPG storage tanks. J. Hazard. Mater. 1988, 20, 41–53. [Google Scholar] [CrossRef]
- Zheng, J.; Ou, K.; Hua, Z.; Zhao, Y.; Hu, J.; Han, B. Experimental and Numerical Studies on High-Pressure Composite Cylinders Subjected to Localized and Engulfing Fire. J. Press. Vessel Technol. 2013, 135, 51405. [Google Scholar] [CrossRef]
- Ruban, S.; Heudier, L.; Jamois, D.; Proust, C.; Bustamante-Valencia, L.; Jallais, S.; Kremer-Knobloch, K.; Maugy, C.; Villalonga, S. Fire risk on high-pressure full composite cylinders for automotive applications. Int. J. Hydrog. Energy 2012, 37, 17630–17638. [Google Scholar] [CrossRef]
- Richardson, S.M.; Saville, G. Blowdown of Vessels and Pipelines. I. Chem. E. Symp. Ser. 1993, 130, 195–209. [Google Scholar]
- Haque, M.A.; Richardson, S.M.; Saville, G.; Chamberlain, G.; Shirvill, L. Blowdown of pressure vessels II. Experimental Validation of Computer Model and Case Studies. Trans. IChemE 1992, 70, 10–17. [Google Scholar]
- Speranza, A.; Terenzi, A. Blowdown of hydrocarbons pressure vessel with partial phase separation. In Applied and Industrial Mathematics in Italy; World Scientific: Singapore, 2005; pp. 508–519. [Google Scholar]
- Incropera, F.P.; Incropera, F.P. Fundamentals of Heat and Mass Transfer; John Wiley: Hoboken, NJ, USA, 2007; ISBN 0471457280. [Google Scholar]
- European Union. Eurocode 3: Design of Steel Structures—Part 1–2: General rules—Structural Fire Design; European Union: City of Brussels, Belgium, 2005. [Google Scholar]
- Andreasen, A.; Eriksen, J.G.I.; Stegelmann, C.; Lynggaard, H. Method improves high-pressure settle-out calculations. Oil Gas J. 2015, 113, 88–96. [Google Scholar]

| Jet Fire | Pool Fire | ||
|---|---|---|---|
| Leak Rate > 2 kg/s | 0.1 kg/s < Leak Rate < 2 kg/s | ||
| Local peak heat load | 350 | 250 | 150 |
| Global average heat load | 100 | 0 | 100 |
| Parameter | Unit | Global Heat Load | Local Heat Load | |
|---|---|---|---|---|
| Pool Fire | Jet Fire | |||
| Tf | K | 1078 | 1212 | 1429 |
| Tg | K | 1078 | 1212 | 1429 |
| αs | -- | 0.85 | 0.85 | 0.85 |
| εs | -- | 1.0 | 1.0 | 1.0 |
| εf | -- | 0.85 | 0.85 | 0.85 |
| H | W/m2 K | 30 | 30 | 100 |
| Q (t = 0) | kW/m2 | 87 | 130 | 311 |
| Vessel Geometry and Design Data | API Sizing Data | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Diameter (m) | Length (T/T m) | Volume (m3) | Surface Area (m2) | Calc. Thickness (mm) | Chosen Thickness (mm) | Pdesign (bar) | Popr (bar) | Allow. Stress (N/mm2) | Relief Flow Calculated (kg/h) | Required Orifice Area (mm2) | API Orifice | Trelief (°C) | F′factor |
| 0.5 | 1.5 | 0.29 | 2.75 | 5.4 | 10.0 | 15 | 5 | 160 | |||||
| 0.5 | 1.5 | 0.29 | 2.75 | 5.4 | 10.0 | 15 | 10 | 160 | 115.6 | 13.7 | D | 306.3 | 0.012 |
| 0.5 | 1.5 | 0.29 | 2.75 | 10.2 | 10.2 | 45 | 15 | 160 | |||||
| 0.5 | 1.5 | 0.29 | 2.75 | 10.2 | 10.2 | 45 | 35 | 160 | 324.8 | 11.7 | D | 227.6 | 0.017 |
| 0.5 | 1.5 | 0.29 | 2.75 | 25.2 | 25.2 | 135 | 45 | 160 | |||||
| 0.5 | 1.5 | 0.29 | 2.75 | 25.2 | 25.2 | 135 | 115 | 160 | 726.8 | 8.2 | D | 185.3 | 0.021 |
| 1 | 3 | 2.36 | 11.00 | 7.7 | 10.0 | 15 | 5 | 160 | |||||
| 1 | 3 | 2.36 | 11.00 | 7.7 | 10.0 | 15 | 10 | 160 | 462.4 | 55.0 | D | 306.3 | 0.012 |
| 1 | 3 | 2.36 | 11.00 | 17.3 | 17.3 | 45 | 15 | 160 | |||||
| 1 | 3 | 2.36 | 11.00 | 17.3 | 17.3 | 45 | 35 | 160 | 1299.1 | 46.8 | D | 227.6 | 0.017 |
| 1 | 3 | 2.36 | 11.00 | 47.4 | 47.4 | 135 | 45 | 160 | |||||
| 1 | 3 | 2.36 | 11.00 | 47.4 | 47.4 | 135 | 115 | 160 | 2907.0 | 32.7 | D | 185.3 | 0.021 |
| 2 | 6 | 18.85 | 43.98 | 12.4 | 12.4 | 15 | 5 | 160 | |||||
| 2 | 6 | 18.85 | 43.98 | 12.4 | 12.4 | 15 | 10 | 160 | 1849.5 | 219.1 | G | 306.3 | 0.012 |
| 2 | 6 | 18.85 | 43.98 | 31.6 | 31.6 | 45 | 15 | 160 | |||||
| 2 | 6 | 18.85 | 43.98 | 31.6 | 31.6 | 45 | 35 | 160 | 5196.3 | 187.3 | F | 227.6 | 0.017 |
| 2 | 6 | 18.85 | 43.98 | 91.9 | 91.9 | 135 | 45 | 160 | |||||
| 2 | 6 | 18.85 | 43.98 | 91.9 | 91.9 | 135 | 115 | 160 | 11,629.4 | 130.8 | F | 185.3 | 0.021 |
| 3 | 9 | 63.62 | 98.96 | 17.1 | 17.1 | 15 | 5 | 160 | |||||
| 3 | 9 | 63.62 | 98.96 | 17.1 | 17.1 | 15 | 10 | 160 | 4161.5 | 494.8 | H | 306.2 | 0.012 |
| 3 | 9 | 63.62 | 98.96 | 45.9 | 45.9 | 45 | 15 | 160 | |||||
| 3 | 9 | 63.62 | 98.96 | 45.9 | 45.9 | 45 | 35 | 160 | 11691.6 | 421.5 | H | 227.6 | 0.017 |
| 3 | 9 | 63.62 | 98.96 | 136.3 | 136.3 | 135 | 45 | 160 | |||||
| 3 | 9 | 63.62 | 98.96 | 136.3 | 136.3 | 135 | 115 | 160 | 26,166.2 | 294.2 | G | 185.3 | 0.021 |
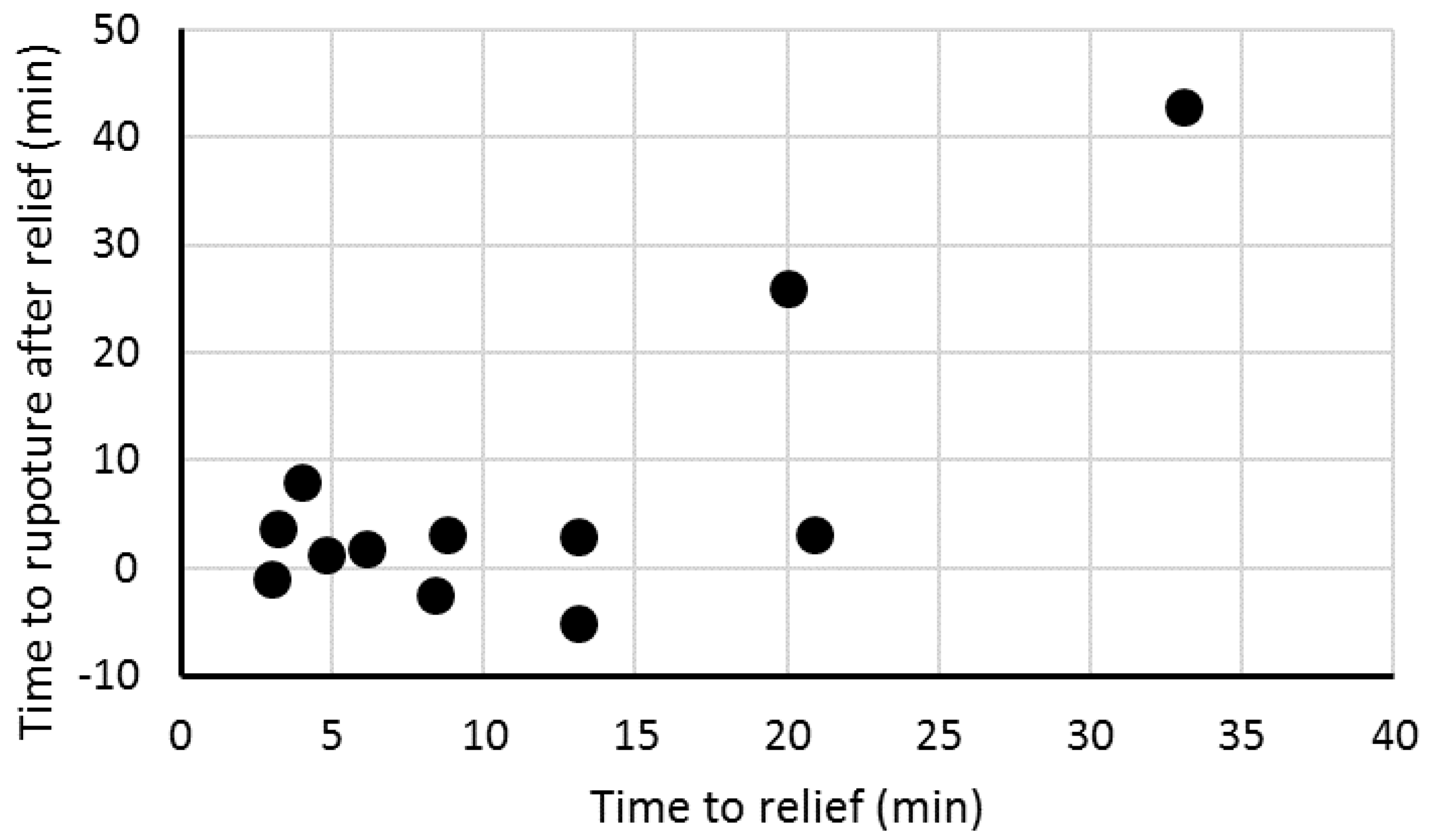
| Vessel Geometry and Design Data | Dynamic Simulation Output Data | Rupture Evaluation | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Diameter (m) | Design Pressure (bar) | Operating Pressure (bar) | Time to Relief (min) | Initial Relief Temperature (°C) | Pool Fire Time to Rupture (min) | Pool Fire Pres. at Rupture (bar) | Jet Fire Time to Rupture (min) | Jet Fire Pres. at Rupture (bar) | Relief Valve Activation (Pool Fire) |
| 0.5 | 15 | 5 | 9.9 | 679.08 | 7 | 13.0 | 2 | 6.4 | FAIL |
| 0.5 | 15 | 10 | 3.2 | 202.87 | 7 | 15.0 | 3 | 14.5 | OK |
| 0.5 | 45 | 15 | 11.6 | 645.03 | 3 | 20.7 | 1 | 15.6 | FAIL |
| 0.5 | 45 | 35 | 3.0 | 124.59 | 2 | 39.6 | 1 | 36.0 | FAIL |
| 0.5 | 135 | 45 | 21.0 | 550.36 | 14 | 67.3 | 8 | 52.9 | FAIL |
| 0.5 | 135 | 115 | 4.0 | 78.54 | 12 | 135.1 | 6 | 126 | OK |
| 1 | 15 | 5 | 14.5 | 679.02 | 10 | 8.5 | 4 | 5.6 | FAIL |
| 1 | 15 | 10 | 4.8 | 202.89 | 6 | 12.2 | 2 | 10.2 | OK |
| 1 | 45 | 15 | 24.2 | 644.94 | 12 | 20.6 | 6 | 16.4 | FAIL |
| 1 | 45 | 35 | 6.1 | 124.42 | 8 | 39.4 | 4 | 36.0 | OK |
| 1 | 135 | 45 | 46.0 | 135.00 | 30 | 66.5 | 14 | 50.0 | FAIL |
| 1 | 135 | 115 | 8.8 | 78.55 | 12 | 135.1 | 5 | 121.2 | OK |
| 2 | 15 | 5 | 28.9 | 678.96 | 8 | 5.9 | 4 | 5.2 | FAIL |
| 2 | 15 | 10 | 8.4 | 202.37 | 6 | 10.7 | 2 | 10.1 | FAIL |
| 2 | 45 | 15 | 54.7 | 644.84 | 22 | 19.2 | 12 | 16.2 | FAIL |
| 2 | 45 | 35 | 13.1 | 124.25 | 16 | 38.8 | 8 | 35.9 | OK |
| 2 | 135 | 45 | 107.3 | 550.28 | 76 | 52.3 | 28 | 48.9 | FAIL |
| 2 | 135 | 115 | 20.0 | 78.48 | 46 | 135.7 | 20 | 119.7 | OK |
| 3 | 15 | 5 | 47.8 | 678.91 | 12 | 5.9 | 6 | 5.2 | FAIL |
| 3 | 15 | 10 | 13.1 | 202.21 | 8 | 12.1 | 3 | 10.3 | FAIL |
| 3 | 45 | 15 | - 1 | - 1 | 32 | 18.5 | 14 | 15.6 | OK |
| 3 | 45 | 35 | 20.9 | 124.21 | 24 | 38.4 | 10 | 35.5 | OK |
| 3 | 135 | 45 | - 1 | - 1 | 112 | 50.8 | 42 | 48.2 | OK |
| 3 | 135 | 115 | 33.1 | 78.48 | 76 | 121.4 | 28 | 118.3 | OK |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andreasen, A.; Borroni, F.; Zan Nieto, M.; Stegelmann, C.; P. Nielsen, R. On the Adequacy of API 521 Relief-Valve Sizing Method for Gas-Filled Pressure Vessels Exposed to Fire. Safety 2018, 4, 11. https://doi.org/10.3390/safety4010011
Andreasen A, Borroni F, Zan Nieto M, Stegelmann C, P. Nielsen R. On the Adequacy of API 521 Relief-Valve Sizing Method for Gas-Filled Pressure Vessels Exposed to Fire. Safety. 2018; 4(1):11. https://doi.org/10.3390/safety4010011
Chicago/Turabian StyleAndreasen, Anders, Filippo Borroni, Marcos Zan Nieto, Carsten Stegelmann, and Rudi P. Nielsen. 2018. "On the Adequacy of API 521 Relief-Valve Sizing Method for Gas-Filled Pressure Vessels Exposed to Fire" Safety 4, no. 1: 11. https://doi.org/10.3390/safety4010011
APA StyleAndreasen, A., Borroni, F., Zan Nieto, M., Stegelmann, C., & P. Nielsen, R. (2018). On the Adequacy of API 521 Relief-Valve Sizing Method for Gas-Filled Pressure Vessels Exposed to Fire. Safety, 4(1), 11. https://doi.org/10.3390/safety4010011