The Effectiveness of Pan-Sharpening Algorithms on Different Land Cover Types in GeoEye-1 Satellite Images
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset and Study Areas
- Frame 1—A natural area, it presents a forest (green area) and nude soil, no man-made features (included between coordinates East 408,000 m–408,500 m and North 4,553,500 m–4,554,000 m);
- Frame 2—A rural area, it mainly presents two kinds of cultivated areas, prevalently covered by vegetation, slightly man-made (included between coordinates East 415,900 m–416,400 m and North 4,548,400 m–4,548,900 m);
- Frame 3—A semi-urban area, it presents a mix of land cover, such as houses, vegetation and nude soil, averagely man-made (included between coordinates East 409,500 m–410,000 m and North 4,545,400 m–4,545,900 m);
- Frame 4—An urban area, it presents few green areas, mostly represented by trees, and a typical urban land cover with houses, strongly man-made (included between coordinates East 407,300 m–407,800 m and North 4,551,900 m–4,552,400 m).
2.2. Classification
2.3. Pan-Sharpening Methods
2.3.1. Intensity-Hue-Saturation
2.3.2. Brovey Transformation
2.3.3. Gram–Schmidt Transformation
2.3.4. Smoothing Filter-Based Intensity Modulation
2.3.5. High-Pass Filter
2.4. Quality Assessment
2.4.1. Universal Image Quality Index (UIQI)
2.4.2. Erreur Relative Globale Adimensionalle de Synthèse (ERGAS)
2.4.3. Zhou’s Spatial Index (ZI)
2.4.4. Spatial ERGAS (S-ERGAS)
3. Results and Discussion
3.1. Classification Results
- Natural area: 75–100%;
- Rural area: 50–75%;
- Semi-urban area: 25–50%;
- Urban area: 0–25%.
3.2. Pan-Sharpening Results
- Weighted methods always perform better than the respective unweighted techniques in terms of spectral correlation;
- Weighted methods tend to maintain the ZI and S-ERGAS values of their respective unweighted methods;
- Low-pass filter-based techniques perform quite well in low-variating land covers, but tend to perform poorly in variegated land cover;
- Low-pass filter-based techniques never present the best performance in terms of spatial similarity with PAN.
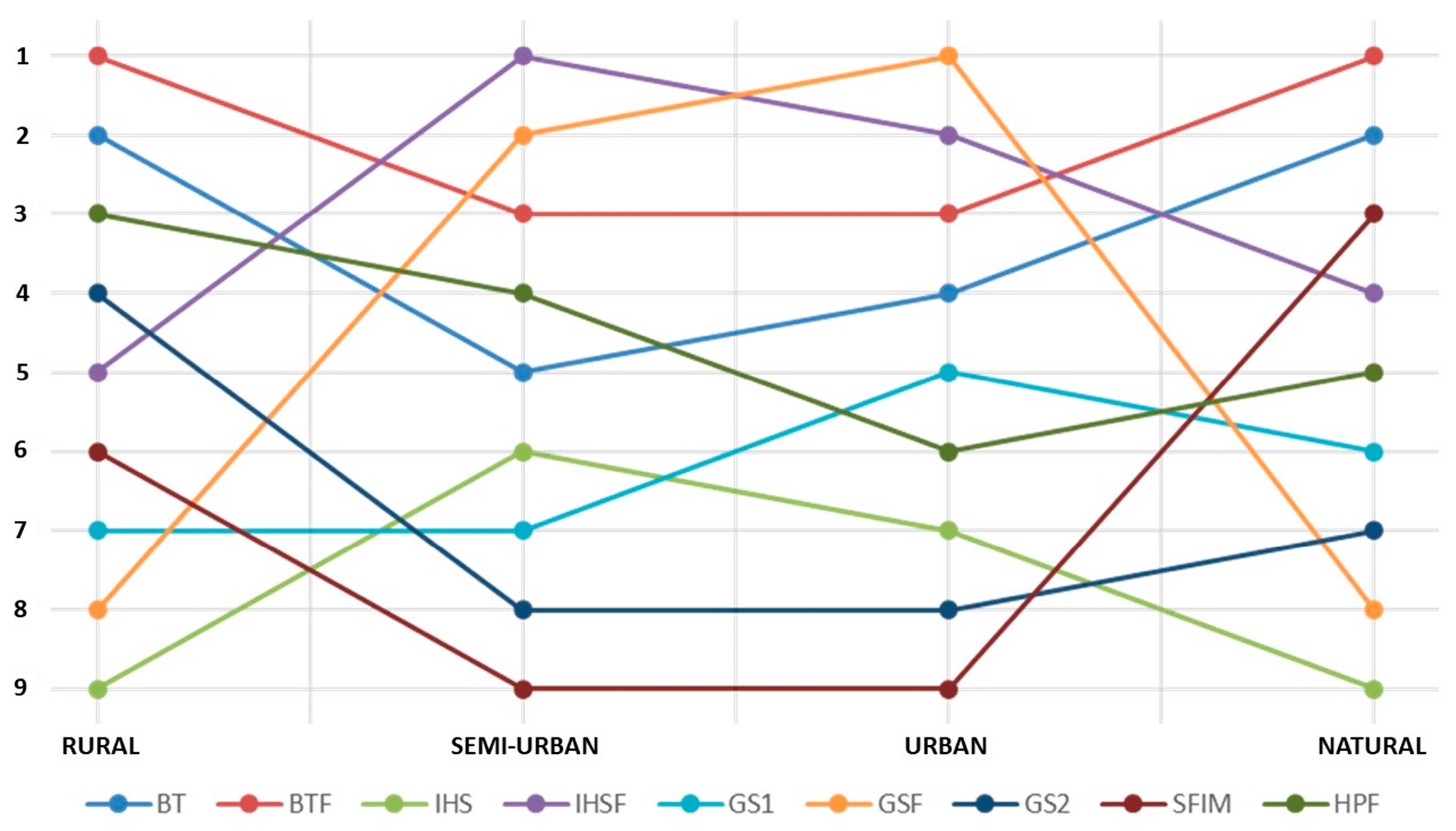
- A ranking is made for the methods in consideration of each indicator, assigning a score from 1 to 9.
- The spectral indicators are then mediated between them, as well as the spatial indicators.
- A general ranking is obtained by averaging the two results.
4. Limitations and Future Research Directions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- De Carvalho Filho, J.G.N.; Carvalho, E.Á.N.; Molina, L.; Freire, E.O. The impact of parametric uncertainties on mobile robots velocities and pose estimation. IEEE Access 2019, 7, 69070–69086. [Google Scholar] [CrossRef]
- Hall, D.L.; Llinas, J. An introduction to multisensor data fusion. Proc. IEEE 1997, 85, 6–23. [Google Scholar] [CrossRef]
- Kong, L.; Peng, X.; Chen, Y.; Wang, P.; Xu, M. Multi-sensor measurement and data fusion technology for manufacturing process monitoring: A literature review. Int. J. Extrem. Manuf. 2020, 2, 022001. [Google Scholar] [CrossRef]
- Stateczny, A.; Bodus-Olkowska, I. Sensor data fusion techniques for environment modelling. In Proceedings of the 2015 16th International Radar Symposium (IRS), Dresden, Germany, 24–26 June 2015; pp. 1123–1128. [Google Scholar] [CrossRef]
- Keenan, T.F.; Davidson, E.; Moffat, A.M.; Munger, W.; Richardson, A.D. Using model-data fusion to interpret past trends, and quantify uncertainties in future projections, of terrestrial ecosystem carbon cycling. Glob. Change Biol. 2012, 18, 2555–2569. [Google Scholar] [CrossRef]
- Fernández Prieto, D. Change detection in multisensor remote-sensing data for desertification monitoring. In Proceedings of the Third International Symposium on Retrieval of Bio- and Geophysical Parameters from SAR Data for Land Applications, Sheffield, UK, 11–14 September 2001; Volume 475. [Google Scholar]
- Schultz, M.; Clevers, J.G.; Carter, S.; Verbesselt, J.; Avitabile, V.; Quang, H.V.; Herold, M. Performance of vegetation indices from Landsat time series in deforestation monitoring. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 318–327. [Google Scholar] [CrossRef]
- Ge, L.; Li, X.; Wu, F.; Turner, I.L. Coastal erosion mapping through intergration of SAR and Landsat TM imagery. In Proceedings of the 2013 IEEE International Geoscience and Remote Sensing Symposium-IGARSS, Melbourne, VIC, Australia, 21–26 July 2013; pp. 2266–2269. [Google Scholar] [CrossRef]
- Sakellariou, S.; Cabral, P.; Caetano, M.; Pla, F.; Painho, M.; Christopoulou, O.; Sfougaris, A.; Dalezios, N.; Vasilakos, C. Remotely sensed data fusion for spatiotemporal geostatistical analysis of forest fire hazard. Sensors 2020, 20, 5014. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Jia, G.; Pohl, C.; Feng, Q.; He, Y.; Gao, H.; Feng, J. Improved monitoring of urbanization processes in China for regional climate impact assessment. Environ. Earth Sci. 2015, 73, 8387–8404. [Google Scholar] [CrossRef]
- Baiocchi, V.; Brigante, R.; Dominici, D.; Milone, M.V.; Mormile, M.; Radicioni, F. Automatic three-dimensional features extraction: The case study of L’Aquila for collapse identification after April 06, 2009 earthquake. Eur. J. Remote Sens. 2014, 47, 413–435. [Google Scholar] [CrossRef]
- Lasaponara, R.; Masini, N. Satellite Remote Sensing: A New Tool for Archaeology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; p. 16. [Google Scholar] [CrossRef]
- Mandanici, E.; Bitelli, G. Preliminary comparison of sentinel-2 and landsat 8 imagery for a combined use. Remote Sens. 2016, 8, 1014. [Google Scholar] [CrossRef]
- Bork, E.W.; Su, J.G. Integrating LIDAR data and multispectral imagery for enhanced classification of rangeland vegetation: A meta analysis. Remote Sens. Environ. 2007, 111, 11–24. [Google Scholar] [CrossRef]
- Amani, M.; Salehi, B.; Mahdavi, S.; Granger, J.; Brisco, B. Wetland classification in Newfoundland and Labrador using multi-source SAR and optical data integration. GIScience Remote Sens. 2017, 54, 779–796. [Google Scholar] [CrossRef]
- Mateo-Sanchis, A.; Piles, M.; Muñoz-Marí, J.; Adsuara, J.E.; Pérez-Suay, A.; Camps-Valls, G. Synergistic integration of optical and microwave satellite data for crop yield estimation. Remote Sens. Environ. 2019, 234, 111460. [Google Scholar] [CrossRef] [PubMed]
- Ehlers, M.; Klonus, S.; Johan Åstrand, P.; Rosso, P. Multi-sensor image fusion for pansharpening in remote sensing. Int. J. Image Data Fusion 2010, 1, 25–45. [Google Scholar] [CrossRef]
- Parente, C.; Santamaria, R. Increasing geometric resolution of data supplied by Quickbird multispectral sensors. Sens. Transducers 2013, 156, 111. [Google Scholar]
- Wang, Z.; Ziou, D.; Armenakis, C.; Li, D.; Li, Q. A comparative analysis of image fusion methods. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1391–1402. [Google Scholar] [CrossRef]
- Thomas, C.; Ranchin, T.; Wald, L.; Chanussot, J. Synthesis of multispectral images to high spatial resolution: A critical review of fusion methods based on remote sensing physics. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1301–1312. [Google Scholar] [CrossRef]
- Garzelli, A.; Nencini, F.; Alparone, L.; Aiazzi, B.; Baronti, S. Pan-sharpening of multispectral images: A critical review and comparison. In Proceedings of the IGARSS 2004. 2004 IEEE International Geoscience and Remote Sensing Symposium, Anchorage, AK, USA, 20–24 September 2004; Volume 1. [Google Scholar] [CrossRef]
- Vivone, G.; Alparone, L.; Chanussot, J.; Dalla Mura, M.; Garzelli, A.; Licciardi, G.A.; Wald, L. A critical comparison among pansharpening algorithms. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2565–2586. [Google Scholar] [CrossRef]
- Falchi, U. IT tools for the management of multi-representation geographical information. Int. J. Eng. Technol. 2018, 7, 65–69. [Google Scholar] [CrossRef]
- Rahmani, S.; Strait, M.; Merkurjev, D.; Moeller, M.; Wittman, T. An adaptive IHS pan-sharpening method. IEEE Geosci. Remote Sens. Lett. 2010, 7, 746–750. [Google Scholar] [CrossRef]
- Masi, G.; Cozzolino, D.; Verdoliva, L.; Scarpa, G. Pansharpening by convolutional neural networks. Remote Sens. 2016, 8, 594. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar] [CrossRef]
- Yang, W.; Zhang, X.; Tian, Y.; Wang, W.; Xue, J.H.; Liao, Q. Deep learning for single image super-resolution: A brief review. IEEE Trans. Multimed. 2019, 21, 3106–3121. [Google Scholar] [CrossRef]
- Li, Z.; Yang, J.; Liu, Z.; Yang, X.; Jeon, G.; Wu, W. Feedback network for image super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 3867–3876. [Google Scholar]
- Rohith, G.; Kumar, L.S. Super-Resolution Based Deep Learning Techniques for Panchromatic Satellite Images in Application to Pansharpening. IEEE Access 2020, 8, 162099–162121. [Google Scholar] [CrossRef]
- Vivone, G. Robust band-dependent spatial-detail approaches for panchromatic sharpening. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6421–6433. [Google Scholar] [CrossRef]
- Xiong, Z.; Guo, Q.; Liu, M.; Li, A. Pan-sharpening based on convolutional neural network by using the loss function with no-reference. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 14, 897–906. [Google Scholar] [CrossRef]
- Jones, E.G.; Wong, S.; Milton, A.; Sclauzero, J.; Whittenbury, H.; McDonnell, M.D. The impact of pan-sharpening and spectral resolution on vineyard segmentation through machine learning. Remote Sens. 2020, 12, 934. [Google Scholar] [CrossRef]
- Vivone, G.; Dalla Mura, M.; Garzelli, A.; Restaino, R.; Scarpa, G.; Ulfarsson, M.O.; Chanussot, J. A new benchmark based on recent advances in multispectral pansharpening: Revisiting pansharpening with classical and emerging pansharpening methods. IEEE Geosci. Remote Sens. Mag. 2020, 9, 53–81. [Google Scholar] [CrossRef]
- Deng, L.J.; Vivone, G.; Paoletti, M.E.; Scarpa, G.; He, J.; Zhang, Y.; Plaza, A. Machine Learning in Pansharpening: A benchmark, from shallow to deep networks. IEEE Geosci. Remote Sens. Mag. 2022, 10, 279–315. [Google Scholar] [CrossRef]
- Jawak, S.D.; Luis, A.J. Improved land cover mapping using high resolution multiangle 8-band WorldView-2 satellite remote sensing data. J. Appl. Remote Sens. 2013, 7, 073573. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, L.; Zhang, G.; Bi, H.; Dalla Mura, M.; Chanussot, J. Superresolution land cover mapping based on pixel-, subpixel-, and superpixel-scale spatial dependence with pansharpening technique. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4082–4098. [Google Scholar] [CrossRef]
- Li, H.; Jing, L.; Tang, Y. Assessment of pansharpening methods applied to WorldView-2 imagery fusion. Sensors 2017, 17, 89. [Google Scholar] [CrossRef] [PubMed]
- Medina, A.; Marcello, J.; Rodriguez, D.; Eugenio, F.; Martin, J. Quality evaluation of pansharpening techniques on different land cover types. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 5442–5445. [Google Scholar] [CrossRef]
- QGIS. Available online: https://www.qgis.org/en/site/about/index.html (accessed on 2 September 2021).
- SAGA; GIS. Available online: http://www.saga-gis.org/en/index.html (accessed on 2 September 2021).
- Planetek Italia–GeoEye-1. Available online: https://www.planetek.it/prodotti/tutti_i_prodotti/geoeye_1 (accessed on 2 September 2021).
- Eo Portal–GeoEye-1. Available online: https://earth.esa.int/web/eoportal/satellite-missions/g/geoeye-1 (accessed on 2 September 2021).
- Rouse, J.W., Jr.; Haas, R.H.; Deering, D.W.; Schell, J.A.; Harlan, J.C. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; NASA: Washington, DC, USA, 1974; No. E75-10354. [Google Scholar]
- Meng, X.; Xiong, Y.; Shao, F.; Shen, H.; Sun, W.; Yang, G.; Zhang, H. A large-scale benchmark data set for evaluating pansharpening performance: Overview and implementation. IEEE Geosci. Remote Sens. Mag. 2020, 9, 18–52. [Google Scholar] [CrossRef]
- Alcaras, E.; Amoroso, P.P.; Parente, C.; Prezioso, G. Remotely Sensed Image Fast Classification and Smart Thematic Map Production. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, 46, 43–50. [Google Scholar] [CrossRef]
- Sisodia, P.S.; Tiwari, V.; Kumar, A. Analysis of supervised maximum likelihood classification for remote sensing image. In Proceedings of the 2014 International Conference on Advances in Computing, Communications and Informatics (ICACCI), Delhi, India, 24–27 September 2014; pp. 1–4. [Google Scholar] [CrossRef]
- Alparone, L.; Wald, L.; Chanussot, J.; Thomas, C.; Gamba, P.; Bruce, L.M. Comparison of pansharpening algorithms: Outcome of the 2006 GRS-S data-fusion contest. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3012–3021. [Google Scholar] [CrossRef]
- Pushparaj, J.; Hegde, A.V. Evaluation of pan-sharpening methods for spatial and spectral quality. Appl. Geomat. 2017, 9, 1–12. [Google Scholar] [CrossRef]
- Carper, W.J.; Lillesand, T.M.; Kiefer, R.W. The use of intensity-hue-saturation transformations for merging SPOT panchromatic and multispectral image data. Photogramm. Eng. Rem. S. 1990, 56, 459–467. [Google Scholar]
- Tu, T.M.; Su, S.; Shyu, H.; Huang, P.S. A new look at IHS-like image fusion methods. Inf. Fusion 2001, 2, 177–186. [Google Scholar] [CrossRef]
- Parente, C.; Pepe, M. Influence of the weights in IHS and Brovey methods for pan-sharpening WorldView-3 satellite images. Int. J. Eng. Technol 2017, 6, 71–77. [Google Scholar] [CrossRef]
- Tu, T.M.; Huang, P.S.; Hung, C.L.; Chang, C.P. A fast intensity-hue-saturation fusion technique with spectral adjustment for IKONOS imagery. IEEE Geosci. Remote Sens. Lett. 2004, 1, 309–312. [Google Scholar] [CrossRef]
- Švab, A.; Oštir, K. High-resolution image fusion: Methods to preserve spectral and spatial resolution. Photogramm. Eng. Remote Sens. 2006, 72, 565–572. [Google Scholar] [CrossRef]
- Pohl, C.; Van Genderen, J.L. Review article multisensor image fusion in remote sensing: Concepts, methods and applications. Int. J. Remote Sens. 1998, 19, 823–854. [Google Scholar] [CrossRef]
- Karakus, P.; Karabork, H. Effect of pansharpened image on some of pixel based and object based classification accuracy. International Archives of the Photogrammetry. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Prague, Czech Republic, 12–19 July 2016; Volume XLI-B7. [Google Scholar] [CrossRef]
- Laben, C.A.; Brower, B.V. Process for Enhancing the Spatial Resolution of Multispectral Imagery Using Pan-Sharpening. U.S. Patent 6011875, 4 January 2000. [Google Scholar]
- Maurer, T. How to pan-sharpen images using the Gram-Schmidt pan-sharpen method-a recipe. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 1, W1. [Google Scholar] [CrossRef]
- Liu, J.G. Smoothing filter-based intensity modulation: A spectral preserve image fusion technique for improving spatial details. Int. J. Remote Sens. 2000, 21, 3461–3472. [Google Scholar] [CrossRef]
- Chavez, P.S., Jr.; Bowell, J.A. Comparison of the spectral information content of Landsat Thematic Mapper and SPOT for three different sites in the Phoenix, Arizona region. Photogramm. Eng. Remote Sens. 1988, 54, 1699–1708. [Google Scholar]
- Karathanassi, V.; Kolokousis, P.; Ioannidou, S. A comparison study on fusion methods using evaluation indicators. Int. J. Remote Sens. 2007, 28, 2309–2341. [Google Scholar] [CrossRef]
- Shahdoosti, H.R.; Ghassemian, H. Fusion of MS and PAN images preserving spectral quality. IEEE Geosci. Remote Sens. Lett. 2014, 12, 611–615. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.C. A universal image quality index. Signal Process. Lett. IEEE 2002, 9, 81–84. [Google Scholar] [CrossRef]
- Nikolakopoulos, K.; Oikonomidis, D. Quality assessment of ten fusion techniques applied on Worldview-2. Eur. J. Remote Sens. 2015, 48, 141–167. [Google Scholar] [CrossRef]
- Wald, L. Quality of High Resolution Synthesised Images: Is There a Simple Criterion. In Proceedings of the Third Conference Fusion of Earth Data: Merging Point Measurements, Raster Maps and Remotely Sensed Images, Sophia Antipolis, France, 26–28 January 2000; pp. 99–103. [Google Scholar]
- Ranchin, T.; Wald, L. Fusion of high spatial and spectral resolution images: The ARSIS concept and its implementation. Photogramm. Eng. Remote Sens. 2000, 66, 49–61. [Google Scholar]
- Zhou, J.; Civco, D.L.; Silander, J.A. A wavelet transform method to merge Landsat TM and SPOT panchromatic data. Int. J. Remote Sens. 1998, 19, 743–757. [Google Scholar] [CrossRef]
- Lillo-Saavedra, M.; Gonzalo, C.; Arquero, A.; Martinez, E. Fusion of multispectral and panchromatic satellite sensor imagery based on tailored filtering in the Fourier domain. Int. J. Remote Sens. 2005, 26, 1263–1268. [Google Scholar] [CrossRef]
- Pleniou, M.; Koutsias, N. Sensitivity of spectral reflectance values to different burn and vegetation ratios: A multi-scale approach applied in a fire affected area. ISPRS J. Photogramm. Remote Sens. 2013, 79, 199–210. [Google Scholar] [CrossRef]
- Lee, J.; Lee, C. Fast and efficient panchromatic sharpening. IEEE Trans. Geosci. Remote Sens. 2009, 48, 155–163. [Google Scholar] [CrossRef]
- Cánovas-García, F.; Pesántez-Cobos, P.; Alonso-Sarría, F. fusionImage: An R package for pan-sharpening images in open source software. Trans. GIS 2020, 24, 1185–1207. [Google Scholar] [CrossRef]
- Alcaras, E.; Della Corte, V.; Ferraioli, G.; Martellato, E.; Palumbo, P.; Parente, C.; Rotundi, A. Comparison of different pan-sharpening methods applied to IKONOS imagery. Geogr. Tech. 2021, 16, 198–210. [Google Scholar] [CrossRef]
- Amolins, K.; Zhang, Y.; Dare, P. Wavelet based image fusion techniques—An introduction, review and comparison. ISPRS J. Photogramm. Remote Sens. 2007, 62, 249–263. [Google Scholar] [CrossRef]
- Dodgson, J.S.; Spackman, M.; Pearman, A.; Phillips, L.D. Multi-Criteria Analysis: A Manual; Department for Communities and Local Government: London, UK, 2009.
- Alcaras, E.; Parente, C.; Vallario, A. Automation of Pan-Sharpening Methods for Pléiades Images Using GIS Basic Functions. Remote Sens. 2021, 13, 1550. [Google Scholar] [CrossRef]
- Saroglu, E.; Bektas, F.; Musaoglu, N.; Goksel, C. Fusion of multisensory sensing data: Assessing the quality of resulting images. ISPRS Arch. 2004, 35, 575–579. [Google Scholar]
- Jeong, D.; Kim, Y. Deep learning based pansharpening using a Laplacian pyramid. Asian Conf. Remote Sens. ACRS 2019, 40, 1–8. [Google Scholar]
- Xu, S.; Zhang, J.; Zhao, Z.; Sun, K.; Liu, J.; Zhang, C. Deep gradient projection networks for pan-sharpening. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 20–25 June 2021; pp. 1366–1375. [Google Scholar] [CrossRef]
- Liu, Q.; Meng, X.; Shao, F.; Li, S. Supervised-unsupervised combined deep convolutional neural networks for high-fidelity pansharpening. Inf. Fusion 2023, 89, 292–304. [Google Scholar] [CrossRef]
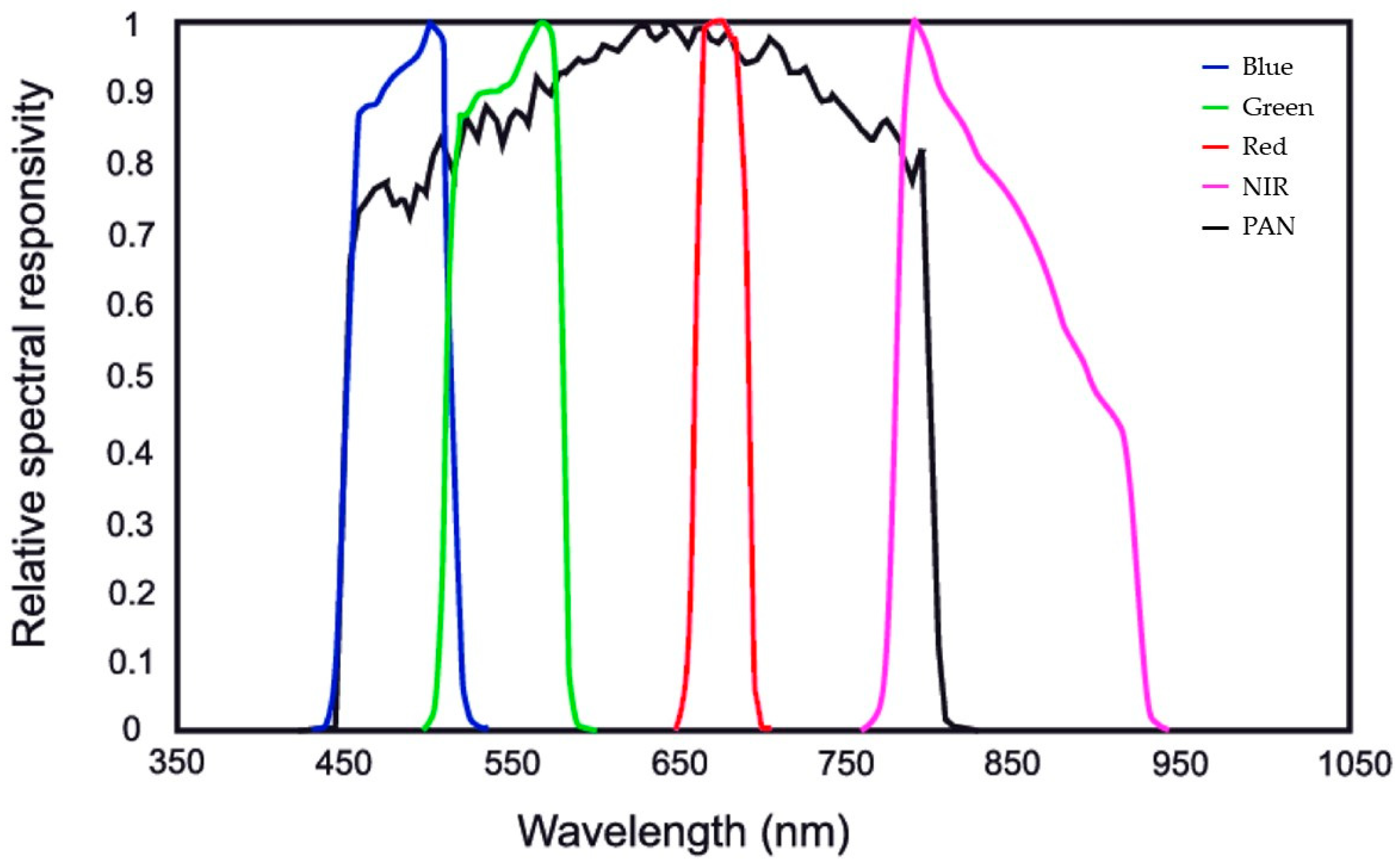










| Bands | Wavelength (nm) | Resolution (m) |
|---|---|---|
| Panchromatic | 450–800 | 0.5 |
| Band 1—Blue | 450–510 | 2 |
| Band 2—Green | 510–580 | 2 |
| Band 3—Red | 655–690 | 2 |
| Band 4—Near Infrared (NIR) | 780–920 | 2 |
| Method | Bands | UIQI | UIQIM | ERGAS | ZI | ZIM | S-ERGAS |
|---|---|---|---|---|---|---|---|
| BT | Blue | 0.812 | 0.842 | 7.458 | 0.950 | 0.923 | 6.250 |
| Green | 0.885 | 0.964 | |||||
| Red | 0.929 | 0.849 | |||||
| NIR | 0.743 | 0.930 | |||||
| BTF | Blue | 0.656 | 0.820 | 4.280 | 0.978 | 0.928 | 6.551 |
| Green | 0.829 | 0.990 | |||||
| Red | 0.953 | 0.907 | |||||
| NIR | 0.842 | 0.838 | |||||
| IHS | Blue | 0.783 | 0.794 | 9.952 | 0.922 | 0.860 | 6.717 |
| Green | 0.746 | 0.947 | |||||
| Red | 0.708 | 0.905 | |||||
| NIR | 0.937 | 0.664 | |||||
| IHSF | Blue | 0.758 | 0.849 | 4.390 | 0.983 | 0.882 | 6.674 |
| Green | 0.789 | 0.990 | |||||
| Red | 0.894 | 0.975 | |||||
| NIR | 0.954 | 0.578 | |||||
| GS1 | Blue | 0.904 | 0.825 | 9.553 | 0.914 | 0.899 | 6.672 |
| Green | 0.836 | 0.946 | |||||
| Red | 0.676 | 0.908 | |||||
| NIR | 0.884 | 0.826 | |||||
| GSF | Blue | 0.827 | 0.860 | 4.981 | 0.983 | 0.777 | 6.748 |
| Green | 0.827 | 0.989 | |||||
| Red | 0.801 | 0.986 | |||||
| NIR | 0.984 | 0.149 | |||||
| GS2 | Blue | 0.861 | 0.877 | 4.841 | 0.956 | 0.860 | 7.363 |
| Green | 0.840 | 0.960 | |||||
| Red | 0.848 | 0.956 | |||||
| NIR | 0.957 | 0.568 | |||||
| SFIM | Blue | 0.745 | 0.851 | 4.018 | 0.963 | 0.896 | 7.059 |
| Green | 0.865 | 0.946 | |||||
| Red | 0.965 | 0.823 | |||||
| NIR | 0.828 | 0.852 | |||||
| HPF | Blue | 0.845 | 0.898 | 3.797 | 0.959 | 0.851 | 7.085 |
| Green | 0.859 | 0.956 | |||||
| Red | 0.931 | 0.915 | |||||
| NIR | 0.956 | 0.574 |
| Method | Bands | UIQI | UIQIM | ERGAS | ZI | ZIM | S-ERGAS |
|---|---|---|---|---|---|---|---|
| BT | Blue | 0.895 | 0.891 | 7.215 | 0.939 | 0.905 | 4.975 |
| Green | 0.914 | 0.947 | |||||
| Red | 0.943 | 0.833 | |||||
| NIR | 0.812 | 0.903 | |||||
| BTF | Blue | 0.664 | 0.837 | 4.226 | 0.979 | 0.917 | 5.152 |
| Green | 0.790 | 0.988 | |||||
| Red | 0.933 | 0.903 | |||||
| NIR | 0.962 | 0.800 | |||||
| IHS | Blue | 0.830 | 0.837 | 9.283 | 0.924 | 0.872 | 5.132 |
| Green | 0.772 | 0.947 | |||||
| Red | 0.767 | 0.917 | |||||
| NIR | 0.977 | 0.700 | |||||
| IHSF | Blue | 0.764 | 0.846 | 4.232 | 0.982 | 0.892 | 5.204 |
| Green | 0.748 | 0.990 | |||||
| Red | 0.881 | 0.978 | |||||
| NIR | 0.991 | 0.619 | |||||
| GS1 | Blue | 0.991 | 0.919 | 6.928 | 0.546 | 0.634 | 4.947 |
| Green | 0.966 | 0.705 | |||||
| Red | 0.990 | 0.376 | |||||
| NIR | 0.729 | 0.910 | |||||
| GSF | Blue | 0.755 | 0.808 | 5.324 | 0.982 | 0.874 | 5.237 |
| Green | 0.760 | 0.990 | |||||
| Red | 0.745 | 0.981 | |||||
| NIR | 0.972 | 0.544 | |||||
| GS2 | Blue | 0.925 | 0.940 | 3.093 | 0.931 | 0.876 | 5.682 |
| Green | 0.906 | 0.937 | |||||
| Red | 0.935 | 0.934 | |||||
| NIR | 0.993 | 0.702 | |||||
| SFIM | Blue | 0.869 | 0.930 | 2.986 | 0.940 | 0.869 | 5.630 |
| Green | 0.909 | 0.914 | |||||
| Red | 0.967 | 0.786 | |||||
| NIR | 0.975 | 0.836 | |||||
| HPF | Blue | 0.923 | 0.948 | 2.655 | 0.933 | 0.844 | 5.570 |
| Green | 0.913 | 0.930 | |||||
| Red | 0.959 | 0.893 | |||||
| NIR | 0.996 | 0.620 |
| Method | Bands | UIQI | UIQIM | ERGAS | ZI | ZIM | S-ERGAS |
|---|---|---|---|---|---|---|---|
| BT | Blue | 0.793 | 0.828 | 7.271 | 0.963 | 0.946 | 6.134 |
| Green | 0.840 | 0.973 | |||||
| Red | 0.890 | 0.927 | |||||
| NIR | 0.787 | 0.923 | |||||
| BTF | Blue | 0.762 | 0.832 | 5.969 | 0.974 | 0.936 | 7.015 |
| Green | 0.830 | 0.987 | |||||
| Red | 0.897 | 0.945 | |||||
| NIR | 0.838 | 0.837 | |||||
| IHS | Blue | 0.812 | 0.835 | 7.859 | 0.954 | 0.929 | 8.120 |
| Green | 0.786 | 0.970 | |||||
| Red | 0.837 | 0.953 | |||||
| NIR | 0.904 | 0.840 | |||||
| IHSF | Blue | 0.812 | 0.852 | 5.836 | 0.979 | 0.929 | 7.250 |
| Green | 0.804 | 0.986 | |||||
| Red | 0.872 | 0.972 | |||||
| NIR | 0.920 | 0.777 | |||||
| GS1 | Blue | 0.832 | 0.835 | 8.053 | 0.952 | 0.930 | 8.398 |
| Green | 0.812 | 0.969 | |||||
| Red | 0.789 | 0.963 | |||||
| NIR | 0.905 | 0.838 | |||||
| GSF | Blue | 0.827 | 0.862 | 5.893 | 0.978 | 0.897 | 7.488 |
| Green | 0.828 | 0.985 | |||||
| Red | 0.832 | 0.982 | |||||
| NIR | 0.962 | 0.641 | |||||
| GS2 | Blue | 0.816 | 0.843 | 6.611 | 0.926 | 0.881 | 8.590 |
| Green | 0.818 | 0.924 | |||||
| Red | 0.818 | 0.932 | |||||
| NIR | 0.919 | 0.740 | |||||
| SFIM | Blue | 0.765 | 0.821 | 6.407 | 0.934 | 0.881 | 8.628 |
| Green | 0.827 | 0.902 | |||||
| Red | 0.890 | 0.836 | |||||
| NIR | 0.804 | 0.854 | |||||
| HPF | Blue | 0.844 | 0.874 | 5.429 | 0.908 | 0.856 | 8.289 |
| Green | 0.840 | 0.909 | |||||
| Red | 0.894 | 0.864 | |||||
| NIR | 0.918 | 0.743 |
| Method | Bands | UIQI | UIQIM | ERGAS | ZI | ZIM | S-ERGAS |
|---|---|---|---|---|---|---|---|
| BT | Blue | 0.781 | 0.842 | 7.488 | 0.954 | 0.952 | 5.056 |
| Green | 0.853 | 0.969 | |||||
| Red | 0.892 | 0.948 | |||||
| NIR | 0.842 | 0.935 | |||||
| BTF | Blue | 0.762 | 0.844 | 6.839 | 0.968 | 0.943 | 5.798 |
| Green | 0.848 | 0.981 | |||||
| Red | 0.896 | 0.953 | |||||
| NIR | 0.868 | 0.872 | |||||
| IHS | Blue | 0.810 | 0.846 | 7.731 | 0.954 | 0.940 | 6.319 |
| Green | 0.802 | 0.967 | |||||
| Red | 0.858 | 0.962 | |||||
| NIR | 0.913 | 0.878 | |||||
| IHSF | Blue | 0.817 | 0.860 | 6.650 | 0.975 | 0.938 | 6.100 |
| Green | 0.820 | 0.982 | |||||
| Red | 0.877 | 0.970 | |||||
| NIR | 0.926 | 0.827 | |||||
| GS1 | Blue | 0.856 | 0.843 | 7.960 | 0.953 | 0.954 | 6.242 |
| Green | 0.834 | 0.966 | |||||
| Red | 0.821 | 0.969 | |||||
| NIR | 0.859 | 0.927 | |||||
| GSF | Blue | 0.851 | 0.863 | 6.756 | 0.974 | 0.946 | 6.176 |
| Green | 0.844 | 0.981 | |||||
| Red | 0.842 | 0.979 | |||||
| NIR | 0.913 | 0.848 | |||||
| GS2 | Blue | 0.826 | 0.826 | 8.042 | 0.915 | 0.905 | 13.206 |
| Green | 0.821 | 0.914 | |||||
| Red | 0.801 | 0.930 | |||||
| NIR | 0.857 | 0.861 | |||||
| SFIM | Blue | 0.723 | 0.800 | 8.407 | 0.912 | 0.873 | 9.166 |
| Green | 0.806 | 0.877 | |||||
| Red | 0.856 | 0.853 | |||||
| NIR | 0.817 | 0.850 | |||||
| HPF | Blue | 0.832 | 0.868 | 6.648 | 0.913 | 0.865 | 8.075 |
| Green | 0.838 | 0.906 | |||||
| Red | 0.883 | 0.872 | |||||
| NIR | 0.921 | 0.771 |
| Rural | Semi-Urban | Urban | Natural | |
|---|---|---|---|---|
| BT | 2 | 5 | 4 | 2 |
| BTF | 1 | 3 | 3 | 1 |
| IHS | 9 | 6 | 7 | 9 |
| IHSF | 5 | 1 | 2 | 4 |
| GS1 | 7 | 7 | 5 | 6 |
| GSF | 8 | 2 | 1 | 8 |
| GS2 | 4 | 8 | 8 | 7 |
| SFIM | 6 | 9 | 9 | 3 |
| HPF | 3 | 4 | 6 | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alcaras, E.; Parente, C. The Effectiveness of Pan-Sharpening Algorithms on Different Land Cover Types in GeoEye-1 Satellite Images. J. Imaging 2023, 9, 93. https://doi.org/10.3390/jimaging9050093
Alcaras E, Parente C. The Effectiveness of Pan-Sharpening Algorithms on Different Land Cover Types in GeoEye-1 Satellite Images. Journal of Imaging. 2023; 9(5):93. https://doi.org/10.3390/jimaging9050093
Chicago/Turabian StyleAlcaras, Emanuele, and Claudio Parente. 2023. "The Effectiveness of Pan-Sharpening Algorithms on Different Land Cover Types in GeoEye-1 Satellite Images" Journal of Imaging 9, no. 5: 93. https://doi.org/10.3390/jimaging9050093
APA StyleAlcaras, E., & Parente, C. (2023). The Effectiveness of Pan-Sharpening Algorithms on Different Land Cover Types in GeoEye-1 Satellite Images. Journal of Imaging, 9(5), 93. https://doi.org/10.3390/jimaging9050093







