Fuzzy Model for the Automatic Recognition of Human Dendritic Cells
Abstract
1. Introduction
2. Material and Methods
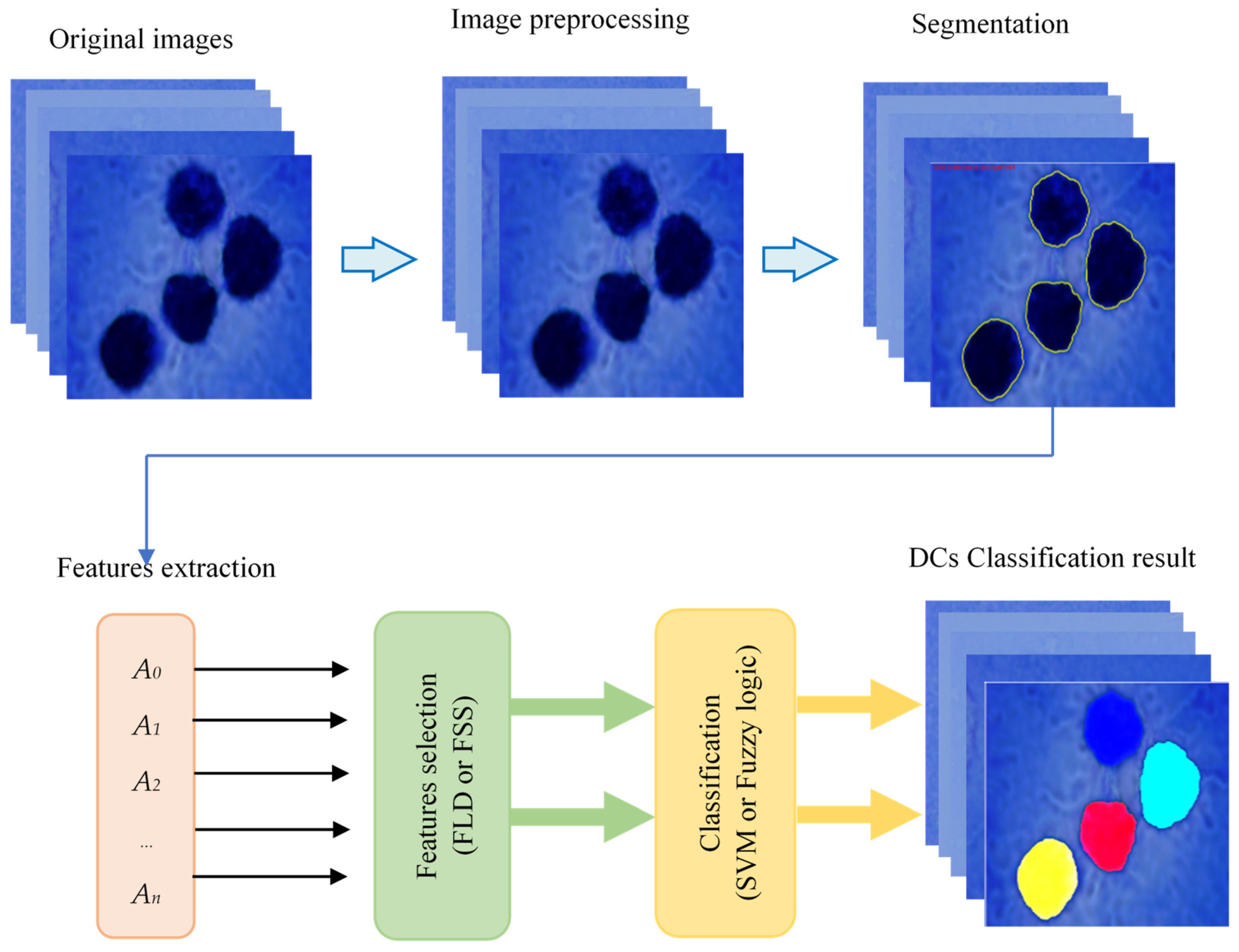
2.1. Description of the Proposed Method
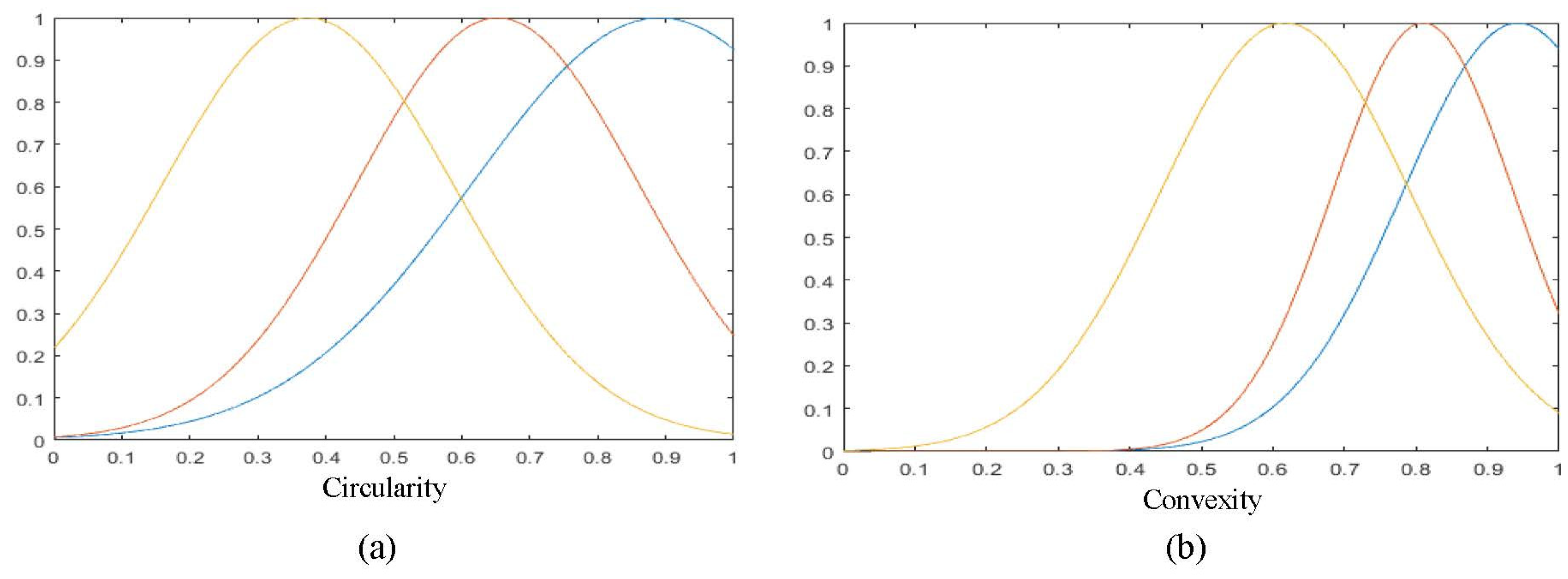
2.2. Shape Characterization
- -
- Class IM: immature DC.
- -
- Class MA: mature DC.
- -
- Class IN: inhibited DC.
2.3. Dimensionality Reduction
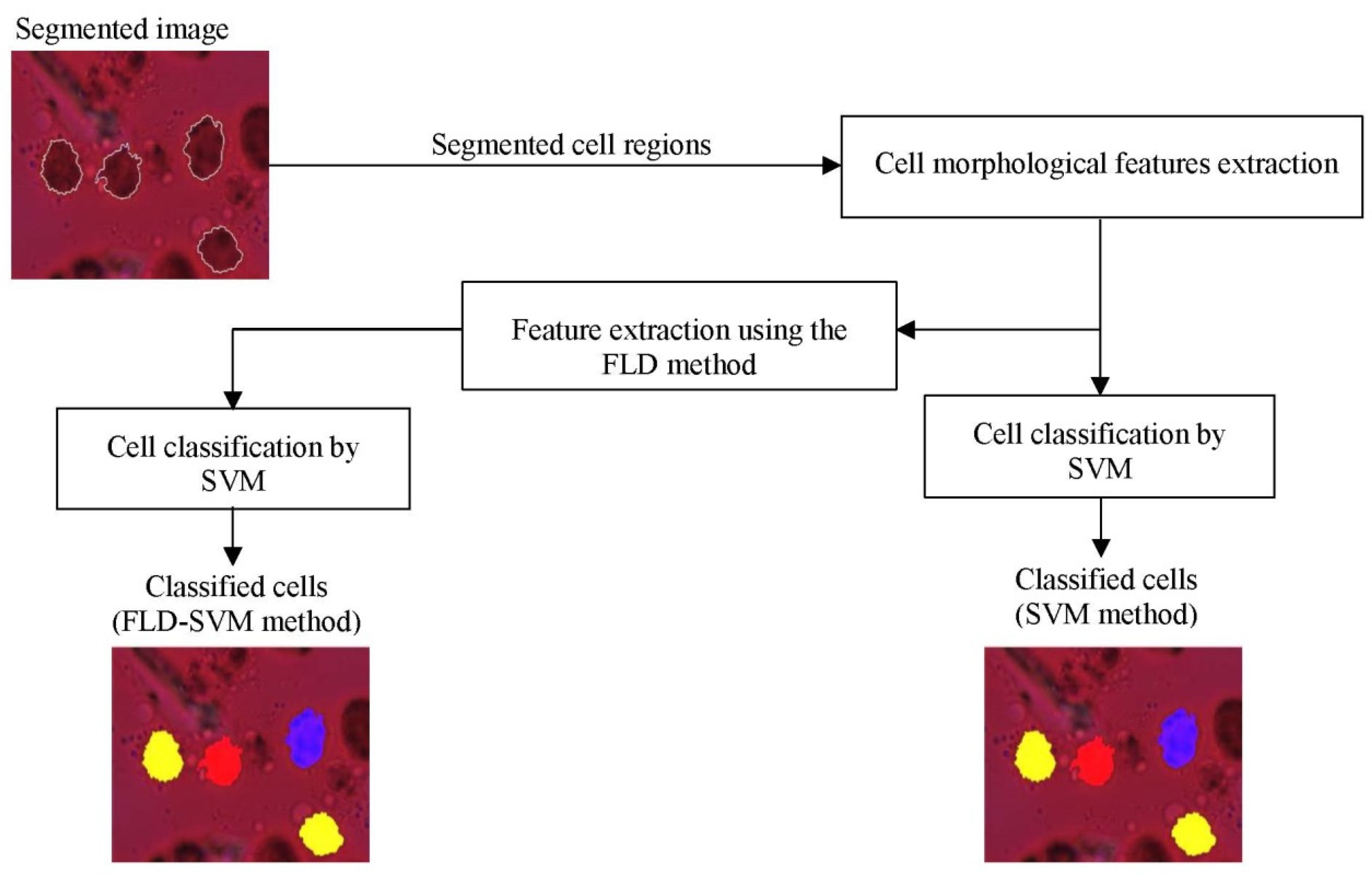
2.4. DC Classification Using SVM Classifier
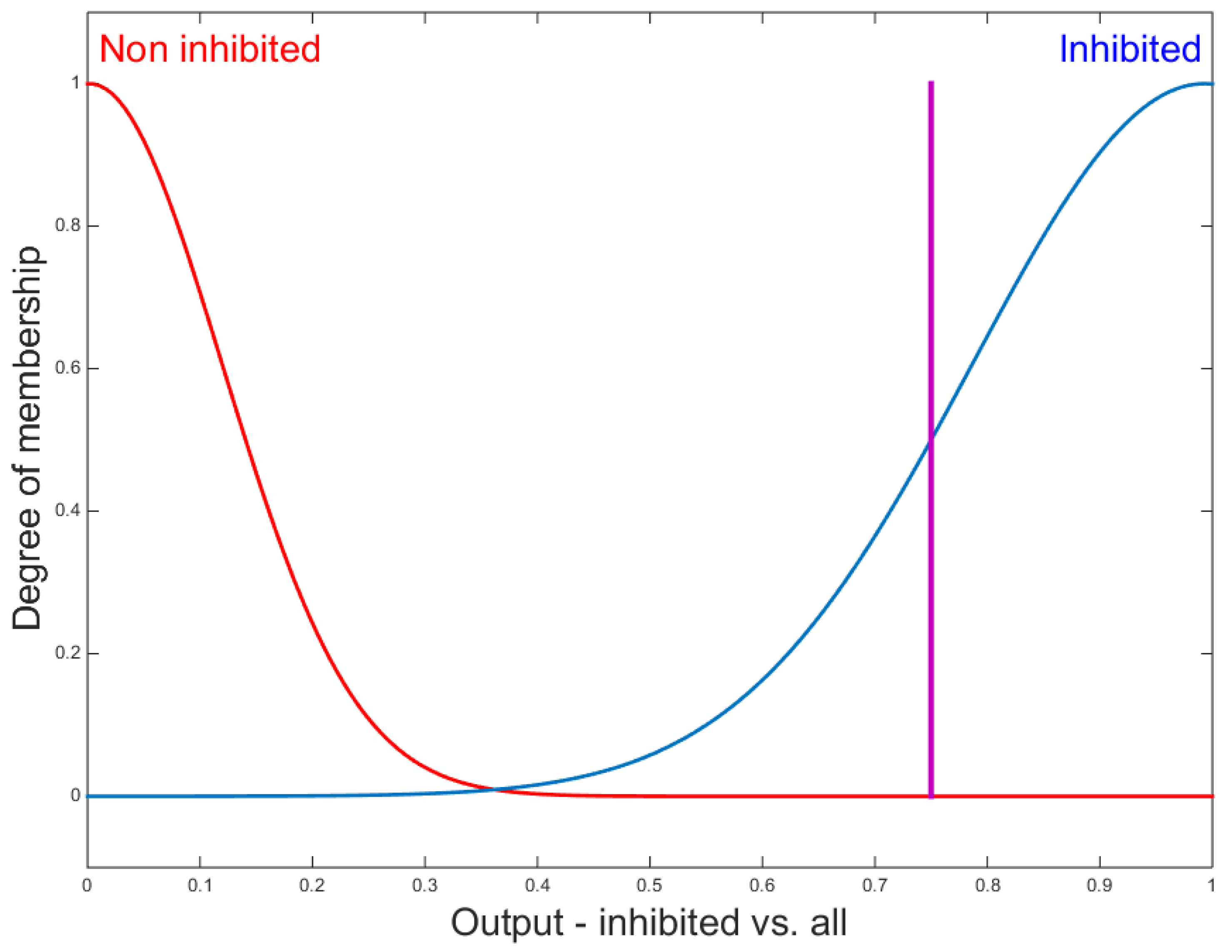
2.5. DC Classification Using Fuzzy Logic
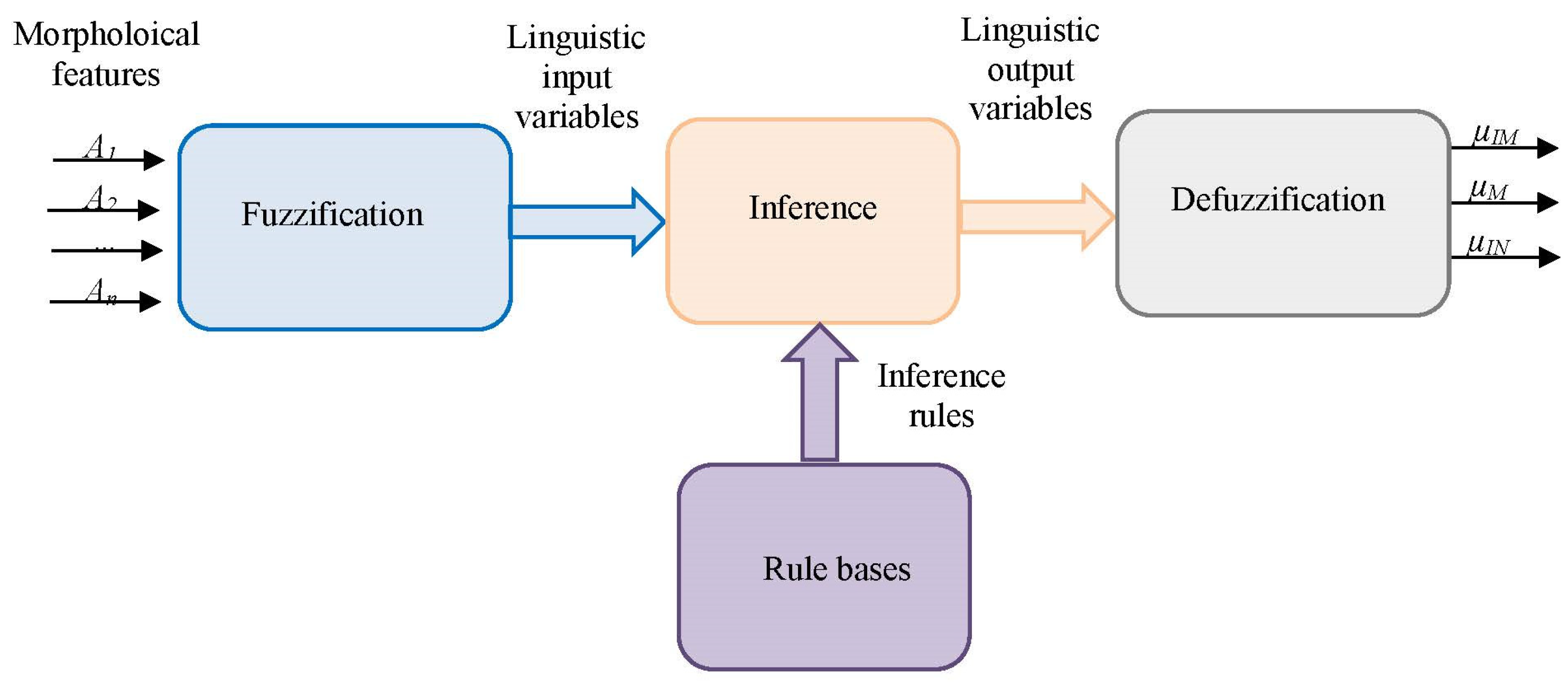
2.5.1. Fuzzy Inference System (FIS)
- ◾
- Fuzzification
- ◾
- Fuzzy inference
- (1)
- The Mamdani method (max min inference method)
- (2)
- The Takagi–Sugeno method (sum-prod inference method)
- ◾
- Defuzzification
- -
- Center of gravity method;
- -
- Maxima method;
- -
- Bisector method.
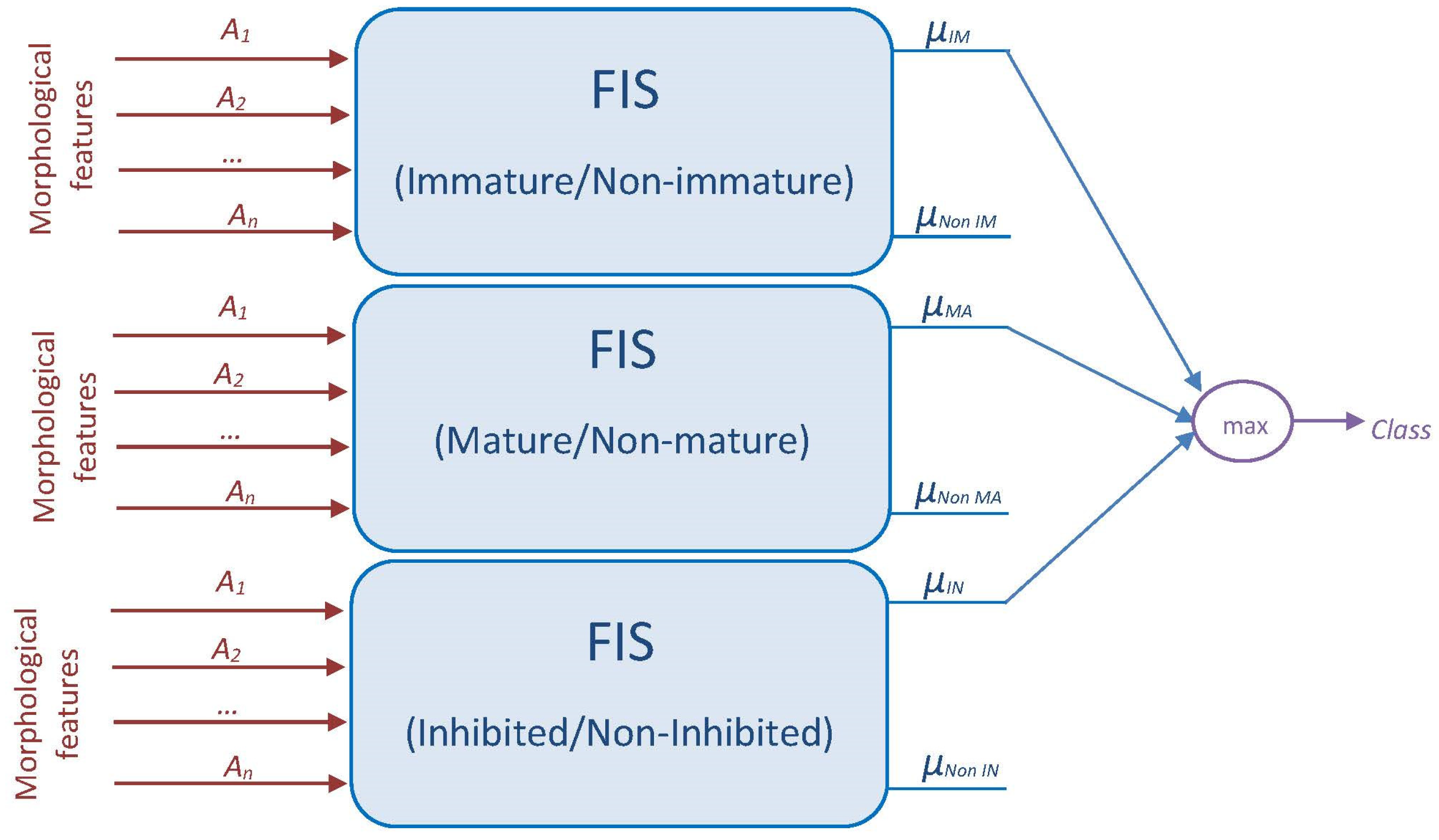
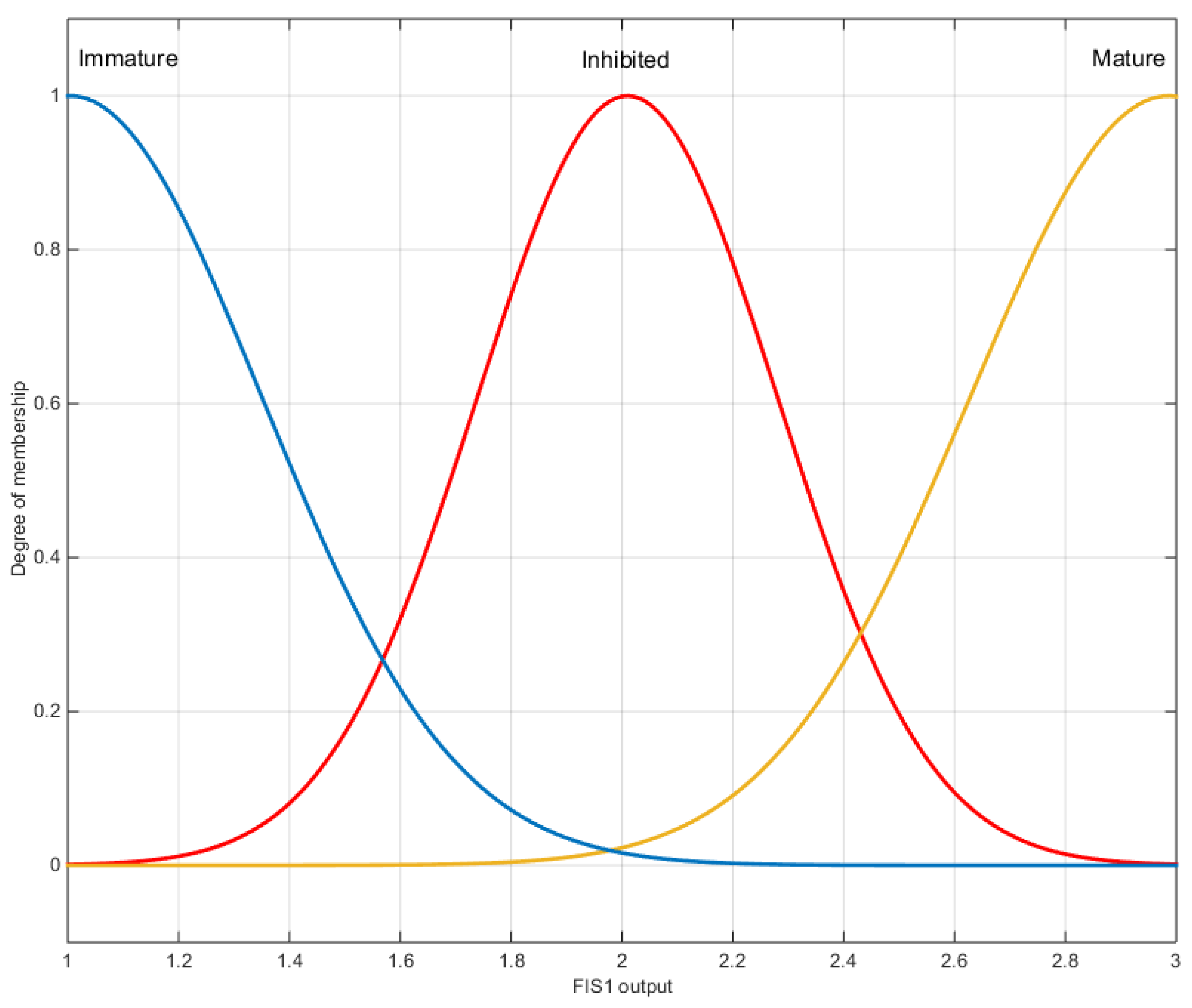
2.5.2. Proposed Fuzzy Systems
3. Results and Discussions
3.1. Classification Results Using SVM and FLD-SVM Classifiers
3.2. Classification Results Using Fuzzy Inference System (FIS)
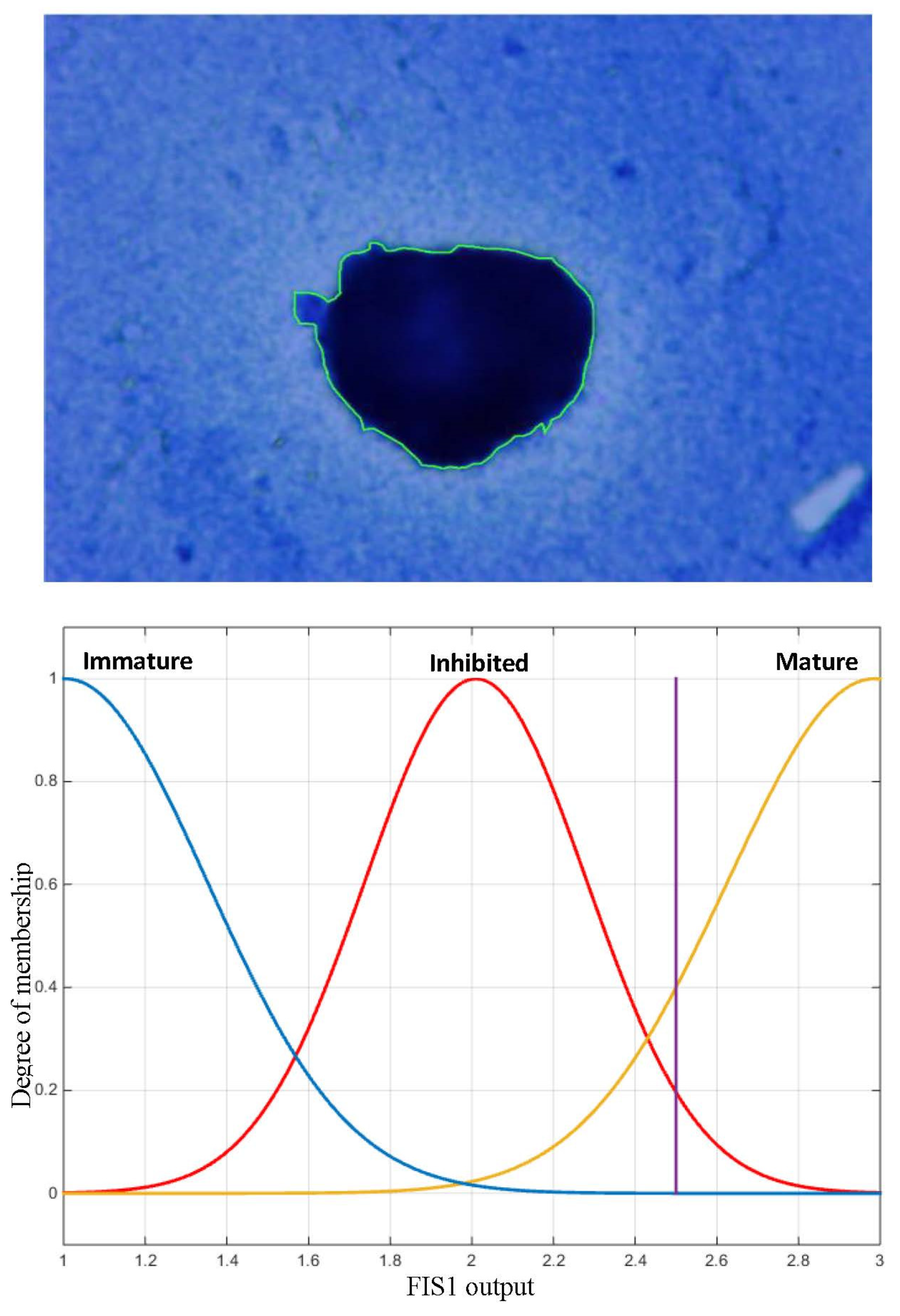
3.3. Interpretation Aiding Tools
4. Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Afssa (Agence Française de Sécurité Sanitaire des Aliments). Évaluation Des Risques Liés à la Présence De Mycotoxines Dans Les Chaînes Alimentaires Humaine Et Animale, Rapport Final; Afssa: Paris, France, 2009; 308p. [Google Scholar]
- Brochard, G.; Le Bacle, C. Mycotoxines en milieu de travail. Origine et propriétés toxiques des principales mycotoxines. INRS Doc. Pour Le Médecin Du Trav. 2009, 119, 299–323. [Google Scholar]
- Milićević, D.R.; Škrinjar, M.; Baltić, T. Real and Perceived Risks for Mycotoxin Contamination in Foods and Feeds: Challenges for Food Safety Control. Toxins 2010, 2, 572–592. [Google Scholar] [CrossRef]
- Marin, S.; Ramos, A.J.; Cano-Sancho, G.; Sanchis, V. Mycotoxins: Occurrence, Toxicology, and Exposure Assessment. Food Chem. Toxicol. 2013, 60, 218–237. [Google Scholar] [CrossRef] [PubMed]
- Galtier, P.; Loiseau, N.; Oswald, I.P.; Puel, O. Toxicologie des mycotoxines: Dangers et risques en alimentation humaine et animale. Bull. Acad. Vét. Fr. 2006, 159, 5–13. [Google Scholar] [CrossRef]
- Reboux, G. Mycotoxines: Effets sur la Santé et Interactions avec d’Autres Composants Organiques. Rev. Française Allergol. Immunol. Clin. 2006, 46, 208–212. [Google Scholar] [CrossRef]
- Hussein, H.S.; Brasel, J.M. Toxicity, Metabolism, and Impact of Mycotoxins on Humans and Animals. Toxicology 2001, 167, 101–134. [Google Scholar] [CrossRef]
- Tozlovanu, M. Evaluation Du Risque De Contamination Alimentaire En Mycotoxines Néphrotoxiques Et Cancérogènes (Notamment L’ochratoxine a): Validation De Biomarqueurs d’Exposition Et d’Effet. Ph.D. Thesis, Institut National Polytechnique de Toulouse (INPT), Toulouse, France, 2008. [Google Scholar]
- Zain, M.E. Impact of Mycotoxins on Humans and Animals. J. Saudi Chem. Soc. 2011, 15, 129–144. [Google Scholar] [CrossRef]
- Wu, F.; Groopman, J.D.; Pestka, J.J. Public Health Impacts of Foodborne Mycotoxins. Annu. Rev. Food Sci. Technol. 2014, 5, 351–372. [Google Scholar] [CrossRef]
- Gauthier, A. Les Mycotoxines Dans L’alimentation Et Leur Incidence Sur La Santé. Ph.D. Thesis, UFR Des Sciences Pharmaceutiques, Université de Bordeaux, Bordeaux, France, 2016. [Google Scholar]
- Hymery, N. Evaluation In Vitro Des Effets Toxiques De Contaminants Alimentaires Sur Les Cellules Dendritiques. Doctoral Thesis, Université de Bretagne Occidentale, Brest, France, 2006. [Google Scholar]
- Ficheux, A.S.; Sibiril, Y.; Parent-Massin, D. Effects of Beauvericin, Enniatin B and Moniliformin on Human Dendritic Cells and Macrophages: An in Vitro Study. Toxicon 2013, 71, 1–10. [Google Scholar] [CrossRef]
- EFSA (European Food Safety Authority) Panel on Contaminants in the Food Chain (CONTAM). Scientific opinion on the risks for animal and public health related to the presence of T-2 and HT-2 toxin in food and feed. EFSA J. 2011, 9, 2481. [Google Scholar] [CrossRef]
- EFSA (European Food Safety Authority) Panel on Contaminants in the Food Chain (CONTAM). Scientific opinion on the risks for public health related to the presence of zearalenone in food. EFSA J. 2011, 9, 2197. [Google Scholar] [CrossRef]
- EFSA (European Food Safety Authority) Panel on Contaminants in the Food Chain (CONTAM). Scientific Opinion on Risks for Animal and Public Health Related to the Presence of Nivalenol in Food and Feed. EFSA J. 2013, 11, 3262. [Google Scholar] [CrossRef]
- Girolomoni, G.; Zambruno, G.; Kanitakis, J. Cellules immunocompétentes. EMC Dermatol. Cosmetol. 2005, 2, 217–231. [Google Scholar] [CrossRef]
- Hymery, N.; Sibiril, Y.; Parent-Massin, D. Improvement of Human Dendritic Cell Culture for Immunotoxicological Investigations. Cell Biol. Toxicol. 2006, 22, 243–255. [Google Scholar] [CrossRef] [PubMed]
- Hymery, N.; Leon, K.; Carpentier, F.G.; Jung, J.L.; Parent-Massin, D. T-2 Toxin Inhibits the Differentiation of Human Monocytes into Dendritic Cells and Macrophages. Toxicol. Vitr. 2009, 23, 509–519. [Google Scholar] [CrossRef]
- Hymery, N.; Sibiril, Y.; Parent-Massin, D. In Vitro Effects of Trichothecenes on Human Dendritic Cells. Toxicol. Vitr. 2006, 20, 899–909. [Google Scholar] [CrossRef]
- Stockmann-Juvala, H.; Alenius, H.; Savolainen, K. Effects of Fumonisin B1 on the Expression of Cytokines and Chemokines in Human Dendritic Cells. Food Chem. Toxicol. 2008, 46, 1444–1451. [Google Scholar] [CrossRef]
- Ficheux, A.S. Évaluation de la Toxicité De Mycotoxines Émergentes Et De Couples De Mycotoxines Sur Les Cellules Humaines d’Origine Hématopoïétique. Ph.D. Thesis, Université de Bretagne Occidentale, Brest, France, 2012. [Google Scholar]
- Yang, Z.; Pan, Y.; Chen, T.; Li, L.; Zou, W.; Liu, D.; Xue, D.; Wang, X.; Lin, G. Cytotoxicity and Immune Dysfunction of Dendritic Cells Caused by Graphene Oxide. Front. Pharmacol. 2020, 11, 1206. [Google Scholar] [CrossRef]
- Yao, X.; Sun, K.; Bu, X.; Zhao, C.; Jin, Y. Classification of White Blood Cells Using Weighted Optimized Deformable Convolutional Neural Networks. Artif. Cells Nanomed. Biotechnol. 2021, 49, 147–155. [Google Scholar] [CrossRef]
- Patil, A.M.; Patil, M.D.; Birajdar, G.K. White Blood Cells Image Classification Using Deep Learning with Canonical Correlation Analysis. IRBM 2021, 42, 378–389. [Google Scholar] [CrossRef]
- Selvaraj, S.; Kanakaraj, B. Naive Bayesian Classifier for Acute Lymphocytic Leukemia Detection. J. Eng. Appl. Sci. 2015, 10, 6888–6892. [Google Scholar]
- Sabino, D.M.U.; da Fontoura Costa, L.; Rizzatti, E.G.; Zago, M.A. A Texture Approach to Leukocyte Recognition. Real-Time Imaging 2004, 10, 205–216. [Google Scholar] [CrossRef]
- Theera-Umpon, N.; Dhompongsa, S. Morphological Granulometric Features of Nucleus in Automatic Bone Marrow White Blood Cell Classification. IEEE Trans. Inform. Technol. Biomed. 2007, 11, 353–359. [Google Scholar] [CrossRef]
- Ghosh, M.; Das, D.; Mandal, S.; Chakraborty, C.; Pala, M.; Maity, A.K.; Surjya, K.P.; Ray, A.K. Statistical Pattern Analysis of White Blood Cell Nuclei Morphometry. In Proceedings of the 2010 IEEE Students Technology Symposium (TechSym), Kharagpur, India, 3–4 April 2010; pp. 59–66. [Google Scholar]
- Mohapatra, S.; Patra, D.; Satpathy, S.; Jena, R.K.; Sethy, S. Automated Morphometric Classification of Acute Lymphoblastic Leukaemia in Blood Microscopic Images Using an Ensemble of Classifiers. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2014, 4, 3–16. [Google Scholar] [CrossRef]
- Prinyakupt, J.; Pluempitiwiriyawej, C. Segmentation of White Blood Cells and Comparison of Cell Morphology by Linear and Naive Bayes Classifiers. Biomed. Eng. Online 2015, 14, 63. [Google Scholar] [CrossRef]
- Kumar, S.; Mishra, S.; Asthana, P. Automated Detection of Acute Leukemia Using K-Mean Clustering Algorithm. In Advances in Computer and Computational Sciences; Springer: Singapore, 2018; pp. 655–670. [Google Scholar]
- Fix, E.; Hodges Jr, J.L. Discriminatory Analysis-Nonparametric Discrimination: Consistency Properties. Int. Stat. Rev. Rev. Int. De Stat. 1951, 57, 238–247. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Tek, F.B.; Dempster, A.; Kale, I. Malaria Parasite Detection in Peripheral Blood Images. In Proceedings of the British Machine Vision Conference 2006 (BMVA), Edinburgh, UK, 4–7 September 2006. [Google Scholar]
- Madhloom, H.T.; Kareem, S.A.; Ariffin, H. A Robust Feature Extraction and Selection Method for the Recognition of Lymphocytes Versus Acute Lymphoblastic Leukemia. In Proceedings of the 2012 International Conference on Advanced Computer Science Applications and Technologies (ACSAT), Kuala Lumpur, Malaysia, 26–28 November 2012; pp. 330–335. [Google Scholar]
- Joshi, M.M.D.; Karode, P.A.H.; Suralkar, P.S.R. White Blood Cells Segmentation and Classification to Detect Acute Leukemia. Int. J. Emerging Trends Technol. Comput. Sci. 2013, 2, 147–151. [Google Scholar]
- Chatap, N.; Shibu, S. Analysis of blood samples for counting leukemia cells using support vector machine and nearest neighbor. J. Comput. Eng. (IOSR-JCE) 2014, 16, 79–87. [Google Scholar] [CrossRef]
- Bhattacharjee, R.; Saini, L.M. Detection of acute lymphoblastic leukemia using watershed transformation technique. In Proceedings of the IEEE International Conference on Signal Processing, Computing and Control (ISPCC), Solan, India, 24–26 September 2015; pp. 383–386. [Google Scholar]
- Purwanti, E.; Calista, E. Detection of Acute Lymphocyte Leukemia Using k-Nearest Neighbor Algorithm Based on Shape and Histogram Features. J. Phys. Conf. Ser. 2017, 853, 012011. [Google Scholar] [CrossRef]
- Rawat, J.; Singh, A.; Bhadauria, H.S.; Virmani, J.; Devgun, J.S. Classification of Acute Lymphoblastic Leukaemia Using Hybrid Hierarchical Classifiers. Multimed. Tools Appl. 2017, 76, 19057–19085. [Google Scholar] [CrossRef]
- Gumble, P.M.; Rode, S.V. Analysis and Classification of Acute Lymphoblastic Leukemia Using KNN Algorithm. Int. J. Recent Innov. Trends Comput. Commun. 2017, 5, 94–98. [Google Scholar]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A training algorithm for optimal margin classifiers. In Proceedings of the 5th Annual Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Vapnik, V. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Hsu, C.W.; Lin, C.J. A Comparison of Methods for Multiclass Support Vector Machines. IEEE Trans. Neural Netw. 2002, 13, 415–425. [Google Scholar] [PubMed]
- Osowski, S.; Markiewicz, T.; Marianska, B.; Moszczynski, L. Feature Generation for the Cell Image Recognition of Myelogenous Leukemia. In Proceedings of the 2004 12th European Signal Processing Conference (EUSIPCO), Vienna, Austria, 6–10 September 2004; pp. 753–756. [Google Scholar]
- Markiewicz, T.; Osowski, S.; Marianska, B.; Moszczynski, L. Automatic Recognition of the Blood Cells of Myelogenous Leukemia Using SVM. In Proceedings of the 2005 IEEE International Joint Conference on Neural Networks (IJCNN), Montreal, QC, Canada, 31 July–4 August 2005. [Google Scholar]
- Ramoser, H.; Laurain, V.; Bischof, H.; Ecker, R. Leukocyte Segmentation and Classification in Blood-Smear Images. In Proceedings of the 2005 IEEE Annual International Conference of the Engineering in Medicine and Biology Society (EMBS), Shanghai, China, 17–18 January 2005; 4; pp. 3371–3374. [Google Scholar]
- Siroic, R.; Markiewicz, T.; Siwek, K. Support Vector Machine and Genetic Algorithm for Efficient Blood Cell Recognition. In Proceedings of the 2007 IEEE International Instrumentation and Measurement Technology Conference (IMTC), Warsaw, Poland, 1–3 May 2007; pp. 1–6. [Google Scholar]
- Tuzel, O.; Yang, L.; Meer, P.; Foran, D.J. Classification of Hematologic Malignancies Using Texton Signatures. Pattern Anal. Appl. 2007, 10, 277–290. [Google Scholar] [CrossRef]
- Mohapatra, S.; Patra, D.; Satpathy, S. An Ensemble Classifier System for Early Diagnosis of Acute Lymphoblastic Leukemia in Blood Microscopic Images. Neural Comput. Appl. 2014, 24, 1887–1904. [Google Scholar] [CrossRef]
- Rezatofighi, S.H.; Soltanian-Zadeh, H. Automatic Recognition of Five Types of White Blood Cells in Peripheral Blood. Comput. Med. Imag. Graph. 2011, 35, 333–343. [Google Scholar] [CrossRef] [PubMed]
- Putzu, L.; Caocci, G.; Di Ruberto, C. Leucocyte Classification for Leukaemia Detection Using Image Processing Techniques. Artif. Intell. Med. 2014, 62, 179–191. [Google Scholar] [CrossRef]
- Putzu, L.; Ruberto, C.D. White Blood Cells Identification and Counting from Microscopic Blood Images. Int. J. Med. Health Biomed. Bioeng. Pharm. Eng. 2013, 7, 15–22. [Google Scholar]
- Basheer, I.A.; Hajmeer, M. Artificial neural networks: Fundamentals, computing, design, and application. J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Long, X.; Cleveland, W.L.; Yao, Y.L. A New Preprocessing Approach for Cell Recognition. IEEE Trans. Inform. Technol. Biomed. 2005, 9, 407–412. [Google Scholar] [CrossRef]
- Mouelhi, A.; Sayadi, M.; Fnaiech, F.; Mrad, K.; Romdhane, K.B. A New Automatic Image Analysis Method for Assessing Estrogen Receptors’ Status in Breast Tissue Specimens. Comput. Biol. Med. 2013, 43, 2263–2277. [Google Scholar] [CrossRef]
- Shanthi, P.; Priya, R.; Priyanka, B. Analysis of Blood Samples Using ANFIS Classification. Int. Res. J. Eng. Technol. 2017, 4, 1460–1461. [Google Scholar]
- Hosseini, M.S.; Zekri, M. Review of Medical Image Classification Using the Adaptive Neuro-Fuzzy Inference System. J. Med. Signals Sens. 2012, 2, 49–60. [Google Scholar] [CrossRef] [PubMed]
- Braiki, M.; Benzinou, A.; Nasreddine, K.; Hymery, N. Automatic human dendritic cells segmentation using k-means clustering and Chan-Vese active contour model. Comput. Methods Programs Biomed. 2020, 195, 105520. [Google Scholar] [CrossRef] [PubMed]
- Díaz, G.; Manzanera, A. Automatic analysis of microscopic images in hematological cytology applications. In Clinical Technologies: Concepts, Methodologies, Tools and Applications; Information Resources Management Association: Wayne, PA, USA, 2011; pp. 325–352. [Google Scholar]
- Saraswat, M.; Arya, K.V. Automated Microscopic Image Analysis for Leukocytes Identification: A Survey. Micron 2014, 65, 20–33. [Google Scholar] [CrossRef]
- Shafique, S.; Tehsin, S. Computer-Aided Diagnosis of Acute Lymphoblastic Leukaemia. Comput. Math. Methods Med. 2018, 2018, 6125289. [Google Scholar] [CrossRef]
- Molina, L.C.; Belanche, L.; Nebot, À. Feature Selection Algorithms: A Survey and Experimental Evaluation. In Proceedings of the 2002 IEEE International Conference on Data Mining, Maebashi, Japan, 9–12 December 2002; pp. 306–313. [Google Scholar]
- Amin, M.M.; Kermani, S.; Talebi, A.; Oghli, M.G. Recognition of acute lymphoblastic leukemia cells in microscopic images using k-means clustering and support vector machine classifier. J. Med. Signals Sens. 2015, 5, 49. [Google Scholar]
- Amin, M.M.; Memari, A.; Samadzadehaghdam, N.; Kermani, S.; Talebi, A. Computer aided detection and classification of acute lymphoblastic leukemia cell subtypes based on microscopic image analysis. Microsc. Res. Techniq. 2016, 79, 908–916. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Beloufa, F. Conception D’un Classifeur A Base Des Règles Floues. Ph.D. Thesis, University Aboubekr Belkaid, Tlemcen, Algeria, 2016. [Google Scholar]
- Mamdani, E.H.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man-Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Sugeno, M. An introductory survey of fuzzy control. Inf. Sci. 1985, 36, 59–83. [Google Scholar] [CrossRef]
- Boujelbene, S.Z.; Mezghani, D.B.A.; Ellouze, N. Systèmes à inférences floues pour la classification phonémique. In Proceedings of the 4th International Conference: Sciences of Electronic, Technologies of Information and Telecommunications (SETIT), Sfax, Tunisia, 25–29 March 2007; pp. 1–7. [Google Scholar]
- Wong, T.T. Performance evaluation of classification algorithms by k-fold and leave-one-out cross validation. Pattern Recognit. 2015, 48, 2839–2846. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Possibility theory, probability theory and multiple-valued logics: A clarification. Ann. Math. Artif. Intell. 2001, 32, 35–66. [Google Scholar] [CrossRef]
- Saffari, A.; Zahiri, S.H.; Khishe, M.; Mosavi, S.M. Design of a Fuzzy Model of Control Parameters of CHIMP Algorithm Optimization for Automatic Sonar Targets Recognition. Iran. J. Mar. Technol. 2022, 9, 1–13. [Google Scholar]
- Saffari, A.; Zahiri, S.H.; Khishe, M. Fuzzy Grasshopper Optimization Algorithm: A Hybrid Technique for Tuning the Control Parameters of GOA Using Fuzzy System for Big Data Sonar Classification. Iran. J. Electr. Electron. Eng. 2022, 18, 2131. [Google Scholar]



| Classifier | Advantages | Limitations |
|---|---|---|
| NB classifier [26,27,28,29,30,31,32] | - Fast and efficient - Simple and easy to implement - Uncorrelated features can be reliably recognized. | - Presumes that all features are independent, which is rarely the case |
| SVM [30,39,41,46,47,48,49,50,51,52,53,54] | - High accuracy for cells classification - Effective for non-linearly separable datasets | - It remains difficult to identify the appropriate kernel function - The hyperplane choices and kernel parameters influence accuracy and performance - Large datasets require a long training time |
| k-NNs classifier [35,36,37,38,39,40,41,42] | - Simple and easy to implement - Recognizes cells with high accuracy | - It is difficult to determine the optimal value of k - Sensitive to irrelevant features |
| MLPs [28,30,39,52,57,58] | - Performs highly accurate recognition of cells - Used to resolve difficult nonlinear issues | - It is a matter to determine the number of neurons and layers. - Requires extensive computational time |
| ANFIS [59,60] | - Powerful classifier that combines advantages of ANN and fuzzy logic - Requires fewer adjustable parameters | - It is challenging to identify appropriate membership functions - Require high computational complexity |
| No. | Feature | Symbol/Formula |
|---|---|---|
| 1 | Area | |
| 2 | Perimeter | |
| 3 | Circularity | |
| 4 | Convexity | |
| 5 | Eccentricity | |
| 6 | Elongation |
| Attribute | Cell 1 | Cell 2 | Cell 3 |
|---|---|---|---|
| Area | 58,888 | 99,755 | 38,897 |
| Perimeter | 870.4980 | 1556.5 | 732.0330 |
| Circularity | 0.9766 | 0.5174 | 0.9121 |
| Convexity | 0.9924 | 0.8797 | 0.9757 |
| Eccentricity | 0.3875 | 0.4294 | 0.5271 |
| Elongation | 1.0847 | 1.1073 | 1.1768 |
| Class | Immature | Mature | Inhibited |
| Classifier | Immature DCs | Mature DCs | Inhibited DCs |
|---|---|---|---|
| SVM | 78.6% | 86% | 62.4% |
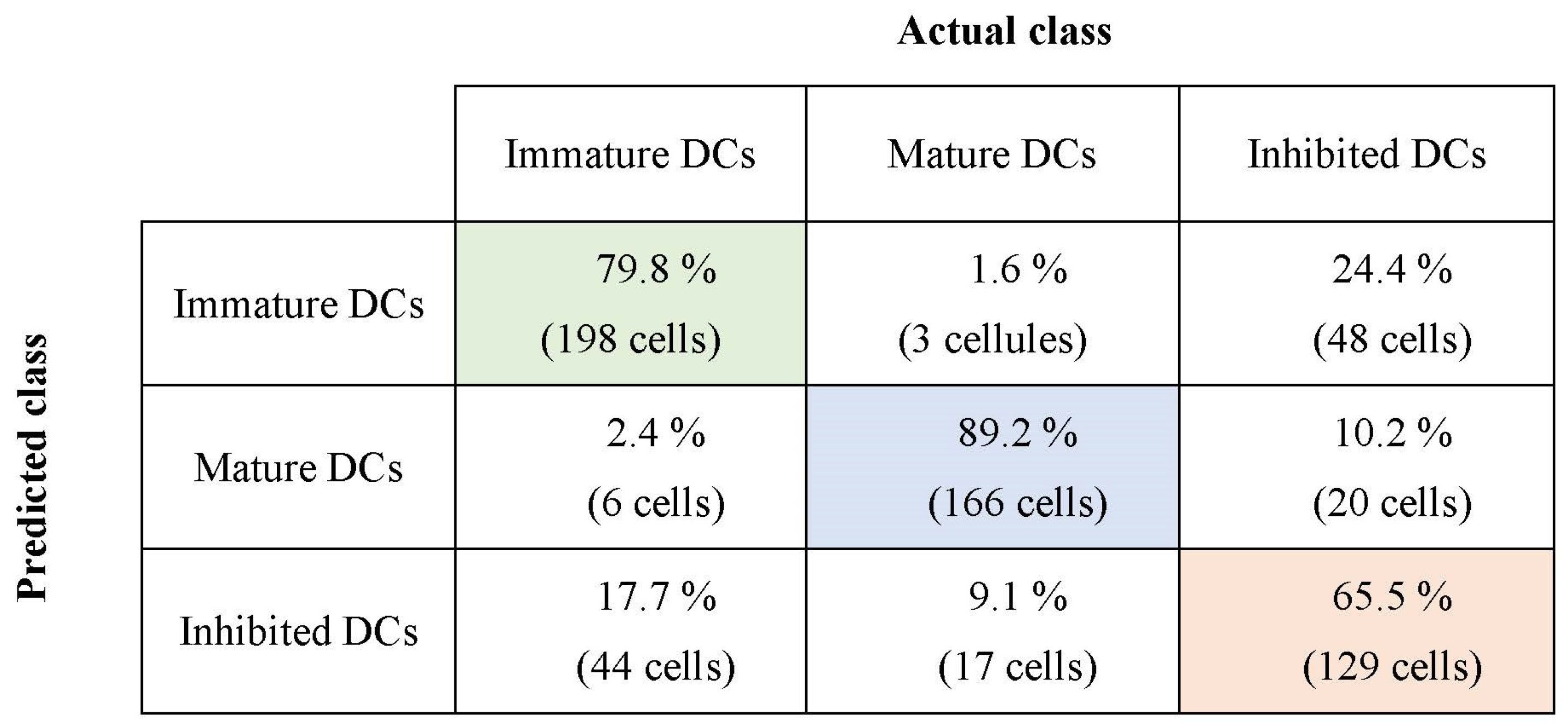
| FLD-SVM | 79.8% | 89.2% | 65.5% |
| Immature DCs | Mature DCs | Inhibited DCs | |
|---|---|---|---|
| FIS1 (all features at the input) | 91.1% | 67.1% | 27.9% |
| FIS1 + FLD | 83.3% | 76.3% | 25.6% |
| FIS1 + FSS | 86.7% | 68.4% | 40.7% |
| Immature DCs | Mature DCs | Inhibited DCs | |
|---|---|---|---|
| FIS2 (all features at the input) | 96.7% | 73.7% | 75.6% |
| FIS2 + FLD | 91.1% | 71.1% | 74.4% |
| FIS2 + FSS | 100% | 96.1% | 94.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Braiki, M.; Nasreddine, K.; Benzinou, A.; Hymery, N. Fuzzy Model for the Automatic Recognition of Human Dendritic Cells. J. Imaging 2023, 9, 13. https://doi.org/10.3390/jimaging9010013
Braiki M, Nasreddine K, Benzinou A, Hymery N. Fuzzy Model for the Automatic Recognition of Human Dendritic Cells. Journal of Imaging. 2023; 9(1):13. https://doi.org/10.3390/jimaging9010013
Chicago/Turabian StyleBraiki, Marwa, Kamal Nasreddine, Abdesslam Benzinou, and Nolwenn Hymery. 2023. "Fuzzy Model for the Automatic Recognition of Human Dendritic Cells" Journal of Imaging 9, no. 1: 13. https://doi.org/10.3390/jimaging9010013
APA StyleBraiki, M., Nasreddine, K., Benzinou, A., & Hymery, N. (2023). Fuzzy Model for the Automatic Recognition of Human Dendritic Cells. Journal of Imaging, 9(1), 13. https://doi.org/10.3390/jimaging9010013











