Nonlinear Reconstruction of Images from Patterns Generated by Deterministic or Random Optical Masks—Concepts and Review of Research
Abstract
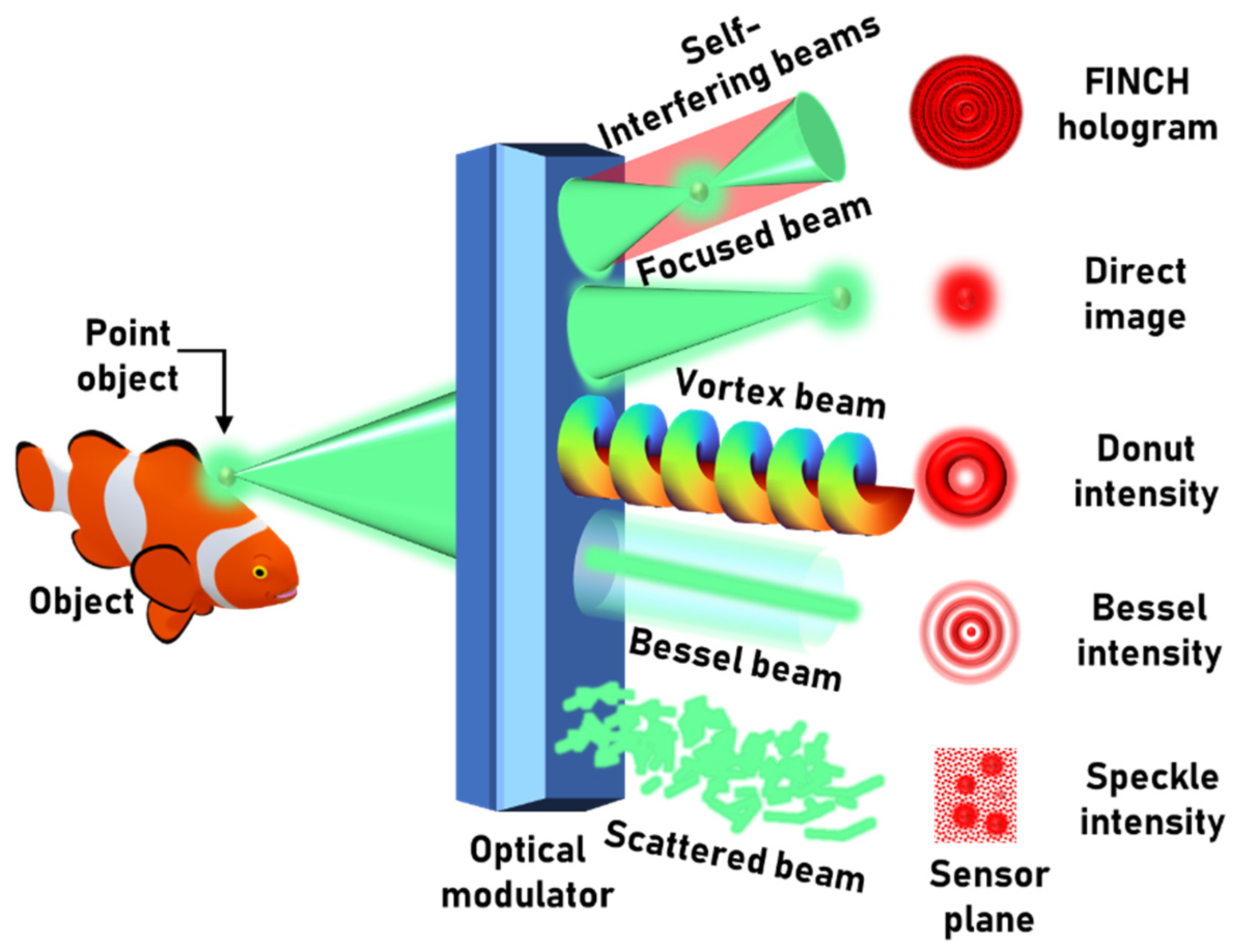
1. Introduction
2. Methodology
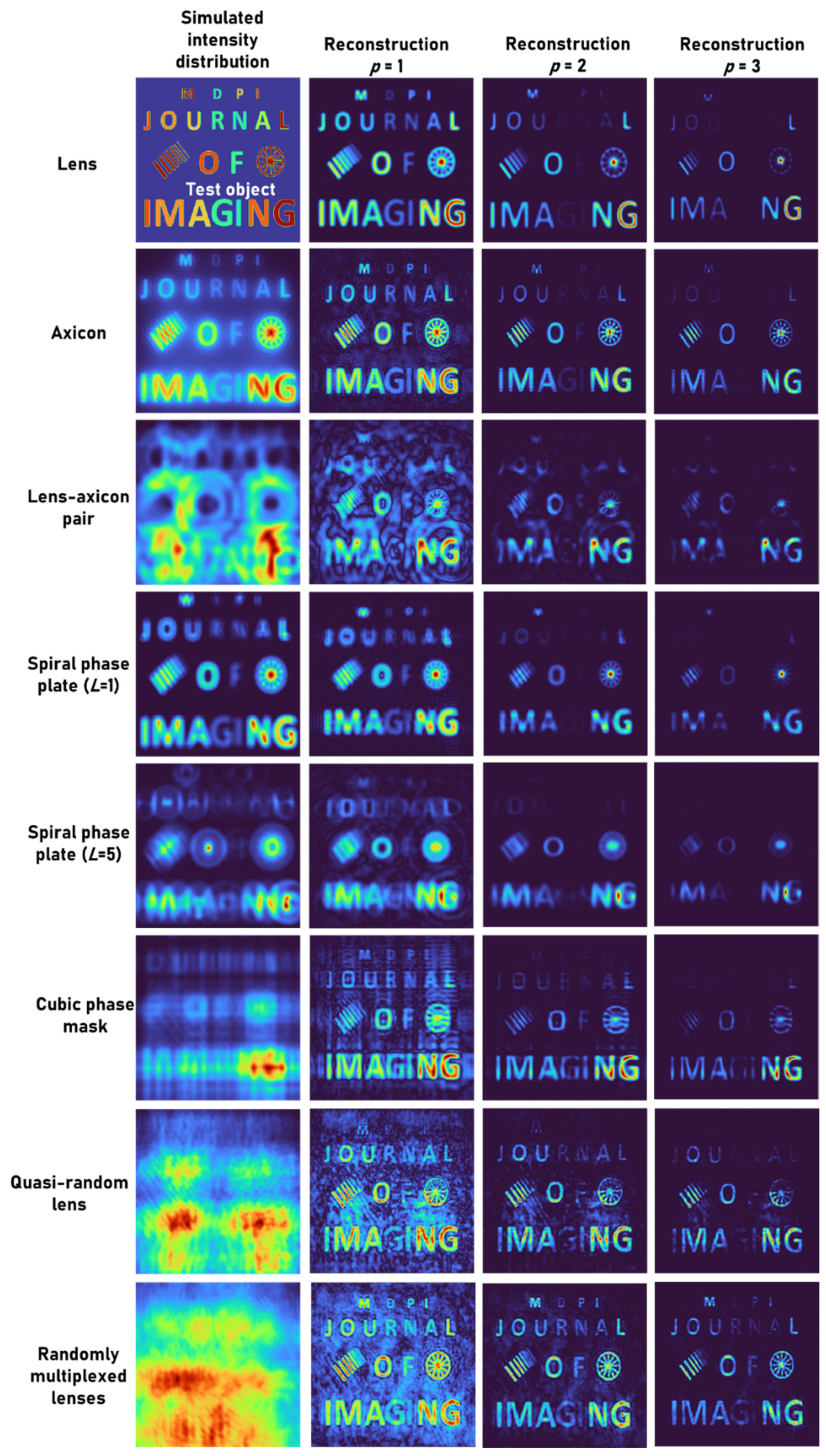
3. Simulation Results
4. Experimental Results
4.1. Lensless I-COACH
4.2. Random Array of Pinholes
4.3. QRL Fabricated Using Electron-Beam Lithography
4.4. QRL Fabricated by Grinding Lens
4.5. Photon-Sieve Axicon
4.6. Diffractive Lens
4.7. Spiral Fresnel Lens
4.8. Lens–Axicon Pair
4.9. FINCH with Polarization Multiplexing
4.10. FINCH with Spatial Random Multiplexing
4.11. Double-Helix Beam with Rotating PSF
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bryngdahl, O. Geometrical transformations in optics. J. Opt. Soc. Am. 1974, 64, 1092–1099. [Google Scholar] [CrossRef]
- Rosen, J.; Vijayakumar, A.; Kumar, M.; Rai, M.R.; Kelner, R.; Kashter, Y.; Bulbul, A.; Mukherjee, S. Recent advances in self-interference incoherent digital holography. Adv. Opt. Photon. 2019, 11, 1–66. [Google Scholar] [CrossRef]
- Liu, J.P.; Tahara, T.; Hayasaki, Y.; Poon, T.-C. Incoherent digital holography: A review. Appl. Sci. 2018, 8, 143. [Google Scholar] [CrossRef]
- Poon, T.-C. Optical scanning holography-a review of recent progress. J. Opt. Soc. Korea. 2009, 13, 406–415. [Google Scholar] [CrossRef][Green Version]
- Rosen, J.; Alford, S.; Anand, V.; Art, J.; Bouchal, P.; Bouchal, Z.; Erdenebat, M.U.; Huang, L.; Ishii, A.; Juodkazis, S.; et al. Roadmap on recent progress in FINCH technology. J. Imaging. 2021, 7, 197. [Google Scholar] [CrossRef]
- Rosen, J.; de Aguiar, H.B.; Anand, V.; Baek, Y.; Gigan, S.; Horisaki, R.; Hugonnet, H.; Juodkazis, S.; Lee, K.; Liang, H.; et al. Roadmap on chaos-inspired imaging technologies (CI2-Tech). Appl. Phys. B 2022, 128, 1–26. [Google Scholar] [CrossRef]
- Rosen, J.; Brooker, G. Digital spatially incoherent Fresnel holography. Opt. Lett. 2007, 32, 912–914. [Google Scholar] [CrossRef]
- Rosen, J.; Siegel, N.; Brooker, G. Theoretical and experimental demonstration of resolution beyond the Rayleigh limit by FINCH fluorescence microscopic imaging. Opt. Express 2011, 19, 26249–26268. [Google Scholar] [CrossRef]
- Bu, Y.; Wang, X.; Li, Y.; Du, Y.; Gong, Q.; Zheng, G.; Ma, F. Tunable edge enhancement by higher-order spiral Fresnel incoherent correlation holography system. J. Phys. D Appl. Phys. 2021, 54, 125103. [Google Scholar] [CrossRef]
- Jeon, P.; Kim, J.; Lee, H.; Kwon, H.S.; Young Kim, D. Comparative study on resolution enhancements in fluorescence-structured illumination Fresnel incoherent correlation holography. Opt. Express 2021, 29, 9231–9241. [Google Scholar] [CrossRef]
- Streibl, N. Phase imaging by the transport equation of intensity. Opt. Commun. 1984, 49, 6–10. [Google Scholar] [CrossRef]
- Paganin, D.; Nugent, K.A. Noninterferometric phase imaging with partially coherent light. Phys. Rev. Lett. 1998, 80, 2586. [Google Scholar] [CrossRef]
- Bromberg, Y.; Katz, O.; Silberberg, Y. Ghost imaging with a single detector. Phys. Rev. A 2009, 79, 053840. [Google Scholar] [CrossRef]
- Cieślak, M.J.; Gamage, K.A.; Glover, R. Coded-aperture imaging systems: Past, present and future development–A review. Radiat. Meas. 2016, 92, 59–71. [Google Scholar] [CrossRef]
- Anand, V.; Rosen, J.; Juodkazis, S. Review of engineering techniques in chaotic coded aperture imagers. Light Adv. Manuf. 2022, 3, 24. [Google Scholar] [CrossRef]
- Ables, J.G. Fourier transform photography: A new method for X-ray astronomy. Publ. Astron. Soc. Aust. 1968, 1, 172–173. [Google Scholar] [CrossRef]
- Dicke, R.H. Scatter-hole cameras for X-rays and gamma rays. Astrophys. J. 1968, 153, L101. [Google Scholar] [CrossRef]
- Woods, J.W.; Ekstrom, M.P.; Palmieri, T.M.; Twogood, R.E. Best linear decoding of random mask images. IEEE Trans. Nucl. Sci. 1975, 22, 379–383. [Google Scholar] [CrossRef][Green Version]
- Fenimore, E.E.; Cannon, T.M. Coded aperture imaging with uniformly redundant arrays. Appl. Opt. 1978, 17, 337–347. [Google Scholar] [CrossRef]
- Dunphy, P.P.; McConnell, M.L.; Owens, A.; Chupp, E.L.; Forrest, D.J.; Googins, J. A balloon-borne coded aperture telescope for low-energy gamma-ray astronomy. Nucl. Instrum. Methods Phys. Res. A Accel. Spectrom. Detect. Assoc. Equip. 1989, 274, 362–379. [Google Scholar] [CrossRef]
- Olmos, P.; Cid, C.; Bru, A.; Oller, J.C.; de Pablos, J.L.; Perez, J.M. Design of a modified uniform redundant-array mask for portable gamma cameras. Appl. Opt. 1992, 31, 4742–4750. [Google Scholar] [CrossRef]
- Arce, G.R.; Brady, D.J.; Carin, L.; Arguello, H.; Kittle, D.S. Compressive coded aperture spectral imaging: An introduction. IEEE Signal. Processing Mag. 2013, 31, 105–115. [Google Scholar] [CrossRef]
- Chi, W.; George, N. Optical imaging with phase-coded aperture. Opt. Express 2011, 19, 4294–4300. [Google Scholar] [CrossRef]
- Rai, M.R.; Vijayakumar, A.; Ogura, Y.; Rosen, J. Resolution enhancement in nonlinear interferenceless COACH with point response of subdiffraction limit patterns. Opt. Express 2019, 27, 391–403. [Google Scholar] [CrossRef]
- Vijayakumar, A.; Kashter, Y.; Kelner, R.; Rosen, J. Coded aperture correlation holography–a new type of incoherent digital holograms. Opt. Express 2016, 24, 12430–12441. [Google Scholar] [CrossRef]
- Vijayakumar, A.; Rosen, J. Interferenceless coded aperture correlation holography–a new technique for recording incoherent digital holograms without two-wave interference. Opt. Express 2017, 25, 13883–13896. [Google Scholar] [CrossRef]
- Rai, M.R.; Vijayakumar, A.; Rosen, J. Non-linear adaptive three-dimensional imaging with interferenceless coded aperture correlation holography (I-COACH). Opt. Express 2018, 26, 18143–18154. [Google Scholar] [CrossRef]
- Ng, S.H.; Anand, V.; Katkus, T.; Juodkazis, S. Invasive and non-invasive observation of occluded fast transient events: Computational Tools. Photonics 2021, 8, 253. [Google Scholar] [CrossRef]
- Vijayakumar, A.; Jayavel, D.; Muthaiah, M.; Bhattacharya, S.; Rosen, J. Implementation of a speckle-correlation-based optical lever with extended dynamic range. Appl. Opt. 2019, 58, 5982–5988. [Google Scholar] [CrossRef]
- Vijayakumar, A.; Katkus, T.; Lundgaard, S.; Linklater, D.P.; Ivanova, E.P.; Ng, S.H.; Juodkazis, S. Fresnel incoherent correlation holography with single camera shot. Opto-Electron. Adv. 2020, 3, 200004. [Google Scholar] [CrossRef]
- Smith, D.; Ng, S.H.; Han, M.; Katkus, T.; Anand, V.; Glazebrook, K.; Juodkazis, S. Imaging with diffractive axicons rapidly milled on sapphire by femtosecond laser ablation. Appl. Phys. B 2021, 127, 1–11. [Google Scholar] [CrossRef]
- Anand, V.; Khonina, S.; Kumar, R.; Dubey, N.; Reddy, A.N.K.; Rosen, J.; Juodkazis, S. Three-dimensional incoherent imaging using spiral rotating point spread functions created by double-helix beams. Nanoscale Res. Lett. 2022, 17, 1–13. [Google Scholar] [CrossRef]
- Anand, V.; Rosen, J.; Ng, S.H.; Katkus, T.; Linklater, D.P.; Ivanova, E.P.; Juodkazis, S. Edge and Contrast Enhancement Using Spatially Incoherent Correlation Holography Techniques. Photonics 2021, 8, 224. [Google Scholar] [CrossRef]
- Anand, V.; Ng, S.H.; Maksimovic, J.; Linklater, D.; Katkus, T.; Ivanova, E.P.; Juodkazis, S. Single shot multispectral multidimensional imaging using chaotic waves. Sci. Rep. 2020, 10, 13902. [Google Scholar] [CrossRef]
- Anand, V.; Ng, S.H.; Katkus, T.; Juodkazis, S. Spatio-spectral-temporal imaging of fast transient phenomena using a random array of pinholes. Adv. Photonics Res. 2021, 2, 2000032. [Google Scholar] [CrossRef]
- Rafayelyan, M.; Brasselet, E. Laguerre–Gaussian modal q-plates. Opt. Lett. 2017, 42, 1966–1969. [Google Scholar] [CrossRef]
- Pachava, S.; Dharmavarapu, R.; Vijayakumar, A.; Jayakumar, S.; Manthalkar, A.; Dixit, A.; Viswanathan, N.K.; Srinivasan, B.; Bhattacharya, S. Generation and decomposition of scalar and vector modes carrying orbital angular momentum: A review. Opt. Eng. 2019, 59, 041205. [Google Scholar] [CrossRef]
- Lin, Y.; Seka, W.; Eberly, J.H.; Huang, H.; Brown, D.L. Experimental investigation of Bessel beam characteristics. Appl. Opt. 1992, 31, 2708–2713. [Google Scholar] [CrossRef]
- Yalizay, B.; Soylu, B.; Akturk, S. Optical element for generation of accelerating Airy beams. J. Opt. Soc. Am. A. 2010, 27, 2344–2346. [Google Scholar] [CrossRef]
- Kelner, R.; Rosen, J.; Brooker, G. Enhanced resolution in Fourier incoherent single channel holography (FISCH) with reduced optical path difference. Opt. Express 2013, 21, 20131–20144. [Google Scholar] [CrossRef]
- Vijayakumar, A.; Bhattacharya, S. Characterization and correction of spherical aberration due to glass substrate in the design and fabrication of Fresnel zone lenses. Appl. Opt. 2013, 52, 5932–5940. [Google Scholar] [CrossRef]
- Reivelt, K.; Saari, P. Optical generation of focus wave modes. JOSA A 2000, 17, 1785–1790. [Google Scholar] [CrossRef]
- Lee, W.M.; Yuan, X.C.; Cheong, W.C. Optical vortex beam shaping by use of highly efficient irregular spiral phase plates for optical micromanipulation. Opt. Lett. 2004, 29, 1796–1798. [Google Scholar] [CrossRef]
- Brasselet, E.; Malinauskas, M.; Žukauskas, A.; Juodkazis, S. Photopolymerized microscopic vortex beam generators: Precise delivery of optical orbital angular momentum. Appl. Phys. Lett. 2010, 97, 211108. [Google Scholar] [CrossRef]
- Demenikov, M.; Harvey, A.R. Image artifacts in hybrid imaging systems with a cubic phase mask. Opt. Express 2010, 18, 8207–8212. [Google Scholar] [CrossRef]
- Vijayakumar, A.; Bhattacharya, S. Quasi-achromatic Fresnel zone lens with ring focus. Appl. Opt. 2014, 53, 1970–1974. [Google Scholar] [CrossRef]
- Ren, O.; Birngruber, R. Axicon: A new laser beam delivery system for corneal surgery. IEEE J. Quantum Electron. 1990, 26, 2305–2308. [Google Scholar] [CrossRef]
- Kumar, M.; Vijayakumar, A.; Rosen, J. Incoherent digital holograms acquired by interferenceless coded aperture correlation holography system without refractive lenses. Sci. Rep. 2017, 7, 11555. [Google Scholar] [CrossRef]
- Zalevsky, Z.; Mendlovic, D.; Dorsch, R.G. Gerchberg–Saxton algorithm applied in the fractional Fourier or the Fresnel domain. Opt. Lett. 1996, 21, 842–844. [Google Scholar] [CrossRef]
- Kumar, M.; Vijayakumar, A.; Rosen, J.; Matoba, O. Interferenceless coded aperture correlation holography with synthetic point spread holograms. Appl. Opt. 2020, 59, 7321–7329. [Google Scholar] [CrossRef]
- Anand, V.; Ng, S.H.; Katkus, T.; Juodkazis, S. White light three-dimensional imaging using a quasi-random lens. Opt. Express 2021, 29, 15551–15563. [Google Scholar] [CrossRef]
- Brooker, G.; Siegel, N.; Wang, V.; Rosen, J. Optimal resolution in Fresnel incoherent correlation holographic fluorescence microscopy. Opt. Express 2011, 19, 5047–5062. [Google Scholar] [CrossRef]
- Prasad, S. Rotating point spread function via pupil-phase engineering. Opt. Lett. 2013, 38, 585–587. [Google Scholar] [CrossRef]
- de Haan, K.; Rivenson, Y.; Wu, Y.; Ozcan, A. Deep-learning-based image reconstruction and enhancement in optical microscopy. Proc. IEEE 2019, 108, 30–50. [Google Scholar] [CrossRef]
- Vijayakumar, A.; Kashter, Y.; Kelner, R.; Rosen, J. Coded aperture correlation holography system with improved performance. Appl. Opt. 2017, 56, F67–F77. [Google Scholar] [CrossRef]
- Praveen, P.A.; Babu, R.R.; Jothivenkatachalam, K.; Ramamurthi, K. Spectral, morphological, linear and nonlinear optical properties of nanostructured benzimidazole metal complex thin films. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2015, 150, 280–289. [Google Scholar] [CrossRef]
- Praveen, P.A.; Babu, R.R.; Ramamurthi, K. Theoretical and experimental investigations on linear and nonlinear optical response of metal complexes doped PMMA films. Mater. Res. Express 2017, 4, 025024. [Google Scholar] [CrossRef]
- Gao, P.; Yang, R. Generating different polarized multiple vortex beams at different frequencies from laminated meta-surface lenses. Micromachines 2022, 13, 61. [Google Scholar] [CrossRef]
- Rai, M.R.; Rosen, J. Noise suppression by controlling the sparsity of the point spread function in interferenceless coded aperture correlation holography (I-COACH). Opt. Express 2019, 27, 24311–24323. [Google Scholar] [CrossRef]
- Bulbul, A.; Hai, N.; Rosen, J. Coded aperture correlation holography (COACH) with a superior lateral resolution of FINCH and axial resolution of conventional direct imaging systems. Opt. Express 2021, 29, 42106–42118. [Google Scholar] [CrossRef]
- Liu, C.; Man, T.; Wan, Y. High-quality interferenceless coded aperture correlation holography with optimized high SNR holograms. Appl. Opt. 2022, 61, 661–668. [Google Scholar] [CrossRef]
- Anand, V.; Han, M.; Maksimovic, J.; Ng, S.H.; Katkus, T.; Klein, A.; Bambery, K.; Tobin, M.J.; Vongsvivut, J.; Juodkazis, S. Single-shot mid-infrared incoherent holography using Lucy-Richardson-Rosen algorithm. Opto-Electron. Sci. 2022, 1, 210006. [Google Scholar] [CrossRef]
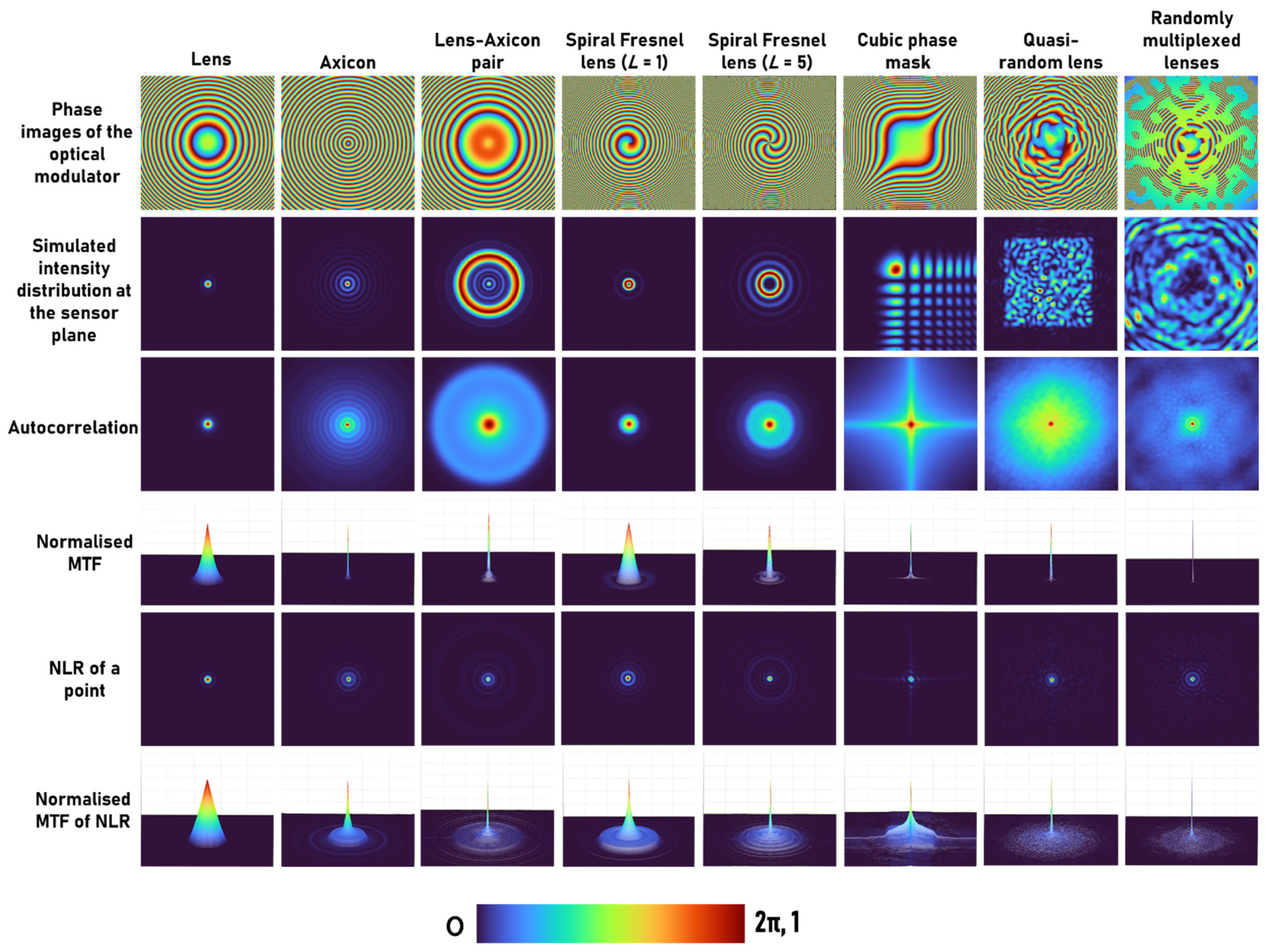
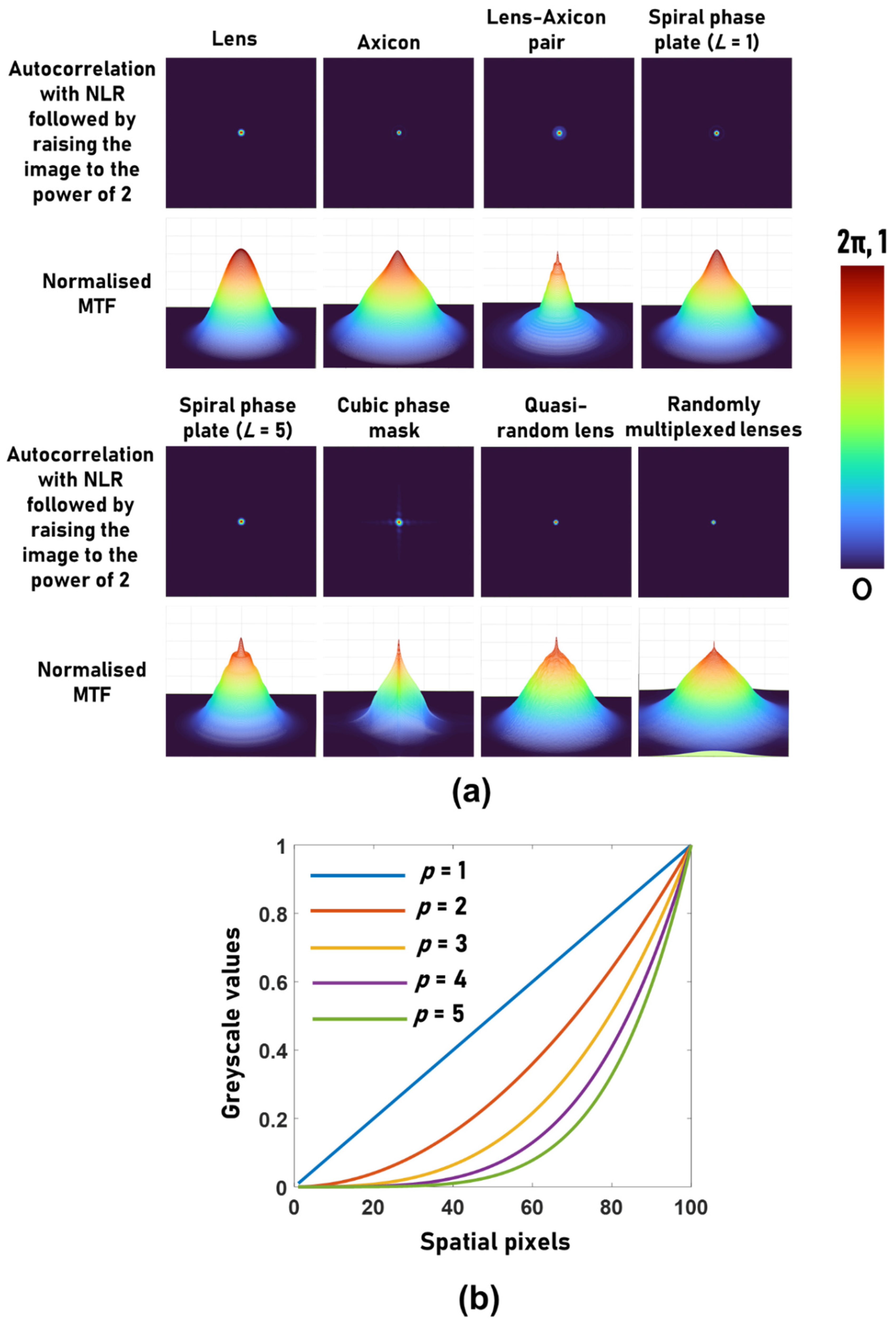












| Peak-to-Background Ratio | Lens | Axicon | Lens–Axicon Pair | Spiral Fresnel Zone Lens L = 1 | Spiral Fresnel Zone Lens L = 5 | Cubic Phase Mask | Quasi-random Lens | Randomly Multiplexed Lenses |
| Autocorrelation | 2518 | 8 | 99 | 925 | 262 | 61 | 23 | 10 |
| NLR | 5957 | 5258 | 3472 | 5739 | 4068 | 18,147 | 7565 | 5977 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smith, D.; Gopinath, S.; Arockiaraj, F.G.; Reddy, A.N.K.; Balasubramani, V.; Kumar, R.; Dubey, N.; Ng, S.H.; Katkus, T.; Selva, S.J.; et al. Nonlinear Reconstruction of Images from Patterns Generated by Deterministic or Random Optical Masks—Concepts and Review of Research. J. Imaging 2022, 8, 174. https://doi.org/10.3390/jimaging8060174
Smith D, Gopinath S, Arockiaraj FG, Reddy ANK, Balasubramani V, Kumar R, Dubey N, Ng SH, Katkus T, Selva SJ, et al. Nonlinear Reconstruction of Images from Patterns Generated by Deterministic or Random Optical Masks—Concepts and Review of Research. Journal of Imaging. 2022; 8(6):174. https://doi.org/10.3390/jimaging8060174
Chicago/Turabian StyleSmith, Daniel, Shivasubramanian Gopinath, Francis Gracy Arockiaraj, Andra Naresh Kumar Reddy, Vinoth Balasubramani, Ravi Kumar, Nitin Dubey, Soon Hock Ng, Tomas Katkus, Shakina Jothi Selva, and et al. 2022. "Nonlinear Reconstruction of Images from Patterns Generated by Deterministic or Random Optical Masks—Concepts and Review of Research" Journal of Imaging 8, no. 6: 174. https://doi.org/10.3390/jimaging8060174
APA StyleSmith, D., Gopinath, S., Arockiaraj, F. G., Reddy, A. N. K., Balasubramani, V., Kumar, R., Dubey, N., Ng, S. H., Katkus, T., Selva, S. J., Renganathan, D., Kamalam, M. B. R., John Francis Rajeswary, A. S., Navaneethakrishnan, S., Inbanathan, S. R., Valdma, S.-M., Praveen, P. A., Amudhavel, J., Kumar, M., ... Anand, V. (2022). Nonlinear Reconstruction of Images from Patterns Generated by Deterministic or Random Optical Masks—Concepts and Review of Research. Journal of Imaging, 8(6), 174. https://doi.org/10.3390/jimaging8060174












