Generation of Ince–Gaussian Beams Using Azocarbazole Polymer CGH
Abstract
:1. Introduction
- The two methods reported for the generation of arbitrary IG beams are LCoS-SLM and DMD, which have a pixel pitch of 3 microns. This results in a small diffraction angle and they are always required to have a 4f Fourier-filtering setup to separate out the zero-order beam from the diffracted beam. The digitally printed hologram on azopolymers has a pixel pitch of 0.8 microns and does not require any optics in the reconstruction setup. This provides a significant reduction in system size footprint compared to SLM/DMD.
- The printed holograms are just 1 mm in size and can be used in an integrated optical device (after printing), which cannot be achieved using SLM/DMD.
- Digital hologram printing allows to print large-sized holograms (25 cm) at a pixel pitch of 0.8 microns, thereby offering a huge space–bandwidth product. This can be beneficial in multiplexing 1000’s of beam modes, which is a crucial requirement in information processing and communication applications. To do the same using SLM/DMD requires spatially tiling SLMs which significantly increases the cost and size footprint.
2. Theory and Methods
2.1. Theory
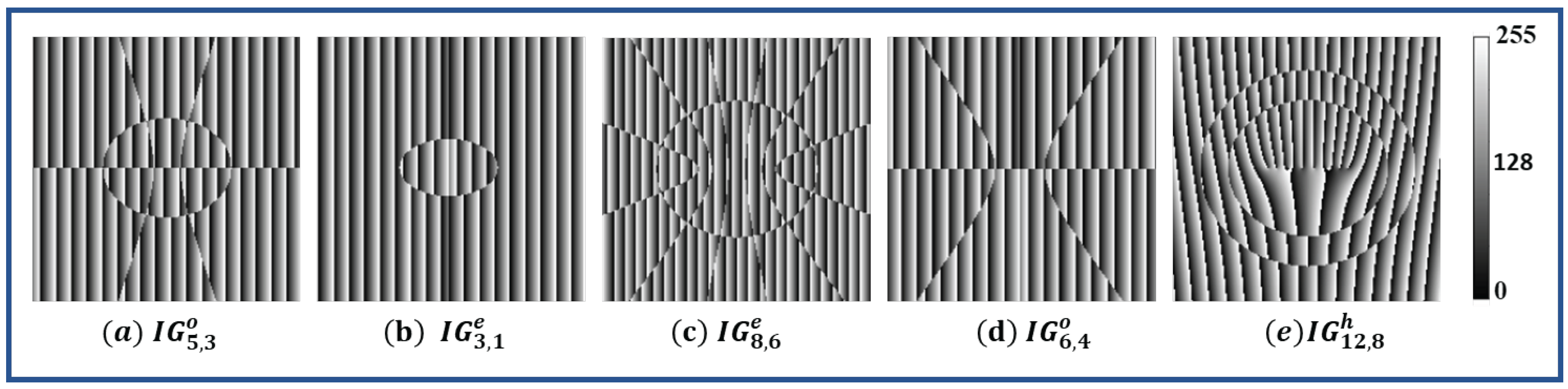
2.1.1. Ince–Gaussian Beam
2.1.2. Azocarbazole Polymer

2.2. Methods
2.2.1. Calculation of Computer-Generated Hologram(CGH)
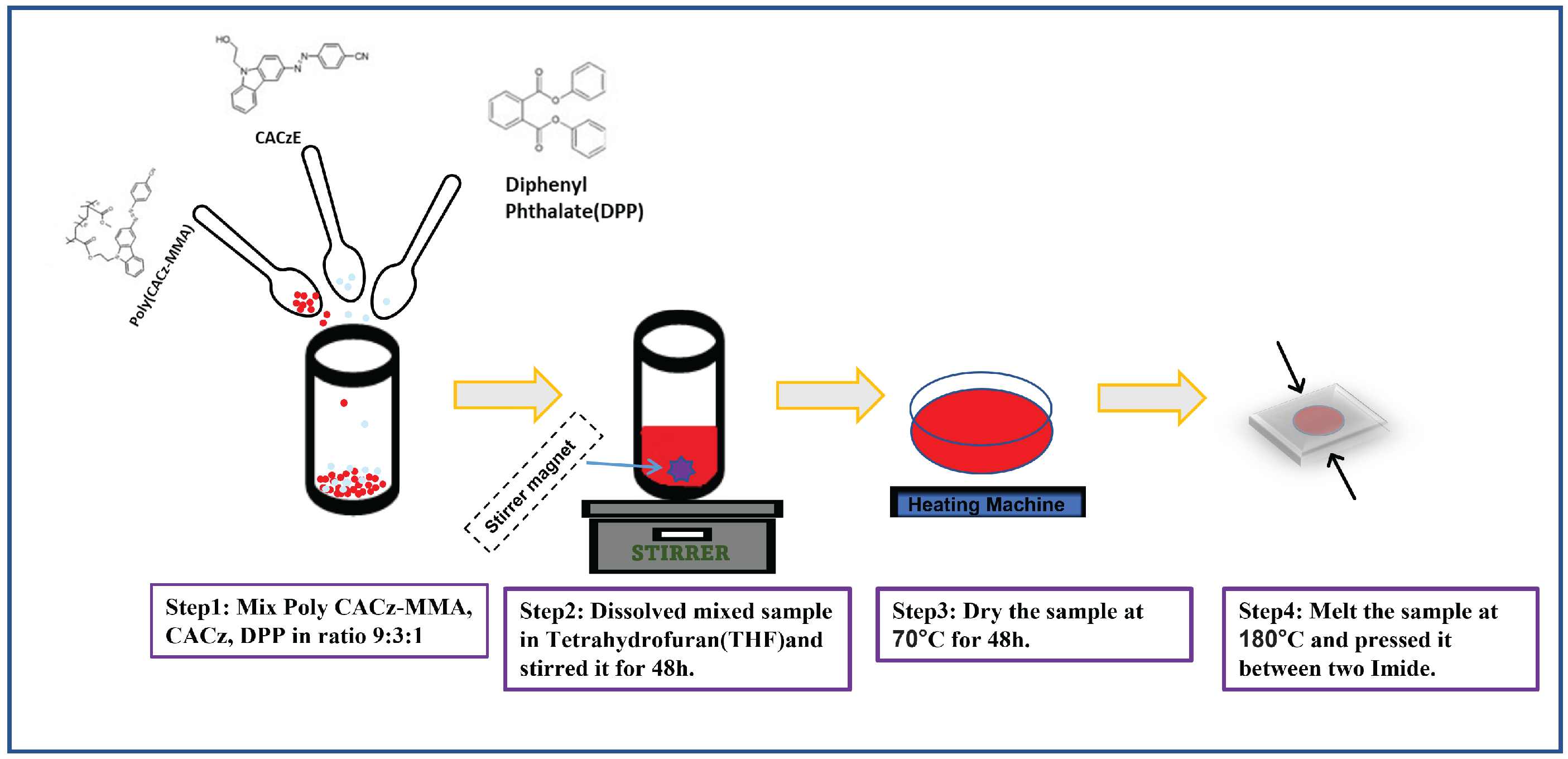
2.2.2. Sample Synthesis
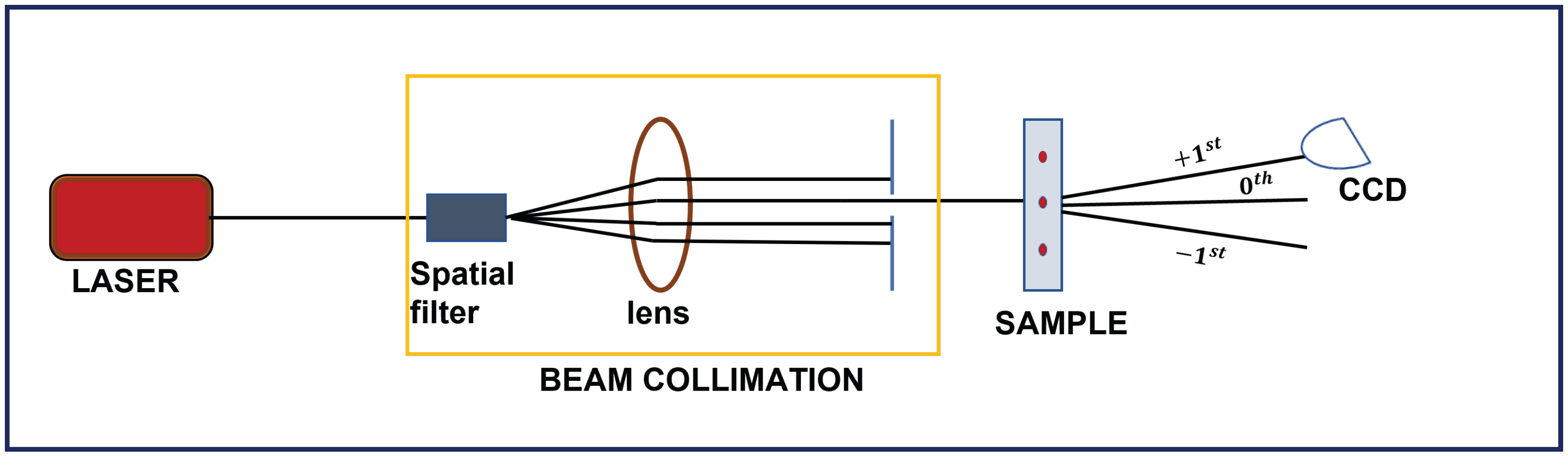
2.2.3. Digital Hologram Printing (DHP)
3. Results
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IG | Ince–Gaussian |
| HG | Hermite Gaussian |
| LG | Laguerre Gaussian |
| CGH | Computer generated hologram |
| DHP | Digital Hologram printing |
| CCD | Charge coupled device |
| SLM | Spatial light modulator |
| MMA | Methyl metacrylate |
| DPP | Diphenyl pthalate |
| THF | Tetrahydrofuran |
| PBS | Polarizing beam splitter |
References
- Bandres, M.A.; Gutiérrez-Vega, J.C. Ince–Gaussian beams. Opt. Lett. 2004, 29, 144–146. [Google Scholar] [CrossRef] [PubMed]
- Jiaqing, L.; Jiming, W.; Chongjun, H.; Tong, W.; Yuangang, L.; Haixia, M.; Youwen, L. Research on the Generation of Ince-Gaussian Vector Optical Field. Acta Opt. Sin. 2019, 39, 0826001. [Google Scholar]
- Baghdasaryan, B.; Fritzsche, S. Enhanced entanglement from Ince-Gaussian pump beams in spontaneous parametric down-conversion. Phys. Rev. A 2020, 102, 052412. [Google Scholar] [CrossRef]
- Sakpal, S.; Milione, G.; Li, M.J.; Nouri, M.; Shahoei, H.; LaFave, T.; Ashrafi, S.; MacFarlane, D. Stability of Ince–Gaussian beams in elliptical core few-mode fibers. Opt. Lett. 2018, 43, 2656–2659. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Chen, Y.; Wang, C.; Wang, J.; Sun, Z.; Cao, M.; Gao, H.; Li, F. Optical storage of Ince–Gaussian modes in warm atomic vapor. Opt. Lett. 2021, 46, 1021–1024. [Google Scholar] [CrossRef] [PubMed]
- Gather, M.; Yun, S. Single-cell biological lasers. Nat. Photonics 2011, 5, 406. [Google Scholar] [CrossRef]
- Yang, Y.; Ren, Y.; Chen, M.; Arita, Y.; Rosales-Guzmán, C. Optical trapping with structured light: A review. Adv. Photonics 2021, 3, 034001. [Google Scholar] [CrossRef]
- Pires, D.; Rocha, J.; Jesus-Silva, A.; Fonseca, E. Optical mode conversion through nonlinear two-wave mixing. Phys. Rev. A 2019, 100, 043819. [Google Scholar] [CrossRef]
- Schwarz, U.T.; Bandres, M.A.; Gutiérrez-Vega, J.C. Observation of Ince–Gaussian modes in stable resonators. Opt. Lett. 2004, 29, 1870–1872. [Google Scholar] [CrossRef] [Green Version]
- Bandres, M.A.; Gutiérrez-Vega, J.C. Ince–Gaussian modes of the paraxial wave equation and stable resonators. JOSA A 2004, 21, 873–880. [Google Scholar] [CrossRef] [Green Version]
- Otsuka, K.; Nemoto, K.; Kamikariya, K.; Miyasaka, Y.; Chu, S.C. Linearly polarized single-frequency oscillations of laser-diode-pumped microchip ceramic Nd: YAG lasers with forced Ince–Gaussian mode operations. Jpn. J. Appl. Phys. 2007, 46, 5865. [Google Scholar] [CrossRef]
- Ren, Y.X.; Fang, Z.X.; Gong, L.; Huang, K.; Chen, Y.; Lu, R.D. Dynamic generation of Ince-Gaussian modes with a digital micromirror device. J. Appl. Phys. 2015, 117, 133106. [Google Scholar] [CrossRef]
- Aguirre-Olivas, D.; Mellado-Villaseñor, G.; Sánchez-de-la Llave, D.; Arrizón, V. Efficient generation of Hermite–Gauss and Ince–Gauss beams through kinoform phase elements. Appl. Opt. 2015, 54, 8444–8452. [Google Scholar] [CrossRef] [PubMed]
- Bentley, J.B.; Davis, J.A.; Bandres, M.A.; Gutiérrez-Vega, J.C. Generation of helical Ince-Gaussian beams with a liquid-crystal display. Opt. Lett. 2006, 31, 649–651. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Li, Y.; Hu, X.; Jin, L. Tailoring Ince-Gaussian arrays based on a computer-generated hologram. Appl. Opt. 2021, 60, 7172–7176. [Google Scholar] [CrossRef]
- Wang, M.Y.; Tang, J.; Wang, H.J.; Ming, Y.; Zhang, Y.; Cui, G.X.; Lu, Y.Q. Generation of second-harmonic Ince-Gaussian beams. Appl. Phys. Lett. 2018, 113, 081105. [Google Scholar] [CrossRef]
- Ohtomo, T.; Chu, S.C.; Otsuka, K. Generation of vortex beams from lasers with controlled Hermite-and Ince-Gaussian modes. Opt. Express 2008, 16, 5082–5094. [Google Scholar] [CrossRef]
- Jin, J.; Pu, M.; Wang, Y.; Li, X.; Ma, X.; Luo, J.; Zhao, Z.; Gao, P.; Luo, X. Multi-Channel Vortex Beam Generation by Simultaneous Amplitude and Phase Modulation with Two-Dimensional Metamaterial. Adv. Mater. Technol. 2017, 2, 1600201. [Google Scholar] [CrossRef]
- Jackin, B.J.; Shirai, M.; Haginaka, H.; Kinashi, K.; Tsutsumi, N.; Sakai, W. Compact and Scalable Large Vortex Array Generation Using Azocarbazole Polymer and Digital Hologram Printing Technique. Nanoscale Res. Lett. 2022, 17, 44. [Google Scholar] [CrossRef]
- Bandres, M.A. Ince Gaussian Beam. 2022. Available online: https://www.mathworks.com/matlabcentral/fileexchange/46222-ince-gaussian-beam (accessed on 20 February 2022).
- Zeleny, E. Ince Polynomial. 2014. Available online: http://demonstrations.wolfram.com/IncePolynomials/ (accessed on 20 February 2022).
- Van Rossum, G.; Drake, F.L. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009. [Google Scholar]
- Kinashi, K.; Fukami, T.; Yabuhara, Y.; Motoishi, S.; Sakai, W.; Kawamoto, M.; Sassa, T.; Tsutsumi, N. Molecular design of azo-carbazole monolithic dyes for updatable full-color holograms. NPG Asia Mater. 2016, 8, e311. [Google Scholar] [CrossRef] [Green Version]
- Kinashi, K.; Nakanishi, I.; Sakai, W.; Tsutsumi, N. Material Design of Azo-Carbazole Copolymers for Preservation Stability with Rewritable Holographic Stereograms. Macromol. Chem. Phys. 2019, 220, 1800456. [Google Scholar] [CrossRef]
- Sun, C. Explicit equations to transform from Cartesian to Elliptic coordinates. Math. Model. Appl. 2017, 2, 43–46. [Google Scholar] [CrossRef] [Green Version]
- Yoshikawa, H.; Tachinami, M. Development of direct fringe printer for computer-generated holograms. In Proceedings of the Practical Holography XIX: Materials and Applications, San Jose, CA, USA, 25–27 January 2005; International Society for Optics and Photonics: Bellingham, WA, USA, 2005; Volume 5742, pp. 259–266. [Google Scholar]
- Chu, X.; Sun, Q.; Wang, J.; Lü, P.; Xie, W.; Xu, X. Generating a Bessel-Gaussian beam for the application in optical engineering. Sci. Rep. 2015, 5, 18665. [Google Scholar] [CrossRef] [PubMed]
- Ez-Zariy, L.; Nebdi, H.; Chafiq, A.; Belafhal, A. Mathieu-Gauss beam and its propagation. Phys. Chem. News 2012, 64, 42–52. [Google Scholar]
- Bandres, M.A.; Gutiérrez-Vega, J.C. Airy-Gauss beams and their transformation by paraxial optical systems. Opt. Express 2007, 15, 16719–16728. [Google Scholar] [CrossRef] [Green Version]
- Karimi, E.; Zito, G.; Piccirillo, B.; Marrucci, L.; Santamato, E. Hypergeometric-gaussian modes. Opt. Lett. 2007, 32, 3053–3055. [Google Scholar] [CrossRef] [Green Version]









Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, S.K.; Haginaka, H.; Jackin, B.J.; Kinashi, K.; Tsutsumi, N.; Sakai, W. Generation of Ince–Gaussian Beams Using Azocarbazole Polymer CGH. J. Imaging 2022, 8, 144. https://doi.org/10.3390/jimaging8050144
Singh SK, Haginaka H, Jackin BJ, Kinashi K, Tsutsumi N, Sakai W. Generation of Ince–Gaussian Beams Using Azocarbazole Polymer CGH. Journal of Imaging. 2022; 8(5):144. https://doi.org/10.3390/jimaging8050144
Chicago/Turabian StyleSingh, Sumit Kumar, Honoka Haginaka, Boaz Jessie Jackin, Kenji Kinashi, Naoto Tsutsumi, and Wataru Sakai. 2022. "Generation of Ince–Gaussian Beams Using Azocarbazole Polymer CGH" Journal of Imaging 8, no. 5: 144. https://doi.org/10.3390/jimaging8050144
APA StyleSingh, S. K., Haginaka, H., Jackin, B. J., Kinashi, K., Tsutsumi, N., & Sakai, W. (2022). Generation of Ince–Gaussian Beams Using Azocarbazole Polymer CGH. Journal of Imaging, 8(5), 144. https://doi.org/10.3390/jimaging8050144








