Abstract
In this paper, we detail a phase-shift implementation in a rotated plane-parallel plate (PPP). Considering the phase-shifting digital holography application, we provide a more precise phase-shift estimation based on PPP thickness, rotation, and mutual inclination of reference and object wavefronts. We show that phase retardation uncertainty implemented by the rotated PPP in a simple configuration is less than the uncertainty of a traditionally used piezoelectric translator. Physical experiments on a phase test target verify the high quality of phase reconstruction.
1. Introduction
Phase-shifting interferometry is a technique of complex amplitude measurement [1]. It is based on the registration and processing of several holograms exposed to phase-shifted reference wavefronts. Its original analog version is very laborious because of complex processing. However, with the development of matrix photo-detectors [2], digital phase-shifting interferometry [3] and phase-shifting digital holography (PSDH) [4] are immensely improved due to the digital implementation [5,6], since now all complex processing (such as registration, developing, and reconstruction) is performed on computers. Due to its straightforward computational realization, high resolution, and precise elimination of spurious zero and minus first diffraction orders in the in-line configuration [7], PSDH has become a popular method for complex amplitude reconstruction.
Since Yamaguchi and Zhang [8] published the first work on phase-shifting digital holography for four phase shifts of , many different implementations of phase shifts and their subsequent processing [9,10] have been proposed. In that way, reductions in the number of the steps to three [11,12] and two [13,14] have been proposed. Furthermore, regarding the phase step values, automatic estimation for unknown values was proposed in works [15,16,17].
Regarding the phase shift implementation as it was realized in the pioneering paper, the most popular one is a piezoelectric translator (PZT). It moves a reference arm mirror with nano-scale precision and, because of a change in the actual length of a light path, the desired phase delay is achieved. Likewise, for this purpose but without mechanical movements, quarter-wave plates [18,19], liquid phase-retarders [13,20,21,22], and spatial light modulators (SLM) [23,24] have been used. While SLM is an expensive solution with a pixelated structure that might decrease imaging resolution, liquid phase-retarders are demanding in terms of precise optical adjustment, since light changes its polarization during retardation.
In papers [25,26,27,28,29,30], phase-shifting with plane-parallel plate (PPP) rotation was described, where a phase-shift was obtained due to path lengthening in the PPP because of its rotation. However, the phase retardation in the rotated PPP was only mentioned without a complete description of the process. Moreover, in [28] phase retardation analysis was performed with trigonometric simplification, which does not correspond to the correct value of the phase delay, and in [29] the equation was published with a misprint.
In PSDH, as in all metrological techniques, the reconstruction quality strongly depends on the quality of an optical system and noise. Noise especially influences the phase measurement in PSDH because of several observations with different phase shifts, resulting in a superposition of noise from each observation. Different factors of the registration system introduce noise in PSDH: an inaccuracy in the phase shift determination, vibration distortion, and sensor noise [20,31,32]. It was found in [32] that the largest distortion of the reconstructed wavefront is introduced by errors associated with the inaccuracy of the phase shift determining, i.e., phase-shift implementation. In papers [33,34,35,36,37] the errors in determining the value of the phase-shift were considered with solutions to reduce these errors. However, these solutions were concentrated on an inhibition of the consequences of the incorrect phase-shift implementations not considering the cause. In the current paper, we aim to investigate the cause of the phase-shift inaccuracy in the rotated PPP and show that this inaccuracy is less than in PZT, which is traditional for PSDH. We thereby provide an effective equivalent to PZT for phase-shift implementation.
2. Phase Retardation in a Rotated Plane-Parallel Plate
An optical plane-parallel plate is a transparent body bounded by two mutually parallel polished surfaces. When placed in the optical path it preserves the light ray direction because of refraction on both surfaces [30]. However, in the case where the PPP is inclined to the optical path (rotated on its axis), the effects of optical path lengthening and lateral displacement of the light ray appear due to refraction on the first surface. Considering both effects, we provide precise phase-shift estimation caused by the rotated PPP.
Figure 1 shows light ray propagation through the PPP. Black arrows illustrate the light path corresponding to the PPP’s initial position (solid black rectangle) with angle and red arrows corresponding to the light path in the rotated PPP (dashed rectangle) when , is the PPP thickness and is the refraction angle. The optical path of a light ray in the PPP’s initial position is , where n is the refractive index of the glass.
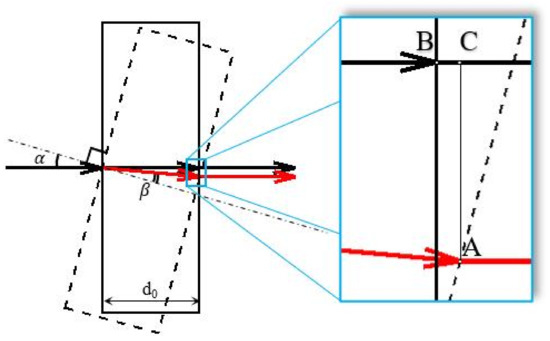
Figure 1.
Path difference in plane-parallel plate. is the PPP rotational angle, the black arrow is the light path with , the red arrow is a light path with , is the PPP thickness, and is the angle of refraction. Zoomed inset shows the detailed location of the shifted light path because of PPP rotation.
To estimate the phase-shift obtained by a wavefront going through the rotated PPP, one needs to subtract the wavefront phases after and before the rotation. For detailed investigation of the accumulated phase shift, we point out the points , and C in the zoomed inset in Figure 1: if the light path goes out from the PPP in the point B, and after PPP rotation, it comes out from the point A. As can be seen from the figure, point A is located further along the optical path than point B, therefore for the correct phase shift estimation, the phase difference must be calculated between points A and C. Thus, length must be considered. In addition, taking into account the PSDH application where reference and object wavefronts create a hologram, mutual spatial displacement (length ) of these wavefronts will result in an additional phase shift if the reference and object wavefronts are inclined to each other. When the angle between the reference and object wavefronts equals zero, there is no lateral phase-shifting effect, but in physical experimental conditions, it is hard to attain a zero value for .
Therefore, to estimate the resulting phase-shift caused by the rotation of the PPP, we have to find the phase difference between wavefronts in points A (after rotation) and C (before rotation) following equation
where is the desired phase delay, is the wavefront phase in point A, is the wavefront phase in point C, is the phase shift because of inclination between the object and reference wavefronts, is the wavelength, n is the PPP refractive index, is the plate thickness, is the light path length in the PPP after rotation, and is the angle between the reference and object wavefronts. Considering all described phases and the law of refraction, we present the resulting equation for the phase shift estimation in the rotated PPP:
3. Phase Retardation Analysis
To illustrate the difference of the proposed equation with the previous phase-shift estimation [28] in the rotated PPP, we have plotted in Figure 2a these phase-shifts depending on rotation angle, . For clarity, we consider the ideally in-line geometry, which means that the angle between the reference and object wavefronts equals zero (), with the PPP thickness mm, , and nm. In Figure 2a, the solid blue curve is for the proposed phase shift estimation and the dashed orange curve is for the estimation from the paper [28]. In the work [28], the authors provide the equation , which is based on trigonometrical simplification and estimates the phase-shift, which is not correct and is smaller than the direct estimation.
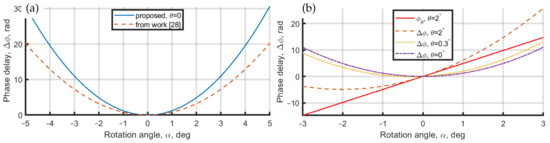
Figure 2.
Phase delay in rotated PPP. (a) Phase delay with no inclination among reference and object wavefronts. The solid blue line is for the proposed phase delay estimation, dashed orange curve is for phase delay from the paper [28]. (b) Phase delay dependence on inclination angle between reference and object wavefronts. The solid red line is phase shift, because of inclination on , a dotted orange curve is phase delay with , a dash-dot purple curve is phase delay with , and dashed orange curve is phase delay with .
Considering the case when the reference and object wavefronts are inclined to each other (), the in Equation (1) creates an almost linear shift of the total phase delay, ; see Figure 2b, where we have plotted two curves of phase shift in PPP with in purple, in yellow, and with deg in orange. A solid red line corresponds to the phase with . The curve is linear; therefore, it only shifts the resulting phase delay without changing its shape. It is seen that shifts the minimum of from to and even small values of (e.g., ) will influence the resulting phase-shift and must be considered for precise estimation of the phase-shift.
4. Uncertainty Estimation
Next, to estimate the stability of the phase delay in PPP, we show in Figure 3 the PPP’s phase delay uncertainty. For the sake of clarity, we have taken . The blue curve in Figure 3a illustrates the phase delay dependence on the PPP rotation angle, ; the solid orange curve is the uncertainty estimation that was calculated as a derivative of the phase delay. The dashed orange curve is the phase uncertainty of the traditional phase-shifting implementation—a piezoelectric translator (PZT). The PPP and PZT uncertainties were calculated based on the parameters of the instruments available in our laboratory. For the rotated PPP, this was the rotatable motorized translation stage (MTS) “Standa mr151-30” (https://www.standa.lt/products/catalog/motorised_positioners?item=9&prod=motorized_rotation_stages&print=1, access date 1 March 2022), in which the smallest rotation step is 0.01 degree and the repeatability equals the step value. For PZT, we estimated the uncertainty based on PZT “Physik Instrumente P-603.1s2” (https://www.physikinstrumente.store/eu/p-603.1s2/, access date 1 March 2022), with a wobble of 7 nm, which resulted in a phase uncertainty of 0.083 rad for the wavelength of 532 nm. Due to the nonlinearity of Equation (2), the PPP uncertainty increases with the rotational angle. In Figure 3a it can be seen that for rotation angles in the range [−3.1:3.1] deg, PPP uncertainty is less than for PZT. Therefore, PPP is more stable in that range. For angles of rotation larger than PPP will perform worse; however, PPP rotation angle in that range corresponds to a phase delay of about rad, which is more than enough for PSDH reconstruction where only a maximum phase-shift is needed.
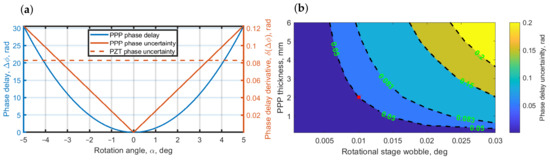
Figure 3.
Phase-shift precision estimation in PPP and PZT. (a) Left y-axis is for the phase delay; right y-axis is for the phase delay uncertainty. The solid blue curve is the phase delay in the rotated PPP, the solid orange curve is the uncertainty of the phase delay in the PPP, and the dashed orange line is the uncertainty of PZT. (b) Rotated PPP phase delay uncertainty map for delay value of rad depending on PPP thickness and rotational stage wobble. Red dot corresponds to the considered MTS wobble of 0.01 deg and PPP thickness of 2 mm.
Mainly, the rotated PPP uncertainty is a function of two parameters: the wobble of a rotational stage and PPP thickness. To estimate the uncertainty for the realization of the required phase delay, we show in Figure 3b an uncertainty contour map of the rotated PPP for the phase delay value of depending on both PPP thickness and MTS wobble. The contours of 0.083 rad and of 0.05 rad correspond to PZT of 7 nm and 4.2 nm wobble, respectively. As can be seen from the map in Figure 3b, a thinner PPP provides smaller errors even with relatively high MTS wobble. The red dot in Figure 3b is for the considered MTS wobble of 0.01 deg and PPP thickness of 2 mm, which corresponds to PZT with a 4.2 nm wobble. Contrary to PZT, MTS has less precision, and to introduce a sufficient phase delay the PPP has to be rotated on a relatively large angle, thus small instabilities in MTS do not impact the phase retardation. Therefore, the proposed implementation of phase retardation surpasses PZT in terms of stability.
5. Experimental Verification
The basic PSDH method reconstructs the object phase from four holograms recorded with shifted phases of the reference beam on 0, , , and [8]. One hundred holograms of each phase step are averaged in order to smooth the noise of the sensor and vibrations. To calculate the phase one must follow the equation
where is the object phase and is the hologram with a phase-shifted reference beam. Such an approach is straightforward and cheap in terms of computational cost.
To compare PSDH reconstructions realized by the proposed rotated PPP and by traditional PZT implementations, we developed the experimental setup with PPP and PZT phase shifts implemented simultaneously. It is presented in Figure 4 and based on a Mach–Zehnder interferometer in the in-line configuration. For phase-shift initialization, a rotation MTS Standa mr151-30 for PPP and PZT “Physik Instrumente P-603.1s2” were utilized. The radiation source was a single-mode laser Lasos CKL 2400, nm; the detector array was the CMOS matrix VEI-830 with resolution and pixel size m; PPP thickness equals 2 mm.
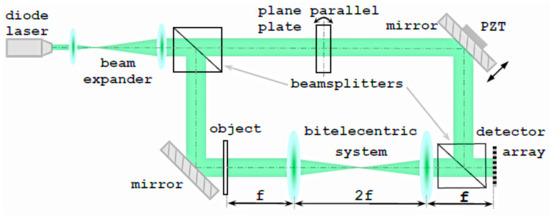
Figure 4.
Experimental setup.
Following Equation (2), to have the desired phase shifts of 0, , , and , the PPP should be rotated on angles , correspondingly. However, considering that even a small inclination between reference and object wavefronts might shift the expected phase delay, we performed an experimental calibration of the PPP phase delay system. The calibration was realized by scanning the PPP rotation angle in the range [−5:5] deg with a consecutive recording of the single-pixel hologram intensity [34]. Thus we present in Figure 5 the solid red curve of that single pixel intensity depending on the PPP rotation angle. The phase-shifts can be estimated by analyzing this curve: the maximums correspond to phase-shifts, minimums correspond to , and halves of the difference of maximum and minimum correspond to with an integer m. Phase-shift simulation in Figure 5 (dash black curve) is calculated by Equation (2), and it is in good agreement with the experimental data.
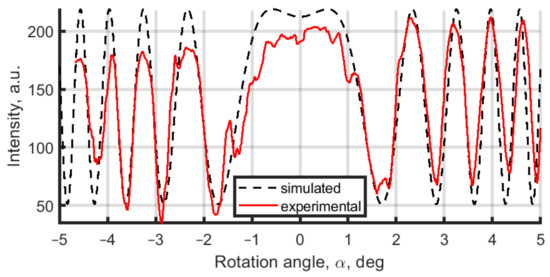
Figure 5.
Hologram’s single pixel intensity dependence from rotational angle of the plane parallel plate.
Figure 6 shows PSDH reconstruction of a phase object by PPP and PZT implementations. For comparison of these reconstructions, we built longitudinal cross-sections in Figure 6c,d. Visually, reconstructions are close to each other with the same spatial resolution. However, in cross-sections, phase deflections of about 0.3 rad are observed. From the theoretical uncertainty estimation in Section 4, we expect that the rotated PPP implementation should perform better. However, we cannot conclude unambiguously that this deflection is the error of PZT implementation since it might be addressed to the influence of noise, e.g., vibrations. Both techniques provide quality imaging with about 10% difference in phase from each other. At least we may conclude that PSDH phase reconstruction with rotated PPP implementation is a cost-effective equivalent for PZT.
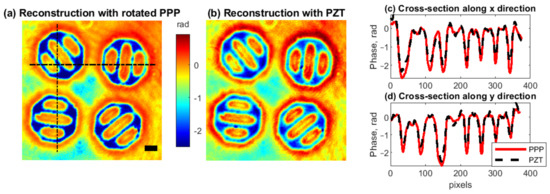
Figure 6.
PSDH reconstructed phase with implementation by rotated PPP (a) and by PZT (b). Longitudinal cross-sections are in subplots (c,d) for x and y directions, correspondingly. Scale bar is 50 m.
6. Conclusions
In this paper, the model of phase-shift estimation in the PSDH with a rotated PPP has been further developed. We have detailed the mathematical equation for phase-shift estimation in the PPP, taking reference and object wavefront mutual inclination into account. Based on the equation, we have estimated the uncertainty of the phase-shift in the rotated PPP and found that PPP implementation is more stable than PZT in a wide range of parameters. It was shown that phase delay will be smaller with a thinner PPP. The thinner PPP thus guarantees higher precision in phase-shift estimation. Moreover, thin optical elements are on-demand in tasks, where embedding of additional elements to the optical scheme is undesirable, to eliminate dispersion broadening. Such restrictions take place in femtosecond holography [38,39,40] where the proposed implementation might now be applied. Additionally, PPP rotation might be realized in multicolor holography with color filters on a registration matrix [41,42,43]. The simplicity and cost-effectiveness of the considered phase-shifter allows widespread use of PSDH, overcoming the PZT technical barrier without loss in the reconstruction quality.
Author Contributions
I.S.: conceptualization, software, validation, investigation, writing—original draft preparation; N.V.P.: conceptualization, methodology, writing—review and editing. All authors have read and agreed to the published version of the manuscript.
Funding
I.S. was supported by the Academy of Finland (project no. 336357, PROFI 6 - TAU Imaging Research Platform); N.V.P. was supported by the Russian Foundation for Basic Research, project No. 21-52-15035/21.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data available through request.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| PSDH | Phase-shifting digital holography |
| PPP | Plane-parallel plate |
| PZT | Piezoelectric translator |
| MTS | Motorized translation stage |
| SLM | Spatial light modulator |
References
- Bruning, J.H.; Herriott, D.R.; Gallagher, J.E.; Rosenfeld, D.P.; White, A.D.; Brangaccio, D.J. Digital Wavefront Measuring Interferometer for Testing Optical Surfaces and Lenses. Appl. Opt. 1974, 13, 2693–2703. [Google Scholar] [CrossRef] [PubMed]
- Boyle, W.S.; Smith, G.E. Charge coupled semiconductor devices. Bell Syst. Tech. J. 1970, 49, 587–593. [Google Scholar]
- Hariharan, P.; Oreb, B.F.; Eiju, T. Digital phase-shifting interferometry: A simple error-compensating phase calculation algorithm. Appl. Opt. 1987, 26, 2504. [Google Scholar] [CrossRef]
- Yamaguchi, I.; Zhang, T. Phase-shifting digital holography. Opt. Lett. 1997, 22, 1268. [Google Scholar] [CrossRef] [PubMed]
- De Groot, P.J.; Deck, L.L.; Su, R.; Osten, W. Contributions of holography to the advancement of interferometric measurements of surface topography. Light Adv. Manuf. 2022, 3, 1. [Google Scholar] [CrossRef]
- Khonina, S.; Khorin, P.G.; Serafimovich, P.G.; Dzyuba, A.P.; Georgieva, A.O.; Petrov, N.V. Analysis of the wavefront aberrations based on neural networks processing of the interferograms with a conical reference beam. Appl. Phys. B 2022, 128, 1–16. [Google Scholar] [CrossRef]
- Latychevskaia, T.; Formanek, P.; Koch, C.; Lubk, A. Off-axis and inline electron holography: Experimental comparison. Ultramicroscopy 2010, 110, 472–482. [Google Scholar] [CrossRef] [Green Version]
- Yamaguchi, I.; Zhang, T. Phase-shifting digital holography. In Digital Holography and Three-Dimensional Display; Springer Series in Optical Sciences; Springer: Boston, MA, USA, 1997; Volume 22, pp. 1268–1270. [Google Scholar] [CrossRef]
- Kim, M.K. Digital Holographic Microscopy; Springer Series in Optical Sciences; Springer: New York, NY, USA, 2011; Volume 162. [Google Scholar] [CrossRef] [Green Version]
- Guo, P.; Devaney, A.J. Digital microscopy using phase-shifting digital holography with two reference waves. Opt. Lett. 2004, 29, 857–859. [Google Scholar] [CrossRef]
- Yamaguchi, I.; Kato, J.; Ohta, S.; Mizuno, J. Image formation in phase-shifting digital holography and applications to microscopy. Appl. Opt. 2001, 40, 6177–6186. [Google Scholar]
- Huang, P.S.; Zhang, S. Fast three-step phase-shifting algorithm. Appl. Opt. 2006, 45, 5086–5091. [Google Scholar] [CrossRef]
- Takaki, Y.; Kawai, H.; Ohzu, H. Hybrid holographic microscopy free of conjugate and zero-order images. Appl. Opt. 1999, 38, 4990–4996. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.F.; Cai, L.Z.; Xu, X.F.; Yang, X.L.; Shen, X.X.; Dong, G.Y.; Wang, Y.R. Two-step phase-shifting interferometry and its application in image encryption. Opt. Lett. 2006, 31, 1414–1416. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Han, B. Advanced iterative algorithm for phase extraction of randomly phase-shifted interferograms. Opt. Lett. 2004, 29, 1671–1673. [Google Scholar]
- Xu, X.F.; Cai, L.Z.; Wang, Y.R.; Meng, X.F.; Sun, W.J.; Zhang, H.; Cheng, X.C.; Dong, G.Y.; Shen, X.X. Simple direct extraction of unknown phase shift and wavefront reconstruction in generalized phase-shifting interferometry: Algorithm and experiments. Opt. Lett. 2008, 33, 776–778. [Google Scholar] [CrossRef] [PubMed]
- Xia, P.; Wang, Q.; Ri, S. Random phase-shifting digital holography based on a self-calibrated system. Opt. Express 2020, 28, 19988–19996. [Google Scholar] [CrossRef]
- Nomura, T.; Murata, S.; Nitanai, E.; Numata, T. Phase-shifting digital holography with a phase difference between orthogonal polarizations. Appl. Opt. 2006, 45, 4873–4877. [Google Scholar] [CrossRef]
- Xia, P.; Ri, S.; Inoue, T.; Awatsuji, Y.; Matoba, O. Dynamic phase measurement of a transparent object by parallel phase-shifting digital holography with dual polarization imaging cameras. Opt. Lasers Eng. 2021, 141, 106583. [Google Scholar]
- Lai, S.; King, B.; Neifeld, M.A. Wave front reconstruction by means of phase-shifting digital in-line holography. Opt. Commun. 2000, 173, 155–160. [Google Scholar]
- Griffin, D.W. Phase-shifting shearing interferometer. Opt. Lett. 2001, 26, 140. [Google Scholar] [CrossRef]
- Cazac, V.; Achimova, E.; Abashkin, V.; Prisacar, A.; Loshmanschii, C.; Meshalkin, A.; Egiazarian, K. Polarization holographic recording of vortex diffractive optical elements on azopolymer thin films and 3D analysis via phase-shifting digital holographic microscopy. Opt. Express 2021, 29, 9217. [Google Scholar] [CrossRef]
- Wang, Z.; Millet, L.; Mir, M.; Ding, H.; Unarunotai, S.; Rogers, J.; Gillette, M.U.; Popescu, G. Spatial light interference microscopy (SLIM). Opt. Express 2011, 19, 1016. [Google Scholar] [CrossRef] [PubMed]
- Tahara, T.; Endo, Y. Multiwavelength-selective phase-shifting digital holography without mechanical scanning. Appl. Opt. 2019, 58, G218–G225. [Google Scholar] [CrossRef] [PubMed]
- Wyant, J.; Shagam, R. Use of electronic phase measurement techniques in optical testing. In Proceedings of the ICO-11 Conference, Madrid, Spain, 10–17 September 1978. [Google Scholar]
- Creath, K. V Phase-Measurement Interferometry Techniques. Prog. Opt. 1988, 26, 349–393. [Google Scholar] [CrossRef]
- Nicola, S.D.; Ferraro, P.; Finizio, A.; Pierattini, G. Wave front reconstruction of Fresnel off-axis holograms with compensation of aberrations by means of phase-shifting digital holography. Opt. Lasers Eng. 2002, 37, 331–340. [Google Scholar] [CrossRef]
- Meneses-Fabian, C.; Rivera-Ortega, U. Phase-Shifting Interferometry by Amplitude Modulation. In Interferometry; Padron, I., Ed.; IntechOpen: Rijeka, Croatia, 2012; Chapter 8. [Google Scholar] [CrossRef] [Green Version]
- Wang, S. Dual Transverse Electro-Optic Modulator in Optical Interferometric Systems. Ph.D. Thesis, Technische Universität München, München, Germany, 2020. [Google Scholar]
- Belashov, A.V.; Petrov, N.V. Improvement of rough surfaces height map reconstruction accuracy in tilt angle illumination digital holography. Opt. Eng. 2020, 59, 1. [Google Scholar] [CrossRef]
- Guo, C.S.; Zhang, L.; Wang, H.T.; Liao, J.; Zhu, Y.Y. Phase-shifting error and its elimination in phase-shifting digital holography. Opt. Lett. 2002, 27, 1687–1689. [Google Scholar] [CrossRef]
- Cordero, R.R.; Molimard, J.; Martínez, A.; Labbe, F. Uncertainty analysis of temporal phase-stepping algorithms for interferometry. Opt. Commun. 2007, 275, 144–155. [Google Scholar] [CrossRef]
- Schwider, J.; Burow, R.; Elssner, K. Digital wave-front measuring interferometry: Some systematic error sources. Appl. Opt. 1983, 22, 3421–3432. [Google Scholar]
- De Groot, P. Phase-shift calibration errors in interferometers with spherical Fizeau cavities. Appl. Opt. 1995, 34, 2856–2863. [Google Scholar] [CrossRef]
- Zhang, H.; Lalor, M.; Burton, D. Error-compensating algorithms in phase-shifting interferometry: A comparison by error analysis. Opt. Lasers Eng. 1999, 31, 381–400. [Google Scholar]
- Guzhov, V.I.; Il’yinykh, S.P.; Khaidukov, D.S.; Vagizov, A.R. Eliminating phase-shift errors in interferometry. Optoelectron. Instrum. Data Process. 2011, 47, 76–80. [Google Scholar] [CrossRef]
- Guzhov, V.I.; Ilinykh, S.P.; Emelyanov, V.A.; Marchenko, I.O. Eliminating the effect of non-linear distortion of profile fringes for structured illumination method. In Proceedings of the 2016 11th International Forum on Strategic Technology, IFOST 2016, Novosibirsk, Russia, 1–3 June 2016; pp. 535–537. [Google Scholar] [CrossRef]
- Kakue, T.; Itoh, S.; Xia, P.; Tahara, T.; Awatsuji, Y.; Nishio, K.; Ura, S.; Kubota, T.; Matoba, O. Single-shot femtosecond-pulsed phase-shifting digital holography. Opt. Express 2012, 20, 20286. [Google Scholar] [CrossRef] [PubMed]
- Hasegawa, S.; Hayasaki, Y. Dynamic control of spatial wavelength dispersion in holographic femtosecond laser processing. Opt. Lett. 2014, 39, 478. [Google Scholar] [CrossRef]
- Petrov, N.V.; Putilin, S.E.; Chipegin, A.A. Time-resolved image plane off-axis digital holography. Appl. Phys. Lett. 2017, 110, 161107. [Google Scholar] [CrossRef]
- Lesnichii, V.V.; Petrov, N.V.; Cheremkhin, P.A. A technique of measuring spectral characteristics of detector arrays in amateur and professional photocameras and their application for problems of digital holography. Opt. Spectrosc. 2013, 115, 557–566. [Google Scholar] [CrossRef]
- Cheremkhin, P.A.; Lesnichii, V.V.; Petrov, N.V. Use of spectral characteristics of DSLR cameras with Bayer filter sensors. J. Phys. Conf. Ser. 2014, 536, 012021. [Google Scholar] [CrossRef]
- Cheremkhin, P.; Shevkunov, I.; Petrov, N. Multiple-wavelength Color Digital Holography for Monochromatic Image Reconstruction. Phys. Procedia 2015, 73, 301–307. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).