Fuzzy Information Discrimination Measures and Their Application to Low Dimensional Embedding Construction in the UMAP Algorithm
Abstract
:1. Introduction
2. Materials and Methods
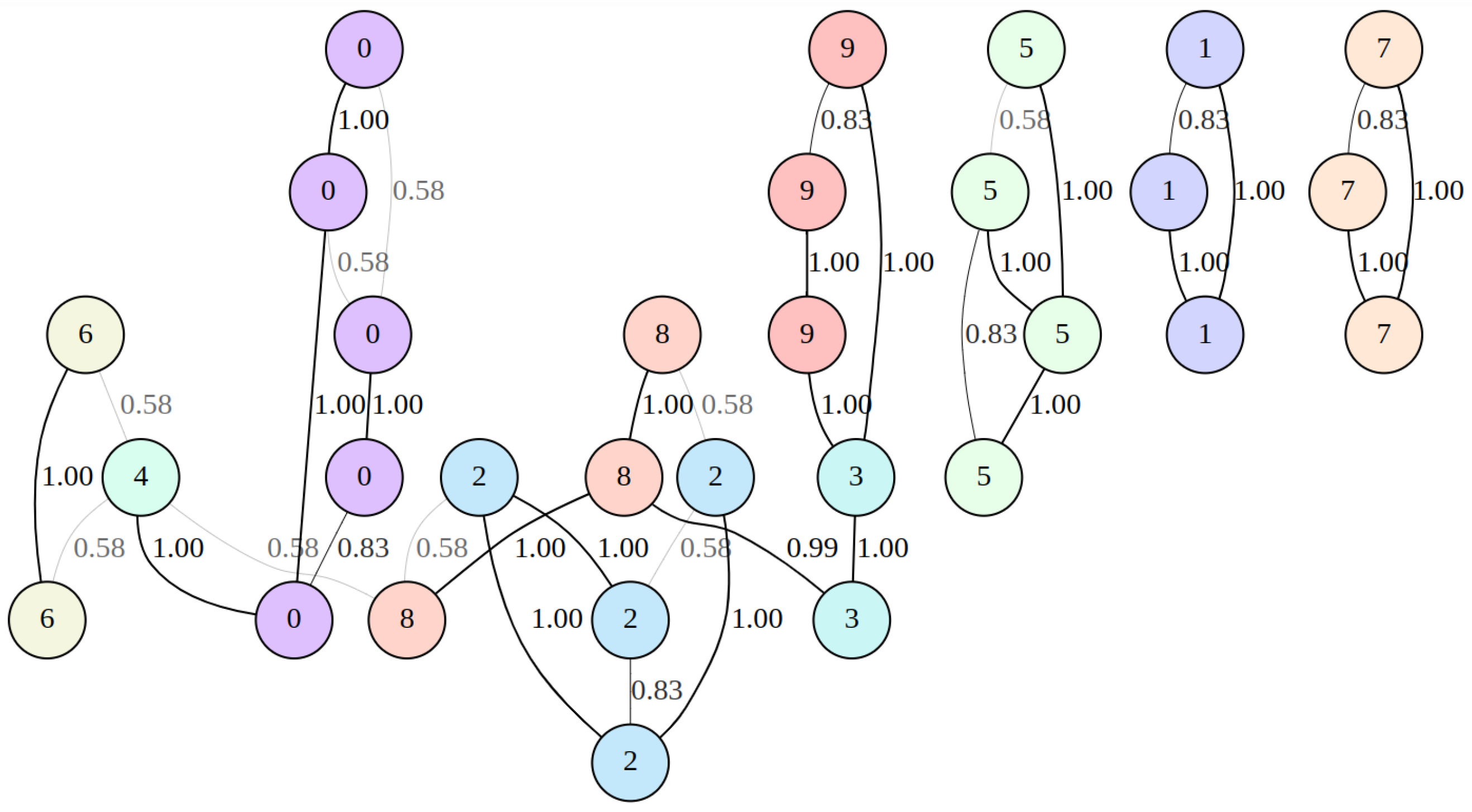
2.1. Fuzzy Weighted Undirected Graph Construction in the UMAP Algorithm
2.2. Loss Function Optimization in the UMAP Algorithm
2.3. Fuzzy Cross Entropy Loss
2.4. Symmetric Fuzzy Cross Entropy Loss
2.5. Modified Fuzzy Cross Entropy Loss
2.6. Adam Optimization Algorithm
| Algorithm 1 Adam | |
| Input: —initial solution, , , —learning step sizes, | |
| 1. | set iteration number to 0 |
| 2. | initialize the and tensors filled with zeros |
| 3. | set |
| 4. | while the stop condition is not met do: |
| 5. | |
| 6. | |
| 7. | |
| 8. | |
| 9. | end loop |
| 10. | return |
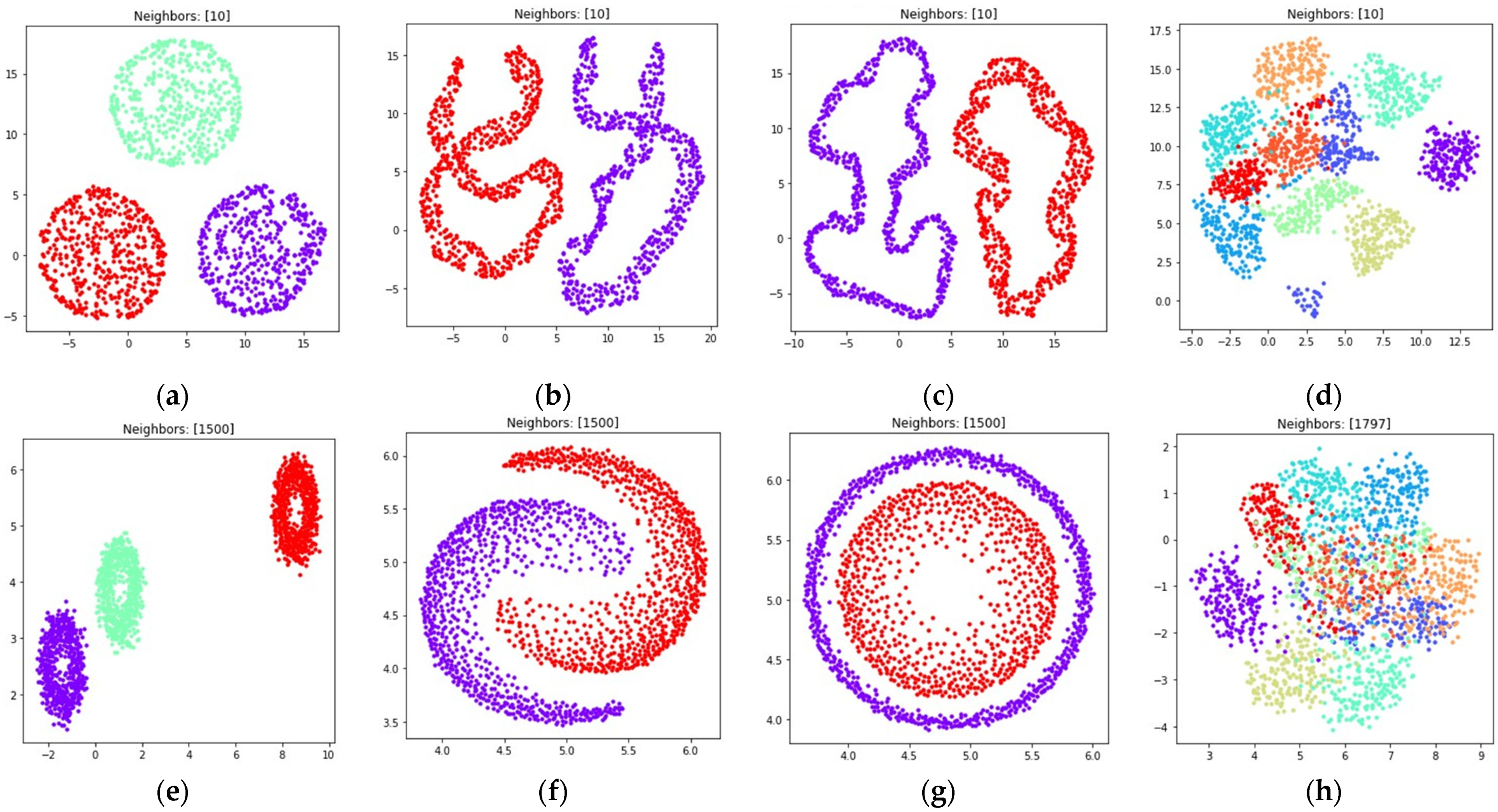
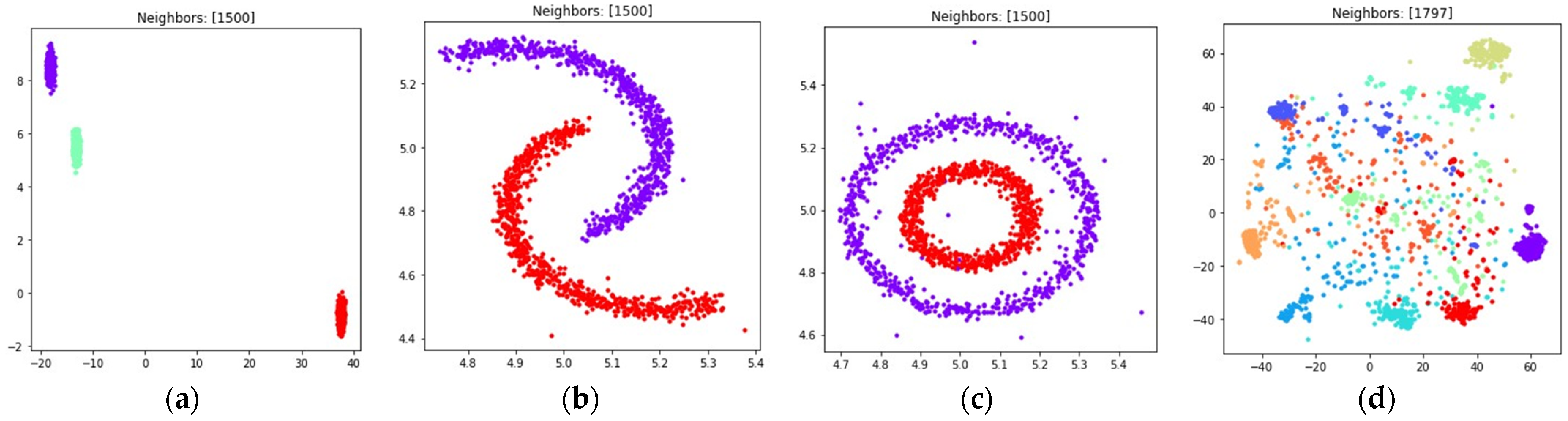
3. Numerical Experiment
3.1. Fuzzy Weighted Adjacency Matrix Construction
3.2. Coefficients Fitting
3.3. Weighted Fuzzy Cross Entropy Loss Optimization
3.4. Fuzzy Cross Entropy Loss Optimization
3.5. Symmetric Fuzzy Cross Entropy Loss Optimization
3.6. Modified Fuzzy Cross Entropy Loss Optimization
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kulikov, A.A. The structure of the local detector of the reprint model of the object in the image. Russ. Technol. J. 2021, 9, 7–13. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Demidova, L.A. Two-stage hybrid data classifiers based on SVM and kNN algorithms. Symmetry 2021, 13, 615. [Google Scholar] [CrossRef]
- Huang, W.; Yin, H. Linear and nonlinear dimensionality reduction for face recognition. In Proceedings of the 2009 16th IEEE International Conference on Image Processing (ICIP), Cairo, Egypt, 7–10 November 2009; pp. 3337–3340. [Google Scholar]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Sammon, J.W. A nonlinear mapping for data structure analysis. IEEE Trans. Comput. 1969, 100, 401–409. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps for dimensionality reduction and data representation. Neural Comput. 2003, 15, 1373–1396. [Google Scholar] [CrossRef] [Green Version]
- Van der Maaten, L.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- McInnes, L.; Healy, J.; Melville, J. UMAP: Uniform manifold approximation and projection for dimension reduction. arXiv 2018, arXiv:1802.03426. [Google Scholar]
- Amid, E.; Warmuth, M.K. TriMap: Large-scale dimensionality reduction using triplets. arXiv 2019, arXiv:1910.00204. [Google Scholar]
- Dorrity, M.W.; Saunders, L.M.; Queitsch, C.; Fields, S.; Trapnell, C. Dimensionality reduction by UMAP to visualize physical and genetic interactions. Nat. Commun. 2020, 11, 1537. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Becht, E.; McInnes, L.; Healy, J.; Dutertre, C.A.; Kwok, I.W.H.; Ng, L.G.; Ginhoux, F.; Newell, E.W. Dimensionality reduction for visualizing single-cell data using UMAP. Nat. Biotechnol. 2019, 37, 38–44. [Google Scholar] [CrossRef] [PubMed]
- Mazher, A. Visualization framework for high-dimensional spatio-temporal hydrological gridded datasets using machine-learning techniques. Water 2020, 12, 590. [Google Scholar] [CrossRef] [Green Version]
- Allaoui, M.; Kherfi, M.L.; Cheriet, A. Considerably improving clustering algorithms using UMAP dimensionality reduction technique: A comparative study. In International Conference on Image and Signal Processing; Springer: Berlin/Heidelberg, Germany, 2020; pp. 317–325. [Google Scholar]
- Hozumi, Y.; Wang, R.; Yin, C.; Wei, G.W. UMAP-assisted K-means clustering of large-scale SARS-CoV-2 mutation datasets. Comput. Biol. Med. 2021, 131, 104264. [Google Scholar] [CrossRef] [PubMed]
- Clément, P.; Bouleux, G.; Cheutet, V. Improved Time-Series Clustering with UMAP dimension reduction method. In Proceedings of the 2020 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 5658–5665. [Google Scholar]
- Weijler, L.; Kowarsch, F.; Wodlinger, M.; Reiter, M.; Maurer-Granofszky, M.; Schumich, A.; Dworzak, M.N. UMAP Based Anomaly Detection for Minimal Residual Disease Quantification within Acute Myeloid Leukemia. Cancers 2022, 14, 898. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, H.; Rudin, C.; Shaposhnik, Y. Understanding how dimension reduction tools work: An empirical approach to deciphering t-SNE, UMAP, TriMAP, and PaCMAP for data visualization. arXiv 2020, arXiv:2012.04456. [Google Scholar]
- Bhandari, D.; Pal, N.R. Some new information measures for fuzzy sets. Inf. Sci. 1993, 67, 209–228. [Google Scholar] [CrossRef]
- Raj Mishra, A.; Jain, D.; Hooda, D.S. On logarithmic fuzzy measures of information and discrimination. J. Inf. Optim. Sci. 2016, 37, 213–231. [Google Scholar] [CrossRef]
- Damrich, S.; Hamprecht, F.A. On UMAP’s true loss function. Adv. Neural Inf. Process. Syst. 2021, 34, 12. [Google Scholar]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharyya, R.; Hossain, S.A.; Kar, S. Fuzzy cross-entropy, mean, variance, skewness models for portfolio selection. J. King Saud Univ. Comput. Inf. Sci. 2014, 26, 79–87. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Dong, W.; Moses, C.; Li, K. Efficient k-nearest neighbor graph construction for generic similarity measures. In Proceedings of the 20th International Conference on World Wide Web, Hyderabad, India, 28 March–1 April 2011; pp. 577–586. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Demidova, L.A.; Gorchakov, A.V. Application of chaotic Fish School Search optimization algorithm with exponential step decay in neural network loss function optimization. Procedia Comput. Sci. 2021, 186, 352–359. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Alpaydin, E.; Kaynak, C. Optical Recognition of Handwritten Digits Data Set. UCI Machine Learning Repository. 1998. Available online: https://archive.ics.uci.edu/ml/datasets/optical+recognition+of+handwritten+digits (accessed on 20 February 2022).
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Lam, S.K.; Pitrou, A.; Seibert, S. Numba: A LLVM-based python JIT compiler. In Proceedings of the Second Workshop on the LLVM Compiler Infrastructure in HPC, Austin, TX, USA, 15 November 2015; pp. 1–6. [Google Scholar]
- Ellson, J.; Gansner, E.R.; Koutsofios, E.; North, S.C.; Woodhull, G. Graphviz and dynagraph—static and dynamic graph drawing tools. In Graph Drawing Software; Springer: Berlin/Heidelberg, Germany, 2004; pp. 127–148. [Google Scholar]
- Li, W.; Tang, Y.M.; Yu, M.K.; To, S. SLC-GAN: An Automated Myocardial Infarction Detection Model Based on Generative Adversarial Networks and Convolutional Neural Networks with Single-Lead Electrocardiogram Synthesis. Inf. Sci. 2022, 589, 738–750. [Google Scholar] [CrossRef]
- Wang, H.Y.; Zhao, J.P.; Zheng, C.H. SUSCC: Secondary Construction of Feature Space based on UMAP for Rapid and Accurate Clustering Large-scale Single Cell RNA-seq Data. Interdiscip. Sci. Comput. Life Sci. 2021, 13, 83–90. [Google Scholar] [CrossRef]
- Hu, H.; Yin, R.; Brown, H.M.; Laskin, J. Spatial segmentation of mass spectrometry imaging data by combining multivariate clustering and univariate thresholding. Anal. Chem. 2021, 93, 3477–3485. [Google Scholar] [CrossRef]
- Chernyshov, K.R. Tsallis Divergence of Order ½ in System Identification Related Problems. In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), Prague, Czech Republic, 29–31 July 2019; pp. 523–533. [Google Scholar]
- Jun, Y.; Jun, Z.; Xuefeng, Y. Two-dimensional Tsallis Symmetric Cross Entropy Image Threshold Segmentation. In Proceedings of the 2012 Fourth International Symposium on Information Science and Engineering, Shanghai, China, 14–16 December 2012; pp. 362–366. [Google Scholar]
- Verma, R.; Merigó, J.M.; Sahni, M. On Generalized Fuzzy Jensen-Exponential Divergence and its Application to Pattern Recognition. In Proceedings of the 2018 IEEE Symposium Series on Computational Intelligence (SSCI), Bangalore, India, 18–21 November 2018; pp. 1515–1519. [Google Scholar]
- Dua, D.; Graff, C. UCI Machine Learning Repository. Irvine, CA: University of California, School of Information and Computer Science. 2019. Available online: http://archive.ics.uci.edu/ml (accessed on 20 February 2022).









| Iteration Limit | |||
|---|---|---|---|
| 1 | 0.9 | 0.999 | 150 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demidova, L.A.; Gorchakov, A.V. Fuzzy Information Discrimination Measures and Their Application to Low Dimensional Embedding Construction in the UMAP Algorithm. J. Imaging 2022, 8, 113. https://doi.org/10.3390/jimaging8040113
Demidova LA, Gorchakov AV. Fuzzy Information Discrimination Measures and Their Application to Low Dimensional Embedding Construction in the UMAP Algorithm. Journal of Imaging. 2022; 8(4):113. https://doi.org/10.3390/jimaging8040113
Chicago/Turabian StyleDemidova, Liliya A., and Artyom V. Gorchakov. 2022. "Fuzzy Information Discrimination Measures and Their Application to Low Dimensional Embedding Construction in the UMAP Algorithm" Journal of Imaging 8, no. 4: 113. https://doi.org/10.3390/jimaging8040113
APA StyleDemidova, L. A., & Gorchakov, A. V. (2022). Fuzzy Information Discrimination Measures and Their Application to Low Dimensional Embedding Construction in the UMAP Algorithm. Journal of Imaging, 8(4), 113. https://doi.org/10.3390/jimaging8040113






