A Green Prospective for Learned Post-Processing in Sparse-View Tomographic Reconstruction
Abstract
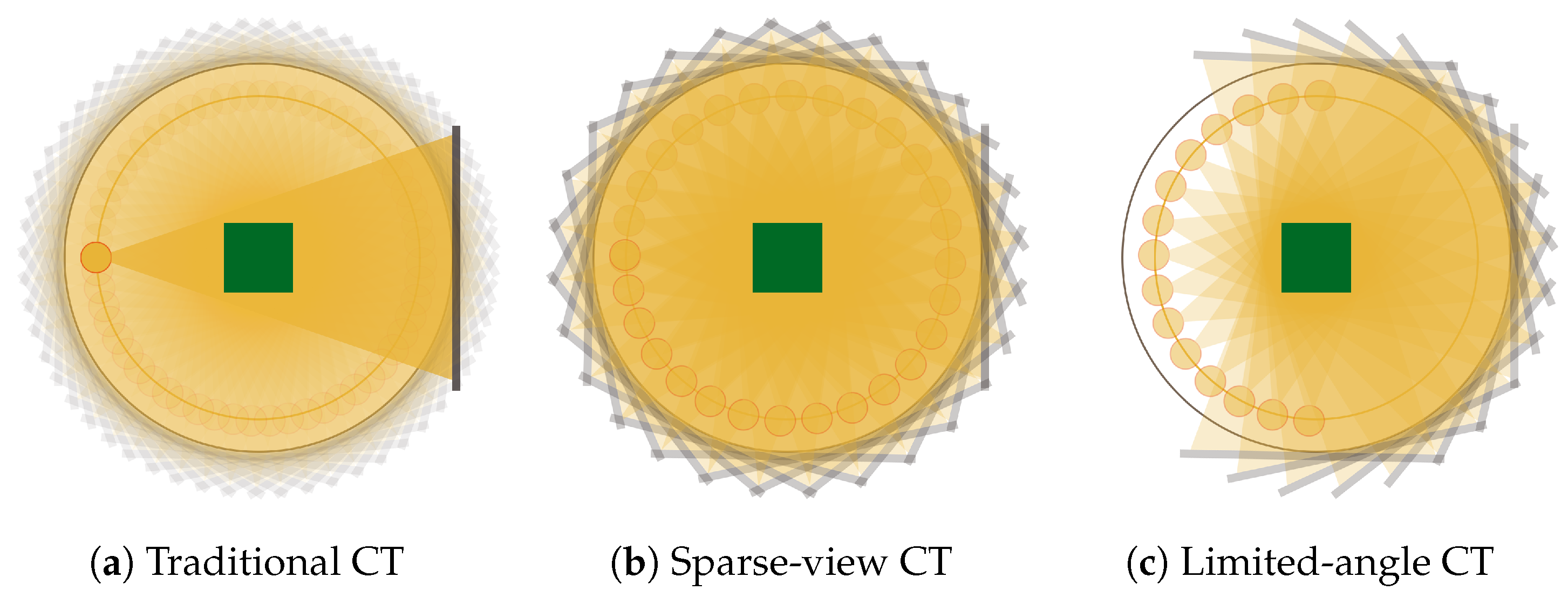
:1. Introduction
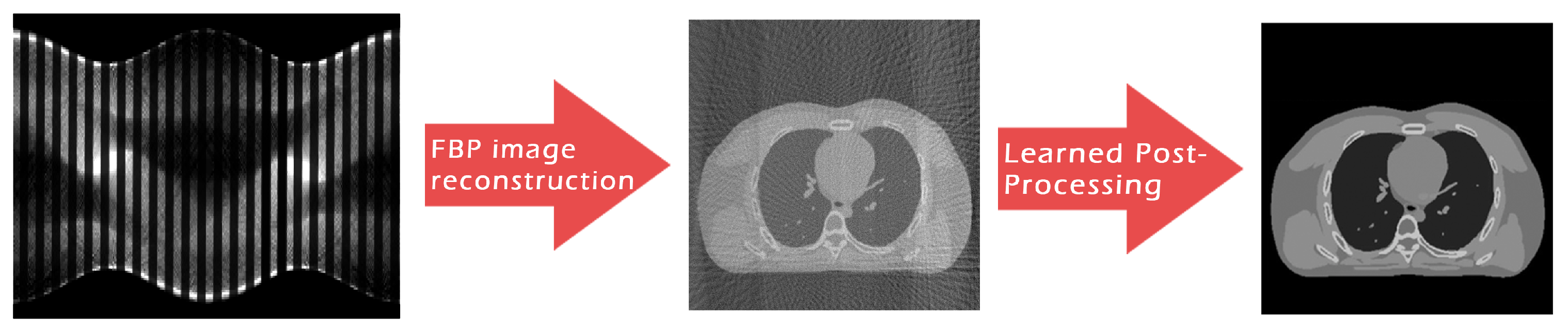
Aim and Contribution of the Paper
2. Methods and Materials
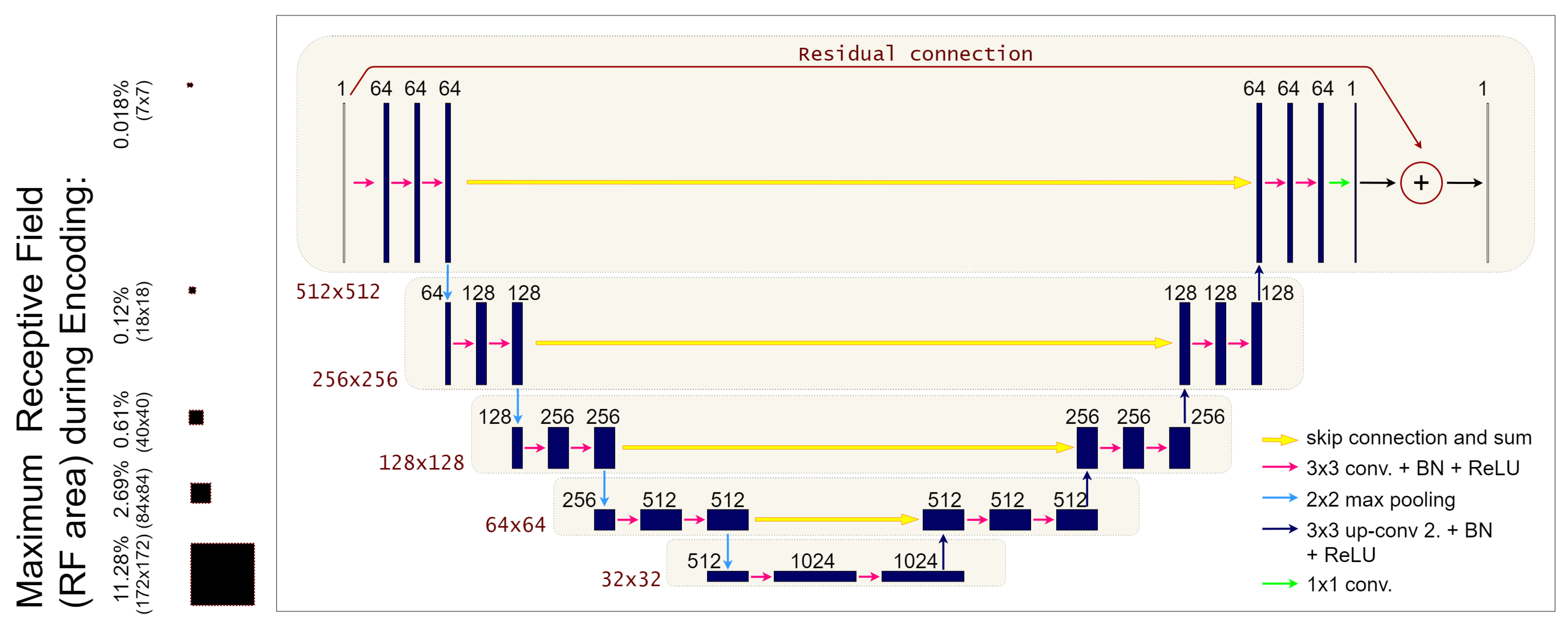
2.1. The ResUNet Architecture
2.2. The 3L-SSNet Architecture
2.3. Receptive Field
2.4. Training of the Networks
2.5. Network Comparison
3. Experimental Results and Discussion
3.1. Metrics for Image Quality Assessment
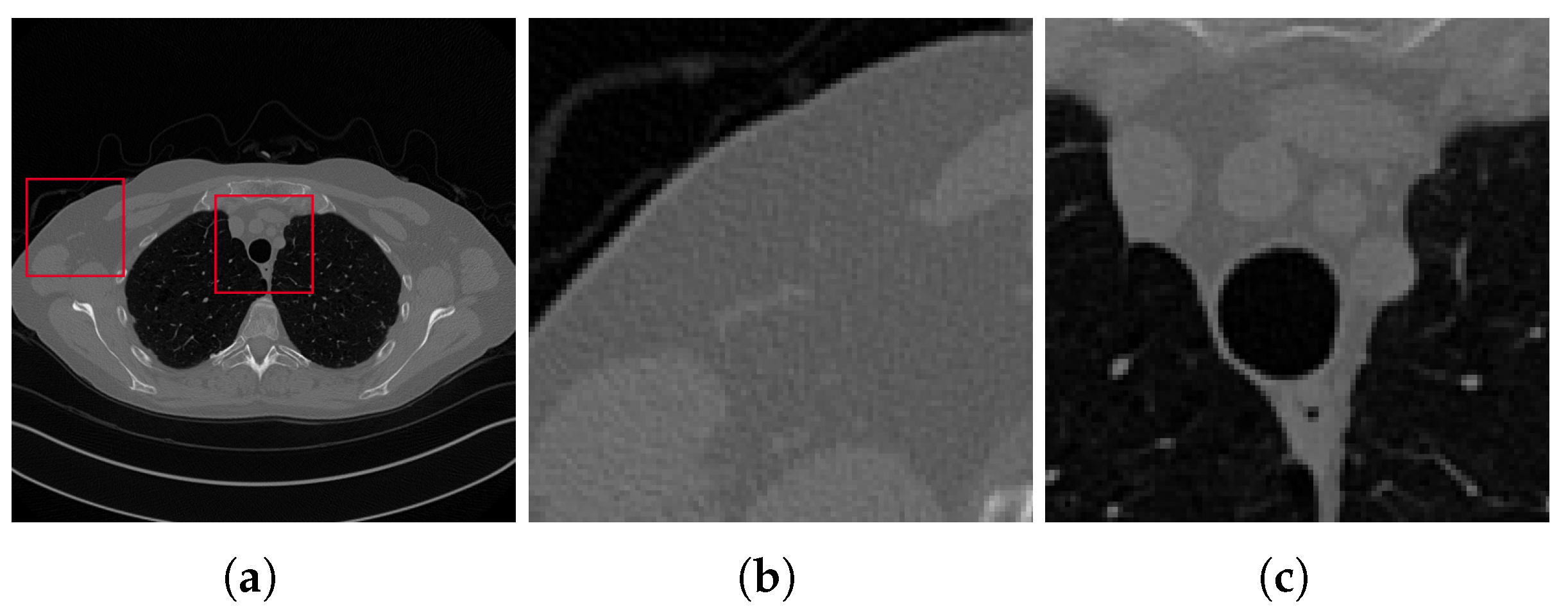
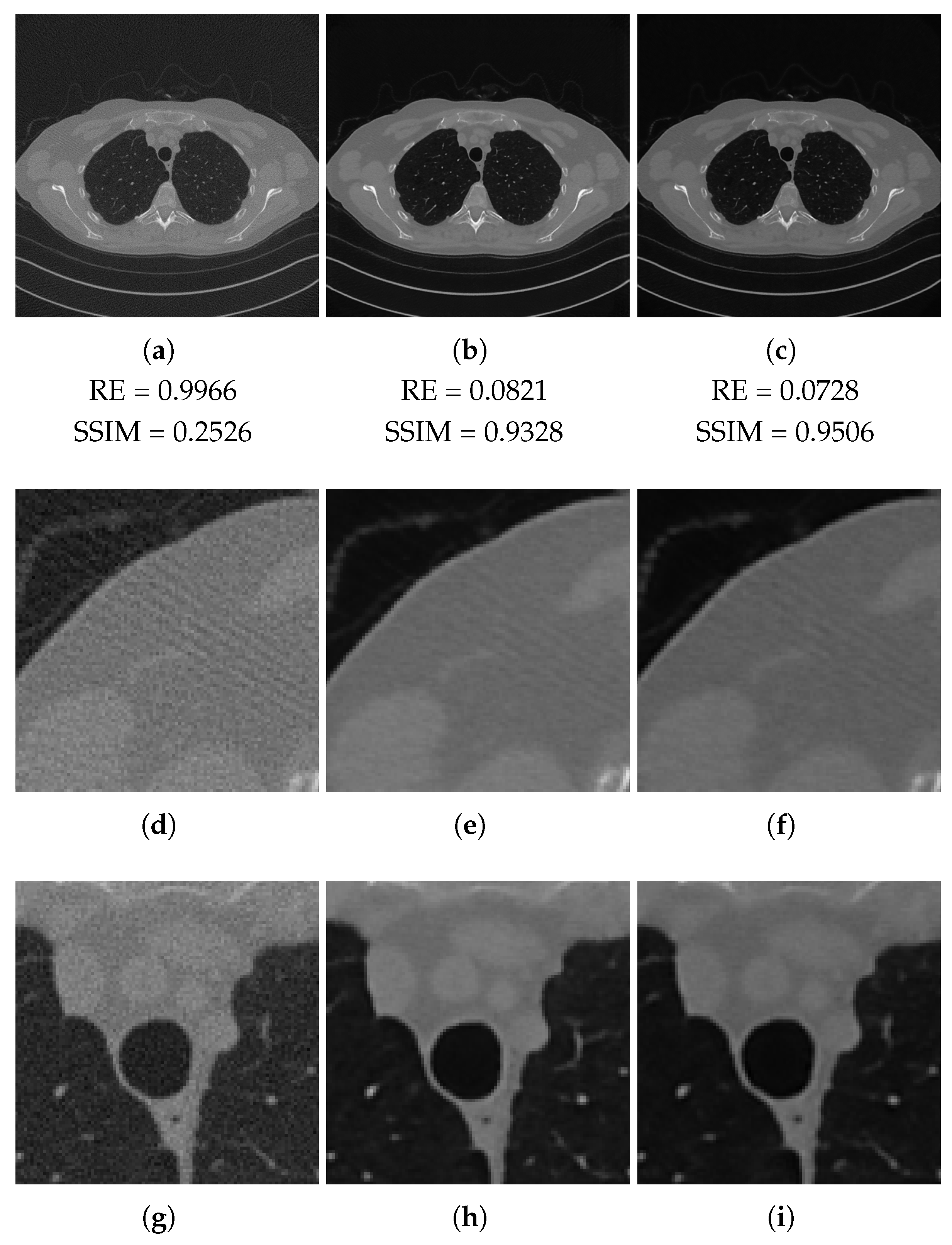
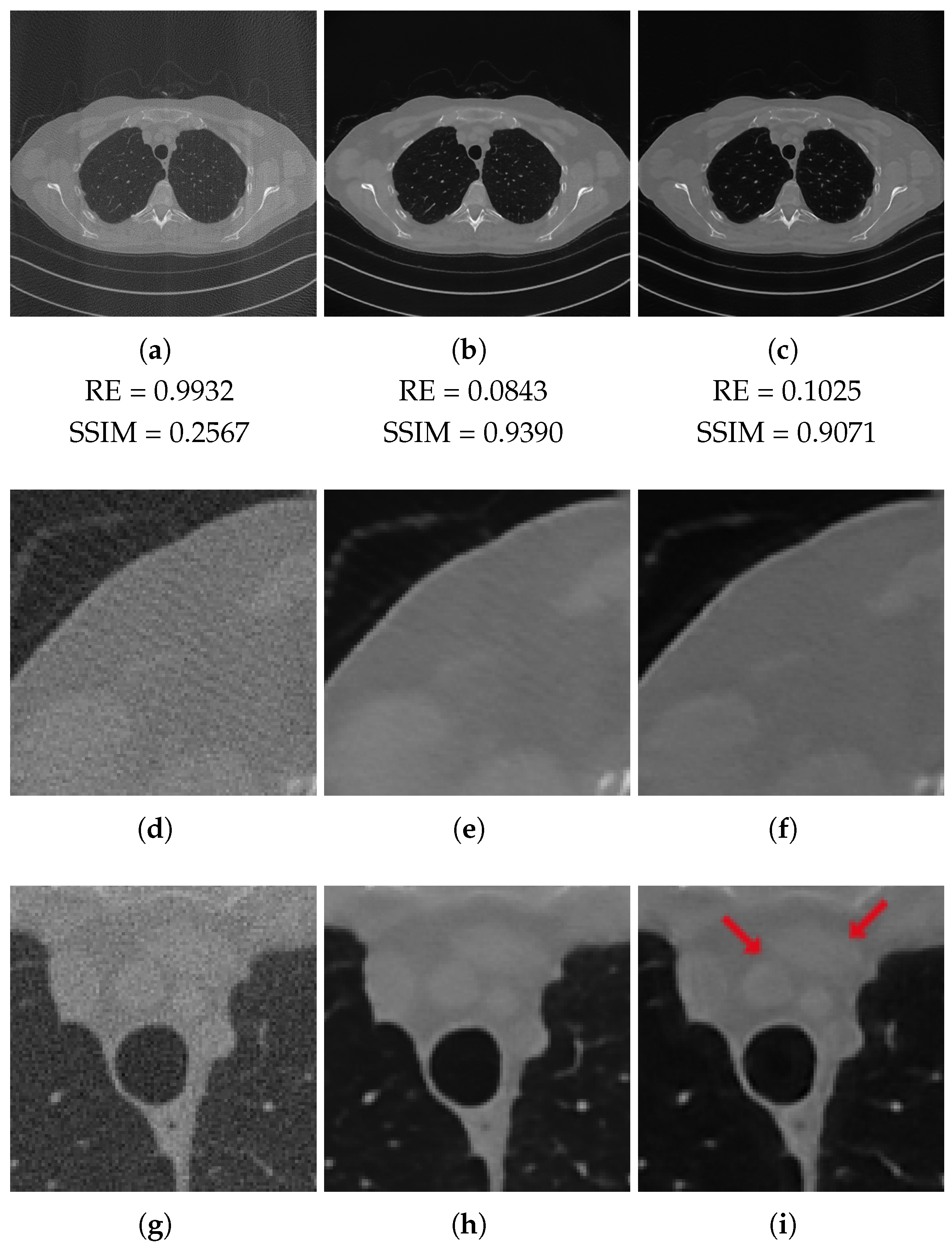
3.2. Results on the Test Set
3.3. Tests on Out-of-Domain Data
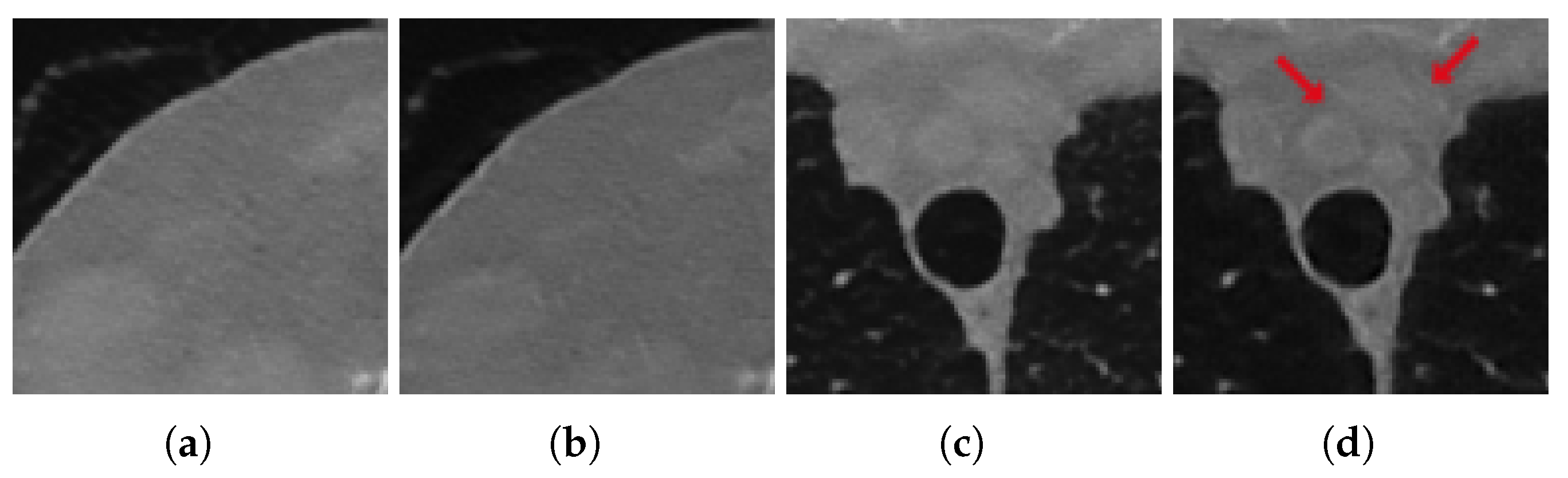
3.3.1. Test on Unseen Noise
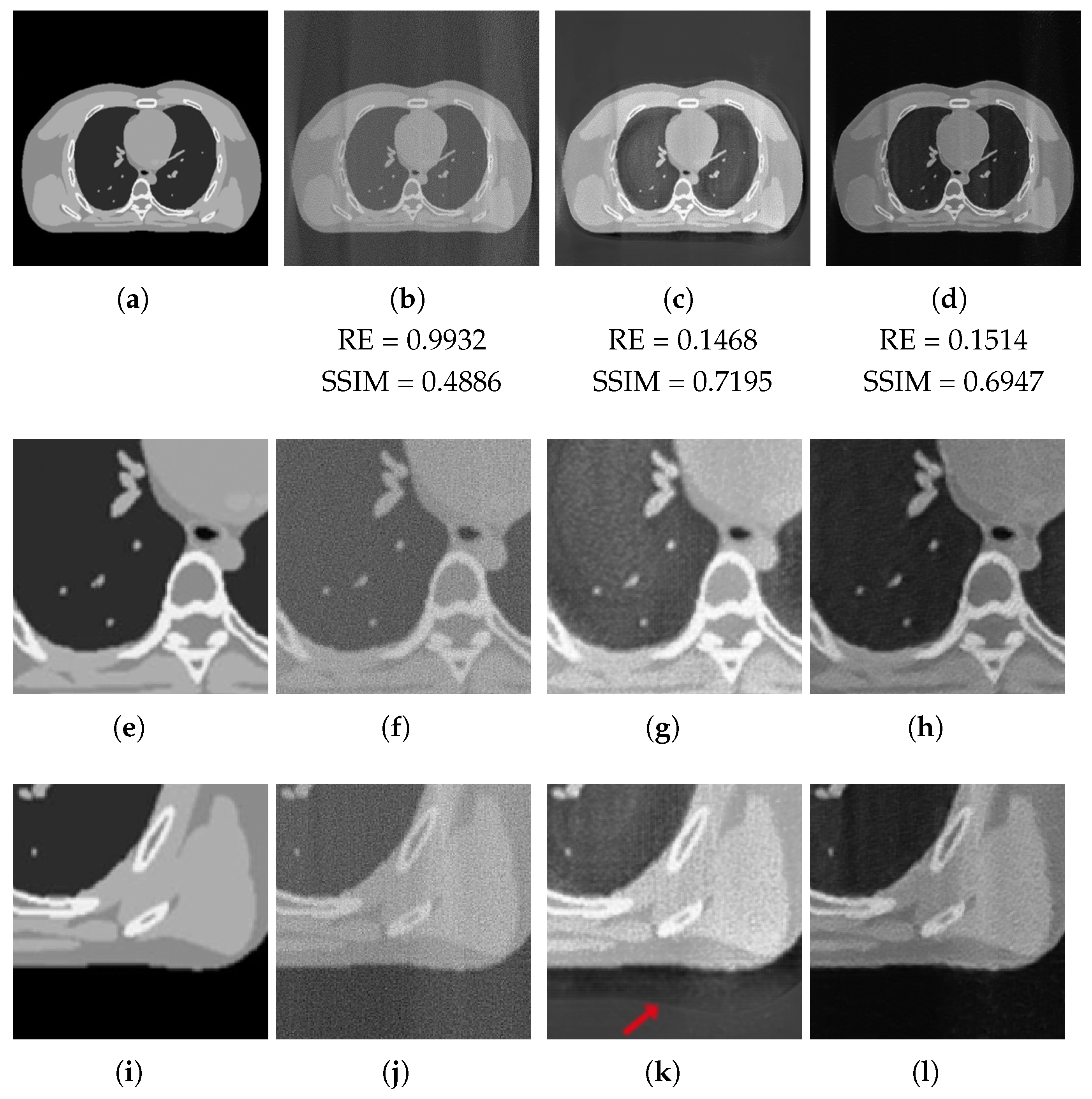
3.3.2. Test on Unseen Image
3.4. Discussion
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arridge, S.; Maass, P.; Öktem, O.; Schönlieb, C.B. Solving inverse problems using data-driven models. Acta Numer. 2019, 28, 1–174. [Google Scholar] [CrossRef] [Green Version]
- McCann, M.T.; Jin, K.H.; Unser, M. Convolutional neural networks for inverse problems in imaging: A review. IEEE Signal Process. Mag. 2017, 34, 85–95. [Google Scholar] [CrossRef] [Green Version]
- Jin, K.H.; McCann, M.T.; Froustey, E.; Unser, M. Deep convolutional neural network for inverse problems in imaging. IEEE Trans. Image Process. 2017, 26, 4509–4522. [Google Scholar] [CrossRef] [Green Version]
- Graff, C.; Sidky, E. Compressive sensing in medical imaging. Appl. Opt. 2015, 54, C23–C44. [Google Scholar] [CrossRef] [Green Version]
- Tian, Z.; Jia, X.; Yuan, K.; Pan, T.; Jiang, S.B. Low Dose CT Reconstruction via Edge-preserving Total Variation Regularization. Phys. Med. Biol. 2011, 56, 5949–5967. [Google Scholar] [CrossRef]
- Jensen, T.L.; Jørgensen, J.H.; Hansen, P.C.; Jensen, S.H. Implementation of an optimal first-order method for strongly convex total variation regularization. BIT Numer. Math. 2012, 52, 329–356. [Google Scholar] [CrossRef] [Green Version]
- Sidky, E.; Chartrand, R.; Boone, J.; Pan, X. Constrained T p V-minimization for enhanced exploitation of gradient sparsity: Application to CT image reconstruction. IEEE J. Transl. Eng. Health Med. 2013, 2, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Liu, L. Model-based Iterative Reconstruction: A Promising Algorithm for Today’s Computed Tomography Imaging. J. Med. Imaging Radiat. Sci. 2014, 45, 131–136. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Loli Piccolomini, E.; Morotti, E. A Model-Based Optimization Framework for Iterative Digital Breast Tomosynthesis Image Reconstruction. J. Imaging 2021, 7, 36. [Google Scholar] [CrossRef]
- Rantala, M.; Vanska, S.; Jarvenpaa, S.; Kalke, M.; Lassas, M.; Moberg, J.; Siltanen, S. Wavelet-based reconstruction for limited-angle X-ray tomography. IEEE Trans. Med. Imaging 2006, 25, 210–217. [Google Scholar] [CrossRef] [PubMed]
- Purisha, Z.; Rimpeläinen, J.; Bubba, T.; Siltanen, S. Controlled wavelet domain sparsity for x-ray tomography. Meas. Sci. Technol. 2017, 29, 014002. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.M.; Dong, B. A review on deep learning in medical image reconstruction. J. Oper. Res. Soc. China 2020, 8, 311–340. [Google Scholar] [CrossRef] [Green Version]
- Ahishakiye, E.; Van Gijzen, M.B.; Tumwiine, J.; Wario, R.; Obungoloch, J. A survey on deep learning in medical image reconstruction. Intell. Med. 2021. [Google Scholar] [CrossRef]
- Zhang, H.; Li, L.; Qiao, K.; Wang, L.; Yan, B.; Li, L.; Hu, G. Image prediction for limited-angle tomography via deep learning with convolutional neural network. arXiv 2016, arXiv:1607.08707. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Li, H.; Mueller, K. Low-dose CT streak artifacts removal using deep residual neural network. In Proceedings of the Fully 3D Conference, Xi’an, China, 18–23 June 2017; pp. 191–194. [Google Scholar]
- Han, Y.; Ye, J.C. Framing U-Net via deep convolutional framelets: Application to sparse-view CT. IEEE Trans. Med. Imaging 2018, 37, 1418–1429. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, T.; Gao, H.; Xing, Y.; Chen, Z.; Zhang, L. DualRes-UNet: Limited Angle Artifact Reduction for Computed Tomography. In Proceedings of the 2019 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC), Manchester, UK, 26 October–2 November 2019; pp. 1–3. [Google Scholar]
- Han, Y.; Ye, J.C. Deep residual learning approach for sparse-view CT reconstruction. Fully Three-Dimensional Image Reconstruction in Radiology and Nuclear Medicine. In Proceedings of the Fully 3D Conference Organization, Xi’an, China, 18–23 June 2017. [Google Scholar]
- Schnurr, A.K.; Chung, K.; Russ, T.; Schad, L.R.; Zöllner, F.G. Simulation-based deep artifact correction with convolutional neural networks for limited angle artifacts. Z. Med. Phys. 2019, 29, 150–161. [Google Scholar] [CrossRef] [PubMed]
- Han, Y.S.; Yoo, J.; Ye, J.C. Deep residual learning for compressed sensing CT reconstruction via persistent homology analysis. arXiv 2016, arXiv:1611.06391. [Google Scholar]
- Huang, Y.; Würfl, T.; Breininger, K.; Liu, L.; Lauritsch, G.; Maier, A. Some investigations on robustness of deep learning in limited angle tomography. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Granada, Spain, 16–20 September 2018; pp. 145–153. [Google Scholar]
- Liu, C.; Huang, Y.; Maier, J.; Klein, L.; Kachelrieß, M.; Maier, A. Robustness Investigation on Deep Learning CT Reconstruction for Real-Time Dose Optimization. arXiv 2020, arXiv:2012.03579. [Google Scholar]
- Schwartz, R.; Dodge, J.; Smith, N.A.; Etzioni, O. Green ai. Commun. ACM 2020, 63, 54–63. [Google Scholar] [CrossRef]
- Strubell, E.; Ganesh, A.; McCallum, A. Energy and policy considerations for deep learning in NLP. arXiv 2019, arXiv:1906.02243. [Google Scholar]
- Strubell, E.; Ganesh, A.; McCallum, A. Energy and Policy Considerations for Modern Deep Learning Research. In Proceedings of the AAAI Conference on Artificial Intelligence, New York, NY, USA, 2–17 February 2020; Volume 34, pp. 13693–13696. [Google Scholar] [CrossRef]
- Asperti, A.; Evangelista, D.; Piccolomini, E.L. A Survey on Variational Autoencoders from a Green AI Perspective. SN Comput. Sci. 2021, 2, 1–23. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Kang, E.; Min, J.; Ye, J.C. A deep convolutional neural network using directional wavelets for low-dose X-ray CT reconstruction. Med. Phys. 2017, 44, e360–e375. [Google Scholar] [CrossRef] [Green Version]
- Ye, J.C.; Han, Y.; Cha, E. Deep convolutional framelets: A general deep learning framework for inverse problems. SIAM J. Imaging Sci. 2018, 11, 991–1048. [Google Scholar] [CrossRef]
- Bubba, T.A.; Kutyniok, G.; Lassas, M.; Maerz, M.; Samek, W.; Siltanen, S.; Srinivasan, V. Learning the invisible: A hybrid deep learning-shearlet framework for limited angle computed tomography. Inverse Probl. 2019, 35, 064002. [Google Scholar] [CrossRef] [Green Version]
- Heinrich, M.; Stille, M.; Buzug, T. Residual U-Net Convolutional Neural Network Architecture for Low-Dose CT Denoising. Curr. Dir. Biomed. Eng. 2018, 4, 297–300. [Google Scholar] [CrossRef]
- Wang, J.; Zeng, L.; Wang, C.; Guo, Y. ADMM-based deep reconstruction for limited-angle CT. Phys. Med. Biol. 2019, 64, 115011. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Zhang, Y.; Zhang, W.; Liao, P.; Li, K.; Zhou, J.; Wang, G. Low-dose CT via convolutional neural network. Biomed. Opt. Express 2017, 8, 679–694. [Google Scholar] [CrossRef] [PubMed]
- Le, H.; Borji, A. What are the Receptive, Effective Receptive, and Projective Fields of Neurons in Convolutional Neural Networks? arXiv 2017, arXiv:1705.07049. [Google Scholar]
- Araujo, A.; Norris, W.; Sim, J. Computing Receptive Fields of Convolutional Neural Networks. Distill 2019, 4, e21. [Google Scholar] [CrossRef]
- McCollough, C. TU-FG-207A-04: Overview of the Low Dose CT Grand Challenge. Med. Phys. 2016, 43, 3759–3760. [Google Scholar] [CrossRef]
- Van Aarle, W.; Palenstijn, W.J.; De Beenhouwer, J.; Altantzis, T.; Bals, S.; Batenburg, K.J.; Sijbers, J. The ASTRA Toolbox: A platform for advanced algorithm development in electron tomography. Ultramicroscopy 2015, 157, 35–47. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A Feature Similarity Index for Image Quality Assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Segars, W.P.; Sturgeon, G.; Mendonca, S.; Grimes, J.; Tsui, B.M. 4D XCAT phantom for multimodality imaging research. Med. Phys. 2010, 37, 4902–4915. [Google Scholar] [CrossRef] [PubMed]
- Russ, T.; Goerttler, S.; Schnurr, A.K.; Bauer, D.F.; Hatamikia, S.; Schad, L.R.; Zöllner, F.G.; Chung, K. Synthesis of CT images from digital body phantoms using CycleGAN. Int. J. Comput. Assist. Radiol. Surg. 2019, 14, 1741–1750. [Google Scholar] [CrossRef] [PubMed]

| Parameters | FLOPs | Training Time | |
|---|---|---|---|
| ResUNet | 209 | ||
| 3L-SSNet | 53 |
| RE | PSNR | SSIM | FSIM | |
|---|---|---|---|---|
| FBP | 0.9966 | 86.42 (33.89) | 0.2924 | 0.5456 |
| ResUNet | 0.0942 | 106.99 (41.95) | 0.9262 | 0.9709 |
| 3L-SSNet | 0.0840 | 107.92 (42.32) | 0.9480 | 0.9627 |
| RE | PSNR | SSIM | FSIM | |
|---|---|---|---|---|
| FBP | 0.9932 | 86.45 (33.90) | 0.2962 | 0.6819 |
| ResUNet | 0.1016 | 106.38 (41.71) | 0.9324 | 0.9478 |
| 3L-SSNet | 0.1309 | 104.34 (40.91) | 0.9021 | 0.9474 |
| FBP | ResUNet | 3L-SSNet | ||||
|---|---|---|---|---|---|---|
| RE | SSIM | RE | SSIM | RE | SSIM | |
| Full-range | 0.9966 | 0.2526 | 0.0966 | 0.9172 | 0.0896 | 0.9295 |
| Half-range | 0.9932 | 0.2567 | 0.0986 | 0.9212 | 0.1162 | 0.8866 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morotti, E.; Evangelista, D.; Loli Piccolomini, E. A Green Prospective for Learned Post-Processing in Sparse-View Tomographic Reconstruction. J. Imaging 2021, 7, 139. https://doi.org/10.3390/jimaging7080139
Morotti E, Evangelista D, Loli Piccolomini E. A Green Prospective for Learned Post-Processing in Sparse-View Tomographic Reconstruction. Journal of Imaging. 2021; 7(8):139. https://doi.org/10.3390/jimaging7080139
Chicago/Turabian StyleMorotti, Elena, Davide Evangelista, and Elena Loli Piccolomini. 2021. "A Green Prospective for Learned Post-Processing in Sparse-View Tomographic Reconstruction" Journal of Imaging 7, no. 8: 139. https://doi.org/10.3390/jimaging7080139
APA StyleMorotti, E., Evangelista, D., & Loli Piccolomini, E. (2021). A Green Prospective for Learned Post-Processing in Sparse-View Tomographic Reconstruction. Journal of Imaging, 7(8), 139. https://doi.org/10.3390/jimaging7080139








