Demonstration of Focusing Wolter Mirrors for Neutron Phase and Magnetic Imaging
Abstract
:1. Introduction
2. Materials and Methods
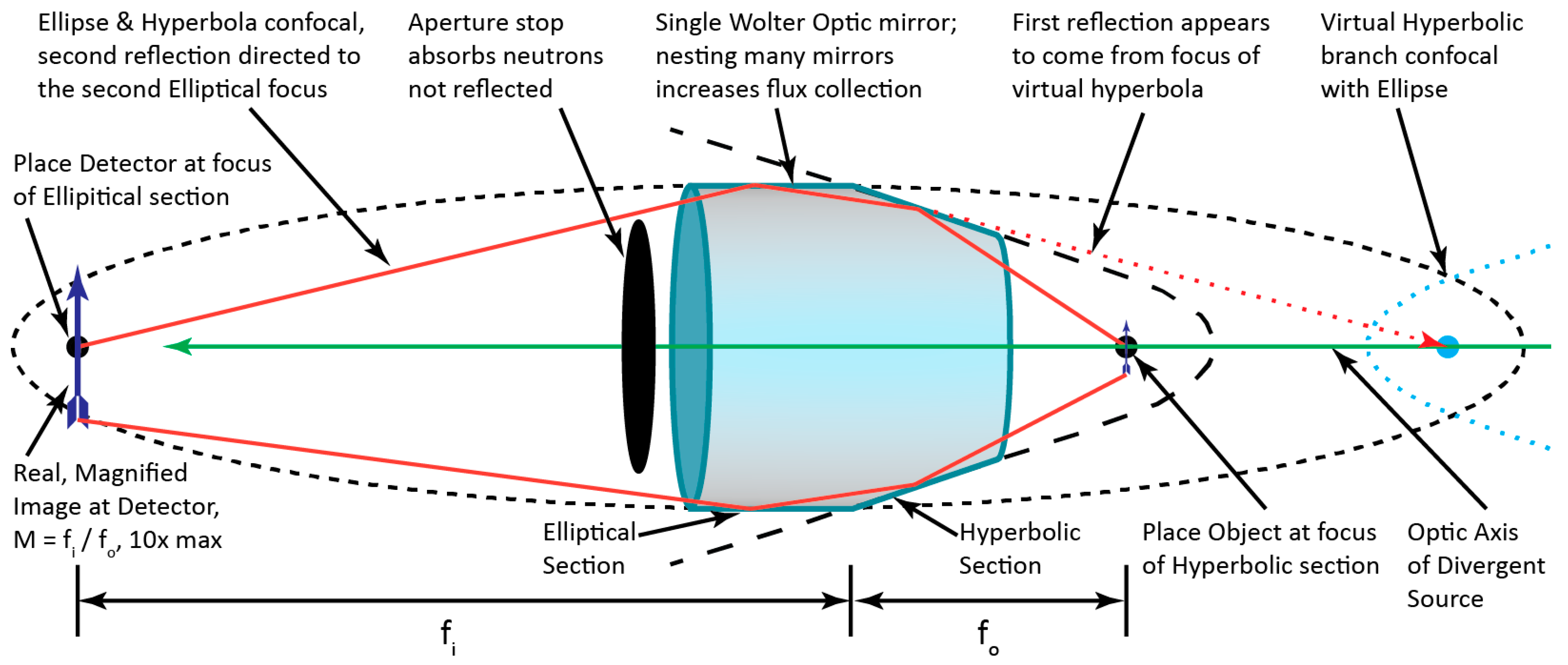
2.1. Wolter Optic
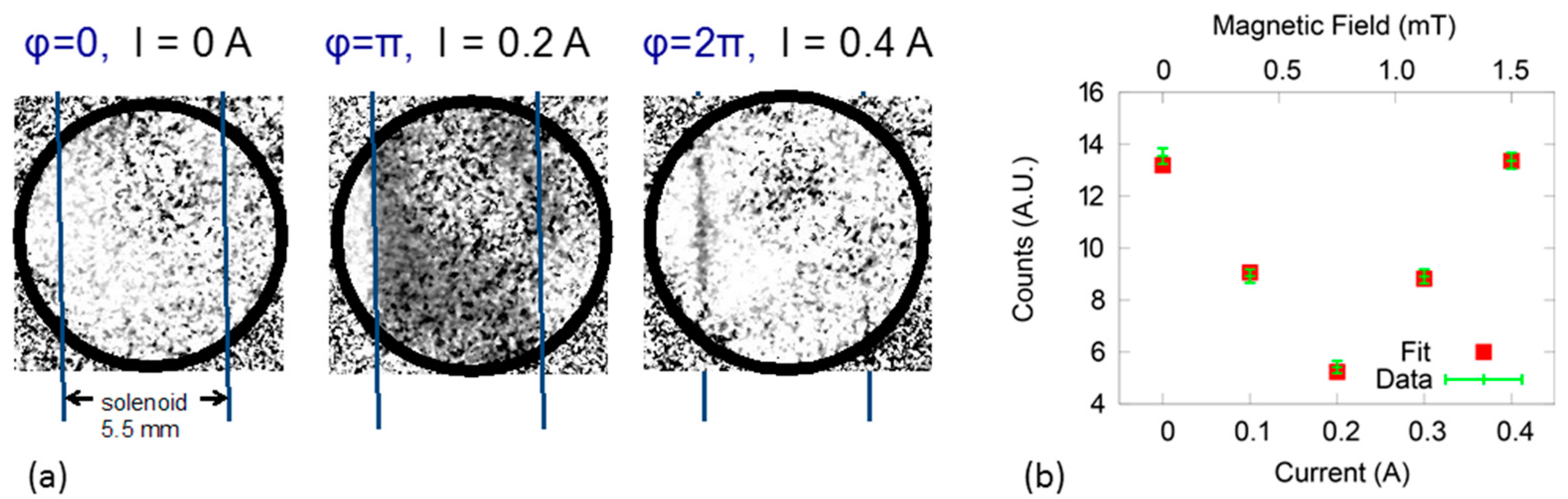
2.2. Wolter Optics, Helium-3 Neutron Imaging of Magnetic Samples (WHIMS)
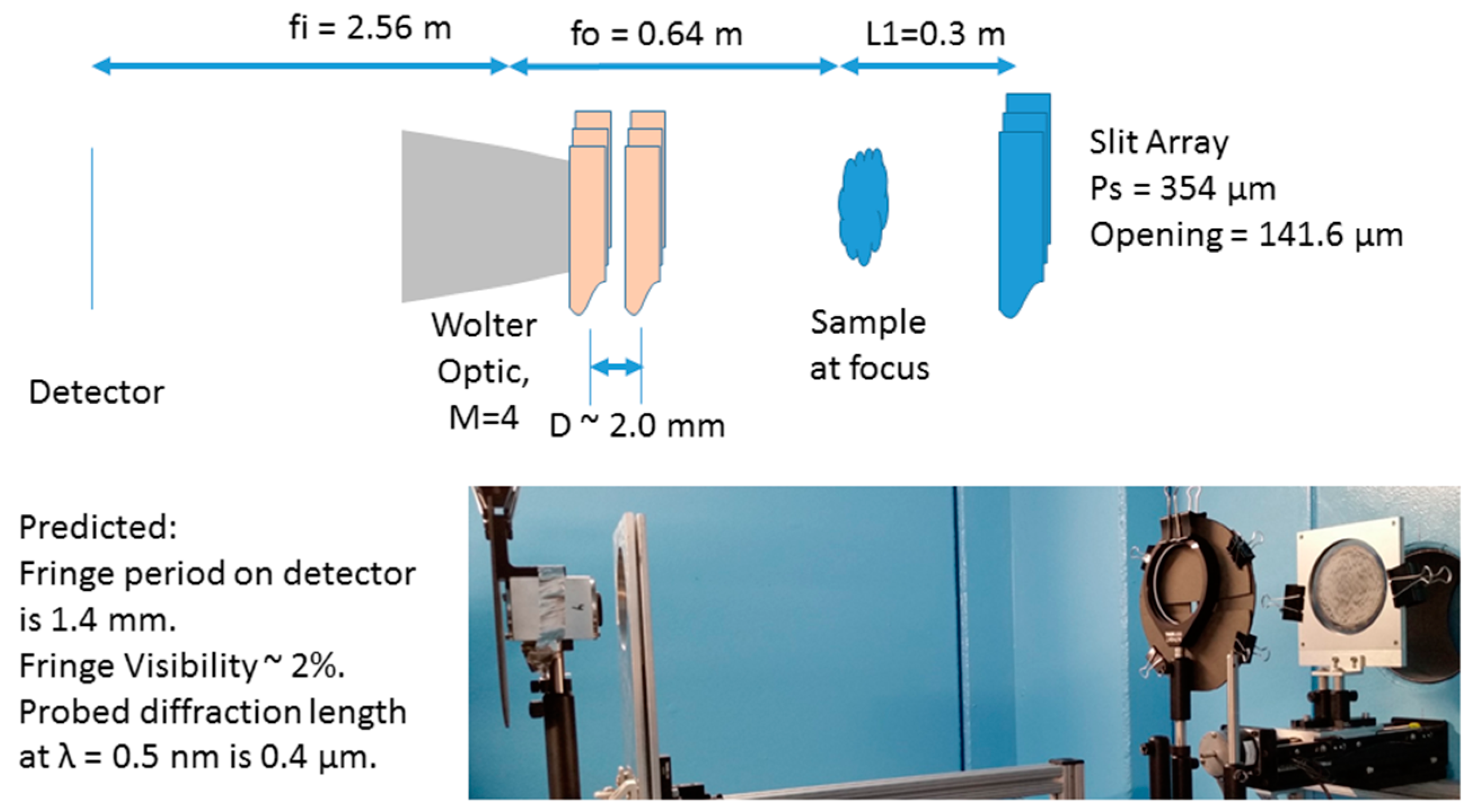
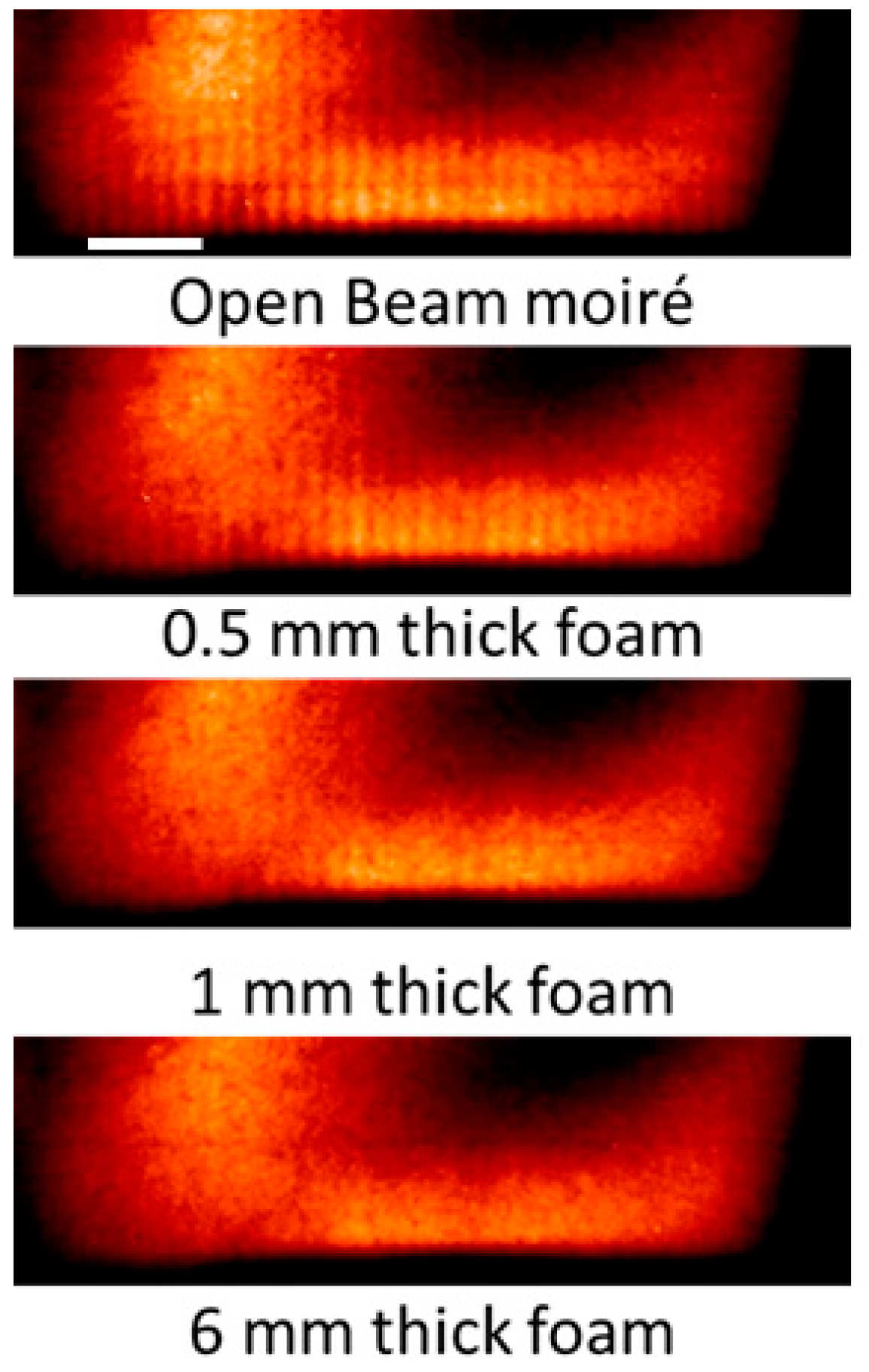
2.3. Wolter Optics Far-Field Interferometry (WOOFF)
3. Results
3.1. WHIMS
3.2. WOOFF
4. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References and Note
- Eskildsen, M.R.; Gammel, P.L.; Isaacs, E.D.; Detlefs, C.; Mortensen, K.; Bishop, D.J. Compound refractive optics for the imaging and focusing of low-energy neutrons. Nature 1998, 391, 563–566. [Google Scholar]
- Kardjilov, N.; Manke, I.; Strobl, M.; Hilger, A.; Treimer, W.; Meissner, M.; Krist, T.; Banhart, J. Three-dimensional imaging of magnetic fields with polarized neutrons. Nat. Phys. 2008, 4, 399–403. [Google Scholar] [CrossRef]
- Treimer, W.; Ebrahimi, O.; Karakas, N.; Prozorov, R. Polarized neutron imaging and three-dimensional calculation of magnetic flux trapping in bulk of superconductors. Phys. Rev. B 2012, 85, 184522. [Google Scholar] [CrossRef]
- Treimer, W. Radiography and tomography with polarized neutrons. J. Magn. Magn. Mater. 2014, 350, 188–198. [Google Scholar] [CrossRef]
- Miao, H.; Panna, A.; Gomella, A.A.; Bennett, E.E.; Znati, S.; Chen, L.; Wen, H. A universal moiré effect and application in X-ray phase-contrast imaging. Nat. Phys. 2016, 12, 830–834. [Google Scholar] [CrossRef] [PubMed]
- Pushin, D.A.; Sarenac, D.; Hussey, D.S.; Miao, H.; Arif, M.; Cory, D.G.; Huber, M.G.; Jacobson, D.L.; LaManna, J.M.; Parker, J.D.; et al. Far-field interference of a neutron white beam and the applications to noninvasive phase-contrast imaging. Phys. Rev. A 2017, 95, 043637. [Google Scholar] [CrossRef]
- Khaykovich, B.; Gubarev, M.V.; Bagdasarova, Y.; Ramsey, B.D.; Moncton, D.E. From X-ray telescopes to neutron scattering: Using axisymmetric mirrors to focus a neutron beam. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2011, 631, 98–104. [Google Scholar] [CrossRef]
- Liu, D.; Hussey, D.; Gubarev, M.V.; Ramsey, B.D.; Jacobson, D.; Arif, M.; Moncton, D.E.; Khaykovich, B. Demonstration of Achromatic Cold-Neutron Microscope Utilizing Axisymmetric Focusing Mirrors. Appl. Phys Lett. 2013, 102, 183508. [Google Scholar] [CrossRef]
- Hussey, D.S.; Brocker, C.; Cook, J.C.; Jacobson, D.L.; Gentile, T.R.; Chen, W.C.; Baltic, E.; Baxter, D.V.; Doskow, J.; Arif, M. A New Cold Neutron Imaging Instrument at NIST. Phys. Procedia 2015, 69, 48–54. [Google Scholar] [CrossRef]
- Certain trade names and company products are mentioned in the text or identified in an illustration in order to adequately specify the experimental procedure and equipment used. In no case does such identification imply recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that the products are necessarily the best available for the purpose.
- Gentile, T.R.; Babcock, E.; Borchers, J.A.; Chen, W.C.; Hussey, D.; Jones, G.L.; Lee, W.T.; Majkzrak, C.F.; O’Donovan, K.V.; Snow, W.M.; et al. Polarized spin filters in neutron scattering. Phys. B Condens. Matter. 2005, 356, 96–102. [Google Scholar] [CrossRef]
- Chen, W.C.; Gentile, T.R.; Erwin, R.; Watson, S.; Ye, Q.; Krycka, K.L.; Maranville, B.B. 3He spin filter based polarized neutron capability at the NIST Center for Neutron Research. J. Phys. Conf. Ser. 2014, 528, 012014. [Google Scholar] [CrossRef]
- Wen, H.; Bennett, E.E.; Hegedus, M.M.; Carroll, S.C. Spatial Harmonic Imaging of X-ray Scattering—Initial Results. IEEE Trans. Med. Imaging 2008, 27, 997–1002. [Google Scholar] [CrossRef] [PubMed]
- Lefmann, K.; Nielsen, K. McStas, a general software package for neutron ray-tracing simulations. Neutron News. 1999, 10, 20–23. [Google Scholar] [CrossRef]
- Willendrup, P.; Farhi, E.; Lefmann, K. McStas 1.7—A new version of the flexible Monte Carlo neutron scattering package. Phys. B Condens. Matter. 2004, 350, E735–E737. [Google Scholar] [CrossRef]
- Wu, H.; Khaykovich, B.; Wang, X.; Hussey, D.S. Wolter mirrors for neutron imaging. Phys. Procedia 2017, 88, 184–189. [Google Scholar] [CrossRef]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussey, D.S.; Wen, H.; Wu, H.; Gentile, T.R.; Chen, W.; Jacobson, D.L.; LaManna, J.M.; Khaykovich, B. Demonstration of Focusing Wolter Mirrors for Neutron Phase and Magnetic Imaging. J. Imaging 2018, 4, 50. https://doi.org/10.3390/jimaging4030050
Hussey DS, Wen H, Wu H, Gentile TR, Chen W, Jacobson DL, LaManna JM, Khaykovich B. Demonstration of Focusing Wolter Mirrors for Neutron Phase and Magnetic Imaging. Journal of Imaging. 2018; 4(3):50. https://doi.org/10.3390/jimaging4030050
Chicago/Turabian StyleHussey, Daniel S., Han Wen, Huarui Wu, Thomas R. Gentile, Wangchun Chen, David L. Jacobson, Jacob M. LaManna, and Boris Khaykovich. 2018. "Demonstration of Focusing Wolter Mirrors for Neutron Phase and Magnetic Imaging" Journal of Imaging 4, no. 3: 50. https://doi.org/10.3390/jimaging4030050
APA StyleHussey, D. S., Wen, H., Wu, H., Gentile, T. R., Chen, W., Jacobson, D. L., LaManna, J. M., & Khaykovich, B. (2018). Demonstration of Focusing Wolter Mirrors for Neutron Phase and Magnetic Imaging. Journal of Imaging, 4(3), 50. https://doi.org/10.3390/jimaging4030050




