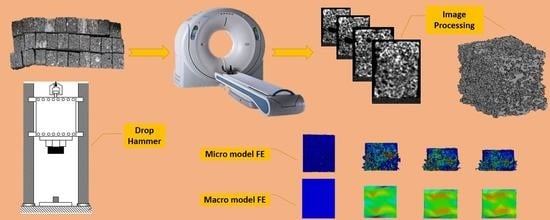
CT-Based Micro-Mechanical Approach to Predict Response of Closed-Cell Porous Biomaterials to Low-Velocity Impact
Abstract
1. Introduction
2. Experimental Tests
2.1. Material
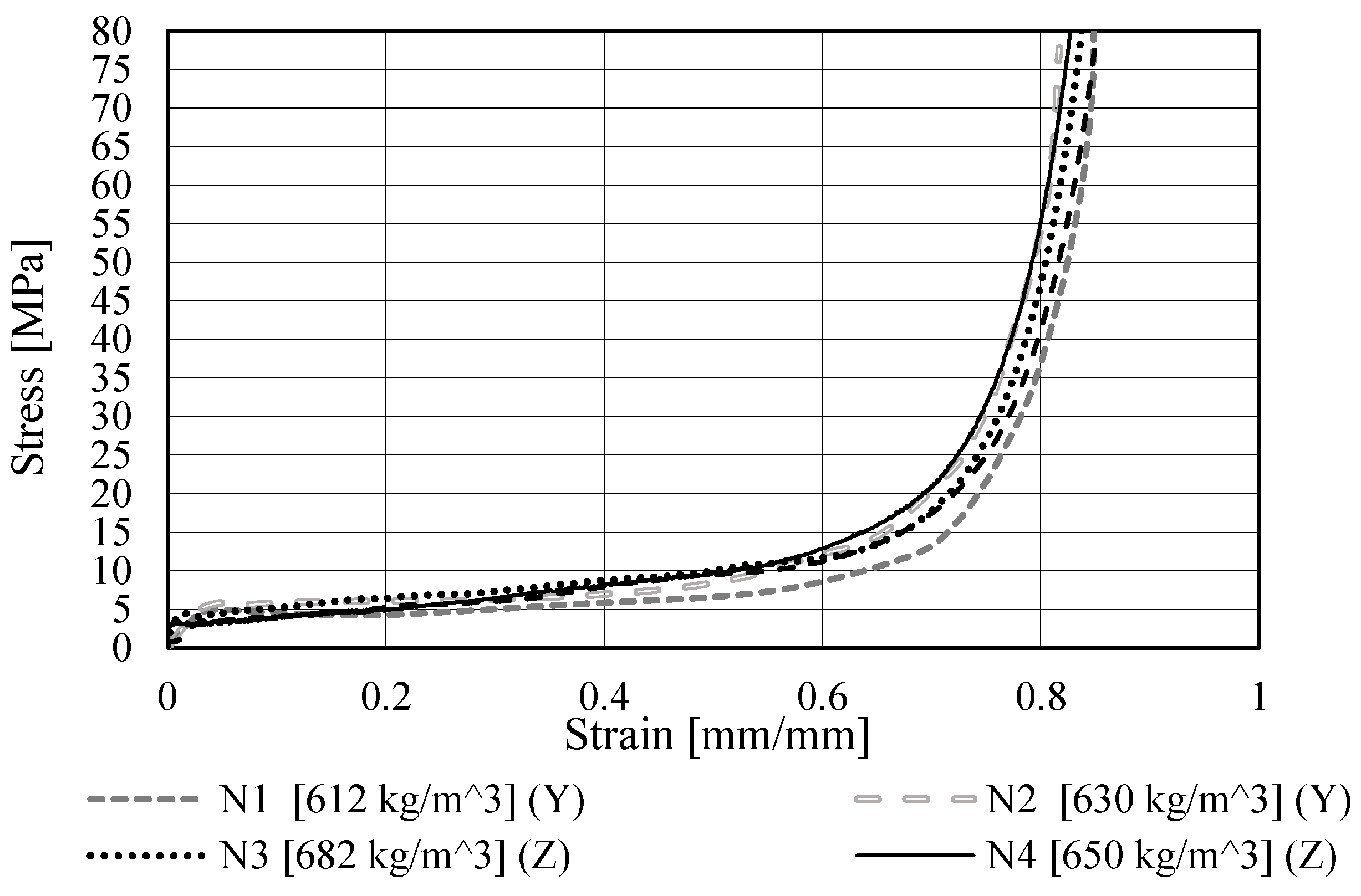
2.2. Compressive Quasi-Static Tests
2.3. Drop Hammer Impact Tests
3. FE Modeling
3.1. Micro-Scale Model
3.2. Macro-Scale Model
4. Results and Discussions
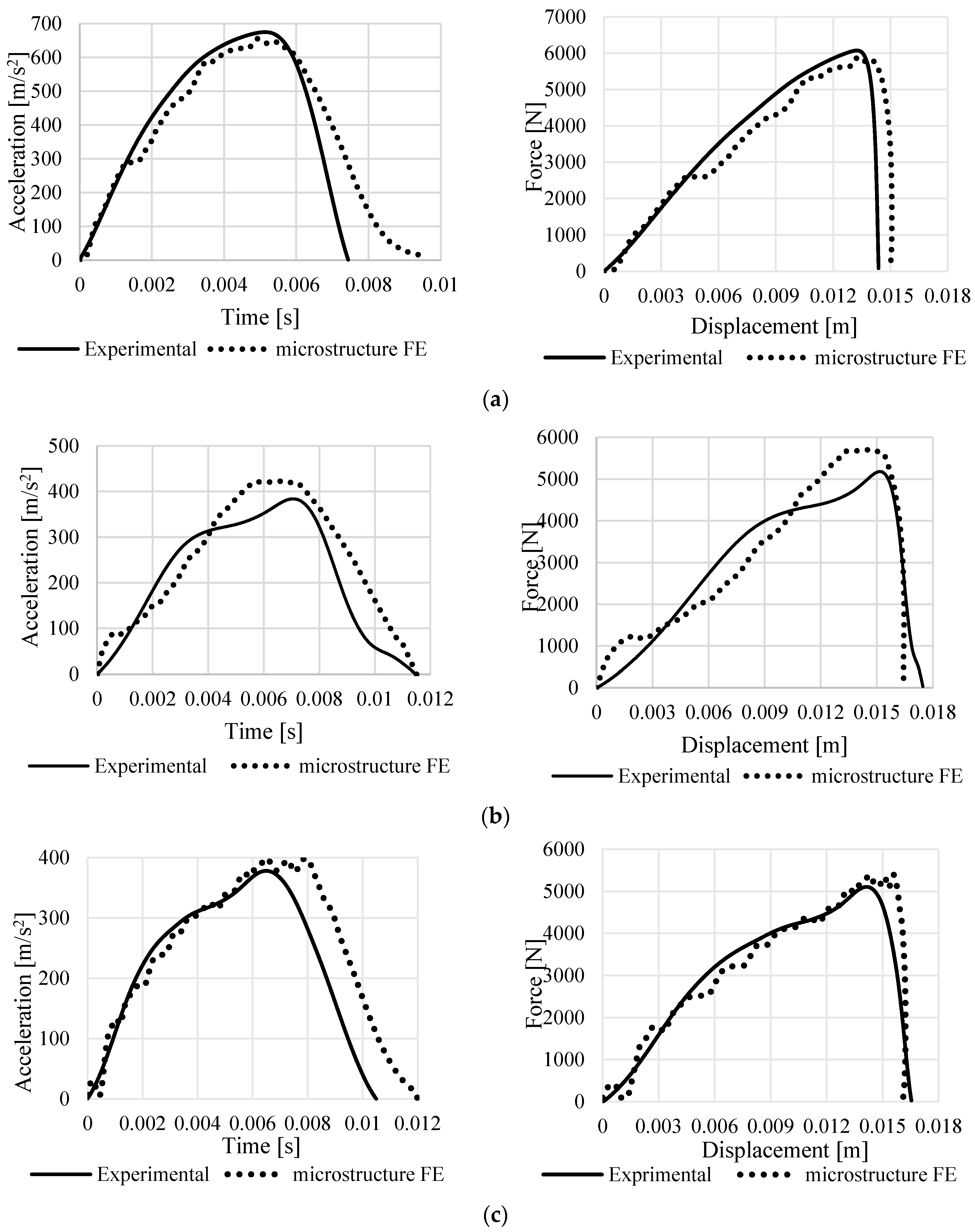
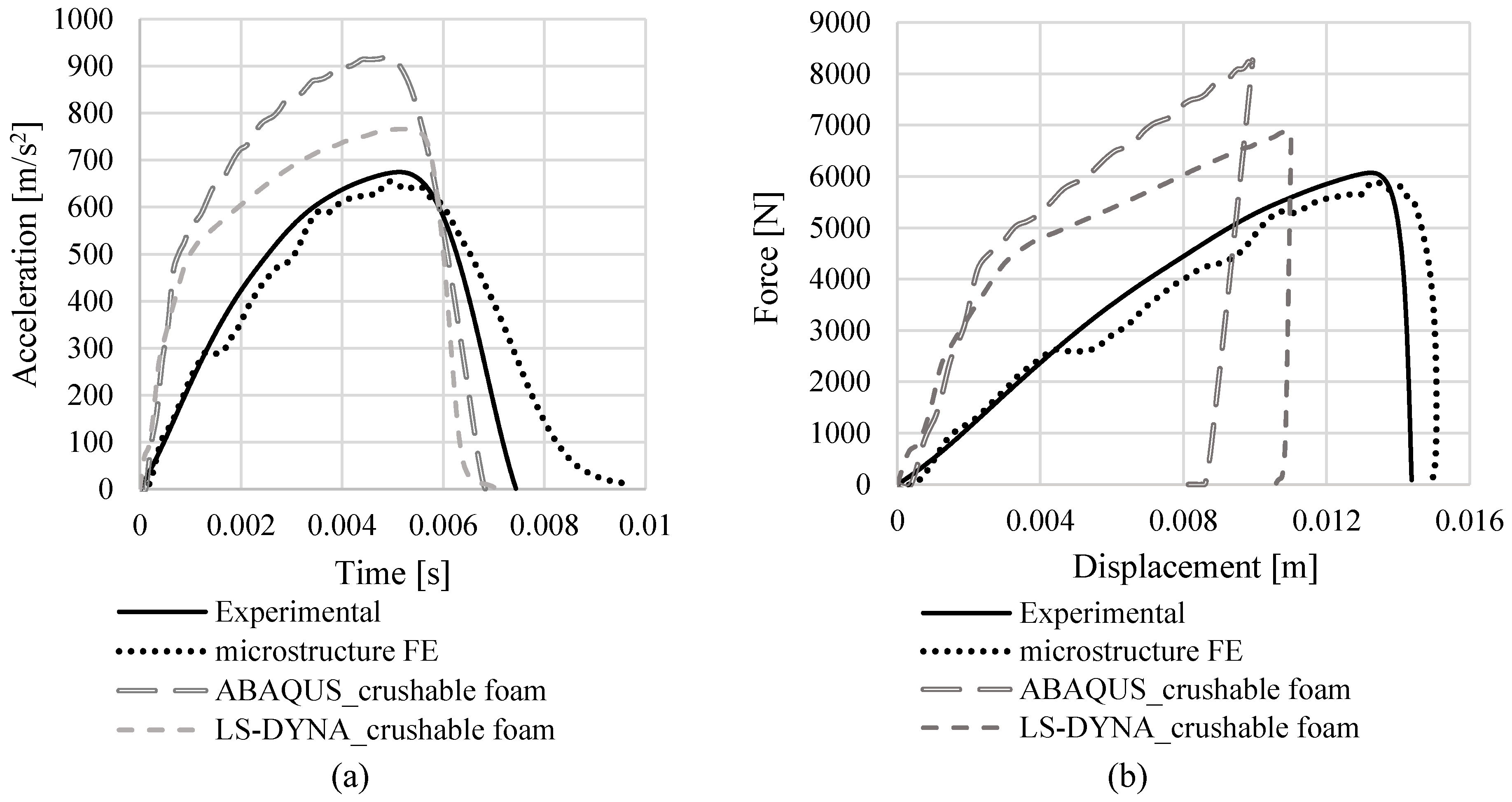
4.1. Validation of the Micro-Scale FE Models
4.2. Comparison of the Results of Micro- and Macro-Scale Models
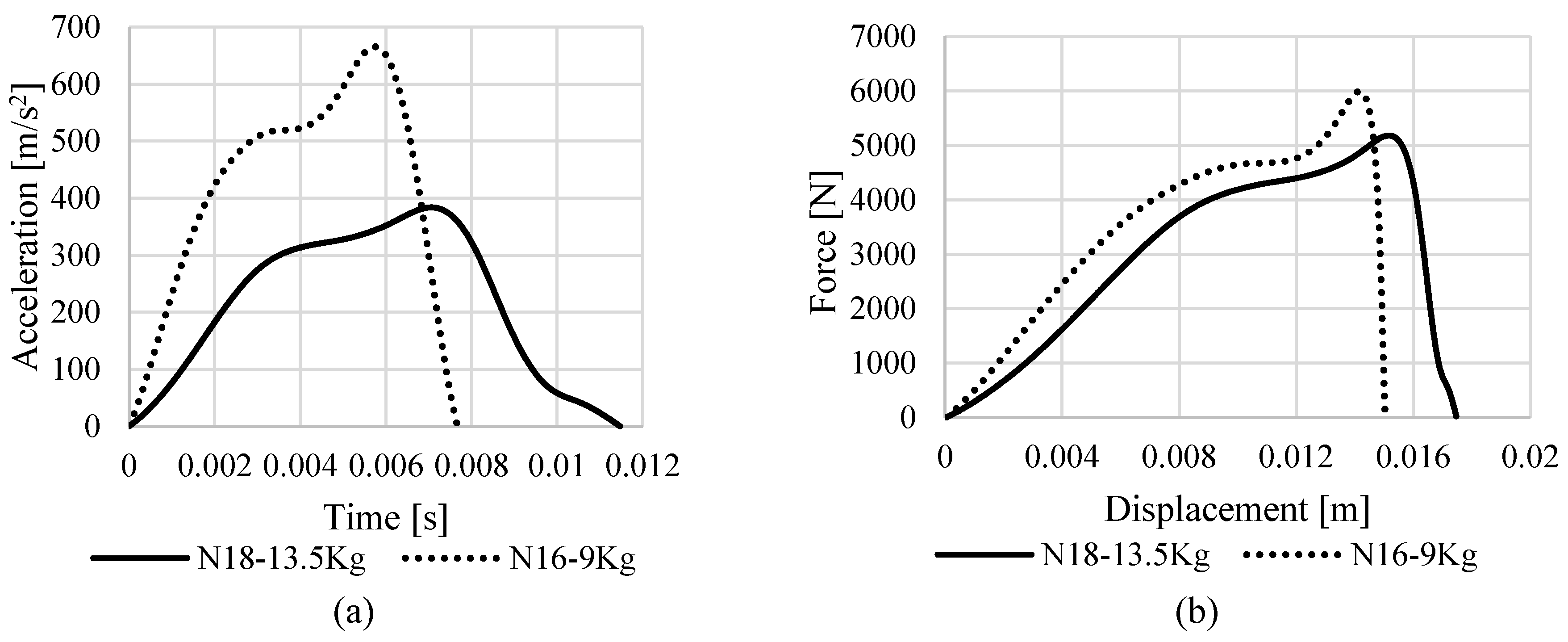
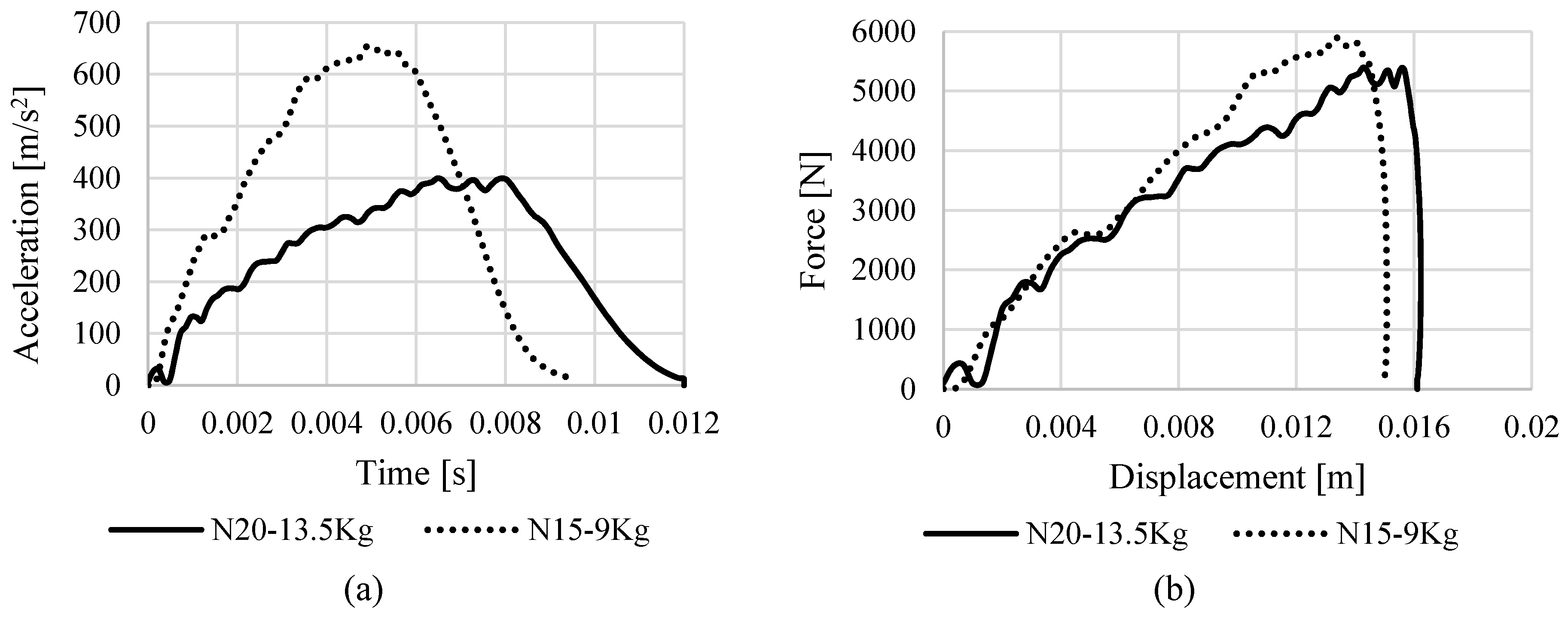
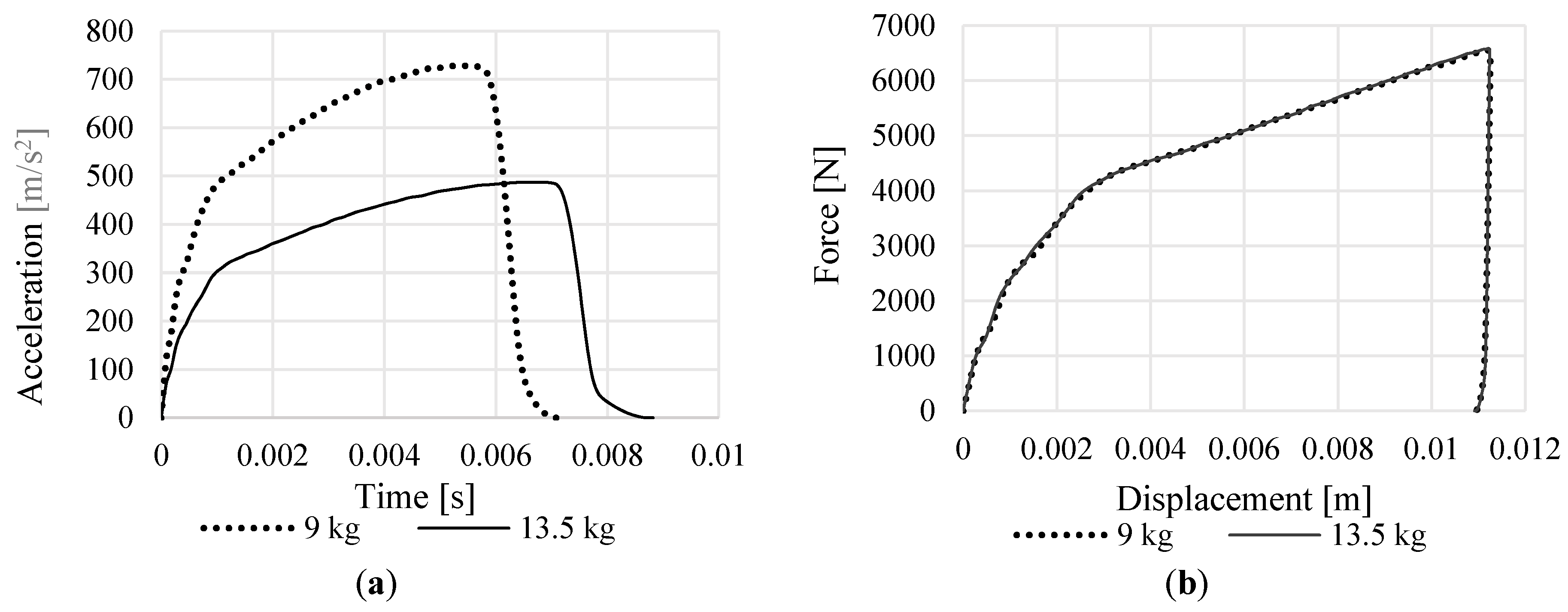
4.3. Effect of Drop Weight Initial Height and Mass
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Hongkong, China, 1997. [Google Scholar]
- Hedayati, R.; Sadighi, M.; Mohammadi-Aghdam, M.; Zadpoor, A.A. Mechanical properties of regular porous biomaterials made from truncated cube repeating unit cells: Analytical solutions and computational models. Mater. Sci. Eng. C 2016, 60, 163–183. [Google Scholar] [CrossRef] [PubMed]
- Warren, W.; Kraynik, A. Linear elastic behavior of a low-density kelvin foam with open cells. J. Appl. Mech. 1997, 64, 787–794. [Google Scholar] [CrossRef]
- Hedayati, R.; Sadighi, M.; Mohammadi Aghdam, M.; Zadpoor, A.A. Mechanical properties of additively manufactured thick honeycombs. Materials 2016, 9, 613. [Google Scholar] [CrossRef] [PubMed]
- Weaire, D.; Phelan, R. Cellular structures in three dimensions. Philos. Trans. R. Soc. Lond. A: Math. Phys. Eng. Sci. 1996, 354, 1989–1997. [Google Scholar] [CrossRef]
- Veyhl, C.; Belova, I.; Murch, G.; Fiedler, T. Finite element analysis of the mechanical properties of cellular aluminium based on micro-computed tomography. Mater. Sci. Eng. A 2011, 528, 4550–4555. [Google Scholar] [CrossRef]
- Miedzińska, D.; Niezgoda, T.; Gieleta, R. Numerical and experimental aluminum foam microstructure testing with the use of computed tomography. Comput. Mater. Sci. 2012, 64, 90–95. [Google Scholar] [CrossRef]
- Bock, J.; Jacobi, A.M. Geometric classification of open-cell metal foams using X-ray micro-computed tomography. Mater. Charact. 2013, 75, 35–43. [Google Scholar] [CrossRef]
- Hedayati, R.; Sadighi, M.; Mohammadi-Aghdam, M.; Zadpoor, A. Mechanical behavior of additively manufactured porous biomaterials made from truncated cuboctahedron unit cells. Int. J. Mech. Sci. 2016, 106, 19–38. [Google Scholar] [CrossRef]
- Hedayati, R.; Sadighi, M.; Mohammadi-Aghdam, M.; Zadpoor, A.A. Mechanics of additively manufactured porous biomaterials based on the rhombicuboctahedron unit cell. J. Mech. Behav. Biomed. Mater. 2016, 53, 272–294. [Google Scholar] [CrossRef] [PubMed]
- Stress Shielding. Available online: https://en.wikipedia.org/wiki/Stress_shielding (accessed on 10 January 2018).
- Banhart, J. Manufacture, characterisation and application of cellular metals and metal foams. Prog. Mater. Sci. 2001, 46, 559–632. [Google Scholar] [CrossRef]
- Ashby, M.F.; Evans, T.; Fleck, N.A.; Hutchinson, J.; Wadley, H.; Gibson, L. Metal Foams: A Design Guide; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Rajendran, R.; Moorthi, A.; Basu, S. Numerical simulation of drop weight impact behaviour of closed cell aluminium foam. Mater. Des. 2009, 30, 2823–2830. [Google Scholar] [CrossRef]
- Li, B.; Zhao, G.; Lu, T. Low strain rate compressive behavior of high porosity closed-cell aluminum foams. Sci. China Tech. Sci. 2012, 55, 451–463. [Google Scholar] [CrossRef]
- Zhang, C.; Tang, L.; Yang, B.; Zhang, L.; Huang, X.; Fang, D. Meso-mechanical study of collapse and fracture behaviors of closed-cell metallic foams. Comput. Mater. Sci. 2013, 79, 45–51. [Google Scholar] [CrossRef]
- Liu, Y.; Gong, W.; Zhang, X. Numerical investigation of influences of porous density and strain-rate effect on dynamical responses of aluminum foam. Comput. Mater. Sci. 2014, 91, 223–230. [Google Scholar] [CrossRef]
- Fang, Q.; Zhang, J.; Zhang, Y.; Liu, J.; Gong, Z. Mesoscopic investigation of closed-cell aluminum foams on energy absorption capability under impact. Compos. Struct. 2015, 124, 409–420. [Google Scholar] [CrossRef]
- Wang, P.; Xu, S.; Li, Z.; Yang, J.; Zhang, C.; Zheng, H.; Hu, S. Experimental investigation on the strain-rate effect and inertia effect of closed-cell aluminum foam subjected to dynamic loading. Mater. Sci. Eng. A 2015, 620, 253–261. [Google Scholar] [CrossRef]
- Andrews, E.; Gioux, G.; Onck, P.; Gibson, L. Size effects in ductile cellular solids. Part II: Experimental results. Int. J. Mech. Sci. 2001, 43, 701–713. [Google Scholar] [CrossRef]
- Mohammadi Nasrabadi, A.; Hedayati, R.; Sadighi, M. Numerical and experimental study of the mechanical response of aluminum foams under compressive loading using ct data. J. Theor. Appl. Mech. 2016, 54, 1357–1368. [Google Scholar] [CrossRef][Green Version]
- Li, Z.; Xi, C.; Jing, L.; Wang, Z.; Zhao, L. Effect of loading rate on the compressive properties of open-cell metal foams. Mater. Sci. Eng. A 2014, 592, 221–229. [Google Scholar] [CrossRef]
- ANSYS Mechanical APDL Basic Analysis Guide. Available online: http://allaboutmetallurgy.com/wp/wp-content/uploads/2016/12/ANSYS-Mechanical-APDL-Basic-Analysis-Guide.pdf (accessed on 10 January 2018).
- Tanwongwan, W.; Carmai, J. Finite element modelling of titanium foam behaviour for dental application. In Proceedings of the World Congress on Engineering 2011, London, UK, 6–8 July 2011. [Google Scholar]
- ABAQUS Theory Manual Version 6.11-1 (R20). Available online: http://130.149.89.49:2080/v6.11/pdf_books/THEORY.pdf (accessed on 10 January 2018).
- Irausquín, I.; Teixeira-Dias, F.; Miranda, V.; Pérez-Castellanos, J.L. Numerical modeling of the compression a closed-cell aluminum foam. In Iberian Conference on Fracture and Structural Integrity; Emerald Group Publishing Limited: Porto, Portugal, 2010. [Google Scholar]
- Khalkhali, A.; Mousavi, S. Multi-objective crashworthiness optimization of the aluminum foam-filled tubes. Int. J. Automot. Eng. 2012, 2, 193–206. [Google Scholar]
- Rizov, V.I. Elastic–plastic response of structural foams subjected to localized static loads. Mater. Des. 2006, 27, 947–954. [Google Scholar] [CrossRef]
- McKown, S.; Mines, R. Impact behaviour of metal foam cored sandwich beams. In Fracture of Nano and Engineering Materials and Structures; Springer: Berlin, Germany, 2006. [Google Scholar]
- Cho, J.U.; Hong, S.J.; Lee, S.K.; Cho, C. Impact fracture behavior at the material of aluminum foam. Mater. Sci. Eng. A 2012, 539, 250–258. [Google Scholar] [CrossRef]
- Wang, J.; Waas, A.M.; Wang, H. Experimental and numerical study on the low-velocity impact behavior of foam-core sandwich panels. Compos. Struct. 2013, 96, 298–311. [Google Scholar] [CrossRef]
- Rajaneesh, A.; Sridhar, I.; Rajendran, S. Numerical modeling of low velocity impact response on metal foam cored sandwich panels. In Proceeding of the 18 th International Conference on Composite Materials, Jeju Island, Korea, 21–26 August 2011. [Google Scholar]
- Flores-Johnson, E.; Li, Q.; Mines, R. Degradation of elastic modulus of progressively crushable foams in uniaxial compression. J. Cell. Plast. 2008, 44, 415–434. [Google Scholar] [CrossRef]
- Motz, C.; Pippan, R. Deformation behaviour of closed-cell aluminium foams in tension. Acta Mater. 2001, 49, 2463–2470. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, J.; Fan, J.; Wang, Z.; Zhao, L. On crushing response of the three-dimensional closed-cell foam based on voronoi model. Mech. Mater. 2014, 68, 85–94. [Google Scholar] [CrossRef]
- Zou, Z.; Reid, S.; Tan, P.; Li, S.; Harrigan, J. Dynamic crushing of honeycombs and features of shock fronts. Int. J. Impact Eng. 2009, 36, 165–176. [Google Scholar] [CrossRef]







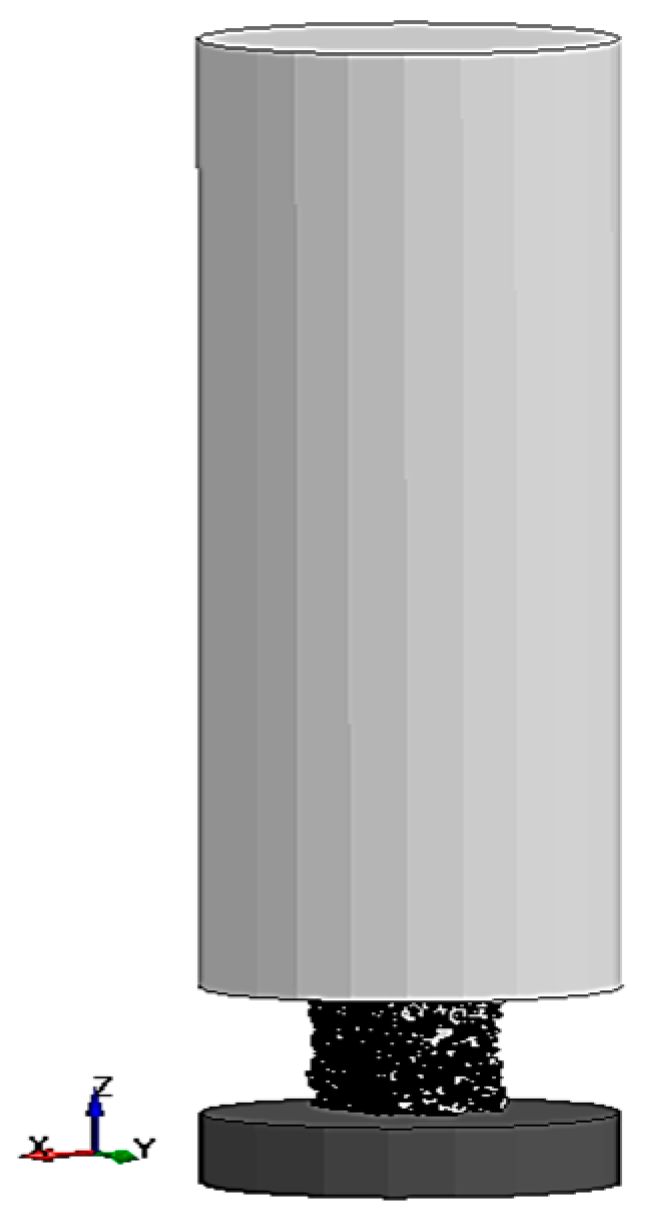
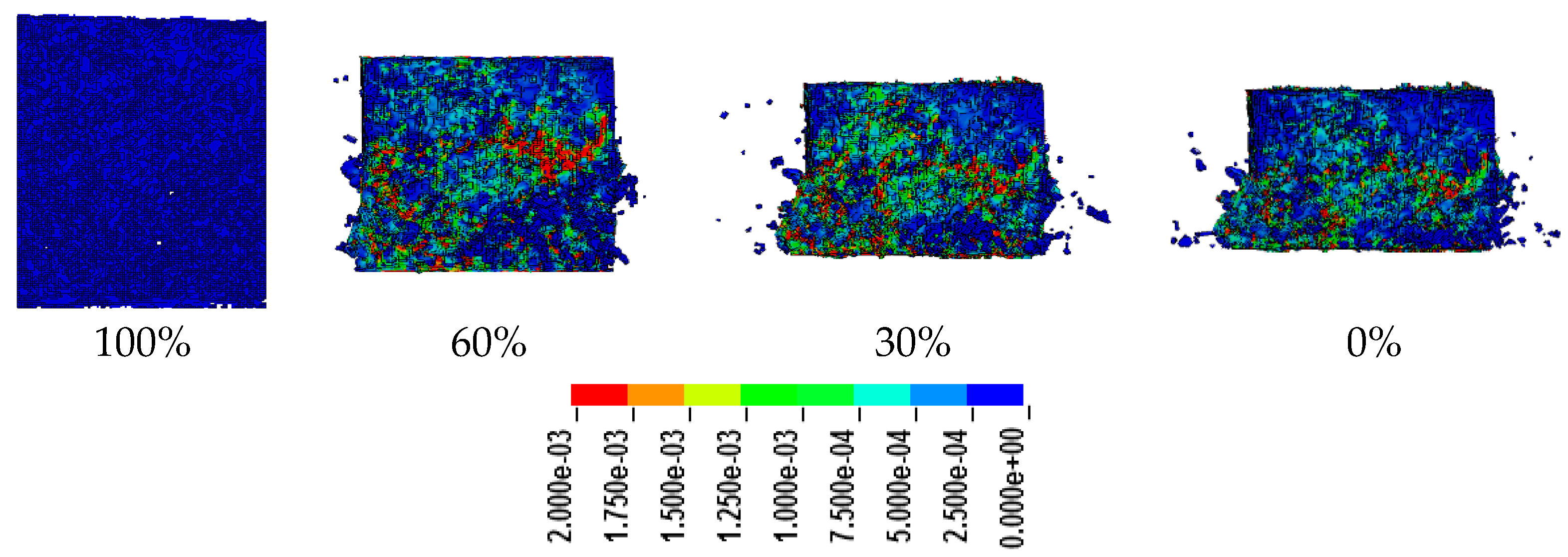
| Property | Value |
|---|---|
| Density (kg/m3) | 2685 |
| Elastic modulus (GPa) | 71 |
| Yield stress (MPa) | 165 |
| Tangent modulus (GPa) | 0.487 |
| Poisson’s ratio | 0.33 |
| Elongation | 2–3.5% |
| Specimen # | Mass (g) | Dimension in Direction (mm) | Dimension in Direction (mm) | Dimension in Direction (mm) | Density | Static Test | Impact Test | ||
|---|---|---|---|---|---|---|---|---|---|
| Elastic | Elastic-Plastic | Drop Weight Mass (kg) | Drop Weight Initial Height (cm) | ||||||
| N1 | 25.09 | 31.57 | 32.33 | 40.18 | 612 | * | |||
| N2 | 25.92 | 32.5 | 31.9 | 39.65 | 630 | * | |||
| N3 | 28.7 | 32.44 | 32.14 | 40.37 | 682 | * | |||
| N4 | 25.74 | 31.38 | 31.78 | 39.7 | 650 | * | |||
| N5 | 25.49 | 31.78 | 32.22 | 39.9 | 624 | * | |||
| N6 | 23.79 | 30.47 | 32.35 | 39.5 | 610 | * | |||
| N7 | 24.9 | 32.75 | 31.8 | 39.84 | 600 | * | |||
| N8 | 32.96 | 32.76 | 31.58 | 39.97 | 797 | * | |||
| N9 | 27.5 | 31.57 | 32.36 | 40.18 | 670 | * | |||
| N10 | 27.7 | 31.98 | 32.55 | 39.78 | 669 | * | |||
| N11 | 27.7 | 31.9 | 32.65 | 40 | 665 | * | |||
| N12 | 27.53 | 32 | 32.69 | 39.64 | 664 | * | |||
| N13 | 27.5 | 31.64 | 32.13 | 40 | 676 | 13.5 | 60 | ||
| N14 | 25.7 | 32.3 | 30.75 | 40.2 | 644 | 13.5 | 60 | ||
| N15 | 27.6 | 32.53 | 32.55 | 39.8 | 655 | 9 | 60 | ||
| N16 | 27.45 | 32.66 | 32.34 | 39.8 | 653 | 9 | 60 | ||
| N17 | 32.3 | 30.95 | 32.41 | 40.3 | 800 | 13.5 | 40 | ||
| N18 | 26.9 | 32.61 | 32.46 | 39.66 | 641 | 13.5 | 40 | ||
| N19 | 30.72 | 32.96 | 32.45 | 40.32 | 714 | 13.5 | 40 | ||
| N20 | 27.7 | 32.1 | 32.53 | 39.83 | 666 | 13.5 | 40 | ||
| Specimen # | Density (kg/m3) | Relative Density (%) | Measured Elastic Modulus (GPa) |
|---|---|---|---|
| N9 | 670 | 25 | 0.118 |
| N10 | 669 | 24.8 | 0.153 |
| N11 | 665 | 24.88 | 0.154 |
| N12 | 664 | 24.7 | 0.152 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koloushani, M.; Hedayati, R.; Sadighi, M.; Mohammadi-Aghdam, M. CT-Based Micro-Mechanical Approach to Predict Response of Closed-Cell Porous Biomaterials to Low-Velocity Impact. J. Imaging 2018, 4, 49. https://doi.org/10.3390/jimaging4030049
Koloushani M, Hedayati R, Sadighi M, Mohammadi-Aghdam M. CT-Based Micro-Mechanical Approach to Predict Response of Closed-Cell Porous Biomaterials to Low-Velocity Impact. Journal of Imaging. 2018; 4(3):49. https://doi.org/10.3390/jimaging4030049
Chicago/Turabian StyleKoloushani, Mehrdad, Reza Hedayati, Mojtaba Sadighi, and Mohammad Mohammadi-Aghdam. 2018. "CT-Based Micro-Mechanical Approach to Predict Response of Closed-Cell Porous Biomaterials to Low-Velocity Impact" Journal of Imaging 4, no. 3: 49. https://doi.org/10.3390/jimaging4030049
APA StyleKoloushani, M., Hedayati, R., Sadighi, M., & Mohammadi-Aghdam, M. (2018). CT-Based Micro-Mechanical Approach to Predict Response of Closed-Cell Porous Biomaterials to Low-Velocity Impact. Journal of Imaging, 4(3), 49. https://doi.org/10.3390/jimaging4030049