Abstract
Background: Probabilistic neighborhood tractography aims to automatically segment brain white matter tracts from diffusion magnetic resonance imaging (dMRI) data in different individuals. It uses reference tracts as priors for the shape and length of the tract, and matching models that describe typical deviations from these. We evaluated new reference tracts and matching models derived from dMRI data acquired from 80 healthy volunteers, aged 25–64 years. Methods: The new reference tracts and models were tested in 50 healthy older people, aged 71.8 ± 0.4 years. The matching models were further assessed by sampling and visualizing synthetic tracts derived from them. Results: We found that data-generated reference tracts improved the success rate of automatic white matter tract segmentations. We observed an increased rate of visually acceptable tracts, and decreased variation in quantitative parameters when using this approach. Sampling from the matching models demonstrated their quality, independently of the testing data. Conclusions: We have improved the automatic segmentation of brain white matter tracts, and demonstrated that matching models can be successfully transferred to novel data. In many cases, this will bypass the need for training data and make the use of probabilistic neighborhood tractography in small testing datasets newly practicable.
1. Introduction
The current work is an extension of original work published at the Medical Image Understanding and Analysis: 21st Annual Conference [1].
Tractography uses diffusion magnetic resonance imaging (dMRI) data to reconstruct in vivo the white matter connections within the brain [2]. Tractography can be used clinically in individual patients [3], but many applications involve group analysis [4]. In the latter, tract characteristics are examined across a patient group of interest, or are compared to a matched control group. In these instances, sources of nuisance variance within and between groups—and in particular, any variability introduced by the tract segmentation method—need to be kept to a minimum to facilitate detection of true biological differences and avoid spurious findings. Probabilistic neighborhood tractography (PNT) aims to reduce operator interaction, and therefore any potential variability that is induced by it, during the tract segmentation process. PNT automatically segments equivalent white matter fasciculi in different subjects by scoring the similarity between a predefined “reference tract” and a group of candidate tracts, which is generated with different initial seed points within a neighborhood [5,6].
Other automated tract segmentation tools have been developed using a range of strategies, such as incorporating prior information about nearby anatomical landmarks [7], or clustering whole-brain streamline sets in some feature space [8,9]. Tractography typically cannot be used for segmentation without manual or automatic refinement, however, due to the accumulation of errors along pathways [10,11], and the use of more sophisticated diffusion models, has led to more false positives [12]. Manual placement of regions of interest (ROIs) or seed points is a common and effective approach [13], although this method is very time-consuming and operator-dependent, for large studies. Automatic ROI or seed registration from an atlas might suffer from registration errors [6], particularly for datasets from the upper and lower extremes of age that might not be appropriately represented by current atlases [14]. Information used for the initialization of tractography should allow for the changes in anatomy due to age, and the PNT priors that are used for the current work seek to achieve this. A similar PNT approach has also been tested for the segmentation of tracts in infants [15].
PNT reference tracts can be generated directly from dMRI data, or from an atlas or similar reference point. In either case, the underlying reference dataset should be representative of the population under study. A suitably large and diverse “training” dataset is subsequently used to capture the variability that is typically observed around each reference tract. However, this set of training data should generally be kept separate from the data that will be used for hypothesis testing to prevent any potential bias during analysis. To avoid the use of valuable testing data in the creation of reference tracts, and for consistency across studies, sets of reference tracts have been created previously and been made freely available (http://www.tractor-mri.org.uk/reference-tracts). The first set was derived from a white matter atlas, which is independent of all new subject data acquired [16,17]. These atlas-based reference tracts improved the results from PNT significantly, although a small proportion of the segmented tracts still needed to be excluded after a visual check, and in some instances the segmented tracts were too short [18]. A second set of reference tracts was created directly from a database of dMRI data acquired from healthy volunteers to address this issue [1], and the current analysis extends this work and focuses on the testing of these data-based reference tracts.
In addition to the reference tract, PNT uses a probabilistic generative model to evaluate candidate tract trajectories for plausibility. This “matching model” describes typical deviations in shape and length that individual white matter tracts make from the reference tract, and is typically fitted using maximum a posteriori estimation. These deviations are due to differences in head shape, brain size, or age. To date, matching models have generally been fitted using study-specific training data, or in an iterative expectation–maximization procedure, but we will demonstrate that they can also be created from an independent set of training data and successfully reused across studies.
In the current work, a new set of reference tracts directly derived from dMRI data are tested and compared with the previous atlas-based reference tracts. We then create PNT matching models from two datasets: a large group of healthy volunteers with a wide age range (25–64 years), and a group of community-dwelling older participants from the Lothian Birth Cohort 1936 (LBC1936; age 71–73 years). While the training data used has a wide age range, in order to represent variability in tract topology due to changes in the brain with age [19], we used testing data from beyond this range in order to demonstrate the wider applicability of our method. We demonstrate different combinations of reference tracts and models by directly sampling from the PNT models, with the aim of assessing the plausibility of the models independently of the data with which they are to be tested.
2. Materials and Methods
2.1. Participants
2.1.1. Training Data
The reference and training data consisted of brain dMRI data from 80 clinically normal, right-handed, healthy volunteers (40 males, 40 females) aged 25–64 years. All of the subjects gave written informed consent. Health status was assessed using medical questionnaires and all structural MRI scans were reported by a fully qualified neuroradiologist. More details can be found in previous publications [20].
2.1.2. Testing Data
The testing data consisted of brain dMRI data from 50 healthy, community-dwelling older participants from the LBC1936, all were born in the same year, with average age 71.8 ± 0.4 years at the time of scanning. More details of this cohort have been published previously [21]. Throughout the manuscript we will refer to the testing data as “LBC1936” data.
2.2. MRI
All brain MRI data were acquired using the same GE Signa Horizon HDxt 1.5 t clinical scanner (General Electric, Milwaukee, WI, USA), equipped with a self-shielding gradient set (33 mT/m maximum gradient strength) and manufacturer-supplied eight-channel phased-array head coil. The same dMRI protocol was used for both training and testing data. The acquisition consisted of seven T2-weighted (T2W; b = 0 s/mm2) and sets of diffusion-weighted (b = 1000 s/mm2) single-shot, spin-echo, echo-planar (EP) imaging volumes, acquired with diffusion gradients applied in 64 non-collinear directions [22] and 2 mm isotropic spatial resolution.
2.3. Image Analysis
dMRI volumes were pre-processed using FSL tools (http://www.fmrib.ox.ac.uk/fsl) to extract the brain [23], remove bulk motion, and correct eddy current induced distortions by registering all subsequent volumes to the first T2W EP volume [24]. The water self-diffusion tensor was calculated, and parametric maps of fractional anisotropy (FA) and mean diffusivity (MD) derived from its eigenvalues using DTIFIT [25]. We used Bayesian Estimation of Diffusion Parameters Obtained using Sampling Techniques modelling Crossing Fibres, (BEDPOSTX; with two fibers per voxel) as the diffusion model for tractography [26].
2.4. Reference Tracts
The two sets of PNT standard reference tracts are available through the TractoR (Tractography with R) project (http://www.tractor-mri.org.uk/) [27]. These represent most of the main pathways in the brain, as described by Hua et al. [17].
2.4.1. Atlas-Based Reference Tracts
These reference tracts are based on the white matter tract atlas made available by Dr. Susumu Mori’s lab at Johns Hopkins University (http://cmrm.med.jhmi.edu/) [17]. The construction of these reference tracts is further explained in [16].
2.4.2. Data-Based Reference Tracts
These reference tracts were created based on manually selected streamlines from the training dataset (Section 2.1.1) used for the current work, representing each tract of interest. Further details about these reference tracts can be found in [1].
2.5. Creation of Matching Models
The model for a tract of interest may be fitted in a supervised fashion by manually choosing a set of training tracts representing good matches to the reference [6], or following an unsupervised approach using an expectation–maximization (EM) algorithm which will train the model and select the best segmentations from each dataset at the same time [5].
We created matching models using the two sets of reference tracts and the two datasets (training and LBC1936 data). With the data-based reference tracts created from the training data, the whole set of 80 training tracts were used to fit a matching model in a supervised fashion [6] (see black paths in Figure 1).
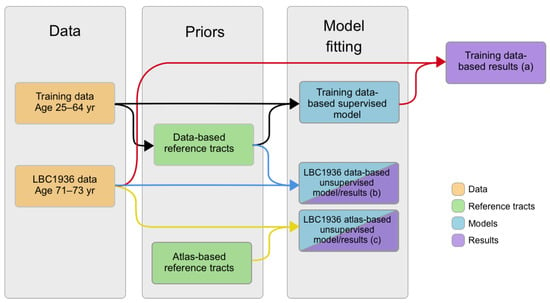
Figure 1.
Flow chart of the processes followed in this manuscript. Black paths show the creation of the data-based reference tracts and training data-based supervised models (which represent the deviations of the training data), using the training data. Color paths show the three cases of tract segmentation performed in the LBC1936 data: red paths use the data-based reference tracts and the training data-based models to segment white matter tracts; blue paths use the data-based reference tracts in the LBC1936 data to create models (which represent the deviations of the tracts corresponding to LBC1936 data), and segment the tracts simultaneously using expectation–maximization (EM); and, yellow paths use the atlas-based reference tracts to create models (which represent the deviations of the tracts corresponding to LBC1936 data), and segment the tracts simultaneously using EM.
We then used an unsupervised approach in the 50 LBC1936 datasets, based on our EM algorithm, whereby the model was trained and applied iteratively using the same data [5]. Using this approach, a matching model was obtained from the LBC1936 data, as well as the best candidate tract for each dataset. We therefore obtained two matching models for each tract of interest, one created from the 80 training datasets (ages 25–64 years) and one created from the 50 LBC1936 datasets (age 71.8 ± 0.4 years).
The unsupervised fitting process was also repeated using the reference tracts, previously created from an atlas [16,17], which are currently provided with the TractoR package. This allows for the new data-based reference tracts to be compared with the previous atlas-based reference tracts.
We therefore obtained three PNT models per tract of interest: (a) a matching model from the training dataset and the data-based reference tract; (b) a matching model from the LBC1936 dataset and the data-based reference tract; and (c) a matching model from the LBC1936 dataset and the atlas-based reference tract. These three cases are represented by the black, blue and yellow paths, respectively, in the flow chart in Figure 1.
2.6. Testing of Reference Tracts and Matching Models
The new reference tracts were used to segment the fasciculi of interest in the LBC1936 data with PNT by evaluating novel candidate tracts for plausibility against each model. This allows us to test the influence of the matching model on the selection of candidate tracts in the LBC1936 data.
We therefore obtained three segmentations for each fasciculus of interest for each LBC1936 dataset: (a) using a supervised matching model from the training dataset and the data-based reference tract; (b) using an unsupervised matching model from the LBC1936 dataset and the data-based reference tract; and (c) using an unsupervised matching model from the LBC1936 dataset and the atlas-based reference tract.
For all of the methods, an additional step based on the same shape models was used to reject false positive streamlines from the final tracts. Briefly, this selection step works by retaining streamlines probabilistically according to the ratio between their matching probabilities and that of the median path. This removes the need to apply a user-defined arbitrary threshold to the connectivity data to exclude voxels with a very low probability of connection. A tract mask is then generated from the retained streamlines of the best matching tract, and truncated to the length of the reference tract [28].
The three resulting groups of segmented tracts were randomly shuffled, and then all of the tracts were visually assessed by an experienced rater (SMM), blinded to the method used. The tracts were considered unacceptable if any significant portion of the tract (i.e., with high visitation count) ran in a direction different from that expected from anatomy, or if they were severely truncated or bent at an unrealistic angle. Tracts with minor spurious branches (low visitation count) were accepted, as their contribution to weighted means would be negligible, although these were not common due to the streamline selection step.
Tract-averaged FA and MD values were then calculated in tracts that passed this visual quality check, weighting the values in each voxel by the streamline visitation count. To compare the three segmentations, the proportions of visually plausible tracts were recorded and the coefficients of variation (CV) of the mean FA and MD values were extracted from the resulting tracts, calculated, and compared. In addition, to obtain an estimate of how the shape and length of the tracts in each case compares to a “ground truth” we estimated the Dice overlaps [29] with the tracts that were represented in a white matter atlas (http://cmrm.med.jhmi.edu/). In this atlas, white matter structures were identified probabilistically by averaging the results of running deterministic tractography on 28 normal subjects (mean age 29 ± 7.9 years) [17]. To obtain the Dice coefficients, for each tract segmented with each of the three PNT tractography cases described above, we summed the segmented tract for each subject to obtain a probabilistic group map in MNI space (Figure 4). Finally, the group map and the probabilistic map from the atlas were both binarized, and the Dice overlaps were calculated.
2.7. Sampling from PNT Models
PNT evaluates candidate tracts for plausibility against the reference tract using a probabilistic generative model. The reference tract is a curve in three-dimensional (3D) standard space, represented by the knot points of a fitted B-spline, which are separated by a fixed distance, d. One of these knot points is known as the “anchor point”, and there are points to one side of this location and points to the other side. (These are nominally designated “left” and “right”, but may in fact go in any direction.)
A PNT model provides parametric distributions for and , the number of steps of length d in the “left” and “right” directions away from the anchor point in plausible tracts, and , with u {−, ..., −1, 1, ..., }, the angle between the uth segment of the observed tract and the equivalent segment of the reference tract (see Figure 2).
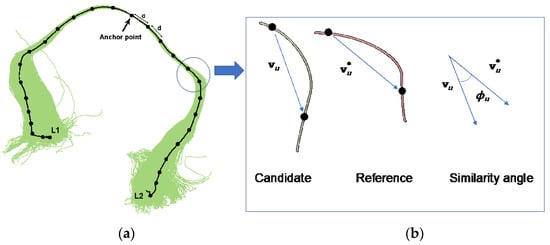
Figure 2.
Graphical representation of a candidate tract (a), the median line is fitted to a B-spline with knot points separated by a distance d (straight-line distance). A B-spline representation is also used for the reference tract. The vector between two consecutive knot points in the candidate and the equivalent knot points in the reference can be compared and the angular deviations obtained. (b) illustrates the shape model used by probabilistic neighborhood tractography (PNT), based on angular deviations , between equivalent tract segments in the reference and candidate tracts, and , respectively. The putative direction of each segment is always away from the anchor point. Adapted from [5,6].
Given a reference tract and a trained tract shape model, the procedure for sampling from the model is therefore as follows:
- Identify the image voxel corresponding to the reference anchor point, and choose a specific starting location from a uniform distribution over that voxel. Note this as the first pseudo-knot point.
- Sample and from their respective distributions, thereby obtaining the length of the sample streamline either side of the anchor point.
- Beginning at the point obtained in step 1, sample sequentially for u {−1, ..., }. In each case, take a step of length d in the direction of from the current pseudo-knot point to arrive at the next pseudo-knot point.
- Return to the point obtained in step 1, and sample sequentially for u {1, ..., }, analogously to step 3.
- Use B-spline interpolation to recover a curve between the sequence of pseudo-knot points.
Steps 3 and 4 above involve some subtlety, since we require samples for , but we have only (from the reference tract) and a sampled (from the model). These jointly specify a locus of equiprobable points in a circle of radius d sin about (see Figure 3).
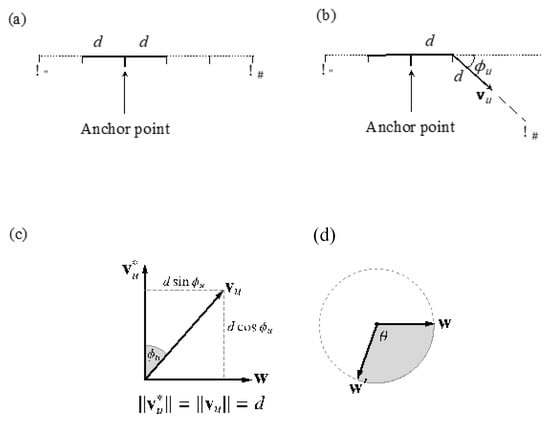
Figure 3.
Graphical representation of the sampling process for step vectors, . (a) From the voxel corresponding to the anchor point, the “left” and “right” tract lengths are sampled from the model length distributions, obtaining the total length of the streamline. (b) From the first step on one side, the vector is sampled, leading to the next knot in the streamline. This vector is obtained from the angle sampled from the model angle distribution at that knot. This is replicated for every step until the distance is reached. The process is then repeated for the “left” tract lengths. (c,d) Geometric representation of the sub-steps for the sampling of : given a reference tract direction, , and an angular deviation from it, (c). These jointly specify a circular locus of possible directions (d), from which a final vector is chosen by additionally sampling θ [0, 2π].
As a result, there are the following substeps involved in each case:
- Sample from the model.
- Establish a point, w, on the plane passing through the origin perpendicular to . The equation of this plane is , so any vector perpendicular to will do. We take , where = (0, 0, 1) unless this is collinear with , in which case we use = (1, 0, 0).
- Sample θ ~ (0, 2π), the angle around the locus circle.
- Rotate w by the angle θ around the unit vector , using Rodrigues’ rotation Formula (1):
- Scale w′ to the radius of the locus circle and translate it along the reference vector, to arrive at the final step vector, , as (2):
2.8. Creating Synthetic Tracts from PNT Models
For each of the reference tract/matching model combinations, we recreated the white matter tracts by sampling the PNT model with 1000 streamlines following the steps above. These samples are a direct illustration of the models, and, as such, allow for the independent assessment of the model before its use for the segmentation of tracts from dMRI data, where each individual’s anatomy would affect the resulting tract. The synthetic tracts that were obtained were visually assessed.
3. Results
3.1. Testing of Reference Tracts and Matching Models
3.1.1. Visual Assessments
The data-based reference tracts were created for 16 major brain white matter fasciculi: the genu and splenium of the corpus callosum, the anterior thalamic radiations (ATR), the arcuate (Arc), uncinate (Unc), and inferior longitudinal fasciculi (ILF), the dorsal and ventral cingula (Cing), and the corticospinal tract (CST), bilaterally.
The use of the data-based reference tracts improved the number of visually acceptable tracts when compared with the same segmentations created from the previous atlas-based reference tracts. Table 1 shows the percentage of successful segmentations for each white matter tract using each method.

Table 1.
Proportion of segmented tracts visually acceptable when using two different matching models and each set of reference tracts as priors.
When comparing tracts that were created with the same LBC1936 data model, the data-based reference tracts improved the consistency of the segmentations, with >92% of successful segmentations for all the tracts. By contrast, atlas-based reference tracts had a lower average performance, particularly due to the poor performance segmenting the ATR, bilaterally, where only 32% and 76% of the cases could be segmented successfully.
When comparing the two models, both perform well, with an average of >98% visually plausible tracts, suggesting that a model can be trained in a separate dataset and still successfully segment the tracts in the LBC1936 data.
Figure 4 shows the group maps that were created by overlaying the segmented tracts from the 50 older age volunteer LBC1936 dataset into standard brain MNI space as maximum intensity projections. These images show that the segmentations obtained from the two sets of reference tracts are similar, except for the left and right ATR, where many of the segmentations using the atlas-based reference followed the wrong path, thereby failing the visual check. Some small differences are, however, obvious in other tracts, specifically regarding their lengths. In particular, the segmentations of the corpus callosum genu, the arcuate fasciculi, and the ventral cingula were longer when using the new data-based reference tracts, with more of the tract being included in the segmentation.
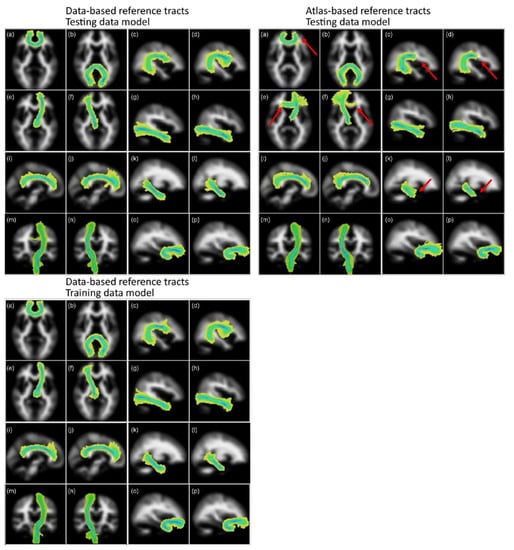
Figure 4.
Group maps projections for the 16 tracts of interest segmented using the data-based (left panel) and atlas-based (right panel) reference tracts. Top panels used a matching model trained in the LBC1936 data, and the bottom panel used a model trained in the training data. The tracts represented are: (a) genu and (b) splenium of the corpus callosum, left and right arcuate fasciculus (c,d), left and right anterior thalamic radiation (e,f), left and right inferior longitudinal fasciculus (g,h), left and right dorsal (i,j) and ventral (k,l) cingulum, left and right corticospinal tracts (m,n) and left and right uncinate fasciculus (o,p). Color scale represents the voxel visitation frequency, from 1 (light yellow) to 50 (dark blue). Maps are projected into the plane of the voxel with maximum visitation value. Red arrows point at the main differences obtained between the resulting tracts derived from atlas-based and data-based reference tracts. Figure adapted from [1].
The group maps from tracts that were generated with each training model showed that the choice of training model had a modest effect on the segmented tracts.
3.1.2. FA and MD Variability
Table 2 shows the mean values and coefficients of variation (CV) of FA and MD, measured along the tracts that were extracted by the three methods. One-way analysis of variance (ANOVA) tests, corrected for multiple comparisons, showed that the parameters measured in tracts that were generated by each method were generally not significantly different. Only the corpus callosum splenium, the right ATR, and CST produced significantly different mean parameters. Without multiple comparison correction, genu (FA), left Cing (FA), and CST (FA and MD) also became significantly different. However, for both the FA and MD, the variation across the 50 LBC1936 datasets is lower for most tracts when generated with the data-based reference tracts.

Table 2.
Averaged values of fractional anisotropy (FA) and mean diffusivity (MD) measured along the tracts segmented with two different matching models, and atlas-based or data-based reference tracts as priors in 50 older age volunteers (LBC1936).
3.1.3. Overlap Analysis
The Dice overlaps between the tract group maps (Figure 4) and the white matter atlas tracts are shown in Table 3. The group maps were created previous to the tract rejection during the visual assessment, and are therefore are unbiased by the rater’s manual intervention. We obtained moderate Dice overlaps for most of the tracts. To illustrate the mismatches, Figure 5 shows the tracts with the lowest overlap, bilateral arcuate, and uncinated fasciculi, created from the atlas-based reference tracts and an unsupervised model.

Table 3.
Dice overlaps between segmented tracts and white matter atlas.
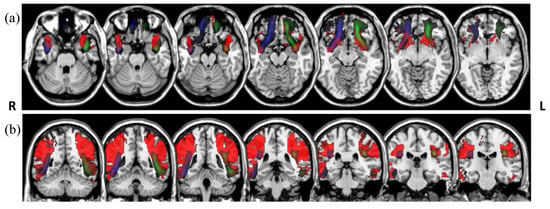
Figure 5.
Overlays of the uncinate (a) and arcuate (b) fasciculi. Atlas tracts represented in red (from [17]) and tracts segmented in the LBC1936 data using atlas-based reference tracts and unsupervised models in green (left) and blue (right), in radiological convention.
The Dice scores suggest that the source of training data used to fit the model appeared to be less influential than the choice of reference tract. To obtain an impression of the relative importance of the reference tracts and the fitted model, the degree of agreement on the best-matching candidate tract was also assessed across the 50 LBC1936 datasets between the three methods. We found that models that were trained with the separate training data or with the LBC1936 data (in the unsupervised framework), but with the reference tracts in common, resulted in agreement on the best candidate tract in an average of 39% of subjects. By contrast, the two models that were fitted in an unsupervised fashion on the same LBC1936 data, but with different reference tracts, agreed only 9% of the time.
3.2. Assessment of Synthetic Tracts Sampled from PNT Models
We sampled the PNT models for the three different combinations of dataset and reference tracts. Figure 6 shows streamline representations of the synthetic tracts that were obtained. We can observe differences in the models trained in each case. The models that were generated from the atlas-based reference tracts reflect the shorter length of the references, particularly for the genu, Arc, and ventral cingulum. The dispersion of the streamlines in each case represents the degree of variability around the reference permitted by the model.
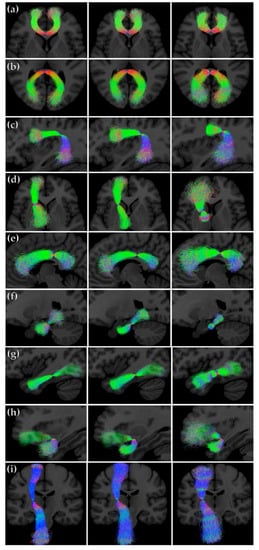
Figure 6.
Streamline representations of the synthetic tracts obtained by sampling from the PNT models generated from the training and LBC1936 data. First column: PNT model from the training dataset using the data-based reference tract; second column: PNT model from the LBC1936 dataset using the data-based reference tract; third column: PNT model from the LBC1936 dataset and the atlas-based reference tract. (a) genu (b) splenium, (c) Arc, (d) ATR, (e) Cing, (f) Cing, ventral, (g) ILF, (h) Unc, and (i) CST.
4. Discussion
The reference tract represents the matching target for PNT automatic segmentation, and it is therefore crucial that this prior epitomizes the topological characteristics of the fasciculus of interest correctly. Instead of using an atlas, the new reference tracts use data directly from a large group of healthy volunteers, with a wide age range, and were able to capture the variability in tract topology better. PNT results were improved, even when the testing data that corresponds to an age group outside the age range used during training to generate the reference tracts or the matching models (71–73 vs. 25–64 years old). The CVs in the parameters measured in the segmentations created from the new set of reference tracts are lower than those created from the atlas-based reference tracts, particularly for the splenium and the ventral cingulum. This suggests a lower variability, introduced by the tract segmentation method, which should facilitate the detection of true biological differences and avoid spurious findings.
The large percentage of successful segmentations obtained in the older population (>98%; Table 1) when using the new reference tracts suggests that these can be used as priors in different populations, and not just in a population matching the training data characteristics. Although the improvement is significant, it is still not sufficient to make manual checking of the segmented tracts entirely unnecessary, but this is true for most automated methods. Further tests would also be required to investigate whether these reference tracts would still be good priors to perform PNT segmentation in diseased populations with potentially large changes in brain topology, such as in the presence of tumors or stroke, but preliminary work suggests that the general approach is robust to even quite substantial mass effects [30].
The most obvious improvement with the new reference tracts is the high success rate that was obtained for the ATR, indicating that the prior for this tract generated from real data is a much better representation of the ATR topology. Another improvement is the extraction of longer segments of some of the tracts of interest, such as the genu of the corpus callosum, the arcuate, and the ventral cingulum, which arises due to the greater difficulty of inferring accurate pathways near the ends of tracts when using an atlas as the reference, leading to a shorter reference tract. The segmentation of a larger section of the genu projections into the frontal cortex (where FA tends to be lower than in the center of the tract) could explain the slightly lower mean values of FA obtained for this tract when using the new reference tracts. There was also a very subtle shift in the overall position of the splenium of the corpus callosum, with the segmentations for this tract being obtained with the atlas-based reference tract being generally closer to the boundary with the ventricles, while the data-based reference produced segmentations within the middle of this fasciculus. This is also reflected in the higher MD and lower FA of the atlas-based splenium, suggesting more partial volume averaging with cerebrospinal fluid from the ventricles.
There could be two main reasons for the differences in parameters that were measured with each method. Firstly, the atlas used to generate the previous reference tracts was obtained using data from subjects with an average age of 29 ± 7.9 years [6], while the training data for the new priors had a wider age range of 25–64 years. The new reference tracts will therefore represent better the characteristics of the white matter in older age, and particularly the changes due to ageing such as atrophy and enlarged ventricles. This is reflected in the better segmentations, and changes to the parameters that were measured, in the tracts running closer to the ventricles, such as the ATR, the CST, and the genu and splenium of the corpus callosum. Secondly, the native-space tractography data used for generating the reference tracts here is a much richer dataset than the subject-averaged tract probability maps that constitute the atlas.
The Dice overlaps obtained when comparing our resulting tracts with a tractography atlas are moderate, ranging between 0.21 and 0.65. The differences in the Dice coefficients between the three approaches that were used in the current work are small, although there is a tendency towards higher overlaps with the tracts generated from the data-based reference tracts, which suggests better segmentations if we consider the atlas as a “ground truth”. However, the overlap was somewhat low in some cases. Figure 5 illustrates the differences between the PNT segmentations and the atlas in the tracts with the lowest overlaps. As we can see, the uncinate fasciculi obtained in the current work have “longer” frontal projections than those in the atlas. For the arcuate fasciculi, we obtained a more focused core of the tracts. In both cases, the differences may be determined by the choice of the underlying diffusion modelling and tractography method. While the atlas was created from deterministic tractography based on the diffusion tensor model [31], we used a ball-and-sticks model with two fiber orientations per voxel [26]. The latter deals better with the issue of crossing fibers, and might have led to the longer projections that we observed in the uncinate fasciculi. The lower amount of “branching” that we obtained in the arcuate fasciculi could, however, be influenced by the streamline selection step that we applied after PNT for the rejection of false positives [28].
We also demonstrated that the source of training data used to fit the model was less influential than the choice of reference tract, and that matching models previously fitted in training data can be used to apply PNT in separate testing datasets. This opens up the possibility of using PNT in small samples of testing data, including individual cases, where the number of datasets might not be large enough for fitting the matching model in an unsupervised fashion.
To assess that the PNT models themselves provided a good representation of the variability of each tract of interest, we sampled from the models to create the synthetic tracts shown in Figure 6. These are an illustration of the models as such, and demonstrate the relative merits of the different models, independently of any particular dataset. These tracts show, however, the influence of the originating reference tract on the models, as can be seen from the longer genu, Arc, and ventral cingulum sampled from the PNT models generated from the new data-based reference tracts. The models can therefore tell us a priori whether they epitomize plausible tracts; for example, if the sampled synthetic tracts are too short, or spread out too much, then the reference tract for a model may be misleading or less informative.
The pre-trained matching models developed here have a number of practical advantages for future studies. Firstly, they reduce both the computational load and the complexity to the user of using PNT for white matter tract segmentation. Indeed, a tract of interest may be feasibly identified from suitably preprocessed dMRI data within a few minutes on a standard workstation. Secondly, they make the approach accessible to small-sample studies, and individual cases, where the lack of readily available training data would have previously made the technique infeasible. However, in certain atypical cohorts, it may still be desirable to fit a study-specific model.
A limitation of the current modeling approach is that all of the angular deviations from the reference tracts by a given angle are equiprobable. A future improvement to these models would be the introduction of anisotropic probability distributions to reflect true brain white matter anatomy more closely. Future work would also include the capability to fit the model from whole-brain tractography data by relaxing the anchor (or seed) point assumption of the reference tracts, which it is currently limited to a small neighborhood of voxels. Some preliminary work on automatic tractography using similar principles has been previously performed using whole-brain tractography [32,33].
We also acknowledge that the resolution and acquisition of the training data is not currently state-of-the-art. However, the reference tracts that are provided in the current work will be valid representations of the expected tract length and shape, regardless of the data that they are to be applied to. There is the possibility that the angular and length distributions represented by the models will have some small connection to the acquisition of the data used for their training, but the training tracts were identified manually to capture accurate tract trajectories, and therefore we believe that the variability that is captured by the models will be mainly related to anatomical variability. In any case, the models can be retrained in other datasets using the EM approach, if required.
In summary, we have created a new set of data-based reference tracts to be used as priors for PNT, which improved the segmentations of 16 tracts of interest. We have also demonstrated that the matching model can be transferred between studies, which will make the use of PNT in small datasets newly practicable, and that matching models can be sampled and independently assessed. The matching models that were created from the training data, using the new set of reference tracts, have been made freely available through the TractoR project (http://www.tractor-mri.org.uk/) [27].
Acknowledgments
LBC1936 was supported by the Age UK-funded Disconnected Mind project, with additional funding from the UK Medical Research Council (MR/M013111/1). MRI scanning for the training dataset was funded under National Institutes of Health grant R01 EB004155-03. The scanning was performed at the Brain Research Imaging Centre, Edinburgh, part of Edinburgh Imaging (www.ed.ac.uk/clinical-sciences/edinburgh-imaging) and the SINAPSE Collaboration (Scottish Imaging Network, A Platform for Scientific Excellence, www.sinapse.ac.uk).
Author Contributions
J.D.C. conceived and designed the experiments, wrote the code, and contributed to writing the paper; S.M.M. performed the experiments, analyzed the data and wrote the paper; M.E.B, I.J.D. and J.M.W contributed to the concept and design, data collection and interpretation of the datasets used in this work and reviewed the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Muñoz Maniega, S.; Bastin, M.E.; Deary, I.J.; Wardlaw, J.M.; Clayden, J.D. Improved reference tracts for unsupervised brain white matter tractography. In Medical Image Understanding and Analysis: 21st Annual Conference, MIUA 2017, Edinburgh, UK, July 11--13, 2017, Proceedings; Valdés Hernández, M., González-Castro, V., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 425–435. ISBN 978-3-319-60964-5. [Google Scholar]
- Tournier, J.D.; Mori, S.; Leemans, A. Diffusion tensor imaging and beyond. Magn. Reson. Med. 2011, 65, 1532–1556. [Google Scholar] [CrossRef] [PubMed]
- Ciccarelli, O.; Catani, M.; Johansen-Berg, H.; Clark, C.; Thompson, A. Diffusion-based tractography in neurological disorders: Concepts, applications, and future developments. Lancet Neurol. 2008, 7, 715–727. [Google Scholar] [CrossRef]
- Johansen-Berg, H.; Behrens, T.E.J. Just pretty pictures? What diffusion tractography can add in clinical neuroscience. Curr. Opin. Neurol. 2006, 19, 379–385. [Google Scholar] [CrossRef] [PubMed]
- Clayden, J.D.; Storkey, A.J.; Muñoz Maniega, S.; Bastin, M.E. Reproducibility of tract segmentation between sessions using an unsupervised modelling-based approach. Neuroimage 2009, 45, 377–385. [Google Scholar] [CrossRef] [PubMed]
- Cllayden, J.D.D.; Storkey, A.J.J.; Bastin, M.E.E. A probabilistic model-based approach to consistent white matter tract segmentation. IEEE Trans. Med. Imaging 2007, 26, 1555–1561. [Google Scholar] [CrossRef] [PubMed]
- Yendiki, A.; Panneck, P.; Srinivasan, P.; Stevens, A.; Zöllei, L.; Augustinack, J.; Wang, R.; Salat, D.; Ehrlich, S.; Behrens, T.; Jbabdi, S.; et al. Automated probabilistic reconstruction of white-matter pathways in health and disease using an atlas of the underlying anatomy. Front. Neuroinform. 2011, 5, 23. [Google Scholar] [CrossRef] [PubMed]
- Parker, G.D.; Marshall, D.; Rosin, P.L.; Drage, N.; Richmond, S.; Jones, D.K. Fast and fully automated clustering of whole brain tractography results using shape-space analysis. In Proceedings of the ISMRM 21st Scientific Meeting & Exhibition, Salt Lake City, UT, USA, 20–26 April 2013; p. 778. [Google Scholar]
- O’Donnell, L.J.; Westin, C.-F.C. Automatic tractography segmentation using a high-dimensional white matter atlas. IEEE Trans. Med. Imaging 2007, 26, 1562–1575. [Google Scholar] [CrossRef] [PubMed]
- Morris, D.M.; Embleton, K.V.; Parker, G.J.M. Probabilistic fibre tracking: Differentiation of connections from chance events. Neuroimage 2008, 42, 1329–1339. [Google Scholar] [CrossRef] [PubMed]
- Jones, D.K. Determining and visualizing uncertainty in estimates of fiber orientation from diffusion tensor MRI. Magn. Reson. Med. 2003, 49, 7–12. [Google Scholar] [CrossRef] [PubMed]
- Maier-Hein, K.H.; Neher, P.F.; Houde, J.-C.; Côté, M.-A.; Garyfallidis, E.; Zhong, J.; Chamberland, M.; Yeh, F.-C.; Lin, Y.-C.; Ji, Q.; Reddick, W.E.; et al. The challenge of mapping the human connectome based on diffusion tractography. Nat. Commun. 2017, 8, 1349. [Google Scholar] [CrossRef] [PubMed]
- Catani, M.; Thiebaut De Schotten, M.A. Diffusion tensor imaging tractography atlas for virtual in vivo dissections. Cortex 2008, 44, 1105–1132. [Google Scholar] [CrossRef] [PubMed]
- Dickie, D.A.; Shenkin, S.D.; Anblagan, D.; Lee, J.; Blesa Cabez, M.; Rodriguez, D.; Boardman, J.P.; Waldman, A.; Job, D.E.; Wardlaw, J.M. Whole brain magnetic resonance image atlases: A systematic review of existing atlases and caveats for use in population imaging. Front. Neuroinform. 2017, 11, 1. [Google Scholar] [CrossRef] [PubMed]
- Anblagan, D.; Bastin, M.E.; Sparrow, S.; Piyasena, C.; Pataky, R.; Moore, E.J.; Serag, A.; Wilkinson, A.G.; Clayden, J.D.; Semple, S.I.; et al. Tract shape modeling detects changes associated with preterm birth and neuroprotective treatment effects. NeuroImage Clin. 2015, 8, 51–58. [Google Scholar] [CrossRef] [PubMed]
- Muñoz Maniega, S.; Bastin, M.; McIntosh, A.; Lawrie, S.; Clayden, J. Atlas-based reference tracts improve automatic white matter segmentation with neighbourhood tractography. In Proceedings of the ISMRM 16th Scientific Meeting & Exhibition, Toronto, ON, Canada, 3–9 May 2008; p. 3318. [Google Scholar]
- Hua, K.; Zhang, J.; Wakana, S.; Jiang, H.; Li, X.; Reich, D.S.; Calabresi, P.A.; Pekar, J.J.; van Zijl, P.C.M.; Mori, S. Tract probability maps in stereotaxic spaces: Analyses of white matter anatomy and tract-specific quantification. Neuroimage 2008, 39, 336–347. [Google Scholar] [CrossRef] [PubMed]
- Penke, L.; Muñoz Maniega, S.; Houlihan, L.M.; Murray, C.; Gow, A.J.; Clayden, J.D.; Bastin, M.E.; Wardlaw, J.M.; Deary, I.J. White matter integrity in the splenium of the corpus callosum is related to successful cognitive aging and partly mediates the protective effect of an ancestral polymorphism in ADRB2. Behav. Genet. 2010, 40, 146–156. [Google Scholar] [CrossRef] [PubMed]
- Bastin, M.E.; Muñoz Maniega, S.; Ferguson, K.J.; Brown, L.J.; Wardlaw, J.M.; MacLullich, A.M.J.; Clayden, J.D. Quantifying the effects of normal ageing on white matter structure using unsupervised tract shape modelling. Neuroimage 2010, 51, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Dickie, D.A.; Mikhael, S.; Job, D.E.; Wardlaw, J.M.; Laidlaw, D.H.; Bastin, M.E. Permutation and parametric tests for effect sizes in voxel-based morphometry of gray matter volume in brain structural MRI. Magn. Reson. Imaging 2015, 33, 1299–1305. [Google Scholar] [CrossRef] [PubMed]
- Deary, I.J.; Gow, A.J.; Taylor, M.D.; Corley, J.; Brett, C.; Wilson, V.; Campbell, H.; Whalley, L.J.; Visscher, P.M.; Porteous, D.J.; et al. The Lothian Birth Cohort 1936: A study to examine influences on cognitive ageing from age 11 to age 70 and beyond. BMC Geriatr. 2007, 7, 28. [Google Scholar] [CrossRef] [PubMed]
- Jones, D.K.; Williams, S.C.R.; Gasston, D.; Horsfield, M.A.; Simmons, A.; Howard, R. Isotropic resolution diffusion tensor imaging with whole brain acquisition in a clinically acceptable time. Hum. Brain Mapp. 2002, 15, 216–230. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.M. Fast robust automated brain extraction. Hum. Brain Mapp. 2002, 17, 143–155. [Google Scholar] [CrossRef] [PubMed]
- Jenkinson, M.; Smith, S.A. Global optimisation method for robust affine registration of brain images. Med. Image Anal. 2001, 5, 143–156. [Google Scholar] [CrossRef]
- Basser, P.J.; Pierpaoli, C. Microstructural and physiological features of tissues elucidated by quantitative-diffusion-tensor MRI. J. Magn. Reson. Ser. B 1996, 111, 209–219. [Google Scholar] [CrossRef]
- Behrens, T.E.J.; Johansen-Berg, H.; Jbabdi, S.; Rushworth, M.F.S.; Woolrich, M.W. Probabilistic diffusion tractography with multiple fibre orientations: What can we gain? Neuroimage 2007, 34, 144–155. [Google Scholar] [CrossRef] [PubMed]
- Clayden, J.D.; Muñoz Maniega, S.; Storkey, A.J.; King, M.D.; Bastin, M.E.; Clark, C.A. TractoR: Magnetic resonance imaging and tractography with R. J. Stat. Softw. 2011, 44, 1–18. [Google Scholar] [CrossRef]
- Clayden, J.D.; King, M.D.; Clark, C.A. Shape modelling for tract selection. In Lecture Notes in Computer Science, Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, London, UK, 20–24 September 2009; Yang, G.Z., Hawkes, D., Rueckert, D., Noble, A., Taylor, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5762, pp. 150–157. [Google Scholar]
- Dice, L.R. Measures of the amount of ecologic association between species. Ecology 1945, 26, 297–302. [Google Scholar] [CrossRef]
- Hill, C.S.; Clayden, J.D.; Kitchen, N.; Bull, J.; Harkness, W.; Clark, C.A. A feasibility study of neighbourhood tractography in the presence of paediatric brain tumours. In Proceedings of the Autumn Meeting of the Society of British Neurological Surgeons, Dublin, Ireland, 28–30 October 2009; p. 1191. [Google Scholar]
- Mori, S.; Crain, B.J.; Chacko, V.P.; van Zijl, P.C. Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann. Neurol. 1999, 45, 265–269. [Google Scholar] [CrossRef]
- Seunarine, K.K.; Clayden, J.D.; Clark, C.A. Whole-brain neighbourhood tractography. In Proceedings of the ISMRM 21th Annual Meeting & Exhibition, Salt Lake City, UT, USA, 20–26 April 2013; p. 2132. [Google Scholar]
- Armitage, P.A.; Muñoz Maniega, S.; Bridson, J.; Poon, M.; Bastin, M.E. Improved white matter tract segmentation reproducibility using global diffusion tensor neighborhood tractography. In Proceedings of the ISMRM 20th Annual Meeting & Exhibition, Melbourne, Australia, 5–11 May 2012; p. 1905. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).