1. Introduction
An observed image
g, which contains additive Gaussian noise with zero mean and standard deviation
, may be modeled as
where
is the original image,
K is a linear bounded operator and
n represents the noise. With the aim of preserving edges in images in [
1] total variation regularization in image restoration was proposed. Based on this approach and assuming that
and
, a good approximation of
is usually obtained by solving
where
is a simply connected domain with Lipschitz boundary and
its volume. Here
denotes the total variation of
u in
and
is the space of functions with bounded variation, i.e.,
if and only if
and
; see [
2,
3] for more details. We recall, that
, if
.
Instead of considering (
1), we may solve the penalized minimization problem
for a given constant
, which we refer to the
-TV model. In particular, there exists a constant
such that the constrained problem (
1) is equivalent to the penalized problem (
2), if
and
K does not annihilate constant functions [
4]. Moreover, under the latter condition also the existence of a minimizer of problem (
1) and (
2) is guaranteed [
4]. There exist many algorithms that solve problem (
1) or problem (
2), see for example [
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23] and references therein.
If in problem (
2) instead of the quadratic
-norm an
-norm is used, we refer to it as the
-TV model. The quadratic
-norm is usually used when Gaussian noise is contained in the image, while the
-norm is more suitable for impulse noise [
24,
25,
26].
If we additionally know (or assume) that the original image lies in the dynamic range
, i.e.,
for almost every (a.e.)
, we incorporate this information into our problems (
1) and (
2) leading to
and
respectively, where
. In order to guarantee the existence of a minimizer of problems (
3) and (
4) we assume in the sequel that
K does not annihilate constant functions. By noting that the characteristic function
is lower semicontinuous this follows by the same arguments as in [
4]. If additionally
, then by [
4] (Prop. 2.1) it follows that there exists a constant
such that problem (
3) is equivalent to problem (
4).
For image restoration box-constraints have been considered for example in [
5,
27,
28,
29]. In [
29] a functional consisting of an
-data term and a Tikhonov-like regularization term (i.e.,
-norm of some derivative of
u) in connection with box-constrained is presented together with a Newton-like numerical scheme. For box-constrained total variation minimization in [
5] a fast gradient-based algorithm, called monoton fast iterative shrinkage/thresholding algorithm (MFISTA), is proposed and a rate of convergence is proven. Based on the alternating direction method of multipliers (ADMM) [
30] in [
27] a solver for the box-constrained
-TV and
-TV model is derived and shown to be faster than MFISTA. In [
28] a primal-dual algorithm for the box-constrained
-TV model and for box-constrained non-local total variation is presented. In order to achieve a constrained solution, which is positive and bounded from above by some intensity value, in [
31] an exponential type transform is applied to the
-TV model. Recently, in [
32] a box-constraint is also incorporated in a total variation model with a combined
-
data fidelity, proposed in [
33], for removing simultaneously Gaussian and impulse noise in images.
Setting the upper bound in the set
C to infinity and the lower bound to 0, i.e.,
and
, leads to a non-negativity constraint. Total variation minimization with a non-negativity constraint is a well-known technique to improve the quality of reconstructions in image processing; see for example [
34,
35] and references therein.
In this paper we are concerned with the problems (
3) and (
4) when the lower bound
and the upper bound
in
C are finite. However, the analysis and the presented algorithms are easily adjustable to the situation when one of the bounds is set to
or
respectively. Note, that a solution of problem (
1) and problem (
2) is in general not an element of the set
C. However, since
g is an observation containing Gaussian noise with zero mean, a minimizer of problem (
2) lies indeed in
C, if
in problem (
2) is sufficiently large and the original image
. This observation however rises the question whether an optimal parameter
would lead to a minimizer that lies in
C. If this would be the case then incorporating the box-constraint into the minimization problem does not gain any improvement of the solution. In particular, there are situations in which a box-constraint is not effecting the solution at all (see
Section 3 below). Additionally, we expect that the box-constrained problems are more difficult to handle and numerically more costly to solve than problem (
1) and problem (
2).
In order to answer the above raised question, we numerically compute optimal values of
for the box-constrained total variation and the non-box-constrained total variation and compare the resulting reconstructions with respect to quality measures. By optimal values we mean here parameters
such that the solutions of problem (
1) and problem (
2) or problem (
3) and problem (
4) coincide. Note, that there exists several methods for computing the regularization parameter; see for example [
36] for an overview of parameter selection algorithms for image restoration. Here we use the pAPS-algorithm proposed in [
36] to compute reasonable
in problem (
2) and problem (
4). For minimizing problem (
4) we derive a semi-smooth Newton method, which should serve us as a good method for quickly computing rather exact solutions. Second order methods have been already proposed and used in image reconstruction; see [
21,
36,
37,
38,
39]. However, to the best of our knowledge till now semi-smooth Newton methods have not been presented for box-constrained total variation minimization. In this setting, differently to the before mentioned approaches, the box-constraint adds some additional difficulties in deriving the dual problems, which have to be calculated to obtain the desired method; see
Section 4 for more details. The superlinear convergence of our method is guaranteed by the theory of semi-smooth Newton methods; see for example [
21]. Note, that our approach differs significantly from the Newton-like scheme presented in [
29], where a smooth objective functional with a box-constraint is considered. This allows in [
29] to derive a Newton method without dualization. Here, our Newton method is based on dualization and may be viewed as a primal-dual (Newton) approach.
We remark, that a scalar regularization parameter might not be the best choice for every image restoration problem, since images usually consist of large uniform areas and parts with fine details, see for example [
36,
38]. It has been demonstrated, for example in [
36,
38,
40,
41] and references therein, that with the help of spatially varying regularization parameters one might be able to restore images visually better than with scalar parameters. In this vein we also consider
and
where
is a bounded continuous function [
42]. We adapt our semi-smooth Newton method to approximately solve these two optimization problems and utilize the pLATV-algorithm of [
36] to compute a locally varying
.
Our numerical results show, see
Section 6, that in a lot of applications the quality of the restoration is more a question of how to choose the regularization parameter then including a box-constraint. However, the solutions obtained by solving the box-constrained versions (
3), (
4) and (
6) are improving the restorations slightly, but not drastically. Nevertheless, we also report on a medical applications where a non-negativity constraint significantly improves the restoration.
We realize that if the noise-level of the corrupted image is unknown, then we may use the information of the image intensity range (if known) to calculate a suitable parameter for problem (
2). Note, that in this situation the optimization problems (
1) and (
3) cannot be considered since
is not at hand. We present a method which automatically computes the regularization parameter
in problem (
2) provided the information that the original image
.
Hence the contribution of the paper is three-sided: (i) We present a semi-smooth Newton method for the box-constrained total variation minimization problems (
3) and (
6). (ii) We investigate the influence of the box-constraint on the solution of the total variation minimization models with respect to the regularization parameter. (iii) In case the noise-level is not at hand, we propose a new automatic regularization parameter selection algorithm based on the box-constraint information.
The outline of the rest of the paper is organized as follows: In
Section 2 we recall useful definitions and the Fenchel-duality theorem which will be used later.
Section 3 is devoted to the analysis of the box-constrained total variation minimization. In particular, we state that in certain cases adding a box-constraint to the considered problem does not change the solution at all. The semi-smooth Newton method for the box-constrained
-TV model (
4) and its multiscale version (
6) is derived in
Section 4 and its numerical implementation is presented in
Section 5. Numerical experiments investigating the usefulness of a box-constraint are shown in
Section 6. In
Section 7 we propose an automatic parameter selection algorithm by using the box-constraint. Finally, in
Section 8 conclusions are drawn.
3. Limitation of Box-Constrained Total Variation Minimization
In this section we investigate the difference between the box-constrained problem (
4) and the non-box-constrained problem (
1). For the case when the operator
K is the identity
I, which is the relevant case in image denoising, we have the following obvious result:
Proposition 1. Let and , then the minimizer of problem (2) lies also in the dynamic range , i.e., . Proof of Proposition 1. Assume
is a minimizer of problem (
2). Define a function
such that
for a.e.
. Then we have that
This implies that
is not a minimizer of problem (
2), which is a contradiction and hence
. ☐
This result is easily extendable to optimization problems of the type
with
and
, since for
, defined as in the above proof, and a minimizer
of problem (
9) the inequalities in (
8) hold as well as
. Problem (
9) has been already considered in [
33,
44,
45] and can be viewed as a generalization of the
-TV model, since
in (
9) yields the
-TV model and
in (
9) yields the
-TV model.
Note, that if an image is only corrupted by impulse noise, then the observed image
g is in the dynamic range of the original image. For example, salt-and-pepper noise contained images may be written as
with
[
46] and for
random-valued impulse noise g is described as
with
d being a uniformly distributed random variable in the image intensity range
. Hence, following Proposition 1, in such cases considering constrained total variation minimization would not change the minimizer and no improvement in the restoration quality can be expected.
This is the reason why we restrict ourselves in the rest of the paper to Gaussian white noise contaminated images and consider solely the -TV model.
It is clear that if a solution of the non box-constrained optimization problem already fulfills the box-constraint, then it is of course equivalent to a minimizer of the box-constraint problem. However, note that the minimizer is not unique in general.
In the following we compare the solution of the box-constrained optimization problem (
4) with the solution of the unconstrained minimization problem (
2).
Proposition 2. Let be a minimizer ofand be a minimizer ofThen we have that - 1.
.
- 2.
.
- 3.
for any .
Proof of Proposition 2. ☐
If in Proposition 2 is constant, then which implies that .
6. Numerical Experiments
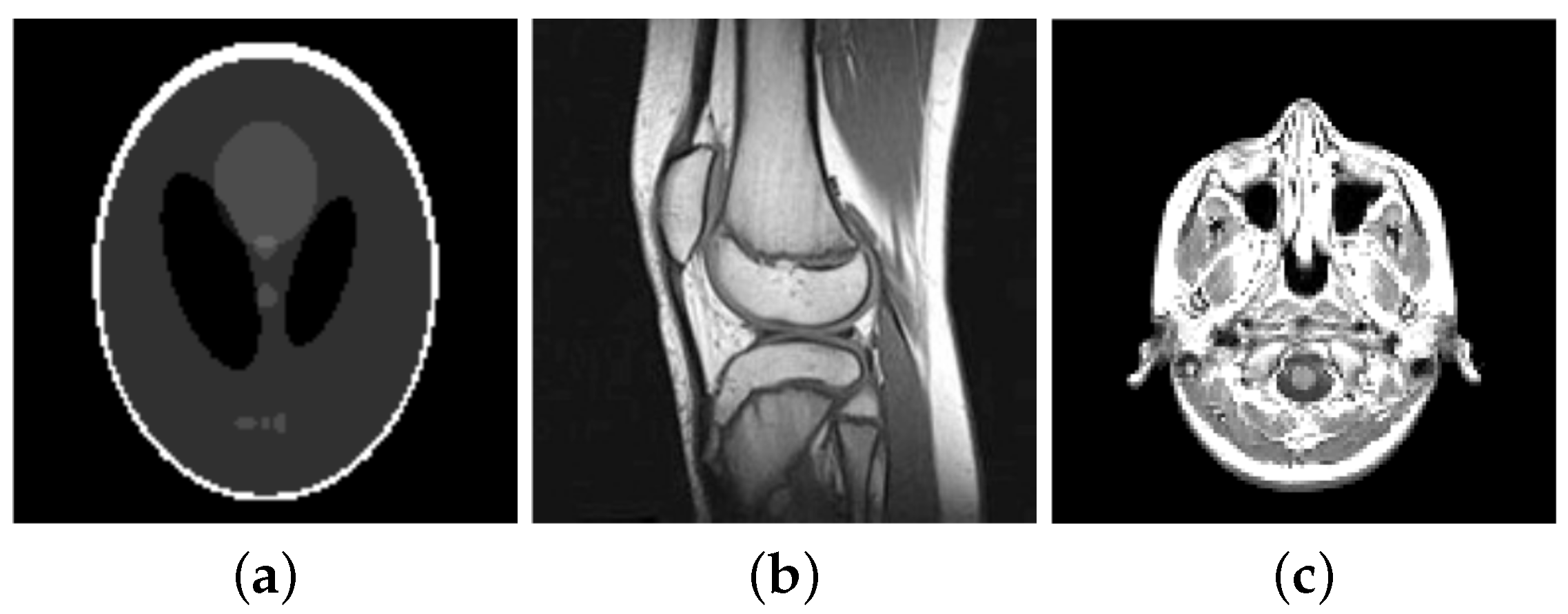
For our numerical studies we consider the images shown in
Figure 1 of size 256 × 256 pixels and in
Figure 2. The image intensity range of all original images considered in this paper is
, i.e.,
and
. Our proposed algorithms automatically transform this images into the dynamic range
, here with
. That is, let
be the original image before any corruption, then
. Moreover, the solution generated by the semi-smooth Newton method is afterwards back-transformed, i.e., the generated solution
is transformed to
. Note that
is not necessarily in
, except
.
As a comparison for the different restoration qualities of the restored image we use the PSNR [
49] (peak signal-to-noise ratio) given by
where
denotes the original image before any corruption and
the restored image, which is widely used as an image quality assessment measure, and the MSSIM [
50] (mean structural similarity), which usually relates to perceived visual quality better than PSNR. In general, when comparing PSNR and MSSIM, large values indicate better reconstruction than small values.
In our experiments we also report on the computational time (in seconds) and the number of iterations (it) needed until the considered algorithms are terminated.
In all the following experiments the parameter is chosen to be 0 for image denoising (i.e., ), since then no additional smoothing is needed, and if (i.e., for image deblurring, image inpainting, for reconstructing from partial Fourier-data, and for reconstructing from sampled Radon-transform).
6.1. Dependency on the Parameter
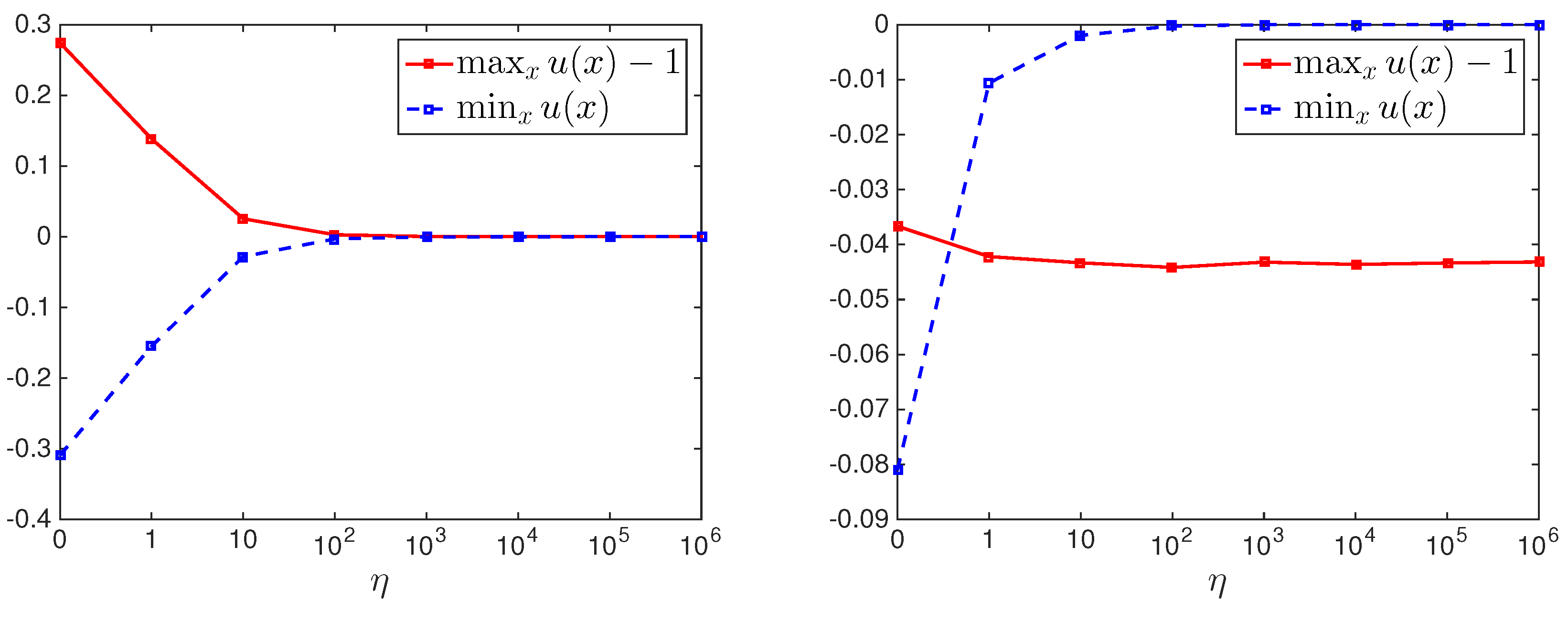
We start by investigating the influence of the parameter
on the behavior of the semi-smooth Newton algorithm and its generated solution. Let us recall, that
is responsible how strictly the box-constraint is adhered. In order to visualize how good the box-constraint is fulfilled for a chosen
in
Figure 3 we depict
and
with
,
, and
u being the back-transformed solution, i.e.,
, where
is obtained via the semi-smooth Newton method. As long as
and
are positive and negative, respectively, the box-constraint is not perfectly adhered. From our experiments for image denoising and image deblurring, see
Figure 3, we clearly see that the larger
the more strictly the box-constraint is adhered. In the rest of our experiments we choose
, which seems sufficiently large to us and the box-constraint seems to hold accurately enough.
6.2. Box-Constrained Versus Non-Box-Constrained
In the rest of this section we are going to investigate how much the solution (and its restoration quality) depends on the box-constraint and if this is a matter on how the regularization parameter is chosen. We start by comparing for different values of
the solutions obtained by the semi-smooth Newton method without a box-constraint (i.e.,
) with the ones generated by the same algorithm with
(i.e., a box-constraint is incorporated). Our obtained results are shown in
Table 1 for image denoising and in
Table 2 for image deblurring. We obtain, that for small
we gain “much” better results with respect to PSNR and MSSIM with a box-constraint than without. The reason for this is that if no box-constraint is used and
is small then nearly no regularization is performed and hence noise, which is violating the box-constraint, is still present. Therefore incorporating a box-constraint is reasonable for these choices of parameters. However, if
is sufficiently large then we numerically observe that the solution of the box-constrained and non-box-constrained problem are the same. This is not surprising, because there exists
such that for all
the solution of problem (
2) is
, see [
4] (Lemma 2.3). That is, for such
the minimizer of problem (
2) is the average of the observation which lies in the image intensity range of the original image, as long as the mean of Gaussian noise is 0 (or sufficiently small). This implies that in such a case the minimizer of problem (
2) and problem (
4) are equivalent. Actually this equivalency already holds if
is sufficiently large such that the respective solution of problem (
2) lies in the dynamic range of the original image, which is the case in our experiments for
. Hence, whether it makes sense or not to incorporate a box-constraint into the considered model depends on the choice of parameters. The third and fourth value of
in
Table 1 and
Table 2 refer to the ones which equalize problem (
2) and problem (
1), and respectively problem (
4) and problem (
3). In the sequel we call such parameters
optimal, since a solution of the penalized problem also solves the related constrained problem. However, we note that these
-values are in general not giving the best results with respect to PSNR and MSSIM, but they are usually close to the results with the largest PSNR and MSSIM. For both type of applications, i.e., image denoising and image deblurring, these optimal
-values are nearly the same for problem (
2) and problem (
1), and respectively problem (
4) and problem (
3) and hence also the PSNR and MSSIM of the respective results are nearly the same. Nevertheless, we mention that for image deblurring the largest PSNR and MSSIM in these experiments is obtained for
with a box-constraint.
In
Table 3 and
Table 4 we also report on an additional strategy. In this approach we threshold (or project) the observation
g such that the box-constraint holds in any pixel and use then the proposed Newton method with
. For large
this is an inferior approach, but for small
this seems to work similar to incorporating a box-constraint, at least for image denoising. However, it is outperformed by the other approaches.
6.3. Comparison with Optimal Regularization Parameters
In order to determine the optimal parameters
for a range of different examples we assume that the noise-level
is at hand and utilize the pAPS-algorithm presented in [
36]. Alternatively, instead of computing a suitable
, we may solve the constrained optimization problems (
1) and (
3) directly by using the alternating direction methods of multipliers (ADMM). An implementation of the ADMM for solving problem (
1) is presented in [
51], which we refer to as the ADMM in the sequel. For solving problem (
3) a possible implementation is suggested in [
27]. However, for comparison purposes we use a slightly different version, which uses the same succession of updates as the ADMM in [
51], see
Appendix B for a description of this version. In the sequel we refer to this algorithm as the box-contrained ADMM. We do not expect the same results for the pAPS-algorithm and the (box-contrained) ADMM, since in the pAPS-algorithm we use the semi-smooth Newton method which generates an approximate solution of problem (
15), that is not equivalent to problem (
1) and problem (
3). In all the experiments in the pAPS-algorithm we set the initial regularization parameter to be
.
6.3.1. pdN versus ADMM
We start by comparing the performance of the proposed primal-dual semi-smooth Newton method (pdN) and the ADMM. In these experiments we assume that we know the optimal parameters , which are then used in the pdN. Note, that a fair comparison of these two methods is difficult, since they are solving different optimization problems, as already mentioned above. However, we still compare them in order to understand better the performance of the algorithms in the sequel section.
The comparison is performed for image denoising and image deblurring and the respective findings are collected in
Table 5 and
Table 6. From there we clearly observe, that the proposed pdN with
reaches in all experiments the desired reconstruction significantly faster than the box-constrained ADMM. While the number of iterations for image denoising is approximately the same for both methods, for image deblurring the box-constrained pdN needs significantly less iterations than the other method. In particular, the pdN needs nearly the same amount of iterations independently of the application. However, more iterations for small
are needed. Note, that the pdN converges at a superlinear rate and hence a faster convergence than the box-constrained ADMM is not surprising but supports the theory.
6.3.2. Image Denoising
In
Table 7 and
Table 8 we summarize our findings for image denoising. We observe that adding a box-constraint to the considered optimization problem leads to a possibly slight improvement in PSNR and MSSIM. While in some cases there is some improvement (see for example the image “numbers”) in other examples no improvement is gained (see for example the image “barbara”). In order to make the overall improvement more visible, in the last row of
Table 7 and
Table 8 we add the average PSNR and MSSIM of all computed restorations. It shows that on average we may expect a gain of around 0.05 PSNR and around 0.001 MSSIM, which is nearly nothing. Moreover, we observe, that the pAPS-algorithm computes the optimal
for the box-constrained problem on average faster than the one for the non-box-constrained problem. We remark, that the box-constrained version needs less (or at maximum the same amount of) iterations as the version with
. The reason for this might be that in each iterations, due to the thresholding of the approximation by the box-constraint, a longer or better step towards the minimizer than by the non-box-constrained pAPS-algorithm is performed. At the same time also the reconstructions of the box-constrained pAPS-algorithm yield higher PSNR and MSSIM than the ones obtained by the pAPS-algorithm with
. The situation seems to be different for the ADMM. On average, the box-constrained ADMM and the (non-box-constrained) ADMM need approximately the same run-time.
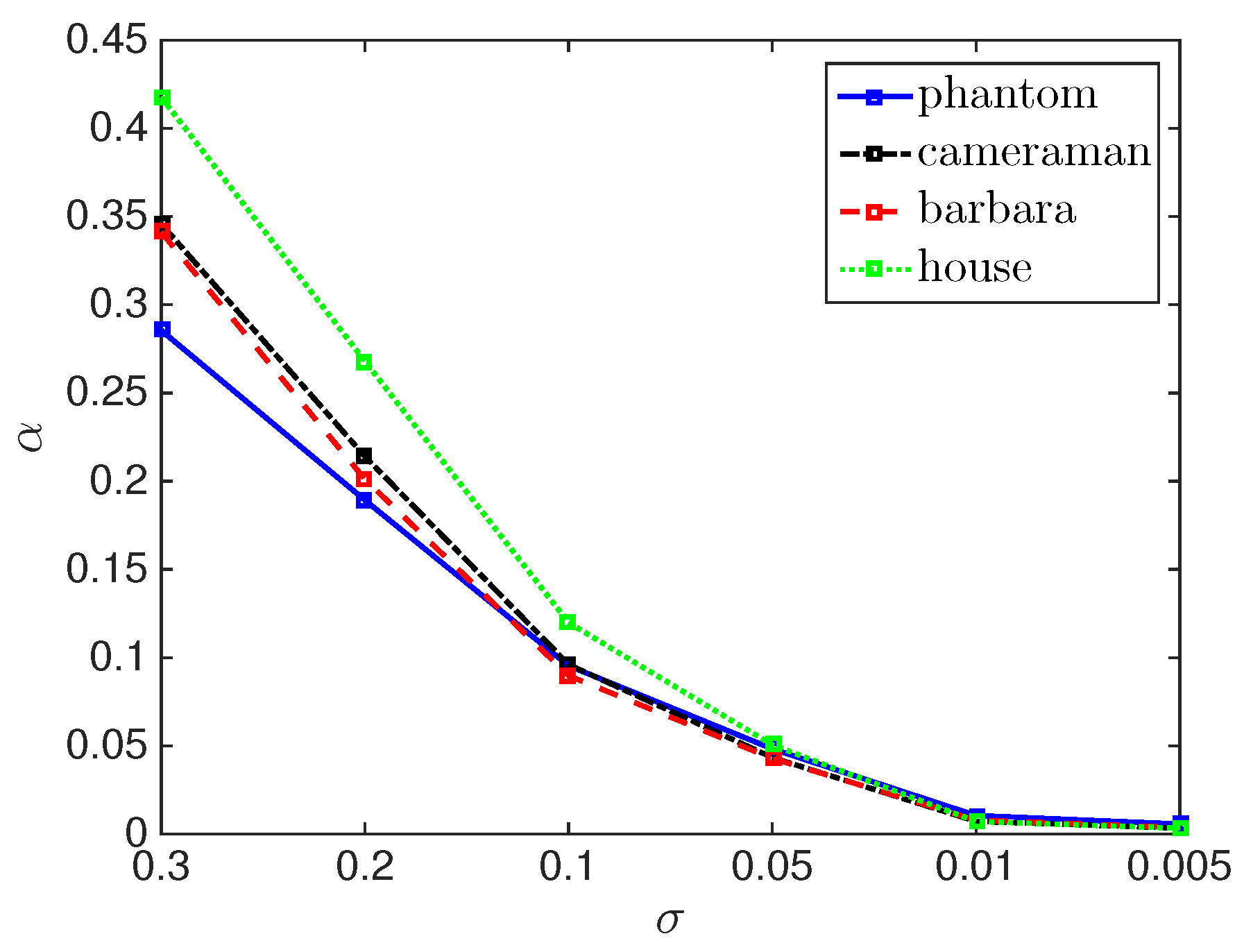
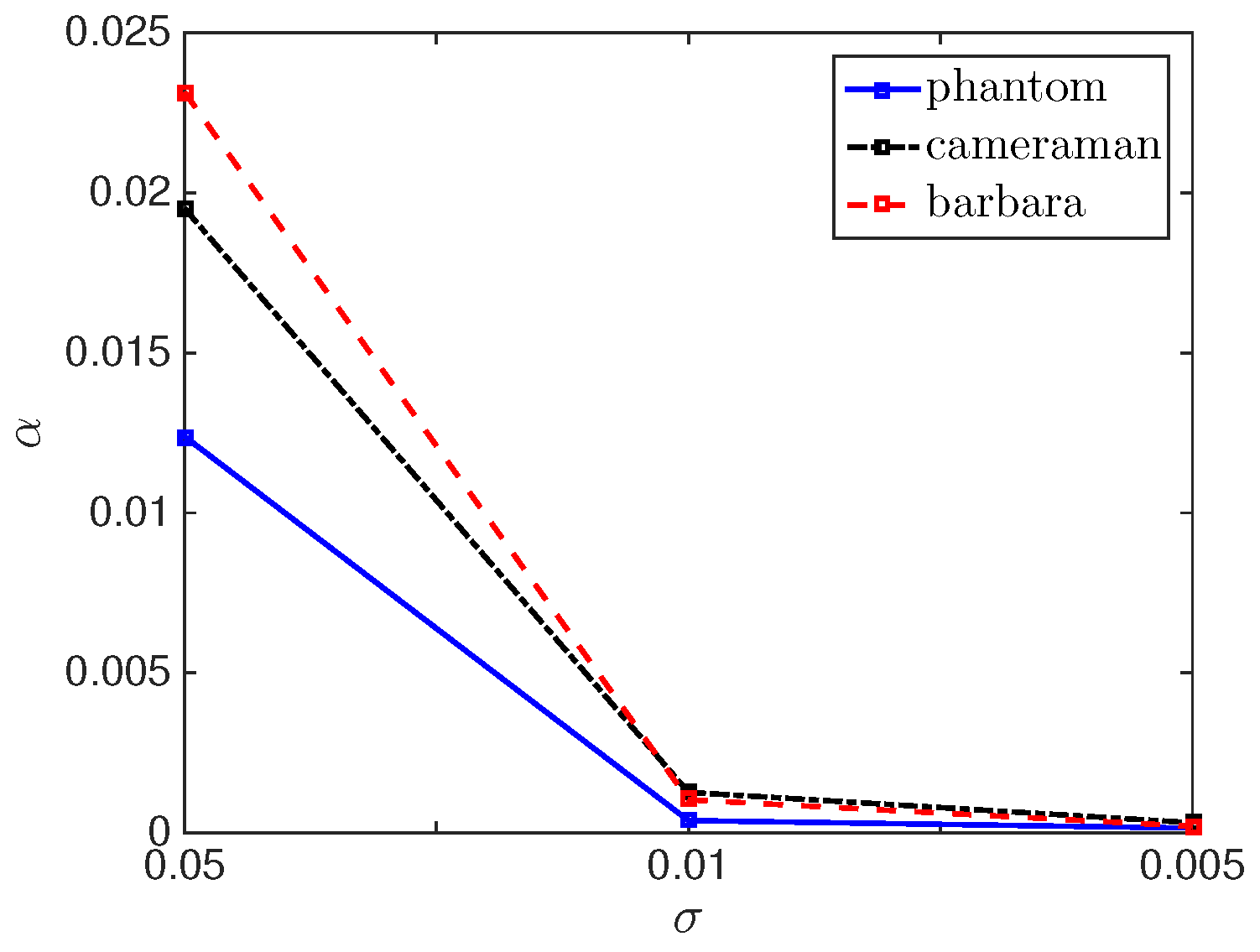
For several examples (i.e., the images “phantom”, “cameraman”, “barbara”, “house”) the choice of the regularization parameter by the box-constrained pAPS-algorithm with respect to the noise-level is depicted in
Figure 4. Clearly, the parameter is selected to be smaller the less noise is present in the image.
We are now wondering whether a box-constraint is more important when the regularization parameter is non-scalar, i.e., when
is a function. For computing suitable locally varying
we use the pLATV-algorithm proposed in [
36], whereby we set in all considered examples the initial (non-scalar) regularization parameter to be constant
. Note, that the continuity assumption on
in problem (
5) and problem (
6) is not needed in our discrete setting, since
is well defined for any
. We approximate such
for problem (
20) with
(unconstrained) and with
(box-constrained) and obtain also here that the gain with respect to PSNR and MSSIM is of the same order as in the scalar case, see
Table 9.
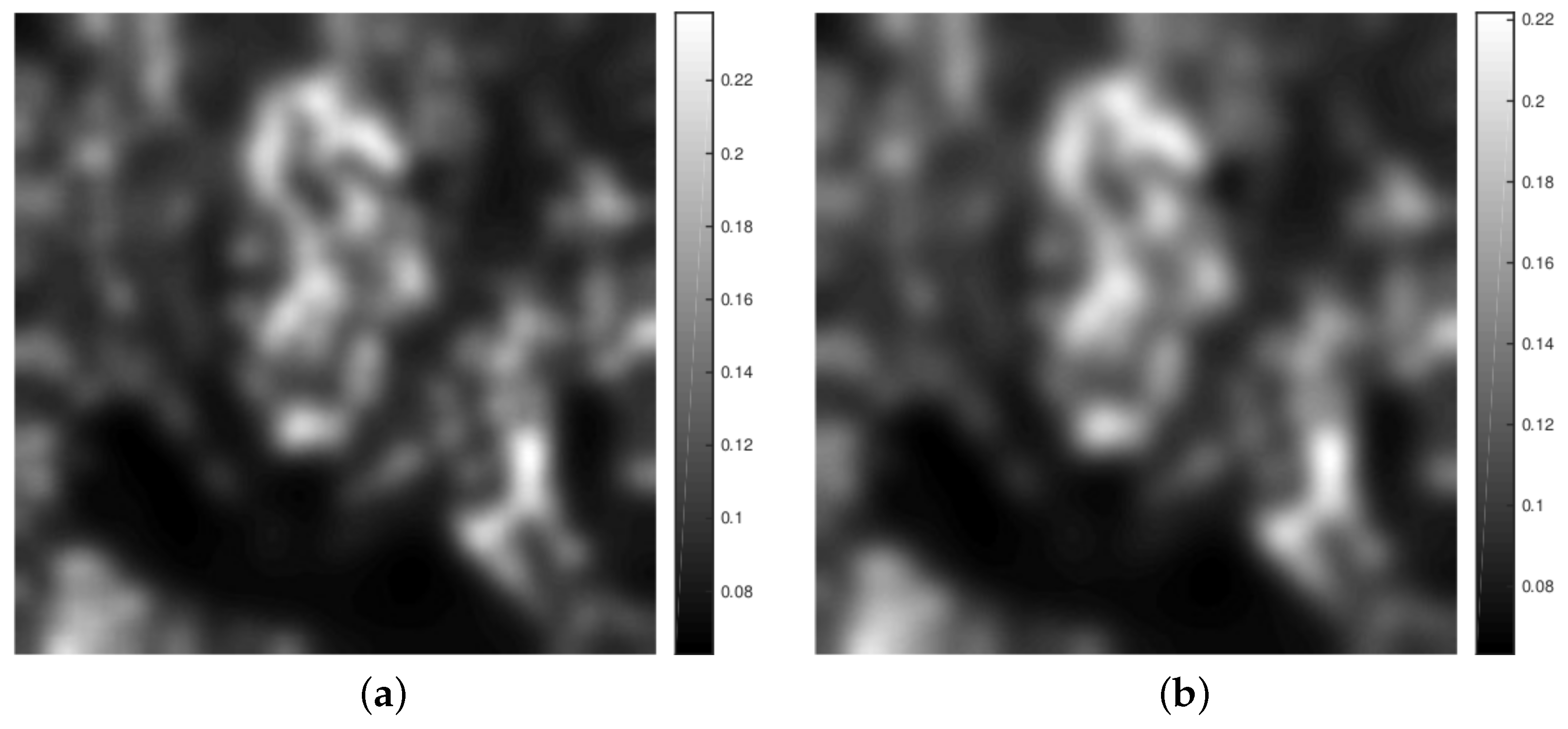
For
and the image “barbara” we show in
Figure 5 the reconstructions generated by the considered algorithms. As indicated by the quality measures, all the reconstructions look nearly alike, whereby in the reconstructions produced by the pLATV-algorithm details, like the pattern of the scarf, are (slightly) better preserved. The spatially varying
of the pLATV-algorithm is depicted in
Figure 6. There we clearly see, that at the scarf around the neck and shoulder the values of
are small, allowing to preserve the details better.
6.3.3. Image Deblurring
Now we consider the images in
Figure 1a–c, convolve them first with a Gaussian kernel of size
and standard deviation 3 and then add some Gaussian noise with mean 0 and standard deviation
. Here we again compare the results obtained by the pAPS-algorithm, the ADMM, and the pLATV-algorithm for the box-constrained and non-box-constrained problems. Our findings are summarized in
Table 10. Also here we observe a slight improvement with a box-constraint with respect to PSNR and MSSIM. The choice of the regularization parameters by the box-constrained pAPS-algorithm is depicted in
Figure 7. In
Figure 8 we present for the image “cameraman” and
the reconstructions produced by the respective methods. Also here, as indicated by the quality measures, all the restorations look nearly the same. The locally varying
generated by the pLATV-algorithm are depicted in
Figure 9.
6.3.4. Image Inpainting
The problem of filling in and recovering missing parts in an image is called image inpainting. We call the missing parts inpainting domain and denote it by . The linear bounded operator K is then a multiplier, i.e., , where is the indicator function of . Note, that K is not injective and hence is not invertible. Hence in this experiment we need to set so that we can use the proposed primal-dual semismooth Newton method. In particular, as mentioned above, we choose .
In the considered experiments the inpainting domain are gray bars as shown in
Figure 10a, where additionally additive white Gaussian noise with
is present. In particular, we consider examples with
. The performance of the pAPS- and pLATV-algorithm with and without a box-constraint reconstructing the considered examples are summarized in
Table 11 and
Table 12. We observe, that adding a box-constraint does not seem to change the restoration considerably. However, as in the case of image denoising, the pAPS-algorithm with box-constrained pdN needs less iterations and hence less time than the same algorithm without a box-constraint to reach the stopping criterion.
Figure 10 shows a particular example for image inpainting and denoising with
. It demonstrates that visually there is nearly no difference between the restoration obtained by the considered approaches. Moreover, we observe that the pLATV-algorithm seems to be not suited to the task of image inpainting. A reason for this might be, that the pLATV-algorithm does not take the inpainting domain correctly into account. This is visible in
Figure 11 where the spatially varying
seems to be chosen small in the inpainting domain, which not necessarily seems to be a suitable choice.
6.3.5. Reconstruction from Partial Fourier-Data
In magnetic resonance imaging one wishes to reconstruct an image which is only given by partial Fourier data and additionally distorted by some additive Gaussian noise with zero mean and standard deviation
. Hence, the linear bounded operator is
, where
is the
Fourier matrix and
S is a downsampling operator which selects only a few output frequencies. The frequencies are usually sampled along radial lines in the frequency domain, in particular in our experiments along 32 radial lines, as visualized in
Figure 12.
In our experiments we consider the images of
Figure 2, transformed to its Fourier frequencies. As already mentioned, we sample the frequencies along 32 radial lines and add some Gaussian noise with zero mean and standard deviation
. In particular, we consider different noise-levels, i.e.,
. We reconstruct the obtained data via the pAPS- and pLATV-algorithm by using the semi-smooth Newton method first with
(no box-constraint) and then with
(with box-constraint). In
Table 13 we collect our findings. We observe that the pLATV-algorithm seems not to be suitable for this task, since it is generating inferior results. For scalar
we observe as before, that a slight improvement with respect to PSNR and MSSIM is expectable when a box-constraint is used. In
Figure 13 we present the reconstructions generated by the considered algorithms for a particular example, demonstrating the visual behavior of the methods.
6.3.6. Reconstruction from Sampled Radon-Data
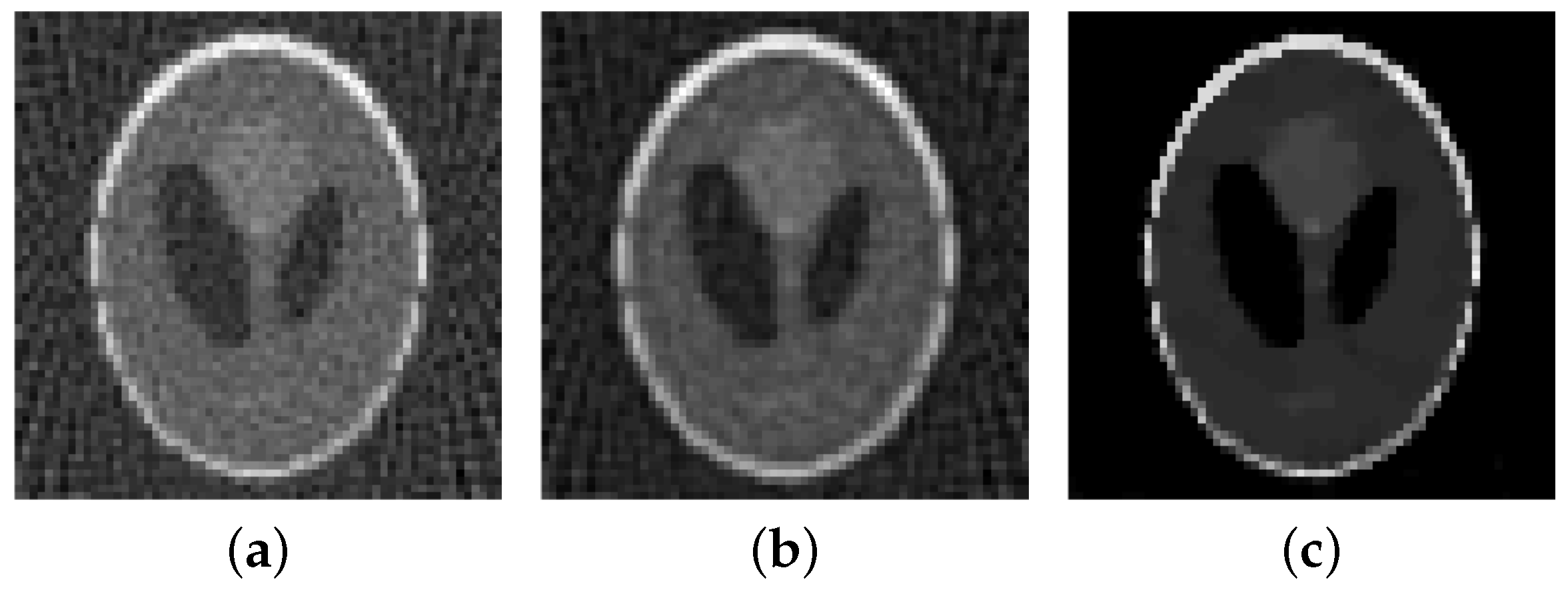
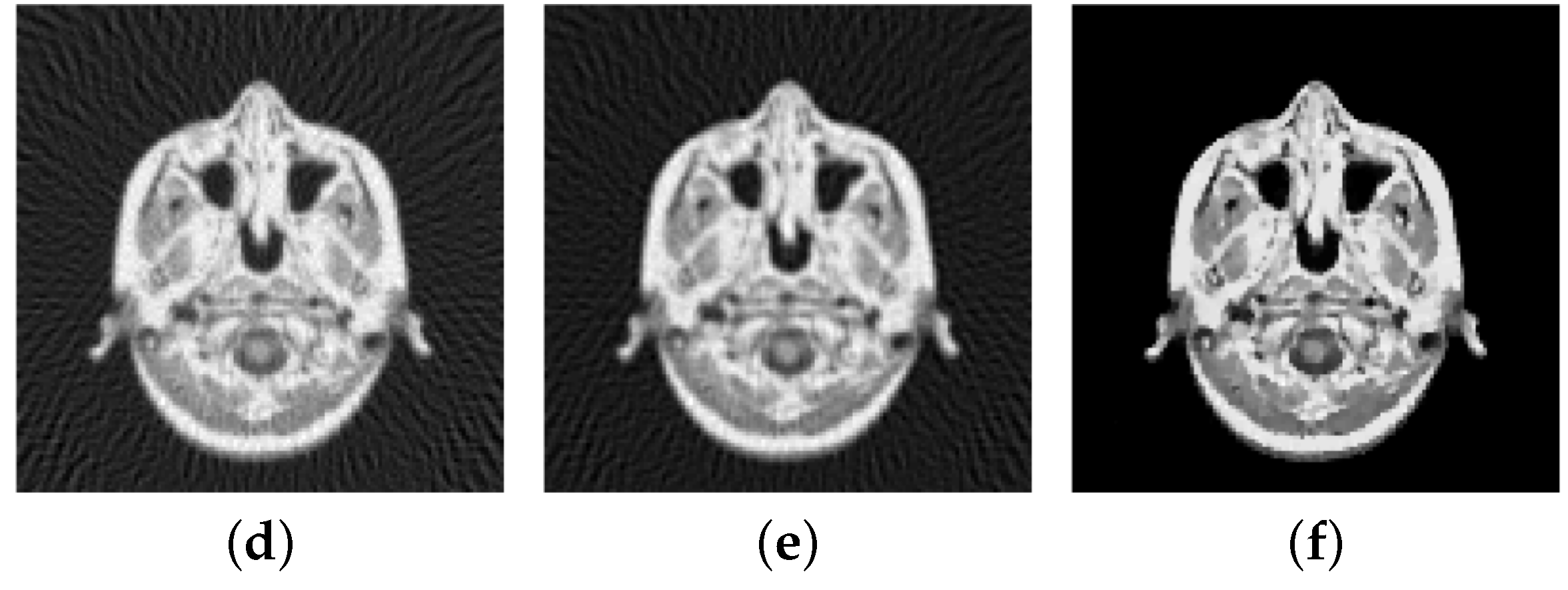
In computerized tomography instead of a Fourier-transform a Radon-transform is used in order to obtain a visual image from the measured physical data. Also here the data is obtained along radial lines. Here we consider the Shepp-Logan phantom, see
Figure 14a, and a slice of a body, see
Figure 15a. The sinogram in
Figure 14a and
Figure 15b are obtained by sampling along 30 and 60 radial lines, respectively, Note, that the sinogram is in general noisy. Here the data is corrupted by Gaussian white noise with standard deviation
, whereby
for the data of the Shepp-Logan phantom and
for the data of the slice of the head. Using the inverse Radon-transform we obtain
Figure 16a,b, which is obviously a suboptimal reconstruction. A more sophisticated approach utilizes the
-TV model which yields the reconstruction depicted in
Figure 16b,e, where we use the pAPS-algorithm and the proposed primal-dual algorithm with
. However, since an image can be assumed to have non-negative values, we may incorporate a non-negativity constraint via the box-constrained
-TV model yielding the result in
Figure 16c,f, which is a much better reconstruction. Also here the parameter
is automatically computed by the pAPS-algorithm and the non-negativity constraint is incorporated by setting
in the semi-smooth Newton method. In order to compute the Radon-matrix in our experiments we used the FlexBox [
52].
Other applications where a box-constraint, and in particular a non-negativity improves the image reconstruction quality significantly include for example magnetic particle imaging, see for example [
53] and references therein.
7. Automated Parameter Selection
We recall, that if the noise-level
is not known, then the problems (
1) and (
3) cannot be considered. Moreover, the selection of the parameter
in problem (
2) cannot be achieved by using the pAPS-algorithm, since this algorithm is based on problem (
1). Note, that also other methods, like the unbiased predictive risk estimator method (UPRE) [
54,
55] and approaches based on the Stein unbiased risk estimator method (SURE) [
56,
57,
58,
59,
60] use knowledge of the noise-level and hence cannot be used for selecting a suitable parameter if
is unknown.
If we assume that
is unknown but the image intensity range of the original image
is known, i.e.,
, then we may use this information for choosing the parameter
in problem (
2). This may be performed by applying the following algorithm:
Box-constrained automatic parameter selection (bcAPS): Initialize (sufficiently small) and set
1. Solve .
2. If increase (i.e., with ), else STOP.
3. Set and continue with step 1. |
Here is an arbitrary parameter chosen manually such that the generated restoration u is not over-smoothed, i.e., there exist such that and/or . In our experiments it turned out that seems to be a reasonable choice, so that the generated solution has the wished property.
Numerical Examples
In our experiments the minimization problem in step 1 of the bcAPS algorithm is approximately solved by the proposed primal-dual semi-smooth Newton method with . We set the initial regularization parameter for image denoising and for image deblurring. Moreover, we set in the bcAPS-algorithm to increase the regularization parameter.
Experiments for image denoising, see
Table 14, show that the bcAPS-algorithm finds suitable parameters in the sense that the PSNR and MSSIM of these reconstructions is similar to the ones obtained with the pAPS-algorithm (when
is known); also compare with
Table 7 and
Table 10. This is explained by the observation that also the regularization parameters
calculated by the bcAPS-algorithm do not differ much from the ones obtained via the pAPS-algorithm. For image deblurring, see
Table 15, the situation is not so persuasive. In particular, the obtained regularization parameter of the two considered methods differ more significantly than before, resulting in different PSNR and MSSIM. However, in the case
the considered quality measures of the generated reconstructions are nearly the same.
We also remark, that in all the experiments the pAPS-algorithm generated reconstructions, which have larger PSNR and MSSIM than the ones obtained by the bcAPS-algorithm. From this observation it seems more useful to know the noise-level than the image intensity range. However, if the noise-level is unknown but the image intensity is known, then the bcAPS-algorithm may be a suitable choice.