Abstract
Watermark is the copy deterrence mechanism used in the multimedia signal that is to be protected from hacking and piracy such a way that it can later be extracted from the watermarked signal by the decoder. Watermarking can be used in various applications such as authentication, video indexing, copyright protection and access control. In this paper a new CDMA (Code Division Multiple Access) based robust watermarking algorithm using customized 8 × 8 Walsh Hadamard Transform, is proposed for the color images and detailed performance and robustness analysis have been performed. The paper studies in detail the effect of spreading code length, number of spreading codes and type of spreading codes on the performance of the watermarking system. Compared to the existing techniques the proposed scheme is computationally more efficient and consumes much less time for execution. Furthermore, the proposed scheme is robust and survives most of the common signal processing and geometric attacks.
1. Introduction
Now-a-days, internet and multimedia technologies have become part and parcel of the human life. The information shared on the world wide web (www) is proliferating day by day. Due to the recent advances in digital technologies, these contents can easily be copied, downloaded and manipulated [1]. Hacking and piracy turns out to be the byproduct of the digital revolutions. To prevent the anonymous manipulation of the digital contents and to protect the copyright, multimedia researchers introduced the copy deterrence mechanism called watermarks which are usually logos, stamps, Gaussian random patterns or pseudo noise sequences that are embedded in the media to be protected. Watermarking does not ensure that the watermarked image is completely secure because there can be intentional manipulations of the image (collusion, confusion and ownership deadlock), which actually try to destroy the embedded watermark or non-intentional manipulations like geometrical and signal processing operations (cropping, scaling, filtering, A/D conversion, etc.) [2]. The embedding algorithm should be designed in such a way that the embedded watermark survives the above mentioned attacks and can be extracted from the attacked image by the decoder. Such algorithms are known as robust and secure algorithms. The introduction of the watermarks should not degrade the perceptual quality of the original image. But as the amount of watermark content in the image to be protected (cover image) increases, the perceptual transparency shows significant reduction [3]. At the same time, more the amount of watermarks, the more robust will be the watermarked image against distortions and attacks. So the most important and desirable properties of the watermarks are perceptual quality and robustness even though there exists trade off among those properties. Along with that the good payload size, reduced false positive rate and information hiding capacity are also expected [4,5].
Watermarks can be added to the digital image by modifying the pixel values as per the values of the watermarks which is known as spatial domain watermarking [6]. Alternately, by altering the transform domain values using common transforms like Discrete Cosine Transform (DCT) [3,4], Discrete Wavelet Transform (DWT) [7,8,9], Fast Walsh Hadamard Transform (FWHT) [10,11] or Fast Fourier Transform (FFT). Even though spatial domain techniques are simple to implement they are less robust against attacks [6]. On the other hand, frequency domain techniques show good robustness and perceptual quality but implementation is complex compared to spatial domain techniques [8]. Some researchers combine two transforms to achieve the advantages of both the transforms [12,13,14]. Watermarking has various applications like authentication, copyright protection, military and satellite applications, broadcast monitoring (ensuring the proper broadcast at the proper timing), transaction tracking/finger printing (finding out the source of leakage of multimedia signal), medical applications and many more [2,3]. Based on the application, the properties should be set and accordingly the embedding and decoding algorithm should be modified.
Among different ways of the watermarking models, the communication based model is the most important and widely used. From a communication point of view, watermarking system can be viewed as a process of communicating a message (watermark), through the fixed bandwidth channel (cover image), from the watermarking embedder to the watermarking decoder [1,3,4,8]. Specifically, some researchers apply the concept of CDMA based communication system in which watermark will be spread using the orthogonal spreading code which is generated using the security key and is added to the selected frequency coefficients [7]. Decoding is usually done using correlation of the received image with the spreading codes. Spread spectrum (SS) watermarking is considered to be the most efficient, secure and robust watermarking scheme which yields high Signal to Noise Ratio (SNR), enhanced robustness and low distortion [1,3]. As in DS-CDMA (Direct Sequence—CDMA), different watermarks are spread using mutually orthogonal codes or different parts of a single watermarks are spread using separate codes [2,4]. The additive noise and signal distortions in communication systems are similar compared with the unintentional manipulations on the image and malicious attacks in watermarking. As the watermark is spread throughout the image bandwidth such that the energy of the embedded watermark in any particular frequency bin is very small, it is difficult for the eavesdropper to detect and destroy the watermark [2]. Most of the existing literatures use a single code to spread and few researchers have worked on multiple mutually orthogonal spreading codes [11,14]. As each part of the watermark is spread throughout the cover image, the length of each spreading code can be increased providing more security. If N independent and orthogonal codes are used, the attacker has to break N codes [3]. The selection of transform for the decomposition of image and the properties of spreading codes determine the efficiency of the data spreading.
This paper is organized as follows. Section 2 explains the proposed algorithm of embedding and decoding followed by the simulation results in Section 3 and finally, Section 4 concludes the paper. Mainly we have used, three different cover images and three different watermarks for analysis as shown in succeeding sections.
2. Walsh Hadamard Transform and Related Works
Walsh Hadamard Transforms (WHT) are generalized version of Fourier transforms. The transformation matrix of the WHT consists of only value of 1 and −1 which directly implies that the calculation of Walsh Hadamard Transform of an image consists of only real additions and subtractions [10]. The elementary matrix of Walsh Hadamard Transform is . Higher order matrices () are calculated as the kronecker product (×) of lower order matrices as given below [15].
where .
The rows of the Hadamard matrix are orthogonal and the transpose (), conjugate () and inverse of the matrix () are the same.
Complexity of calculating the Walsh Hadamard Transform is O(Nlog2N) real additions and subtractions. Equations of forward Walsh Hadamard Transform of a one dimensional matrix u(m) is
are binary values
are binary values
The two dimensional transform is found out by calculating the one dimensional WHT of the rows first followed by WHT of the columns. The transformation matrix can be Walsh ordered or Hadamard ordered. Walsh ordered matrix has elements arranged in increasing order of frequency (sequency). Sequency is the more generalized 24 term for frequency which is the number of sign changes among the elements of a row in the matrix. But Hadamard matrix has elements arranged in hadamard order (0, 4, 6, 2, 3, 7, 5, 1).
The inverse and forward transformations are identical except for a scalar multiplication factor. WHTs are computationally very efficient and hardware implementations are cost effective as both forward and inverse transformations can be done through the same block which reduces the space, complexity and cost considerably [11,14]. Most of the energy is contained in less than 50% of the coefficients yielding good energy compaction properties and high resiliency towards low quality compression. So WHT turns out to be the best choice for robust, low cost implementations [2,11].
Only few numbers of researchers worked on FWHT based algorithms. F. Rajkumar et al. combined the image decomposition method, Singular Value Decomposition (SVD) and FWHT and used the entropy (measure of randomness of the pixel values) of the blocks to decide the block to embed the watermark [14]. In [16], Anthony et al. developed a robust watermarking algorithm, but computationally, it takes more time as both watermark and original image are to be frequency transformed. The watermark is embedded in the coefficients selected by the security key. Moreover the DC coefficients of each block should be stored in a separate file. Some of the researchers used complex Hadamard transform. Aris et.al. have applied FWHT on the watermark and has added to the DC coefficients of the host image and they could achieve good visual perception [17]. In [18], the authors tried to add the watermark in the Hadamard coefficients. But no attack analysis is performed instead they studied the effect of scaling factor on the embedding process. In [19], Ishikawa et.al. proposed an illumination based watermarking technique which used a combination of FWHT and DCT. With this technique they were able to attain 100% accuracy and robustness against compression. In [9] complex Hadamard transform is used and the watermark is embedded in the phase of the transform coefficients. Santi. P. Marity et al. used spread spectrum based watermarking using FWHT. They have incorporated characteristics of Human Visual System (HVS) also to make the system more robust and perceptually better [20]. Combining HVS and FWHT offered good robustness against fading as well. The VLSI implementation of the similar algorithm has been done using FPGA which can be used for the blind assessment of Quality of Service (QoS) of the wireless fading channel. In [21] authors have combined the effect of DCT and FWHT. FWHT of the watermark to be embedded is calculated before embedding into the DC coefficients. DCT of each of the 8 × 8 blocks is calculated to extract the DC coefficients of each block and they showed that the proposed technique is better than DCT based technique. E.E. Abdullah et al. combined Single Value Decomposition and FWHT and formulated a high rate, robust and easily implementable algorithm [22]. E. Mwangi used the rows of the Hadamard matrix to spread the watermark using CDMA technique and spread watermark is embedded into the selected DWT coefficients [23].
3. Proposed Algorithm
The proposed algorithm makes use of CDMA based spread spectrum concept, explained earlier, for embedding and decoding the watermark. The spreading codes used are the hadamard codes which are orthogonal codes.
3.1. Computational Efficient Calculation
In this paper the computation of WHT is done using a customised algorithm developed for calculating 8 × 8 WHT cells. The algorithm has been implemented in MATLAB (2013) using the idea of fast computation of Discrete Fourier Transform (DFT), without using any loops and using only matrix additions and subtractions. With this customized technique, computation of WHT of an 8 × 8 image takes only 0.15 milliseconds which is considerably less than the time for execution using existing MATLAB implementation which consumed 1 milliseconds for the same applied image. The cyclomatic complexity of the proposed algorithm is found to be equal to one which means that there is a single path from input to output. On the other hand cyclomatic complexity of MATLAB implemented WHT and DCT is 12. A new, computationally efficient CDMA based watermarking algorithm using above mentioned WHT is formulated with a specific selection of frequency coefficients which has better robustness and performance compared to the existing similar algorithms using other transforms like DCT [3]. Variation of robustness with change in spreading code length, number of spreading codes and type of spreading code is studied in detail.
3.2. Embedding Algorithm
Even though watermarking of the color images are not done by most of the researchers, some of the existing algorithms watermark in all the three (R,G,B) color planes, and some of the researchers embed only in the blue plane as changes in the blue component will not be perceived by the human eye much. Here, the color image to be watermarked is converted to YUV format and the watermark is embedded only in the Y plane based on the property of human visual system (HVS) which states that the human eye is more vulnerable to changes in the color component compared to that in the intensity component [9]. The Y matrix that is to be watermarked is divided into k number of 8 × 8 blocks (i1, i2, i3, i4, …, ik). Each of these blocks is transformed using Fast Walsh Hadamard Transform to get the transformed blocks (h1, h2, h3, h4, …, hk). The binary watermark (B) is converted into one dimensional string (b1, b2, b3 …, bn) each of the values either 1 or −1. For spreading, r numbers of, polar orthogonal hadamard codes are used. As shown in Figure 1 mutually similar mid band coefficients along the 3rd, 4th, 5th and 6th rows are selected for embedding the watermark and rest of the coefficients are left unchanged. Mid frequency coefficients are selected as the changes on them do not cause much changes to the perceptual quality compared to the lower frequency coefficients. In addition, these mid band frequencies are less affected by compression. The selected frequency coefficients along xth row are made into a single vector rx such that length of rx is same as that of spreading codes used. Each bit of the watermark in each modifying row is spread using different spreading codes, then, spread watermarks are added to the selected coefficient vector.
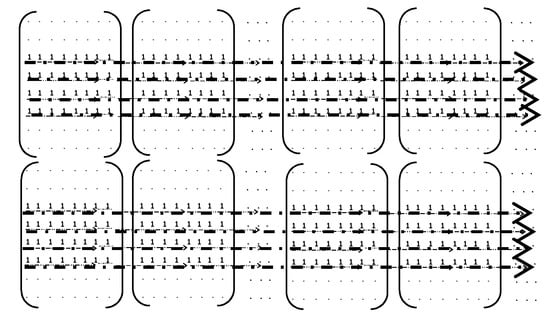
Figure 1.
Location of mid band coefficients used for embedding.
The embedding equation is,
where α is the modulation index or gain of embedding (selected based on the allowed distortion and the required robustness), rx is the xth row used for watermarking and is the FWHT of the xth row of the watermarked image. Watermarked image can be obtained after finding the inverse FWHT of all the watermarked blocks and reconstructing into their original locations. After watermarking, the Y plane is replaced back and the image is converted back to RGB format.
3.3. Decoding Algorithm
The received watermarked image is converted to YUV format and Y plane is split into 8 × 8 blocks as in the embedding side. The split block is transformed to frequency domain using Walsh Hadamard Transform (FWHT). The same orthogonal, Hadamard spreading codes are generated as at the embedding side and the correlation of the modified rows with each of the spreading codes is calculated. The sign of the correlation value determines the embedded watermark bits. If the correlation value is negative the embedded watermark bit is assumed to be 0 and if it is positive the embedded watermark bit is considered to be 1. Embedder and decoder outputs are shown below in Figure 2.
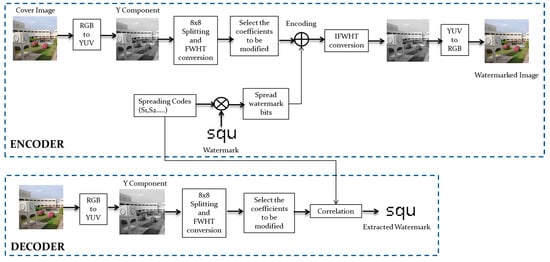
Figure 2.
Embedding and Decoding procedure.
4. Performance Evaluation and Simulation Results
4.1. Performance Measures
The performance of the algorithm is measured and compared based on the following metrics. Mean Square Error (MSE), is the measure of the deviation of watermarked image from the original cover image, which is given by,
where C is the original cover image intensity, WI is watermarked image Intensity, m and n are the width and height of the cover image. Peak Signal to Noise Ratio (PSNR) is the measure of similarity of the original cover image and the watermarked image. It is the direct measure of perceptual quality.
To quantify the quality of the extracted watermark the Bit Error Rate (BER) is used as indication of the similarity of the original binary watermark and extracted watermark. The BER counts the bit by bit difference between the original watermark and the extracted watermark, thus indicating the efficiency and robustness of the watermarking algorithm against image distortions and attacks.
4.2. Computational Complexity and Execution Time
A 512 × 512 sized Lena image is watermarked with a 64 × 64 sized watermark and the time taken for embedding and decoding using the proposed algorithm is measured on HP Laptop EliteBook 8470p with Windows 7 Operating System, 8 GB RAM, clock speed of 2.8 GHz with Intel i5 core CPU. It is found that the total time consumed by the algorithm is 0.665 s.
Compared to DCT based algorithms [3] and FWHT based algorithms, the proposed algorithm takes much less time. The time taken by different algorithms for embedding the same sized watermark is compared in the Table 1 given below.

Table 1.
Execution Time for Different Algorithms.
4.3. Perceptual Quality
Compared to DCT based techniques, the proposed algorithm shows less perceptual quality. When we watermark the 512 × 512 as shown in Figure 3, with a 32 × 32 bit of watermark, proposed technique yields a PSNR value of 41.8 dB and similar DCT technique [3] shows a PSNR value of 50.8dB. Even though the PSNR of the proposed algorithm is numerically less, however, the resultant perceptual quality for PSNR of 41.8 dB is high.

Figure 3.
(a) Cover Image (b) Watermark (c) Decoder output.
4.4. Robustness Analysis
FWHT is resilient to low quality compression compared to other common transforms like DCT and DWT. Lena image, of size 512 × 512 shown in Figure 4 below is watermarked with a watermark of size 32 × 32. Figure 5 below shows that as the compression quality decreases, the extracted watermark is getting distorted and the BER at the extractor increases. Compared to the other algorithms, the proposed algorithm is able to withstand low quality compression up to a quality factor of 15. Comparison of robustness of the proposed algorithm and DCT has been done in the case of various attacks as shown in Table 2. The results reinforce the fact that proposed technique is more robust to all the tested attacks compared to the similar DCT algorithm.

Figure 4.
(a) Lena Image (b) 32 × 32 watermark.
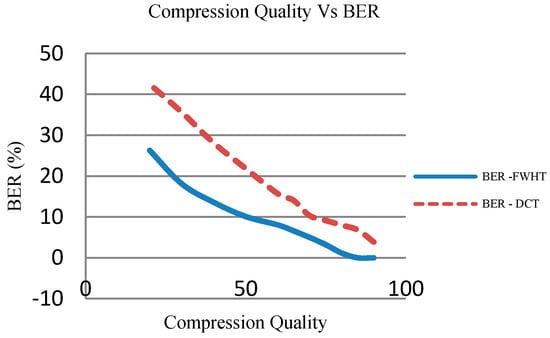
Figure 5.
Compression Quality Vs BER for proposed technique (FWHT) and for similar DCT technique.

Table 2.
Extracted watermark After Different Attacks.
4.5. Effect of Spreading Code Length on Robustness
The 512 × 512 Lena image is watermarked with a 16 × 16 watermark. For watermarking, three different lengths spreading codes, 512 bits, 256 bits and 128 bits are used. When we use 512 bits spreading code the whole row is used for embedding and for 256 bits and 128 bits only half and quarters of the selected coefficients respectively in a row are used for embedding. The BER performance is shown in Figure 6. Robustness of the algorithm in each of the above cases is noted and tabulated Table 3. It can be seen that the 512 bit spreading code is more resistant to compression (JPEG) compared to others and in the case of detailed attack analysis also 512 bit spreading codes show best robustness against all the attacks and 128 bit code the least.
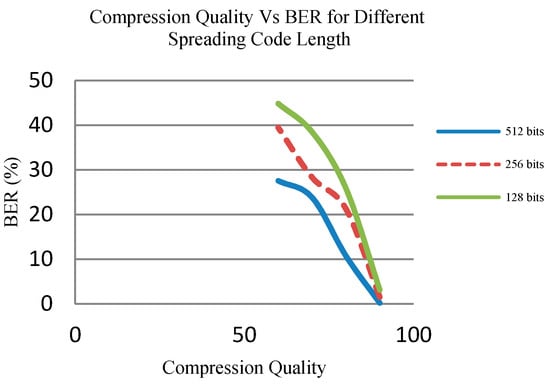
Figure 6.
Compression Quality Vs BER in the case of different spreading code length.

Table 3.
Extracted watermark after different attacks in the case of different spread code length.
4.6. Effect of Number of Watermark Bits on Robustness
As the number of embedded watermark bits increases the robustness of the algorithm against attacks also increases as shown in Figure 7. On the other hand, there occurs degradations in the perceptual quality of the watermarked image. Different watermarks used for simulations are shown in Figure 8.
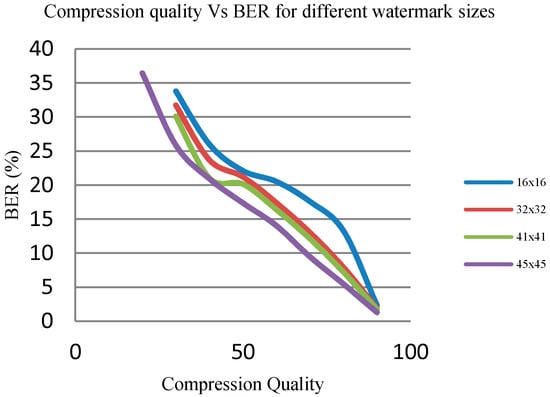
Figure 7.
Compression Quality Vs BER in the case of different watermark sizes.
Figure 8.
Watermarks used (a) 16 × 16 bits (b) 32 × 32 bits (c) 41 × 41bits (d) 45 × 45 bits.
4.7. Effect of Number of Spreading Codes on Robustness
As the number of spreading codes increases, the number of bits of watermark that can be embedded also increases. When we use 4 spreading codes, in each of the selected mid band row 4 bits can be embedded and as per the proposed algorithm total of 1024 bits watermark can be embedded at the maximum in a 512 × 512 image. Same way with one spreading code 256 bits and with 16 spreading codes 4096 bits watermark can be embedded. Different watermarks used in this section are shown in Figure 9. So, in effect as the number of spreading codes increases, the number of watermark bits that can be embedded and thus the robustness increases as shown in Figure 10.
Figure 9.
Watermarks used (a) 16 × 16 bits (b) 32 × 32 bits (c) 64 × 64bits.
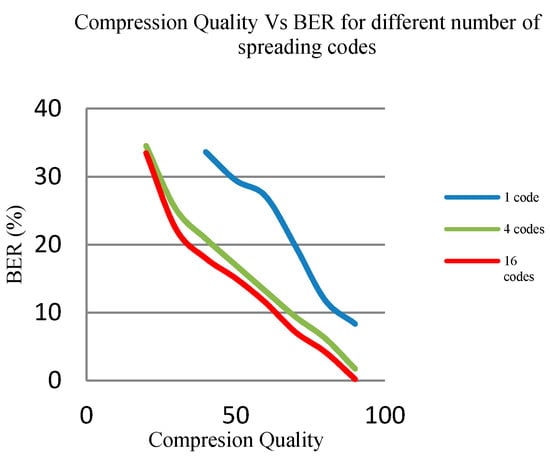
Figure 10.
Compression Quality Vs BER in the case of different number of spreading codes.
4.8. Effect of Type of Spreading Codes on Robustness
Researchers used many types of codes for spreading the watermark bits. Gold code, PN code, Hadamard codes are the commonly used spreading codes. The effect of the different types of spreading codes on the performance of the proposed FWHT based algorithm is studied in detail. We have used Gold code, Hadamard code and MATLAB generated PN codes for spreading. Figure 11 shows that Hadamard codes have better performance against compression (JPEG) and PN codes are the worst. Detailed analysis of the robustness of the algorithm against different attacks reveals that Hadamard and Gold code sequences show almost similar robustness. As shown in Figure 12, only in the case of blurring attack PN codes outperforms Hadamard sequences.
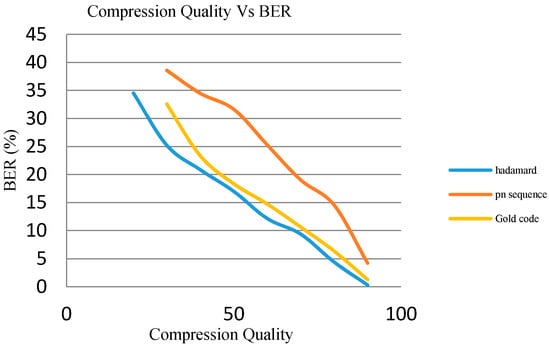
Figure 11.
Compression Quality Vs BER in the case of different types of spreading codes.
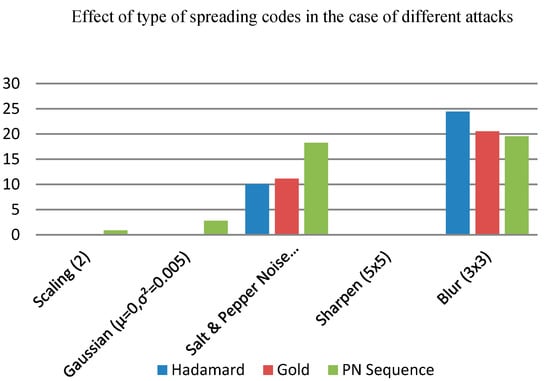
Figure 12.
BER after different attacks in the case of different types of spreading codes.
5. Conclusions
This paper did a detailed analysis of digital image watermarking, its various properties and applications. Proposed a CDMA based spread spectrum technique of watermarking using customized 8 × 8 Fast Walsh Hadamard Transform for color images and compared the performance with similar existing DCT based algorithm. Simulation results showed that the proposed algorithm exhibits better robustness against attacks at a specified gain and is highly resilient to low quality compression compared to DCT algorithm. Analyzed in detail the effect of number, length and type of spreading codes on the robustness of the algorithm. Another major advantage of the proposed technique is low computational complexity and thus the low cost. The only drawback of FWHT is its low information hiding capacity and thus the low perceptual quality. So, the proposed algorithm is a good candidate for applications that require computationally efficient, low cost and robust watermarking.
Author Contributions
Suja conceived, designed and performed the experiments; Suja and T.Naser analyzed the data. A.Afaq and Fahad involved in the discussions and analysis of the results. Suja wrote the paper and T.Naser reviewed the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Vassaux, B.; Bas, P.; Chassery, J.M. A New CDMA Technique for Digital Image Watermarking. In Proceedings of the 2001 International Conference on Image Processing, Thessaloniki, Greece, 7–10 October 2001; Volume 3, pp. 983–986. [Google Scholar]
- Al-Haj, A.M. Advanced Techniques in Multimedia Watermarking: Image, Video and Audio Applications; Information Science Reference: Hershey, PA, USA, 2010. [Google Scholar]
- Cox, J.; Kilian, J.; Leighton, F.T.; Shamoon, T. Secure Spread Spectrum Watermarking for Multimedia. IEEE Trans. Image Process. 1997, 6, 1673–1687. [Google Scholar] [CrossRef] [PubMed]
- Samee, M.K.; Gotze, J. CDMA Based Reversible and Blind Watermarking Scheme for Images. Int. J. Future Comput. Commun. 2013, 2, 138. [Google Scholar] [CrossRef]
- Shrivastava, V.; Saini, L.K. A Survey of Digital Watermarking Techniques and its Applications. Int. J. Comput. Sci. Trends Technol. IJCST 2014, 2, 303–313. [Google Scholar]
- Bamatraf, A.; Ibrahim, R.; Najib, M. A New Digital Watermarking Algorithm Using Combination of Least Significant Bit (LSB) and Inverse Bit. J. Comput. 2011, 3, 1–8. [Google Scholar]
- Masoumi, M.; Rezaei, M.; Hamza, A.B. A blind spatio-temporal data hiding for video ownership verification in frequency domain. AEU-Int. J. Electron. Commun. 2015, 69, 1868–1879. [Google Scholar] [CrossRef]
- Patil, P.; Bormane, D.S. DWT Based Invisible Watermarking Technique for Digital Images. Int. J. Eng. Adv. Technol. IJEAT 2013, 2, 603–605. [Google Scholar]
- Vishwanatham, V.M.; Reddy, G.S.; Jagadeesh, P. A Hybrid Digital Watermarking Algorithm for Colour Images Based on DWT and DCT; Annals Computer Science Series: Mirton, Romania, 2012. [Google Scholar]
- Khan, M.I.; Sarkar, M.I.H. An Efficient Image Watermarking Scheme Using BFS Technique Based on Hadamard Transform. Smart Comput. Rev. 2013, 3, 298–308. [Google Scholar]
- Lee, L.T.; Pai, Y.T. DS-CDMA based Watermarking: A low power, high security algorithm for embedded systems. Int. J. Innov. Comput. Inf. Control 2010, 7, 5893–5908. [Google Scholar]
- Anju, R. Modified Algorithm for Digital Image Watermarking Using Combined DCT and DWT. Int. J. Inf. Comput. Technol. 2013, 3, 691–700. [Google Scholar]
- Garimella, A.; Satyanarayana, M.V.V.; Murugesh, P.S.; Niranjan, U.C. ASIC for Digital Color Image Watermarking. In Proceedings of the IEEE 11th Digital Signal Processing Workshop and IEEE Signal Processing Education Workshop, Taos Ski Valley, NM, USA, 1–4 August 2004; pp. 292–296. [Google Scholar]
- Chaturvedi, N. Comparison of Digital Image watermarking Methods DWT & DWT-DCT on the Basis of PSNR. Int. J. Innov. Res. Sci. Eng. Technol. 2012, 1, 147–153. [Google Scholar]
- Franklin, R.V.; GRS, M.; Santhi, V. Entropy based Robust Watermarking Scheme using Hadamard Transformation Technique. Int. J. Comput. Appl. 2011, 12, 14–21. [Google Scholar]
- Shen, J.; Tan, S.H.; Anthony, T.S.H. A Robust Digital Image-in-Image Watermarking Algorithm Using the Fast Hadamard Transform. In Proceedings of the 2003 International Symposium on Circuits and Systems, Bangkok, Thailand, 25–28 May 2003. [Google Scholar]
- Marjuni, A.; Logeswaran, R.; Ahmad Fauzi, M. F. An image watermarking scheme based on fast Walsh Hadamard transformation and discrete Cosine transformation. In Proceedings of the International Conference on Networking and Information Technology, Manila, Philippines, 11–12 June 2010; pp. 289–293. [Google Scholar]
- Shanthakumari, R.; Parvathavarthini, S. An Adapative Watermarking Process in Hadamard Transform. Int. J. Adv. Inf. Technol. 2014, 4, 1. [Google Scholar]
- Ishikawa, Y.; Uehira, K.; Yanaka, K. Practical evaluation of illumination watermarking technique using orthogonal transforms. J. Display Technol. 2010, 6, 351–358. [Google Scholar] [CrossRef]
- Maity, S.P.; Kundu, M.K. A Blind CDMA Image Watermarking Scheme in Wavelet Domain. In Proceedings of the IEEE International Conference on Image Processing-ICIP 2004, Singapore, 24–27 October 2004; Volume 4, pp. 2633–2636. [Google Scholar]
- Wah, W.H. Image Watermarking and Data Hiding Techniques. Ph.D. Thesis, Hong Kong University of Science and Technology, Hong Kong, China, August 2003. [Google Scholar]
- Abdallah, E.E.; Hamza, A.B.; Bhattacharya, P. Robust block based image watermarking scheme using fast Hadamard transformation and single value decomposition. In Proceedings of the 18th International Conference on Pattern Recognition, Hong Kong, China, 20–24 August 2006; Volume 3, pp. 673–676. [Google Scholar]
- Mwangi, E. A wavelet based image watermarking scheme with a CDMA/Hadamard embedding technique. In Proceedings of the 9th International Symposium on Signal Processing and Its Applications, Sharjah, UAE, 12–15 February 2007; pp. 1–4. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).