Abstract
3D reconstruction and 3D printing of subject-specific anatomy is a promising technology for supporting clinicians in the visualisation of disease progression and planning for surgical intervention. In this context, the 3D model is typically obtained from segmentation of magnetic resonance imaging (MRI), computed tomography (CT) or echocardiography images. Although these modalities allow imaging of the tissues in vivo, assessment of quality of the reconstruction is limited by the lack of a reference geometry as the subject-specific anatomy is unknown prior to image acquisition. In this work, an optical method based on 3D digital image correlation (3D-DIC) techniques is used to reconstruct the shape of the surface of an ex vivo porcine heart. This technique requires two digital charge-coupled device (CCD) cameras to provide full-field shape measurements and to generate a standard tessellation language (STL) file of the sample surface. The aim of this work was to quantify the error of 3D-DIC shape measurements using the additive manufacturing process. The limitations of 3D printed object resolution, the discrepancy in reconstruction of the surface of cardiac soft tissue and a 3D printed model of the same surface were evaluated. The results obtained demonstrated the ability of the 3D-DIC technique to reconstruct localised and detailed features on the cardiac surface with sub-millimeter accuracy.
1. Introduction
Additive manufacturing (AM) of cardiovascular structures offers clinicians the opportunity to visualise and manipulate a 3D object, highlighting its morphology and physical size and supporting surgeons in the planning of complex interventions [1]. The generation of the 3D object generally consists of three phases:
- Imaging of the anatomy of interest using computed tomography (CT), magnetic resonance imaging (MRI) or ultrasound (US) imaging;
- Image post-processing to create the 3D representation of the object (e.g., segmentation) and conversion of the 3D model to a file format suitable for the AM procedure such as standard tessellation language (STL);
- The 3D printing process, which involves the editing and loading of the STL file into a slicing software environment that makes the STL file readable by the 3D printer (g-code).
An alternative approach to the above-mentioned imaging modalities for surface reconstruction is provided by stereo-optical systems (e.g., two cameras) that can reconstruct the 3D surface of an object from two different views with an accuracy comparable to the microCT (µCT) technique [2]. Stereo-optical methods are very versatile because they can be employed to image samples at different length scales. For instance, using microscopy techniques such as atomic force microscopy (AFM), scanning tunneling microscopy (STM), near field scanning optical microscopy (NFSOM) and scanning electron microscopy (SEM), 3D surface profile measurements at the microscale can be achieved. However, these techniques have some disadvantages that limit their applicability in reconstructing the surface of soft biological tissues [3].
Using two calibrated cameras, 3D reconstruction is achieved by performing triangulation of the 2D coordinates of correspondence points (pixels) identified in the two images. However, before the triangulation procedure, matching algorithms can be used to address the correspondence problem [4]. Digital image correlation (DIC), a non-contact optical method, can be used to match the same neighbourhood of pixels, called subsets, in the image pair with sub-pixel accuracy [5]. The degree of similarity between subsets is computed using a correlation criterion [6]. To successfully determine the correlation between image pairs, the sample surface must have a stochastic distribution of distinctive features (e.g., speckle pattern) that can be artificially created [7].
The combination of a stereo vision system and the DIC method, allowing so-called 3D-DIC methods, has seen widespread use in several engineering fields also including biomedical applications [8]. Being a non-contact and full-field technique, the DIC method has significant potential to characterise strain in soft tissues, providing a localised measure of strain on the tissue surface without affecting physical properties. Furthermore, recent developments of this technique have enabled extension to real-time measurements of physiological human parameters in vivo [9,10]. In addition, 3D-DIC may find an application in the cardiac strain imaging field [11], which has clinical applications in assessment of the functionality of the heart and to diagnose the progression of cardiovascular disease (CVD) [12]. Clinical imaging techniques such as Ultrasound [13], tagged Magnetic Resonance Imaging [14] and radiography [15] are typically used to track in vivo deformation of cardiac tissues. 3D-DIC provides measurements at high spatial resolution offering the potential to validate measurements obtained with these lower resolution imaging techniques.
In the 3D printing context, the output of 3D-DIC shape measurements provides appropriate data for 3D model generation. In fact, in contrast with CT, MRI and US techniques that require a post-processing phase to create the 3D model, 3D-DIC directly provides a 3D point cloud describing the object surface, suitable for straightforward conversion to STL format. In the current work, we use the 3D-DIC method to generate a 3D model of the surface of an ex vivo porcine heart.
The aim of this paper is threefold:
- (i)
- To describe the creation of the 3D model of the cardiac surface for the AM process using 3D-DIC;
- (ii)
- To evaluate the change in geometry between the reconstructed 3D shape of the cardiac surface and the reconstructed 3D shape of the 3D printed cardiac surface;
- (iii)
- To assess the accuracy of the 3D printer using µCT to compare this with results from DIC evaluation.
This approach allows evaluation of errors associated with both the DIC reconstruction technique and the 3D printing process.
2. Materials and Methods
The workflow implemented in this paper is outlined in Figure 1 and includes the following steps: (a) stereo imaging of the cardiac tissue surface and 3D shape reconstruction using the 3D-DIC method (3DsurfCTS); (b) 3D model and STL generation of the cardiac surface; (c) 3D printing of the model of the cardiac surface; (d) stereo imaging of the 3D printed cardiac surface and repeated 3D shape reconstruction using the 3D-DIC method (3Dsurf3DM); (e) evaluation of the geometric discrepancy between the two reconstructed surfaces (3DsurfCTS and 3Dsurf3DM); (f) comparison of the geometrical discrepancy with the 3D printer accuracy assessed through µCT measurements.
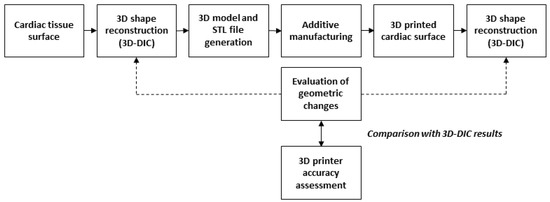
Figure 1.
Outline of the study.
2.1. Cardiac Tissue Stereo Imaging and 3D Model Generation
The surface of a porcine heart collected from a local abattoir was prepared for DIC analysis applying a speckle pattern using the approach described in a previous work [16]. Briefly, the cardiac surface was firstly coated with a blue dye (Methylene blue, Sigma-Aldrich Company Ltd, Dorset, UK) to create a dark background, then white speckles were applied with an airbrush (124 kPA working pressure, 0.3 mm nozzle diameter, approximately 15 cm spraying distance, Iwata Hi-Line HP-CH, Anest Iwata-Medea Inc., Portland, OR, USA.) using white spray paint (Com-Art, Anest Iwata-Medea Inc., Portland, OR, USA). Two different image views of the cardiac tissue surface were captured using two 8-bit CCD digital cameras (Flea2-13S2, Point Grey Research Inc., Vancouver, BC, Canada) with 1024 × 768 pixel resolution (Figure 2A) and 25 mm focal length lenses. The cameras were placed at a distance from the cardiac tissue of approximately 45 mm ensuring the entire sample surface (52 mm × 40 mm) was within the camera field of view (FOV). Under these conditions, image magnification and image resolution were 0.07 and 50 μm/pixel, respectively. The internal (focal length, principal points and lens distortion coefficients) and external (orientation and position of one camera with respect to the other) camera parameters were computed with the Matlab stereo calibration application (Matlab R2015b, Mathworks, Natick, MA, USA) using twenty images pairs of a 9 × 7 square chequerboard (4 mm internal square size) captured at different positions and orientation.
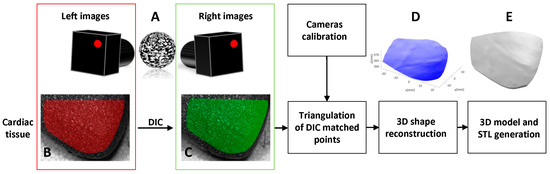
Figure 2.
Schematic representation describing the process implemented to reconstruct and generate the 3D model of the cardiac surface using the 3D-DIC technique. (A) Stereo-imaging of the cardiac tissue surface (for the sake of clarity, the cardiac sample has been rendered as a sphere); (B) Polygonal region of interest (ROI) identified on the image of the cardiac tissue surface (red dots) captured by the left camera; (C) The corresponding points (green dots) on the image of the cardiac tissue surface as if it were seen by the right camera computed by the DIC analysis; (D) 3D shape reconstruction of the cardiac tissue surface using the cameras calibration data and the triangulation of the corresponding 2D coordinates; (E) 3D model and STL generation of the reconstructed cardiac tissue surface.
A polygonal-shaped region of interest (ROI) was identified on the cardiac tissue surface of the left image containing 449,095 pixels (Figure 2B). To provide a dense mapping of the correspondence points between the left and right image (Figure 2C), DIC analysis was performed on the ROI using a subset size of 21 × 21 pixels and a step size (distance between subsets) of 3 pixels. DIC processing was carried out with Ncorr [17], an open source Matlab program. Using the camera calibration data, triangulation of the correspondence points enabled 3D shape reconstruction of the cardiac tissue surface (Figure 2D). This reconstructed surface is referred to as 3DsurfCTS. Subsequently, a 3D model and STL file of the reconstructed surface were produced using the Matlab surf2solid.m and stlwrite.m functions, respectively [18,19], as shown in Figure 2E. These functions generate a surface from X, Y and Z point data using Delaunay triangulation and then create a solid volume by extending the surface to specified boundaries which is then written to an STL file.
2.2. Additive Manufacturing and Stereo Imaging of the 3D Printed Object
A 3D printed model of the cardiac tissue surface was created with an X400 PRO V3 (German RepRap, GmbH, Feldkirchen, Germany) fused deposition modeling 3D printer using polylactic acid (PLA) filament (1.75 mm diameter). The STL file was loaded into 3D printer slicing software (Simplify3D). The 3D model was oriented orthogonally to the printer bed. The printer settings used were: printing speed 900 mm/s, infill percentage 20%, layer height 0.1 mm. In accordance with the ‘white on black’ approach used to mark the soft tissue during the speckle pattern application, the 3D printed object was coated firstly with black spray paint (Fast dry enamel, PlasticKote, Wolvega, The Netherlands) and then speckles were applied as before using the airbrush.
The 3D printed model, shown in Figure 3A, was imaged using the same stereo-optical setup and DIC parameters as before and a polygonal-shaped region of interest (ROI) was identified on the left image containing 447,613 pixels. The same procedure was used as before to obtain a 3D reconstruction of the surface of the 3D printed model. This reconstructed surface is referred to as 3Dsurf3DM.

Figure 3.
(A) 3D printed object with the applied speckle pattern and the ROI (green) used to reconstruct 3Dsurf3DM; (B) Sub-region on the 3D printed model used to assess the accuracy of the rigid registration process.
To study variation in quality between the two applied speckle patterns, a morphological analysis [20] of the speckle pattern on the cardiac tissue surface and the 3D printed model surface was performed.
2.3. Comparison of Reconstructed Tissue Surface with Reconstructed 3D Model Surface
The 3D point cloud of the reconstructed cardiac tissue surface (3DsurfCTS) and the 3D point cloud of the reconstructed 3D printed model surface (3Dsurf3DM) were aligned using a rigid registration process based on the iterative closest point (ICP) algorithm, which computed the rotation matrix and translation vector to transform 3Dsurf3DM to the same coordinate system as 3DsurfCTS. Afterwards, a triangular mesh was created over each surface and linear interpolation was used to obtain the Z coordinates of each surface over an identical grid of points in X and Y coordinates. The discrepancy in the Z coordinate between 3DsurfCTS and 3Dsurf3DM was computed along with the maximum absolute discrepancy and the 95th percentile of the measured deviations [21]. Furthermore, to verify the accuracy and robustness of the rigid registration process, the changes in geometry between 3DsurfCTS and 3Dsurf3DM were also assessed using a sub-region of the 3D printed cardiac surface, depicted in Figure 3B.
2.4. Measurement of 3D Printer Geometric Accuracy with µCT
An estimate of the spatial errors inherent in the 3D printing process was also obtained by printing small, simple shapes which were then imaged in a µCT scanner. Due to the acquisition volume constraints of the µCT machine, the full printed cardiac surface could not be used. Four test objects containing different sized slits, lines, holes and hemispheres were designed in tinkerCAD software [22]. Slit width ranged from 0.2 mm to 4 mm, the hole and hemisphere radii ranged from 0.5 mm to 4 mm and the lines were printed with thickness 1 to 4 mm (see Figure 4). The test objects were exported from tinkerCAD as STL files and then imported into simplify3D software for slicing. Print settings were similar to those used for the cardiac surface, although printing speed was increased by approximately 50% (1400 mm/s).

Figure 4.
Photographs of the four printed test objects, with variable hole sizes (top left); variable hemispheres (top right); lines (bottom left) and slits (bottom right).
Once printed, each test object was placed within a Skyscan 1172 µCT scanner (Bruker, Kontich, Belgium). Scanner settings were adjusted such that the reconstructed voxel size (filtered back projection) was 12 µm. Following image acquisition and reconstruction, the linear dimensions of each feature in each object were measured manually in three places using DataViewer software (SkyScan, Version 1.4.4, Kontich, Belgium). Measured dimensions were compared with the original dimensions of the geometry design.
3. Results
3.1. 3D Shape Reconstruction and Speckle Pattern Quality
The focal lengths of the cameras obtained from camera calibration differed by approximately 1 mm from the physical size stated by the manufacturer, while the principal points in pixel unit (cx and cy) and distortion coefficients (k1, k2) for the left and right camera were: (520, 398), (495, 421) and (−0.6777, 114.3260), (−0.6549, 103.7227), respectively. Overall, the intrinsic and extrinsic camera parameters obtained were in good agreement with the physical set-up of the stereo system. The 3D reconstruction assessed using a control object with known geometry suggested measurement accuracy of the order of 15 µm.
The assessment of the quality of the two speckle patterns is reported in Figure 5, which describes the cumulative percentage of speckles with a radius belonging to a specific interval.
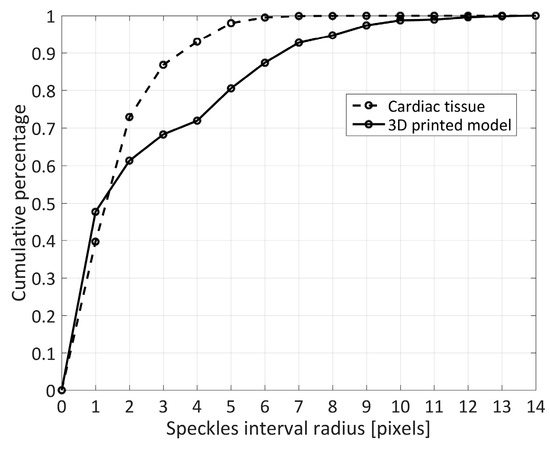
Figure 5.
Cumulative percentage of speckles radius.
The 3D shape reconstruction of the cardiac tissue surface (3DsurfCTS) and the 3D printed model surface (3Dsurf3DM) are shown in Figure 6A,B, respectively. The dataset of the reconstructed surfaces is available as Supplementary Materials.
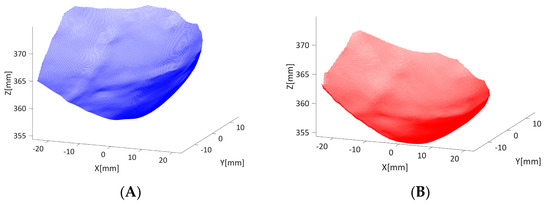
Figure 6.
(A) 3D reconstruction of the cardiac tissue surface (3DsurfCTS); (B) 3D reconstruction of the 3D printed model surface (3Dsurf3DM).
3.2. Geometric Deviations between 3DsurfCTS and 3Dsurf3DM
The geometric deviations between 3DsurfCTS and 3Dsurf3DM in the Z direction are described in the following section for both the whole surface (WS) and sub-region (SR) reconstructions. The largest absolute difference between 3DsurfCTS-WS and 3Dsurf3DM-WS was 1.06 mm with 95% of the values less than 0.41 mm. The largest absolute difference between 3DsurfCTS-WS and 3Dsurf3DM-SR was 1.15 mm with 95% of the values less than 0.42 mm. Figure 7 shows contour plots of the difference in Z coordinate between 3DsurfCTS-WS and 3Dsurf3DM-WS (Figure 7A) and between 3DsurfCTS-WS and 3Dsurf3DM-SR (Figure 7B). The probability distribution of obtaining a given deviation between the two surfaces at any point is reported in Figure 7C.
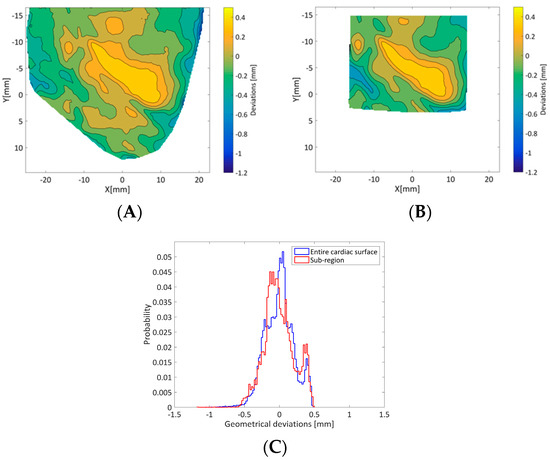
Figure 7.
Contour plot of the geometric deviations in the Z direction: (A) between 3DsurfCTS-WS and 3Dsurf3DM-WS and (B) between 3DsurfCTS-WS and 3Dsurf3DM-SR. (C) Histogram indicating the probability distribution of the geometrical deviations between the two surfaces.
3.3. µCT Measurements of 3D Printer Geometric Accuracy
The mean absolute difference over the three measurements between µCT dimensions and those of the original design for the four test objects (see Figure 4) is summarized in Figure 8. This illustrates the presence of errors at ~0.1 mm although with some features this can rise to be as large as 0.35 mm.
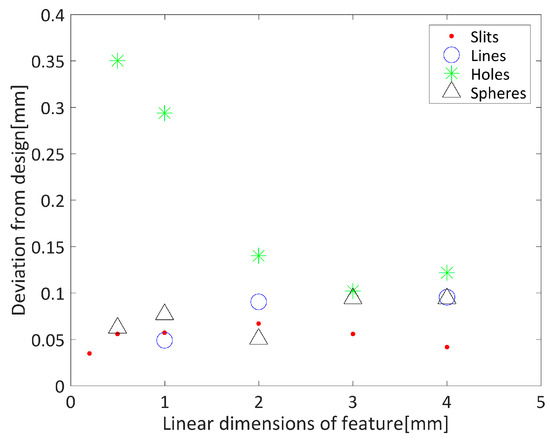
Figure 8.
Summary of linear dimension measurements as compared to the computer-aided design (CAD) for the four test objects.
4. Discussion
In this paper, we have reported the use of an optical technique based on digital image correlation (DIC) to reconstruct the cardiac surface of an ex vivo porcine heart including localised features (coronary artery branches). To the best of our knowledge, this is the first effort to quantify the error of 3D-DIC shape measurements on the cardiac tissue surface with local geometrical variations using an additive manufacturing process. The use of a 3D printed model to present a controlled surface geometry to the 3D-DIC technique removes the uncertainty associated with the form of the initial soft tissue geometry. The comparison between the reconstructed 3D surface of the cardiac tissue (3DsurfCTS) and that of the 3D printed model (3Dsurf3DM) consisted of two steps: (1) a rigid transformation that computed the rotation and translation matrix to align the two surfaces; (2) calculation of the discrepancy between Z coordinates after linear interpolation to common X and Y locations.
The 3D-DIC shape measurements were achieved using two different speckle patterns generated on two different materials (soft tissue and PLA), therefore, since the outcome of DIC measurements strongly depends on the quality of the speckle pattern, the evaluation of the speckle morphology in the two patterns provided information about the quality and similarity of these two patterns. In particular, the two distributions of the cumulative percentage of speckle sizes (Figure 5) demonstrated most speckles (~70%) had a radius included in the range of 2–3 pixels, which are the recommended values for speckle sizes in DIC analysis [5].
The rigid transformation process did not have a significant impact on the result of the geometrical comparisons as the 95th percentile of the results shown in Figure 7A,B differed by only 10 µm.
Overall, 95% of the geometrical discrepancy between 3DsurfCTS and 3Dsurf3DM was lower than 0.42 mm, with larger deviation close to the edge of the ROI. Such behaviour can be explained both by poorer performance of DIC near the edges of the ROI, resulting in reduced accuracy in the 3D reconstruction, and by differences in the size of the object in the field of view in each case that forced different ROIs to be used for each reconstruction. However, considering the uncertainty introduced by the 3D printer, assessed through gold standard µCT measurements, the final error achieved by the 3D-DIC method in shape reconstruction is expected to be less than 0.3 mm. Therefore, the geometrical discrepancies reported in this study support sub-millimeter accuracy of 3D-DIC shape measurements. This represents a spatial resolution that is less than 1% of the field of view of the stereo images used for the reconstruction. Reconstruction of the geometry used in this study is arguably more challenging than studies in the literature which report surface reconstruction of either objects that do not have local geometrical variations (e.g., flat plates [23]) or that can be fitted to a simpler geometry (e.g., cylinder [23]), allowing straightforward error computation relative to the ground truth geometry.
Although the influence of the DIC parameters on the accuracy of the surface reconstruction is not the main focus of this work, the subset size may strongly affect the 3D reconstruction process and, hence, the resulting 3D printed model and discrepancy between 3DsurfCTS and 3Dsurf3DM. It is well known that whilst larger subset sizes increase the accuracy of the correlation and the precision in displacement measurements, detailed features of the object surface are not preserved [24]. Therefore, in the current study best practice was followed to obtain at least three speckles within each subset [5], resulting in a subset size of 21 pixels. This is reasonably small relative to the ROI in order to minimize smoothing of object surface features.
The results presented in Figure 8 suggest that holes are the most difficult feature to print at small sizes, but that typical errors are of the order of 0.1 mm. The maximum error obtained is of the same order as the 95% interval of the discrepancy between the two reconstructed surfaces. These results are consistent with the manufacturer’s quoted position accuracy in the XY plane of ± 0.1 mm. However, direct interpretation of these results in the context of the 3D printed cardiac surface is complicated by the PLA layering process. It has been shown, for example, that the geometric error in fused deposition modelling is strongly related to a number of parameters including the deposition angle [25]. Errors of up to approximately 0.8 mm have been previously reported when considering a number of different print designs, with a range of machine settings [25]. This suggests that 3D print accuracy measured in this study is towards the higher end of what might be expected.
Whilst these results suggest that the dominant source of error between the two reconstructions arises from the 3D-DIC process, further reduction in reconstruction error may be possible through further optimisation of stereo camera hardware and DIC parameter variation.
Finally, results obtained in this work will support the development of future work that will focus on the use of the 3D-DIC technique to characterise epicardial deformations in isolated beating hearts to provide a detailed validation of strain measurements obtained using clinical imaging modalities (e.g., ultrasound), as already discussed in the introduction.
Limitations
Limitations that may contribute to discrepancy between the reconstructed 3D surfaces originate from the 3D-DIC workflow including speckle pattern quality [20], stereo camera calibration [26], choice of the shape function, interpolation scheme and correlation criterion used in the DIC analysis [27], and selection of the subset and step size [28]. Variation in the accuracy of the additive manufacturing process may be expected using different 3D printing methods (e.g., stereolithography), however, a comparison between techniques was not performed in this study.
This study reports an evaluation of geometry under static conditions, in order to make a direct comparison between the geometry reconstructed from images of cardiac tissue and the 3D printed model. As a result, this does not assess the challenges associated with dynamic deformation of the cardiac surface which will be encountered if the 3D-DIC technique is extended to measure the beating heart.
5. Conclusions
In conclusion, in this paper, we have described the use of the additive manufacturing process to validate shape reconstruction measurements performed with the 3D-DIC method. The accuracy of the 3D printer and discrepancy between 3D surfaces reconstructed from cardiac tissue and a 3D print of the same geometry were evaluated. In particular, considering the resolution of the 3D printer, the error associated with the 3D-DIC measurement supports the use of this technique to accurately reconstruct localised features of complex surfaces with errors less than 1% of the field of view.
Supplementary Materials
The figures and dataset of the reconstructed surfaces are available online at https://doi.org/10.15131/shef.data.5426683.
Acknowledgments
This work is funded by the European Commission through the H2020 Marie Skłodowska-Curie European VPH-CaSE Training Network (www.vph-case.eu), GA No. 642612.
Author Contributions
Paolo Ferraiuoli, John W. Fenner and Andrew J. Narracott conceived and designed the experiments; Paolo Ferraiuoli performed the experiments; Paolo Ferraiuoli and Jonathan C. Taylor analyzed the data; Emily Martin and Jonathan C. Taylor contributed to the measurement of 3D printer accuracy with µCT; Paolo Ferraiuoli wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Giannopoulos, A.A.; Mitsouras, D.; Yoo, S.-J.; Liu, P.P.; Chatzizisis, Y.S.; Rybicki, F.J. Applications of 3D printing in cardiovascular diseases. Nat. Rev. Cardiol. 2016, 13, 701–718. [Google Scholar] [CrossRef] [PubMed]
- Cosentino, D.; Zwierzak, I.; Schievano, S.; Díaz-zuccarini, V.; Fenner, J.W.; Narracott, A.J. Uncertainty assessment of imaging techniques for the 3D reconstruction of stent geometry. Med. Eng. Phys. 2014, 36, 1062–1068. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Luo, H.; Du, Y.; Lu, H. Fluorescent stereo microscopy for 3D surface profilometry and deformation mapping. Opt. Express 2013, 21, 11808–11818. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Kieu, H.; Nguyen, H.; Le, M. Digital image correlation in experimental mechanics and image registration in computer vision: Similarities, differences and complements. Opt. Lasers Eng. 2015, 65, 18–27. [Google Scholar] [CrossRef]
- Schreier, H.; Orteu, J.-J.; Sutton, M.A. Image Correlation for Shape, Motion and Deformation Measurements; Springer: Boston, MA, USA, 2009. [Google Scholar]
- Pan, B.; Qian, K.; Xie, H.; Asundi, A. Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review. Meas. Sci. Technol. 2009, 20, 62001. [Google Scholar] [CrossRef]
- Dong, Y.L.; Pan, B. A Review of Speckle Pattern Fabrication and Assessment for Digital Image Correlation. Exp. Mech. 2017, 57, 1161–1181. [Google Scholar] [CrossRef]
- Palanca, M.; Tozzi, G.; Cristofolini, L. The use of digital image correlation in the biomechanical area: A review. Int. Biomech. 2016, 3, 1–21. [Google Scholar] [CrossRef]
- Shao, X.; Dai, X.; Chen, Z.; He, X. Real-time 3D digital image correlation method and its application in human pulse monitoring. Appl. Opt. 2016, 55, 696–704. [Google Scholar] [CrossRef] [PubMed]
- Xue, Y.; Su, Y.; Zhang, C.; Xu, X.; Gao, Z.; Wu, S.; Zhang, Q.; Wu, X. Full-field wrist pulse signal acquisition and analysis by 3D Digital Image Correlation. Opt. Lasers Eng. 2017, 98, 76–82. [Google Scholar] [CrossRef]
- Hokka, M.; Mirow, N.; Nagel, H.; Irqsusi, M.; Vogt, S.; Kuokkala, V. In-vivo deformation measurements of the human heart by 3D Digital Image Correlation. J. Biomech. 2015, 48, 2217–2220. [Google Scholar] [CrossRef] [PubMed]
- Dandel, M.; Lehmkuhl, H.; Knosalla, C.; Suramelashvili, N.; Hetzer, R. Strain and strain rate imaging by echocardiography—Basic concepts and clinical applicability. Curr. Cardiol. Rev. 2009, 5, 133–148. [Google Scholar] [CrossRef] [PubMed]
- RLopata, G.P.; Nillesen, M.M.; Thijssen, J.M.; Kapusta, L.; de Korte, C.L. Three-dimensional cardiac strain imaging in healthy children using RF-data. Ultrasound Med. Biol. 2011, 37, 1399–1408. [Google Scholar] [CrossRef] [PubMed]
- Azhari, H.; Weiss, J.L.; Rogers, W.J.; Siu, C.; Zerhouni, A.; Shapiro, E.P. Noninvasive quantification of principal strains in normal canine hearts using tagged MRI images in 3-D. Am. J. Physiol. Heart Circ. Physiol. 1993, 264, 205–216. [Google Scholar]
- Hashima, A.R.; Young, A.A.; McCulloch, A.D.; Waldman, L.K. Nonhomogeneous analysis of epicardial strain distributions during acute myocardial ischemia in the dog. J. Biomech. 1993, 26, 19–35. [Google Scholar] [CrossRef]
- Ferraiuoli, P.; Fenner, J.W.; Narracott, A.J. Analysis of Speckle Pattern Quality and Uncertainty for Cardiac Strain Measurements Using 3D Digital Image Correlation. In VipIMAGE 2017, 1st ed.; Tavares, J.M.R.S., Jorge, R.M.N., Eds.; Springer International Publishing: Basel, Switzerland, 2018; Volume 27. [Google Scholar]
- Blaber, J.; Adair, B.; Antoniou, A. Ncorr: Open-Source 2D Digital Image Correlation Matlab Software. Exp. Mech. 2015, 55, 1105–1122. [Google Scholar] [CrossRef]
- Sven Holcombe. Surf2solid—Make a Solid Volume from a Surface for 3D Printing. Available online: https:www.mathworks.com/matlabcentral/fileexchange/42876-surf2solid-make-a-solid-volume-from-a-surface-for-3d-printing (accessed on 13 July 2017).
- Sven Holcombe. Stlwrite (Filename, Varargin). Available online: www.mathworks.com/matlabcentral/fileexchange/20922-stlwrite-filename--varargin- (accessed on 13 July 2017).
- Lecompte, D.; Smits, A.; Bossuyt, S.; Sol, H.; Vantomme, J.; Van Hemelrijck, D.; Habraken, A.M. Quality assessment of speckle patterns for digital image correlation. Opt. Lasers Eng. 2006, 44, 1132–1145. [Google Scholar] [CrossRef]
- Van Eijnatten, M.; Rijkhorst, E.J.; Hofman, M.; Forouzanfar, T.; Wolff, J. The accuracy of ultrashort echo time MRI sequences for medical additive manufacturing. Dentomaxillofac. Radiol. 2016, 45, 20150424. [Google Scholar] [CrossRef] [PubMed]
- Autodesk, “TinkerCAD”. Available online: https://www.tinkercad.com (accessed on 12 October 2017).
- Yu, L.; Pan, B. Color Stereo-Digital Image Correlation Method Using a Single 3CCD Color Camera. Exp. Mech. 2017, 57, 649–657. [Google Scholar] [CrossRef]
- Harvent, J.; Coudrin, B.; Brèthes, J.-J.; Orteu, L.; Devy, M. Shape Measurement Using a New Multi-step Stereo-DIC Algorithm That Preserves Sharp Edges. Exp. Mech. 2015, 55, 167–176. [Google Scholar] [CrossRef]
- Boschetto, A.; Bottini, L. Accuracy prediction in fused deposition modeling. Int. J. Adv. Manuf. Technol. 2014, 73, 913–928. [Google Scholar] [CrossRef]
- Balcaen, R.; Wittevrongel, L.; Reu, P.L.; Lava, P.; Debruyne, D. Stereo-DIC Calibration and Speckle Image Generator Based on FE Formulations. Exp. Mech. 2017, 57, 703–718. [Google Scholar] [CrossRef]
- Lava, P.; Cooreman, S.; Coppieters, S.; De Strycker, M.; Debruyne, D. Assessment of measuring errors in DIC using deformation fields generated by plastic FEA. Opt. Lasers Eng. 2009, 47, 747–753. [Google Scholar] [CrossRef]
- Sun, Y.; Pang, J.H.L. Study of optimal subset size in digital image correlation of speckle pattern images. Opt. Lasers Eng. 2007, 45, 967–974. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).