Radial Distortion from Epipolar Constraint for Rectilinear Cameras
Abstract
:1. Introduction
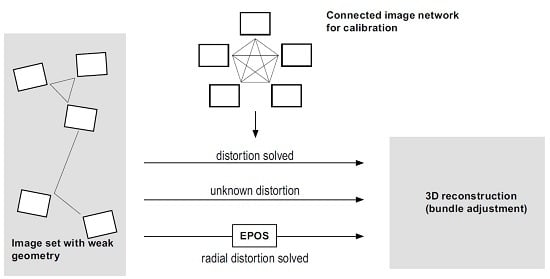
2. Related Work
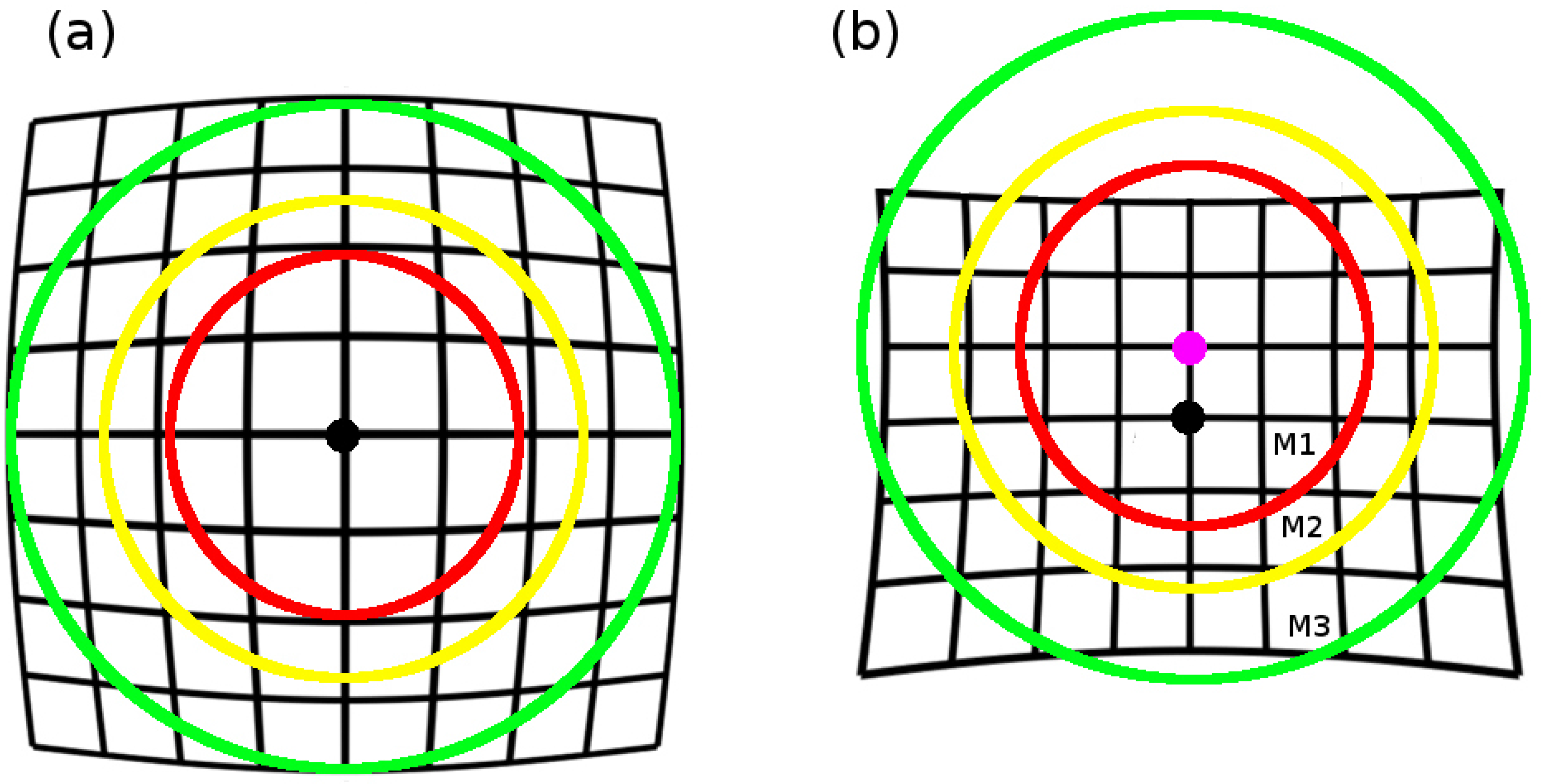
3. Iterative Solution for Radial Distortion
| Algorithm 1 EPOS algorithm. |
|
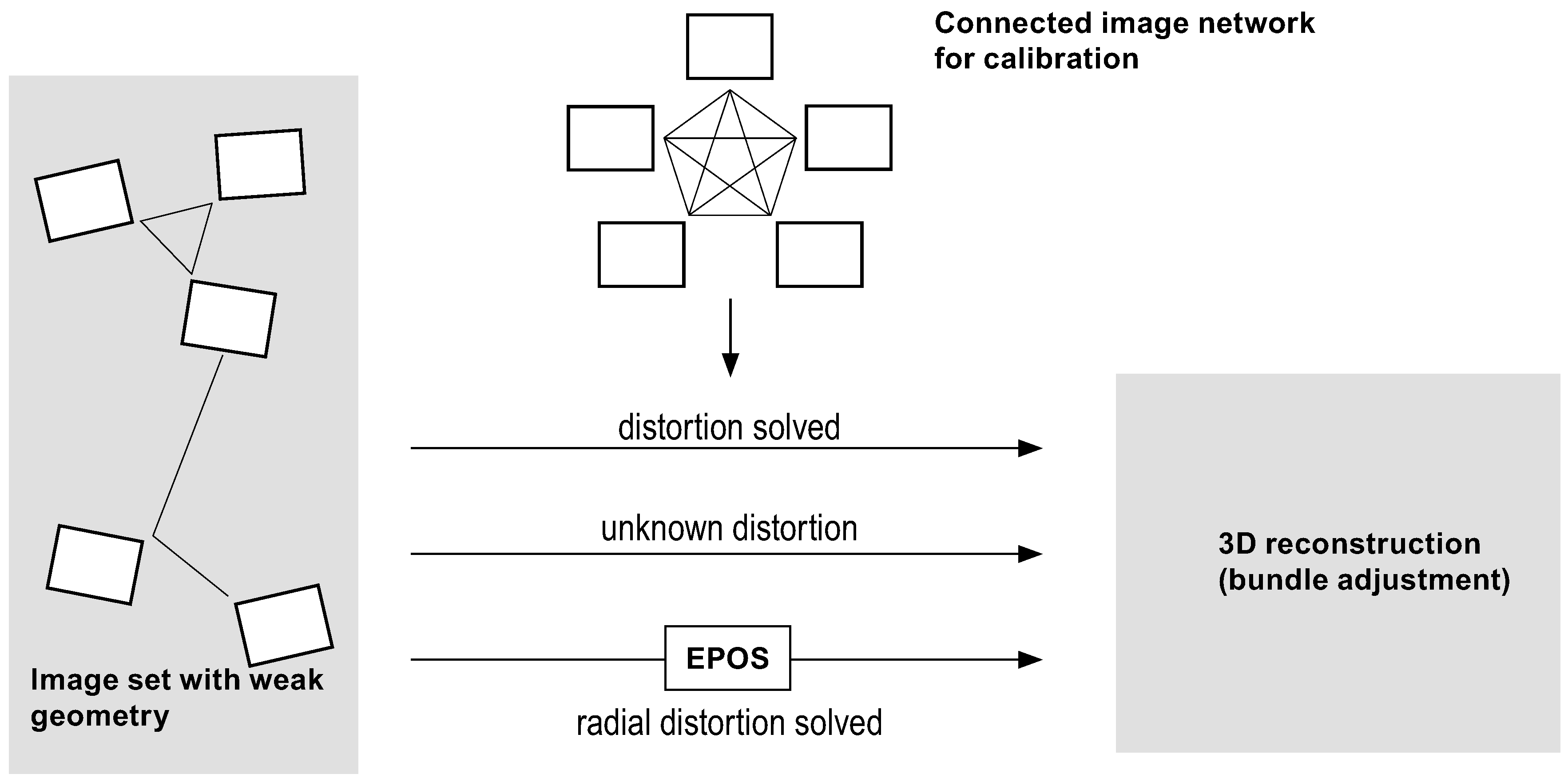
4. Finding the Center of Distortion
4.1. Symmetry Ratio Measure
4.2. Symmetry Landscape
4.3. Local Search
4.4. Implementation of the Proposed Method: EPOS
4.5. Extension to Non-Rectilinear Lenses
5. Results and Discussion
5.1. Simulated Data
5.2. Real Data from In Situ Images
5.3. Computational Efficiency
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nicolae, C.; Nocerino, E.; Menna, F.; Remondino, F. Photogrammetry applied to Problematic artefacts. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40, 451–456. [Google Scholar] [CrossRef]
- Lehtola, V.V.; Kurkela, M.; Hyyppä, H. Automated image-based reconstruction of building interiors—A case study. Photogramm. J. Finl. 2014, 1, 1–13. [Google Scholar] [CrossRef]
- Brown, D.C. Close-range camera calibration. Photogramm. Eng. 1971, 37, 855–866. [Google Scholar]
- Fryer, J.G.; Brown, D.C. Lens distortion for close-range photogrammetry. Photogramm. Eng. Remote Sens. 1986, 52, 51–58. [Google Scholar]
- Fraser, C.; Shortis, M. Variation of distortion within the photographic field. Photogramm. Eng. Remote Sens. 1992, 58, 851–855. [Google Scholar]
- Kim, D.; Shin, H.; Oh, J.; Sohn, K. Automatic radial distortion correction in zoom lens video camera. J. Electron. Imaging 2010, 19, 043010. [Google Scholar] [CrossRef]
- Fraser, C.; Al-Ajlouni, S. Zoom-dependent camera calibration in digital close-range photogrammetry. Photogramm. Eng. Remote Sens. 2006, 72, 1017–1026. [Google Scholar] [CrossRef]
- Remondino, F.; Fraser, C. Digital camera calibration methods: considerations and comparisons. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2006, 36, 266–272. [Google Scholar]
- Strecha, C.; Hansen, W.V.; Gool, L.V.; Fua, P.; Thoennessen, U. On Benchmarking Camera Calibration and Multi-View Stereo for High Resolution Imagery. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2008, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8.
- Bouguet, J.Y. Camera Calibration Toolbox for Matlab. Available online: http://www.vision.caltech.edu/bouguetj/calib_doc/ (accessed on 1 July 2016).
- Photometrix. Australis—Camera Calibration Software. Available online: http://www.photometrix.com.au/australis/ (accessed on 1 July 2016).
- Jeong, Y.; Nister, D.; Steedly, D.; Szeliski, R.; Kweon, I. Pushing the Envelope of Modern Methods for Bundle Adjustment. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1605–1617. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Agarwal, S.; Curless, B.; Seitz, S.M. Multicore Bundle Adjustment. In Proceedings of the 2011 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011; pp. 3057–3064.
- Lourakis, M.I.A.; Argyros, A.A. SBA: A software package for generic sparse bundle adjustment. ACM Trans. Math. Softw. 2009, 36, 1–30. [Google Scholar] [CrossRef]
- Furukawa, Y.; Ponce, J. Accurate Camera Calibration from Multi-View Stereo and Bundle Adjustment. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2008, Anchorage, AK, USA, 23–28 June 2008; pp. 1–8.
- Snavely, N.; Seitz, S.; Szeliski, R. Photo Tourism: Exploring Photo Collections in 3D. ACM Trans. Graph. (TOG) 2006, 25, 835–846. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Wu, C. Critical Configurations for Radial Distortion Self-Calibration. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014.
- Fraser, C.S. Automatic camera calibration in close range photogrammetry. Photogramm. Eng. Remote Sens. 2013, 79, 381–388. [Google Scholar] [CrossRef]
- Farid, H.; Popescu, A.C. Blind removal of lens distortion. J. Opt. Soc. Am. A 2001, 18, 2072–2078. [Google Scholar] [CrossRef]
- Zhang, Z. On the Epipolar Geometry between Two Images with Lens Distortion. In Proceedings of the 13th International Conference on Pattern Recognition, Vienna, Austria, 25–29 August 1996; Volume 1, pp. 407–411.
- Fitzgibbon, A.W. Simultaneous Linear Estimation of Multiple View Geometry and Lens Distortion. In Proceedings of the 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR 2001, Kauai, HI, USA, 8–14 December 2001; Volume 1, pp. 125–132.
- Kukelova, Z.; Pajdla, T. A Minimal Solution to Radial Distortion Autocalibration. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 2410–2422. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Fang, S. Correcting large lens radial distortion using epipolar constraint. Appl. Opt. 2014, 53, 7355–7361. [Google Scholar] [CrossRef] [PubMed]
- Brito, J.H.; Angst, R.; Koser, K.; Pollefeys, M. Radial Distortion Self-Calibration. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Portland, OR, USA, 23–28 June 2013; pp. 1368–1375.
- Willson, R.G.; Shafer, S.A. What is the center of the image? J. Opt. Soc. Am. A 1994, 11, 2946–2955. [Google Scholar] [CrossRef]
- Hartley, R.; Kang, S.B. Parameter-free radial distortion correction with center of distortion estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 1309–1321. [Google Scholar] [CrossRef] [PubMed]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Lowe, D. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Snavely, N. Bundler: Structure from Motion (SFM) for Unordered Image Collections. Available online: http://www.cs.cornell.edu/ snavely/bundler/ (accessed on 11 October 2014).
- Olsson, C.; Enqvist, O. Stable Structure from Motion for Unordered Image Collections; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6688, pp. 524–535. [Google Scholar]
- McGlone, C.; Mikhail, E.; Bethel, J. Manual of Photogrammetry, 5th ed.; American Society of Photogrammetry: Bethesda, MD, USA, 2005. [Google Scholar]
- Wu, C. VisualSFM: A Visual Structure from Motion System. Available online: http://ccwu.me/vsfm/doc.html (accessed 1 July 2016).

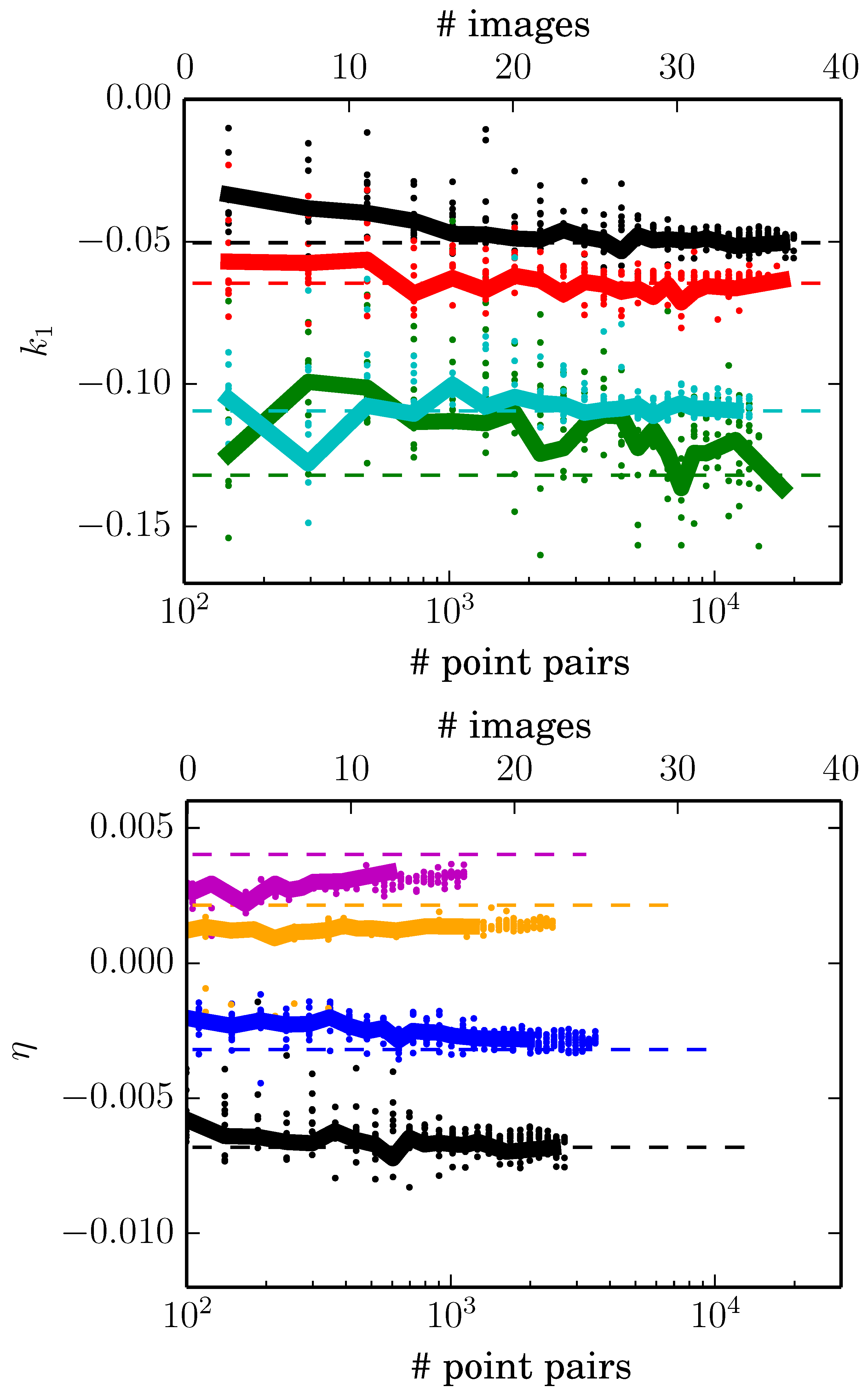


| Data Set Figure 5a | Std dev (EPOS) | Reference | |
|---|---|---|---|
| Nikon D700 24 mm | −0.04868 | 0.00273 | −0.05038 |
| Olympus 14 mm | −0.06319 | 0.00271 | −0.06460 |
| Nikon D7100 18 mm | −0.10748 | 0.00257 | −0.10949 |
| Panasonic DMC 6 mm | −0.12107 | 0.01227 | −0.13201 |
| Dataset Figure 5b | Std dev (EPOS) | Reference η | |
| 24 mm | −0.00659 | 0.00037 | −0.00681 |
| 28 mm | −0.00282 | 0.00025 | −0.00319 |
| 35 mm | 0.00139 | 0.00015 | 0.00213 |
| 50 mm | 0.00308 | 0.00022 | 0.00402 |
| Data Set | # Images | VSFM # | VSFM f | Reference f | Ref. η | EPOS η | VSFM η |
|---|---|---|---|---|---|---|---|
| Dipoli | 10 | 10 | 372.2 | 361.5 | |||
| Sofa | 9 | 2 | 354.6 | 361.5 | N/A | ||
| Combined | 3 | 602.0 | 361.5 | N/A | |||
| Bookshelf | 5 | 5 | 803.6 | 821.7 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lehtola, V.V.; Kurkela, M.; Rönnholm, P. Radial Distortion from Epipolar Constraint for Rectilinear Cameras. J. Imaging 2017, 3, 8. https://doi.org/10.3390/jimaging3010008
Lehtola VV, Kurkela M, Rönnholm P. Radial Distortion from Epipolar Constraint for Rectilinear Cameras. Journal of Imaging. 2017; 3(1):8. https://doi.org/10.3390/jimaging3010008
Chicago/Turabian StyleLehtola, Ville V., Matti Kurkela, and Petri Rönnholm. 2017. "Radial Distortion from Epipolar Constraint for Rectilinear Cameras" Journal of Imaging 3, no. 1: 8. https://doi.org/10.3390/jimaging3010008
APA StyleLehtola, V. V., Kurkela, M., & Rönnholm, P. (2017). Radial Distortion from Epipolar Constraint for Rectilinear Cameras. Journal of Imaging, 3(1), 8. https://doi.org/10.3390/jimaging3010008