ODDM: Integration of SMOTE Tomek with Deep Learning on Imbalanced Color Fundus Images for Classification of Several Ocular Diseases
Abstract
1. Introduction
- Seven different types of ODs, including NOR, AMD, DR, MAC, PDR, NPDR, and GLU, are classified using the proposed ODDM. The proposed ODDM has the ability to extract the dominant features from CFIs that can be helpful in the accurate classification of ODs. Furthermore, this study also simplifies the proposed ODDM by reducing the number of trainable parameters to obtain a significant classifier.
- SM-TOM is used to handle the imbalance class issue of the OD dataset, and the Grad-CAM heatmap technique is employed to highlight the infected region that occurred in the eye due to ODs.
- Ablation experiments are performed to evaluate the effectiveness of the proposed ODDM, and the ANOVA and Tukey HSD (Honestly Significant Difference) post hoc tests are used to show the statistical significance of the proposed ODDM. Also, the proposed ODDM obtained 97.19% accuracy, which is superior to that of modern state-of-the-art (SOTA) approaches.
2. Literature Review
| Ref | Year | Method | Dataset Name | No of Diseases | Outcomes |
|---|---|---|---|---|---|
| Lenka et al. [62] | 2025 | GCN | DRISTHI-GS | 02 | Accuracy = 97.43% |
| Hu et al. [63] | 2025 | FundusNet | UKBB and EyePACS | 02 | AUC = 77.00% |
| Kansal et al. [64] | 2025 | TL + LDA + BiLSTM | ODIR | 08 | Accuracy 98.04% |
| Butt et al. [65] | 2025 | CNN | DDR | 05 | Accuracy = 95.92% |
| Nguyen et al. [66] | 2024 | ResNet-152 | Eye diseases using UFI | 02 | Accuracy = 96.47% |
| Li et al. [67] | 2024 | CNN | TRIPOD | 02 | Accuracy = 92.04% |
| Al-Fahdawi et al. [68] | 2024 | HRNet | OIA-ODIR | 08 | Accuracy = 88.56% |
| Hussain et al. [69] | 2024 | CNN | OHD | 02 | Accuracy = 96.15% |
| Hemelings et al. [70] | 2023 | CNN | AIROGS | 02 | Accuracy = 85.84% |
| Sengar et al. [71] | 2023 | CNN | RFMiD | 02 | Accuracy = 90.02% |
| Thanki [72] | 2023 | DCNN | DRISTHI-GS | 02 | Accuracy = 75.30% |
| Nazir et al. [73] | 2021 | CNN | EYEPACS datasets | 02 | Accuracy = 97.13% |
| Bodapati et al [74] | 2021 | DCNN | APTOS 2019 | 01 | Accuracy = 84.31% |
| Khan et al. [75] | 2021 | VGG-19 | APTOS 2019 | 04 | Accuracy = 97.47% |
| Sarki et al. [76] | 2021 | CNN | Messidor-2 | 01 | Accuracy = 81.33% |
| Pahuja et al. [77] | 2022 | SVM and CNN | APTOS 2019 | 02 | Accuracy = 85.42% |
| Vidivelli et al. [78] | 2025 | CNN | ODIR | 05 | Accuracy = 89.64% |
| Farag et al. [79] | 2022 | CBAM | APTOS 2019 | 02 | Accuracy = 93.45% |
| Vives et al. [80] | 2021 | CNN | APTOS 2019 | 02 | Accuracy = 94.54% |
| Zhang et al. [81] | 2022 | CNN | APTOS 2019 | 02 | Accuracy = 96.15% |
| Gangwar et al. [82] | 2021 | ResNet-50 | APTOS 2019 | 02 | Accuracy = 92.39% |
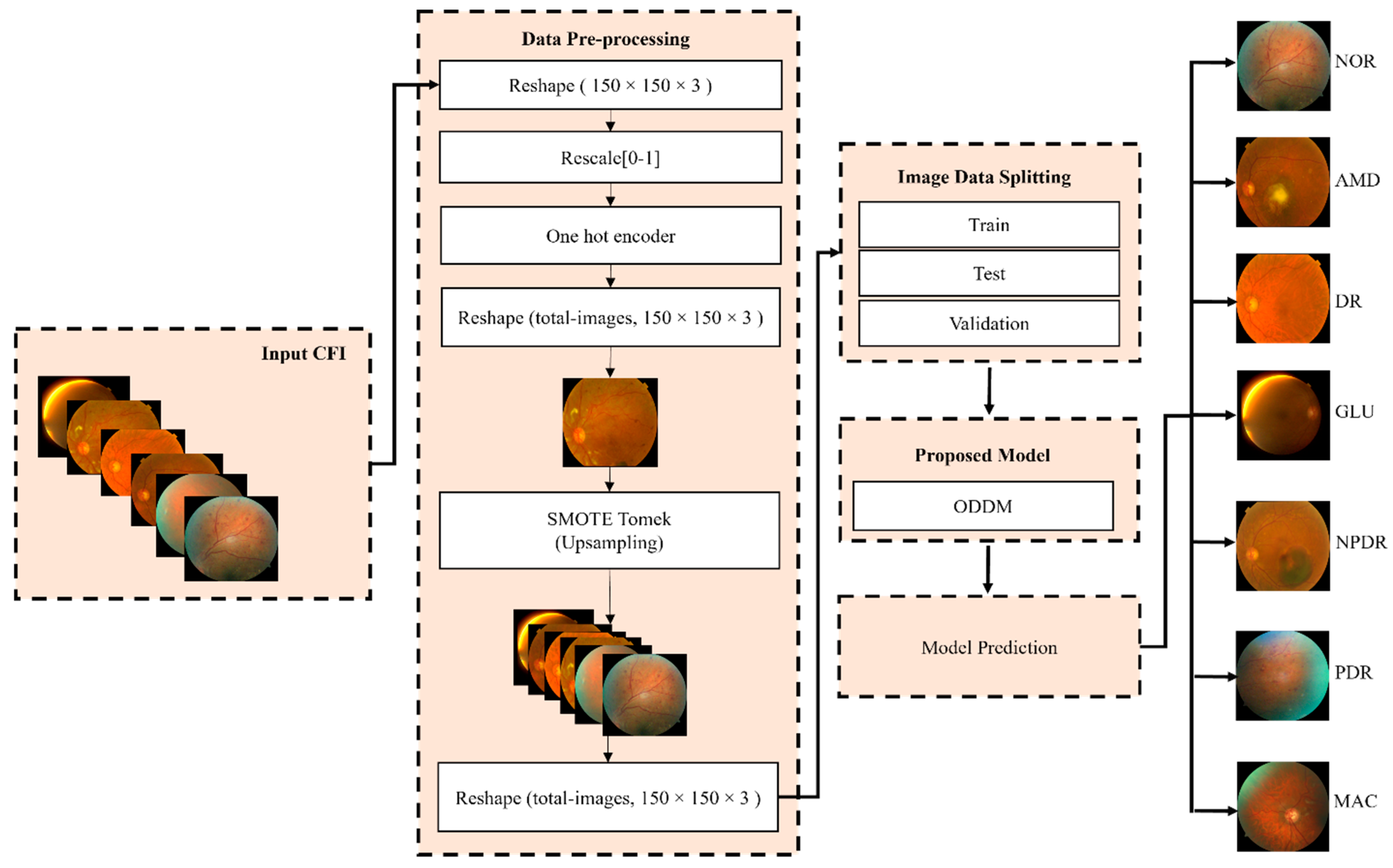
3. Materials and Methods
3.1. Workflow of ODDM for Classification of ODs
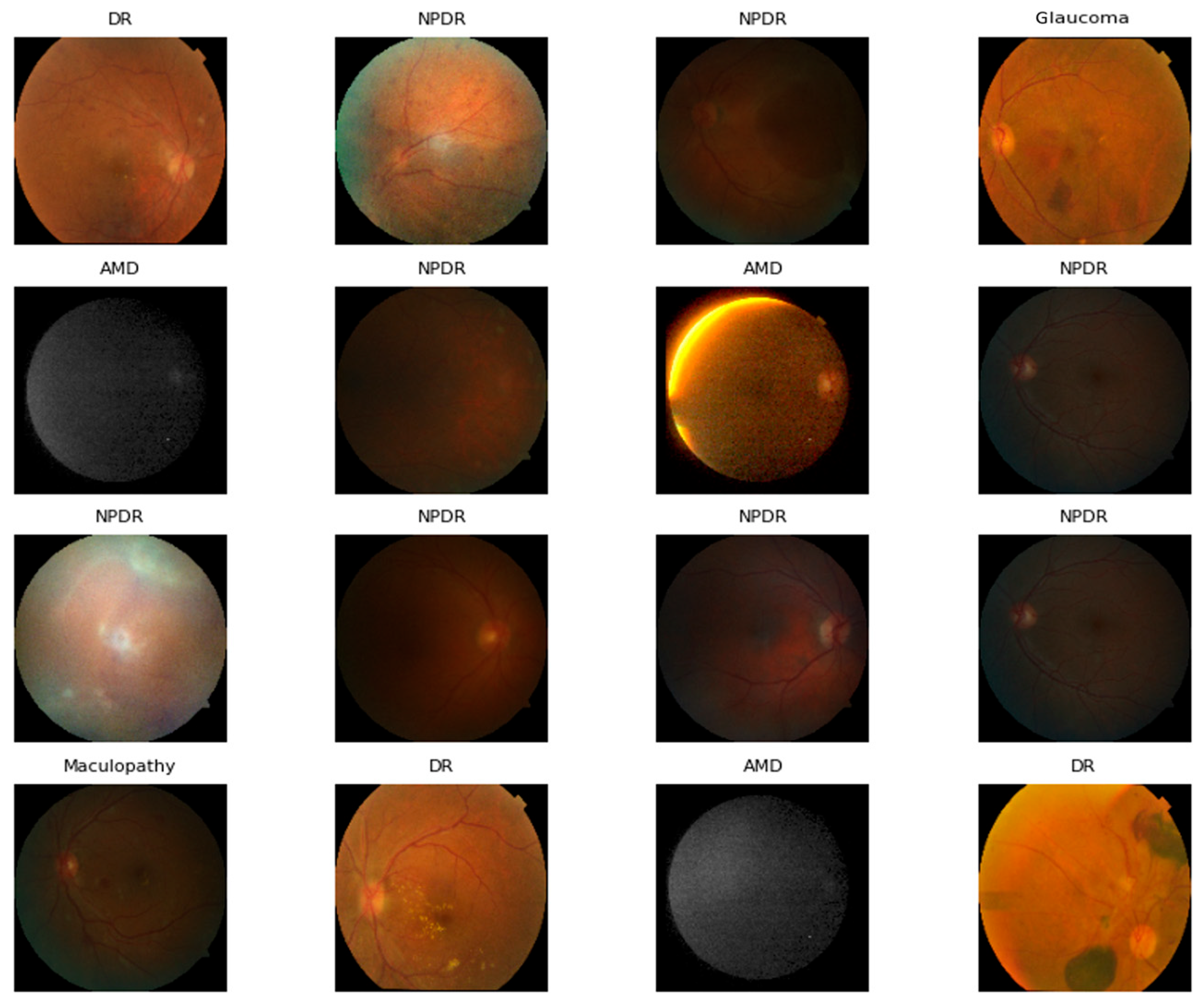
3.2. Dataset Description
3.3. Handling Imbalanced Classes of OD Dataset Using SM-TOM
| Algorithm 1: SMOTE Tomek algorithm for increasing the number of CFI of the minority class. |
| Quantity of synthetic CFI images to compensate the original CFI in the minority classes of ODs. |
| is a collection of samples that are generated using Smote Tomek. |
| do: and not in O is a borderline sample. End if End |
| is a set containing synthetic samples. |
| 4: For all in do: For do: ← choose a random sample from ← + j * ( is a random number in (0, 1), is a synthetic CFI. add to End For End For |
| 5: |
3.4. K-Fold Cross-Validation
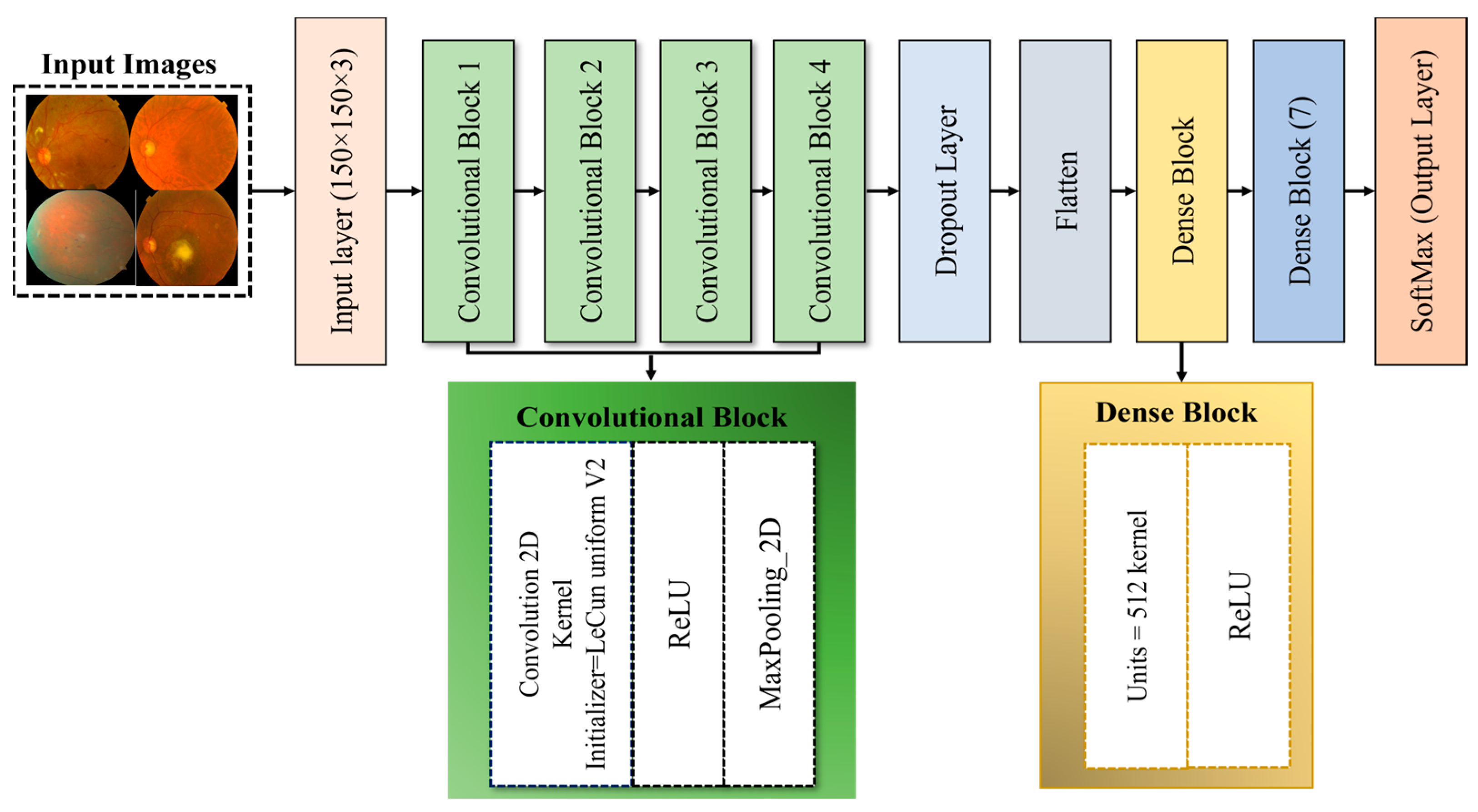
3.5. Proposed ODDM
3.5.1. ConvL_Bs of ODDM
3.5.2. Flatten Layer
3.5.3. D_LB of Proposed ODDM
3.6. Performance Evaluation
3.7. ANOVA and Tukey’s HSD Post Hoc Test
3.8. Proposed Algorithm
| Algorithm 2: | Classification of ocular diseases using CFI. |
| Input: | = CFI |
| Output: | Ocular Diseases Classification |
| PRE-PROCESSING: Z1 | |
| 1 | |
| 2 | |
| 3 | |
| SYNTHETIC IMAGES USING SM-TOM: Z2 | |
| 4 | See Algorithm (1) |
| PROPOSED ODDM MODEL: Z3 | |
| 5 | For i in Add Conv_2D in See Equation (5) Add ReLU in See Equations (7) and (8) Add M_PL in See Equations (1)–(4) End Add F_LT in See Equation (6) Add D_BL in For j in D_BL: Add ReLU in D_BL See Equations (7) and (8) Add SoftMax in D_BL See Equation (9) End End |
| TRAINING & VALIDATION SPLIT FOR ODDM MODEL: Z4 | |
| 6 | Training set: , Validation set: |
| 7 | For f = 1 : | on A3 |
| 8 | Training Image: |
| 9 | : training CFI image in epoch runs (r) |
| 10 | |
| 11 | End |
| 12 | |
| PERFORMANCE EVALUATION PARAMETERS: Z5 | |
| 13 | For Z = 1:5% Z represents the no. of performance evaluators. Parameters: See Equations (10)–(14) End |
| 14 | Select Best Model in terms of Z |
| 15 | End |
4. Results and Discussions
4.1. Experimental Setups and Hyperparameters of Proposed ODDM and Baseline Models
4.2. Results of Proposed ODDM and Baseline Models
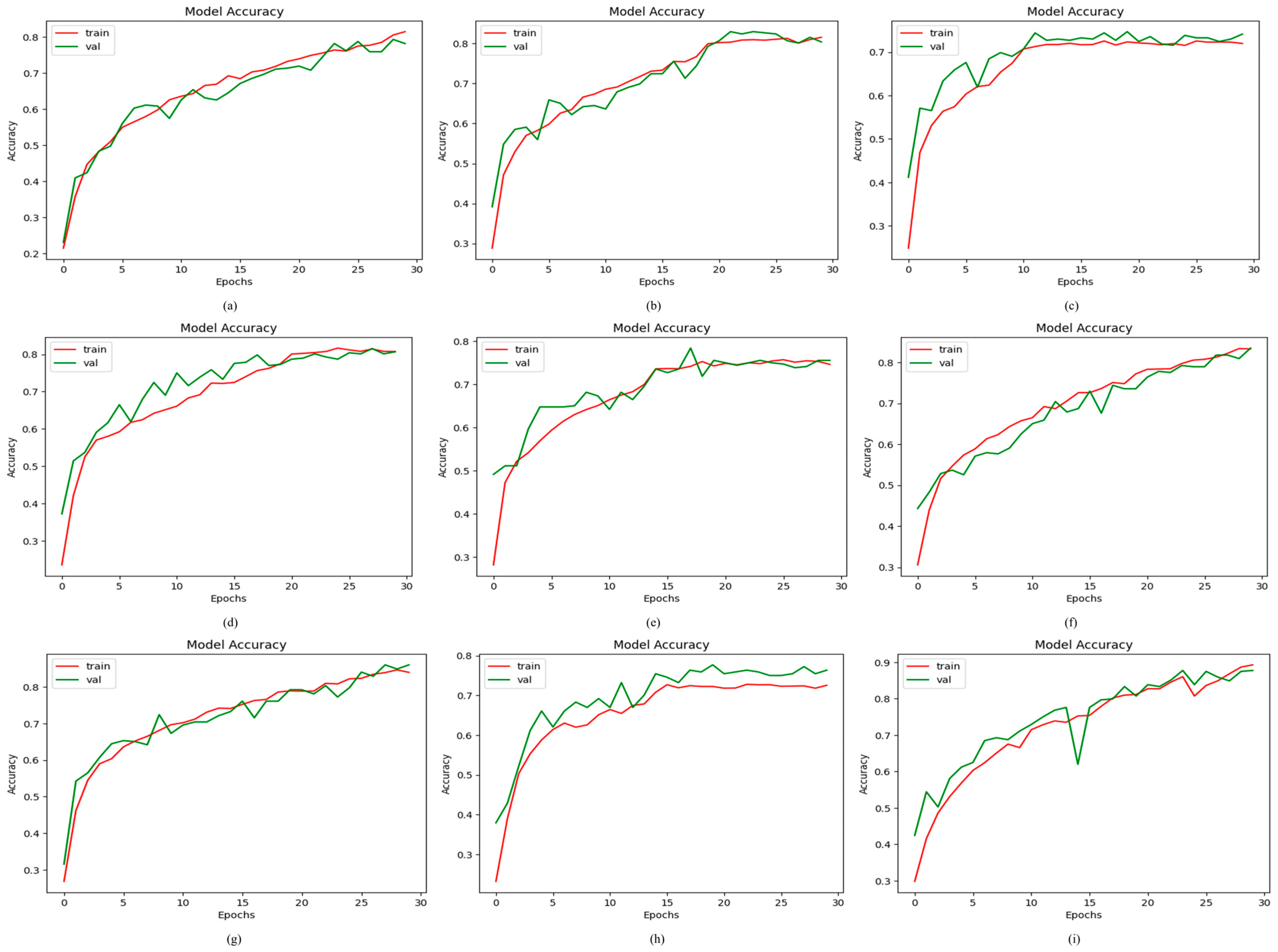
4.2.1. Results of Proposed ODDM in Terms of Accuracy
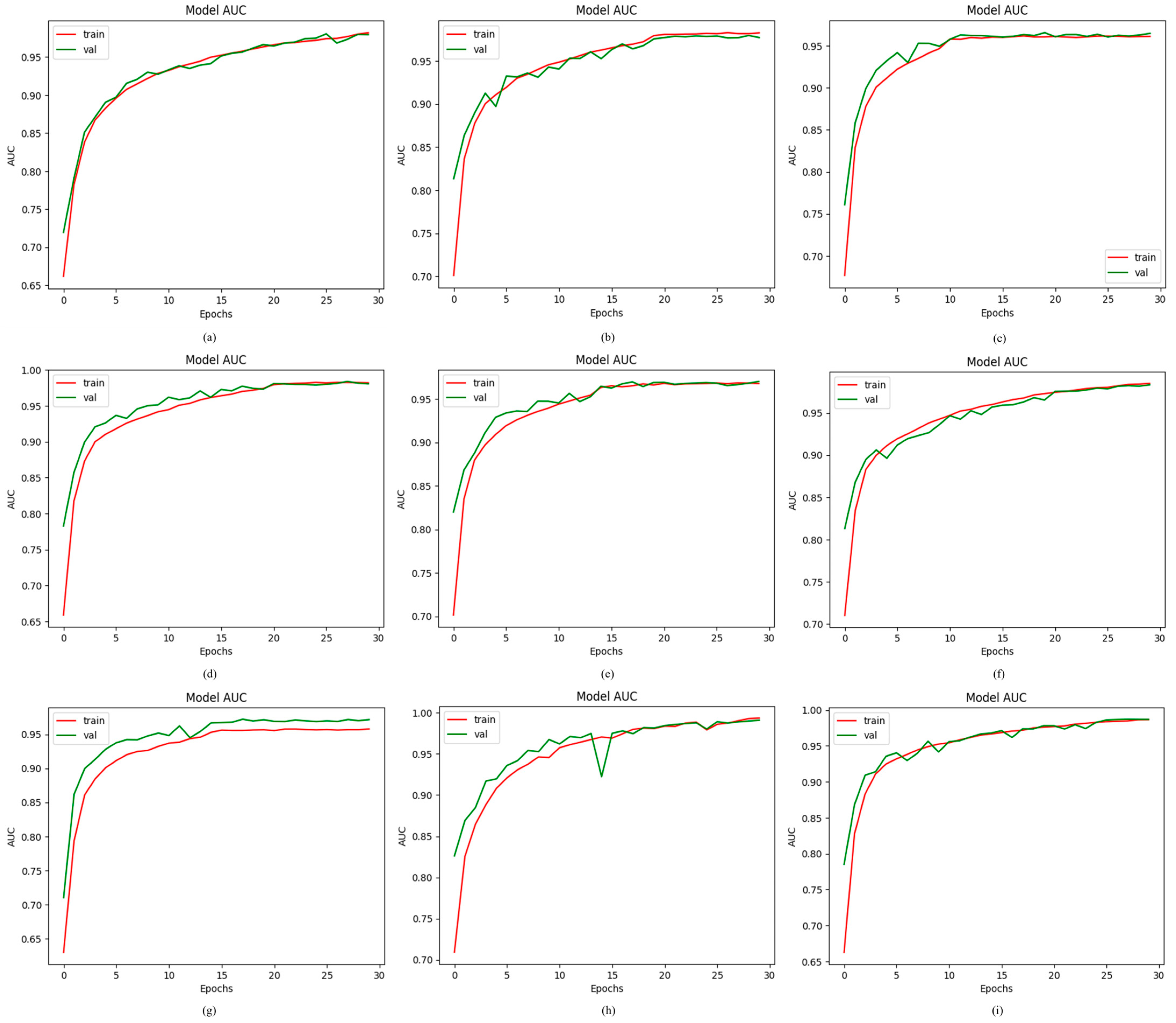
4.2.2. Results of Proposed ODDM in Terms of AUC
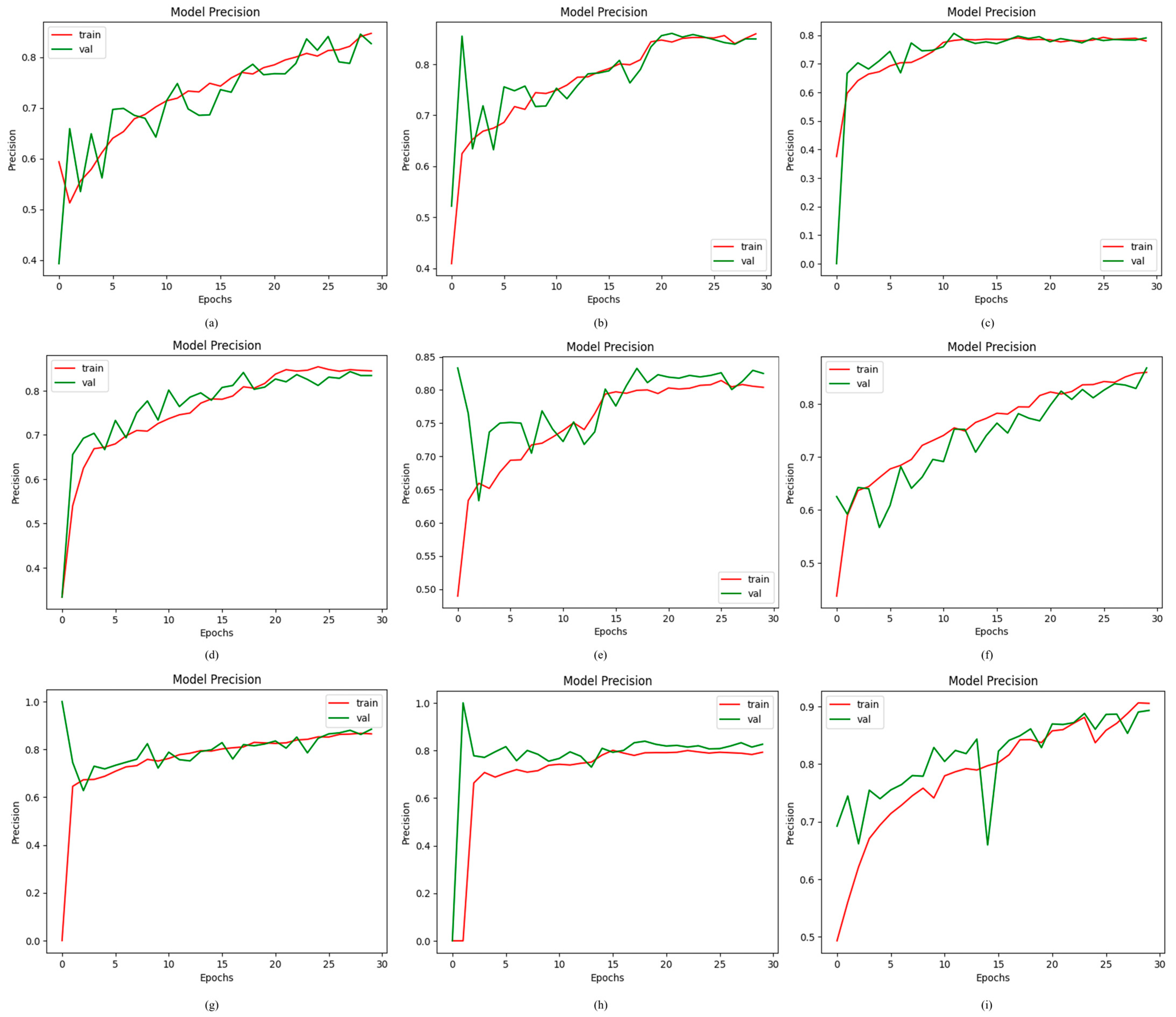
4.2.3. Results of Proposed ODDM in Terms of Precision
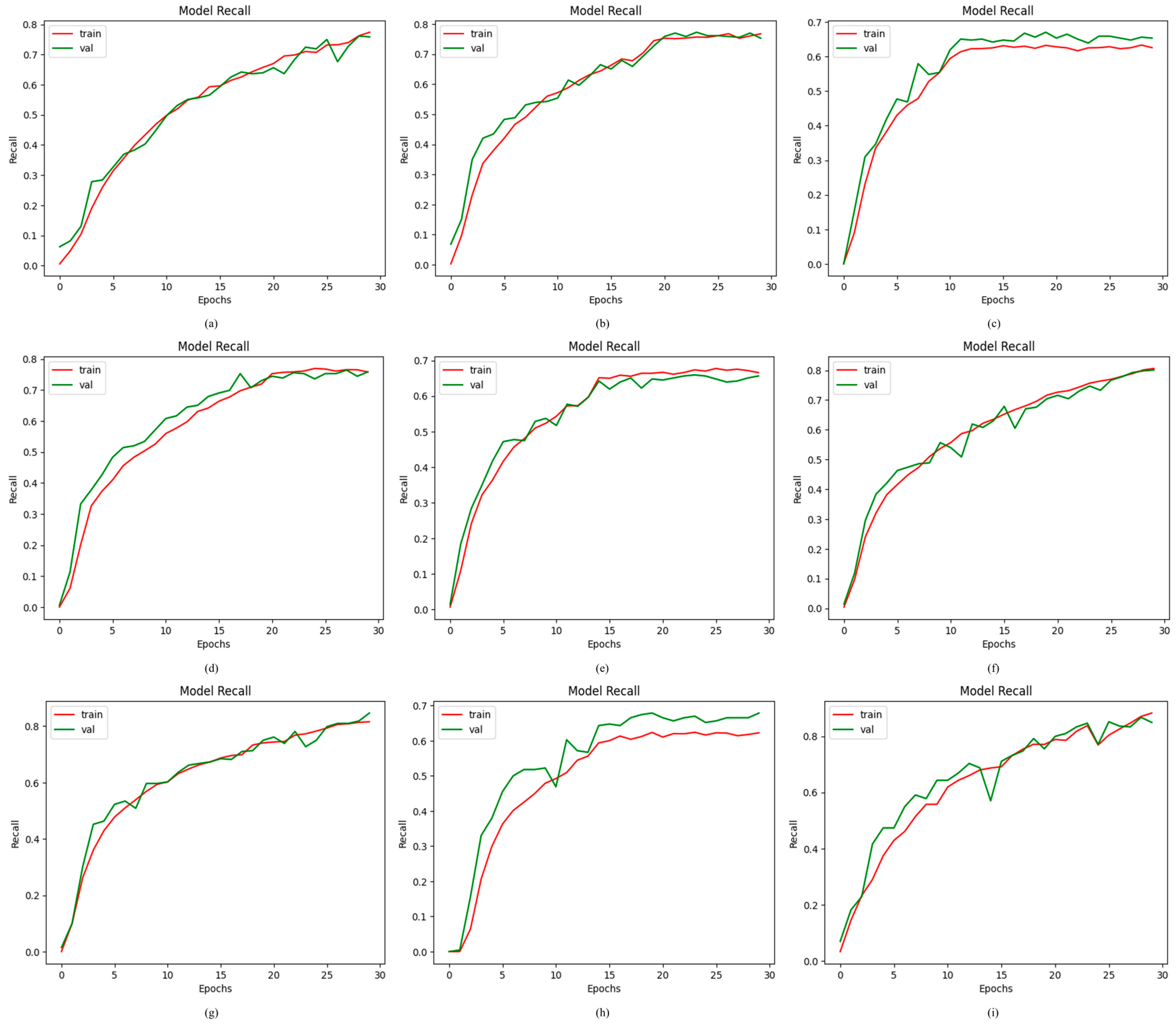
4.2.4. Results of Proposed ODDM in Terms of Recall
4.2.5. Results of Proposed ODDM in Terms of F1-Score
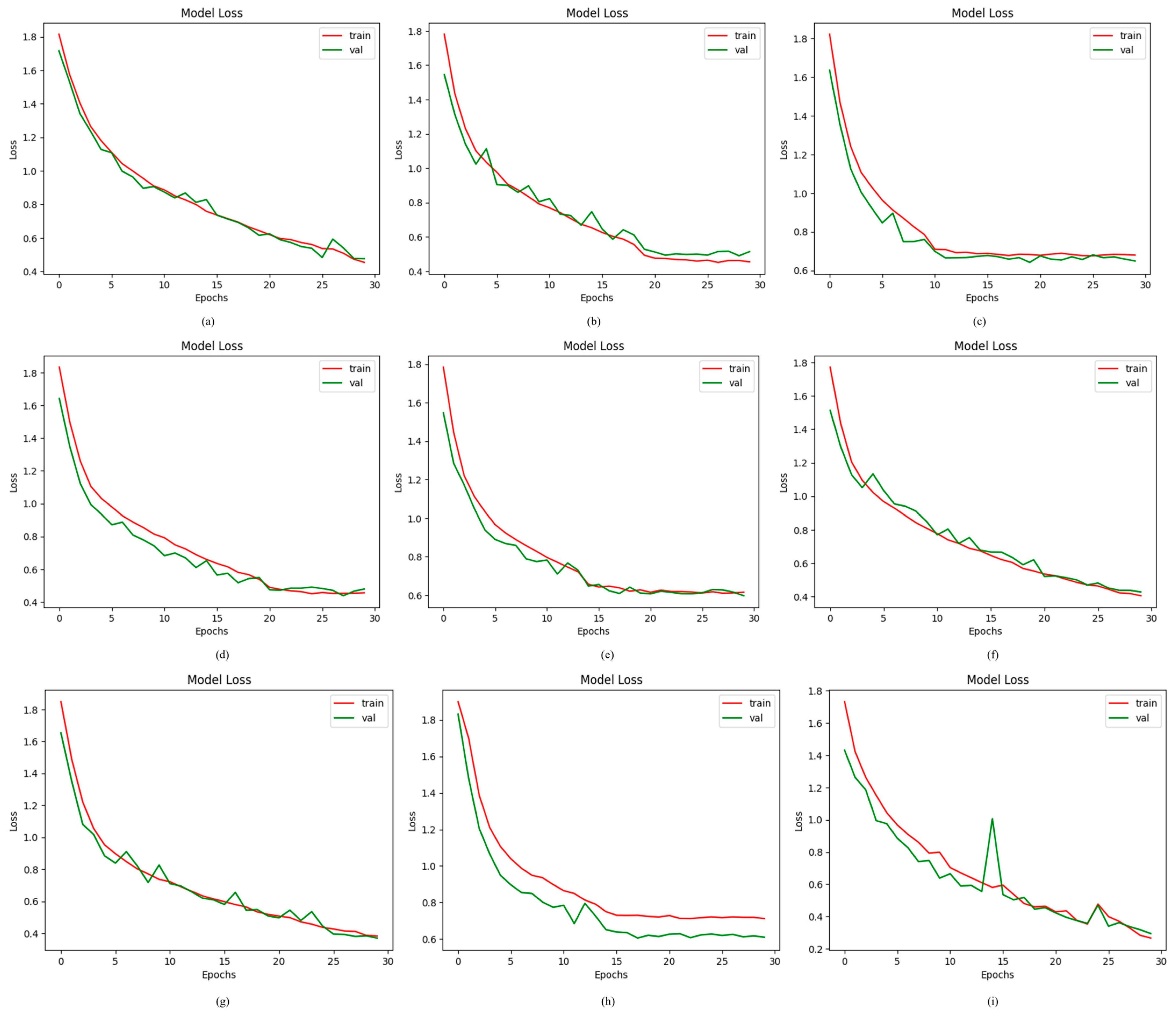
4.2.6. Results of Proposed ODDM in Terms of Loss
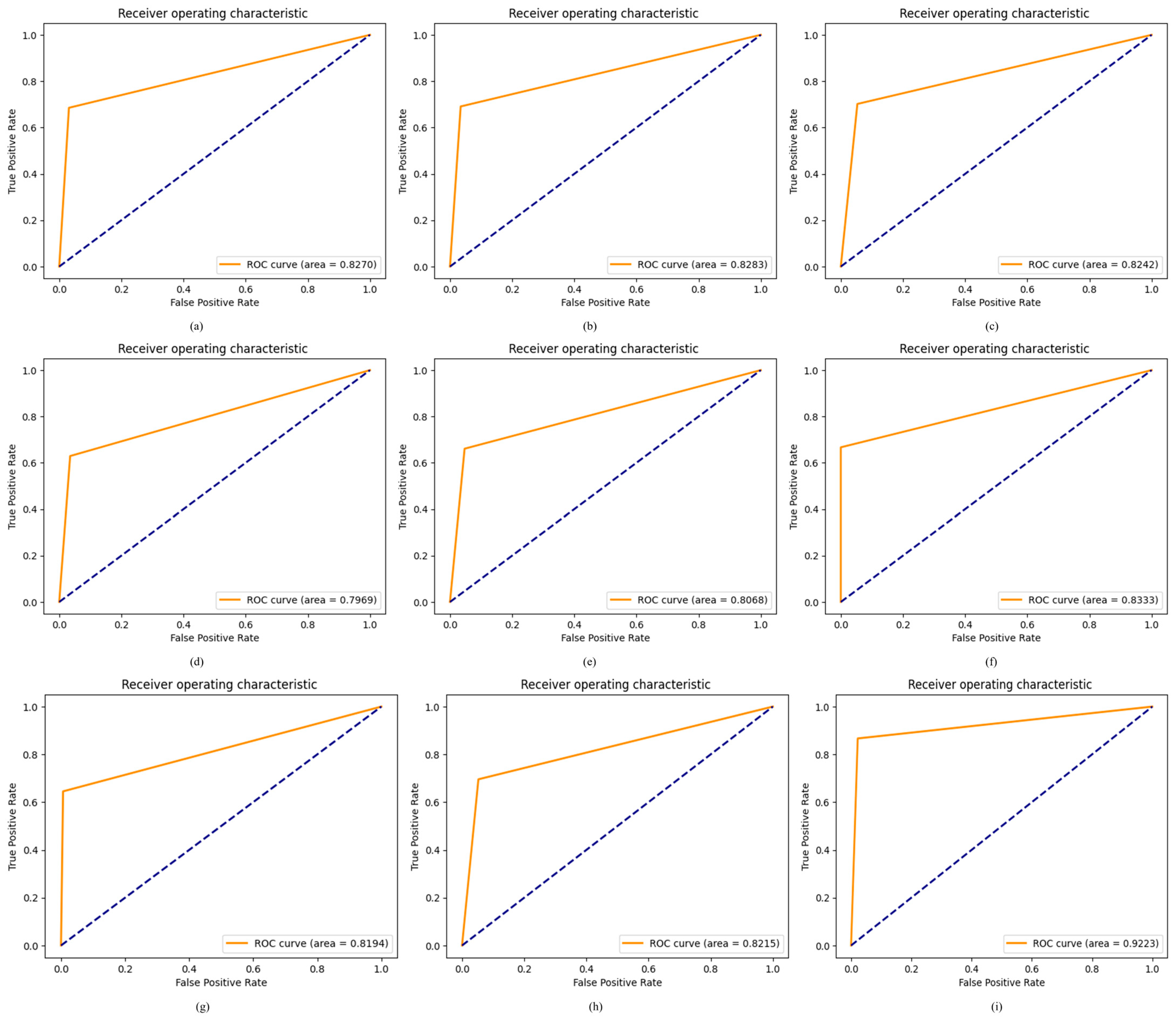
4.2.7. Results of Proposed ODDM in Terms of ROC
4.2.8. Results of Proposed ODDM in Terms of AU ROC
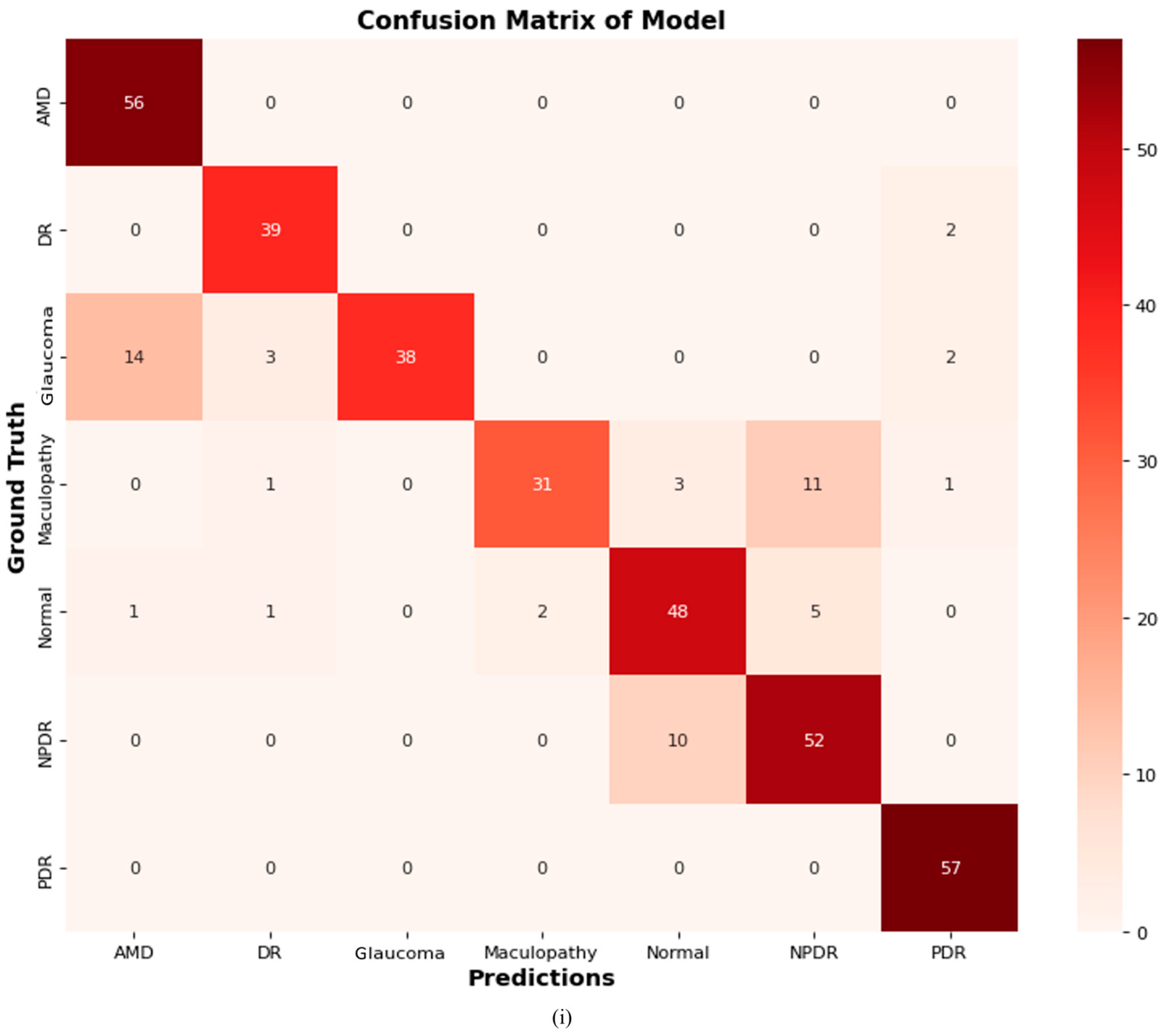
4.2.9. Confusion Matrix of Proposed ODDM
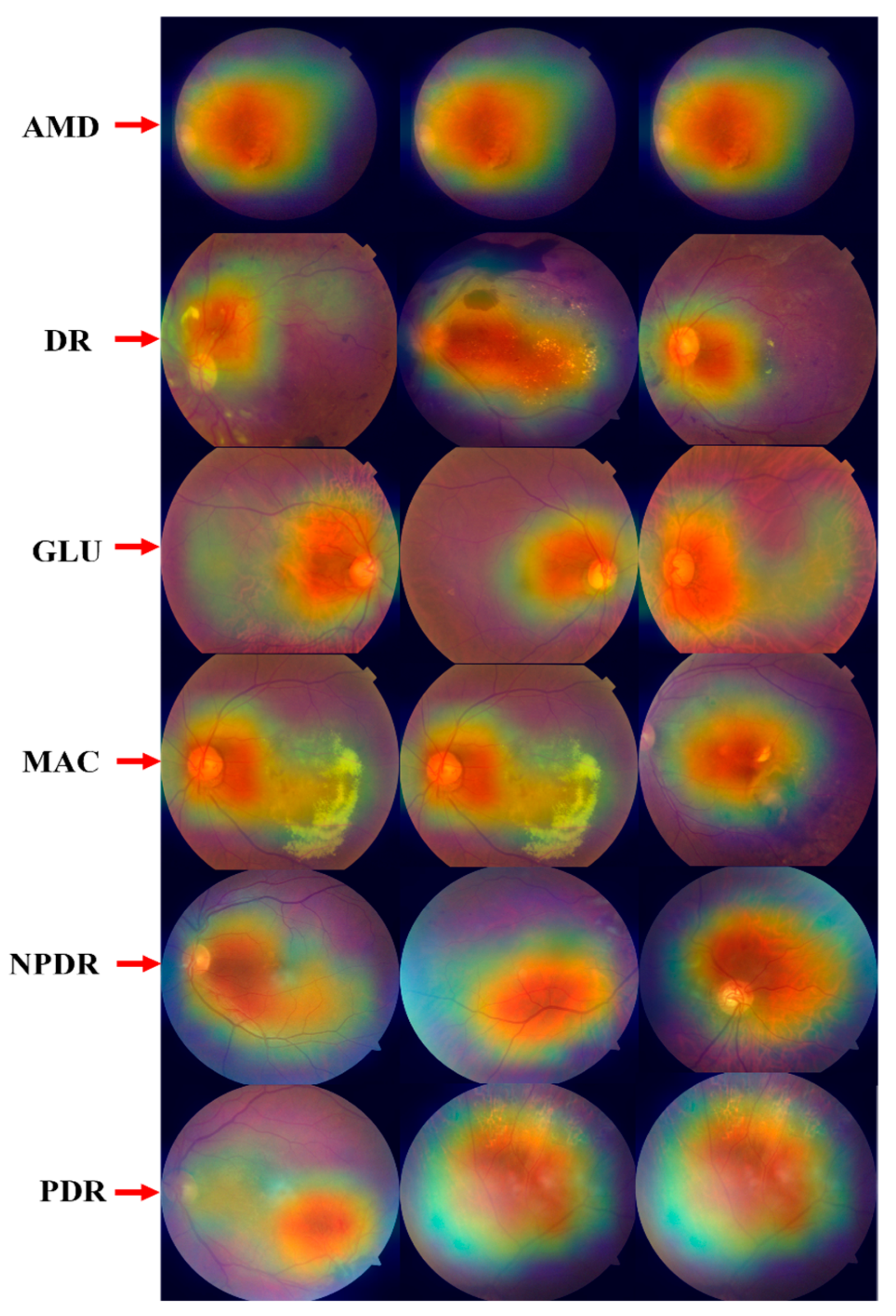
4.2.10. GRAD-CAM Visualization of Proposed ODDM
4.3. Ablation Experiments
4.4. Results of ANOVA and Tukey’s HSD Post Hoc Test
4.5. Comparison of Proposed ODDM with SOTA
4.6. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ODs | Ocular Diseases |
| CFIs | Color Fundus Images |
| DL | Deep Learning |
| CNN | Convolutional Neural Network |
| NOR | Normal |
| AMD | Age-Related Macular Degeneration |
| DR | Diabetic Retinopathy |
| GLU | Glaucoma |
| MAC | Maculopathy |
| NPDR | Non-Proliferative Diabetic Retinopathy |
| PDR | Proliferative Diabetic Retinopathy |
References
- Flaxman, S.R.; Bourne, R.R.; Resnikoff, S.; Ackland, P.; Braithwaite, T.; Cicinelli, M.V.; Zheng, Y. Global causes of blindness and distance vision impairment 1990–2020: A systematic review and meta-analysis. Lancet Glob. Health 2017, 5, e1221–e1234. [Google Scholar] [CrossRef]
- Wiedemann, P. LOVE your eyes—World Sight Day 2022. Int. J. Ophthalmol. 2022, 15, 1567. [Google Scholar] [CrossRef] [PubMed]
- Wong, W.L.; Su, X.; Li, X.; Cheung, C.M.G.; Klein, R.; Cheng, C.Y.; Wong, T.Y. Global prevalence of age-related macular degeneration and disease burden projection for 2020 and 2040: A systematic review and meta-analysis. Lancet Glob. Health 2014, 2, e106–e116. [Google Scholar] [CrossRef]
- Cheyne, C.P.; Burgess, P.I.; Broadbent, D.M.; García-Fiñana, M.; Stratton, I.M.; Criddle, T.; Jones, L. Incidence of sight-threatening diabetic retinopathy in an established urban screening programme: An 11-year cohort study. Diabet. Med. 2021, 38, e14583. [Google Scholar] [CrossRef]
- Schultz, N.M.; Bhardwaj, S.; Barclay, C.; Gaspar, L.; Schwartz, J. Global burden of dry age-related macular degeneration: A targeted literature review. Clin. Ther. 2021, 43, 1792–1818. [Google Scholar] [CrossRef]
- Wild, S.; Roglic, G.; Green, A.; Sicree, R.; King, H. Global prevalence of diabetes: Estimates for the year 2000 and projections for 2030. Diabetes Care 2004, 27, 1047–1053. [Google Scholar] [CrossRef] [PubMed]
- Lim, G.; Bellemo, V.; Xie, Y.; Lee, X.Q.; Yip, M.Y.; Ting, D.S. Different fundus imaging modalities and technical factors in AI screening for diabetic retinopathy: A review. Eye Vis. 2020, 7, 21. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Li, C.; Ye, J.; Qiao, Y.; Gu, L. Multi-label ocular disease classification with a dense correlation deep neural network. Biomed. Signal Process. Control. 2021, 63, 102167. [Google Scholar] [CrossRef]
- Wang, J.; Yang, L.; Huo, Z.; He, W.; Luo, J. Multi-label classification of fundus images with efficientnet. IEEE Access 2020, 8, 212499–212508. [Google Scholar] [CrossRef]
- Azzopardi, G.; Strisciuglio, N.; Vento, M.; Petkov, N. Trainable COSFIRE filters for vessel delineation with application to retinal images. Med. Image Anal. 2015, 19, 46–57. [Google Scholar] [CrossRef]
- Zhang, Z.; Srivastava, R.; Liu, H.; Chen, X.; Duan, L.; Kee Wong, D.W.; Liu, J. A survey on computer aided diagnosis for ocular diseases. BMC Med. Inform. Decis. Mak. 2014, 14, 80. [Google Scholar] [CrossRef]
- Sarhan, M.H.; Nasseri, M.A.; Zapp, D.; Maier, M.; Lohmann, C.P.; Navab, N.; Eslami, A. Machine learning techniques for ophthalmic data processing: A review. IEEE J. Biomed. Health Inform. 2020, 24, 3338–3350. [Google Scholar] [CrossRef]
- Burlina, P.M.; Joshi, N.; Pekala, M.; Pacheco, K.D.; Freund, D.E.; Bressler, N.M. Automated grading of age-related macular degeneration from color fundus images using deep convolutional neural networks. JAMA Ophthalmol. 2017, 135, 1170–1176. [Google Scholar] [CrossRef]
- Chen, X.; Xu, Y.; Duan, L.; Yan, S.; Zhang, Z.; Wong, D.W.K.; Liu, J. Multiple ocular diseases classification with graph regularized probabilistic multi-label learning. In Proceedings of the Computer Vision—ACCV 2014: 12th Asian Conference on Computer Vision, Singapore, 1–5 November 2014; Revised Selected Papers, Part IV 12. Springer International Publishing: Cham, Switzerland, 2015; pp. 127–142. [Google Scholar]
- Li, Z.; Keel, S.; Liu, C.; He, Y.; Meng, W.; Scheetz, J.; He, M. An automated grading system for detection of vision-threatening referable diabetic retinopathy on the basis of color fundus photographs. Diabetes Care 2018, 41, 2509–2516. [Google Scholar] [CrossRef]
- Richards, B.A.; Lillicrap, T.P.; Beaudoin, P.; Bengio, Y.; Bogacz, R.; Christensen, A.; Kording, K.P. A deep learning framework for neuroscience. Nat. Neurosci. 2019, 22, 1761–1770. [Google Scholar] [CrossRef]
- Wang, Z.; Keane, P.A.; Chiang, M.; Cheung, C.Y.; Wong, T.Y.; Ting, D.S.W. Artificial intelligence and deep learning in ophthalmology. In Artificial Intelligence in Medicine; Springer International Publishing: Cham, Switzerland, 2022; pp. 1519–1552. [Google Scholar]
- Gulshan, V.; Peng, L.; Coram, M.; Stumpe, M.C.; Wu, D.; Narayanaswamy, A.; Webster, D.R. Development and validation of a deep learning algorithm for detection of diabetic retinopathy in retinal fundus photographs. JAMA 2016, 316, 2402–2410. [Google Scholar] [CrossRef]
- Litjens, G.; Ciompi, F.; Wolterink, J.M.; de Vos, B.D.; Leiner, T.; Teuwen, J.; Išgum, I. State-of-the-art deep learning in cardiovascular image analysis. JACC Cardiovasc. Imaging 2019, 12 Pt 1, 1549–1565. [Google Scholar] [CrossRef] [PubMed]
- Esteva, A.; Kuprel, B.; Novoa, R.A.; Ko, J.; Swetter, S.M.; Blau, H.M.; Thrun, S. Dermatologist-level classification of skin cancer with deep neural networks. Nature 2017, 542, 115–118. [Google Scholar] [CrossRef] [PubMed]
- Sureyya Rifaioglu, A.; Doğan, T.; Jesus Martin, M.; Cetin-Atalay, R.; Atalay, V. DEEPred: Automated protein function prediction with multi-task feed-forward deep neural networks. Sci. Rep. 2019, 9, 7344. [Google Scholar] [CrossRef]
- Sultan, A.S.; Elgharib, M.A.; Tavares, T.; Jessri, M.; Basile, J.R. The use of artificial intelligence, machine learning and deep learning in oncologic histopathology. J. Oral Pathol. Med. 2020, 49, 849–856. [Google Scholar] [CrossRef] [PubMed]
- Diaz-Pinto, A.; Morales, S.; Naranjo, V.; Köhler, T.; Mossi, J.M.; Navea, A. CNNs for automatic glaucoma assessment using fundus images: An extensive validation. Biomed. Eng. Online 2019, 18, 29. [Google Scholar] [CrossRef] [PubMed]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Cen, L.P.; Ji, J.; Lin, J.W.; Ju, S.T.; Lin, H.J.; Li, T.P.; Zhang, M. Automatic detection of 39 fundus diseases and conditions in retinal photographs using deep neural networks. Nat. Commun. 2021, 12, 4828. [Google Scholar] [CrossRef]
- Dubey, S.; Dixit, M. Recent developments on computer aided systems for diagnosis of diabetic retinopathy: A review. Multimed. Tools Appl. 2023, 82, 14471–14525. [Google Scholar] [CrossRef]
- Ashraf, M.N.; Hussain, M.; Habib, Z. Review of Various Tasks Performed in the Preprocessing Phase of a Diabetic Retinopathy Diagnosis System. Curr. Med. Imaging 2020, 16, 397–426. [Google Scholar] [CrossRef]
- Kyei, S.; Kwasi Gyaami, R.; Abowine, J.B.; Zaabaar, E.; Asiedu, K.; Boadi-Kusi, S.B.; Ayerakwah, P.A. Risk of major myopia-associated non-communicable ocular health disorders in Ghana. PLoS ONE 2024, 19, e0297052. [Google Scholar] [CrossRef]
- Bali, A.; Mansotra, V. Analysis of deep learning techniques for prediction of eye diseases: A systematic review. Arch. Comput. Methods Eng. 2024, 31, 487–520. [Google Scholar] [CrossRef]
- Sharma, H.; Wasim, J.; Sharma, P. Analysis of eye disease classification by fundus images using different machine/deep/transfer learning techniques. In Proceedings of the 2024 4th International Conference on Innovative Practices in Technology and Management (ICIPTM), Noida, India, 21–23 February 2024; pp. 1–6. [Google Scholar]
- Hassan, M.U.; Al-Awady, A.A.; Ahmed, N.; Saeed, M.; Alqahtani, J.; Alahmari, A.M.M.; Javed, M.W. A transfer learning enabled approach for ocular disease detection and classification. Health Inf. Sci. Syst. 2024, 12, 36. [Google Scholar] [CrossRef]
- Hasnain, M.A.; Malik, H.; Asad, M.M.; Sherwani, F. Deep learning architectures in dental diagnostics: A systematic comparison of techniques for accurate prediction of dental disease through x-ray imaging. Int. J. Intell. Comput. Cybern. 2024, 17, 161–180. [Google Scholar] [CrossRef]
- Tahir, A.; Malik, H.; Chaudhry, M.U. Multi-classification Deep Learning Models for Detecting Multiple Chest Infection Using Cough and Breath Sounds. In Deep Learning for Multimedia Processing Applications; CRC Press: Boca Raton, FL, USA, 2024; pp. 216–249. [Google Scholar]
- Malik, H.; Anees, T. Federated learning with deep convolutional neural networks for the detection of multiple chest diseases using chest X-rays. Multimed. Tools Appl. 2024, 83, 63017–63045. [Google Scholar] [CrossRef]
- Malik, H.; Anees, T. Multi-modal deep learning methods for classification of chest diseases using different medical imaging and cough sounds. PLoS ONE 2024, 19, e0296352. [Google Scholar] [CrossRef]
- Abd El-Khalek, A.A.; Balaha, H.M.; Alghamdi, N.S.; Ghazal, M.; Khalil, A.T.; Abo-Elsoud, M.E.A.; El-Baz, A. A concentrated machine learning-based classification system for age-related macular degeneration (AMD) diagnosis using fundus images. Sci. Rep. 2024, 14, 2434. [Google Scholar] [CrossRef]
- Vidivelli, S.; Padmakumari, P.; Parthiban, C.; DharunBalaji, A.; Manikandan, R.; Gandomi, A.H. Optimising deep learning models for ophthalmological disorder classification. Sci. Rep. 2025, 15, 3115. [Google Scholar] [CrossRef] [PubMed]
- Li, N.; Kondo, N.; Ogawa, Y.; Shiraga, K.; Shibasaki, M.; Pinna, D.; Suzuki, T. Fundus camera-based precision monitoring of blood vitamin A level for Wagyu cattle using deep learning. Sci. Rep. 2025, 15, 4125. [Google Scholar] [CrossRef] [PubMed]
- Sarki, R.; Ahmed, K.; Wang, H.; Zhang, Y. Automated detection of mild and multi-class diabetic eye diseases using deep learning. Health Inf. Sci. Syst. 2020, 8, 32. [Google Scholar] [CrossRef]
- Anoop, B.K. Binary classification of DR-diabetic retinopathy using CNN with fundus colour images. Mater. Today Proc. 2022, 58, 212–216. [Google Scholar]
- Pawar, B.; Lobo, S.N.; Joseph, M.; Jegannathan, S.; Jayraj, H. Validation of artificial intelligence algorithm in the detection and staging of diabetic retinopathy through fundus photography: An automated tool for detection and grading of diabetic retinopathy. Middle East Afr. J. Ophthalmol. 2021, 28, 81–86. [Google Scholar] [CrossRef]
- Farag, M.M.; Fouad, M.; Abdel-Hamid, A.T. Automatic severity classification of diabetic retinopathy based on densenet and convolutional block attention module. IEEE Access 2022, 10, 38299–38308. [Google Scholar] [CrossRef]
- Vadduri, M.; Kuppusamy, P. Enhancing Ocular Healthcare: Deep Learning-Based multi-class Diabetic Eye Disease Segmentation and Classification. IEEE Access 2023, 11, 137881–137898. [Google Scholar] [CrossRef]
- Tan, Y.Y.; Kang, H.G.; Lee, C.J.; Kim, S.S.; Park, S.; Thakur, S.; Cheng, C.Y. Prognostic potentials of AI in ophthalmology: Systemic disease forecasting via retinal imaging. Eye Vis. 2024, 11, 17. [Google Scholar] [CrossRef]
- Oliveira, J.S.; Franco, F.O.; Revers, M.C.; Silva, A.F.; Portolese, J.; Brentani, H.; Nunes, F.L. Computer-aided autism diagnosis based on visual attention models using eye tracking. Sci. Rep. 2021, 11, 10131. [Google Scholar] [CrossRef]
- Li, B.; Barney, E.; Hudac, C.; Nuechterlein, N.; Ventola, P.; Shapiro, L.; Shic, F. Selection of Eye-Tracking Stimuli for Prediction by Sparsely Grouped Input Variables for Neural Networks: Towards Biomarker Refinement for Autism. In Proceedings of the ACM Symposium on Eye Tracking Research and Applications, Stuttgart, Germany, 2–5 June 2020; pp. 1–8. [Google Scholar]
- Raghavendra, U.; Fujita, H.; Bhandary, S.V.; Gudigar, A.; Tan, J.H.; Acharya, U.R. Deep convolution neural network for accurate diagnosis of glaucoma using digital fundus images. Inf. Sci. 2018, 441, 41–49. [Google Scholar] [CrossRef]
- dos Santos Ferreira, M.V.; de Carvalho Filho, A.O.; de Sousa, A.D.; Silva, A.C.; Gattass, M. Convolutional neural network and texture descriptor-based automatic detection and diagnosis of glaucoma. Expert Syst. Appl. 2018, 110, 250–263. [Google Scholar] [CrossRef]
- Prananda, A.R.; Frannita, E.L.; Hutami, A.H.T.; Maarif, M.R.; Fitriyani, N.L.; Syafrudin, M. Retinal nerve fiber layer analysis using deep learning to improve glaucoma detection in eye disease assessment. Appl. Sci. 2022, 13, 37. [Google Scholar] [CrossRef]
- Sheraz, H.; Shehryar, T.; Khan, Z.A. Two stage-network: Automatic localization of Optic Disc (OD) and classification of glaucoma in fundus images using deep learning techniques. Multimed. Tools Appl. 2024, 84, 12949–12977. [Google Scholar] [CrossRef]
- Liu, Z.; Huang, W.; Wang, Z.; Jin, L.; Congdon, N.; Zheng, Y.; Liu, Y. Evaluation of a self-imaging OCT for remote diagnosis and monitoring of retinal diseases. Br. J. Ophthalmol. 2024, 108, 1154–1160. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.Q.; Sun, G.; Khalid, M.; Imran, A.; Bilal, A.; Azam, M.; Sarwar, R. A novel fusion of genetic grey wolf optimization and kernel extreme learning machines for precise diabetic eye disease classification. PLoS ONE 2024, 19, e0303094. [Google Scholar] [CrossRef]
- Wykoff, C.C.; Do, D.V.; Goldberg, R.A.; Dhoot, D.S.; Lim, J.I.; Du, W.; Clark, W.L. Ocular and Systemic Risk Factors for Disease Worsening Among Patients with NPDR: Post Hoc Analysis of the PANORAMA Trial. Ophthalmol. Retin. 2024, 8, 399–408. [Google Scholar] [CrossRef]
- Chelaramani, S.; Gupta, M.; Agarwal, V.; Gupta, P.; Habash, R. Multi-task knowledge distillation for eye disease prediction. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Virtual, 5–9 January 2021; pp. 3983–3993. [Google Scholar]
- Lu, D.; Heisler, M.; Lee, S.; Ding, G.W.; Navajas, E.; Sarunic, M.V.; Beg, M.F. Deep-learning based multiclass retinal fluid segmentation and detection in optical coherence tomography images using a fully convolutional neural network. Med. Image Anal. 2019, 54, 100–110. [Google Scholar] [CrossRef]
- Szeskin, A.; Yehuda, R.; Shmueli, O.; Levy, J.; Joskowicz, L. A column-based deep learning method for the detection and quantification of atrophy associated with AMD in OCT scans. Med. Image Anal. 2021, 72, 102130. [Google Scholar] [CrossRef]
- Aamir, M.; Irfan, M.; Ali, T.; Ali, G.; Shaf, A.; Al-Beshri, A.; Mahnashi, M.H. An adoptive threshold-based multi-level deep convolutional neural network for glaucoma eye disease detection and classification. Diagnostics 2020, 10, 602. [Google Scholar] [CrossRef]
- Devalla, S.K.; Renukanand, P.K.; Sreedhar, B.K.; Subramanian, G.; Zhang, L.; Perera, S.; Girard, M.J. DRUNET: A dilated-residual U-Net deep learning network to segment optic nerve head tissues in optical coherence tomography images. Biomed. Opt. Express 2018, 9, 3244–3265. [Google Scholar] [CrossRef]
- Arsalan, M.; Haider, A.; Park, C.; Hong, J.S.; Park, K.R. Multiscale triplet spatial information fusion-based deep learning method to detect retinal pigment signs with fundus images. Eng. Appl. Artif. Intell. 2024, 133, 108353. [Google Scholar] [CrossRef]
- Haider, A.; Arsalan, M.; Lee, M.B.; Owais, M.; Mahmood, T.; Sultan, H.; Park, K.R. Artificial Intelligence-based computer-aided diagnosis of glaucoma using retinal fundus images. Expert Syst. Appl. 2022, 207, 117968. [Google Scholar] [CrossRef]
- Haider, A.; Arsalan, M.; Park, C.; Sultan, H.; Park, K.R. Exploring deep feature-blending capabilities to assist glaucoma screening. Appl. Soft Comput. 2023, 133, 109918. [Google Scholar] [CrossRef]
- Lenka, S.; Lazarus, M.Z.; Panda, G. Glaucoma detection from retinal fundus images using graph convolution-based multi-task model. E-Prime-Adv. Electr. Eng. Electron. Energy 2025, 11, 100931. [Google Scholar] [CrossRef]
- Hu, W.; Li, K.; Gagnon, J.; Wang, Y.; Raney, T.; Chen, J.; Zhang, B. FundusNet: A Deep-Learning Approach for Fast Diagnosis of Neurodegenerative and Eye Diseases Using Fundus Images. Bioengineering 2025, 12, 57. [Google Scholar] [CrossRef]
- Kansal, I.; Khullar, V.; Sharma, P.; Singh, S.; Hamid, J.A.; Santhosh, A.J. Multiple model visual feature embedding and selection method for an efficient ocular disease classification. Sci. Rep. 2025, 15, 5157. [Google Scholar] [CrossRef]
- Butt, M.; Awang Iskandar, D.N.F.; Khan, M.A.; Latif, G.; Bashar, A. MEDCnet: A Memory Efficient Approach for Processing High-Resolution Fundus Images for Diabetic Retinopathy Classification Using CNN. Int. J. Imaging Syst. Technol. 2025, 35, e70063. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Le, D.T.; Bum, J.; Kim, S.; Song, S.J.; Choo, H. Retinal disease diagnosis using deep learning on ultra-wide-field fundus images. Diagnostics 2024, 14, 105. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, R.; Dong, L.; Shi, X.; Zhou, W.; Wu, H.; Wei, W. Predicting systemic diseases in fundus images: Systematic review of setting, reporting, bias, and models’ clinical availability in deep learning studies. Eye 2024, 38, 1246–1251. [Google Scholar] [CrossRef]
- Al-Fahdawi, S.; Al-Waisy, A.S.; Zeebaree, D.Q.; Qahwaji, R.; Natiq, H.; Mohammed, M.A.; Deveci, M. Fundus-deepnet: Multi-label deep learning classification system for enhanced detection of multiple ocular diseases through data fusion of fundus images. Inf. Fusion 2024, 102, 102059. [Google Scholar] [CrossRef]
- Hussain, S.K.; Ramay, S.A.; Shaheer, H.; Abbas, T.; Mushtaq, M.A.; Paracha, S.; Saeed, N. Automated Classification of Ophthalmic Disorders Using Color Fundus Images. Kurd. Stud. 2024, 12, 1344–1348. [Google Scholar]
- Hemelings, R.; Elen, B.; Schuster, A.K.; Blaschko, M.B.; Barbosa-Breda, J.; Hujanen, P.; Stalmans, I. A generalizable deep learning regression model for automated glaucoma screening from fundus images. npj Digit. Med. 2023, 6, 112. [Google Scholar] [CrossRef]
- Sengar, N.; Joshi, R.C.; Dutta, M.K.; Burget, R. EyeDeep-Net: A multi-class diagnosis of retinal diseases using deep neural network. Neural Comput. Appl. 2023, 35, 10551–10571. [Google Scholar] [CrossRef]
- Thanki, R. A deep neural network and machine learning approach for retinal fundus image classification. Healthc. Anal. 2023, 3, 100140. [Google Scholar] [CrossRef]
- Nazir, T.; Nawaz, M.; Rashid, J.; Mahum, R.; Masood, M.; Mehmood, A.; Hussain, A. Detection of diabetic eye disease from retinal images using a deep learning based CenterNet model. Sensors 2021, 21, 5283. [Google Scholar] [CrossRef]
- Bodapati, J.D.; Shaik, N.S.; Naralasetti, V. Deep convolution feature aggregation: An application to diabetic retinopathy severity level prediction. Signal Image Video Process. 2021, 15, 923–930. [Google Scholar] [CrossRef]
- Khan, M.S.M.; Ahmed, M.; Rasel, R.Z.; Khan, M.M. Cataract detection using convolutional neural network with VGG-19 model. In Proceedings of the 2021 IEEE World AI IoT Congress (AIIoT), Online, 10–13 May 2021; IEEE: New York, NY, USA, 2021; pp. 0209–0212. [Google Scholar]
- Sarki, R.; Ahmed, K.; Wang, H.; Zhang, Y.; Wang, K. Convolutional neural network for multi-class classification of diabetic eye disease. EAI Endorsed Trans. Scalable Inf. Syst. 2022, 9, e5. [Google Scholar] [CrossRef]
- Pahuja, R.; Sisodia, U.; Tiwari, A.; Sharma, S.; Nagrath, P. A Dynamic Approach of Eye Disease Classification Using Deep Learning and Machine Learning Model. In Proceedings of Data Analytics and Management; Springer: Singapore, 2022; pp. 719–736. [Google Scholar]
- Vives-Boix, V.; Ruiz-Fernández, D. Diabetic retinopathy detection through convolutional neural networks with synaptic metaplasticity. Comput. Methods Programs Biomed. 2021, 206, 106094. [Google Scholar] [CrossRef]
- Zhang, C.; Lei, T.; Chen, P. Diabetic retinopathy grading by a source-free transfer learning approach. Biomed. Signal Process. Control. 2022, 73, 103423. [Google Scholar] [CrossRef]
- Gangwar, A.K.; Ravi, V. Diabetic retinopathy detection using transfer learning and deep learning. In Evolution in Computational Intelligence: Frontiers in Intelligent Computing: Theory and Applications (FICTA 2020); Springer: Singapore, 2021; Volume 1, pp. 679–689. [Google Scholar]
- Malik, H.; Farooq, M.S.; Khelifi, A.; Abid, A.; Qureshi, J.N.; Hussain, M. A comparison of transfer learning performance versus health experts in disease diagnosis from medical imaging. IEEE Access 2020, 8, 139367–139386. [Google Scholar] [CrossRef]
- Malik, H.; Anees, T.; Din, M.; Naeem, A. CDC_Net: Multi-classification convolutional neural network model for detection of COVID-19, pneumothorax, pneumonia, lung Cancer, and tuberculosis using chest X-rays. Multimed. Tools Appl. 2023, 82, 13855–13880. [Google Scholar] [CrossRef]
- Khan, A.H.; Malik, H.; Khalil, W.; Hussain, S.K.; Anees, T.; Hussain, M. Spatial Correlation Module for Classification of Multi-Label Ocular Diseases Using Color Fundus Images. Comput. Mater. Contin. 2023, 76, 133–150. [Google Scholar] [CrossRef]
- Malik, H.; Anees, T. BDCNet: Multi-classification convolutional neural network model for classification of COVID-19, pneumonia, and lung cancer from chest radiographs. Multimed. Syst. 2022, 28, 815–829. [Google Scholar] [CrossRef]
- Hasnain, M.A.; Ali, S.; Malik, H.; Irfan, M.; Maqbool, M.S. Deep learning-based classification of dental disease using X-rays. J. Comput. Biomed. Inform. 2023, 5, 82–95. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Riaz, S.; Naeem, A.; Malik, H.; Naqvi, R.A.; Loh, W.K. Federated and Transfer Learning Methods for the Classification of Melanoma and Nonmelanoma Skin Cancers: A Prospective Study. Sensors 2023, 23, 8457. [Google Scholar] [CrossRef]
- Majidpour, J.; Rashid, T.A.; Thinakaran, R.; Batumalay, M.; Dewi, D.A.; Hassan, B.A.; Arabi, H. NSGA-II-DL: Metaheuristic optimal feature selection with Deep Learning Framework for HER2 classification in Breast Cancer. IEEE Access 2024, 12, 38885–38898. [Google Scholar]
- Cuevas, A.; Febrero, M.; Fraiman, R. An anova test for functional data. Comput. Stat. Data Anal. 2004, 47, 111–122. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Tukey’s honestly significant difference (HSD) test. Encycl. Res. Des. 2010, 3, 1–5. [Google Scholar]
- Hairani, H.; Anggrawan, A.; Priyanto, D. Improvement performance of the random forest method on unbalanced diabetes data classification using Smote-Tomek Link. JOIV Int. J. Inform. Vis. 2023, 7, 258–264. [Google Scholar] [CrossRef]
- Malik, H.; Anees, T. Deep Learning-based Classification of COVID-19 Variants and Lung Cancer Using CT Scans. J. Comput. Biomed. Inform. 2023, 6, 238–269. [Google Scholar]
- Bhati, A.; Gour, N.; Khanna, P.; Ojha, A. Discriminative kernel convolution network for multi-label ophthalmic disease detection on imbalanced fundus image dataset. Comput. Biol. Med. 2023, 153, 106519. [Google Scholar] [CrossRef]
- Xiao, Y.; Ding, X.; Liu, S.; Ma, Y.; Zhang, T.; Xiang, Z.; Zhou, X. Fusion-Attention Diagnosis Network (FADNet): An end-to-end framework for optic disc segmentation and ocular disease classification. Inf. Fusion 2025, 124, 103333. [Google Scholar] [CrossRef]
- Hanfi, R.; Mathur, H.; Shrivastava, R. Hybrid attention-based deep learning for multi-label ophthalmic disease detection on fundus images. Graefe’s Arch. Clin. Exp. Ophthalmol. 2025. Online ahead of print. [Google Scholar]
- Rani, A.A.; Karthikeyini, C.; Ravi, C.R. Eye Disease Prediction Using Deep Learning and Attention on Oct Scans. SN Comput. Sci. 2024, 5, 1065. [Google Scholar] [CrossRef]
- Pandey, P.U.; Ballios, B.G.; Christakis, P.G.; Kaplan, A.J.; Mathew, D.J.; Tone, S.O.; Wong, J.C. Ensemble of deep convolutional neural networks is more accurate and reliable than board-certified ophthalmologists at detecting multiple diseases in retinal fundus photographs. Br. J. Ophthalmol. 2024, 108, 417–423. [Google Scholar] [CrossRef] [PubMed]






| No. of Ocular Classes | Ocular Diseases | No. of CFIs |
|---|---|---|
| 0 | AMD | 273 |
| 1 | DR | 318 |
| 2 | MAC | 270 |
| 3 | NPDR | 368 |
| 4 | NOR | 576 |
| 5 | PDR | 404 |
| 6 | GLU | 363 |
| Total | 2572 | |
| No. of Ocular Classes | Ocular Diseases | No. of CFI |
|---|---|---|
| 0 | AMD | 576 |
| 1 | DR | 576 |
| 2 | MAC | 576 |
| 3 | NPDR | 576 |
| 4 | NOR | 576 |
| 5 | PDR | 576 |
| 6 | GLU | 576 |
| Total | 4032 | |
| Folds | AMD | DR | MAC | NPDR | NOR | PDR | GLU | Total |
|---|---|---|---|---|---|---|---|---|
| 1 | 144 | 144 | 144 | 144 | 144 | 144 | 144 | 1008 |
| 2 | 144 | 144 | 144 | 144 | 144 | 144 | 144 | 1008 |
| 3 | 144 | 144 | 144 | 144 | 144 | 144 | 144 | 1008 |
| 4 | 144 | 144 | 144 | 144 | 144 | 144 | 144 | 1008 |
| Total | 576 | 576 | 576 | 576 | 576 | 576 | 576 | 4032 |
| Layer Type | Output Shape | Parameters |
|---|---|---|
| Con_conv2d_(Conv2D) | (None, 146, 146, 16) | 1216 |
| MPL_average_pooling2d_(AveragePooling2D) | (None, 73, 73, 16) | 0 |
| Con_conv2d_1_(Conv2D) | (None, 69, 69, 32) | 12,832 |
| MPL_average_pooling2d_1_(AveragePooling2D) | (None, 34, 34, 32) | 0 |
| Con_conv2d_2_(Conv2D) | (None, 30, 30, 64) | 51,264 |
| MPL_average_pooling2d_2_(AveragePooling2D) | (None, 15, 15, 64) | 0 |
| Con_conv2d_3_(Conv2D) | (None, 11, 11, 128) | 204,928 |
| MPL_average_pooling2d_3_(AveragePooling2D) | (None, 5, 5, 128) | 0 |
| DO_dropout_(Dropout) | (None, 5, 5, 128) | 0 |
| FLT_flatten_(Flatten) | (None, 3200) | 0 |
| D_Dense_(Dense) | (None, 512) | 819,456 |
| DO_dropout_1_(Dropout) | (None, 512) | 0 |
| D_dense_1_(Dense) | (None, 7) | 1799 |
| Total params: | 1,091,495 | |
| Trainable params: | 1,091,495 | |
| Non-trainable params: | 0 | |
| Hyperparameters | Value |
|---|---|
| Learning rate | 0.00001 |
| Batch size | 32 |
| Momentum | 0.9 |
| No. of iterations | 30 epochs |
| Activation function | ReLU, SoftMax |
| Optimizer | RMSprop |
| Models | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) | AUC (%) |
|---|---|---|---|---|---|
| R5 | 73.33 | 79.23 | 66.13 | 74.19 | 96.66 |
| R6 | 85.14 | 88.66 | 83.02 | 84.94 | 98.57 |
| R1 | 83.42 | 86.58 | 79.41 | 83.18 | 98.46 |
| R4 | 79.46 | 82.74 | 75.46 | 78.91 | 98.17 |
| R2 | 80.80 | 83.77 | 75.73 | 81.04 | 97.85 |
| R3 | 73.13 | 80.39 | 64.36 | 73.05 | 96.04 |
| R7 | 83.15 | 84.63 | 81.01 | 82.32 | 98.12 |
| Proposed ODDM (Without SM-TOM) | 77.15 | 83.73 | 66.81 | 75.12 | 96.31 |
| Proposed ODDM (With SM-TOM) | 97.19 | 95.23 | 88.74 | 88.31 | 98.94 |
| Experiments | Proposed Model | SM-TOM | Image Size | Accuracy |
|---|---|---|---|---|
| 1 | ODDM | × | 150 × 150 × 3 | 77.15% |
| 2 | ODDM | ✓ | 150 × 150 × 3 | 97.19% |
| Test | F-Statistics | p-Value |
|---|---|---|
| ANOVA | 17.31 | 0.0021 |
| Comparison | Mean Difference | p-Value | Statistically Significant? |
|---|---|---|---|
| Proposed ODDM (With SM-TOM) vs. R1 | 6.96 | 0.005 | Yes |
| Proposed ODDM (With SM-TOM) vs. R2 | 8.18 | 0.004 | Yes |
| Proposed ODDM (With SM-TOM) vs. R3 | 12.02 | 0.003 | Yes |
| Proposed ODDM (With SM-TOM) vs. R4 | 8.85 | 0.042 | Yes |
| Proposed ODDM (With SM-TOM) vs. R5 | 11.92 | 0.003 | Yes |
| Proposed ODDM (With SM-TOM) vs. R6 | 6.01 | 0.001 | Yes |
| Proposed ODDM (With SM-TOM) vs. R7 | 7.02 | 0.002 | Yes |
| Ref | Year | Models | No. of ODs | Ocular Diseases | Accuracy |
|---|---|---|---|---|---|
| [78] | 2025 | CNN | GLU, DR, Hypertension, Myopia, and Cataract | 89.64% | |
| [94] | 2025 | Attention Module | 3 | Myopia, Normal, and Other Ocular Diseases | 90.40% |
| [95] | 2025 | Attention Module | 2 | Multiple Ophthalmology | 95.30% |
| [96] | 2024 | Attention with Inception-V3 | 4 | NOR, DME, CNV, and Drusen | 96.00% |
| [68] | 2024 | Deep-Net | 5 | DR, AMD, Hypertension, GLU, and Cataract | 74.62% |
| [97] | 2024 | CNN | 2 | GLU and Normal | 72.70% |
| [42] | 2022 | CBAM | 2 | DR and Normal | 95.00% |
| [81] | 2022 | TL | 2 | DR and Normal | 91.20% |
| [82] | 2021 | CNN | 2 | DR and Normal | 82.18% |
| [70] | 2023 | CNN | 2 | GLU and Normal | 92.50% |
| [93] | 2023 | CNN | 3 | DR, Cataract, and GLU | 93.14% |
| [73] | 2023 | CNN | 2 | GLU and Normal | 83.00% |
| Proposed ODDM with SM-TOM | 7 | DR, AMD, MAC, GLU, NPDR, PDR, and NOR | 97.19% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qureshi, A.D.A.; Malik, H.; Naeem, A.; Hassan, S.N.; Jeong, D.; Naqvi, R.A. ODDM: Integration of SMOTE Tomek with Deep Learning on Imbalanced Color Fundus Images for Classification of Several Ocular Diseases. J. Imaging 2025, 11, 278. https://doi.org/10.3390/jimaging11080278
Qureshi ADA, Malik H, Naeem A, Hassan SN, Jeong D, Naqvi RA. ODDM: Integration of SMOTE Tomek with Deep Learning on Imbalanced Color Fundus Images for Classification of Several Ocular Diseases. Journal of Imaging. 2025; 11(8):278. https://doi.org/10.3390/jimaging11080278
Chicago/Turabian StyleQureshi, Afraz Danish Ali, Hassaan Malik, Ahmad Naeem, Syeda Nida Hassan, Daesik Jeong, and Rizwan Ali Naqvi. 2025. "ODDM: Integration of SMOTE Tomek with Deep Learning on Imbalanced Color Fundus Images for Classification of Several Ocular Diseases" Journal of Imaging 11, no. 8: 278. https://doi.org/10.3390/jimaging11080278
APA StyleQureshi, A. D. A., Malik, H., Naeem, A., Hassan, S. N., Jeong, D., & Naqvi, R. A. (2025). ODDM: Integration of SMOTE Tomek with Deep Learning on Imbalanced Color Fundus Images for Classification of Several Ocular Diseases. Journal of Imaging, 11(8), 278. https://doi.org/10.3390/jimaging11080278










