1. Introduction
Hyperspectral imaging (HSI) collects information from a three-dimensional space. It has two spatial resolutions and one spectral resolution. Spectral resolutions indicate how many bands are present in the image. Precision agriculture relies heavily on the evaluation of soil nutrients, and precise nutrient analysis can maximize crop production and fertilizer use while reducing environmental impact. The current laboratory soil examination is costly and time-consuming. It will be reduced based on strategies like Visible and Near-Infrared (VNIR) Reflectance Spectroscopy with machine-learning methods. According to [
1], VNIR spectroscopy monitors soil reflectance across wavelengths, gathering information about soil characteristics such as pH value, electrical conductivity, organic carbon, nitrogen, potassium, and phosphorus. However, the spectral data acquired is frequently high-dimensional, resulting in duplicate information that might degrade the performance of ML models. This requires optimal band selection, a strategy for identifying important spectral bands for better nutrition prediction. Several optimization methods have been used for this purpose, including genetic methods (GA), particle swarm optimization (PSO), and, more recently, Battle Royale Optimization (BRO) [
2].
VNIR spectroscopy, which covers a wavelength range of 400 to 2500 nm, is extremely sensitive to soil components such as moisture, organic matter, and minerals. Numerous studies have demonstrated the effectiveness of VNIR in forecasting soil nutrients. The authors in [
3] demonstrated the use of VNIR to predict organic carbon and other essential soil parameters in diverse soil types, highlighting the promise of the method in rapid soil evaluation. Furthermore, the authors in [
4] used VNIR spectra to assess the organic carbon and clay content of the soil with high precision. Random Forest (RF), Support Vector Machines (SVM), and Artificial Neural Networks (ANN) have demonstrated great promise in improving soil-nutrient prediction based on VNIR spectral data. The author [
5] used RF and SVM in VNIR data to estimate soil organic carbon and nitrogen content with good precision compared to typical laboratory studies.
Despite the effectiveness of VNIR spectroscopy, the great complexity of the data presents problems [
6]. Band-selection strategies attempt to minimize dimensionality by finding the most informative spectral bands, which improves both the accuracy of soil-nutrient forecasts and the computational efficiency of machine-learning models. Traditional band-selection approaches include Principal Component Analysis (PCA), GA, and PSO [
7]. However, these strategies might occasionally result in poor selection due to their inability to balance exploration and exploitation within the search space. Recently, the Battle Royale Optimization (BRO) algorithm has developed as a robust metaheuristic approach for tackling optimization issues, such as band selection in high-dimensional data. BRO is modeled after Battle Royale games in which agents engage in an arena until only one remains, simulating the search for the global optimum [
8,
9]. SVM with VNIR spectral data to forecast organic carbon, nitrogen, and other nutrients in the soil with good accuracy. The use of band-selection approaches, such as those provided by BRO, in these machine-learning models has been proven to greatly increase prediction accuracy [
10]. The competitiveness of BRO enables effective exploration of the search space, making it especially suitable in difficult applications like band selection for VNIR spectroscopy. BRO enhances band selection for VNIR-based soil-nutrient prediction by iteratively choosing bands that deliver the most information to ML models. BRO algorithm to optimize band selection for nitrogen and phosphorus prediction from VNIR data, and their findings surpassed established optimization approaches such as GA and PSO in terms of precision and computation time [
11,
12].
The authors in [
13] investigated the performance of GA, PSO, and BRO in optimizing band selection for soil-nutrient prediction. They discovered that BRO improved prediction accuracy while also drastically reducing the computing time required for model training [
14]. The author [
15] demonstrated that BRO-based band selection combined with ANN outperformed previous optimization techniques to forecast soil nutrients such as potassium and nitrogen. Several comparison studies have demonstrated the superiority of BRO over traditional optimization approaches.
Despite the positive findings of employing BRO for band selection in VNIR-based soil-nutrient prediction, some obstacles still exist. The integration of several machine-learning techniques with BRO may require more studies to achieve model stability and generalizability [
16]. Furthermore, the author used emphasized the need for standardized data sets and benchmarking frameworks for a fair comparison of various optimization techniques [
17]. Furthermore, as VNIR technology and sensor resolution advance, controlling the growing dimensionality of spectral data will become more difficult. BRO and other metaheuristic optimization approaches will need to be modified to deal with the increasing complexity of the data. The following contributions to our proposed work are:
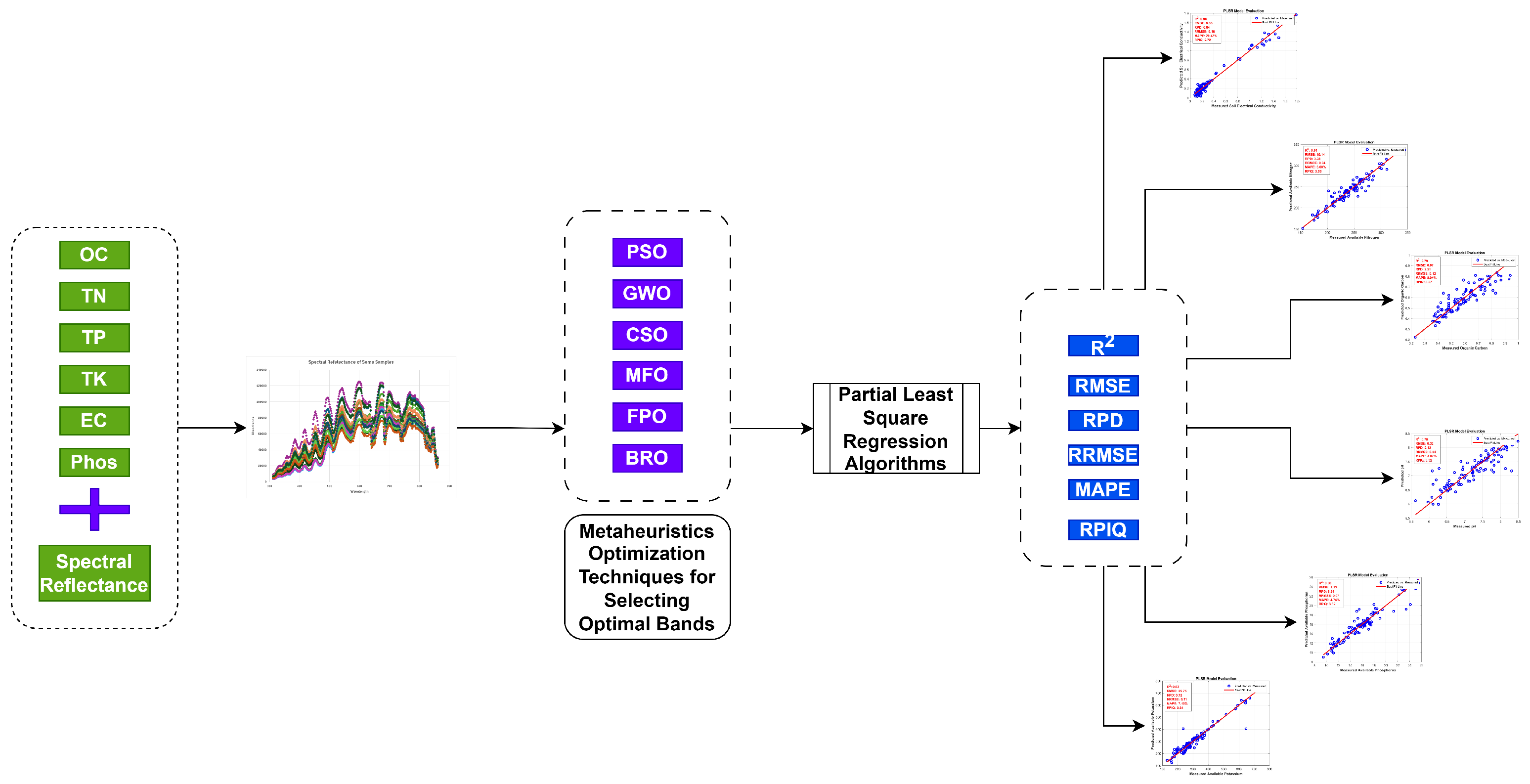
The integration of hyperspectral spectroradiometer data and machine-learning algorithms for soil-nutrient analysis.
The use of spectral reflectance to enhance correlations with soil-nutrient properties.
The application of metaheuristic optimization techniques for selecting relevant bands in hyperspectral data from spectroradiometers.
Estimation of soil-nutrient content using the Battle Royale Optimization (BRO) and Partial Least Squares Regression (PLSR)-based machine-learning algorithms.
3. Results and Discussion
Hyperspectral imaging captures detailed reflectance information across numerous narrow spectral bands, allowing for precise analysis of soil properties based on their spectral signatures. Each Equations (
19)–(
22), combines an intercept with weighted reflectance values at particular wavelengths, where the coefficients represent the influence of each wavelength on the OC estimation. A positive coefficient indicates that a higher reflectance at that wavelength correlates with a higher organic carbon content, while a negative coefficient suggests an inverse relationship. In organic carbon, the mean value is 0.5812 with a standard deviation (SD) of 0.1485, and the coefficient of variation (CV) is 25.55%, which is a moderate variability in these soil-nutrient content. In terms of ED, the mean is 0.386, and the mean is lower at 0.2. The SD is 0.4154, and the CV is 10.76%, suggesting relatively low variability in ED. The phosphorus shows a mean value of 16.11, a median of 16.05, an SD of 3.6511, and a CV of 22.66%, indicating moderate variability in the phosphorus content. AK has the highest variability with a mean of 318.65, a median of 282, a high SD of 122.0962, and a CV of 41.77%, indicating a large spread in potassium levels. The mean nitrogen level is 240.78, close to the median of 239.5, with an SD of 34.2524 and a CV of 14.23%, showing moderate variability. The pH values are relatively stable, with a mean of 7.2604, a median of 7.31, an SD of 0.6727, and the lowest CV of 9.2%, indicating minimal variation. Based on BRO optimization algorithms, we derived the equations for calculating all soil-nutrient content based on low, medium, and high values, which are shown in
Table 2.
Hyperspectral imaging allows for a detailed assessment of soil properties, and these Equations (
15)–(
18) use selected wavelengths to estimate pH, with the coefficients indicating the influence of each wavelength on the prediction of pH. Full-level pH uses wavelengths at 458.43 nm, 764.82 nm, and 880.92 nm. The positive coefficient for 458.43 nm suggests that higher reflectance at this wavelength is associated with an increase in soil pH. In contrast, the negative coefficient for 764.82 nm indicates that the increase in reflectance at this wavelength slightly decreases the predicted pH. The coefficient for 880.92 nm is very small and shows a minimal positive influence on the pH value. Low-level pH uses wavelengths at 535.22 nm, 556.28 nm, and 453.47 nm, all with negative coefficients. This suggests that a higher reflectance in these wavelengths correlates with a decrease in soil pH at lower levels, indicating more acidic soil. The substantial negative coefficient for 535.22 nm implies a significant inverse relationship with pH, whereas the smaller negative values for 556.28 nm and 453.47 nm show less but still notable influence. The medium-level pH involves wavelengths at 411.62 nm, 871.87 nm, and 883.93 nm. The positive coefficients for all three wavelengths suggest that as the reflectance at these wavelengths increases, so does the predicted pH. This indicates that a higher reflectance correlates with more alkaline soil at medium pH levels. High-level pH uses wavelengths at 949.86 nm, 814.15 nm, and 877.91 nm.
Figure 3 describes the evaluations of the PLSR model to predict soil nutrients in four different pH categories:
Figure 3a: full levels,
Figure 3b: low levels,
Figure 3c: medium levels, and
Figure 3d: high levels. Performance metrics were analyzed based on all subplots for comparison, including
, RMSE, RPD, MAPE, and RPIQ. The full strength of PH shows a very low
of 0.13, the predictive power for the week level, and an RMSE of 0.08, showing a reasonable error rate. RPD and MAPE show that the model does not perform well compared to all the levels. For low pH levels,
improves by a certain amount to 0.52, showing moderate predictive power. RMSE (0.15) is lower than in full levels, but RPD of 1.48 and MAPE of 1.59%, indicating better accuracy and model performance for this subset. The model’s
remains relatively low at 0.35, indicating a poor fit. RMSE (0.04) is smaller, suggesting less error in prediction, but RPD (1.16) and MAPE (3.23%) still point to a modest model performance in the medium pH range. The model shows the best fit at high pH levels, with an
R2 of 0.45 and a low RMSE of 0.17, demonstrating an improvement in predictive accuracy. The RPD (1.36) and MAPE (1.75%) suggest that the model is fairly accurate for higher pH values and performs better than in other subsets. In summary, the model performs poorly for the full pH range (a) but shows moderate improvements for (b) low and (d) high pH levels. The medium pH range (c) has a performance similar to that of the full pH range, with minimal improvement.
Full-level OC uses wavelengths at 411.62 nm, 772.57 nm, and 811.09 nm. The negative coefficients for 411.62 and 772.57 nm imply that increased reflectance at these wavelengths is associated with a lower OC content. In contrast, the positive coefficient for 811.09 nm indicates a direct correlation with OC levels. Low-level OC incorporates wavelengths at 771.02 nm, 456.78 nm, and 755.48 nm. The large negative coefficient for 771.02 nm suggests a strong inverse relationship with OC at low levels. The near-zero coefficients for 456.78 nm and 755.48 nm imply a minimal impact on the OC estimation at these wavelengths. Medium-level OC involves wavelengths at 771.02 nm, 714.75 nm, and 937.91 nm. The positive coefficient for 771.02 nm and negative coefficients for 714.75 nm and 937.91 nm indicate that reflectance at these wavelengths affects the OC content differently, highlighting the complexity of medium-level OC estimation. High-level OC uses wavelengths at 551.43 nm, 601.49 nm, and 896.96 nm, all with negative coefficients.
Figure 4 describes predictions for organic carbon (OC) across four levels.
Figure 4a: Full levels has an
R2 of 0.87 and an RMSEP of 0.15, reflecting strong prediction accuracy with minimal error. However, in
Figure 4b: low levels, the
R2 drops to 0.81, and RMSEP increases to 0.19, suggesting a slight decrease in accuracy, with the data points more spread out from the regression line.
Figure 4c: Medium levels show similar performance with an
R2 of 0.79 and an RMSEP of 0.21, indicating continued moderate prediction accuracy. Finally,
Figure 4d: high levels sees an
R2 of 0.74 and an RMSEP of 0.25, reflecting the poorest performance with the most scattered points and highest prediction errors.
Phosphorus is a crucial soil nutrient, and these equations help predict its availability based on the reflectance characteristics of soil at specific spectral bands. Full-level AP uses wavelengths at 771.02 nm, 915.46 nm, and 933.42 nm. Equation (
23) has a base value of 18.831, which represents the starting estimate of the phosphorus content. In Equation (
24), low-level AP uses wavelengths at 468.32 nm, 812.62 nm, and 565.99 nm. The intercept (11.16) represents the base phosphorus content for low levels. Equation (
25) medium-level AP incorporates wavelengths at 698.96 nm, 933.42 nm, and 849.19 nm. Equation (
26) High-level AP uses wavelengths at 501.07, 418.39, and 430.17 nm.
Figure 5 describes the predictions for AP at four different levels. For
Figure 5a: Full levels, the model achieves an
R2 of 0.85 and an RMSEP of 2.45, indicating solid predictive performance. As we move to
Figure 5b low levels,
decreases to 0.78, and RMSEP increases to 2.89, showing a slight reduction in accuracy with a wider spread of data points. In
Figure 5c medium levels, the
R2 further decreases to 0.75 with an RMSEP of 3.12, reflecting a further decline in model performance. Lastly,
Figure 5d: High levels show the lowest
of 0.70 and an RMSEP of 3.54, where the data points exhibit the largest deviation from the regression line. This progression highlights that the model’s predictive power for AP decreases as the levels move from full to high, with notable inaccuracies at higher levels.
Nitrogen is a critical soil nutrient that influences plant growth, and these equations use spectral information to predict nitrogen availability, enabling efficient, noninvasive soil analysis. In Equation (
27), full-level AN is estimated using wavelengths at 499.44 nm, 761.71 nm, and 849.19 nm. This suggests that these wavelengths are inversely related to nitrogen availability when levels are low, as shown in Equation (
28). Medium-level AN is predicted using wavelengths at 411.62 nm, 772.57 nm, and 811.09 nm. The intercept is 271.02, representing the base nitrogen content for medium-level soils. All coefficients for these wavelengths are negative, indicating that higher reflectance values at these specific wavelengths reduce nitrogen content in soil at medium levels, as shown in Equation (
29).
For AN,
Figure 6a: full levels show an
of 0.82 and an RMSEP of 3.31, demonstrating good prediction accuracy across the entire dataset.
Figure 6b: Low levels has an
R2 of 0.76 and an RMSEP of 3.77, showing a moderate decrease in performance, as demonstrated by the increased data spread around the regression line. In
Figure 6c: medium levels, the model performs similarly to low levels, with an
R2 of 0.75 and an RMSEP of 3.84. The general trend indicates that the model performance is consistent in the low and medium levels but slightly less accurate compared to the full levels, as the data become more scattered at these levels, which is shown in
Figure 6.
Potassium is an essential nutrient for plant growth, and these equations predict its availability based on the spectral reflectance of the soil at selected wavelengths. Full-level AK is predicted using wavelengths at 771.02 nm, 774.12 nm, and 882.43 nm. The equation starts with a base potassium value of 175.47 as shown in Equation (
30). All the coefficients for these wavelengths are negative, meaning that the increase in reflectance at these wavelengths is associated with a decrease in potassium content. This suggests that at full potassium levels, higher reflectance in these spectral bands correlates with lower available potassium in the soil. In Equation (
31), medium-level AK is estimated using wavelengths at 777.22 nm, 858.28 nm, and 852.22 nm. However, the positive coefficient for 936.41 nm suggests that a higher reflectance at this wavelength leads to an increase in the available potassium at high levels, as shown in Equation (
32).
This
Figure 7 compares the predicted versus measured values of AK at three different levels: full, medium, and high. In
Figure 7a: full levels, the model shows an
R2 of 0.83 and an RMSEP (Root Mean Square Error of Prediction) of 3.26, indicating a good fit where the predicted values align closely with the measured data. In
Figure 7b: medium levels,
slightly drops to 0.78 with an RMSEP of 3.89, reflecting a moderate decrease in model accuracy, as seen by the slight increase in the scatter around the regression line. For
Figure 7c: high levels, the model performs worse with an
R2 of 0.71 and an RMSEP of 4.12, showing a larger spread of points around the regression line.
Equation (
33) provided an estimate of the EC of the soil at full levels using hyperspectral reflectance data from specific wavelengths. EC is a key measure of the capacity of the soil to conduct electrical current, which is closely related to the concentration of dissolved salts in the soil and serves as an indicator of soil salinity and fertility. The equation starts with a base EC value of 0.5953, which represents the foundational level of conductivity. The positive coefficient for the wavelength of 772.57 nm indicates that a higher reflectance at this wavelength is associated with an increase in soil conductivity. This suggests that in this specific spectral band, soil reflectance is positively correlated with higher concentrations of salts or other conductive materials.
This
Figure 8 contains a single plot of soil nutrients in EC, where the model demonstrates an
R2 of 0.91 and an RMSEP of 0.17. The tight clustering of points along the regression line suggests that the model is very accurate in predicting EC values. High
and low RMSEP show strong predictive performance with minimal errors.
The available potassium levels in the soil are evaluated as full, high, and medium availability. For example, the BRO algorithm performed best for full potassium with an
of 0.31, an RMSE of 110.23, and an RPD of 1.21. In high potassium availability, BRO again outperformed others with an
R2 of 0.35, RMSE of 104.73, and RPD of 1.25. For medium potassium, BRO had an
R2 of 0.26, RMSE of 33.22, and RPD of 1.17, indicating moderate precision, which is shown in
Table 3,
Table 4 and
Table 5.
Nitrogen availability is divided into full, low, and medium levels. For full nitrogen, BRO demonstrated better accuracy with an
R2 of 0.16 and an RMSE of 31.33. In low nitrogen, the BRO algorithm also outperformed others with
R2 = 0.14 and RMSE = 19.32. Similarly, for medium nitrogen, BRO showed the highest
R2 value of 0.21 and RMSE of 19.53, making it the most suitable algorithm for this nutrient as well in
Table 6,
Table 7 and
Table 8.
The availability of phosphorus is classified as full, high, low, and medium. The BRO algorithm consistently achieved the highest
values in all categories, notably performing well in high phosphorus with
= 0.71 and RMSE = 0.61. For low phosphorus, BRO had an
R2 of 0.68, RMSE of 0.29, and a high RPIQ of 1.57, which indicates high prediction precision in
Table 9,
Table 10,
Table 11 and
Table 12.
For electrical conductivity, the BRO algorithm achieved the best performance in the full category with an
R2 of 0.32 and an RMSE of 0.34, as shown in
Table 13. In
Table 14,
Table 15 and
Table 16 organic carbon in the soil is assessed in the full, high, low, and medium categories. For full OC, the BRO algorithm again performed better with an
of 0.12 and RMSE of 0.14. In the high availability of OC, BRO had a very strong
R2 value of 0.48 and a low RMSE of 0.04. For low OC, BRO maintained its high precision with
= 0.43 and RMSE = 0.04. In the medium OC case, BRO delivered an
R2 of 0.35 and an RMSE of 0.06, making it consistently superior across the OC levels.
The soil pH is analyzed with full, high, low, and medium availability. BRO consistently showed high accuracy, with the highest
values in all categories. In particular, for high pH, BRO achieved an
R2 of 0.45 and an RMSE of 0.17, making it the top performer for this soil property, as shown in
Table 17,
Table 18,
Table 19 and
Table 20.
Figure 9 provides a comparative analysis of different regression techniques (BFO, CGO, IFO, GWO, WFO and PSO) for five parameters:
Figure 9a: organic carbon (OC),
Figure 9b: available nitrogen (AN),
Figure 9c: available potassium (AK),
Figure 9d: Soil pH, and
Figure 9e available phosphorus (AP), based on their
values. For OC
Figure 9a, BFO demonstrates the highest performance with a median
close to 0.8, while other techniques, such as PSO, show lower medians, around 0.3. In AN
Figure 9b, BFO again performs well with a median
of approximately 0.65, while PSO shows a lower performance, with a median of around 0.3. For AK
Figure 9c, BFO maintains the highest median
near 0.6, while PSO lags with a median closer to 0.3. In terms of soil pH
Figure 9d, BFO shows a strong performance with a median
around 0.6, and PSO continues to underperform, with a median of around 0.2. Finally, for AP
Figure 9e, BFO and CGO have similar medians close to 0.7, while PSO displays the lowest median
, below 0.3. Overall, BFO consistently outperforms other techniques in all parameters, while PSO shows the weakest performance.