Dual-Attention-Based Block Matching for Dynamic Point Cloud Compression
Abstract
1. Introduction
- (1)
- We propose a multi-scale, end-to-end DPC compression framework, which jointly optimizes MC/ME, motion compression, and residual compression.
- (2)
- The proposed hierarchical point cloud ME/MC scheme is a multi-scale inter-prediction scheme, which predicts motion vectors at different scales and improves inter-frame prediction accuracy.
- (3)
- The designed dual-attention-based KNN block matching (DA-KBM) network efficiently measures feature correlation between points in adjacent frames. It strengthens the predicted motion flow and further improves the inter-prediction efficiency.
2. Related Works
2.1. Rule-Based Point Cloud Compression
2.1.1. 2D-Projection-Based Methods
2.1.2. 3D-Based Methods
2.2. Learning-Based Point Cloud Compression
2.2.1. Voxelization-Based Methods
2.2.2. Octree-Based Methods
2.2.3. Point-Based Methods
2.2.4. Sparse Tensors-Based Methods
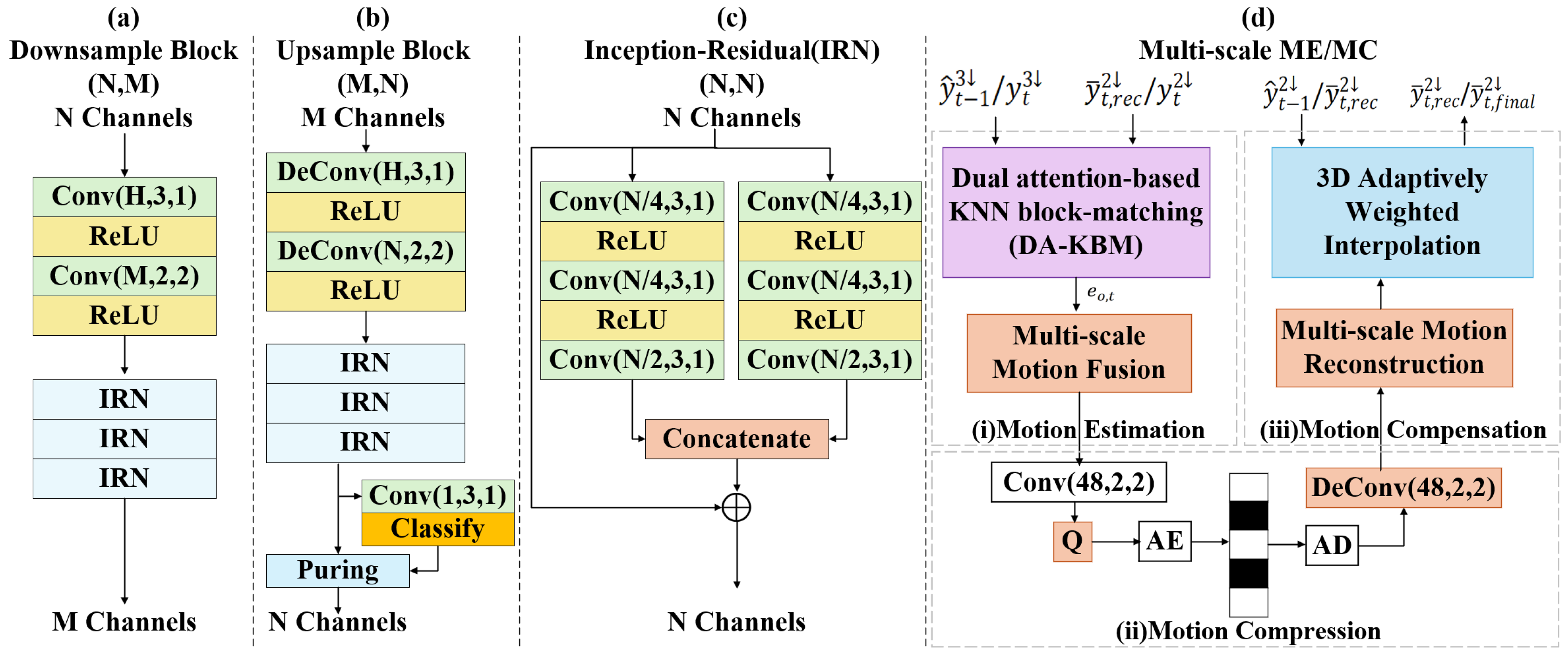
3. Proposed Method
3.1. Overview of Proposed DPCs Compression Network
3.2. Feature Extraction Module
3.3. Multi-Resolution-Based Inter-Prediction
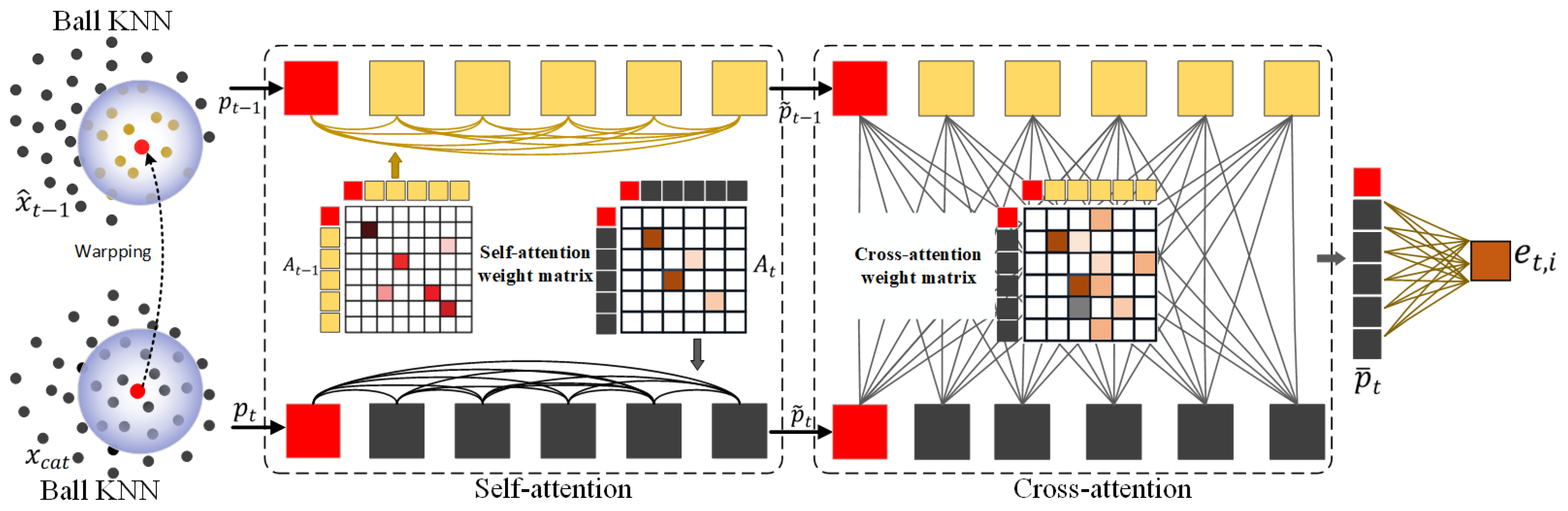
3.3.1. Dual Attention-Based KNN Block Matching (DA-KBM)
3.3.2. Motion Compensation Module
3.4. Residual Compression Module
3.5. Point Cloud Reconstruction Module
3.6. Loss Function
4. Experiments
4.1. Datasets
4.2. Training Details
4.3. Baseline Settings
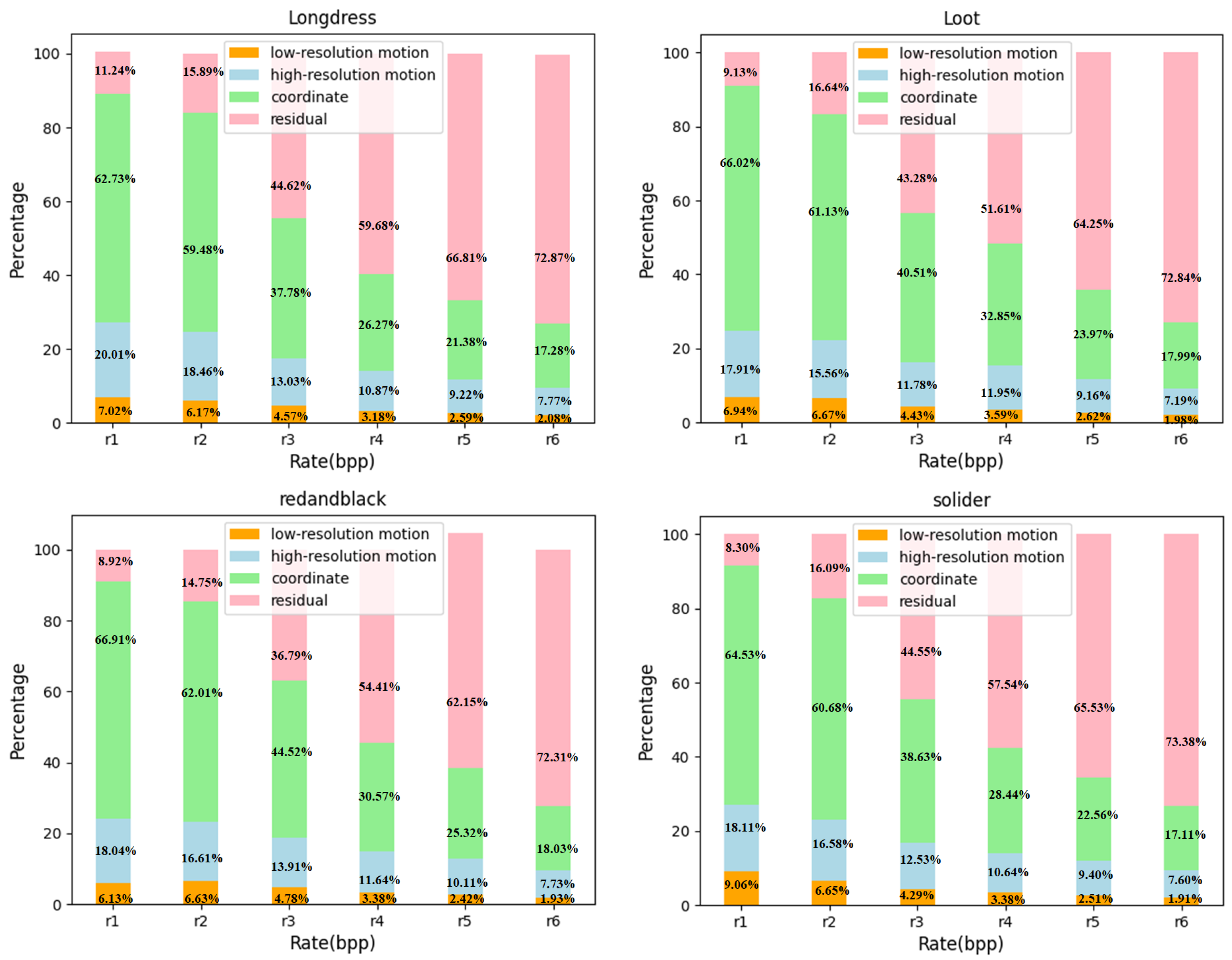
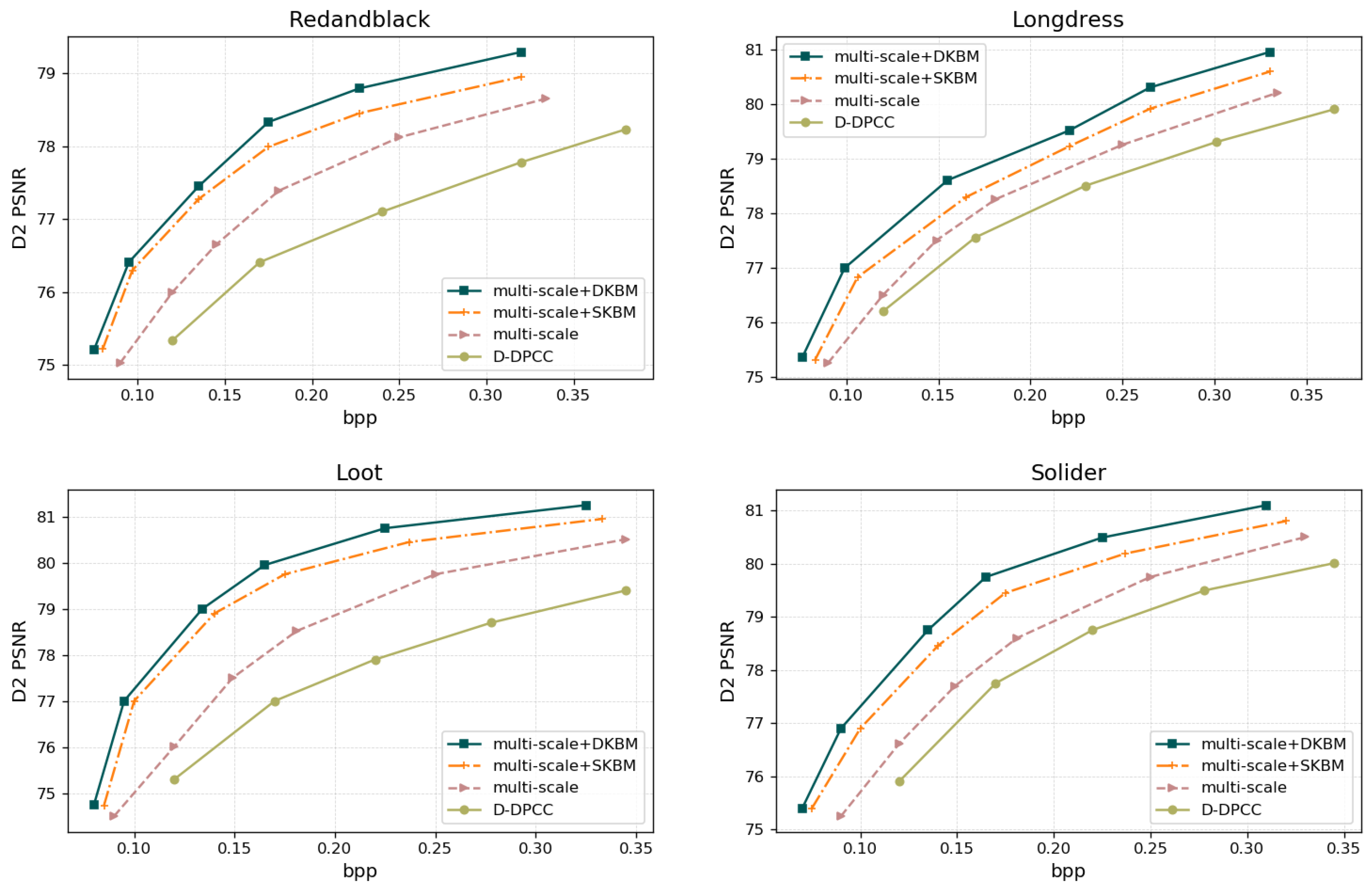
4.4. Experimental Results
4.5. Ablation Study
4.6. Model Complexity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Silva, A.L.; Oliveira, P.; Durães, D.; Fernandes, D.; Névoa, R.; Monteiro, J.; Melo-Pinto, P.; Machado, J.; Novais, P. A framework for representing, building and reusing novel state-of-the-art three-dimensional object detection models in point clouds targeting self-driving applications. Sensors 2023, 23, 6427. [Google Scholar] [CrossRef]
- Ryalat, M.; Almtireen, N.; Elmoaqet, H.; Almohammedi, M. The Integration of Two Smarts in the Era of Industry 4.0: Smart Factory and Smart City. In Proceedings of the 2024 IEEE Smart Cities Futures Summit (SCFC), Marrakech, Morocco, 29–31 May 2024; pp. 9–12. [Google Scholar]
- Hanif, S. The Aspects of Authenticity in the Digitalization of Cultural Heritage: A Drifting Paradigm. In Proceedings of the 2023 International Conference on Sustaining Heritage: Innovative and Digital Approaches (ICSH), Sakhir, Bahrain, 18–19 June 2023; pp. 39–44. [Google Scholar]
- Wang, K.; Sheng, L.; Gu, S.; Xu, D. VPU: A Video-Based Point Cloud Upsampling Framework. IEEE Trans. Image Process. 2022, 31, 4062–4075. [Google Scholar] [CrossRef]
- Li, Z.; Li, G.; Li, T.H.; Liu, S.; Gao, W. Semantic Point Cloud Upsampling. IEEE Trans. Multimed. 2023, 25, 3432–3442. [Google Scholar] [CrossRef]
- Akhtar, A.; Li, Z.; Auwera, G.V.d.; Li, L.; Chen, J. PU-Dense: Sparse Tensor-Based Point Cloud Geometry Upsampling. IEEE Trans. Image Process. 2022, 31, 4133–4148. [Google Scholar] [CrossRef] [PubMed]
- Sangaiah, A.K.; Anandakrishnan, J.; Kumar, S.; Bian, G.-B.; AlQahtani, S.A.; Draheim, D. Point-KAN: Leveraging Trustworthy AI for Reliable 3D Point Cloud Completion With Kolmogorov Arnold Networks for 6G-IoT Applications. IEEE Internet Things J. 2025. [Google Scholar] [CrossRef]
- Yu, X.; Rao, Y.; Wang, Z.; Lu, J.; Zhou, J. AdaPoinTr: Diverse Point Cloud Completion With Adaptive Geometry-Aware Transformers. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 14114–14130. [Google Scholar] [CrossRef]
- Xiao, H.; Xu, H.; Li, Y.; Kang, W. Multi-Dimensional Graph Interactional Network for Progressive Point Cloud Completion. IEEE Trans. Instrum. Meas. 2023, 72, 2501512. [Google Scholar] [CrossRef]
- He, L.; Zhu, W.; Xu, Y. Best-effort projection based attribute compression for 3D point cloud. In Proceedings of the 23rd Asia-Pacific Conference on Communications, Perth, WA, Australia, 11–13 December 2017; pp. 1–6. [Google Scholar]
- Zhu, W.; Ma, Z.; Xu, Y.; Li, L.; Li, Z. View-Dependent Dynamic Point Cloud Compression. IEEE Trans. Circuits Syst. Video Technol. 2021, 31, 765–781. [Google Scholar] [CrossRef]
- Schwarz, S.; Preda, M.; Baroncini, V.; Budagavi, M.; Cesar, P.; Chou, P.A.; Cohen, R.A.; Krivokuća, M.; Lasserre, S.; Li, Z.; et al. Emerging mpeg standards for point cloud compression. IEEE J. Emerg. Sel. Top. Circuits Syst. 2018, 9, 133–148. [Google Scholar] [CrossRef]
- de Queiroz, R.L.; Chou, P.A. Motion-Compensated Compression of Dynamic Voxelized Point Clouds. IEEE Trans. Image Process. 2017, 26, 3886–3895. [Google Scholar] [CrossRef]
- Hong, H.; Pavez, E.; Ortega, A.; Watanabe, R.; Nonaka, K. Fractional Motion Estimation for Point Cloud Compression. In Proceedings of the 2022 Data Compression Conference (DCC), Snowbird, UT, USA, 22–25 March 2022; pp. 369–378. [Google Scholar]
- Connor, M.; Kumar, P. Fast construction of k-nearest neighbor graphs for point clouds. IEEE Trans. Vis. Comput. Graph. 2010, 16, 599–608. [Google Scholar] [CrossRef]
- Mekuria, R.; Blom, K.; Cesar, P. Design, Implementation, and Evaluation of a Point Cloud Codec for Tele-Immersive Video. IEEE Trans. Circuits Syst. Video Technol. 2017, 27, 828–842. [Google Scholar] [CrossRef]
- Santos, C.; Gonçalves, M.; Corrêa, G.; Porto, M. Block-Based Inter-Frame Prediction for Dynamic Point Cloud Compression. In Proceedings of the 2021 IEEE International Conference on Image Processing (ICIP), Anchorage, AK, USA, 19–22 September 2021; pp. 3388–3392. [Google Scholar]
- Gao, L.; Fan, T.; Wan, J.; Xu, Y.; Sun, J.; Ma, Z. Point Cloud Geometry Compression Via Neural Graph Sampling. In Proceedings of the 2021 IEEE International Conference on Image Processing (ICIP), Anchorage, AK, USA, 19–22 September 2021; pp. 3373–3377. [Google Scholar]
- Huang, T.; Liu, Y. 3D Point Cloud Geometry Compression on Deep Learning. In Proceedings of the 27th ACM Internation Conference on Multimedia (MM), Nice, France, 21–25 October 2019; pp. 890–898. [Google Scholar]
- Pang, J.; Lodhi, M.A.; Tian, D. GRASP-Net: Geometric Residual Analysis and Synthesis for Point Cloud Compression. In Proceedings of the 1st International Workshop on Advances in Point Cloud Compression, Lisboa, Portugal, 14 October 2022; pp. 11–19. [Google Scholar]
- Guarda, A.F.R.; Rodrigues, N.M.M.; Pereira, F. Adaptive Deep Learning-Based Point Cloud Geometry Coding. IEEE J. Sel. Top. Signal Process. 2021, 15, 415–430. [Google Scholar] [CrossRef]
- Wang, J.; Ding, D.; Li, Z.; Ma, Z. Multiscale Point Cloud Geometry Compression. In Proceedings of the 2021 Data Compression Conference (DCC), Snowbird, UT, USA, 23–26 March 2021; pp. 73–82. [Google Scholar]
- Wang, J.; Zhu, H.; Liu, H.; Ma, Z. Lossy Point Cloud Geometry Compression via End-to-End Learning. IEEE Trans. Circuits Syst. Video Technol. 2021, 31, 4909–4923. [Google Scholar] [CrossRef]
- Huang, L.; Wang, S.; Wong, K.; Liu, J.; Urtasun, R. OctSqueeze: Octree-Structured Entropy Model for LiDAR Compression. In Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 13–19 June 2020; pp. 1310–1320. [Google Scholar]
- Biswas, S.; Liu, J.; Wong, K.; Wang, S.; Urtasun, R. MuSCLE: Multi Sweep Compression of LiDAR using Deep Entropy Models. Adv. Neural Inf. Process. Syst. 2020, 33, 22170–22181. [Google Scholar]
- Que, Z.; Lu, G.; Xu, D. VoxelContext-Net: An Octree based Framework for Point Cloud Compression. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 6038–6047. [Google Scholar]
- Fu, C.; Li, G.; Song, R.; Gao, W.; Liu, S. OctAttention: Octree-Based Large-Scale Contexts Model for Point Cloud Compression. In Proceedings of the Conference on Artificial Intelligence(AAAI), Virtual, 22 February–1 March 2022; Volume 36, pp. 625–633. [Google Scholar]
- Akhtar, A.; Li, Z.; der Auwera, G.V. Inter-Frame Compression for Dynamic Point Cloud Geometry Coding. IEEE Trans. Image Process. 2024, 33, 584–594. [Google Scholar] [CrossRef]
- Fan, T.; Gao, L.; Xu, Y.; Li, Z.; Wang, D. D-DPCC: Deep Dynamic Point Cloud Compression via 3D Motion Prediction. In Proceedings of the 31st International Joint Conference on Artificial Intelligence (IJCAI-22), Vienna, Austria, 23–29 July 2022; pp. 898–904. [Google Scholar]
- Xia, S.; Fan, T.; Xu, Y.; Hwang, J.-N.; Li, Z. Learning Dynamic Point Cloud Compression via Hierarchical Inter-frame Block Matching. arXiv 2023, arXiv:2305.05356. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Cui, T.; Fang, Z. Occupancy Map-Based Low-Complexity Motion Prediction for Video-Based Point Cloud Compression. J. Vis. Commun. Image Represent. 2024, 100, 104110. [Google Scholar] [CrossRef]
- Wang, W.; Ding, G.; Ding, D. Leveraging Occupancy Map to Accelerate Video-Based Point Cloud Compression. J. Vis. Commun. Image Represent. 2024, 104, 104292. [Google Scholar] [CrossRef]
- Garcia, D.C.; de Queiroz, R.L. Intra-Frame Context-Based Octree Coding for Point-Cloud Geometry. In Proceedings of the 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 1807–1811. [Google Scholar]
- Thanou, D.; Chou, P.A.; Frossard, P. Graph-Based Compression of Dynamic 3D Point Cloud Sequences. IEEE Trans. Image Process. 2016, 25, 1765–1778. [Google Scholar] [CrossRef]
- Quach, M.; Valenzise, G.; Dufaux, F. Learning Convolutional Transforms for Lossy Point Cloud Geometry Compression. In Proceedings of the 2019 IEEE International Conference on Image Processing (ICIP), Taipei, Taiwan, 22–25 September 2019; pp. 4320–4324. [Google Scholar]
- Quach, M.; Valenzise, G.; Dufaux, F. Improved Deep Point Cloud Geometry Compression. In Proceedings of the 2020 IEEE 22nd International Workshop on Multimedia Signal Processing (MMSP), Tampere, Finland, 21–24 September 2020; pp. 1–6. [Google Scholar]
- Sun, C.; Yuan, H.; Mao, X.; Lu, X.; Hamzaoui, R. Enhancing Octree-Based Context Models for Point Cloud Geometry Compression With Attention-Based Child Node Number Prediction. IEEE Signal Process. Lett. 2024, 31, 1835–1839. [Google Scholar] [CrossRef]
- Fan, T.; Gao, L.; Xu, Y.; Wang, D.; Li, Z. Multiscale Latent-Guided Entropy Model for LiDAR Point Cloud Compression. IEEE Trans. Circuits Syst. Video Technol. 2023, 33, 7857–7869. [Google Scholar] [CrossRef]
- Song, R.; Fu, C.; Liu, S.; Li, G. Efficient Hierarchical Entropy Model for Learned Point Cloud Compression. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 14368–14377. [Google Scholar]
- Lodhi, M.A.; Pang, J.; Tian, D. Sparse Convolution Based Octree Feature Propagation for Lidar Point Cloud Compression. In Proceedings of the 2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Rhodes Island, Greece, 4–10 June 2023; pp. 1–5. [Google Scholar]
- Qi, C.R.; Su, H.; Mo, K.; Guibas, L.J. PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition(CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 652–660. [Google Scholar]
- Qi, C.R.; Yi, L.; Su, H.; Guibas, L.J. PointNet++: Deep hierarchical feature learning on point sets in a metric space. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5099–5108. [Google Scholar]
- You, K.; Gao, P. Patch-based deep autoencoder for point cloud geometry compression. In Proceedings of the ACM International Conference on Multimedia Asia (MMAsia ’21), Gold Coast, Australia, 1–3 December 2021; pp. 1–7. [Google Scholar]
- Xie, L.; Gao, W.; Fan, S.; Yao, Z. PDNet: Parallel Dual-branch Network for Point Cloud Geometry Compression and Analysis. In Proceedings of the 2024 Data Compression Conference (DCC), Snowbird, UT, USA, 19–22 March 2024; p. 596. [Google Scholar]
- Zhou, Y.; Zhang, X.; Ma, X.; Xu, Y.; Zhang, K.; Zhang, L. Dynamic point cloud compression with spatio-temporal transformer-style modeling. In Proceedings of the 2024 Data Compression Conference (DCC), Snowbird, UT, USA, 19–22 March 2024; pp. 53–62. [Google Scholar]
- Choy, C.; Gwak, J.; Savarese, S. 4D Spatio-Temporal ConvNets: Minkowski Convolutional Neural Networks. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 3070–3079. [Google Scholar]
- Ballé, J.; Laparra, V.; Simoncelli, E.P. End-to-End Optimized Image Compression. In Proceedings of the 5th International Conference on Learning Representations (ICLR 2017), Toulon, France, 24–26 April 2017. [Google Scholar]
- Cao, K.; Xu, Y.; Lu, Y.; Wen, Z. Owlii Dynamic Human Mesh Sequence Dataset. In Proceedings of the 122nd MPEG Meeting, Ljubljana, Slovenia, 16–20 July 2018. ISO/IEC JTC1/SC29/WG11 Doc.m42816. [Google Scholar]
- d’Eon, E.; Harrison, B.; Myers, T.; Chou, P.A. 8i Voxelized Full Bodies—A Voxelized Point Cloud Dataset; ISO/IEC JTC1/SC29 Joint WG11/WG1 (MPEG/JPEG) Input Document WG11M40059/WG1M74006; ISO: Geneva, Switzerland, 2017. [Google Scholar]
- Mammou, K.; Chou, P.A.; Flynn, D.; Krivokuca, M. PCC Test Model Category 13 v2; ISO/IEC JTC1/SC29/WG11 MPEG Output Document N17762; ISO: Ljubljana, Slovenia, 2018. [Google Scholar]
- Bernardini, F.; Mittleman, J.; Rushmeier, H.; Silva, C.; Taubin, G. The ball-pivoting algorithm for surface reconstruction. IEEE Trans. Vis. Comput. Graph. 1999, 5, 349–359. [Google Scholar] [CrossRef]



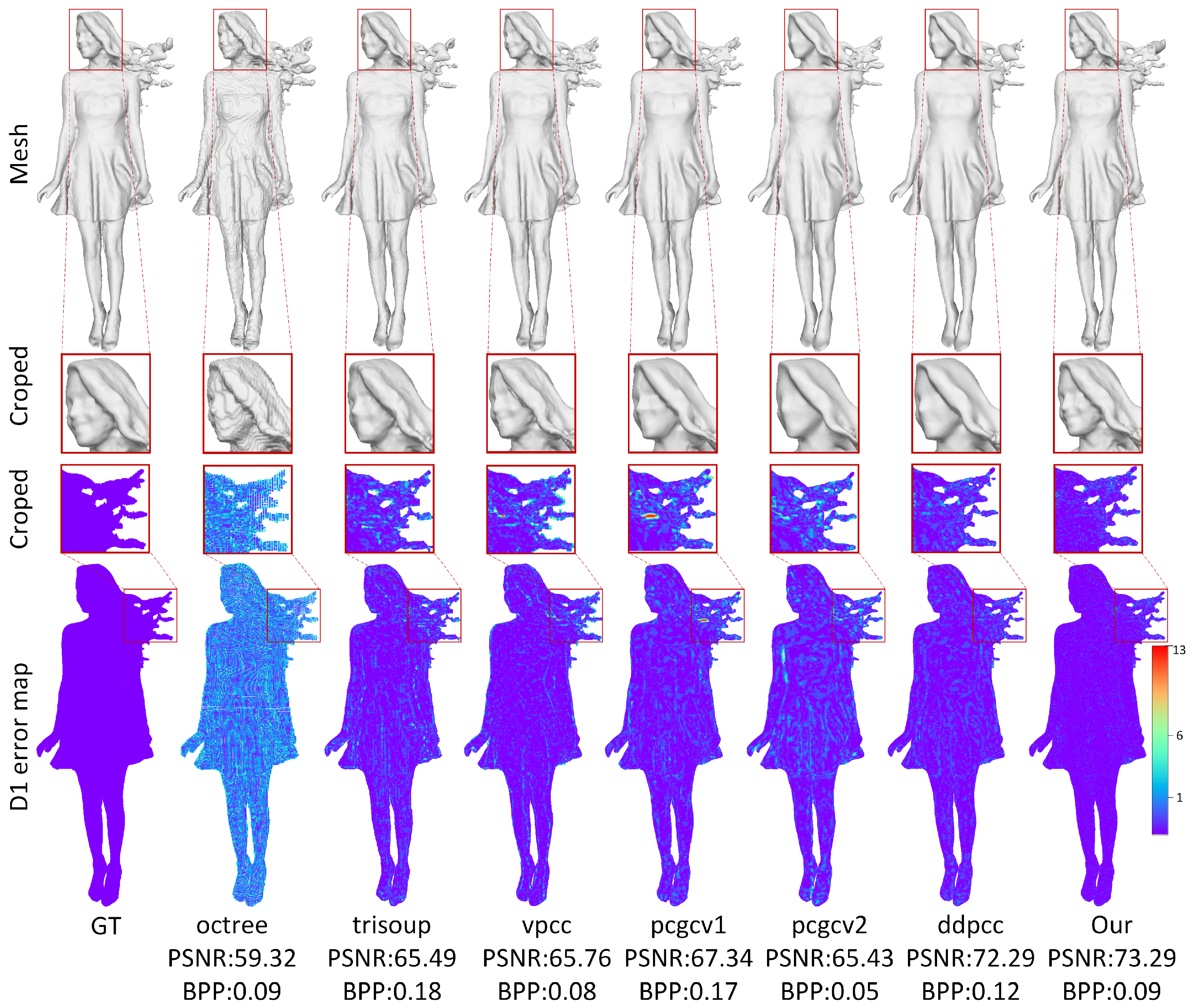
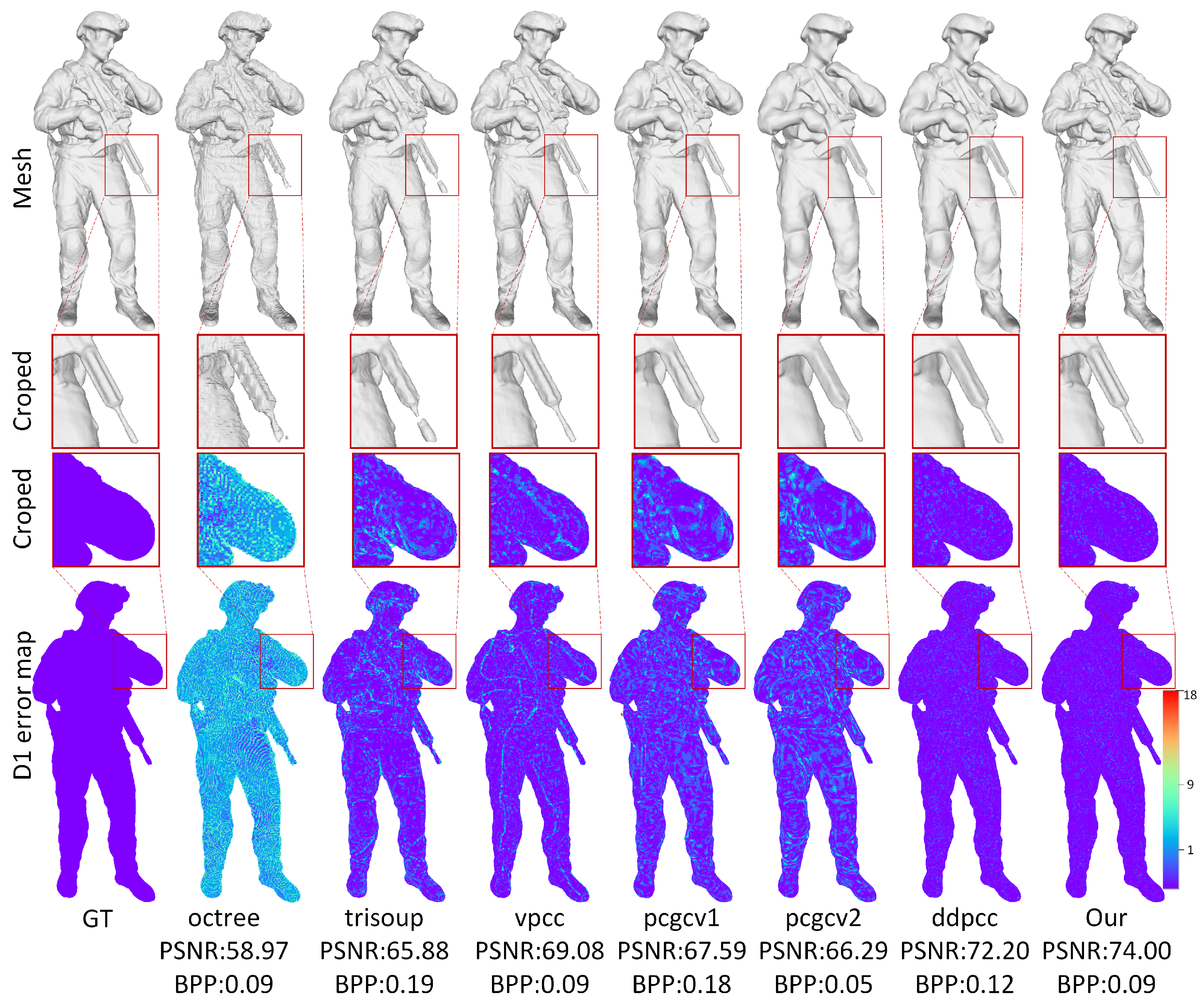

| Dataset | Sequence | BD-Rate with D1 PSNR (dB) | |||||
| G-PCC (octree) | G-PCC (trisoup) | V-PCC | PCGCv1 | PCGCv2 | D-DPCC | ||
| 8iVFBv2 | soldier | −98.21% | −96.28% | −76.87% | −93.31% | −43.09% | −33.45% |
| longdress | −97.32% | −94.24% | −73.43% | −83.76% | −31.25% | −26.57% | |
| loot | −98.58% | −95.57% | −78.87% | −93.12% | −43.55% | −32.89% | |
| redandblack | −96.70% | −93.37% | −75.93% | −84.21% | −41.58% | −20.03% | |
| Average with D1 | −97.70% | −94.86% | −76.27% | −88.60% | −39.86% | −28.24% | |
| Dataset | Sequence | BD-Rate with D2 PSNR (dB) | |||||
| G-PCC (octree) | G-PCC (trisoup) | V-PCC | PCGCv1 | PCGCv2 | D-DPCC | ||
| 8iVFBv2 | soldier | −93.40% | −92.03% | −71.23% | −70.35% | −33.55% | −16.87% |
| longdress | −92.68% | −91.52% | −68.58% | −68.73% | −27.83% | −12.33% | |
| loot | −93.78% | −92.42% | −73.34% | 74.03% | −45.37% | −23.89% | |
| redandblack | −91.98% | −90.28% | −72.77% | −71.28% | −22.45% | −12.38% | |
| Average with D2 | −92.96% | −91.56% | −71.48% | −71.09% | −32.34% | −16.37% | |
| Dataset | Sequence | BD-PSNR with D1 PSNR (dB) | |||||
| G-PCC (octree) | G-PCC (trisoup) | V-PCC | PCGCv1 | PCGCv2 | D-DPCC | ||
| 8iVFBv2 | soldier | 13.17 | 10.37 | 5.37 | 9.31 | 3.63 | 2.92 |
| longdress | 12.48 | 9.76 | 4.63 | 8.35 | 2.73 | 2.44 | |
| loot | 15.02 | 10.07 | 5.54 | 9.28 | 3.68 | 2.78 | |
| redandblack | 10.73 | 9.33 | 5.05 | 8.42 | 3.55 | 2.03 | |
| Average with D1 | 12.85 | 9.88 | 5.15 | 8.84 | 3.39 | 2.54 | |
| Dataset | Sequence | BD-PSNR with D2 PSNR (dB) | |||||
| G-PCC (octree) | G-PCC (trisoup) | V-PCC | PCGCv1 | PCGCv2 | D-DPCC | ||
| 8iVFBv2 | soldier | 11.65 | 10.11 | 4.13 | 4.07 | 3.03 | 1.63 |
| longdress | 10.92 | 9.38 | 4.27 | 4.43 | 2.55 | 1.33 | |
| loot | 13.87 | 10.18 | 4.56 | 4.98 | 3.88 | 2.42 | |
| redandblack | 9.75 | 9.36 | 4.32 | 4.16 | 2.13 | 1.38 | |
| Average with D2 | 11.54 | 9.75 | 4.32 | 4.41 | 2.89 | 1.69 | |
| Dataset | Sequence | BD-Rate with D1 PSNR (dB) | |||||
| K = 5 | K = 7 | K = 9 | K = 11 | K = 13 | K = 15 | ||
| 8iVFBv2 | soldier | −30.22% | −31.45% | −33.45% | −34.72% | −35.57% | −36.34% |
| longdress | −23.16% | −24.38% | −26.57% | −28.31% | −29.27% | −29.96% | |
| loot | −29.88% | −30.62% | −32.89% | −33.97% | −35.43% | −36.21% | |
| redandblack | −17.08% | −18.11% | −20.03% | −21.47% | −22.53% | −23.03% | |
| Average with D1 | −25.08% | −26.14% | −28.24% | −29.61% | −30.70% | −31.39% | |
| Dataset | Sequence | BD-Rate with D2 PSNR (dB) | |||||
| K = 5 | K = 7 | K = 9 | K = 11 | K = 13 | K = 15 | ||
| 8iVFBv2 | soldier | −13.07% | −14.23% | −16.87% | −17.43% | −18.26% | −19.17% |
| longdress | −9.03% | −10.27% | −12.33% | −13.66% | −14.57% | −15.81% | |
| loot | −20.02% | −21.83% | −23.89% | −24.21% | −25.37% | −26.09% | |
| redandblack | −9.43% | −10.71% | −12.38% | −13.17% | −14.65% | −15.20% | |
| Average with D2 | −12.89% | −14.26% | −16.37% | −17.12% | −18.12% | −18.89% | |
| Average Coding Time | 2.21 | 2.36 | 2.57 | 3.10 | 3.90 | 4.60 | |
| Dataset | Sequence | BD-Rate with D1 PSNR (dB) | ||
|---|---|---|---|---|
| Heads = 1 | Heads = 2 | Heads = 3 | ||
| 8iVFBv2 | soldier | 2.92 | 3.21 | 3.27 |
| longdress | 2.44 | 2.73 | 2.79 | |
| loot | 2.78 | 2.92 | 3.01 | |
| redandblack | 2.03 | 2.25 | 2.32 | |
| Average with D1 | 2.54 | 2.77 | 2.84 | |
| Methods | Enc/Dec (s/Frame) | FLOPs | #Params. |
|---|---|---|---|
| PCGCv1 | 4.2/1.8 | 7.2 G | 6.34 M |
| PCGCv2 | 1.1/1.0 | 4.8 G | 3.44 M |
| D-DPCC | 1.67/1.67 | 5.4 G | 3.87 M |
| VPCC | 90.7/2.1 | - | - |
| G-PCC (octree) | 2.1/0.8 | - | - |
| G-PCC (trisoup) | 3.2/1.1 | - | - |
| Proposed | 2.57/2.57 | 6.0 G | 4.23 M |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Wang, Y.; Zhu, Q. Dual-Attention-Based Block Matching for Dynamic Point Cloud Compression. J. Imaging 2025, 11, 332. https://doi.org/10.3390/jimaging11100332
Sun L, Wang Y, Zhu Q. Dual-Attention-Based Block Matching for Dynamic Point Cloud Compression. Journal of Imaging. 2025; 11(10):332. https://doi.org/10.3390/jimaging11100332
Chicago/Turabian StyleSun, Longhua, Yingrui Wang, and Qing Zhu. 2025. "Dual-Attention-Based Block Matching for Dynamic Point Cloud Compression" Journal of Imaging 11, no. 10: 332. https://doi.org/10.3390/jimaging11100332
APA StyleSun, L., Wang, Y., & Zhu, Q. (2025). Dual-Attention-Based Block Matching for Dynamic Point Cloud Compression. Journal of Imaging, 11(10), 332. https://doi.org/10.3390/jimaging11100332






