Overcoming Dimensionality Constraints: A Gershgorin Circle Theorem-Based Feature Extraction for Weighted Laplacian Matrices in Computer Vision Applications
Abstract
1. Introduction
2. Materials and Methods
2.1. Datasets
2.1.1. Extended MNIST (EMNSIT) Dataset
2.1.2. Cats vs. Dogs (CVD) Dataset
2.1.3. Malaria Cell (MC) Dataset
2.2. Methodology
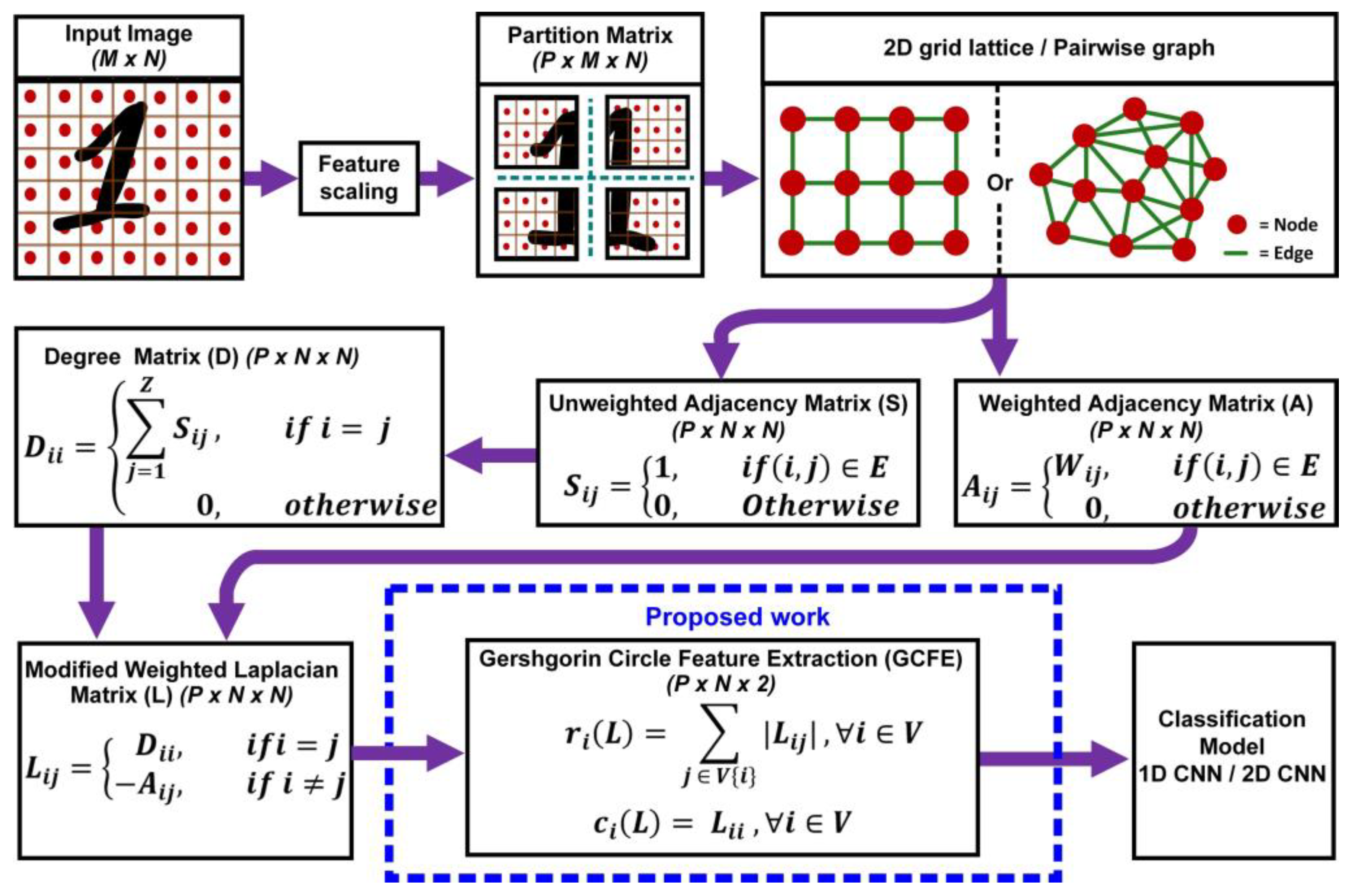
2.2.1. Preprocessing
2.2.2. Modified Weighted Laplacian (MWL) Matrix
2.2.3. Gershgorin Circle Feature Extraction
2.2.4. Classification
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Balaban, A.T. Applications of graph theory in chemistry. J. Chem. Inf. Comput. Sci. 1985, 25, 334–343. [Google Scholar] [CrossRef]
- Majeed, A.; Rauf, I. Graph theory: A comprehensive survey about graph theory applications in computer science and social networks. Inventions 2020, 5, 10. [Google Scholar] [CrossRef]
- Norcliffe-Brown, W.; Vafeias, S.; Parisot, S. Learning conditioned graph structures for interpretable visual question answering. In Proceedings of the Advances in Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; Volume 31, pp. 1–10. [Google Scholar]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps and spectral techniques for embedding and clustering. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 3–8 December 2001; Volume 13, pp. 1–7. [Google Scholar]
- He, X.; Niyogi, P. Locality preserving projections. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 8–13 December 2003; Volume 16, pp. 1–8. [Google Scholar]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed]
- Tenenbaum, J.B.; Silva, V.D.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Cai, D.; Niyogi, P. Laplacian score for feature selection. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 5–8 December 2005; Volume 18, pp. 1–8. [Google Scholar]
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.; Müller, K.-R. Kernel Principal Component Analysis. In Proceedings of the International Conference on Artificial Neural Networks, Lausanne, Switzerland, 8–10 October 1997; Springer: Berlin/Heidelberg, Germany, 1997; pp. 583–588. [Google Scholar]
- Chapelle, O.; Weston, J.; Schölkopf, B. Learning the Kernel Matrix with Semidefinite Programming. J. Mach. Learn. Res. 2002, 3, 1–48. [Google Scholar]
- Ross, D.; Lim, J.; Lin, R.-S.; Yang, M.-H. Incremental Learning for Robust Visual Tracking. Int. J. Comput. Vis. 2008, 77, 125–141. [Google Scholar] [CrossRef]
- Gershgorin, S.A. Über die Abgrenzung der Eigenwerte einer Matrix. Izv. Akad. Nauk. SSSR 1931, 6, 749–754. [Google Scholar]
- Bejarano, D.; Ibargüen-Mondragón, E.; Gómez-Hernández, E.A. A stability test for non linear systems of ordinary differential equations based on the gershgorin circles. Contemp. Eng. Sci. 2018, 11, 4541–4548. [Google Scholar] [CrossRef]
- Wang, F.; Wang, Y.; Cheung, G.; Yang, C. Graph sampling for matrix completion using recurrent Gershgorin disc shift. IEEE Trans. Signal Process. 2020, 68, 2814–2829. [Google Scholar] [CrossRef]
- Xie, X.; Huang, J.; Tan, E.; He, F.; Liu, Z. Stability Criterion and Stability Analysis of Three-Phase Grid-Connected Rectifier System Based on Gerschgorin Circle Theorem. Electronics 2022, 11, 3270. [Google Scholar] [CrossRef]
- Varga, R.S.; Krautstengl, A. On Geršgorin-type problems and ovals of Cassini. Electron. Trans. Numer. Anal. 1999, 8, 15–20. [Google Scholar]
- Varga, R.S. Geršgorin and His Circles; Springer: Berlin/Heidelberg, Germany, 2010; Volume 36. [Google Scholar]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Song, Y.-Y.; Ying, L.U. Decision tree methods: Applications for classification and prediction. Shanghai Arch. Psychiatry 2015, 27, 130. [Google Scholar] [PubMed]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Lake Tahoe, NV, USA, 3–6 December 2012; Volume 25. [Google Scholar]
- Cohen, G.; Afshar, S.; Tapson, J.; Schaik, A.V. EMNIST: Extending MNIST to handwritten letters. In Proceedings of the 2017 International Joint Conference on Neural Networks, Anchorage, AK, USA, 14–19 May 2017; pp. 2921–2926. [Google Scholar]
- Kaggle Dogs vs. Cats. Kaggle 2013. Available online: https://www.kaggle.com/c/dogs-vs-cats (accessed on 1 February 2024).
- Rajaraman, S.; Antani, S.K.; Poostchi, M.; Silamut, K.; Hossain, M.A.; Maude, R.J.; Jaeger, S.; Thoma, G.R. pre-trained convolutional neural networks as feature extractors toward improved malaria parasite detection in thin blood smear images. PeerJ 2018, 6, e4568. [Google Scholar] [CrossRef]
- Patel, S.A.; Yildirim, A. Non-stationary neural signal to image conversion framework for image-based deep learning algorithms. Front. Neuroinform. 2023, 17, 1081160. [Google Scholar] [CrossRef] [PubMed]
- Patel, S.A. Image_GCFE[Sourecode]. 2023. Available online: https://github.com/sahaj432/Image_GCFE.git (accessed on 12 February 2024).
- Zhang, Z.; Wang, J. MLLE: Modified locally linear embedding using multiple weights. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 4 December 2006; Volume 19. [Google Scholar]
- Donoho, D.L.; Grimes, C. Hessian eigenmaps: Locally linear embedding techniques for high-dimensional data. Proc. Natl. Acad. Sci. USA 2003, 100, 5591–5596. [Google Scholar] [CrossRef] [PubMed]




| Datasets | Instances | Classes | Type | Distribution of Classes |
|---|---|---|---|---|
| EMNIST | ||||
| E_Balanced | 131,600 | 47 | 1D | Balanced |
| E_ByClass | 814,255 | 62 | 1D | Imbalanced |
| E_ByMerge | 814,255 | 47 | 1D | Imbalanced |
| E_Digits | 280,000 | 10 | 1D | Imbalanced |
| E_Letter | 145,600 | 26 | 1D | Imbalanced |
| E_MNIST | 70,000 | 10 | 1D | Imbalanced |
| CVD | 25,000 | 2 | 3D | Balanced |
| MC | 27,558 | 2 | 3D | Balanced |
| Approach No. | Dataset | Type of Comparison | Type of Graph | Classification Architecture | Performance Metric |
|---|---|---|---|---|---|
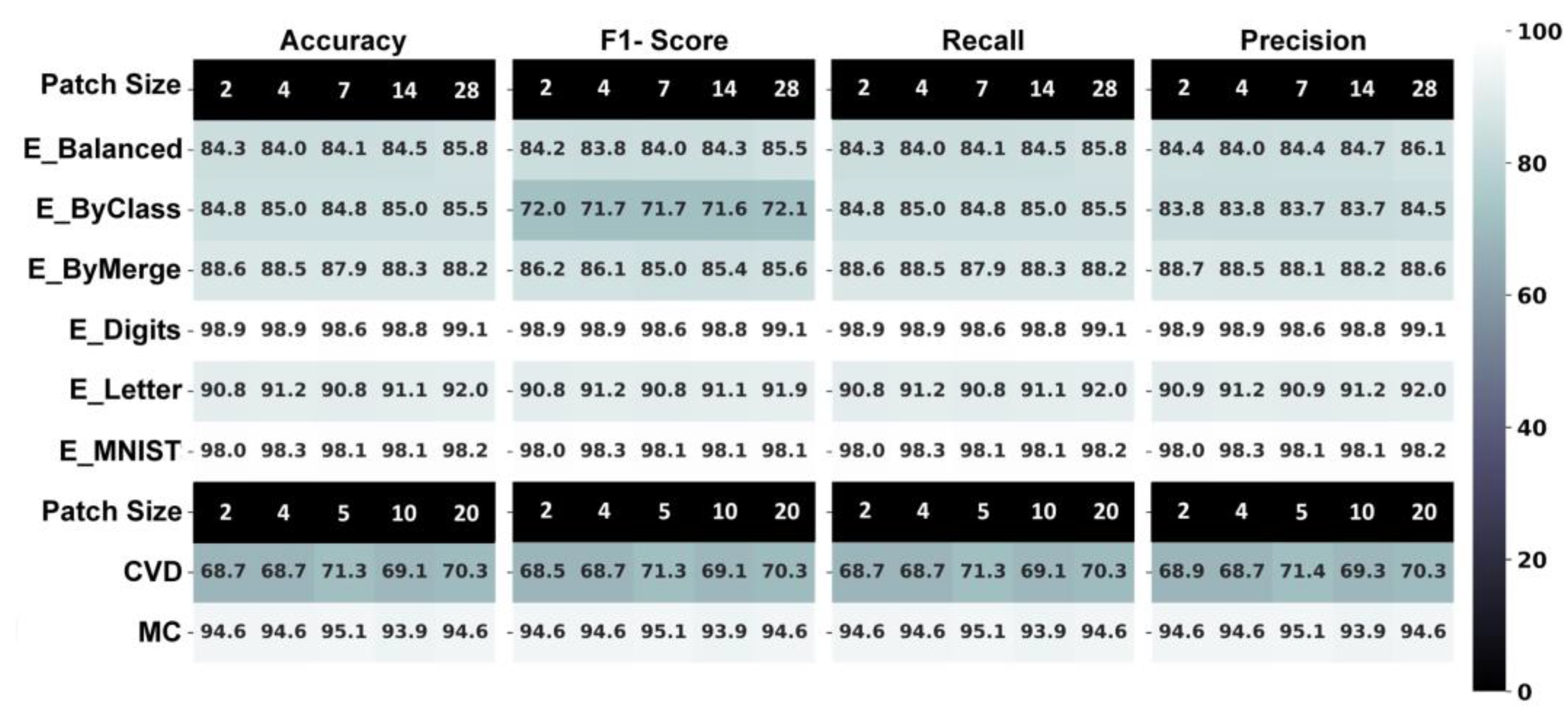
| 1 | E_Balanced, E_ByClass, E_ByMerge, E_Digits, E_Letter, E_MNIST, CVD, MC | Comparison between GCFE of all datasets with different image patch sizes. | 2D-Grid | 2D-CNN | Accuracy |
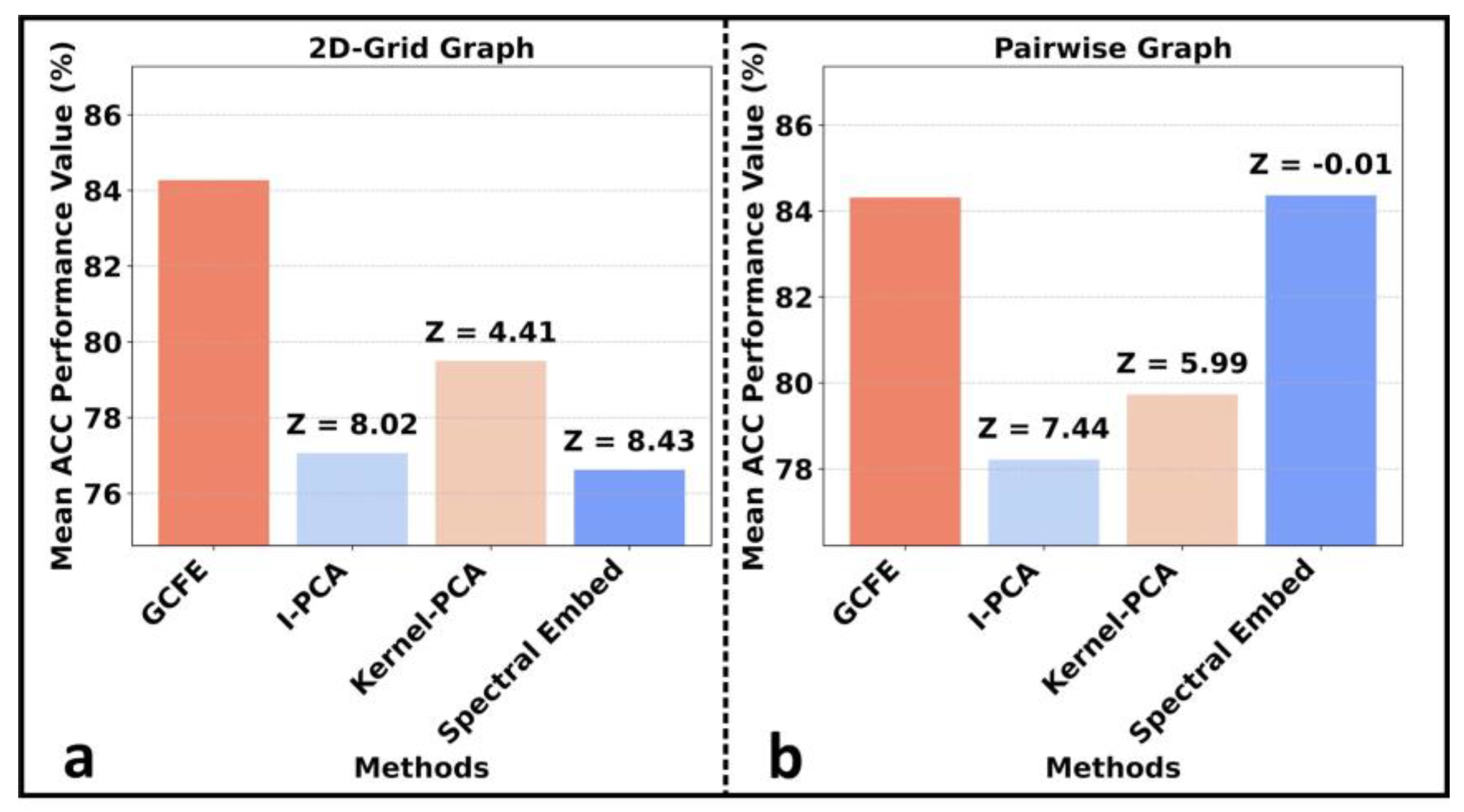
| 2 | E_Balanced, CVD, MC | Comparison between GCFE, Laplacian, I-PCA, Kernel-PCA, and spectral embedding with different image patch sizes. | 2D-Grid, pairwise | 2D-CNN, 1D-CNN | Accuracy, Z-Score |
| 3 | E_MNIST | Comparison between GCFE, Isomap, LLE, MLLE, and Hessian Eigenmap with different image patch sizes. | K-NN | 1D-CNN | Accuracy |
| Datasets | GCFE (2D CNN) | Laplacian (2D CNN) | GCFE (1D CNN) | I-PCA | Kernel-PCA (RBF) | Spectral Embed. | Raw Image |
|---|---|---|---|---|---|---|---|
| Graph type—2D-Grid | |||||||
| E_Balanced_P2 | 84.329 t = ≈6 | 84.553 | 83.797 t = ≈6 | 76.468 t = ≈225 | 78.138 t* = ≈12 | 75.787 t* = ≈3 | 86.617 |
| E_Balanced_P4 | 83.978 t = ≈6 | 85.010 | 84.691 t = ≈6 | 76.499 t = ≈926 | 79.776 t* = ≈107 | 76.329 t* = ≈54 | 86.117 |
| E_Balanced_P7 | 84.117 t = ≈16 | 84.595 | 84.329 t = ≈16 | 78.223 t = ≈2010 | 80.585 t* = ≈1163 | 77.755 t* = ≈1136 | 85.659 |
| CVD_P2 | 68.681 t = ≈32 | 71.518 | 66.045 t = ≈32 | 62.722 t = ≈10,475 | ~ | 61.318 t* = ≈1182 | 70.773 |
| MC_P2 | 94.581 t = ≈38 | 93.783 | 92.646 t = ≈38 | 63.691 t = ≈6944 | ~ | 62.796 t* = ≈1256 | 92.186 |
| Graph type—Pairwise | |||||||
| E_Balanced_P2 | 84.744 t = ≈5 | 85.372 | 84.989 t = ≈5 | 78.595 t = ≈194 | 79.287 t* = ≈11 | 77.638 t* = ≈1 | 86.617 |
| E_Balanced_P4 | 84.276 t = ≈5 | 85.255 | 84.148 t = ≈5 | 77.297 t = ≈917 | 80.553 t* = ≈111 | 95.86 t* = ≈55 | 86.117 |
| E_Balanced_P7 | 83.237 t = ≈8 | 84.074 | 83.808 t = ≈8 | 78.755 t = ≈1912 | 79.351 t* = ≈1122 | 79.595 t* = ≈1182 | 85.659 |
| CVD_P2 | 69.684 t = ≈27 | 70.773 | 69.025 t = ≈27 | ~ | ~ | 63.954 t* = ≈1337 | 70.773 |
| MC_P2 | 92.597 t = ≈33 | 92.938 | 92.670 t = ≈33 | ~ | ~ | 63.570 t* = ≈1407 | 92.186 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patel, S.A.; Yildirim, A. Overcoming Dimensionality Constraints: A Gershgorin Circle Theorem-Based Feature Extraction for Weighted Laplacian Matrices in Computer Vision Applications. J. Imaging 2024, 10, 121. https://doi.org/10.3390/jimaging10050121
Patel SA, Yildirim A. Overcoming Dimensionality Constraints: A Gershgorin Circle Theorem-Based Feature Extraction for Weighted Laplacian Matrices in Computer Vision Applications. Journal of Imaging. 2024; 10(5):121. https://doi.org/10.3390/jimaging10050121
Chicago/Turabian StylePatel, Sahaj Anilbhai, and Abidin Yildirim. 2024. "Overcoming Dimensionality Constraints: A Gershgorin Circle Theorem-Based Feature Extraction for Weighted Laplacian Matrices in Computer Vision Applications" Journal of Imaging 10, no. 5: 121. https://doi.org/10.3390/jimaging10050121
APA StylePatel, S. A., & Yildirim, A. (2024). Overcoming Dimensionality Constraints: A Gershgorin Circle Theorem-Based Feature Extraction for Weighted Laplacian Matrices in Computer Vision Applications. Journal of Imaging, 10(5), 121. https://doi.org/10.3390/jimaging10050121






