Advances in Real-Time 3D Reconstruction for Medical Endoscopy
Abstract
1. Introduction
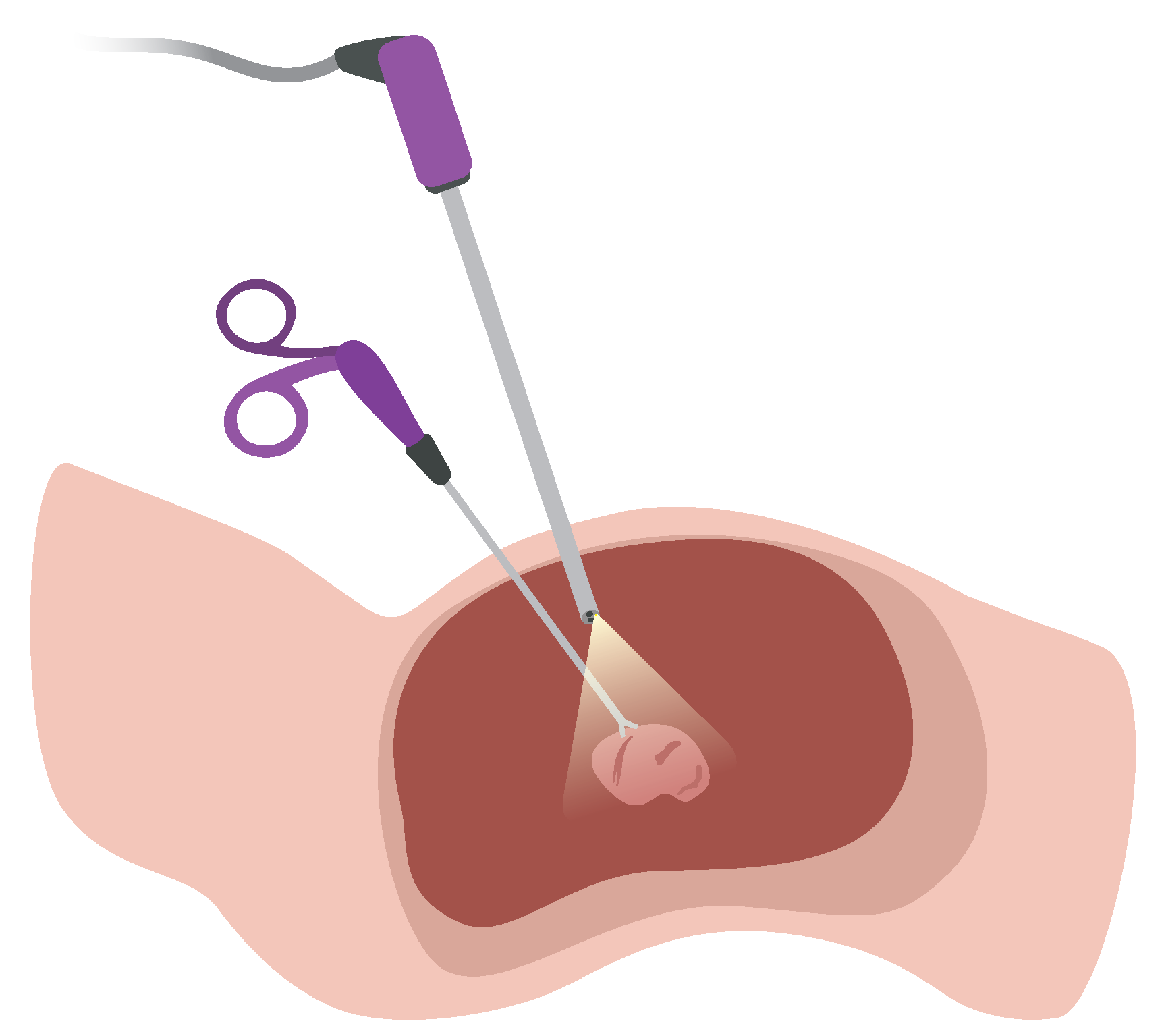
2. Evaluation Tools
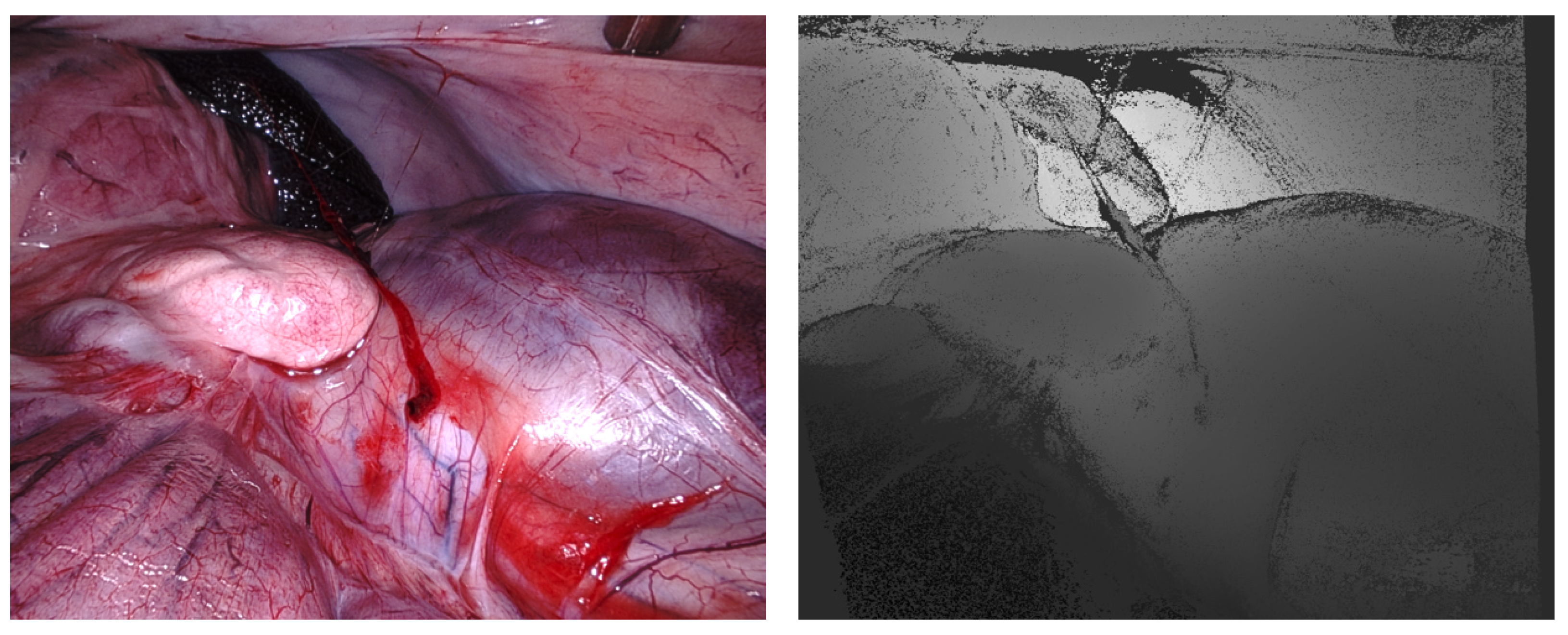
2.1. Disparity Map vs. Point Cloud
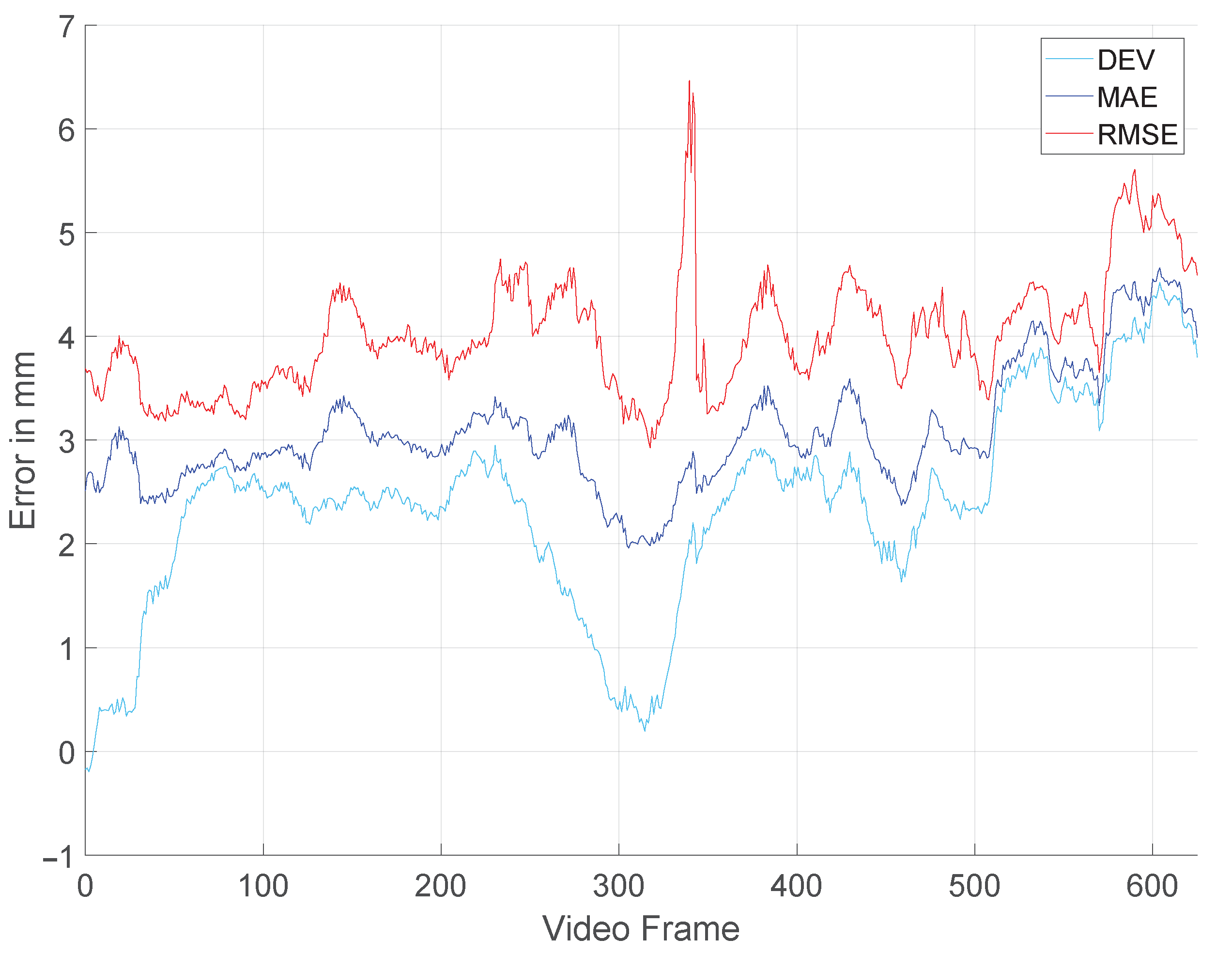
2.2. Metrics for Comparison
2.3. Datasets
2.4. Comparability between Contributions
2.5. GPU vs. FPGA
3. Monocular: Passive Methods
| Monocular Contribution (Active/Passive, Self Evaluated) | Error in mm | FPS in Hz | Hardware AMD, Intel, NVIDIA (Santa Clara, CA, USA) | Image Size in px |
|---|---|---|---|---|
| Sfm from tracking [51] | RMSE = 1.9 | 33 | 2.5 GHz CPU NVIDIA Quadro FX 570 | n.a. |
| SLAM Dense Surface Reconstruction [52] | RMSE = 2.54 | 1.6 | Intel Xenon 2.8 GHz NVIDIA GTX 970 | |
| ORBSLAM [53] | RMSE = 3–4.1 | 1.7 | Intel i5 3337U 1.8 GHz | n.a. |
| Endo-Depth- and-Motion [54] | RMSE = 11.02 | 3.1 | AMD Ryzen 9 3900X NVIDIA RTX 2080 Ti | n.a. |
| VCSEL single point laser distance sensing [55] | MAE = 0.04 | 5000 | n.a | n.a. |
| 3D Scanner Structured Light [56] | MAE = 0.1 | 30 | n.a. | |
| Infrared coded Structured Light [57] | MAE = 0.12 | n.a. | n.a. | |
| Multispectral Structured Light [58] | MAE = 0.64–0.88 | 0.02 | Intel i7 3770 3.9 GHz |
3.1. Structure from Motion (SfM)
3.2. Simultaneous Localization and Mapping (SLAM)
4. Monocular: Active Methods
4.1. Structured Light (SL)
4.2. Time of Flight (ToF)
4.3. Laser Distance Sensing
5. Binocular: Passive Methods
5.1. Deterministic Stereo Matching
| Binocular Contribution (Middlebury Dataset) | Error in % | FPS in Hz | Hardware AMD, Intel, NVIDIA (Santa Clara, CA, USA) Inrevium (Shibuya, Tokyo, Japan) | Image Size in px | Disparity Range in px |
|---|---|---|---|---|---|
| Cross-based Support Regions [95] | 3.94 | 49.7 | NVIDIA GTX 1070 | 16 | |
| Guided Image Filtering [96] | 5.55 | 17 | NVIDIA GTX 480 | 40 | |
| Weakly-Textured Scenes [97] | 5.78 | 1 | NVIDIA GTX 8800 | 48 | |
| High-quality Stereo Vision [49] | 6.17 | 31.79 | Intel (Altera) EP4SGX230 FPGA | 96 | |
| Two Pass Adaptive Support Weights [98] | 6.20 | 62 | NVIDIA GTX 580 | 32 | |
| Hardware Guided Image Filtering [47] | 6.36 | 60 | Inrevium Kintex-7 FPGA | 64 | |
| Line-wise HRM [99] | 6.68 | 13 | NVIDIA Tesla C 2070 | n.a. | |
| Real-time BFV [100] | 7.65 | 57 | NVIDIA GTX 8800 | 16 | |
| Belief Propagation [101] | 7.69 | 16 | NVIDIA GTX 7900 | 16 | |
| High-def SM on FPGA [48] | 8.20 | 60 | Intel (Altera) EP3SL150 FPGA | 64 | |
| Embedded Real-time Systems [44] | 9.73 | 573.7 | NVIDIA GTX 280 | 15 |
| Binocular Contribution (Self Evaluated) | Error in mm | FPS in Hz | Hardware AMD, Intel, NVIDIA (Santa Clara, CA, USA) | Image Size in px | Disparity Range in px |
|---|---|---|---|---|---|
| Semi-dense Surface reconstruction [102] | RMSE = 3.2 | 2.64 | NVIDIA Quadro K5000 | n.a. | |
| Semi-dense Surface reconstruction [1] | MAE = 1.06 | 15 | NVIDIA Quadro FX 5800 | n.a. | |
| GPU/CPU Surface reconstruction [103] | MAE = 1.55 | 30 | Intel i7 930 NVIDIA Tesla C 2070 | n.a. | |
| Novel enhancement to HRM [104] | MAE = 2.06 | 14.5 | CPU | n.a. | n.a. |
| CPU Surface reconstruction [86] | MAE = 2.6 | 20 | CPU | n.a. | |
| Fraunhofer HHI stereo pipeline [15] | MAE = 3.44 (SCARED Dataset) | 45 | NVIDIA RTX 3090 | n.a. |
5.2. Deep Learning Photogrammetry
| Binocular Contribution (KITTI Dataset) | Error in % | FPS in HZ | Hardware | Image Size in px | Disparity Range in px |
|---|---|---|---|---|---|
| UASNet [119] | 1.64 | 3.3 | 2.5 GHz CPU | ≤150 | |
| ACVNet [120] | 1.65 | 5 | 2 × NVIDIA RTX 3090 | ≤150 | |
| LeaStereo [121] | 1.65 | 3.3 | NVIDIA V 100 | ≤150 | |
| CVCNet [122] | 1.74 | 13.5 | 2 × NVIDIA RTX 2080 Ti | ≤150 | |
| HITNet [123] | 1.98 | 50 | NVIDIA GTX Titan V | ≤150 | |
| HSM [124] | 2.14 | 7 | NVIDIA GTX Titan X | ≤150 | |
| DeepPruner [125] | 2.15 | 5.5 | 4 × NVIDIA GTX Titan X | ≤150 | |
| DispNetC [126] | 4.05 | 15 | NVIDIA GTX Titan X | ≤150 | |
| MADNet [127] | 4.66 | 50 | NVIDIA GTX 1080 Ti | ≤150 | |
| StereoNet [128] | 4.83 | 60 | NVIDIA GTX Titan X | ≤150 | |
| FP-Stereo [50] | 7.9 | 147 | Xilinx ZCU102 (FPGA) | 128 | |
| CNN L12 [129] | n.a. | 60 | NVIDIA GTX Titan X | n.a. |
6. Multi-Ocular: Passive Methods
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stoyanov, D.; Visentini-Scarzanella, M.; Pratt, P.; Yang, G.Z. Real-Time Stereo Reconstruction in Robotically Assisted Minimally Invasive Surgery. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention: MICCAI International Conference on Medical Image Computing and Computer-Assisted Intervention, Beijing, China, 20–24 September 2010; Volume 13, pp. 275–282. [Google Scholar] [CrossRef]
- Lin, B.; Johnson, A.; Qian, X.; Sanchez, J.; Sun, Y. Simultaneous Tracking, 3D Reconstruction and Deforming Point Detection for Stereoscope Guided Surgery. In Proceedings of the Augmented Realitcy Environments for Medical Imaging and Computer-Assisted Interventions, Nagoya, Japan, 22–26 September 2013; Liao, H., Linte, C.A., Masamune, K., Peters, T.M., Zheng, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 35–44. [Google Scholar] [CrossRef]
- Bogdanova, R.; Boulanger, P.; Zheng, B. Depth Perception of Surgeons in Minimally Invasive Surgery. Surg. Innov. 2016, 23, 515–524. [Google Scholar] [CrossRef] [PubMed]
- Breedveld, P.; Wentink, M. Eye-hand coordination in laparoscopy—An overview of experiments and supporting aids. Minim. Invasive Ther. Allied Technol. 2009, 10, 155–162. [Google Scholar] [CrossRef] [PubMed]
- Way, L.; Stewart, L.; Gantert, W.; Liu, K.; Lee, C.; Whang, K.; Hunter, J. Causes and Prevention of Laparoscopic Bile Duct Injuries: Analysis of 252 Cases from a Human Factors and Cognitive Psychology Perspective. Ann. Surg. 2003, 237, 460–469. [Google Scholar] [CrossRef] [PubMed]
- Skogås, J.G.; Myhre, H.O.; Ødegård, A.; Kiss, G. Imaging for Minimally Invasive Surgery. Surg. Sci. 2016, 7, 333–341. [Google Scholar] [CrossRef]
- Erpenbeck, D.; Lemke, N.; Wittenberg, T.; Rosenthal, J.C.; Kauff, P.; Bergen, T. Evaluierung von 3D-Rekonstruktionsverfahren in der Stereo-Laparoskopie. In Proceedings of the 15th Annual Conference of the German Society for Computer- and Robot-Assisted Surgery (CURAC 2016), Bern, Schwitzerland, 29 September–1 October 2016; pp. 58–63, ISBN 978-3-86247-595-7. [Google Scholar]
- Liu, X.; Karmarkar, P.; Voit, D.; Frahm, J.; Weiss, C.; Kraitchman, D.; Bottomley, P. Real-Time High-Resolution MRI Endoscopy at up to 10 Frames per Second. BME Front. 2021, 2021, 6185616. [Google Scholar] [CrossRef] [PubMed]
- Trucco, E.; Verri, A. Introductory Techniques for 3-D Computer Vision; Prentice Hall PTR: Hoboken, NJ, USA, 1998; ISBN 978-0-13-261108-4. [Google Scholar]
- Min, D.; Yea, S.; Arican, Z.; Vetro, A. Disparity search range estimation: Enforcing temporal consistency. In Proceedings of the 2010 IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas, TX, USA, 14–19 March 2010; pp. 2366–2369. [Google Scholar] [CrossRef]
- Sara, R. Finding the Largest Unambiguous Component of Stereo Matching. In Proceedings of the Computer Vision—ECCV 2002, Copenhagen, Denmark, 28–31 May 2002; pp. 900–914. [Google Scholar] [CrossRef]
- Cyganek, B.; Borgosz, J. An Improved Variogram Analysis of the Maximum Expected Disparity in Stereo Images. In Proceedings of the SCIA’03: Proceedings of the 13th Scandinavian Conference on Image Analysis, Halmstad, Sweden, 29 June–2 July 2003; Volume 2749, pp. 640–645. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Groch, A.; Hempel, S.; Speidel, S.; Höller, K.; Engelbrecht, R.; Penne, J.; Seitel, A.; Röhl, S.; Yung, K.; Bodenstedt, S.; et al. In-vitro Evaluation von endoskopischer Oberflächenrekonstruktion mittels Time-of-Flight-Kameratechnik. In Proceedings of the Bildverarbeitung für die Medizin 2011: Algorithmen–Systeme–Anwendungen, Lübeck, Germany, 20–22 March 2011; pp. 184–188. [Google Scholar] [CrossRef]
- Allan, M.; McLeod, A.J.; Wang, C.C.; Rosenthal, J.C.; Hu, Z.; Gard, N.; Eisert, P.; Fu, K.; Zeffiro, T.; Xia, W.; et al. Stereo Correspondence and Reconstruction of Endoscopic Data Challenge. arXiv 2021, arXiv:2101.01133. [Google Scholar] [CrossRef]
- Scharstein, D.; Hirschmüller, H.; Kitajima, Y.; Krathwohl, G.; Nešić, N.; Wang, X.; Westling, P. High-Resolution Stereo Datasets with Subpixel-Accurate Ground Truth. In Proceedings of the 36th Conference on Pattern Recognition, Münster, Germany, 2–5 September 2014; pp. 31–42. [Google Scholar] [CrossRef]
- Edwards, P.; Psychogyios, D.; Speidel, S.; Maier-Hein, L.; Stoyanov, D. SERV-CT: A disparity dataset from CT for validation of endoscopic 3D reconstruction. arXiv 2020, arXiv:2012.11779. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R. Root mean square error (RMSE) or mean absolute error (MAE)? Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Menze, M.; Geiger, A. Object scene flow for autonomous vehicles. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3061–3070. [Google Scholar] [CrossRef]
- Schauwecker, K. Real-time stereo vision on FPGAs with SceneScan. In Proceedings of the Forum Bildverarbeitung, Karlsruhe, Germany, 29–30 November 2018; p. 339. [Google Scholar]
- Scharstein, D.; Szeliski, R. A Taxonomy and Evaluation of Dense Two-Frame Stereo Correspondence Algorithms. Int. J. Comput. Vis. 2002, 47, 7–42. [Google Scholar] [CrossRef]
- Scharstein, D.; Szeliski, R. High-accuracy stereo depth maps using structured light. In Proceedings of the 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Madison, WI, USA, 18–20 June 2003; Volume 1. [Google Scholar] [CrossRef]
- Scharstein, D.; Pal, C. Learning Conditional Random Fields for Stereo. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 16 July 2007; pp. 1–8. [Google Scholar] [CrossRef]
- Hirschmuller, H.; Scharstein, D. Evaluation of Cost Functions for Stereo Matching. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 16 July 2007; pp. 1–8. [Google Scholar] [CrossRef]
- Stiller, C.; Kammel, S.; Pitzer, B.; Ziegler, J.; Werling, M.; Gindele, T.; Jagszent, D. Team AnnieWAY’s Autonomous System. In Proceedings of the Robot Vision, Second International Workshop, RobVis 2008, Auckland, New Zealand, 18–20 February 2008; pp. 248–259. [Google Scholar] [CrossRef]
- Mountney, P.; Stoyanov, D.; Yang, G.-Z.; Mylonas, G.; Deligianni, F.; Darzi, A.; Lerotic, M.; Chung, A.J.; Clark, J.; Valibeik, S.; et al. Hamlyn Centre Laparoscopic/Endoscopic Video Datasets. 2021. Available online: https://hamlyn.doc.ic.ac.uk/vision/ (accessed on 9 September 2022).
- Mountney, P.; Stoyanov, D.; Yang, G.Z. Three-Dimensional Tissue Deformation Recovery and Tracking. IEEE Signal Process. Mag. 2010, 27, 14–24. [Google Scholar] [CrossRef]
- Stoyanov, D.; Mylonas, G.P.; Deligianni, F.; Darzi, A.; Yang, G.Z. Soft-Tissue Motion Tracking and Structure Estimation for Robotic Assisted MIS Procedures. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2005, Palm Springs, CA, USA, 26–29 October 2005; Duncan, J.S., Gerig, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 139–146. [Google Scholar] [CrossRef]
- Lerotic, M.; Chung, A.; Clark, J.; Valibeik, S.; Yang, G.Z. Dynamic View Expansion for Enhanced Navigation in Natural Orifice Transluminal Endoscopic Surgery. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention: MICCAI International Conference on Medical Image Computing and Computer-Assisted Intervention, New York, NY, USA, 6–10 September 2008; Volume 11, pp. 467–475. [Google Scholar] [CrossRef]
- Pratt, P.; Stoyanov, D.; Visentini-Scarzanella, M.; Yang, G.Z. Dynamic Guidance for Robotic Surgery Using Image-Constrained Biomechanical Models. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention: MICCAI International Conference on Medical Image Computing and Computer-Assisted Intervention, Beijing, China, 20–24 September 2010; Volume 13, pp. 77–85. [Google Scholar] [CrossRef]
- Giannarou, S.; Visentini-Scarzanella, M.; Yang, G.Z. Probabilistic Tracking of Affine-Invariant Anisotropic Regions. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 130–143. [Google Scholar] [CrossRef]
- Ye, M.; Giannarou, S.; Meining, A.; Yang, G.Z. Online Tracking and Retargeting with Applications to Optical Biopsy in Gastrointestinal Endoscopic Examinations. Med. Image Anal. 2015, 30, 144–157. [Google Scholar] [CrossRef] [PubMed]
- Ye, M.; Johns, E.; Handa, A.; Zhang, L.; Pratt, P.; Yang, G. Self-Supervised Siamese Learning on Stereo Image Pairs for Depth Estimation in Robotic Surgery. In Proceedings of the Hamlyn Symposium on Medical Robotics, London, UK, 25–28 June 2017; pp. 27–28. [Google Scholar] [CrossRef]
- Geiger, A.; Roser, M.; Urtasun, R. Efficient Large-Scale Stereo Matching. In Proceedings of the Computer Vision—ACCV 2010, Queenstown, New Zealand, 8–12 November 2010; pp. 25–38. [Google Scholar] [CrossRef]
- Ozyoruk, K.B.; Gokceler, G.I.; Coskun, G.; Incetan, K.; Almalioglu, Y.; Mahmood, F.; Curto, E.; Perdigoto, L.; Oliveira, M.; Sahin, H.; et al. EndoSLAM Dataset and An Unsupervised Monocular Visual Odometry and Depth Estimation Approach for Endoscopic Videos: Endo-SfMLearner. arXiv 2020, arXiv:2006.16670. [Google Scholar] [CrossRef] [PubMed]
- Rau, A.; Bano, S.; Jin, Y.; Azagra, P.; Morlana, J.; Sanderson, E.; Matuszewski, B.J.; Lee, J.Y.; Lee, D.J.; Posner, E.; et al. SimCol3D—3D Reconstruction during Colonoscopy Challenge. arXiv 2023, arXiv:2307.11261. [Google Scholar]
- Penza, V.; Ciullo, A.; Moccia, S.; Mattos, L.; De Momi, E. EndoAbS Dataset: Endoscopic Abdominal Stereo Image Dataset for Benchmarking 3D Stereo Reconstruction Algorithms. Int. J. Med. Robot. Comput. Assist. Surg. 2018, 14, e1926. [Google Scholar] [CrossRef]
- Bobrow, T.L.; Golhar, M.; Vijayan, R.; Akshintala, V.S.; Garcia, J.R.; Durr, N.J. Colonoscopy 3D video dataset with paired depth from 2D-3D registration. Med. Image Anal. 2023, 90, 102956. [Google Scholar] [CrossRef]
- Rau, A.; Edwards, P.; Ahmad, O.; Riordan, P.; Janatka, M.; Lovat, L.; Stoyanov, D. Implicit domain adaptation with conditional generative adversarial networks for depth prediction in endoscopy. Int. J. Comput. Assist. Radiol. Surg. 2019, 14, 1167–1176. [Google Scholar] [CrossRef] [PubMed]
- HajiRassouliha, A.; Taberner, A.; Nash, M.; Nielsen, P. Suitability of recent hardware accelerators (DSPs, FPGAs, and GPUs) for computer vision and image processing algorithms. Signal Process. Image Commun. 2018, 68, 101–119. [Google Scholar] [CrossRef]
- Ghorpade, J.; Parande, J.; Kulkarni, M.; Bawaskar, A. GPGPU Processing in CUDA Architecture. arXiv 2012, arXiv:1202.4347. [Google Scholar] [CrossRef]
- Pauwels, K.; Tomasi, M.; Alonso, J.D.; Ros, E.; Hulle, M. A Comparison of FPGA and GPU for Real-Time Phase-Based Optical Flow, Stereo, and Local Image Features. IEEE Trans. Comput. 2012, 61, 999–1012. [Google Scholar] [CrossRef]
- Qasaimeh, M.; Denolf, K.; Lo, J.; Vissers, K.; Zambreno, J.; Jones, P.H. Comparing Energy Efficiency of CPU, GPU and FPGA Implementations for Vision Kernels. In Proceedings of the 2019 IEEE International Conference on Embedded Software and Systems (ICESS), Las Vegas, NV, USA, 2–3 June 2019; pp. 1–8. [Google Scholar] [CrossRef]
- Humenberger, M.; Zinner, C.; Weber, M.; Kubinger, W.; Vincze, M. A Fast Stereo Matching Algorithm Suitable for Embedded Real-Time Systems. Comput. Vis. Image Underst. 2010, 114, 1180–1202. [Google Scholar] [CrossRef]
- Feng, X.; Jiang, Y.; Yang, X.; Du, M.; Li, X. Computer vision algorithms and hardware implementations: A survey. Integration 2019, 69, 309–320. [Google Scholar] [CrossRef]
- Carballo-Hern’andez, W.; Pelcat, M.; Berry, F. Why is FPGA-GPU Heterogeneity the Best Option for Embedded Deep Neural Networks? arXiv 2021, arXiv:2102.01343. [Google Scholar] [CrossRef]
- Ttofis, C.; Theocharides, T. High-quality real-time hardware stereo matching based on guided image filtering. In Proceedings of the 2014 Design, Automation & Test in Europe Conference & Exhibition (DATE), Dresden, Germany, 24–28 March 2014; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, K.; Chang, T.S.; Lafruit, G.; Kuzmanov, G.K.; Verkest, D. Real-Time High-Definition Stereo Matching on FPGA. In Proceedings of the 19th ACM/SIGDA International Symposium on Field Programmable Gate Arrays (FPGA’11), Monterey, CA, USA, 27 February–1 March 2011; pp. 55–64. [Google Scholar] [CrossRef]
- Wang, W.; Yan, J.; Xu, N.; Wang, Y.; Hsu, F.H. Real-time high-quality stereo vision system in FPGA. In Proceedings of the 2013 International Conference on Field-Programmable Technology (FPT), Kyoto, Japan, 9–11 December 2013; pp. 358–361. [Google Scholar] [CrossRef]
- Zhao, J.; Liang, T.; Feng, L.; Ding, W.; Sinha, S.; Zhang, W.; Shen, S. FP-Stereo: Hardware-Efficient Stereo Vision for Embedded Applications. arXiv 2020, arXiv:2006.03250. [Google Scholar]
- Sun, D.; Liu, J.; Linte, C.A.; Duan, H.; Robb, R.A. Surface Reconstruction from Tracked Endoscopic Video Using the Structure from Motion Approach. In Proceedings of the Augmented Reality Environments for Medical Imaging and Computer-Assisted Interventions, Nagoya, Japan, 22–26 September 2013; Springer: Berlin/Heidelberg, Germany, 2013; pp. 127–135. [Google Scholar] [CrossRef]
- Chen, L.; Tang, W.; John, N.W.; Wan, T.R.; Zhang, J.J. SLAM-based dense surface reconstruction in monocular Minimally Invasive Surgery and its application to Augmented Reality. Comput. Methods Programs Biomed. 2018, 158, 135–146. [Google Scholar] [CrossRef] [PubMed]
- Mahmoud, N.; Cirauqui, I.; Hostettler, A.; Doignon, C.; Soler, L.; Marescaux, J.; Montiel, J.M. ORBSLAM-based endoscope tracking and 3D reconstruction. In Computer-Assisted and Robotic Endoscopy; Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2017; Volume 10170, pp. 72–83. [Google Scholar] [CrossRef]
- Recasens, D.; Lamarca, J.; Fácil, J.M.; Montiel, J.M.M.; Civera, J. Endo-Depth-and-Motion: Localization and Reconstruction in Endoscopic Videos using Depth Networks and Photometric Constraints. arXiv 2021, arXiv:2103.16525. [Google Scholar] [CrossRef]
- Vilches, S.; Zappe, H.; Ataman, Ç. Multi-Point Fiber-Optic Distance Sensor for Endoscopic Surgery Monitoring. IEEE Photonics Technol. Lett. 2023, 35, 883–886. [Google Scholar] [CrossRef]
- Schmalz, C.; Forster, F.; Schick, A.; Angelopoulou, E. An endoscopic 3D scanner based on structured light. Med. Image Anal. 2012, 16, 1063–1072. [Google Scholar] [CrossRef]
- Jia, T.; Zhou, Z.; Gao, H.; Wang, B. Depth Measurement Based on Infrared Coded Structured Light. Hongwai Yu Jiguang Gongcheng/Infrared Laser Eng. 2015, 44, 1628–1632. [Google Scholar] [CrossRef]
- Lin, J.; Clancy, N.T.; Elson, D.S. An endoscopic structured light system using multispectral detection. Int. J. Comput. Assist. Surg. 2015, 10, 1941–1950. [Google Scholar] [CrossRef] [PubMed]
- Godard, C.; Aodha, O.M.; Brostow, G.J. Digging Into Self-Supervised Monocular Depth Estimation. arXiv 2018, arXiv:1806.01260. [Google Scholar]
- Yang, Y.; Shao, S.; Yang, T.; Wang, P.; Yang, Z.; Wu, C.; Liu, H. A geometry-aware deep network for depth estimation in monocular endoscopy. Eng. Appl. Artif. Intell. 2023, 122, 105989. [Google Scholar] [CrossRef]
- Vélez, A.F.M.; Marcinczak, J.M.; Grigat, R.R. Structure from motion based approaches to 3D reconstruction in minimal invasive laparoscopy. In Proceedings of the 9th International Conference on Image Analysis and Recognition, ICIAR 2012; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2012; pp. 296–303. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision, 2nd ed.; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Malti, A.; Bartoli, A.; Collins, T. Template-Based Conformal Shape-from-Motion-and-Shading for Laparoscopy. In Proceedings of the Information Processing in Computer-Assisted Interventions; Abolmaesumi, P., Joskowicz, L., Navab, N., Jannin, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1–10. [Google Scholar] [CrossRef]
- Malti, A. Variational Formulation of the Template-Based Quasi-Conformal Shape-from-Motion from Laparoscopic Images. Int. J. Adv. Comput. Sci. Appl. 2014, 5, 162–172. [Google Scholar] [CrossRef][Green Version]
- Wang, R.; Price, T.; Zhao, Q.; Frahm, J.M.; Rosenman, J.; Pizer, S. Improving 3D surface reconstruction from endoscopic video via fusion and refined reflectance modeling. In Proceedings of the Medical Imaging 2017: Image Processing, Orlando, FL, USA, 12–14 February 2017; Styner, M.A., Angelini, E.D., Eds.; International Society for Optics and Photonics SPIE: Bellingham, WA, USA, 2017; pp. 80–86. [Google Scholar] [CrossRef]
- Turan, M.; Pilavci, Y.Y.; Ganiyusufoglu, I.; Araújo, H.; Konukoglu, E.; Sitti, M. Sparse-then-Dense Alignment based 3D Map Reconstruction Method for Endoscopic Capsule Robots. arXiv 2017, arXiv:1708.09740. [Google Scholar] [CrossRef]
- Widya, A.R.; Monno, Y.; Imahori, K.; Okutomi, M.; Suzuki, S.; Gotoda, T.; Miki, K. 3D Reconstruction of Whole Stomach from Endoscope Video Using Structure-from-Motion. In Proceedings of the 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBC 2019, Berlin, Germany, 23–27 July 2019; pp. 3900–3904. [Google Scholar] [CrossRef]
- Rukhovich, D.; Mouritzen, D.; Kaestner, R.; Rufli, M.; Velizhev, A. Estimation of Absolute Scale in Monocular SLAM Using Synthetic Data. arXiv 2019, arXiv:1909.00713. [Google Scholar]
- Cadena, C.; Carlone, L.; Carrillo, H.; Latif, Y.; Scaramuzza, D.; Neira, J.; Reid, I.; Leonard, J.J. Past, Present, and Future of Simultaneous Localization and Mapping: Toward the Robust-Perception Age. IEEE Trans. Robot. 2016, 32, 1309–1332. [Google Scholar] [CrossRef]
- Mur-Artal, R.; Montiel, J.M.M.; Tardós, J.D. ORB-SLAM: A Versatile and Accurate Monocular SLAM System. arXiv 2015, arXiv:1502.00956. [Google Scholar] [CrossRef]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 2564–2571. [Google Scholar] [CrossRef]
- Mahmoud, N.; Collins, T.; Hostettler, A.; Soler, L.; Doignon, C.; Montiel, J. Live Tracking and Dense Reconstruction for Hand-held Monocular Endoscopy. IEEE Trans. Med Imaging 2018, 24, 3074–3086. [Google Scholar] [CrossRef]
- Blender Foundation. Home of the Blender Project—Free and Open 3D Creation Software. Available online: https://www.blender.org/ (accessed on 9 September 2022).
- Geng, J. Structured-light 3D surface imaging: A tutorial. Adv. Opt. Photonics 2011, 3, 128–160. [Google Scholar] [CrossRef]
- Albitar, C.; Graebling, P.; Doignon, C. Robust Structured Light Coding for 3D Reconstruction. In Proceedings of the 2007 IEEE 11th International Conference on Computer Vision, Rio de Janeiro, Brazil, 14–21 October 2007; pp. 1–6. [Google Scholar] [CrossRef]
- Lee, D.; Schachter, B. Two Algorithms for Constructing a Delaunay Triangulation. Int. J. Parallel Program. 1980, 9, 219–242. [Google Scholar] [CrossRef]
- Vollmer, J.; Mencl, R.; Müller, H. Improved Laplacian Smoothing of Noisy Surface Meshes. Comput. Graph. Forum 1999, 18, 131–138. [Google Scholar] [CrossRef]
- Kazhdan, M.; Bolitho, M.; Hoppe, H. Poisson Surface Reconstruction. In Proceedings of the Fourth Eurographics Symposium on Geometry Processing, SGP ’06, Cagliari, Italy, 26–28 June 2006; Eurographics Association: Eindhoven, The Netherlands, 2006; pp. 61–70. [Google Scholar] [CrossRef]
- Recherche, E.; Automatique, E.; Antipolis, S.; Zhang, Z. Iterative Point Matching for Registration of Free-Form Curves and Surfaces. Int. J. Comput. Vis. 1992, 13, 119–152. [Google Scholar] [CrossRef]
- Foix, S.; Alenya, G.; Torras, C. Lock-in Time-of-Flight (ToF) Cameras: A Survey. IEEE Sens. J. 2011, 11, 1917–1926. [Google Scholar] [CrossRef]
- Kolb, A.; Barth, E.; Koch, R.; Larsen, R. Time-of-Flight Sensors in Computer Graphics. In Proceedings of the EUROGRAPHICS (State of the Art Report); Eurographics Association: Eindhoven, The Netherlands, 2009. [Google Scholar] [CrossRef]
- Kolb, A.; Barth, E.; Koch, R. ToF-sensors: New dimensions for realism and interactivity. In Proceedings of the 2008 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, CVPR Workshops, Anchorage, AK, USA, 23–28 June 2008; pp. 1–6. [Google Scholar] [CrossRef]
- Laković, N.; Brkić, M.; Batinić, B.; Bajić, J.; Rajs, V.; Kulundžić, N. Application of low-cost VL53L0X ToF sensor for robot environment detection. In Proceedings of the 2019 18th International Symposium INFOTEH-JAHORINA (INFOTEH), Jahorina, East Sarajevo, Bosnia and Herzegovina, 23–28 June 2019; pp. 1–4. [Google Scholar] [CrossRef]
- De Ponte Müller, F. Survey on Ranging Sensors and Cooperative Techniques for Relative Positioning of Vehicles. Sensors 2017, 17, 271. [Google Scholar] [CrossRef] [PubMed]
- Groch, A.; Haase, S.; Wagner, M.; Kilgus, T.; Kenngott, H.; Schlemmer, H.P.; Hornegger, J.; Meinzer, H.P.; Maier-Hein, L. Optimierte endoskopische Time-of-Flight Oberflächenrekonstruktion durch Integration eines Struktur-durch-Bewegung-Ansatzes. In Proceedings of the Bildverarbeitung für die Medizin 2012: Algorithmen–Systeme—Anwendungen, Berlin, Germany, 18–20 March 2012; Springer: Berlin/Heidelberg, Germany, 2012. Chapter V9. pp. 39–44. [Google Scholar] [CrossRef]
- Roehl, S.; Bodenstedt, S.; Suwelack, S.; Kenngott, H.; Mueller-Stich, B.; Dillmann, R.; Speidel, S. Real-time surface reconstruction from stereo endoscopic images for intraoperative registration. In Proceedings of the MedicalImaging 2011: Visualization, Image-Guided Procedures, and Modeling, Lake Buena Vista, FL, USA, 13–15 February 2011; Society of Photo-Optical Instrumentation Engineers SPIE: Bellingham, WA, USA, 2011; Volume 7964, pp. 338–350. [Google Scholar] [CrossRef]
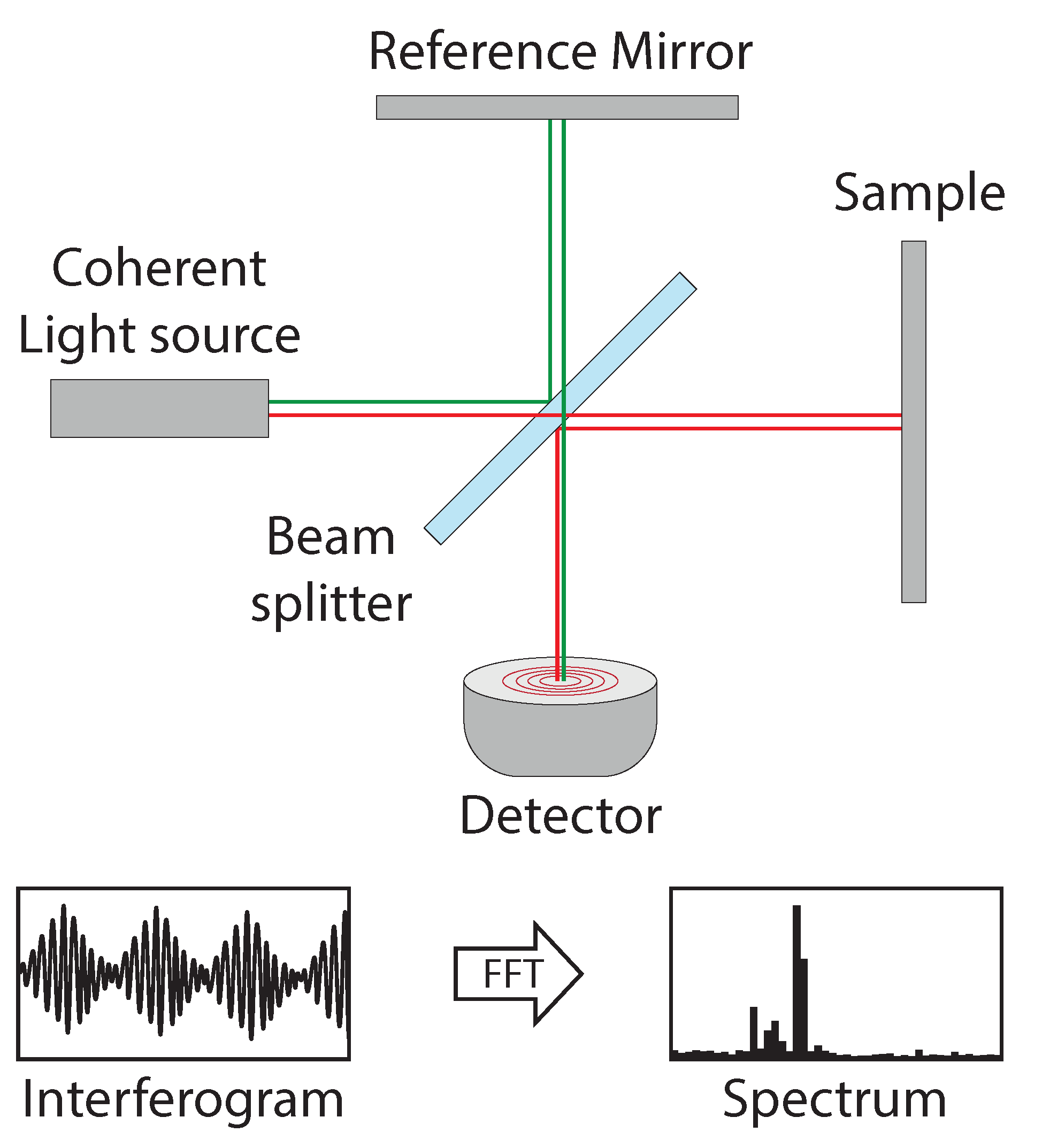
- Giacomo, P. The Michelson interferometer. Microchim. Acta 1987, 93, 19–31. [Google Scholar] [CrossRef]
- Horlick, G. Introduction to Fourier Transform Spectroscopy. Appl. Spectrosc. 1968, 22, 617–626. [Google Scholar] [CrossRef]
- Conen, N.; Luhmann, T. Overview of photogrammetric measurement techniques in minimally invasive surgery using endoscopes. ISPRS—Int. Arch. Photogramm. Remote. Spat. Inf. Sci. 2017, XLII-2/W4, 33–40. [Google Scholar] [CrossRef]
- Lucesoli, A.; Criante, L.; Simoni, F.; Di Donato, A.; Rozzi, T.; Farabollini, B.; Bonifazi, F. Quantitative endoscopy by FOLCI-based distance sensor. In Proceedings of the IEEE Sensors, Lecce, Italy, 26–29 October 2008; pp. 870–873. [Google Scholar] [CrossRef]
- Moon, S.; Choi, E.S. VCSEL-based swept source for low-cost optical coherence tomography. Biomed. Opt. Express 2017, 8, 1110–1121. [Google Scholar] [CrossRef]
- Hariyama, T.; Sandborn, P.A.M.; Watanabe, M.; Wu, M.C. High-accuracy range-sensing system based on FMCW using low-cost VCSEL. Opt. Express 2018, 26, 9285–9297. [Google Scholar] [CrossRef]
- Praveen, S. Efficient Depth Estimation Using Sparse Stereo-Vision with Other Perception Techniques. In Coding Theory; IntechOpen: London, UK, 2019; Chapter 7. [Google Scholar] [CrossRef]
- Liu, Y.; Aggarwal, J. 3.12—Local and Global Stereo Methods. In Handbook of Image and Video Processing (Second Edition), 2nd ed.; Communications, Networking and Multimedia; Bovik, A., Ed.; Academic Press: Burlington, NJ, USA, 2005; pp. 297–308. [Google Scholar] [CrossRef]
- Lee, S.; Hong, H. Near-real-time stereo matching method using both cross-based support regions in stereo views. Opt. Eng. 2018, 57, 023103. [Google Scholar] [CrossRef]
- Hosni, A.; Bleyer, M.; Rhemann, C.; Gelautz, M.; Rother, C. Real-Time local stereo matching using guided image filtering. In Proceedings of the 2011 IEEE International Conference on Multimedia and Expo (ICME), Barcelona, Spain, 11–15 July 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Yang, Q.; Engels, C.; Akbarzadeh, A. Near Real-time Stereo for Weakly-Textured Scenes. In Proceedings of the British Machine Vision Conference, Leeds, UK, 1–4 September 2008; BMVA Press: Durham, UK, 2008; pp. 1–10. [Google Scholar] [CrossRef]
- Kowalczuk, J.; Psota, E.T.; Perez, L.C. Real-Time Stereo Matching on CUDA Using an Iterative Refinement Method for Adaptive Support-Weight Correspondences. IEEE Trans. Circuits Syst. Video Technol. 2013, 23, 94–104. [Google Scholar] [CrossRef][Green Version]
- Riechert, C.; Zilly, F.; Mueller, M.; Kauff, P. Real-time disparity estimation using line-wise hybrid recursive matching and cross-bilateral median up-sampling. In Proceedings of the 21st International Conference on Pattern Recognition (ICPR2012), Tsukuba Science City, Japan, 11–15 November 2012; pp. 3168–3171, ISBN 978-4-9906441-0-9. [Google Scholar]
- Zhang, K.; Lu, J.; Lafruit, G.; Lauwereins, R.; Gool, L.V. Real-time accurate stereo with bitwise fast voting on CUDA. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision Workshops, ICCV Workshops, Kyoto, Japan, 27 September–4 October 2009; pp. 794–800. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, L.; Yang, R.; Wang, S.; Liao, M.; Nistér, D. Real-time Global Stereo Matching Using Hierarchical Belief Propagation. In Proceedings of the British Machine Vision Conference, Edinburgh, UK, 4–7 September 2006; Volume 6, pp. 989–998. Available online: https://bmva-archive.org.uk/bmvc/2006/papers/324.pdf (accessed on 12 March 2024).
- Totz, J.; Thompson, S.; Stoyanov, D.; Gurusamy, K.; Davidson, B.; Hawkes, D.; Clarkson, M. Fast Semi-dense Surface Reconstruction from Stereoscopic Video in Laparoscopic Surgery. In Proceedings of the IPCAI, Fukuoka, Japan, 28 June 2014; pp. 206–215. [Google Scholar] [CrossRef]
- Roehl, S.; Bodenstedt, S.; Suwelack, S.; Kenngott, H.; Mueller-Stich, B.P.; Dillmann, R.; Speidel, S. Dense GPU-enhanced surface reconstruction from stereo endoscopic images for intraoperative registration. Med Phys. 2012, 39, 1632–1645. [Google Scholar] [CrossRef] [PubMed]
- Singh, T.; Alsadoon, A.; Prasad, P.; Alsadoon, O.H.; Venkata, H.S.; Alrubaie, A. A novel enhanced hybrid recursive algorithm: Image processing based augmented reality for gallbladder and uterus visualisation. Egypt. Inform. J. 2020, 21, 105–118. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, J.; Chu, R. Objective Evaluation Criteria for Shooting Quality of Stereo Cameras over Short Distance. Radioengineering 2015, 24, 305–313. [Google Scholar] [CrossRef]
- Patoommakesorn, K.; Vignat, F.; Villeneuve, F. The 3D Edge Reconstruction from 2D Image by Using Correlation Based Algorithm. In Proceedings of the 2019 IEEE 6th International Conference on Industrial Engineering and Applications (ICIEA), Tokyo, Japan, 12–15 April 2019; pp. 372–376. [Google Scholar] [CrossRef]
- Lin Chen, F.R.; Heipke, C. Feature detection and description for image matching: From hand-crafted design to deep learning. Geo-Spat. Inf. Sci. 2021, 24, 58–74. [Google Scholar] [CrossRef]
- Zhang, K.; Lu, J.; Lafruit, G. Cross-Based Local Stereo Matching Using Orthogonal Integral Images. IEEE Trans. Circuits Syst. Video Technol. 2009, 19, 1073–1079. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, L.; Yang, R.; Stewénius, H.; Nistér, D. Stereo Matching with Color-Weighted Correlation, Hierarchical Belief Propagation, and Occlusion Handling. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 492–504. [Google Scholar] [CrossRef]
- Felzenszwalb, P.; Huttenlocher, D. Efficient belief propagation for early vision. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR 2004, Washington, DC, USA, 27 June–2 July 2004; Volume 1, p. I. [Google Scholar] [CrossRef]
- Fischler, M.A.; Bolles, R.C. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Kauff, P.; Brandenburg, N.; Karl, M.; Schreer, O. Fast Hybrid Block- And Pixel-Recursive Disparity Analysis For Real-Time Applications In Immersive Tele-Conference Scenarios. In Proceedings of the 9-th International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision, Plzen, Czech Republic, 5–9 February 2001; pp. 198–205. [Google Scholar]
- Waizenegger, W.; Feldmann, I.; Schreer, O.; Kauff, P.; Eisert, P. Real-time 3D body reconstruction for immersive TV. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 360–364. [Google Scholar] [CrossRef]
- Zuiderveld, K. Contrast Limited Adaptive Histogram Equalization; Academic Press Professional, Inc.: Cambridge, MA, USA, 1994; pp. 474–485. ISBN 0-12-336156-7. [Google Scholar] [CrossRef]
- Yoon, K.J.; Kweon, I.S. Locally adaptive support-weight approach for visual correspondence search. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 2, pp. 924–931. [Google Scholar] [CrossRef]
- He, K.; Sun, J.; Tang, X. Guided Image Filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1397–1409. [Google Scholar] [CrossRef]
- Choudhary, B.K.; Kumar, N.; And, S.; Shanker, P. Pyramid method in image processing. J. Inf. Syst. Commun. 2012, 3, 269. [Google Scholar]
- Song, J.; Zhu, Q.; Lin, J.; Ghaffari, M. BDIS: Bayesian Dense Inverse Searching Method for Real-Time Stereo Surgical Image Matching. IEEE Trans. Robot. 2022, 39, 1388–1406. [Google Scholar] [CrossRef]
- Mao, Y.; Liu, Z.; Li, W.; Dai, Y.; Wang, Q.; Kim, Y.T.; Lee, H.S. UASNet: Uncertainty Adaptive Sampling Network for Deep Stereo Matching. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 6311–6319. [Google Scholar] [CrossRef]
- Xu, G.; Cheng, J.; Guo, P.; Yang, X. ACVNet: Attention Concatenation Volume for Accurate and Efficient Stereo Matching. arXiv 2022, arXiv:2203.02146. [Google Scholar]
- Cheng, X.; Zhong, Y.; Harandi, M.; Dai, Y.; Chang, X.; Drummond, T.; Li, H.; Ge, Z. Hierarchical Neural Architecture Search for Deep Stereo Matching. arXiv 2020, arXiv:2010.13501. [Google Scholar]
- Zhu, X.; Guo, K.; Fang, H.; Chen, L.; Ren, S.; Hu, B. Cross View Capture for Stereo Image Super-Resolution. IEEE Trans. Multimed. 2021, 24, 3074–3086. [Google Scholar] [CrossRef]
- Tankovich, V.; Häne, C.; Fanello, S.R.; Zhang, Y.; Izadi, S.; Bouaziz, S. HITNet: Hierarchical Iterative Tile Refinement Network for Real-time Stereo Matching. arXiv 2020, arXiv:2007.12140. [Google Scholar]
- Yang, G.; Manela, J.; Happold, M.; Ramanan, D. Hierarchical Deep Stereo Matching on High-Resolution Images. arXiv 2019, arXiv:1912.06704. [Google Scholar] [CrossRef]
- Duggal, S.; Wang, S.; Ma, W.C.; Hu, R.; Urtasun, R. DeepPruner: Learning Efficient Stereo Matching via Differentiable PatchMatch. arXiv 2019, arXiv:1909.05845. [Google Scholar]
- Mayer, N.; Ilg, E.; Hausser, P.; Fischer, P.; Cremers, D.; Dosovitskiy, A.; Brox, T. A Large Dataset to Train Convolutional Networks for Disparity, Optical Flow, and Scene Flow Estimation. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 4040–4048. [Google Scholar] [CrossRef]
- Tonioni, A.; Tosi, F.; Poggi, M.; Mattoccia, S.; Di Stefano, L. Real-Time self-adaptive deep stereo. arXiv 2019, arXiv:1810.05424. [Google Scholar]
- Khamis, S.; Fanello, S.R.; Rhemann, C.; Kowdle, A.; Valentin, J.P.C.; Izadi, S. StereoNet: Guided Hierarchical Refinement for Real-Time Edge-Aware Depth Prediction. arXiv 2018, arXiv:1807.08865. [Google Scholar]
- Garg, R.; G, V.K.B.; Reid, I.D. Unsupervised CNN for Single View Depth Estimation: Geometry to the Rescue. arXiv 2016, arXiv:1603.04992. [Google Scholar]
- Zhou, K.; Meng, X.; Cheng, B. Review of Stereo Matching Algorithms Based on Deep Learning. Comput. Intell. Neurosci. 2020, 2020, 8562323. [Google Scholar] [CrossRef] [PubMed]
- Žbontar, J.; LeCun, Y. Computing the stereo matching cost with a convolutional neural network. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1592–1599. [Google Scholar] [CrossRef]
- Huo, J.; Zhou, C.; Yuan, B.; Yang, Q.; Wang, L. Real-Time Dense Reconstruction with Binocular Endoscopy Based on StereoNet and ORB-SLAM. Sensors 2023, 23, 2074. [Google Scholar] [CrossRef] [PubMed]
- Mayer, N.; Ilg, E.; Fischer, P.; Hazirbas, C.; Cremers, D.; Dosovitskiy, A.; Brox, T. What Makes Good Synthetic Training Data for Learning Disparity and Optical Flow Estimation? arXiv 2018, arXiv:1801.06397. [Google Scholar] [CrossRef]
- Chen, Z.; Marzullo, A.; Alberti, D.; Lievore, E.; Fontana, M.; De Cobelli, O.; Musi, G.; Ferrigno, G.; De Momi, E. FRSR: Framework for real-time scene reconstruction in robot-assisted minimally invasive surgery. Comput. Biol. Med. 2023, 163, 107121. [Google Scholar] [CrossRef]
- Bardozzo, F.; Collins, T.; Forgione, A.; Hostettler, A.; Tagliaferri, R. StaSiS-Net: A stacked and siamese disparity estimation network for depth reconstruction in modern 3D laparoscopy. Med. Image Anal. 2022, 77, 102380. [Google Scholar] [CrossRef] [PubMed]
- Benjamens, S.; Dhunnoo, P.; Mesko, B. The state of artificial intelligence-based FDA-approved medical devices and algorithms: An online database. NPJ Digit. Med. 2020, 3, 118. [Google Scholar] [CrossRef]
- Food and Drug Administration. Proposed Regulatory Framework for Modifications to AI/ML-Based Software as a Medical Device. 2019. Available online: https://www.regulations.gov/document/FDA-2019-N-1185-0001 (accessed on 9 October 2023).
- Heinrichs, M.; Rodehorst, V.; Hellwich, O. Efficient Semi-Global Matching for Trinocular Stereo. In Proceedings of the PIA 2007—Photogrammetric Image Analysis, Munich, Germany, 19–21 September 2007. [Google Scholar]
- Conen, N.; Luhmann, T.; Maas, H.G. Development and Evaluation of a Miniature Trinocular Camera System for Surgical Measurement Applications. PFG-Photogramm. Remote Sens. Geoinf. Sci. 2017, 85, 127–138. [Google Scholar] [CrossRef]
- Hirschmüller, H. Stereo Processing by Semi-Global Matching and Mutual Information. IEEE Trans. Pattern Anal. Mach. 2008, 30, 328–341. [Google Scholar] [CrossRef]
- Hassanfiroozi, A.; Huang, Y.P.; Javidi, B.; Shieh, H.P. Hexagonal liquid crystal lens array for 3D endoscopy. Opt. Express 2015, 23, 971–981. [Google Scholar] [CrossRef]
- Hassanfiroozi, A. Dual layer electrode liquid crystal lens for 2D/3D tunable endoscopy imaging system. Opt. Express 2016, 24, 8527–8538. [Google Scholar] [CrossRef] [PubMed]


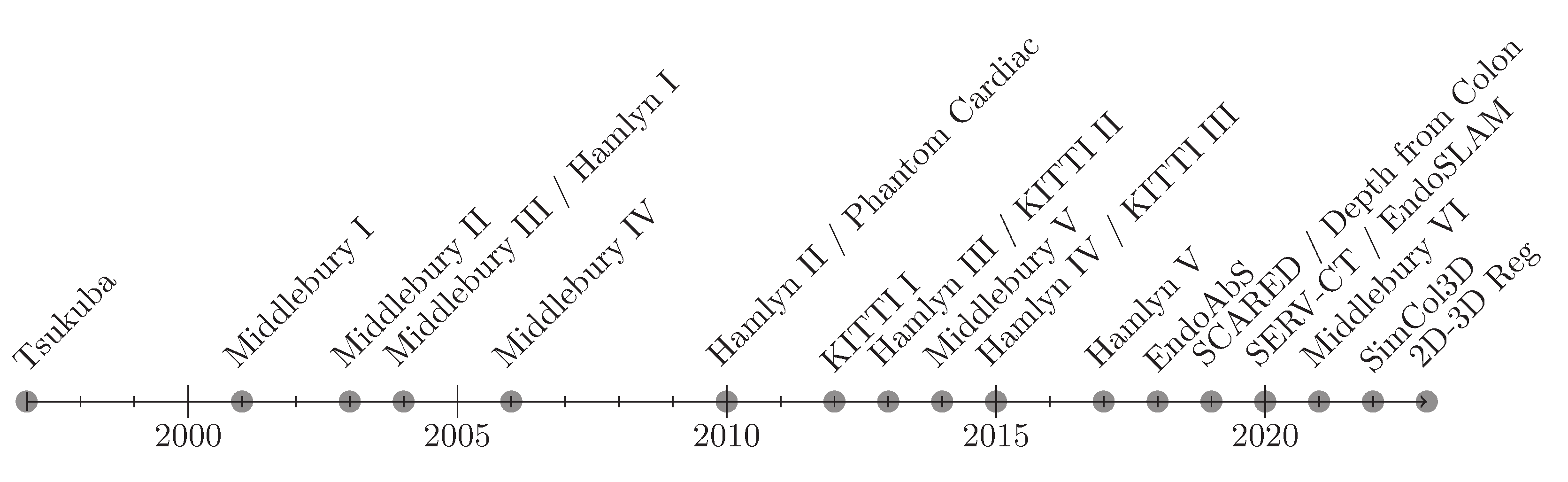
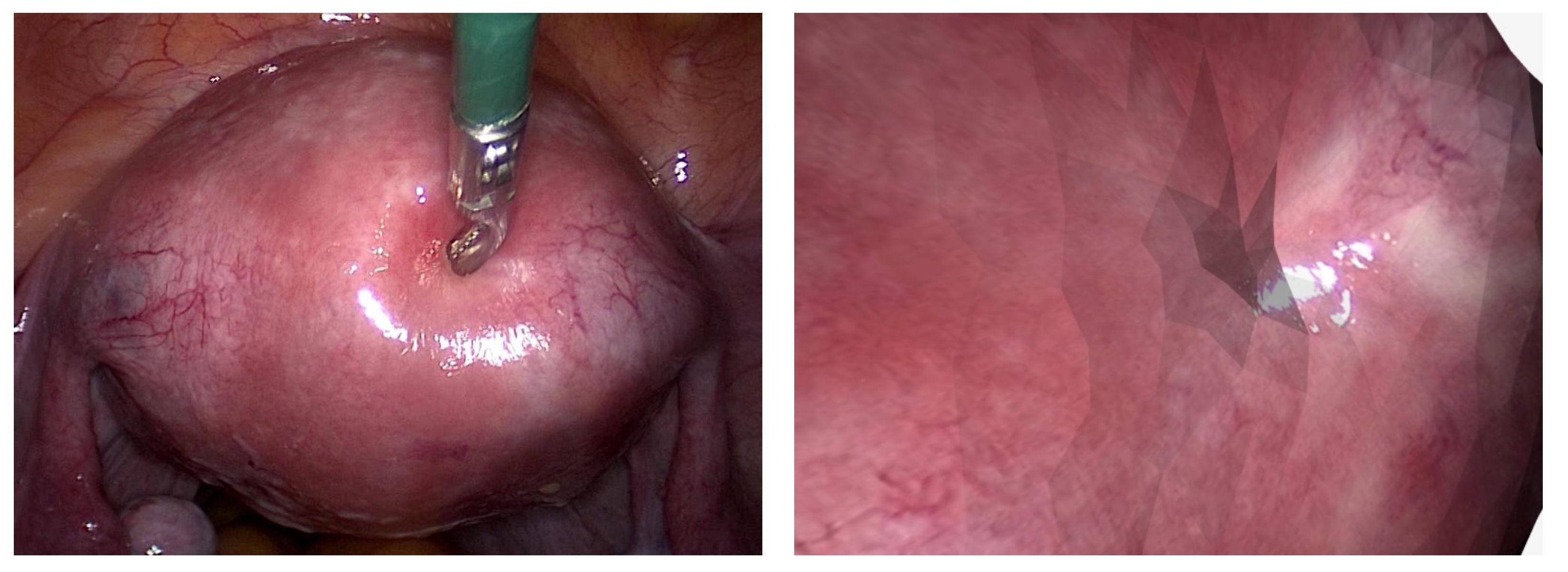
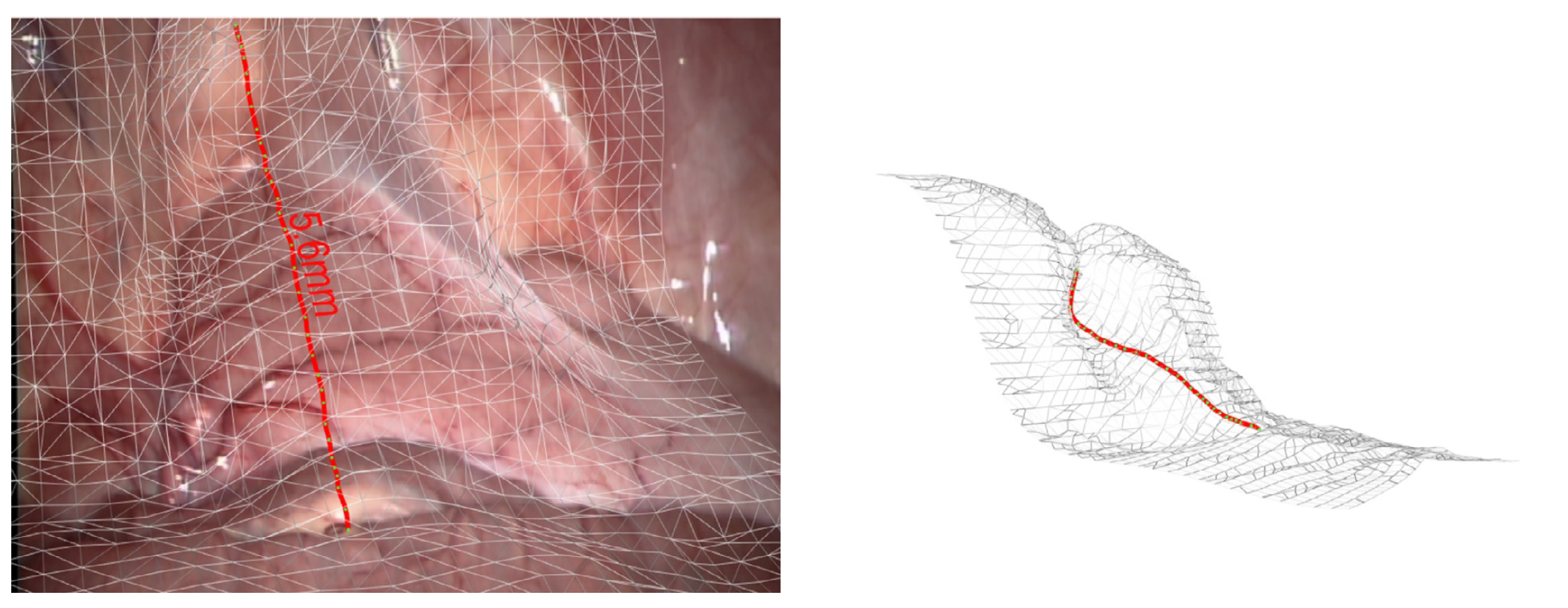
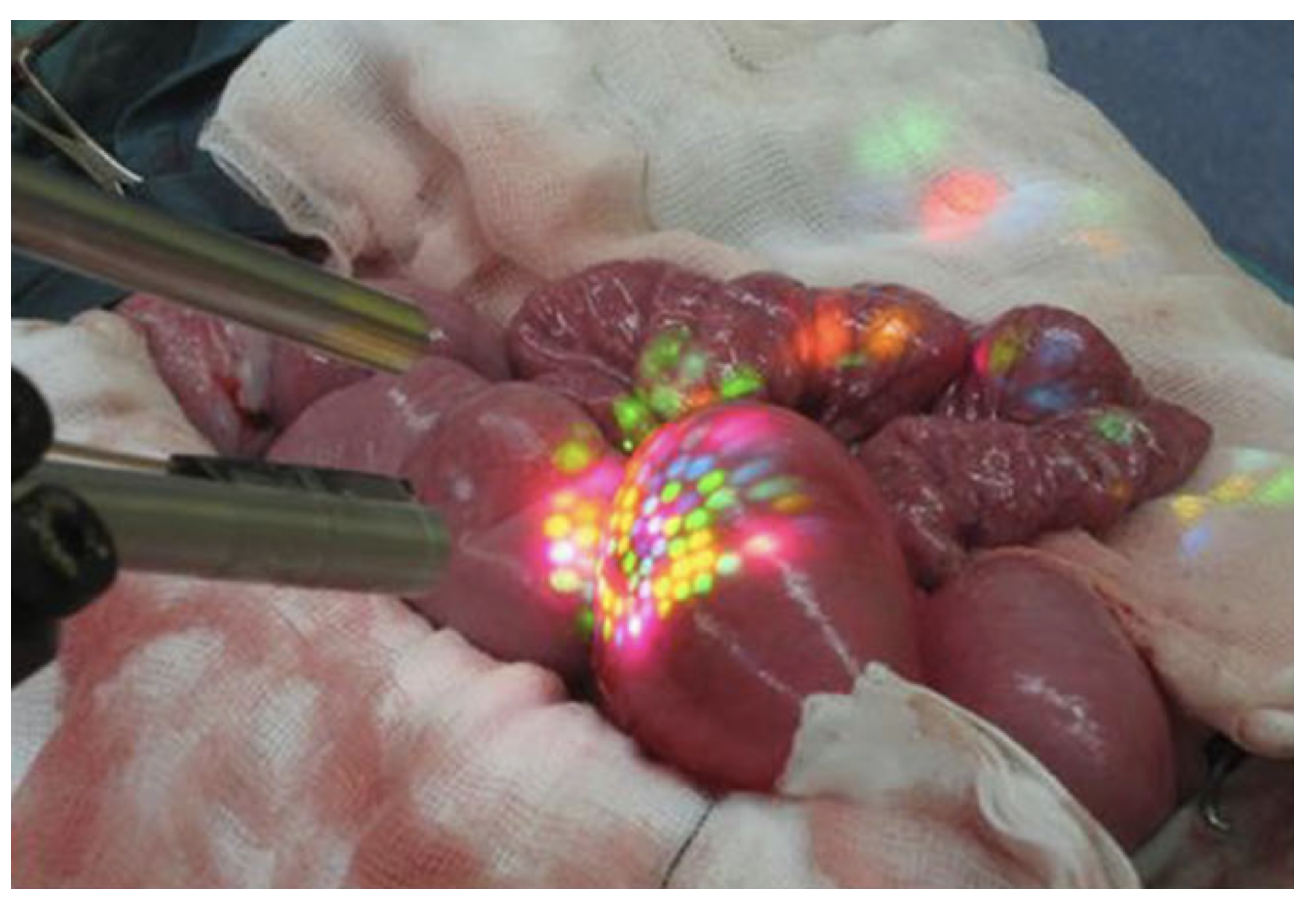
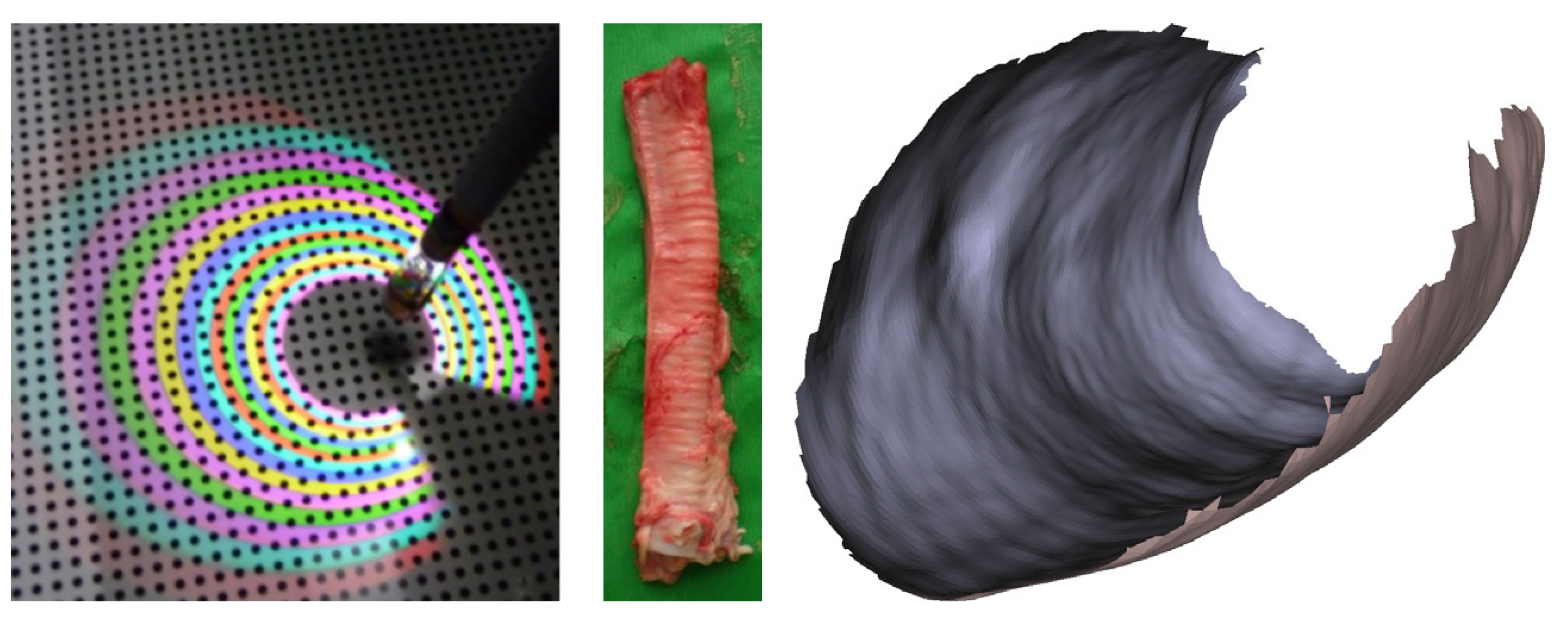





| Dataset | Static | Dynamic | Ground Truth (GT) Type | Remarks |
|---|---|---|---|---|
| EndoSlam | – | X | Structured Light | Monoscopic image sequence |
| SimCol3D | – | X | CT data | Monoscopic images & videos |
| 2D-3D Registration | – | X | 3D Model | Monoscopic videos |
| Depth from Colon | – | X | 3D Model | Monoscopic image sequence |
| Hamlyn | – | X | partly available | Mono- & Stereoscopic |
| Tsukuba | X | – | Manual segmentation | The first dataset with GT |
| Middlebury | X | – | Structured Light | Stereo images |
| Kitti | – | X | LiDAR | Stereoscopic videos |
| SCARED | – | X | Structured Light | Stereoscopic videos |
| SERV-CT | X | – | CT data | Stereoscopic images |
| EndoAbs | X | – | Laser | Stereoscopic & Synthetic 3D Models |
| Phantom Cardiac | – | X | CT data | Stereoscopic videos |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Richter, A.; Steinmann, T.; Rosenthal, J.-C.; Rupitsch, S.J. Advances in Real-Time 3D Reconstruction for Medical Endoscopy. J. Imaging 2024, 10, 120. https://doi.org/10.3390/jimaging10050120
Richter A, Steinmann T, Rosenthal J-C, Rupitsch SJ. Advances in Real-Time 3D Reconstruction for Medical Endoscopy. Journal of Imaging. 2024; 10(5):120. https://doi.org/10.3390/jimaging10050120
Chicago/Turabian StyleRichter, Alexander, Till Steinmann, Jean-Claude Rosenthal, and Stefan J. Rupitsch. 2024. "Advances in Real-Time 3D Reconstruction for Medical Endoscopy" Journal of Imaging 10, no. 5: 120. https://doi.org/10.3390/jimaging10050120
APA StyleRichter, A., Steinmann, T., Rosenthal, J.-C., & Rupitsch, S. J. (2024). Advances in Real-Time 3D Reconstruction for Medical Endoscopy. Journal of Imaging, 10(5), 120. https://doi.org/10.3390/jimaging10050120










