Harmonizing Image Forgery Detection & Localization: Fusion of Complementary Approaches
Abstract
:1. Introduction
2. Related Work
2.1. Image Forgery Detection and Localization Methods
2.2. Fusion Methods
2.2.1. Feature-Level Fusion
2.2.2. Pixel-Level Fusion
3. Selection & Complementariness of Image Forgery Detection Methods
3.1. Experimental Setup
3.1.1. Image Forgery Detection Algorithms
3.1.2. Evaluation Datasets
3.1.3. Performance Metrics
3.1.4. Theoretical Oracle Fusion & Complementary F1 Delta Metric
3.2. Performance & Complementariness Results
4. Proposed Fusion Method
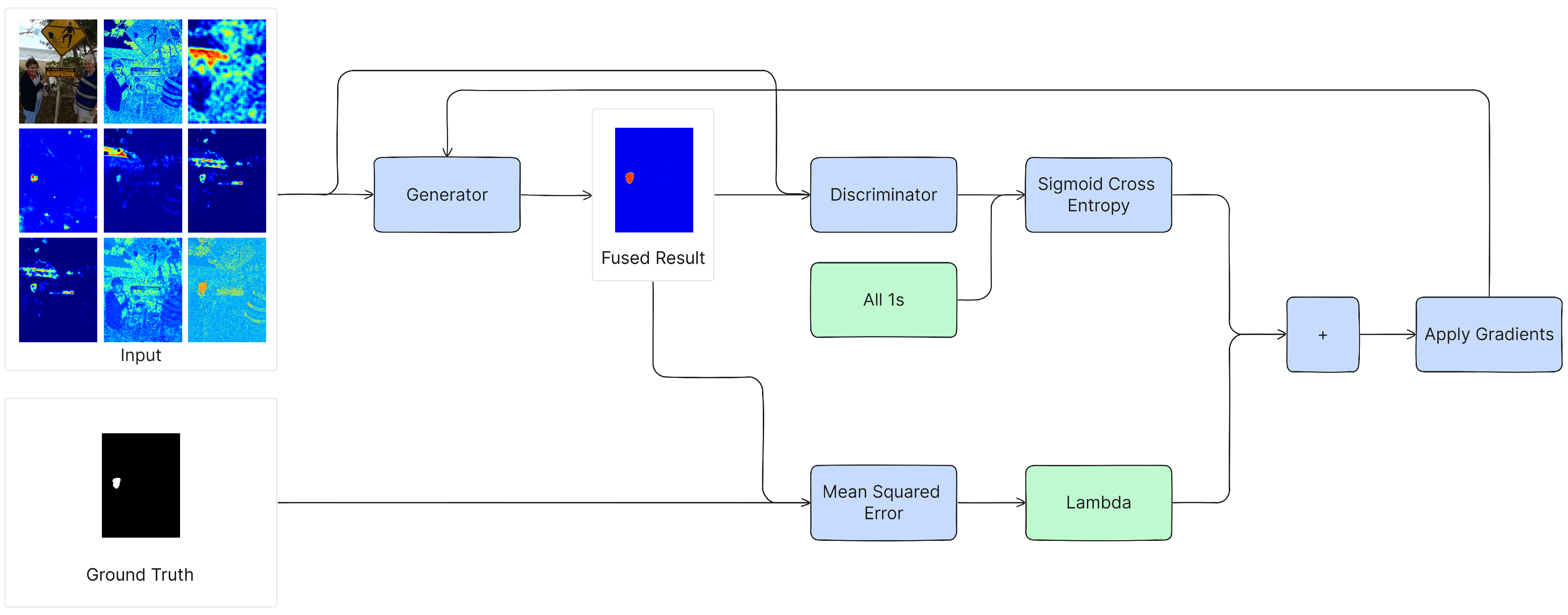
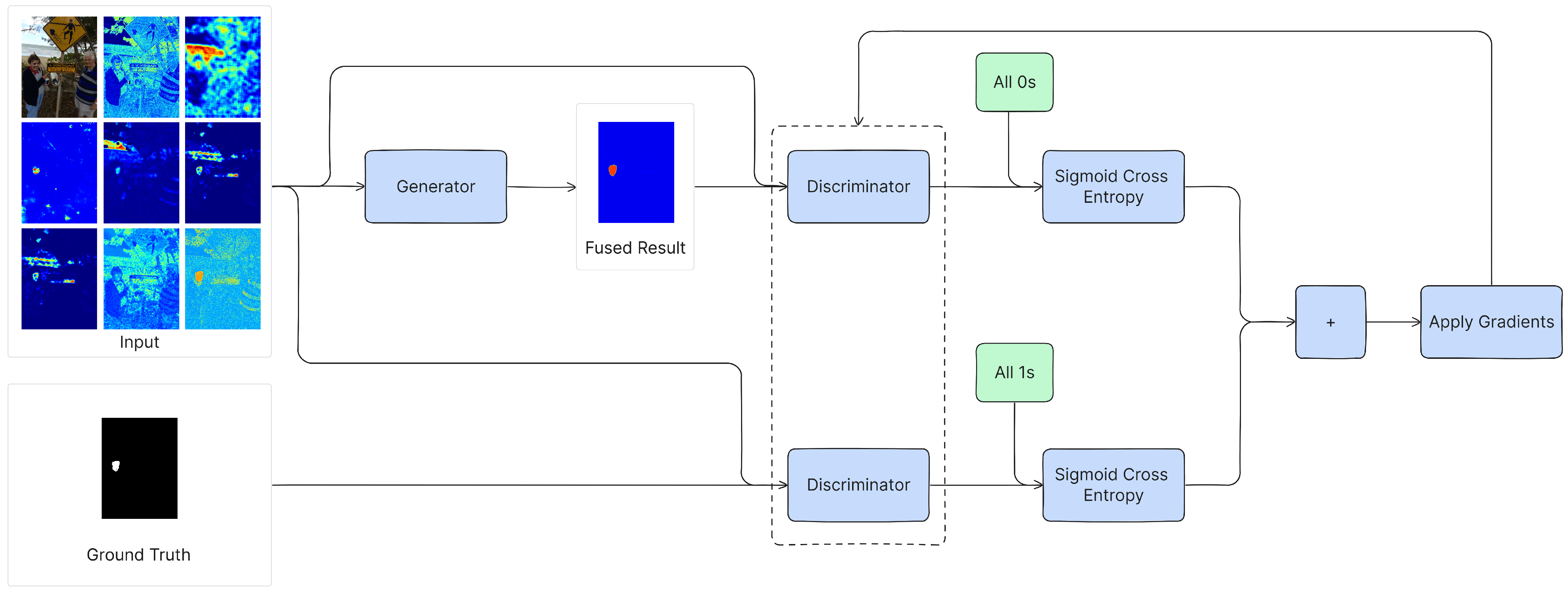
4.1. Training Methodology
4.1.1. Generator
4.1.2. Discriminator
4.2. Inference Methodology
5. Evaluation of Proposed Fusion Method
5.1. Experimental Setup
5.1.1. Training Setup
5.1.2. Evaluation Setup
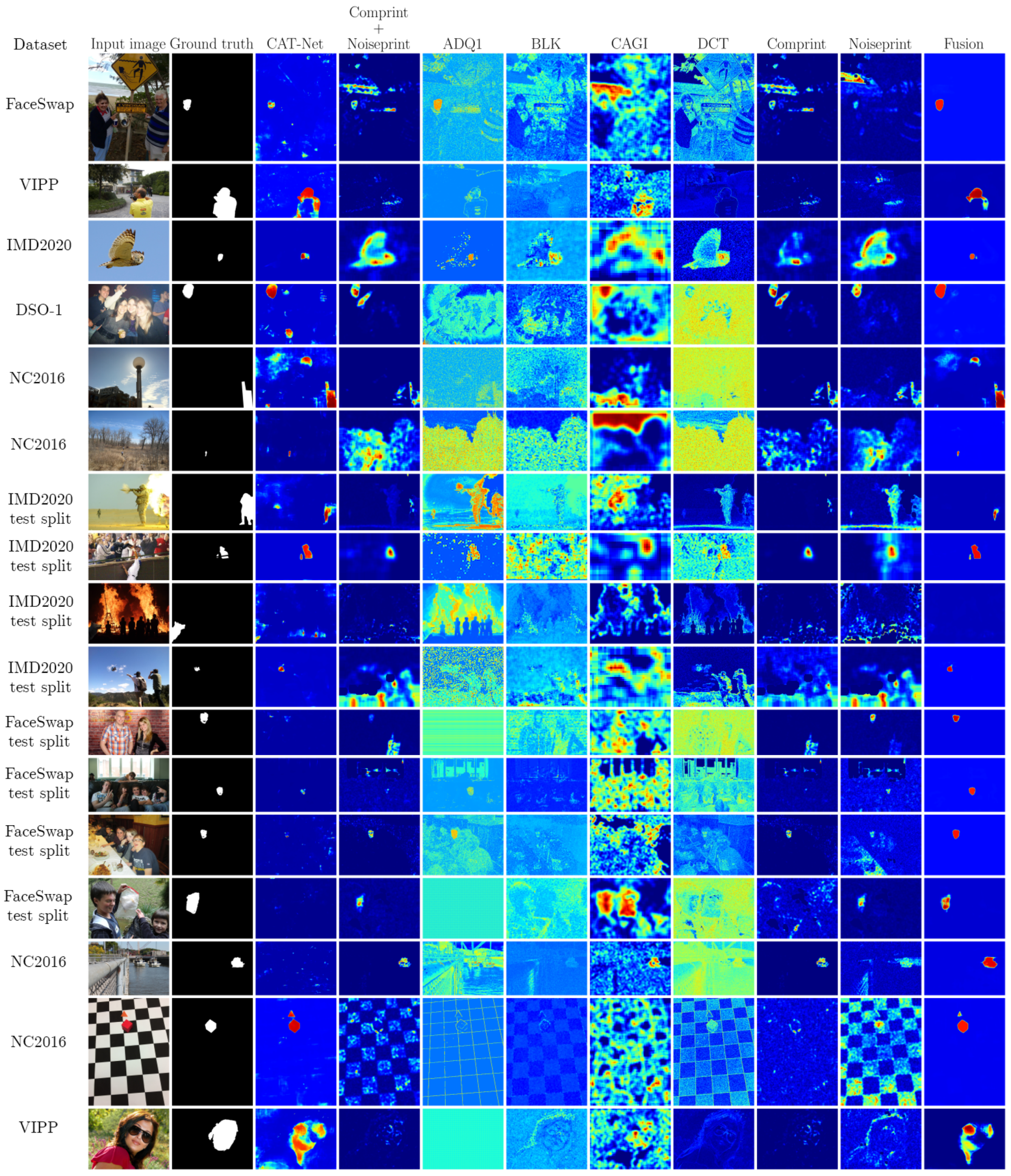
5.2. Results
5.2.1. Image Forgery Localization Performance
5.2.2. Image Forgery Detection Performance
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Performance and Complementarity Tables
| Dataset: VIPP [32] | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Algorithm | F1 | Complementary F1 Delta | |||||||
| CAT-Net | ADQ1 | BLK | CAGI | DCT | Compr | Compr | Noisepr + Noisepr | ||
| CAT-Net [27] | 0.716 | - | 0.039 | 0.049 | 0.019 | 0.045 | 0.037 | 0.091 | 0.088 |
| ADQ1 [23] | 0.503 | 0.246 | - | 0.087 | 0.072 | 0.054 | 0.122 | 0.155 | 0.146 |
| BLK [20] | 0.431 | 0.334 | 0.160 | - | 0.117 | 0.097 | 0.154 | 0.206 | 0.175 |
| CAGI [21] | 0.438 | 0.299 | 0.144 | 0.111 | - | 0.095 | 0.134 | 0.187 | 0.180 |
| DCT [22] | 0.432 | 0.329 | 0.132 | 0.096 | 0.100 | - | 0.147 | 0.198 | 0.184 |
| Comprint [11] | 0.496 | 0.257 | 0.138 | 0.089 | 0.075 | 0.083 | - | 0.095 | 0.139 |
| Compr + Noisepr [11] | 0.581 | 0.227 | 0.087 | 0.057 | 0.044 | 0.050 | 0.011 | - | 0.062 |
| Noiseprint [17] | 0.556 | 0.248 | 0.090 | 0.050 | 0.062 | 0.060 | 0.079 | 0.086 | - |
| Dataset: IMD2020 [29] | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Algorithm | F1 | Complementary F1 Delta | |||||||
| CAT-Net | ADQ1 | BLK | CAGI | DCT | Compr | Compr + Noisepr | Noisepr | ||
| CAT-Net [27] | 0.850 | - | 0.001 | 0.003 | 0.003 | 0.002 | 0.006 | 0.008 | 0.006 |
| ADQ1 [23] | 0.292 | 0.560 | - | 0.064 | 0.087 | 0.074 | 0.138 | 0.173 | 0.150 |
| BLK [20] | 0.263 | 0.590 | 0.093 | - | 0.096 | 0.085 | 0.169 | 0.201 | 0.162 |
| CAGI [21] | 0.297 | 0.556 | 0.083 | 0.062 | - | 0.098 | 0.151 | 0.181 | 0.146 |
| DCT [22] | 0.313 | 0.538 | 0.052 | 0.035 | 0.081 | - | 0.135 | 0.163 | 0.134 |
| Comprint [11] | 0.297 | 0.466 | 0.040 | 0.041 | 0.058 | 0.058 | - | 0.071 | 0.087 |
| Compr + Noisepr [11] | 0.437 | 0.421 | 0.029 | 0.027 | 0.041 | 0.040 | 0.025 | - | 0.034 |
| Noiseprint [17] | 0.396 | 0.461 | 0.046 | 0.029 | 0.048 | 0.052 | 0.082 | 0.075 | - |
| Dataset: DSO-1 [33] | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Algorithm | F1 | Complementary F1 Delta | |||||||
| CAT-Net | ADQ1 | BLK | CAGI | DCT | Compr | Compr + Noisepr | Noisepr | ||
| CAT-Net [27] | 0.675 | - | 0.029 | 0.072 | 0.072 | 0.019 | 0.176 | 0.202 | 0.201 |
| ADQ1 [23] | 0.420 | 0.301 | - | 0.082 | 0.149 | 0.024 | 0.365 | 0.405 | 0.396 |
| BLK [20] | 0.456 | 0.291 | 0.043 | - | 0.131 | 0.014 | 0.349 | 0.386 | 0.378 |
| CAGI [21] | 0.512 | 0.235 | 0.053 | 0.076 | - | 0.013 | 0.291 | 0.331 | 0.322 |
| DCT [22] | 0.347 | 0.347 | 0.082 | 0.123 | 0.179 | - | 0.420 | 0.470 | 0.466 |
| Comprint [11] | 0.763 | 0.088 | 0.016 | 0.043 | 0.040 | 0.004 | - | 0.055 | 0.081 |
| Compr + Noisepr [11] | 0.813 | 0.063 | 0.008 | 0.029 | 0.030 | 0.003 | 0.004 | - | 0.038 |
| Noiseprint [17] | 0.810 | 0.067 | 0.007 | 0.025 | 0.025 | 0.003 | 0.034 | 0.042 | - |
| Dataset: OpenForensics [30] | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Algorithm | F1 | Complementary F1 Delta | |||||||
| CAT-Net | ADQ1 | BLK | CAGI | DCT | Compr | Compr + Noisepr | Noisepr | ||
| CAT-Net [27] | 0.948 | - | 0.001 | 0.001 | 0.002 | 0.001 | 0.012 | 0.012 | 0.009 |
| ADQ1 [23] | 0.483 | 0.466 | - | 0.020 | 0.046 | 0.027 | 0.252 | 0.277 | 0.225 |
| BLK [20] | 0.263 | 0.686 | 0.240 | - | 0.086 | 0.178 | 0.386 | 0.453 | 0.411 |
| CAGI [21] | 0.294 | 0.657 | 0.235 | 0.056 | - | 0.182 | 0.365 | 0.429 | 0.389 |
| DCT [22] | 0.423 | 0.526 | 0.087 | 0.019 | 0.053 | - | 0.299 | 0.329 | 0.274 |
| Comprint [11] | 0.630 | 0.331 | 0.105 | 0.019 | 0.028 | 0.092 | - | 0.108 | 0.151 |
| Compr + Noisepr [11] | 0.711 | 0.249 | 0.049 | 0.006 | 0.012 | 0.041 | 0.028 | - | 0.058 |
| Noiseprint [17] | 0.671 | 0.286 | 0.037 | 0.003 | 0.012 | 0.025 | 0.110 | 0.098 | - |
| Dataset: FaceSwap [31] | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Algorithm | F1 | Complementary F1 Delta | |||||||
| CAT-Net | ADQ1 | BLK | CAGI | DCT | Compr | Compr + Noisepr | Noisepr | ||
| CAT-Net [27] | 0.449 | - | 0.068 | 0.016 | 0.044 | 0.032 | 0.099 | 0.130 | 0.105 |
| ADQ1 [23] | 0.282 | 0.235 | - | 0.023 | 0.048 | 0.024 | 0.127 | 0.173 | 0.153 |
| BLK [20] | 0.106 | 0.359 | 0.199 | - | 0.109 | 0.104 | 0.265 | 0.318 | 0.249 |
| CAGI [21] | 0.184 | 0.310 | 0.146 | 0.031 | - | 0.084 | 0.210 | 0.259 | 0.203 |
| DCT [22] | 0.191 | 0.290 | 0.115 | 0.019 | 0.077 | - | 0.192 | 0.244 | 0.192 |
| Comprint [11] | 0.351 | 0.199 | 0.057 | 0.020 | 0.043 | 0.032 | - | 0.074 | 0.125 |
| Compr + Noisepr [11] | 0.412 | 0.168 | 0.041 | 0.011 | 0.031 | 0.022 | 0.013 | - | 0.060 |
| Noiseprint [17] | 0.347 | 0.208 | 0.086 | 0.008 | 0.040 | 0.035 | 0.128 | 0.125 | - |
| Dataset: Coverage [34] | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Algorithm | F1 | Complementary F1 Delta | |||||||
| CAT-Net | ADQ1 | BLK | CAGI | DCT | Compr | Compr + Noisepr | Noisepr | ||
| CAT-Net [27] | 0.573 | - | 0.003 | 0.005 | 0.032 | 0.004 | 0.037 | 0.043 | 0.027 |
| ADQ1 [23] | 0.211 | 0.365 | - | 0.040 | 0.094 | 0.023 | 0.146 | 0.165 | 0.128 |
| BLK [20] | 0.242 | 0.335 | 0.008 | - | 0.073 | 0.010 | 0.123 | 0.141 | 0.107 |
| CAGI [21] | 0.298 | 0.307 | 0.006 | 0.017 | - | 0.009 | 0.104 | 0.118 | 0.086 |
| DCT [22] | 0.222 | 0.355 | 0.012 | 0.030 | 0.085 | - | 0.139 | 0.157 | 0.120 |
| Comprint [11] | 0.349 | 0.261 | 0.009 | 0.017 | 0.053 | 0.013 | - | 0.063 | 0.046 |
| Compr + Noisepr [11] | 0.368 | 0.248 | 0.008 | 0.015 | 0.049 | 0.011 | 0.044 | - | 0.030 |
| Noiseprint [17] | 0.332 | 0.268 | 0.007 | 0.017 | 0.053 | 0.010 | 0.063 | 0.066 | - |
| Dataset: NC2016 [35] | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Algorithm | F1 | Complementary F1 Delta | |||||||
| CAT-Net | ADQ1 | BLK | CAGI | DCT | Compr | Compr + Noisepr | Noisepr | ||
| CAT-Net [27] | 0.487 | - | 0.017 | 0.034 | 0.055 | 0.010 | 0.094 | 0.107 | 0.097 |
| ADQ1 [23] | 0.206 | 0.298 | - | 0.077 | 0.129 | 0.032 | 0.220 | 0.251 | 0.227 |
| BLK [20] | 0.233 | 0.287 | 0.050 | - | 0.092 | 0.028 | 0.186 | 0.218 | 0.192 |
| CAGI [21] | 0.293 | 0.250 | 0.039 | 0.030 | - | 0.026 | 0.139 | 0.169 | 0.146 |
| DCT [22] | 0.183 | 0.313 | 0.055 | 0.079 | 0.137 | - | 0.239 | 0.266 | 0.239 |
| Comprint [11] | 0.398 | 0.183 | 0.027 | 0.021 | 0.037 | 0.024 | - | 0.060 | 0.073 |
| Compr + Noisepr [11] | 0.439 | 0.154 | 0.018 | 0.012 | 0.026 | 0.009 | 0.019 | - | 0.022 |
| Noiseprint [17] | 0.413 | 0.171 | 0.021 | 0.013 | 0.030 | 0.010 | 0.059 | 0.048 | - |
References
- Verdoliva, L. Media Forensics and DeepFakes: An overview. IEEE J. Sel. Top. Signal Process. 2020, 14, 910–932. [Google Scholar] [CrossRef]
- Korus, P. Digital image integrity—A survey of protection and verification techniques. Digit. Signal Process. 2017, 71, 1–26. [Google Scholar] [CrossRef]
- Salvi, D.; Liu, H.; Mandelli, S.; Bestagini, P.; Zhou, W.; Zhang, W.; Tubaro, S. A Robust Approach to Multimodal Deepfake Detection. J. Imaging 2023, 9, 122. [Google Scholar] [CrossRef] [PubMed]
- Wodajo, D.; Atnafu, S. Deepfake Video Detection Using Convolutional Vision Transformer. arXiv 2021, arXiv:2102.11126. [Google Scholar]
- Masood, M.; Nawaz, M.; Malik, K.M.; Javed, A.; Irtaza, A.; Malik, H. Deepfakes generation and detection: State-of-the-art, open challenges, countermeasures, and way forward. Appl. Intell. 2023, 53, 3974–4026. [Google Scholar] [CrossRef]
- Korus, P.; Huang, J. Multi-Scale Fusion for Improved Localization of Malicious Tampering in Digital Images. IEEE Trans. Image Process. 2016, 25, 1312–1326. [Google Scholar] [CrossRef]
- Li, H.; Luo, W.; Qiu, X.; Huang, J. Image forgery localization via integrating tampering possibility maps. IEEE Trans. Inf. Forensics Secur. 2017, 12, 1240–1252. [Google Scholar] [CrossRef]
- Iakovidou, C.; Papadopoulos, S.; Kompatsiaris, Y. Knowledge-Based Fusion for Image Tampering Localization. In Proceedings of the Artificial Intelligence Applications and Innovations, 16th IFIP WG 12.5 International Conference, AIAI 2020, Neos Marmaras, Greece, 5–7 June 2020; Maglogiannis, I., Iliadis, L., Pimenidis, E., Eds.; Springer: Cham, Switzerland, 2020; pp. 177–188. [Google Scholar]
- Charitidis, P.; Kordopatis-Zilos, G.; Papadopoulos, S.; Kompatsiaris, I. Operation-wise Attention Network for Tampering Localization Fusion. In Proceedings of the 2021 International Conference on Content-Based Multimedia Indexing (CBMI), Lille, France, 28–30 June 2021. [Google Scholar]
- Siopi, M.; Kordopatis-Zilos, G.; Charitidis, P.; Kompatsiaris, I.; Papadopoulos, S. A Multi-Stream Fusion Network for Image Splicing Localization. In Proceedings of the International Conference on Multimedia Modeling, Bergen, Norway, 9–12 January 2023; Springer: Cham, Switzerland, 2023; pp. 611–622. [Google Scholar]
- Mareen, H.; Vanden Bussche, D.; Guillaro, F.; Cozzolino, D.; Van Wallendael, G.; Lambert, P.; Verdoliva, L. Comprint: Image Forgery Detection and Localization Using Compression Fingerprints. In Proceedings of the Pattern Recognition, Computer Vision, and Image Processing—ICPR 2022 International Workshops and Challenges, Montreal, QC, Canada, 21–25 August 2022; Rousseau, J.J., Kapralos, B., Eds.; Springer: Cham, Switzerland, 2023; pp. 281–299. [Google Scholar] [CrossRef]
- Liu, B.; Pun, C.M. Deep fusion network for splicing forgery localization. In Proceedings of the Proceedings of the European Conference on Computer Vision (ECCV) Workshops, Munich, Germany, 8–14 September 2018. [Google Scholar]
- Yerushalmy, I.; Hel-Or, H. Digital image forgery detection based on lens and sensor aberration. Int. J. Comput. Vis. 2011, 92, 71–91. [Google Scholar] [CrossRef]
- Mayer, O.; Stamm, M.C. Accurate and efficient image forgery detection using lateral chromatic aberration. IEEE Trans. Inf. Forensics Secur. 2018, 13, 1762–1777. [Google Scholar] [CrossRef]
- Popescu, A.; Farid, H. Exposing digital forgeries in color filter array interpolated images. IEEE Trans. Signal Process. 2005, 53, 3948–3959. [Google Scholar] [CrossRef]
- Lin, X.; Li, C.T. Refining PRNU-based detection of image forgeries. In Proceedings of the 2016 Digital Media Industry Academic Forum (DMIAF), Santorini, Greece, 4–6 July 2016; pp. 222–226. [Google Scholar] [CrossRef]
- Cozzolino, D.; Verdoliva, L. Noiseprint: A CNN-based camera model fingerprint. IEEE Trans. Inf. Forensics Secur. 2019, 15, 144–159. [Google Scholar] [CrossRef]
- Ghosh, A.; Zhong, Z.; Boult, T.E.; Singh, M. SpliceRadar: A Learned Method For Blind Image Forensics. In Proceedings of the CVPR Workshops, Long Beach, CA, USA, 16–20 June 2019; pp. 72–79. [Google Scholar]
- Huh, M.; Liu, A.; Owens, A.; Efros, A.A. Fighting Fake News: Image Splice Detection via Learned Self-Consistency. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Li, W.; Yuan, Y.; Yu, N. Passive detection of doctored JPEG image via block artifact grid extraction. Signal Process. 2009, 89, 1821–1829. [Google Scholar] [CrossRef]
- Iakovidou, C.; Zampoglou, M.; Papadopoulos, S.; Kompatsiaris, Y. Content-aware detection of JPEG grid inconsistencies for intuitive image forensics. J. Vis. Commun. Image Represent. 2018, 54, 155–170. [Google Scholar] [CrossRef]
- Ye, S.; Sun, Q.; Chang, E.C. Detecting Digital Image Forgeries by Measuring Inconsistencies of Blocking Artifact. In Proceedings of the 2007 IEEE International Conference on Multimedia and Expo, Beijing, China, 2–5 July 2007; pp. 12–15. [Google Scholar] [CrossRef]
- Lin, Z.; He, J.; Tang, X.; Tang, C.K. Fast, automatic and fine-grained tampered JPEG image detection via DCT coefficient analysis. Pattern Recognit. 2009, 42, 2492–2501. [Google Scholar] [CrossRef]
- Bianchi, T.; Piva, A. Image Forgery Localization via Block-Grained Analysis of JPEG Artifacts. IEEE Trans. Inf. Forensics Secur. 2012, 7, 1003–1017. [Google Scholar] [CrossRef]
- Bianchi, T.; De Rosa, A.; Piva, A. Improved DCT coefficient analysis for forgery localization in JPEG images. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 2444–2447. [Google Scholar] [CrossRef]
- Barni, M.; Nowroozi, E.; Tondi, B. Higher-order, adversary-aware, double JPEG-detection via selected training on attacked samples. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos, Greece, 28 August–2 September 2017; pp. 281–285. [Google Scholar] [CrossRef]
- Kwon, M.J.; Nam, S.H.; Yu, I.J.; Lee, H.K.; Kim, C. Learning JPEG Compression Artifacts for Image Manipulation Detection and Localization. Int. J. Comput. Vis. 2022, 130, 1875–1895. [Google Scholar] [CrossRef]
- Coccomini, D.A.; Caldelli, R.; Falchi, F.; Gennaro, C. On the Generalization of Deep Learning Models in Video Deepfake Detection. J. Imaging 2023, 9, 89. [Google Scholar] [CrossRef]
- Novozámský, A.; Mahdian, B.; Saic, S. IMD2020: A Large-Scale Annotated Dataset Tailored for Detecting Manipulated Images. In Proceedings of the 2020 IEEE Winter Applications of Computer Vision Workshops (WACVW), Snowmass, CO, USA, 1–5 March 2020; pp. 71–80. [Google Scholar] [CrossRef]
- Le, T.; Nguyen, H.H.; Yamagishi, J.; Echizen, I. OpenForensics: Large-Scale Challenging Dataset For Multi-Face Forgery Detection And Segmentation In-The-Wild. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021. [Google Scholar]
- Zhou, P.; Han, X.; Morariu, V.I.; Davis, L.S. Two-Stream Neural Networks for Tampered Face Detection. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Fontani, M.; Bianchi, T.; De Rosa, A.; Piva, A.; Barni, M. A Framework for Decision Fusion in Image Forensics Based on Dempster–Shafer Theory of Evidence. IEEE Trans. Inf. Forensics Secur. 2013, 8, 593–607. [Google Scholar] [CrossRef]
- de Carvalho, T.J.; Riess, C.; Angelopoulou, E.; Pedrini, H.; de Rezende Rocha, A. Exposing Digital Image Forgeries by Illumination Color Classification. IEEE Trans. Inf. Forensics Secur. 2013, 8, 1182–1194. [Google Scholar] [CrossRef]
- Wen, B.; Zhu, Y.; Subramanian, R.; Ng, T.T.; Shen, X.; Winkler, S. Coverage—A Novel Database for Copy-Move Forgery Detection. In Proceedings of the IEEE International Conference on Image processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 161–165. [Google Scholar]
- Guan, H.; Kozak, M.; Robertson, E.; Lee, Y.; Yates, A.N.; Delgado, A.; Zhou, D.; Kheyrkhah, T.; Smith, J.; Fiscus, J. MFC Datasets: Large-Scale Benchmark Datasets for Media Forensic Challenge Evaluation. In Proceedings of the 2019 IEEE Winter Applications of Computer Vision Workshops (WACVW), Waikoloa, HI, USA, 7–11 January 2019; pp. 63–72. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Zhu, J.; Park, T.; Isola, P.; Efros, A.A. Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- Zeng, Y.; Lin, Z.; Yang, J.; Zhang, J.; Shechtman, E.; Lu, H. High-Resolution Image Inpainting with Iterative Confidence Feedback and Guided Upsampling. In Proceedings of the Computer Vision—ECCV 2020: 16th European Conference, Glasgow, UK, 23–28 August 2020. [Google Scholar]
- Vitoria, P.; Raad, L.; Ballester, C. ChromaGAN: An Adversarial Approach for Picture Colorization. arXiv 2019, arXiv:1907.09837. [Google Scholar]
- Ledig, C.; Theis, L.; Huszar, F.; Caballero, J.; Aitken, A.P.; Tejani, A.; Totz, J.; Wang, Z.; Shi, W. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Pang, Y.; Lin, J.; Qin, T.; Chen, Z. Image-to-Image Translation: Methods and Applications. IEEE Trans. Multimed. 2021, 24, 3859–3881. [Google Scholar] [CrossRef]
- Isola, P.; Zhu, J.; Zhou, T.; Efros, A.A. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015: 18th International Conference, Munich, Germany, 5–9 October 2015. [Google Scholar]
- Miyato, T.; Kataoka, T.; Koyama, M.; Yoshida, Y. Spectral Normalization for Generative Adversarial Networks. arXiv 2018, arXiv:1802.05957. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An Image is Worth 16 × 16 Words: Transformers for Image Recognition at Scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Guillaro, F.; Cozzolino, D.; Sud, A.; Dufour, N.; Verdoliva, L. TruFor: Leveraging All-Round Clues for Trustworthy Image Forgery Detection and Localization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 17–24 June 2023; pp. 20606–20615. [Google Scholar]
- Wu, H.; Chen, Y.; Zhou, J. Rethinking Image Forgery Detection via Contrastive Learning and Unsupervised Clustering. arXiv 2023, arXiv:2308.09307. [Google Scholar]
| Input Type | |||
|---|---|---|---|
| Algorithm | Artifact | RGB | Other |
| ADQ1 [23] | JPEG | ✓ | DCT analysis |
| DCT [22] | JPEG | ✓ | DCT analysis |
| BLK [20] | JPEG | ✓ | - |
| CAGI [21] | JPEG | ✓ | - |
| Noiseprint [17] | camera-based | ✓ | - |
| Comprint [11] | JPEG | ✓ | - |
| Comprint + Noiseprint [11] | camera-based & JPEG | ✓ | - |
| CAT-Net [27] | JPEG & DCT | ✓ | DCT filter |
| Dataset | #fake | #real | Format | Notes | Usage |
|---|---|---|---|---|---|
| IMD2020 [29] | 2010 | 414 | PNG & JPEG | Various forgery types | Training & Evaluation |
| OpenForensics [30] | 18,895 | N/A | JPEG | Synthetic face swapping | Training & Evaluation |
| FaceSwap [31] | 879 | 1651 | JPEG | Face swaps with FaceSwap-app | Training & Evaluation |
| VIPP [32] | 62 | 69 | JPEG | Uses double JPEG compression | Evaluation |
| DSO-1 [33] | 100 | 100 | PNG | Only splicing | Evaluation |
| Coverage [34] | 100 | 100 | TIF | Only copy-moves | Evaluation |
| NC2016 [35] | 546 | 874 | JPEG | Splicing, copy-moves and inpainting | Evaluation |
| Algorithm | F1 Score | ||||||
|---|---|---|---|---|---|---|---|
| VIPP | IMD2020 | DSO-1 | OpenForensics | FaceSwap | Coverage | NC2016 | |
| CAT-Net [27] | 0.717 | 0.850 | 0.675 | 0.948 | 0.449 | 0.573 | 0.487 |
| ADQ1 [23] | 0.503 | 0.292 | 0.420 | 0.483 | 0.282 | 0.211 | 0.206 |
| BLK [20] | 0.431 | 0.263 | 0.456 | 0.263 | 0.106 | 0.242 | 0.233 |
| CAGI [21] | 0.437 | 0.297 | 0.512 | 0.294 | 0.184 | 0.298 | 0.293 |
| DCT [22] | 0.432 | 0.313 | 0.347 | 0.423 | 0.191 | 0.222 | 0.183 |
| Comprint [11] | 0.496 | 0.297 | 0.763 | 0.630 | 0.351 | 0.349 | 0.398 |
| Comprint + Noiseprint [11] | 0.581 | 0.437 | 0.813 | 0.711 | 0.412 | 0.368 | 0.439 |
| Noiseprint [17] | 0.556 | 0.396 | 0.810 | 0.671 | 0.347 | 0.332 | 0.413 |
| Best oracle fusion of 2 methods | 0.807 | 0.857 | 0.877 | 0.961 | 0.579 | 0.616 | 0.594 |
| Oracle fusion of all methods | 0.830 | 0.864 | 0.914 | 0.965 | 0.653 | 0.653 | 0.626 |
| Maximum | 0.700 | 0.776 | 0.822 | 0.924 | 0.435 | 0.488 | 0.514 |
| Minimum | 0.673 | 0.637 | 0.793 | 0.897 | 0.558 | 0.478 | 0.476 |
| Proposed fusion method | 0.733 | - | 0.753 | - | - | 0.538 | 0.510 |
| Algorithm | F1 Score | ||
|---|---|---|---|
| IMD2020 Test | OpenForensics Test | FaceSwap Test | |
| CAT-Net [27] | 0.863 | 0.952 | 0.448 |
| ADQ1 [23] | 0.340 | 0.479 | 0.322 |
| BLK [20] | 0.274 | 0.256 | 0.134 |
| CAGI [21] | 0.316 | 0.290 | 0.211 |
| DCT [22] | 0.336 | 0.418 | 0.220 |
| Comprint [11] | 0.424 | 0.626 | 0.421 |
| Comprint + Noiseprint [11] | 0.457 | 0.710 | 0.466 |
| Noiseprint [17] | 0.408 | 0.667 | 0.409 |
| Best oracle fusion of 2 methods | 0.873 | 0.961 | 0.584 |
| Oracle fusion of all methods | 0.883 | 0.965 | 0.647 |
| Maximum | 0.806 | 0.926 | 0.439 |
| Minimum | 0.672 | 0.898 | 0.580 |
| Proposed fusion method | 0.869 | 0.966 | 0.814 |
| Algorithm | AUC | |||||
|---|---|---|---|---|---|---|
| VIPP | IMD2020 | DSO-1 | FaceSwap | Coverage | NC2016 | |
| CAT-Net [27] | 0.807 | 0.933 | 0.786 | 0.661 | 0.697 | 0.758 |
| ADQ1 [23] | 0.634 | 0.686 | 0.654 | 0.727 | 0.506 | 0.603 |
| BLK [20] | 0.592 | 0.553 | 0.579 | 0.496 | 0.508 | 0.525 |
| CAGI [21] | 0.644 | 0.615 | 0.650 | 0.498 | 0.530 | 0.558 |
| DCT [22] | 0.649 | 0.611 | 0.410 | 0.574 | 0.505 | 0.498 |
| Comprint [11] | 0.614 | 0.644 | 0.960 | 0.526 | 0.545 | 0.566 |
| Comprint + Noiseprint [11] | 0.630 | 0.634 | 0.960 | 0.533 | 0.556 | 0.597 |
| Noiseprint [17] | 0.608 | 0.543 | 0.861 | 0.517 | 0.534 | 0.534 |
| Maximum | 0.700 | 0.803 | 0.881 | 0.579 | 0.609 | 0.672 |
| Minimum | 0.734 | 0.750 | 0.775 | 0.738 | 0.618 | 0.696 |
| Proposed fusion method | 0.790 | - | 0.792 | - | 0.671 | 0.686 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mareen, H.; De Neve, L.; Lambert, P.; Van Wallendael, G. Harmonizing Image Forgery Detection & Localization: Fusion of Complementary Approaches. J. Imaging 2024, 10, 4. https://doi.org/10.3390/jimaging10010004
Mareen H, De Neve L, Lambert P, Van Wallendael G. Harmonizing Image Forgery Detection & Localization: Fusion of Complementary Approaches. Journal of Imaging. 2024; 10(1):4. https://doi.org/10.3390/jimaging10010004
Chicago/Turabian StyleMareen, Hannes, Louis De Neve, Peter Lambert, and Glenn Van Wallendael. 2024. "Harmonizing Image Forgery Detection & Localization: Fusion of Complementary Approaches" Journal of Imaging 10, no. 1: 4. https://doi.org/10.3390/jimaging10010004
APA StyleMareen, H., De Neve, L., Lambert, P., & Van Wallendael, G. (2024). Harmonizing Image Forgery Detection & Localization: Fusion of Complementary Approaches. Journal of Imaging, 10(1), 4. https://doi.org/10.3390/jimaging10010004












