Recycling of Lead Pastes from Spent Lead–Acid Batteries: Thermodynamic Constraints for Desulphurization
Abstract
:1. Introduction
2. Thermodynamic Models for Lead Species
| Reactions | , and Cumulative Formation Constants, , | Reference and Remarks |
|---|---|---|
| PbCO3(cr) ⇄ Pb2+ + CO32− | −13.76 ± 0.15 (2σ) | [14] |
| Pb2+ + CO32− ⇄ PbCO3(aq) | 6.87 ± 0.09 (2σ) | [21] |
| Pb2+ + 2CO32− ⇄ Pb(CO3)22− | 10.41 ± 0.18 (2σ) | [22] |
| Pb2+ + CO32− + Cl− ⇄ Pb(CO3)Cl− | 7.23 ± 0.74 (2σ) | [21] |
| PbO(cr) + 2H+ ⇄ Pb2+ + H2O(l) | 12.59 | [23], EQ3/6 database |
| Pb2+ + H2O(l) ⇄ PbOH+ + H+ | −7.46 | [24] |
| Pb2+ + 2H2O(l) ⇄ Pb(OH)2(aq) + 2H+ | −17.05 ± 0.10 (2σ) | [15] |
| Pb2+ + 3H2O(l) ⇄ Pb(OH)3− + 3H+ | −27.99 ± 0.15 (2σ) | [15] |
| PbC2O4(cr) ⇄ Pb2+ + C2O42− | −11.13 ± 0.15 (2σ) | [12] A |
| Pb2+ + C2O42− ⇄ PbC2O4(aq) | 5.85 ± 0.10 (2σ) | [12] A |
| Pb2+ + 2C2O42− ⇄ Pb(C2O4)22− | 8.05 ± 0.15 (2σ) | [12] A |
| Pb2+ + C6H5O73− ⇄ PbC6H5O7− | 7.28 | [19] |
| Pb2+ + Cl− ⇄ PbCl+ | 1.48 | [25] |
| Pb2+ + 2Cl− ⇄ PbCl2(aq) | 2.03 | [25] |
| Pb2+ + 3Cl− ⇄ PbCl3− | 1.86 | [25] |
| PbSO4(cr) ⇄ Pb2+ + SO42− | −7.78 | [26] |
| PbO•PbSO4(cr) + 2H+ ⇄ Pb2+ + SO42− + H2O(l) | 2.66 ± 0.05 | This study |
| Na2C2O4(cr) ⇄ 2Na+ + C2O42− | −2.61 ± 0.05 | This study |
| K2C2O4(cr) ⇄ 2K+ + C2O42− | −1.00 ± 0.06 | This study |
| H2C2O4 (aq) ⇄ 2H+ + C2O42− | −6.07 | [13] |
| HC2O4− ⇄ H+ + C2O42− | −4.36 | [13] |
| PbO2(cr) + 2H+ ⇄ Pb2+ + H2O(l) + 0.5O2(g) | 7.75 | [27] |
3. Results
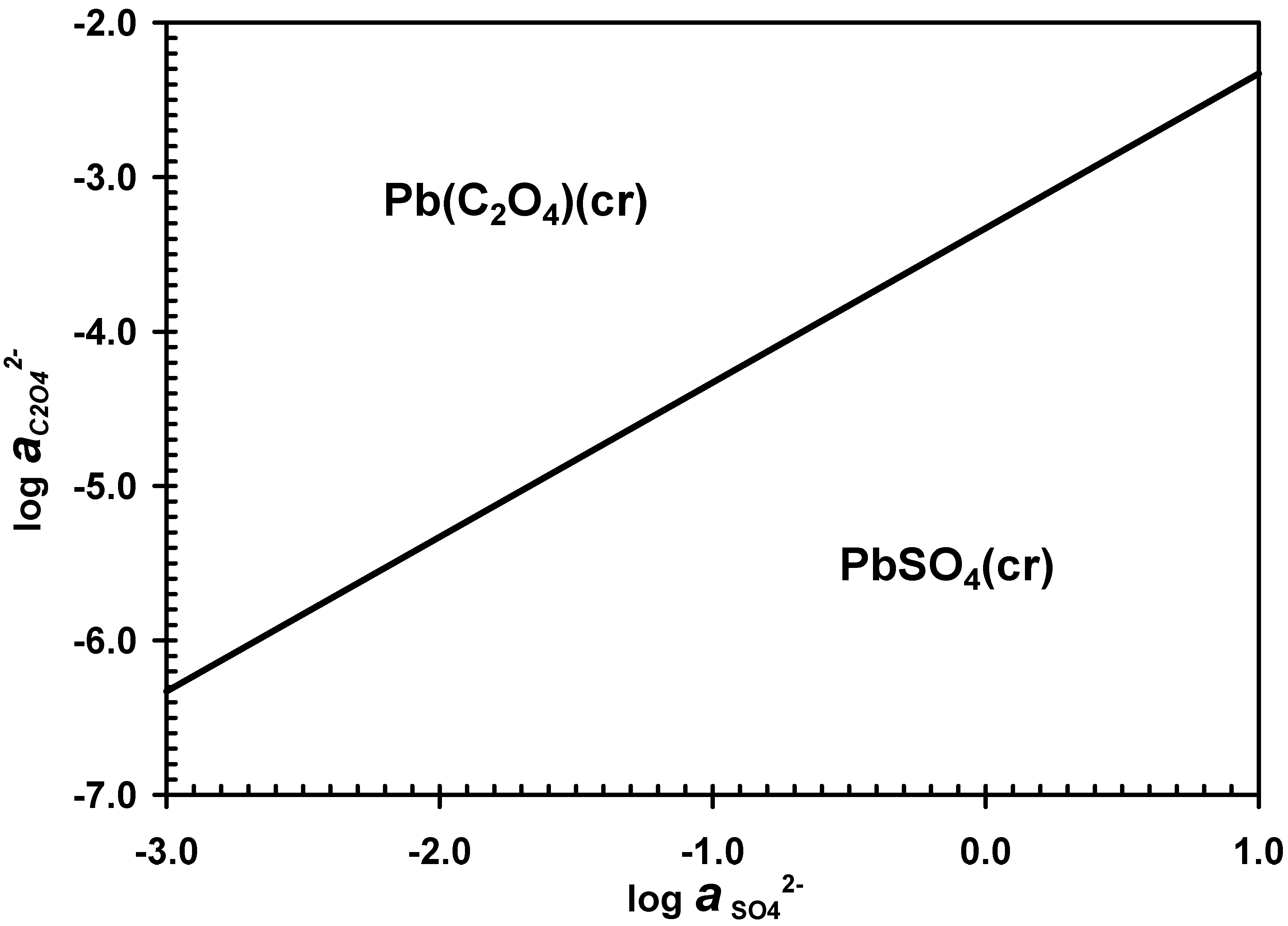
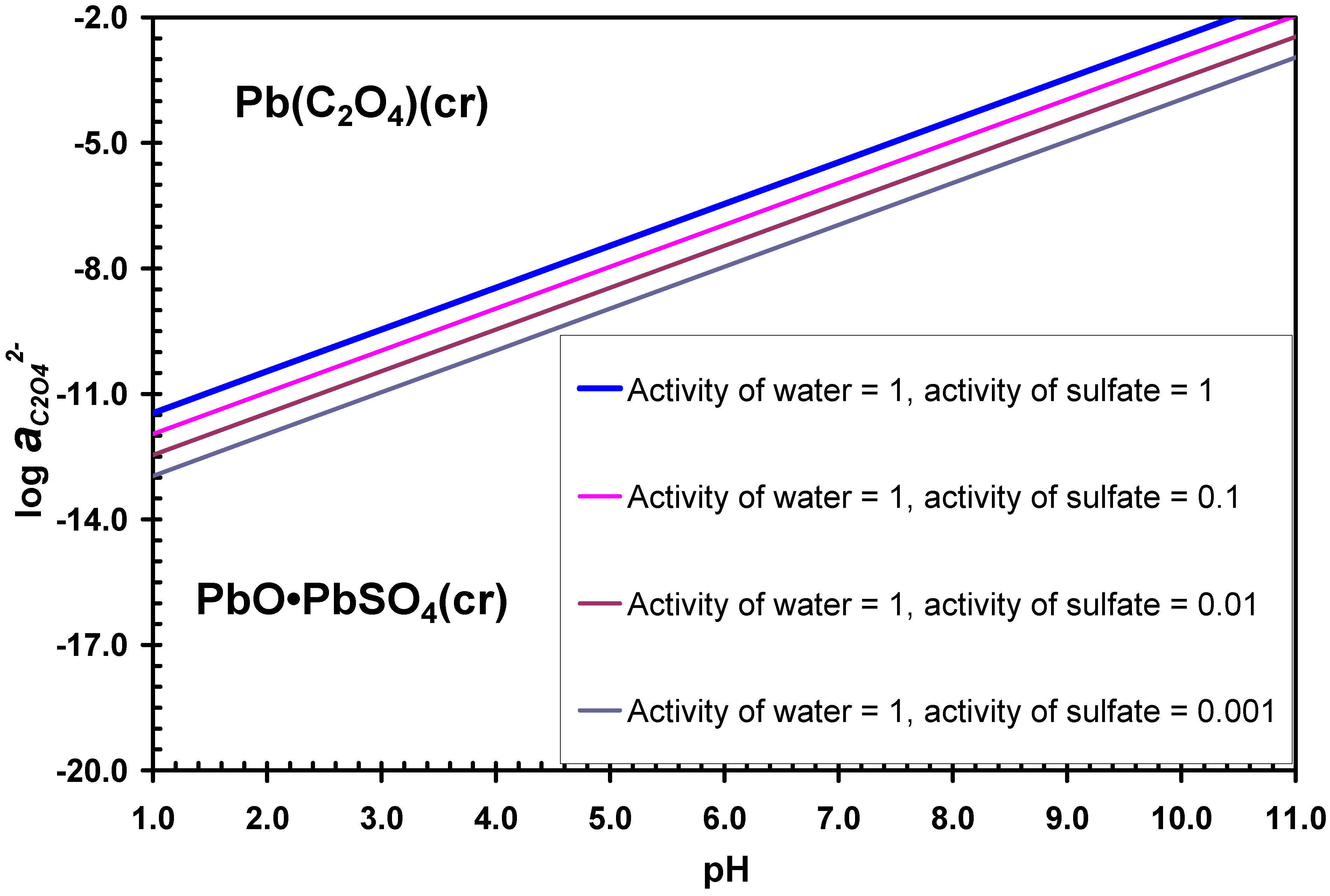
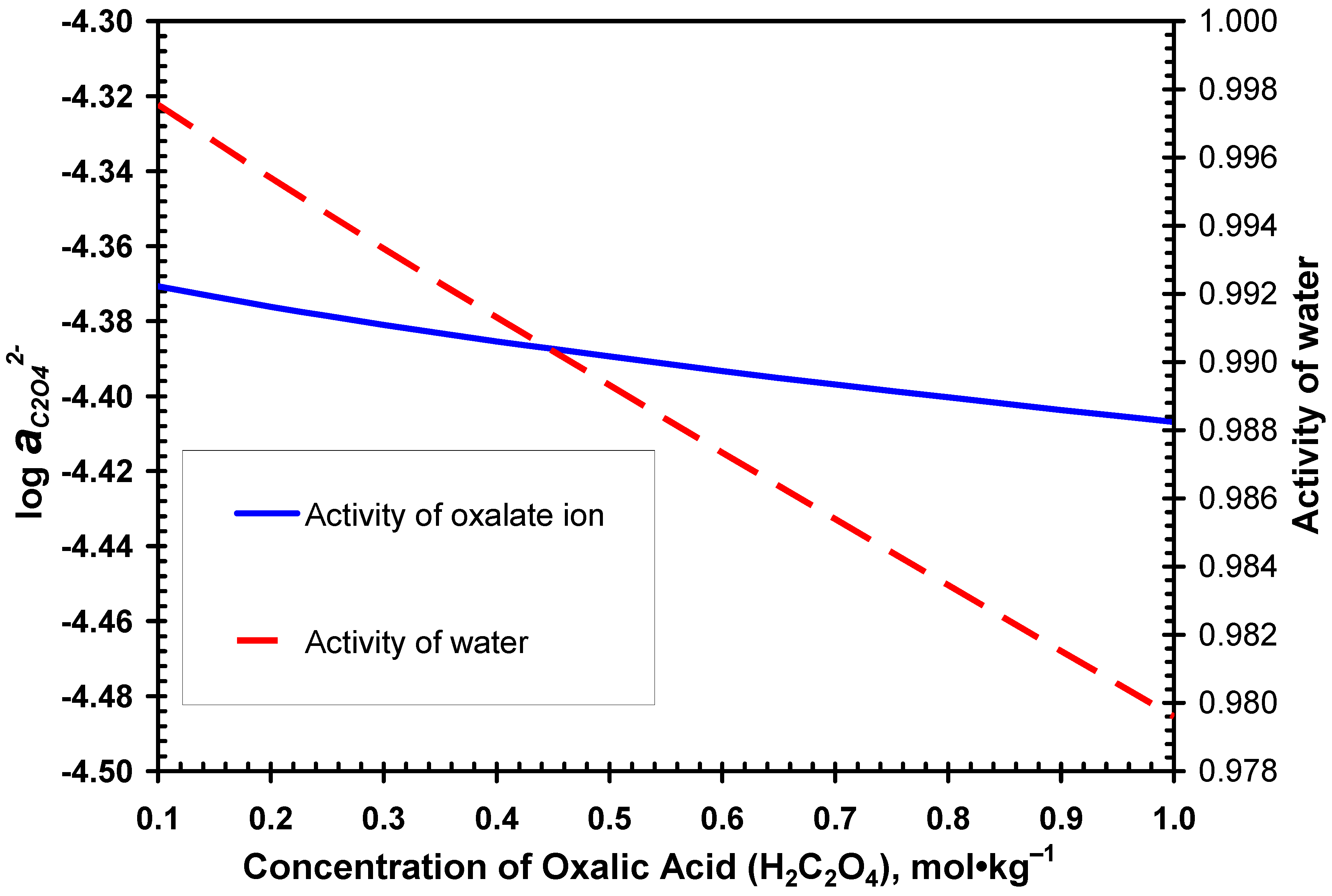
3.1. Desulphurization in Oxalate-Bearing Media
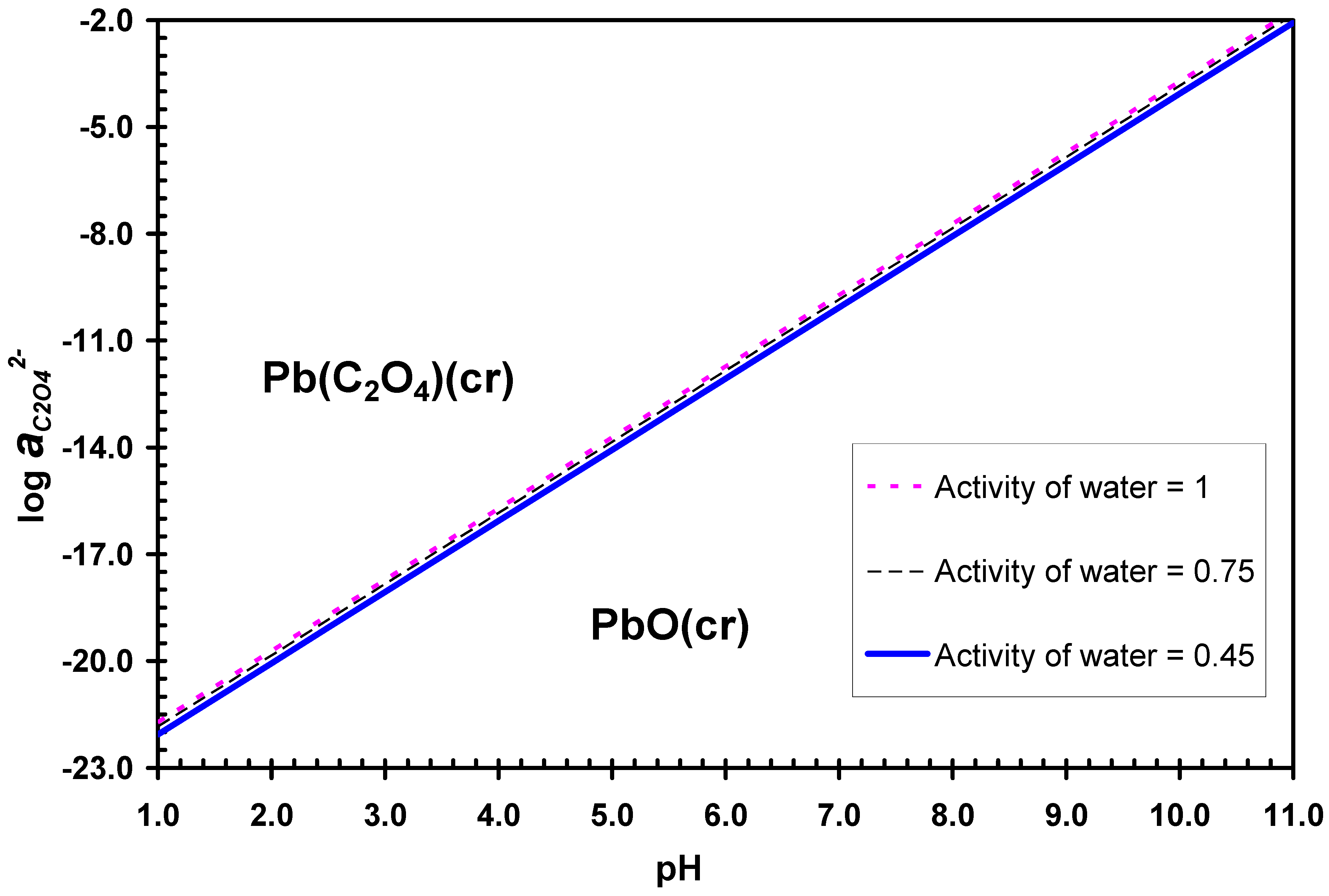
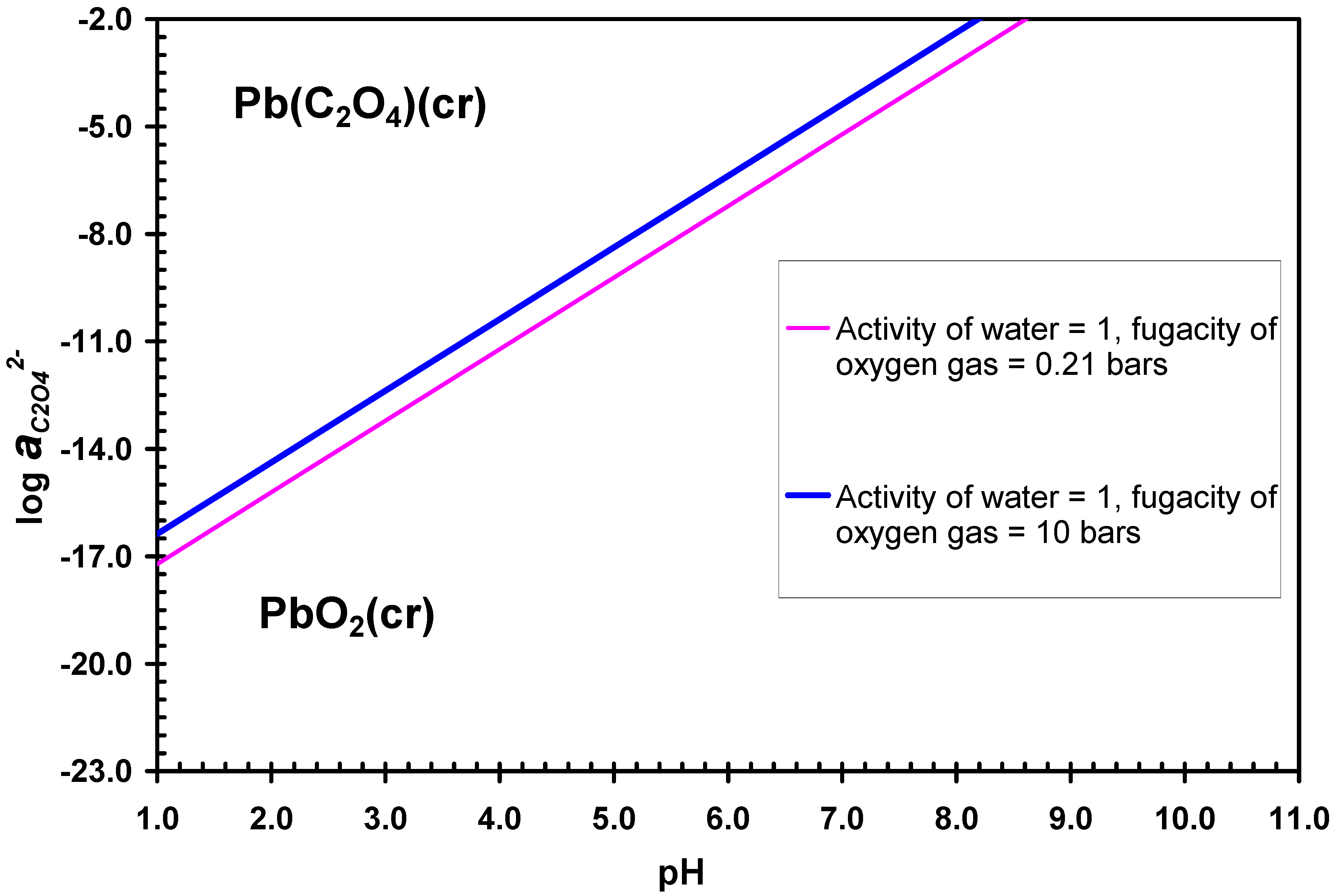
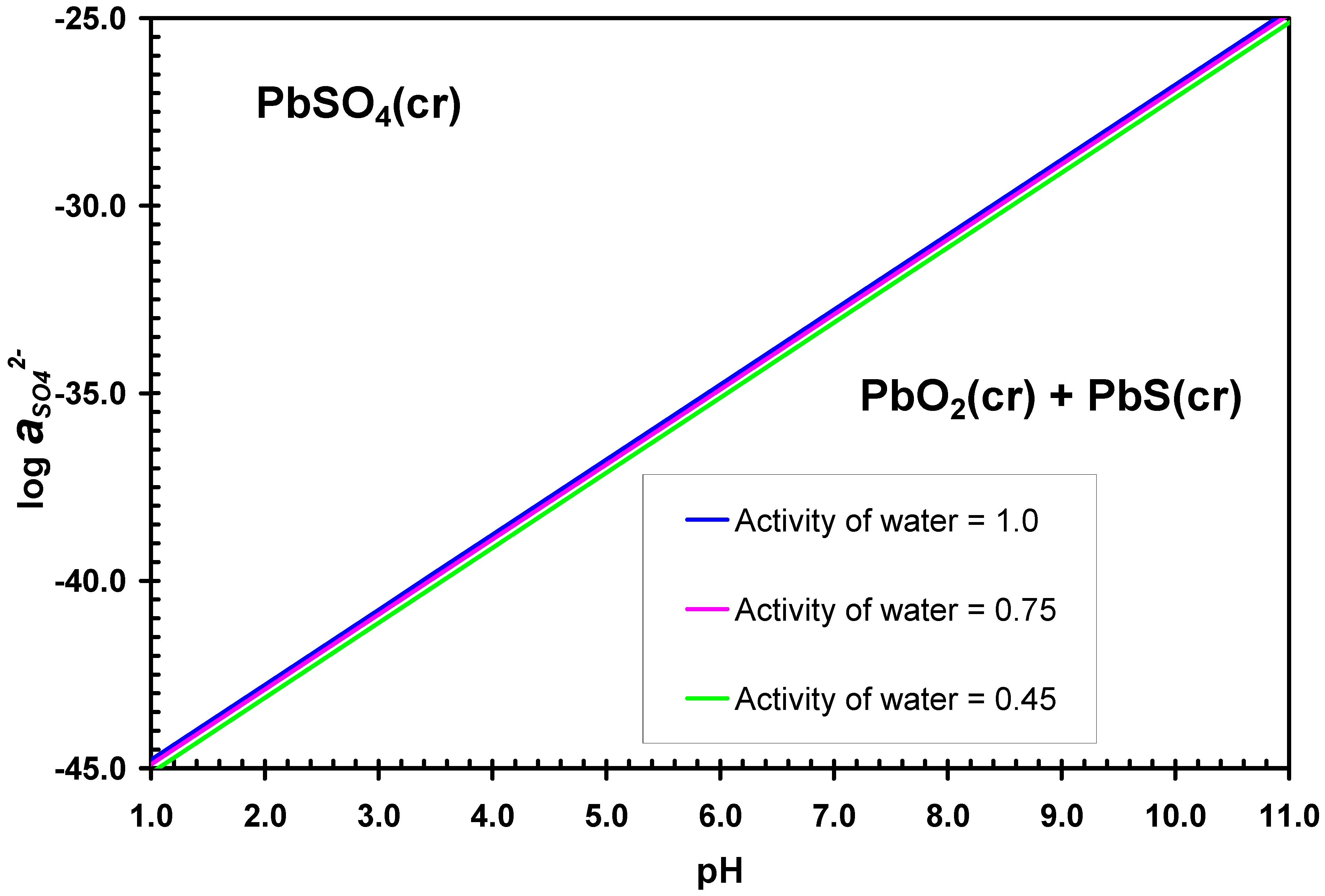
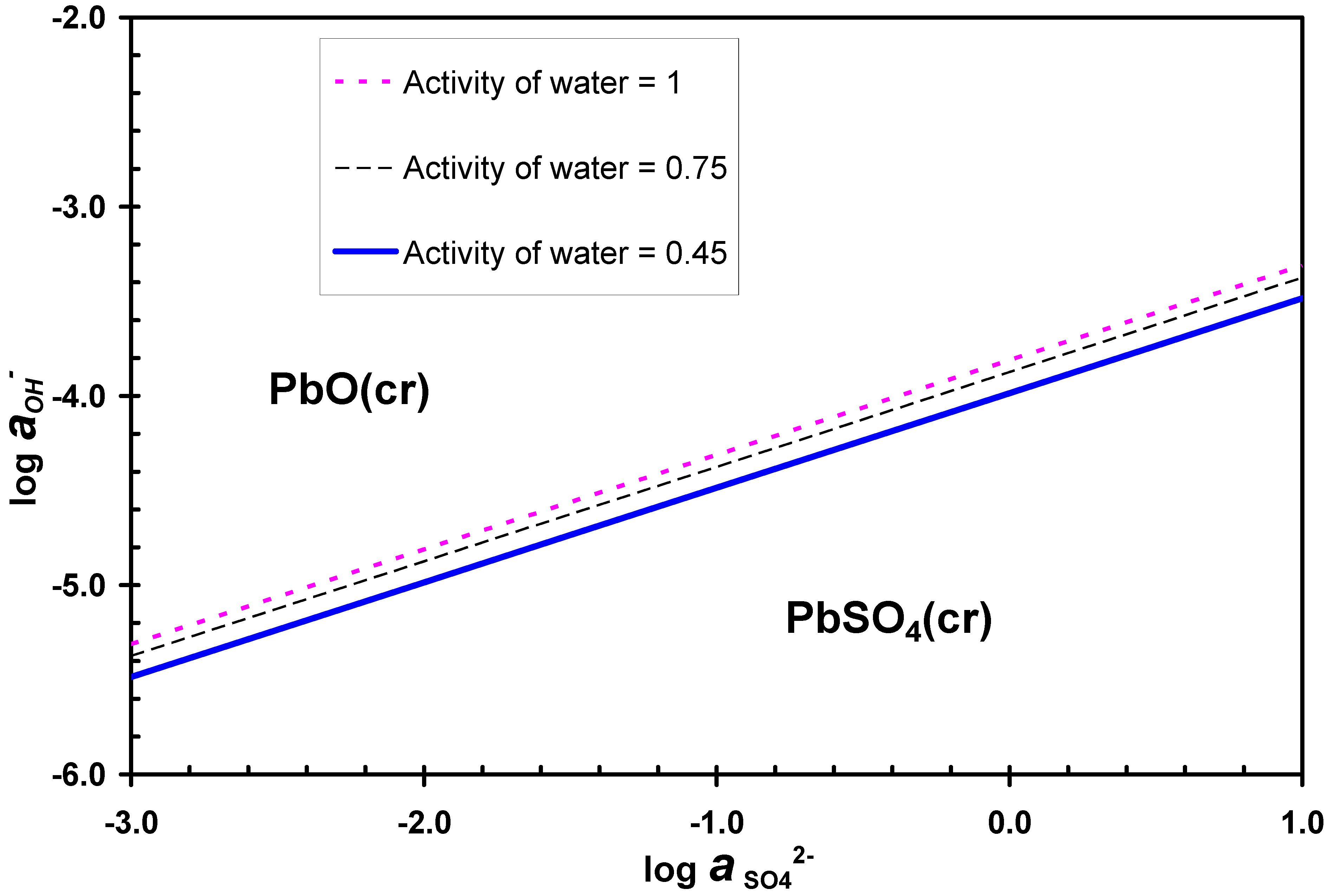
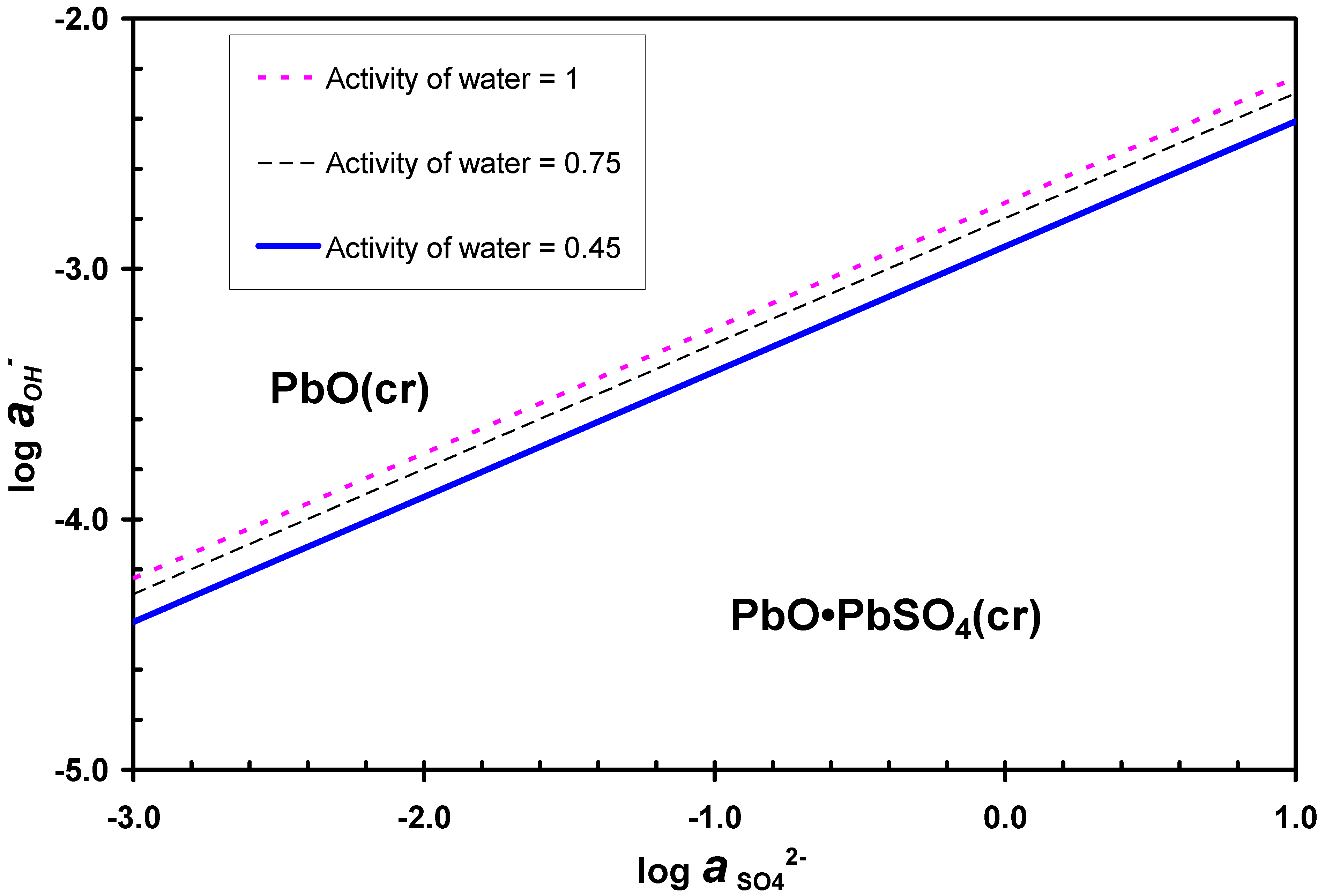
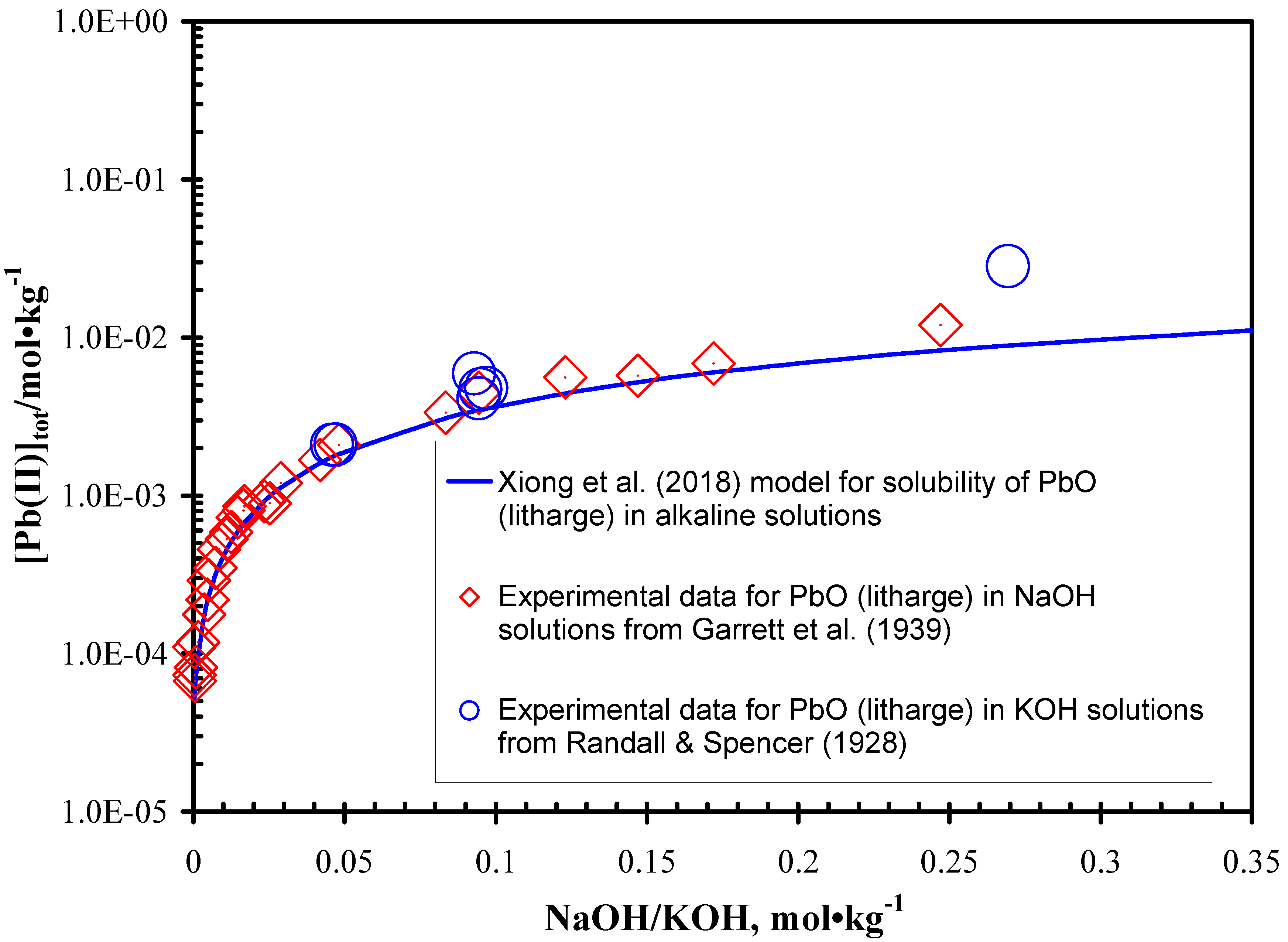
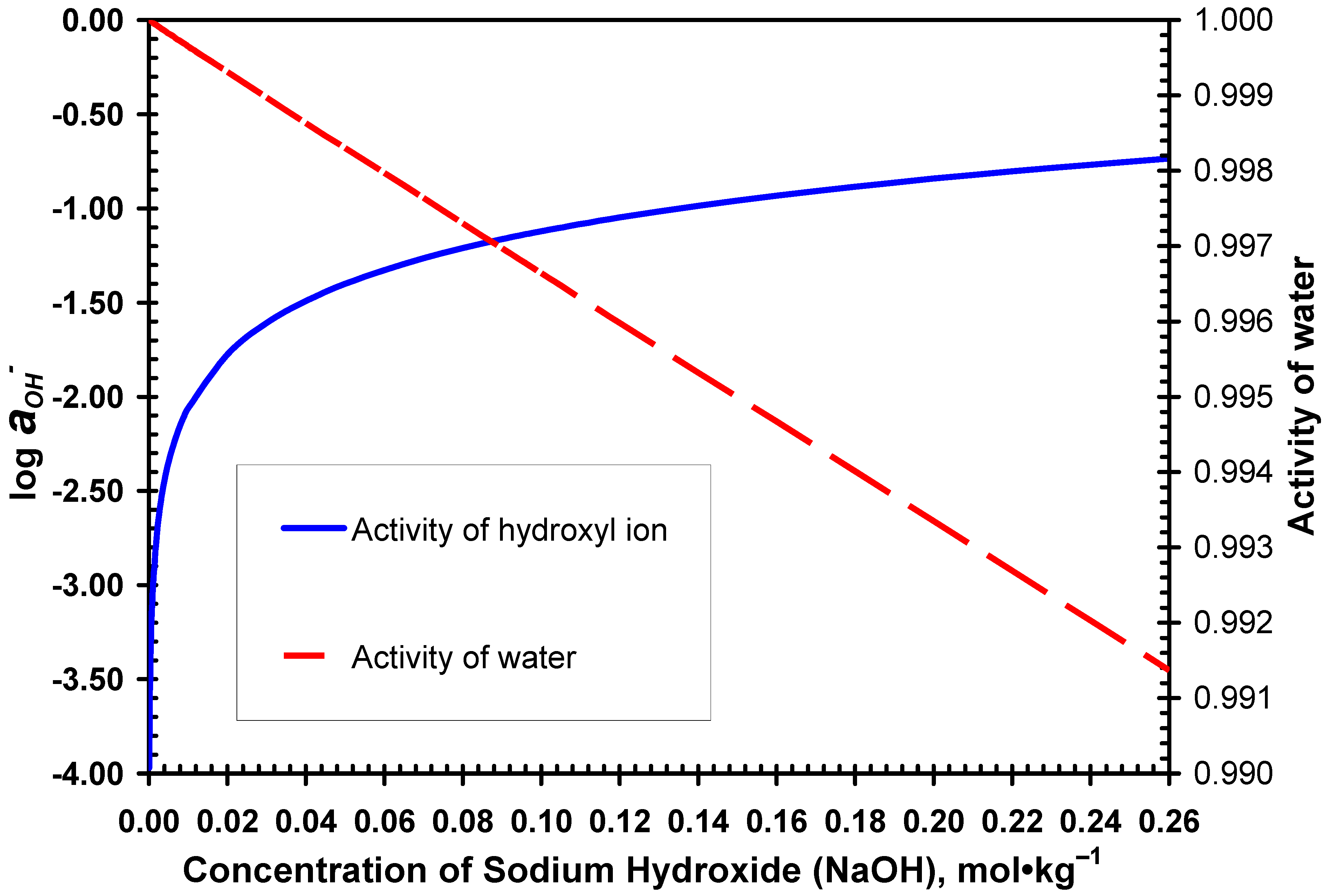
3.2. Desulphurization in Alkaline Solutions
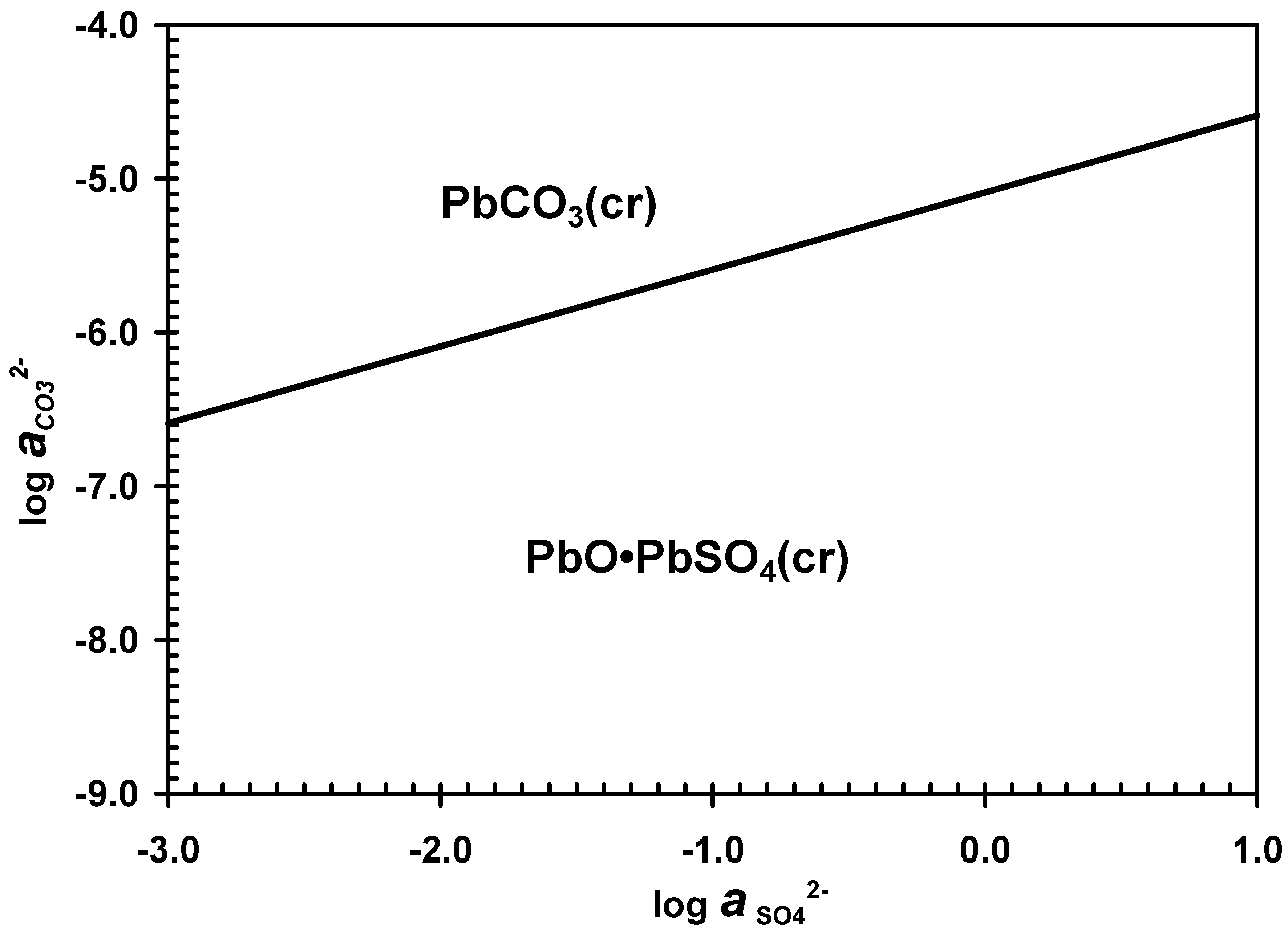
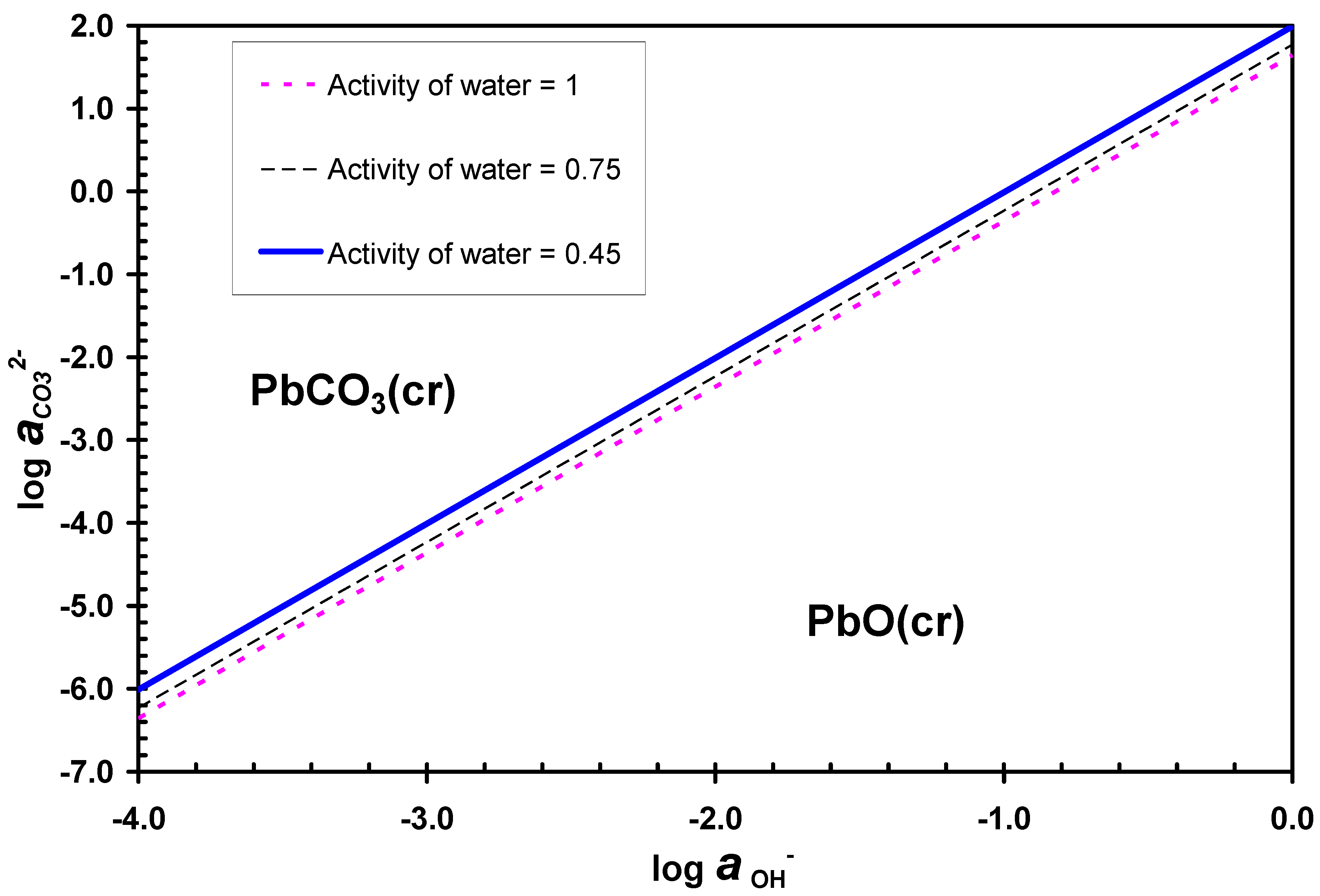
3.3. Desulphurization in Carbonate Media
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reich, S.; Leitus, G.; Shalev, S. Measurement of corrosion content of archaeological lead artifacts by their Meissner response in the superconducting state; a new dating method. New J. Phys. 2003, 5, 99.1–99.9. [Google Scholar] [CrossRef]
- Ellis, T.W.; Mirza, A.H. The refining of secondary lead for use in advanced lead-acid batteries. J. Power Sources 2010, 195, 4525–4529. [Google Scholar] [CrossRef]
- Buzatu, T.; Ghica, G.V.; Petrescu, I.M.; Iacob, G.; Buzatu, M.; Niculescu, F. Studies on mathematical modeling of the leaching process in order to efficiently recover lead from the sulfate/oxide lead paste. Waste Manag. 2017, 60, 723–733. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.S.; Shih, Y.J.; Huang, Y.H. Recovery of lead from smelting fly ash of waste lead-acid battery by leaching and electrowinning. Waste Manag. 2016, 52, 212–220. [Google Scholar] [CrossRef]
- Xie, B.; Yang, T.; Liu, W.; Zhang, D.; Chen, L. Recovery of Lead from Spent Lead Paste by Pre-desulfurization and Low-Temperature Reduction Smelting. JOM 2020, 72, 3195–3203. [Google Scholar] [CrossRef]
- Huang, K.; Liu, H.-Y.; Dong, H.-L.; Lin, M.; Ruan, J.-J. A novel approach to recover lead oxide from spent lead acid batteries by desulfurization and crystallization in sodium hydroxide solution after sulfation. Resour. Conserv. Recycl. 2021, 167, P105385. [Google Scholar] [CrossRef]
- Ma, C.; Shu, Y.; Chen, H. Recycling lead from spent lead pastes using oxalate and sodium oxalate and preparation of novel lead oxide for lead-acid batteries. RSC Adv. 2015, 5, 94895–94902. [Google Scholar] [CrossRef]
- Zhang, X.; Li, L.; Fan, E.; Xue, Q.; Bian, Y.; Wu, F.; Chen, R. Toward sustainable and systematic recycling of spent rechargeable batteries. Chem. Soc. Rev. 2018, 47, 7239–7302. [Google Scholar] [CrossRef]
- Chen, T.T.; Dutrizac, J.E. The mineralogical characterization of lead-acid battery paste. Hydrometallurgy 1996, 40, 223–245. [Google Scholar] [CrossRef]
- Deng, X.; Liu, W.; Zhang, D.; Chen, L.; Liu, Z.; Yang, T. Hydrothermal desulfurization of spent lead paste based on comproportionation reaction. Sep. Purif. Technol. 2021, 259, 118115. [Google Scholar] [CrossRef]
- Che, J.; Zhang, W.; Xia, L.; Chen, J.; Wen, P.; Ma, B.; Wang, C. A Facile and Environmentally Friendly Approach for Lead Recovery from Lead Sulfate Residue via Mechanochemical Reduction: Phase Transformation and Reaction Mechanism. ACS Sustain. Chem. Eng. 2021, 9, 10227–10239. [Google Scholar] [CrossRef]
- Xiong, Y.-L.; Kirkes, L.; Westfall, T.; Roselle, R. Experimental determination of solubilities of lead oxalate (PbC2O4(cr)) in a NaCl medium to high ionic strengths, and the importance of lead oxalate in low temperature environments. Chem. Geol. 2013, 342, 128–137. [Google Scholar] [CrossRef]
- Thakur, P.; Xiong, Y.-L.; Borkowski, M. Improved thermodynamic model for the complexation of trivalent actinides and lanthanide with oxalic acid to high ionic strength. Chem. Geol. 2015, 413, 7–17. [Google Scholar] [CrossRef] [Green Version]
- Xiong, Y.-L. Experimental determination of lead carbonate solubility at high ionic strengths: A Pitzer model description. Mon. Chem. Chem. Mon. 2015, 146, 1433–1443. [Google Scholar] [CrossRef]
- Xiong, Y.-L.; Kirkes, L.; Westfall, T.; Knox, J.; Marrs, C.; Burton, H. A Pitzer model for lead oxide solubilities in the presence of borate to high ionic strength. J. Solut. Chem. 2018, 47, 1905–1925. [Google Scholar] [CrossRef]
- Wolery, T.J.; Xiong, Y.-L.; Long, J. Verification and Validation Plan/Validation Document for EQ3/6 Version 8.0a for Actinide Chemistry; Document Version 8.10; ERMS 550239; Sandia National laboratories: Carlsbad, NM, USA, 2010.
- Xiong, Y.-L. WIPP Verification and Validation Plan/Validation Document for EQ3/6 Version 8.0a for Actinide Chemistry, Revision 1, Document Version 8.20. Supersedes ERMS 550239; ERMS 555358; Sandia National Laboratories: Carlsbad, NM, USA, 2011.
- Domski, P.S. Memo AP-173, EQ3/6 Database Update: DATA0.FM2. Memorandum to WIPP Records, 27 October 2015; ERMS 564914; Sandia National Laboratories: Carlsbad, NM, USA, 2015.
- Domski, P.S.; Xiong, Y.-L. Prediction of Baseline Actinide Solubilities with an Updated EQ3/6 Thermodynamic Database (DATA0.FM2) in Response EPA Completeness Comment 3-C-3 for CRA 2014; ERMS 565032; Sandia National Laboratories: Carlsbad, NM, USA, 2015.
- Xiong, Y.-L.; Domski, P.S. Updating the WIPP Thermodynamic Database, Revision 1, Supersedes ERMS 565730; ERMS 566047; Sandia National Laboratories: Carlsbad, NM, USA, 2016.
- Woosley, R.J.; Millero, F.J. Pitzer model for the speciation of lead chloride and carbonate complexes in natural waters. Mar. Chem. 2013, 149, 1–7. [Google Scholar] [CrossRef]
- Easley, R.A.; Byrne, R.H. The ionic strength dependence of lead(II) carbonate complexation in perchlorate media. Geochim. Cosmochim. Acta 2011, 75, 5638–5647. [Google Scholar] [CrossRef]
- Wolery, T.J.; Jarek, R.L. Software User’s Manual EQ3/6 (Version 8.0); Sandia National Laboratories: Albuquerque, NM, USA, 2003.
- Powell, K.J.; Brown, P.L.; Byrne, R.H.; Gajda, T.; Hefter, G.; Luez, A.-K.; Sjöberg, S.; Wanner, H. Experimental Determination of Lead Carbonate Solubility at High Ionic Strengths: A Pitzer Model Description. Pure Appl. Chem. 2009, 81, 2425. [Google Scholar] [CrossRef] [Green Version]
- Millero, F.J.; Byrne, R.H. Use of Pitzer equations to determine the media effect on the formation of lead chloro complexes. Geochim. Cosmochim. Acta 1984, 48, 1145–1150. [Google Scholar] [CrossRef]
- Paige, C.R.; Kornicker, W.A.; Hileman, O.E., Jr.; Snodgrass, W.J. Modeling solution equilibra for uranium ore processing: The PbSO4-H2SO4-H2O and PbSO4-Na2SO4-H2O systems. Geochim. Cosmochim. Acta 1992, 56, 1165–1173. [Google Scholar] [CrossRef]
- Wagman, D.D.; Evans, W.H.; Parker, V.B.; Schumm, R.H.; Halow, I. The NBS Tables of Chemical Thermodynamic Properties. Selected Values for Inorganic and C1 and C2 Organic Substances in SI Units; National Standard Reference Data System: Gaithersburg, MD, USA, 1982.
- Choppin, G.R.; Bond, A.H.; Borkowski, M.; Bronikowski, M.G.; Chen, J.-F.; Lis, S.; Mizera, J.; Pokrovsky, O.S.; Wall, N.A.; Xia, Y.-X.; et al. Waste Isolation Pilot Plant Actinide Source Term Test Program: Solubility Studies and Development of Modeling Parameter; SAND99-0943s; Sandia National Laboratories Report: Albuquerque, NM, USA, 2001.
- Xiong, Y. Experimental determination of solubilities of tri-calcium di-citrate tetrahydrate [Ca3[C3H5O(COO)3]2•4H2O], earlandite, in NaCl and MgCl2 solutions to high ionic strengths. Appl. Geochem. 2021, 125, 104856. [Google Scholar] [CrossRef]
- Felmy, A.R.; Onishi, L.M.; Foster, N.S.; Rustad, J.R.; Rai, D.; Mason, M.J. An aqueous thermodynamic model for the Pb2+–Na+–K+–Ca2+–Mg2+–H+–Cl−–SO42−–H2O system to high concentration: Application to WIPP brines. Geochim. Cosmochim. Acta 2000, 64, 3615–3628. [Google Scholar] [CrossRef]
- Gadd, G.M. Geomycology. In Fungal Applications in Sustainable Environmental Biotechnology; Springer: Cham, Switzerland, 2016; pp. 371–401. [Google Scholar]
- McBride, M.B.; Kelch, S.; Schmidt, M.; Zhou, Y.; Aristilde, L.; Martinez, C.E. Lead solubility and mineral structures of coprecipitated lead/calcium oxalates. Environ. Sci. Technol. 2019, 53, 13794–13801. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.; Shu, Y.; Chen, H. Leaching of spent lead paste by oxalate and sodium oxalate solution and prepared leady oxide powder in nitrogen and air for lead acid battery. J. Electrochem. Soc. 2016, 163, A2240. [Google Scholar] [CrossRef]
- Ma, Y.; Huang, P.; Cao, J.; Zhang, J.; Huang, Y.; Chen, B. Analysis of a more sustainable method for recycling waste lead batteries: Surface renewal promotes desulfurization agent regeneration. Waste Manag. 2022, 137, 319–328. [Google Scholar] [CrossRef]
- Yang, T.; Xie, B.; Liu, W.; Zhang, D.; Chen, L. An environment-friendly process of lead recovery from spent lead paste. Sep. Purif. Technol. 2020, 233, 116035. [Google Scholar] [CrossRef]
- Abdul-Samad, F.A.; Thomas, J.H.; Williams, P.A.; Symes, R.F. Chemistry of formation of lanarkite, Pb2OSO4. Mineral. Mag. 1982, 46, 499–501. [Google Scholar] [CrossRef]
- Menczel, B.; Apelblat, A.; Korin, E. The molar enthalpies of solution and solubilities of ammonium, sodium and potassium oxalates in water. J. Chem. Thermodyn. 2004, 36, 41–44. [Google Scholar] [CrossRef]
- Yu, W.; Zhang, P.; Yang, J.; Li, M.; Hu, Y.; Liang, S.; Wang, J.; Li, S.; Xiao, K.; Hou, H.; et al. A low-emission strategy to recover lead compound products directly from spent lead-acid battery paste: Key issue of impurities removal. J. Clean. Prod. 2019, 210, 1534–1544. [Google Scholar] [CrossRef]
- Randall, M.; Spencer, H.M. Solubility of lead monoxide and basic lead carbonate in alkaline solutions. J. Am. Chem. Soc. 1928, 50, 1572–1583. [Google Scholar] [CrossRef]
- Garrett, A.B.; Vellenga, S.; Fontana, C.M. The solubility of red, yellow, and black lead oxides (2) and hydrated lead oxide in alkaline solutions. The character of the lead-bearing ion. J. Am. Chem. Soc. 1939, 61, 367–373. [Google Scholar] [CrossRef]
- Liu, W.F.; Deng, X.B.; Zhang, D.C.; Yang, T.Z.; Lin, C.H.E.N. A clean process of lead recovery from spent lead paste based on hydrothermal reduction. Trans. Nonferrous Met. Soc. China 2018, 28, 2360–2367. [Google Scholar] [CrossRef]
- Gamsjäger, H.; Fluch, A.; Swinehart, J.H. The effect of potential aqueous pollutants on the solubility of Pb+ 2 in cerussite—Calcite phase. Mon. Chem. Chem. Mon. 1984, 115, 251–259. [Google Scholar] [CrossRef]
- Li, X.; Azimzadeh, B.; Martinez, C.E.; McBride, M.B. Pb mineral precipitation in solutions of sulfate, carbonate and phosphate: Measured and modeled Pb solubility and Pb2+ activity. Minerals 2021, 11, 620. [Google Scholar] [CrossRef]
- Ma, Y.-J.; Qiu, K.-Q. Recovery of lead from lead paste in spent lead acid battery by hydrometallurgical desulfurization and vacuum thermal reduction. Waste Manag. 2015, 40, 151–156. [Google Scholar] [CrossRef]
- Hua, C.; Pan, J.; Li, Z.; Wang, K.; Sun, Y.; Li, D.; Li, T. A new desulfation process of spent lead paste via cyclic utilization of CO2–NH3•H2O. J. Clean. Prod. 2022, 349, 131307. [Google Scholar] [CrossRef]
- Wei, W.; Han, X.; Shao, Y.; Xie, W.; Zhang, Y.; Yao, Y.; Zhao, W.; Han, R.; Li, S.; Zheng, C. Comparing the effects of humic acid and oxalic acid on Pb (II) immobilization by a green synthesized nanocrystalline hydroxyapatite. Chemosphere 2021, 285, 131411. [Google Scholar] [CrossRef]
- Sonmez, M.S.; Kumar, R.V. Leaching of waste battery paste components. Part 2: Leaching and desulphurisation of PbSO4 by citric acid and sodium citrate solution. Hydrometallurgy 2009, 95, 82–86. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, W.; Yang, H.; Li, L.; Yang, J. Preparation of ultrafine PbO powders from lead paste in spent lead acid battery. Chin. J. Nonferrous Met. 2010, 20, 132–136. (In Chinese) [Google Scholar]
- Zhu, X.; Li, L.; Sun, X.; Yang, D.; Gao, L.; Liu, J.; Kumar, R.V. Preparation of basic lead oxide from spent lead acid battery paste via chemical conversion. Hydrometallurgy 2012, 117–118, 24–31. [Google Scholar] [CrossRef]
- Yang, J.; Kumar, R.V.; Singh, D.P. Combustion synthesis of PbO from lead carboxylate precursors relevant to developing a new method for recovering components from spent lead-acid batteries. J. Chem. Technol. Biotechnol. 2012, 87, 1480–1488. [Google Scholar] [CrossRef]


| Pitzer Binary Interaction Parameters | |||||
|---|---|---|---|---|---|
| Species i | Species j | β(0) | β(1) | Cφ | Reference |
| Na+ | Pb(CO3)22− | 0.4168 | 1.74 | −0.3161 | [14] |
| Na+ | Pb(CO3)Cl− | 0.2419 | 0.29 | −0.1802 | [14] |
| Na+ | Pb(OH)3− | 0.3354 | 0.29 | 0 | [15] |
| Na+ | PbCl3− | −0.0605 | 0 | 0.091 | [12] |
| Pb2+ | Cl− | 0.26 | 1.64 | 0.088 | [25] |
| PbCl+ | Cl− | 0.15 | 0 | 0 | [25] |
| K+ | Pb(C2O4)22− | 0 | −1.86 ± 0.20 | 0.198 ± 0.09 | [12] |
| Na+ | Pb(C2O4)22− | 0 | −1.86 ± 0.20 | 0.198 ± 0.09 | [12] |
| PbNO3+ | NO3− | −0.75 | 0.34 | 0 | [12] |
| Na+ | C2O42− | −0.2770 | 1.74 | 0.122 | [13] |
| K+ | C2O42− | −0.2770 | 1.74 | 0.122 | This work, using Na+/C2O42− from [13] as an analog |
| Na+ | PbC6H5O7− | 0.535 | 0.29 | 0.0196 | [20] |
| Mg2+ | PbC6H5O7− | 1.97 | 1.74 | 0.0771 | [20] |
| Na+ | C6H5O73− | 0.0877 | 5.22 | 0.047 | [28] |
| Mg2+ | C6H5O73− | 0.9330 | 4.4 | 0 | [29] |
| Pitzer Mixing Interaction Parameters and Interaction Parameters Involving Neutral Species | |||||
| Species i | Species j | Species k | λij or θij | ζijk | Reference |
| HCO3− | Pb(CO3)22− | 0.2956 | [14] | ||
| CO32− | Pb(CO3)22− | 0.2707 | [14] | ||
| Cl− | PbCO3(aq) | −0.02 | [21] | ||
| Na+ | PbCO3(aq) | Cl− | 0 | −0.145 | [21] |
| SO42− | Pb(OH)2(aq) | −0.5581 | [15] | ||
| SO42− | Pb(OH)3− | −0.4046 | [15] | ||
| Na+ | Pb2+ | 0.10 | [30] | ||
| Cl− | PbCl2(aq) | −0.14 ± 0.04 | [12] | ||
| Na+ | PbCl2(aq) | −0.11 | [30] | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiong, Y. Recycling of Lead Pastes from Spent Lead–Acid Batteries: Thermodynamic Constraints for Desulphurization. Recycling 2022, 7, 45. https://doi.org/10.3390/recycling7040045
Xiong Y. Recycling of Lead Pastes from Spent Lead–Acid Batteries: Thermodynamic Constraints for Desulphurization. Recycling. 2022; 7(4):45. https://doi.org/10.3390/recycling7040045
Chicago/Turabian StyleXiong, Yongliang. 2022. "Recycling of Lead Pastes from Spent Lead–Acid Batteries: Thermodynamic Constraints for Desulphurization" Recycling 7, no. 4: 45. https://doi.org/10.3390/recycling7040045
APA StyleXiong, Y. (2022). Recycling of Lead Pastes from Spent Lead–Acid Batteries: Thermodynamic Constraints for Desulphurization. Recycling, 7(4), 45. https://doi.org/10.3390/recycling7040045





