Facility Location Problems: Models, Techniques, and Applications in Waste Management

Abstract

This paper presents a brief description of some existing models of facility location problems (FLPs) in solid waste management. The study provides salient information on commonly used distance functions in location models along with their corresponding mathematical formulation. Some of the optimization techniques that have been applied to location problems are also presented along with an appropriate pseudocode algorithm for their implementation. Concerning the models and solution techniques, the survey concludes by summarizing some recent studies on the applications of FLPs to waste collection and disposal. It is expected that this paper will contribute in no small measure to an integrated solid waste management system with specific emphasis on issues associated with waste collection, thereby boosting the drive for effective and efficient waste collection systems. The content will also provide early career researchers with some necessary starting information required to formulate and solve problems relating to FLP.

1. Introduction

One of the critical issues that borders on solid waste management in developing countries is centered on the collection of waste. For an effective integrated solid waste management (ISWM) system, locating the collection points is very crucial. Governments and other stakeholders have made several investments but with limited results in combating the challenges associated with effective waste collection. Although much of the generated and stored waste find their way to the designated collection points, due to the lack of effective collection systems, these wastes constitute public challenges thereby creating unsanitary issues and consequently adding to environmental pollution [1,2,3,4]. Thus, this review study focuses on the well-researched facility location problem (FLP) regarding locating waste collection facilities such as recycling centers, waste-to-energy facilities, or containers/bins within a waste collection network.

Several studies have considered methods for addressing the problem of facility selection through the use of mathematical analyses and computer simulations. For instance, in a similar fashion to FLP, one study [5] reported an approach for selecting construction materials in an engineering design project. An extensive range of models exists in the literature for describing practical problems of optimization involving service point locations in waste management, and some of these mathematical formulations are discussed in this study (see [6,7,8,9,10,11,12,13,14,15,16,17,18] for examples). The differences and similarities in these models are discussed more succinctly under the application section as many of them find direct applications in solid waste management where municipal authorities are often confronted with the enormous challenge of locating waste collection facilities as well as landfills within their municipalities because of limited financial resources.

FLP deal with the question of how to select from a given set of potential locations, a cost-effective subset of sites to place new facilities or retain existing ones. A facility could represent any service facility such as an electric power plant, hospital, food production plant, a warehouse (depot), petrol station, government office, etc. FLPs are an essential class of problems in logistic management. Facility location and the assignment of entities to such facilities usually determine the distribution pattern and the associated characteristics (e.g., time, cost, and efficiency) of the facility. The placement of one or more facilities and the assignment of customers in an optimal version not only improve the flow of materials and services offered by the facilities to customers but also utilize the facilities in an optimum manner, thus preventing the use of duplicated or redundant facilities [19]. Technological advancement has made it somewhat easier to design cost-efficient facility locations for municipal solid waste collection especially for large areas. In this sense, the Web-Geographical Information System (Web-GIS) oriented technologies are noteworthy, and their applications have been reported elsewhere [20,21,22].

The most common approach for formulating FLP models in the literature is through the use of integer programming (IP). IP is a form of linear programming in which some or all the decision variables are restricted to be non-negative integer values. When all the variables take on integer values, then it is called a pure integer programming problem. On the other hand, the mixed-integer programming (MIP) model is a variation where some variables are real, and some are integers, or at least one variable is an integer. It may have a binary variable, which can be used to identify if any entity is active or not by being assigned 1 or 0, respectively [23].

Optimization algorithms for solving FLP models can be grouped under two categories of exact and approximation algorithms. Exact algorithms guarantee optimal solutions to the problems being addressed. However, a significant disadvantage of exact methods is that, as the size of the problem increases, the time required to arrive at the optimal solution usually becomes huge. This drawback led to the construction of approximation algorithms, which generally start with a single solution or a predetermined set of solutions while trying to identify a near-optimal solution for the optimization problem. In contrast to the exact techniques, approximate or heuristic algorithms use some specific rules-of-thumb to guide the algorithm towards the problem’s feasible region. These rules often provide some modifications to the incumbent solution as well as procedures for the further exploration of the solution space of the problem. The identification and specification of these sets of rules and connecting them appropriately within the framework of the algorithm are crucial for successful implementation of approximate algorithms.

The remaining part of this paper is structured as follows: Section 2 describes the methodology adopted for the conducted survey, while Section 3 discusses the notion of distance function. In contrast, Section 4 describes a few significant variants of FLP and their corresponding mathematical models. Some optimization algorithms for solving FLP models are discussed in Section 5, while some applications of FLP in waste management are highlighted in Section 6. The concluding remarks are given in Section 7.

2. Methodology

This survey article follows a narrative approach describing important models in FLP that have been adapted to problems relating to waste management, especially the collection stage of the system. One of the objectives of the paper is to provide first-hand information on the existing models and solution approaches to emerging research in related fields, thus the collection of materials was such that original documents on model formulations and solution designs were given priority. All the journal materials were obtained from Google Scholar database. The study considered only research carried out between 2006 and 2020 in narrating the applications of FLP in waste management.

3. Distance Function in Facility Location

In the process of finding optimal locations for a set of facilities, a remarkable phenomenon is the pattern of travel distances among service customers. Customers always appreciate the placement of facilities not being too far from a service point. Ogryczak [24] observed that most classical FLP focus on the minimization of the mean distance or the maximum distance to the facilities. Usually, these distances are measured over the set Z^x with their values in Z; however, because Zⁿ is not a vector space, the notion of distances is often extended, and this gives rise to the general definition in R^x (the real line). Thus, the distance functioned between points x and y denoted as d(x,y) satisfies the basic properties of a metric distance.

For a more general notation, the distance function between the points x = (x_1, x_{2, …,} x_x) and y = (y_1, y_{2, …,} y_x) is denoted by d_k,p(x,y) and is called the Minkowski distance of order p and is defined as:

$$d_{k,p}\left(x,y\right)={\left({\displaystyle \sum _{i=1}^n{k}_i{\left|x_i-y_i\right|}^p}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$p$}\right.}$$

(1)

When k₁ = k₂ = ··· = k_x = k_p, Equation (1) becomes

$$d_{k,p}\left(x,y\right)=k{\left({\displaystyle \sum _{i=1}^n{\left|x_i-y_i\right|}^p}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$p$}\right.}$$

(2)

where k is the weight of the distance function d_k,p and Equation (2) is called the weighted d_k,p − norm. However, suppose k₁ = k₂ = ··· = k_x = 1, then Equation (1) becomes

$$d_{k,p}\left(x,y\right)={\left({\displaystyle \sum _{i=1}^n{\left|x_i-y_i\right|}^p}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$p$}\right.}$$

(3)

Equation (3) denotes the d_k,p − norm. Uster and Love [25] showed that distances estimated based on the d_k,p − norm are more accurate than those in the weighted d_k,p − norm. According to Equation (3), some distances are defined in the following:

• Rectilinear distance: This distance describes, for instance, the distance that a vehicle will cover over a square block in a city layout where no one-way routes exist. It is given by

  $$d_{k,1}\left(x,y\right)={\displaystyle \sum _{i=1}^n\left|x_i-y_i\right|}$$

  (4)

  Since it is simple to analyze distance compared to some other forms of distance, it has become popular among researchers [26].
• Euclidean distance: This is defined for p = 2 as follows:

  $$d_{k,2}\left(x,y\right)={\left({\displaystyle \sum _{i=1}^n{\left|x_i-y_i\right|}^2}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$$

  (5)

  Equation (5) is the meter rule distance because it gives exactly what would be obtained if the distance between two points was measured with a ruler.
• The Chebyshev distance: This distance is defined for p = ∞ as follows:

  $$d_{k,\infty }\left(x,y\right)=\underset{p\to \infty }{\lim }{\left({\displaystyle \sum _{i=1}^n{\left|x_i-y_i\right|}^p}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$p$}\right.}=\max \left(\left|x_1-y_1\right|,\dots ,\left|x_n-y_n\right|\right)$$

  (6)

By simple inspection, it is evident that d_k,1 and d_k,∞ assume discrete values. Thus, from a practical viewpoint, the parameter d_k,2 being continuous is widely used because of its rotation invariance [27].

For each category of FLP, there is a corresponding suitable distance function. For instance, in the analytic models of FLP, the travel distances follow the rectilinear metric. In contrast, in network problems consisting of nodes and arcs, distances are measured concerning the shortest path. The discrete models can usually make use of all kinds of distance functions [28].

4. Classification of Facility Location Problems

FLPs are not uniquely classified in literature. Location problems may be divided into four classes: analytic, network, continuous, and discrete models. The analytic models are based on simple assumptions, such as the fixed costs of locating a facility. They are hardly used to express real-world problems. The network models are frequently encountered in transportation planning and other applications that allow tours on routes represented on a network. Mladenovi et al. [29] classified FLP into continuous and discrete problems. In the continuous models, facilities to be located are placed anywhere in the chosen plane and therefore computations are required to determine the best locations with respect to the distances of the demand points (customers’ locations). Furthermore, in continuous location models, customers are grouped (using appropriate techniques) and the centroid of each group is determined. Each centroid then becomes the best location for each group (cluster). This approach of locating facilities is very applicable in highly sensitive strategic planning.

In most practical real cases, estimates in continuous models make discrete models become practicable. Discrete models handle the allocation of customers to a set of potential location points (usually predetermined either from the results of the continuous model or random selection based on past experiences). In other words, the objective in a discrete model is to select the required number of locations for facilities from a set of known locations, and then allocate customers to receive service from exactly one of these facilities at minimum cost [19].

Discrete models usually consist of three main components of facilities to be located, a set of locations, and demand points. The facilities have certain features such as total number, type, and costs. There are two cases identified for the number of facilities. The first is the single facility problem in which only one new facility is to be opened. The more general case is the multi-facility problem where more than one facility is established simultaneously. Facilities in location-allocation problems can also come in different types such as situations where facilities are designed to provide only one or more services. One other major consideration is the satisfaction of demands at these facilities. This in turn gives rise to the variants of uncapacitated and capacitated FLP. Based on these features, a number of discrete and continuous models have been proposed in the literature for several areas of application. Some of these are described in the subsections. Afterward, some solution approaches to FLPs are described with their possible algorithms.

4.1. Single Facility Location Problem (SFLP)

The SFLP belongs to the most straightforward class of location problems. Its involve the location of a unique new facility in a plane intending to minimize the sum of distances (Euclidean or rectilinear) between the proposed new facility and existing (planar) locations. A simple general formulation of the problem is

$$Z_1=\min \left\{f\left(\overline{x}\right):f\left(\overline{x}\right)={\displaystyle \sum _{i=1}^n{w}_{i}d\left(\overline{x},p_i\right)}\right\}$$

(7)

where $\overline{x}$ = (x, y) is the distance coordinate of the location of the new facility; d(x_i,y_i) is the distance between the new facility and the planar locations; p_i = (u_i,v_i) are the coordinates of the planar locations; w_i represents the weight of existing facilities; i and n are the index and number of existing facilities, respectively.

4.2. Multi-Facility Location Problem (MFLP)

In a MFLP, more than one new facility are to be optimally located, such that each newly located facility is connected to at least one other new facility. A typical objective function is formulated as follows. Let N be a set of the new facilities to be located so that |N| = n and M_i a set of the existing facilities such that |M| = m. Define w_ji ≥ 0 as the weight between each j$\in$N and i$\in$M by a unit distance; v_jk ≥ 0 is the weight between each j,k$\in$N by unit distance; d(X_j, p_i) is the distance between the location of j$\in$N and i$\in$M d(X_j, X_k) is the distance between the location of j,k$\in$N; and p_i = (a_i, b_i) is the location coordinates of i$\in$M; The objective function is:

$$Z_2=\min \left({\displaystyle \sum _{1\le j<k\le n}{v}_{jk}d\left(X_j,X_k\right)+{\displaystyle \sum _{j=1}^n{\displaystyle \sum _{i=1}^m{w}_{ji}d\left(X_j,p_i\right)}}}\right)$$

(8)

The model in Equation (8) is a minisum model that finds the locations of new facilities such that the total cost function (sum of costs directly proportional to the distances between the new facilities, and costs directly proportional to the distances between new and existing facilities [27]) is minimized.

4.3. Fixed Costs Capacitated Facility Location Problem (FC-CFLP)

In an FC-CFLP, the objective is to minimize the fixed costs associated with the potential facilities. The FC-CFLP is a minisum problem because it seeks to minimize the sum of the cost of flow between facilities and customers. The fixed cost is a one-time expenditure that varies from location to location, which is expected to be recovered during the entire life of the facility. To formulate the problem as a mathematical model, the following sets are defined: C is the set of all n customers indexed with i; F is the set of all candidate facilities indexed with j. The fixed cost for opening facility j is c_j. The transportation cost from facility j to customer i is t_ij; a_j is the capacity of facility j$\in$F and β_i is the demand of customer i$\in$C The decision variables are: x_j = 1 if facility j is open, and 0 if otherwise; y_ij = 1 if a customer i is assigned to facility j, and 0 if otherwise. The mixed integer programming model of the problem is as follows:

$$Z_3=\min \left({\displaystyle \sum _{i\in C}{\displaystyle \sum _{j\in F}\left(t_{ij}{y}_{ij}+c_j{x}_j\right)}}\right)\in$$

(9)

$$\begin{array}{l}\mathrm{such} \mathrm{that}\\ {\displaystyle \sum _{i\in C}{y}_{ij}=1}, \mathrm{for} \mathrm{all} \mathrm{facility} j\end{array}$$

(10)

$${\displaystyle \sum _{i\in C}{\beta }_i{y}_{ij}\le {\alpha }_j{x}_j}, \mathrm{for} \mathrm{all} \mathrm{facility} j$$

(11)

$${\displaystyle \sum _{i\in C}{y}_{ij}\ge x_j}, \mathrm{for} \mathrm{all} \mathrm{facility} j$$

(12)

$$x_j,y_{ij}\in \left\{0,1\right\}, \mathrm{for} \mathrm{all} i,j$$

(13)

The objective function in Equation (9) minimizes the total cost (transportation and fixed cost) associated with an open facility. The constraint in Equation (10) ensures that each customer is allocated to only one facility. Equation (11) defines capacity constraints, and it ensures that the total demand of customer i assigned to facility j does not exceed the capacity of j. By constraints in Equation (12), a number of open facilities must not exceed the total number of customers in the system. Equation (13) is the integer constraint.

4.4. Capacitated p-Median Facility Location Problem (CpMFLP)

This is a discrete problem where the list of potential depots is the same as the list of customers. The selected depots are called the medians or concentrators. A p-median problem is defined as follows. Consider a connected graph consisting of customers with associated network distances from each other, P new facilities are to be opened to satisfy the demands of these customers. A p-median problem optimally locates the P facilities so that the sum of the weighted distances in the network between the customers and their respective closest facility is the smallest [30]. p-Median problems are widely studied because of their relevance to most real-life issues.

The CpMFLP is a variant of the capacitated FLP (CFLP) when fixed costs associated with potential facilities are not considered. Using the approach of Lorena and Senne [31] with a little modification, the problem is described with the following notations. N = {1,2,...,n} is the set of customers to be allocated to potential medians; y_ij = 1 if the customer i is assigned to the median j, or 0, otherwise x_j = 1 if the median j is selected, or 0, otherwise. Other parameters are: P is the number of facilities to be opened; d_i is the demand of customer i; q_j is the capacity of the facility j; and c_ij is the shipment cost from facility j to the customer i. The integer programming formulation of the problem is Constraint sets in Equation (15) impose that each customer must be allocated to only one median. Equation (16) prevents the total number of opened facilities from exceeding the number of facilities required. Full median capacity is ensured by constraint in Equation (17).

$$Z_4=\min \left({\displaystyle \sum _{i\in N}{\displaystyle \sum _{j\in N}{c}_{ij}{y}_{ij}}}\right)$$

(14)

$$\begin{array}{l}\mathrm{such} \mathrm{that}\\ {\displaystyle \sum _{i\in N}{y}_{ij}=1}, \mathrm{for} \mathrm{all} \mathrm{median} j\end{array}$$

(15)

$${\displaystyle \sum _{i\in C}{x}_j}=P, \mathrm{for} \mathrm{all} \mathrm{median} j$$

(16)

$${\displaystyle \sum _{i\in N}{d}_i{y}_{ij}\le q_j{x}_j}, \mathrm{for} \mathrm{all} \mathrm{median} j$$

(17)

$$x_j,y_{ij}\in \left\{0,1\right\}, \mathrm{for} \mathrm{all} i,j$$

(18)

4.5. Covering Location Problems (SCLP)

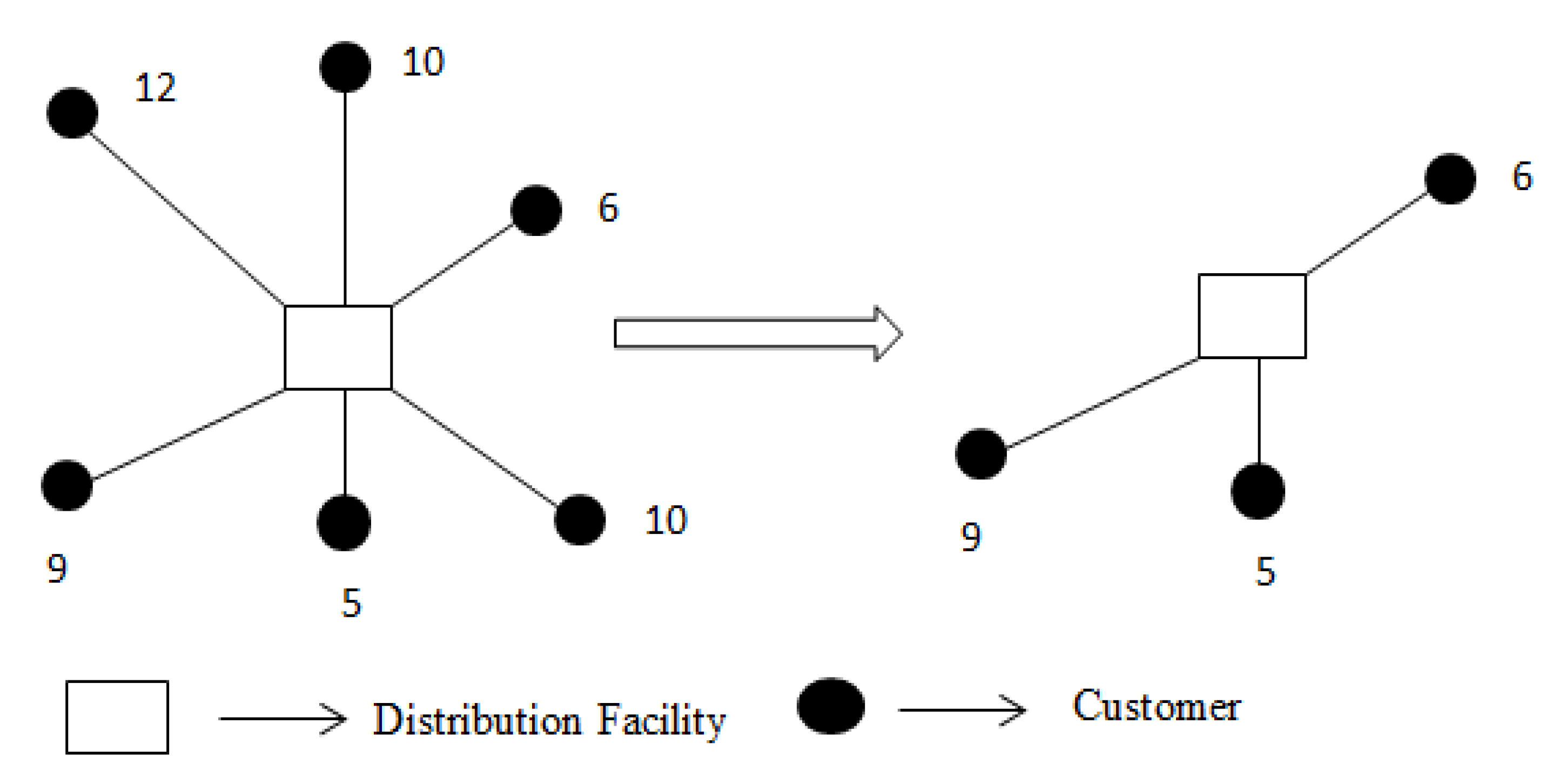
In SCLP, customers are allowed to receive services from potential facilities depending on the distances between the customers and the facilities. A customer’s demand/request can only be satisfied at a facility provided the distance between the customer and the facility is equal or less than a predefined value known as the threshold distance or coverage radius. There are two cases of SCLP depending on the extent of coverage on the demands of customers. When all the demand points are covered, the problem is called a total SCLP, and when only some locations are included, the problem is a partial SCLP. In Figure 1 (left side), the demand points are represented on the customer nodes with the corresponding distances between the distribution facility and the customers. Suppose we are interested in covering only customers located within a maximum distance of 9 km of all the customers represented in the plane (left side of Figure 1), Figure 1 (right side) shows that the distribution facility can serve only three customers. The coverage radius in the above illustration was measured as a distance; however, the value may be measured with other quantities like time and cost.

The symmetric total covering problem (STCP) is a typical example of a total covering problem, while the maximum covering location problem (MCLP) belongs to the family of partial covering problems. These two variants are discussed as follows.

4.5.1. Symmetrical Total Covering Problem (STCP)

This problem was first formulated by Jans and Degraeve [32] for a lottery problem. Two variables x_j and y_ij are defined on a set S, the set of all demand points, as x_j = 1 if the facility j$\in$S covers a point, 0, otherwise, y_ij = 1 if the facility includes the customer j$\in$S and 0, otherwise. The integer programming formulation is:

$$Z_5=\min \left({\displaystyle \sum _{j\in S}{c}_j{x}_j}\right)$$

(19)

$$\begin{array}{l}\mathrm{such} \mathrm{that}\\ {\displaystyle \sum _{i\in S}{y}_{ij}{x}_j\ge 1}, \mathrm{for} \mathrm{all} \mathrm{facility} j\end{array}$$

(20)

$$x_j,y_{ij}\in \left\{0,1\right\}, \mathrm{for} \mathrm{all} i,j,$$

(21)

where c_j is the cost associated with a facility j. The objective function minimizes the total cost of covering all the demand points. The constraint in Equation (20) ensures that each customer is covered by at least one facility.

4.5.2. Maximum Covering Location Problem (MCLP)

The problem reported by Berman and colleagues [33] is a partial SCLP and has the objective of maximizing the total satisfying demands in the network with a limited maximum number of facilities. The integer programming model is:

$$Z_6=\max \left({\displaystyle {\sum }_i{\sigma }_i{a}_i}\right)$$

(22)

$$\begin{array}{l}\mathrm{such} \mathrm{that}\\ a_i\le {\displaystyle {\sum }_j{y}_{ij}{x}_j}, \mathrm{for} \mathrm{all} i\end{array}$$

(23)

$${\displaystyle {\sum }_j{x}_j}\le p,$$

(24)

$$a_i,y_{ij},x_j\in \left\{0,1\right\}, \mathrm{for} \mathrm{all} i,j$$

(25)

σ_i is the request of customers i; the maximum number of the limited facility is p. The two decision variables are: x_j = 1 if a facility is located at j or 0, otherwise a_i = 1 if the demand of the customer i is not satisfied and 0, otherwise. y_ij is the same as in Section 4.5.1. Equation (23) means a_i = 0 if ${\displaystyle {\sum }_j{y}_{ij}=0}$ and hence the need of the customer i is satisfied. If ${\displaystyle {\sum }_j{y}_{ij}=1}$, then, the converse holds. This equation represents the capacity limitations. Equation (24) ensures that the number of activated facilities cannot exceed the maximum number of available facilities.

4.6. Undesirable Facility Location Problem (UFLP)

The UFLP belongs to a class of FLPs known as the maxisum models. Unlike the p-median problems where the desirability of facilities allows for the minimization of the objective function relating to distance or cost, in maxisum models, the concern is how to locate facilities far from the intended users. For instance, because of the health and environmental implications, locating landfill facilities close to waste collection points may be undesirable. Daskin [34] proposed an IP model for the UFLP with the following parameters: P is the number of expected facilities to be opened; σ_i is the demand of customer i; d_ij is the distance between customer i and facility j; x_j is the same as in Section 4.5.1; y_ij = 1 if the requirement of customer i is satisfied by facility j, and 0, if otherwise. The mathematical representation is:

$$Z_7=\min \left({\displaystyle {\sum }_i{\displaystyle {\sum }_j{\sigma }_i{d}_{ij}{y}_{ij}}}\right)$$

(26)

$$\begin{array}{l}\mathrm{such} \mathrm{that}\\ {\displaystyle {\sum }_j{y}_{ij}=1}, \mathrm{for} \mathrm{all} i\end{array}$$

(27)

$${\displaystyle {\sum }_j{x}_j}=P$$

(28)

$$y_{ij}\le x_j, \mathrm{for} \mathrm{all} i,j,$$

(29)

$$x_j,y_{ij}\in \left\{0,1\right\}, \mathrm{for} \mathrm{all} i,j$$

(30)

The objective function in Equation (26) minimizes the weighted sum of demands and distances with the limitations of Equations (27)–(30).

5. Solution Techniques for FLP

Every optimization algorithm aims to obtain the best available solution from the feasible solution space, and several methods have been proposed and described in the literature for solving the FLP optimally. Many of these methods generate inexact solutions as experiments have shown that the FLP falls in the class of NP-hard combinatorial problems. That are problems for which there is no known polynomial-time algorithm for their solution. Krarup and Pruzan [35] verified that the uncapacitated plant location problem, a simple form of the FLP, is NP-hard.

For this reason, exact methods are usually sacrificed for inexact methods to arrive at near-optimal solutions. Thus, there are two categories of techniques available for FLPs: precise and heuristics (approximate) methods. In many cases, however, solutions that start with exact methods are usually concluded with heuristic approaches to obtain desirable optimal solutions.

Heuristics can be viewed as methods of arriving at an approximate solution to a problem, that is, guessing a solution to a problem which is considered good enough. Thus, making use of heuristic methods in finding the resolution of a problem is to apply a rule of thumb, which is generally under the control of the computer to explore available paths and reasonable guesses to arrive at an optimal solution. It is a search mechanism that checks all possible alternatives to obtain the best. Heuristics are problem-dependent. In other words, a heuristic is usually defined for the particular problem it seeks to solve. Meta-heuristics, a form of heuristics, differ from basic heuristics in that they are problem-independent techniques and can generally be adapted to different types of problems. In the literature, a number of these approximate methods have been proposed to provide near-optimal solutions to the FLP. Below are some of the widely used techniques for solving facility location-related problems.

5.1. Branch-and-Bound

The branch-and-bound (BB) is by far the most widely used exact method for solving large-scale NP-hard optimization problems [36]. The BB algorithm searches the space of the feasible solution of a given problem for the best solution. Since the number of possible solutions grows exponentially, only an implicit search of the solution space is possible. At the start of the process, only one subset of the solution space exists and is the complete solution space having an optimal solution set at 1. Successively, a pool of unexplored subsets is generated and represented as nodes in a search tree. These nodes are then processed by an iterative algorithm with the following components: node insertion, estimation of bounds, and branching.

This method is popular with many authors and has been incorporated into some software for suitable problem instances. In 2010, Kim and Kim [37] applied the technique to determine the locations of long-term care facilities by using some dominance properties that identify partial solutions dominated by other solutions and subsequently remove such dominated solutions from the solution space. Beresnev [38] proposed a BB algorithm for finding an optimal non-cooperative solution to a competitive FLP where competing parties open their facilities successively intending to capture a good number of customers, thereby maximizing their profits.

To describe a simple algorithm for the BB technique, consider a simple optimization problem φ(X,f), where X is the search space and f:X→R is the cost function. A new sub-problem $L\subseteq X(X\in L)$ is selected at each iteration of the algorithm, where L is a list of unexplored subproblems. A pseudocode for implementing the BB technique based on this information is given as follows:

The Pseudocode of Branch and Bound

1: input: $L=\left\{X\right\}$, initialized $\overline{x}$ (the current solution); 2: while L = ϕ do 3: select the subproblem $l\in L$ to explore 4: if a solution ${\overline{x}}^{\prime }\in \left\{x\in l,f\left(x\right)<f\left(\overline{x}\right)\right\}$ can be found do 5: set $\overline{x}={\overline{x}}^{\prime }$; 6: end if 7: if l cannot be pruned do 8: partition l into l1, l2,..., lp; 9: insert l1, l2,..., lp into l 10: end if 11: remove l from L; 12: end 13: return $\overline{x}$ (the best solution found in the process).

5.2. Lagrangian Relaxation Heuristic

Another method commonly used for solving FLP models is the Lagrangian relaxation (LR) heuristic, which, according to many studies, is both powerful and rich in analysis for solving NP-hard combinatorial optimization problems. The main idea behind the method is to identify one or more “complicating” constraints (see [39]) and then attach a multiplier vector, also known as the penalty cost to this set of constraints before adding it to the objective function [40]. The resulting problem is called the Lagrangian problem, and the objective function is known as the Lagrangian dual function. Maximizing the dual purpose gives the best lower bound value on the actual function of the original problem. Relaxing an integer programming problem in this sense generally produces an easy-to-solve issue [41].

It is easy to infer from the preceding that there are two main concerns in the application of LR. The first is the strategic choice of the set of constraints to relax. Often, this can be done by isolating one or more exciting sub-problems and then relaxing the other restrictions as described above. Another way is to dualize a set of linking constraints (that is, set of constraints where two constraints are represented) into the objective function [42]. This latter approach is common when applying Lagrangian relaxation to facility location problems [43]. The second concern involves the tactical process of finding and updating numerical values of the Lagrangian multipliers. To achieve this, the subgradient optimization method is a handy tool, which takes advantage of the problem structure and constructs a numerical scheme similar to most gradient methods. Comparing different ways, Beasley [41] suggested that the technique will nearly always outperform other applicable methods.

The use of LR and subgradient optimization methods are not new to problems formulated as FLPs. In fact, due to the NP-hard nature of this class of problems, many heuristics proposed for finding optimal solutions are usually based on initial solutions provided by solving the Lagrangian problem of the original question. Some of the applications of the LR heuristics to FLP models may be found in other studies [40,44,45]. The following pseudocode describes the LR process.

The Pseudocode of LR Heuristics

1: Identify the complicating constraint(s) or “easy” subproblem(s) of the primal problem; 2: Initialize all the parameters; 3: while stopping condition is unsatisfied do 4: Solve the subproblems to obtain the lower bound values for the decision variables; 5: Update the vector of Lagrangian multipliers using subgradient optimization method; 6: Construct primal problem solution; 7: end 8: return the best solution to the primal problem

5.3. Constructive and Local Search

Constructive search algorithms build an optimal solution to a problem from scratch by repeatedly extending the current known solution until a complete solution is found. The method generally improves solutions than random methods. It is often used to initialize many metaheuristic algorithms for obtaining near-optimal solutions. The algorithm is usually thought of as being fast, as they are often a single-pass approach [46]. Local search methods, on their part, consider the neighborhood of the existing current solution for possible replacement. That is, a local search algorithm takes a complete solution and tries to improve it through local moves within the neighborhood. Often, constructive algorithms are used to initiate solutions that local search heuristics build on to provide optimal solutions. Generally, a local search follows the hill-climbing search process until the best solution is reached.

5.4. Tabu Search

The Tabu search (TS) is a meta-heuristic approach that allows a form of hill-climbing to overcome the local search optimal [47]. The technique is based on the neighborhood, also known as the short term memory of the search, in a way that prevents movement in cycles [48]. In this way, moves in subsequent iterations that take the current solution to points in the feasible space, which have previously been explored, are avoided. The search space and its neighborhood structure are two fundamental elements of the TS algorithm. When different definitions of the search space for a given problem are considered, the neighborhood structures inevitably change to a certain degree [49]. A typical example is the capacitated FLP, where the search space may be defined with respect to the location variable. In this case, the neighborhood structure will usually involve moves that change the status of one location and open facilities from one place to another.

The Pseudocode of Tabu Search

1: input: initial solution $s\in S$, best solution so far $s^{\prime }$; 2: initialize: k = 0 (iteration counter), Tabu-Memory; 3: repeat 4: Generate Candidate Set $V=N\left(s,k\right)\left(N\left(s,k\right)=N\left(s\right)-Tabu list\right)$; 5: find the best solution $s\in V$; 6: Update: s′ = s, Tabu-Memory 7: k = k + 1; 8: until the stop criterion is met 9: return xα.

5.5. Large Neighborhood Search

The broad large neighborhood search (LNS) is a meta-heuristic and was first proposed by Shaw [50]. A comprehensive description of the algorithm was provided by Pisinger and Ropke [51]. Unlike most neighborhood search methods where the neighborhood containing the solution is usually explicitly defined, the LNS makes use of a destroy-repair approach to define an implicit region of the solution. The destroy technique removes part of a current solution while the repair method re-inserts the eliminated candidate solution(s), thus rebuilding the solution structure. In the LNS, a solution neighborhood J(x) is defined as a solution. This neighborhood can then be explored by the destroy method, followed by the repair method. The algorithm is designed in such a way that it prevents a search of the entire neighborhood. Instead, only a random sample of it is explored at a time. The prefix “large” is appended to the LNS heuristic because, at the destruct phase, a large portion of the solution can be removed.

In describing the LNS algorithm, three essential variables are usually considered: x_α is the best-observed solution during the search, x is the current solution, and x_p is a solution under probation of destructor repair, and two functions d(·) and r(·) correspond to the destruct and improve method, respectively. It is essential to consider carefully the degree of freedom allowed at the destruct phase of the algorithm. The removal of a very small or substantial part of the solution may result in a poor solution. Hence, a mild degree is usually desirable. The methods of solution removal and re-insertion are best applied to problems that can be decomposed to the main and sub-problems. At the destruction phase, an infeasible solution is produced and then converted to a feasible solution by the repair method. Thus, it is right to say an LNS alternates between infeasible and viable solutions.

The adaptive broad neighborhood search (ALNS) is an extension of the LNS heuristic. The first proposition of this extension was reported by Ropke and Pisinger [52]. This method allows multiple applications of the destroy-repair method within the same search. A weight value that controls the frequency of attempt by each way is assigned. This assignment, however, undergoes dynamical re-adjustment as the search progresses to allow problem adaptation. The use of multiple destroy-repair methods indicates that the ALNS enables the creation of various neighborhoods. The following is a pseudocode that represents the descriptions above. Note that c(·) is used to evaluate the objective function, and the accept function of Line 5 can be implemented as suitable to the user as long as the current solution is improved.

The Pseudocode of LNS

1: input: a feasible solution x; 2: xα = x; 3: repeat 4: $x_p=r(d\left(x\right)$; 5: if accept(xp,x) then 6: x = xp; 7: end if 8: if c(xp) < c(xα) then 9: xα = xp; 10: end if 11: until the stop criterion is met 12: return xα.

5.6. Particle Swarm Optimization

PSO is a swarm intelligence-based metaheuristic inspired by the schooling and flocking patterns of birds and fishes [53]. The first work on PSO was published by Eberhart and Kennedy [54]. Particle swarm optimization (PSO), as a form of stochastic optimization, does not require an operator to extract a new set of a candidate solution. This is sharply in contrast to most evolutionary search (ES) methods. It is, however, similar to ES heuristics in that it also searches the population of the potential solution.

Furthermore, unlike the mutation stage of the ES, the PSO relies on information exchange between particles in the population. One can, therefore, say a PSO utilizes a set of agents, called particles, to search a solution space for the optimum value of a given problem. These particles move at a trajectory determined by a rule that merges the current velocity of a particle, its exploration histories, and neighbors [55]. Parsopoulos and Vrahatic [56] described PSO in the following way: Assume n is the dimensional search space and X_i = {x_i1,x_i2,...,x_in} is the vector space of the i^th particle; f is the index of the lowest function valued particle (i.e., the best particle of the swarm); b_i = {b_i1,b_i2,...,b_in} is the best previous position of i^th the particle; V_i = {v_i1,v_i2,...,v_in} is the velocity of the i^th particle.

The updating rule of particles moving through the search space is given by the following equations representing their velocities and position coordinates, respectively:

$$V_i^{j+1}=\beta \left(w{V}_i^j+k_1{\tau }_{i1}^j\left(b_i^j-X_i^j\right)+k_2{\tau }_{i2}^j\left(b_f^j-X_i^j\right)\right)$$

(31)

and

$$X_i^{j+1}=X_i^j+V_i^{j+1}$$

(32)

for i = 1,2,...,S, where S is the size of the population; β is the control parameter for the swarm velocity; w is the inertial weight; k₁ and k₂ are the cognitive and social parameters, respectively; τ_i1, τ_i2$\in$[0,1] are uniformly distributed random numbers. The convergence behavior of PSO is well determined by an appropriate choice of w. To facilitate a search of new solution space, experimental results have indicated that this can be done by initializing w in no small value. In contrast, for fine-tuning results, a low w can be used. Hence, a gradual reduction of the weight value can generate a good result. The pseudocode for implementing PSO is given as follows.

The Pseudocode of PSO

1: input: randomly initialized position and velocity of particles, Xi and Vi; 2: initialize: k = 0 (iteration counter); 3: repeat 4: for i = 1 to S do 5: evaluate the fitness function (the cost function to be minimized); 6: update: bi and bj; 7: update: Vi and Xi; 8: end for 8: k = k + 1; 9: until the stopping criterion is met 10: return X* (the global minimum)

5.7. Ant Colony Optimization and Variants

Ant colony optimization (ACO) and its variants are metaheuristic methods inspired by the way real ants find the shortest paths from their nest to food sources. The ants communicate through the release of a chemical substance known as pheromones. This substance influences the behavioral pattern of other ants in the same environment. ACO makes use of a constructive algorithm to create a solution by a sequence of probabilistic decisions where every move extends an incomplete solution by adding a new solution component until a complete solution is obtained. The series of steps can be viewed as a path through a corresponding decision graph [57].

The implementation of an ACO starts by initializing the values of the pheromones by which a solution is constructed through a transition rule. Once a solution is obtained, the set of local pheromones is updated immediately. Local search is then employed to search for an improved resolution and based on the best global solution obtained at different iterations, the comprehensive pheromone information is updated accordingly.

The Pseudocode of ACO and Variants

1: input: randomly initialized pheromone values; 2: initialize: k = 0 (iteration counter); 3: repeat 4: for i = 1 to n (the number of ants) do 5: construct a solution; 6: update local pheromone values; 7: end for 8: k = k + 1; 9: until the stopping criterion is met 10: return pheromone values for the best solution.

5.8. Simulated Annealing

Simulated annealing (SA) is a technique adapted from the metal annealing process [58]. It is a probability-based method for finding the global minimum of a cost function that possesses more than one local minimum [59]. The SA algorithm comprises a non-homogeneous discrete-time Markov chain at a current state x(t) such that if x(t) = i, a neighborhood j(i) is chosen at random. Given a finite set S, the probability that any j$\in$S(i) is selected is q_ij. Once such j is selected, the next state x(t + 1) is computed as follows: if J(j) ≤ J(i), then x(t + 1) = j. However, if J(j) > J(i), then x(t + 1) = I with the possibility $P\left[x\left(t+1\right)\right]=\exp \left[\frac{-J\left(j\right)-J\left(i\right)}{T\left(t\right)}\right]$, otherwise, $P\left[x\left(t+1\right)\right]=i$.

In essence,

$$P\left[x\left(t+1\right)=j|x\left(t\right)=i\right]=q_{ij}\cdot \exp \left[\frac{-1}{T\left(t\right)}\max \left\{0,J\left(j\right)-J\left(i\right)\right\}\right],\forall j\ne i,j\in S\left(i\right)$$

(33)

and

$$P\left[x\left(t+1\right)=j|x\left(t\right)=i\right]=0 \mathrm{if} j\ne i,j\notin S\left(i\right)$$

(34)

where J is a real-valued cost function defined on S; set $S\left(i\right)\subset S-\left\{i\right\}$ for each i$\in$S is the neighborhood of i; T is a non-increasing function such that T:Z⁺→(0,∞) called the cooling schedule; and T(t) is the temperature at time t. Other assumptions of the technique are: x(0)$\in$ and j$\in$S(i) if and only if i$\in$S(j).

5.9. Genetic Algorithm

The genetic search (GA) algorithm mimics the natural evolution process [60]. The algorithm makes use of significant properties of the evolutionary system such as the population of chromosomes, selection of chromosomes according to fitness, production of new offspring through crossover, and the random mutation of the new family [61]. The GA algorithm searches through a space of chromosomes, which often take the form of a bit string with two possible values of 0 and 1 called the alleles by changing from one population to another. In the search process, a fitness score is assigned to each chromosome in the current population. The rating assigned is dependent on the solvability index of the chromosomes to the particular problem under study.

Generally, the GA works with three major operators. The selection operator chooses chromosomes for reproduction according to their fitness scores. In short, the selection operator preserves the best current solution while keeping the size of the population constant. It does this by eliminating from the population the wrong answers and reproducing copies of the good ones simultaneously. The crossover operator mimics the natural recombination process between organisms by exchanging two chromosomes to reproduce two new offspring. The mutation operator maintains the diversity from one generation of the chromosome population to another by the introduction of new features into the solution pool. More comprehensive details on this technique and some of those discussed above can be found in [62].

The Pseudocode of GA

1: input: Itmax (maximum iteration), n (population size); 2: initialize: current set of the solution: pool, k = 0; 3: repeat 4: for i = 1 to n do 5: select the solutions randomly a,b; 6: crossover(a,b) and generate the new solution: newsol; 7: mutation(newsol); 8: update pool by adding newsol; 9: end for 10: selection(pool); 11: k = k + 1; 12: until the stopping criterion is met 13: return best solution found in the process.

6. Application of Facility Location Problems in Waste Management

Waste management comprises six stages, namely: generation, collection, transport, sorting processing, and disposal. For any successful waste management practice, the efficient planning of the waste collection is essential, not only because of its impact on the total cost of waste management but also due to the environmental implications of uncollected wastes. However, to effectively collect the generated wastes, the number of collection points and their corresponding locations are required to serve the collection requests of customers in any given community. These factors largely determine the level of success that may be attained at the collection phase of waste management. Thus, modeling an optimal collection system always revolves around these two variables: the number of collection facilities and the locations of these facilities. Importantly, the location of facilities in waste management is not restricted to the collection facilities alone. Other facilities such as the treatment centers, recycling centers, and landfills may also be the subject of consideration when applying FLPs in waste management practices.

Due to the associated cost of waste collection, municipal authorities are beginning to engage the participation of optimization analysts in the quest to ascertain the maximum number of facilities required for daily collection and the optimal locations of the facilities. This has given rise to some studies on waste collection FLPs, many of which have been reported in the literature. Badran and El-Hagar [6] proposed a MIP model to optimize the municipal waste collection in Port Said, Egypt. The model presented in their study can select between the different candidate locations for collection facilities to minimize the total cost of municipal waste management. The results they obtained showed that the best model would include 27 locations. Hazardous wastes, usually products of industrial processes and characterized by either their ignitability, corrosiveness, reactivity, or toxicity, form the basis of a study by Alumur and Kara [7]. Their proposed MIP model locates treatment and disposal centers and finds the appropriate choice of technology for the treatment centers. The study used the CPLEX solver to obtain a solution to the optimization model. Erkut et al. [8] proposed a mixed-integer linear programming (MILP) model with multiple criteria for solving the location problem at the regional level of waste collection leading to a solution that was obtained using a technique known as the lexicographic minimax approach. The facilities considered in their study include transfer stations, material recovery facilities, incinerators, and sanitary landfills. A similar approach was used by Tralhão and colleagues [9] who considered a multi-objective modeling approach for urban sorted waste.

In a study conducted in Nardo, a city in the southern part of Italy, Ghiani and colleagues [10] described an IP model for the capacitated location of collection facilities. Their proposed IP model considered capacitating each facility so that all customers’ demands are satisfied every day. The study also introduced the quality of service in the model so that each customer is served by the collection site nearest to him. Their model minimized the total number of facilities to be opened among the set of candidate facilities. It also determined the optimal assignment of customers to opened facilities, as well as allocating waste bins to these facilities so that all the demands were satisfied. They solved the optimization model directly on a solver and proposed a construction heuristic for obtaining approximate solutions. Building on this work, Ghiani and co-workers [11] introduced an additional feature of zoning to determine service territories. Exact and approximate techniques were proposed to implement the model. A considerable number of studies on the location of landfills have also been reported in the literature, a summary of some of these studies may be found in a study by Eiselt and Marianov [12]. Some recently proposed studies on the applications of FLPs in waste collection are presented in

Table 1. Some recent studies on the applications of facility location problems (FLPs) to waste management.

Study	Objective	Mathematical Model	Method		Waste Specification	Data/Application Area
			Exact	Approximate
Chauhan and Singh [63]	Selection of sustainable disposal locations	Multi-criteria	-	Fussy optimization	Healthcare waste	Case study: India
Zhao et al. [64]	Minimization of total cost and risk of locating waste facilities and finding optimal transportation routes	MILP	CPLEX for single-objective problems	The customized multi-objective optimization approach	Hazardous waste	Hypothetical and realistic cases from Sichuan Province, China
Yadav et al. [65]	Minimization of the number of facility locations under uncertainty	Stochastic	-	Interval analysis heuristic	-	Hypothetical case study
Hu et al. [66]	Minimization of multi-objective function	MIP	CCG	-	Waste-to-energy	Case study: Shanghai, China
Boonmee et al. [67]	Minimization of total cost in the supply chain of sellable waste	MIP	-	PSO + differential evolution	Post-disaster wastes	Theoretical datasets
Wichapa and Khokhajaikiat [14]	Minimization of multi-objective functions comprising of the total cost and the final priority weight	Fuzzy analytical hierarchy process (FAHP) and hybrid FAHP and goal programming	LINGO	-	Infectious waste	Case study: Northeast Thailand
Aydemir-Karadag [15]	Maximization of total annual profit	MIP	CPLEX	-	Hazardous waste	Case study: Turkey
Rabbani et al. [68]	Minimization of multi-objective functions comprising of the total cost, total transportation risk of hazardous waste related to population exposure, and site risk	MIP	Linearized version solved by CPLEX	Nondominated Sorting Genetic Algorithm (NSGA) and multi-objective (MOPSO)	Hazardous waste	Hypothetical instance
Rabbani et al. [69]	Minimization of multi-objective function (total cost, total site risk, transportation risk)	MIP	-	GA + Monte Carlo	-	Randomly generated dataset
Rathore and Sarmah [16]	Optimal selection of transfer stations for segregated and unsegregated wastes	MIP	CPLEX + ArcGIS	-	Segregated and unsegregated wastes	Case study: Bilaspur, India
Asefi et al. [17]	Minimization of the total cost of facility location and transportation	MILP	CPLEX	VNS + SA	Solid waste	Case study: Tehran, Iran
Gergin et al. [70]	Optimal site locations for healthcare wastes	Multiple FLP as MIP	-	Artificial Bee Colony based clustering algorithm	Healthcare waste	Real-life problem: Turkey
Toutouh et al. [71]	Optimal locations of garbage accumulation points	MIP	-	PageRank Method + Multi-objective Evolutionary Algorithm	Solid waste (garbage)	Case study: Uruguay and Argentina
Adeleke and Ali [72]	Minimization of the number of activated waste collection sites	IP	-	Lagrangian heuristic	Solid waste	Hypothetical instance: Lagos, Nigeria

CCG = column-and-constraint generation; MILP = mixed integer linear programming; VNS = variable neighborhood search; MIP = mixed-integer programming; SA = simulated annealing; PSO = particle swarm optimization; IP = integer programming; CPLEX and LINGO are optimization solvers suitable for implementing FLP models.

.

7. Conclusions

This paper presents a brief survey of literature on facility location problems (FLPs). To convey the concept of this class of problems, the study tried to review the underlying ideas of the distance function, which are very important in FLPs. Several mathematical models were reviewed, along with some optimization methods that have been used to find near-optimal solutions because of the complexity of the problems. This survey concludes by describing some critical studies where FLPs are directly applied on waste collection, a vital activity of waste management. The content of this paper will provide early career researchers with some necessary starting information required to formulate and solve problems relating to FLPs.

As part of the contribution, this survey study provides a number of managerial insights for stakeholders in the waste management industries as well as other related industries where the proposed model can be utilized. These are highlighted in the following:

• The study provides tangible information on some existing FLP models that have been applied to the problems associated with locating waste collection facilities. These models with little modifications can be utilized to address some current challenges arising from waste collection in many developing urban centers.
• The various optimization algorithms described for solving the existing mathematical models can serve as tools for designing more efficient approximating techniques that will be capable of finding quality solutions to very large-scale problems. Waste collection managers can utilize the ideas in the existing models and solution techniques presented in this study to handle problem-specific factors that are necessary to improve the quality of services they provide at their various customers’ locations.
• The information presented regarding the application of FLPs to waste management is sufficient to guide the stakeholders in the current trends of collection approaches being adopted in different regions of the world.