A Three-Dimensional Hydraulic Stack Model for Redox Flow Batteries Considering Porosity Variations in Porous Felt Electrodes and Bypass Flow in Side Gaps
Abstract
1. Introduction
2. Mathematical Model
2.1. Assumptions
- The electrolyte is an incompressible Newtonian fluid fully filled in the system with constant volume, density and viscosity.
- The electrolyte flow is within the laminar regime.
- The electrolyte and porous electrode are assumed to be isotropic and homogeneous.
- The electrolyte is assumed to be balanced, so no ion diffusion or water transport across the membrane is considered.
- Gassing side reactions, self-discharge reactions and shunt currents are assumed to be negligible.
- Constant temperature is assumed for the system with the heat transfer and thermal effects neglected.
- The gravitational effect of electrolytes is assumed to be negligible.
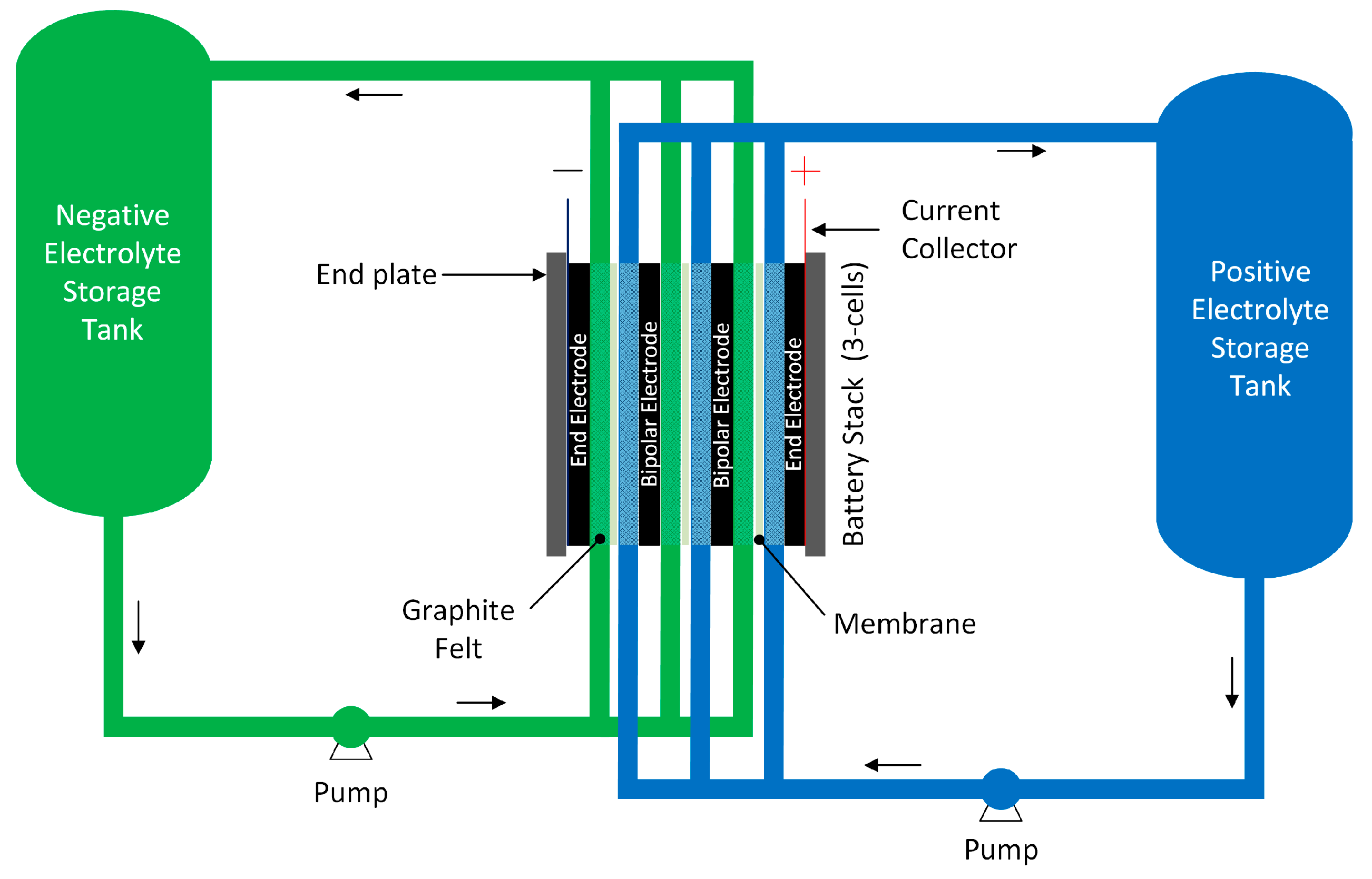
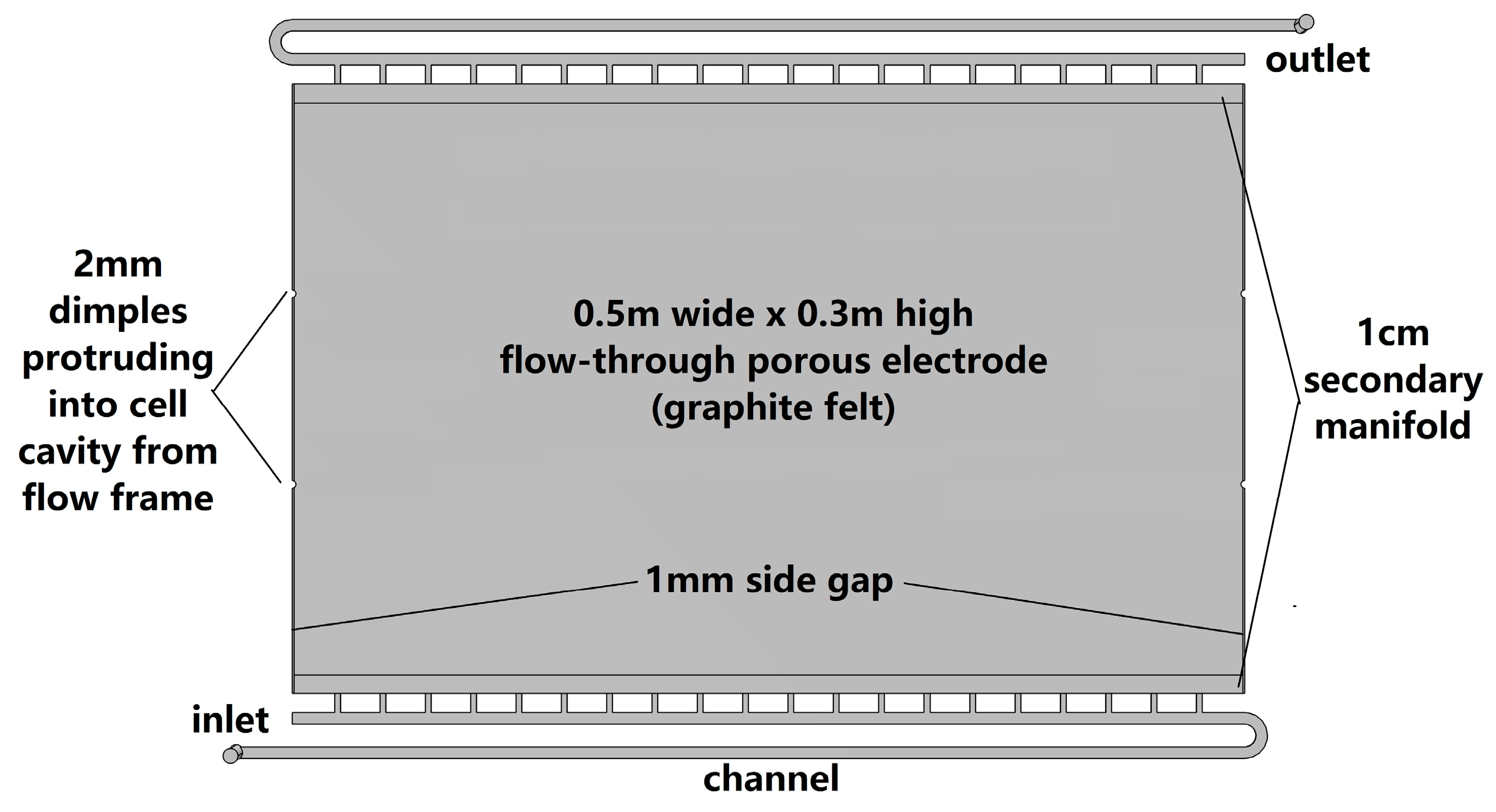
2.2. Geometry
2.3. Governing Equations
2.4. Boundary Conditions
2.5. System Specifications
3. Results and Discussion
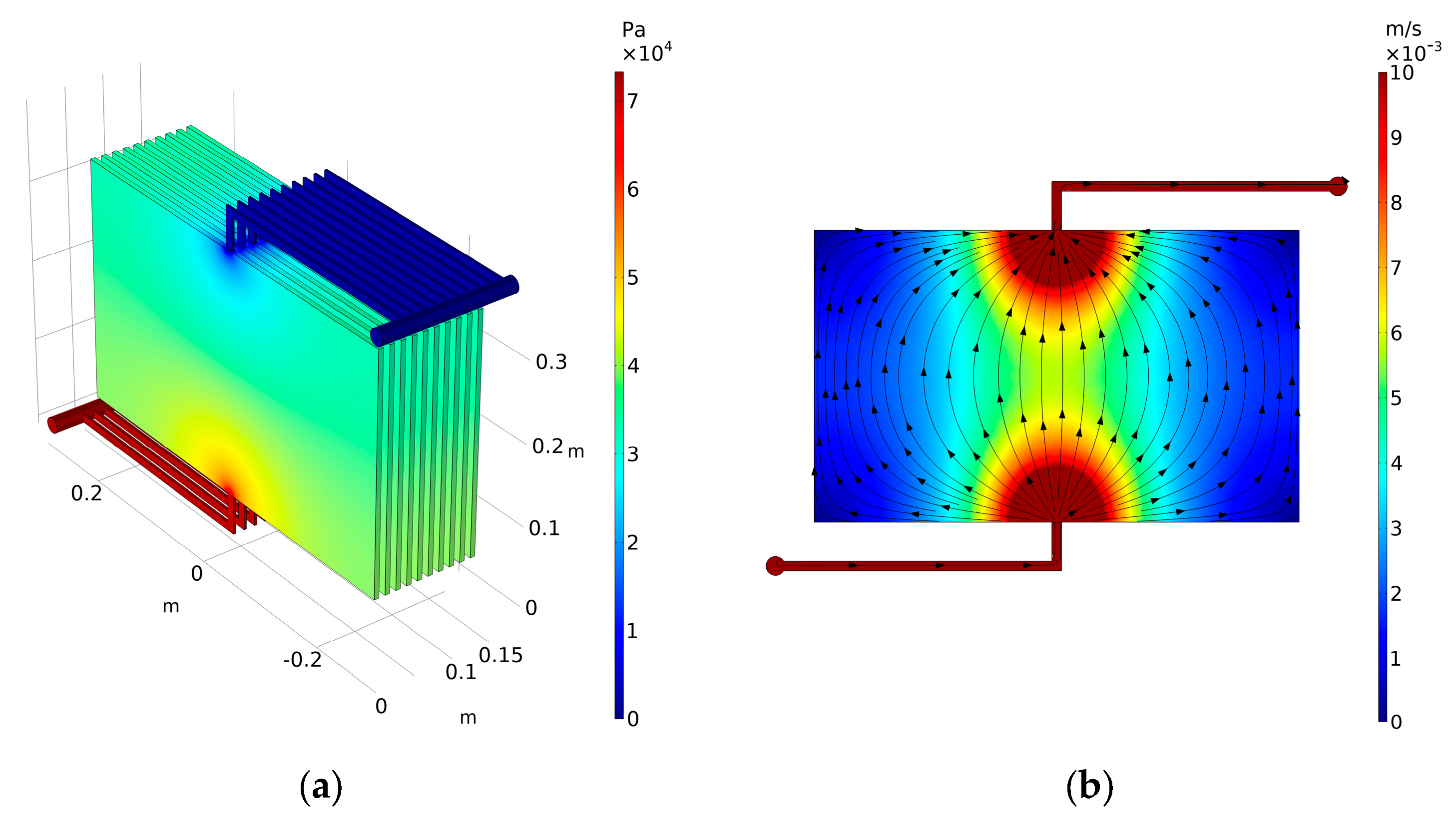
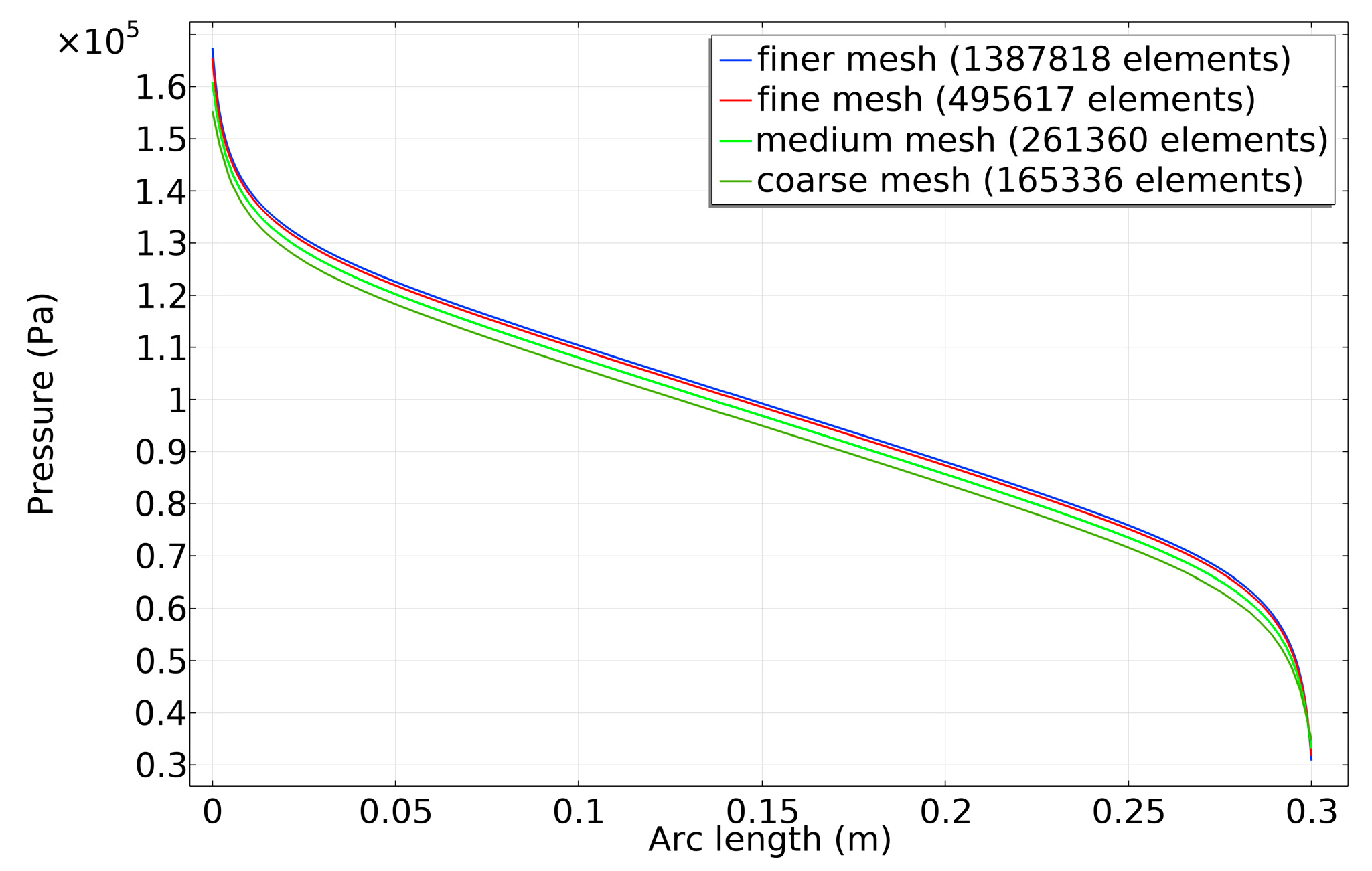
3.1. Case 1: Validation
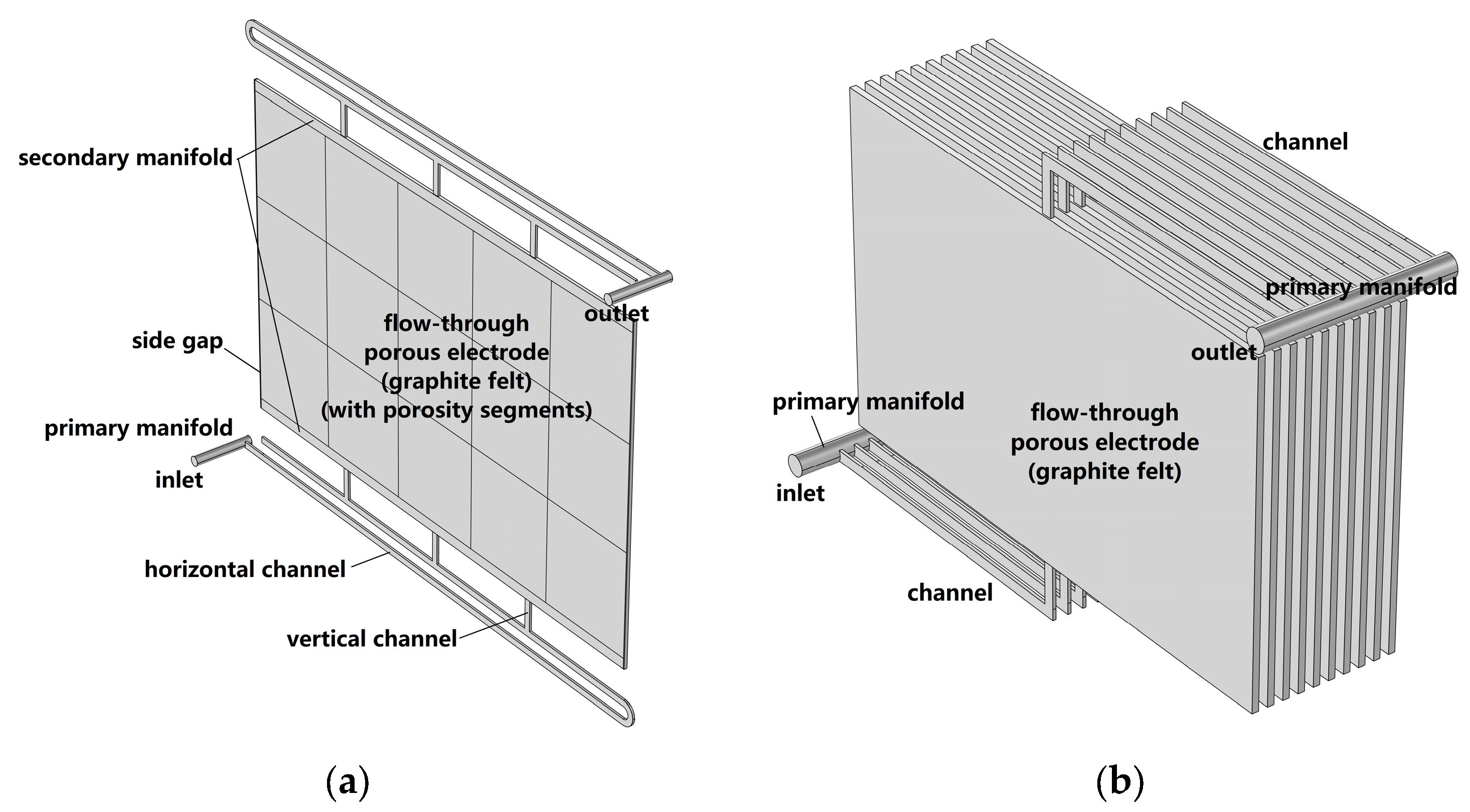
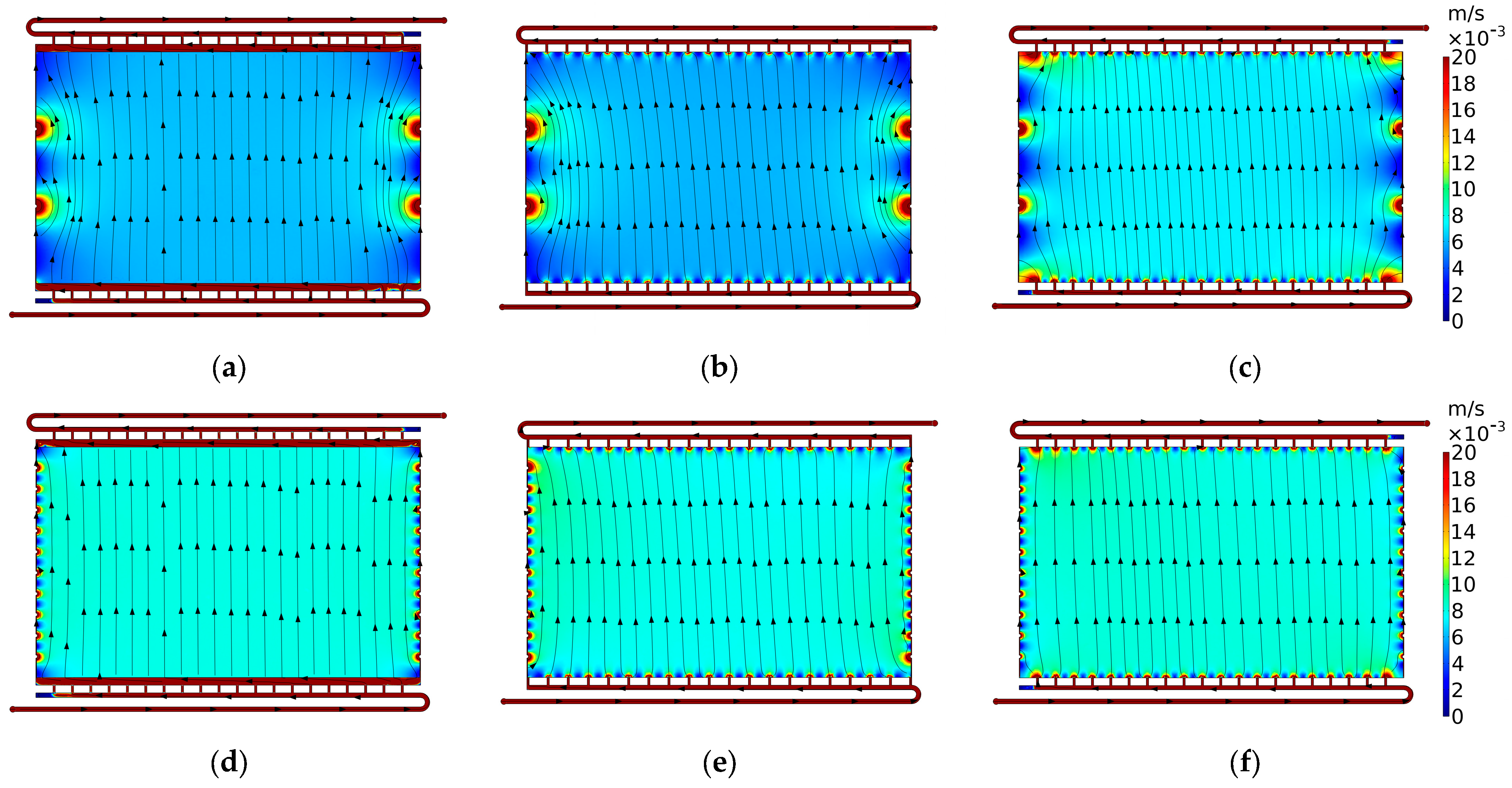
3.2. Case 2: Typical Flow Frame
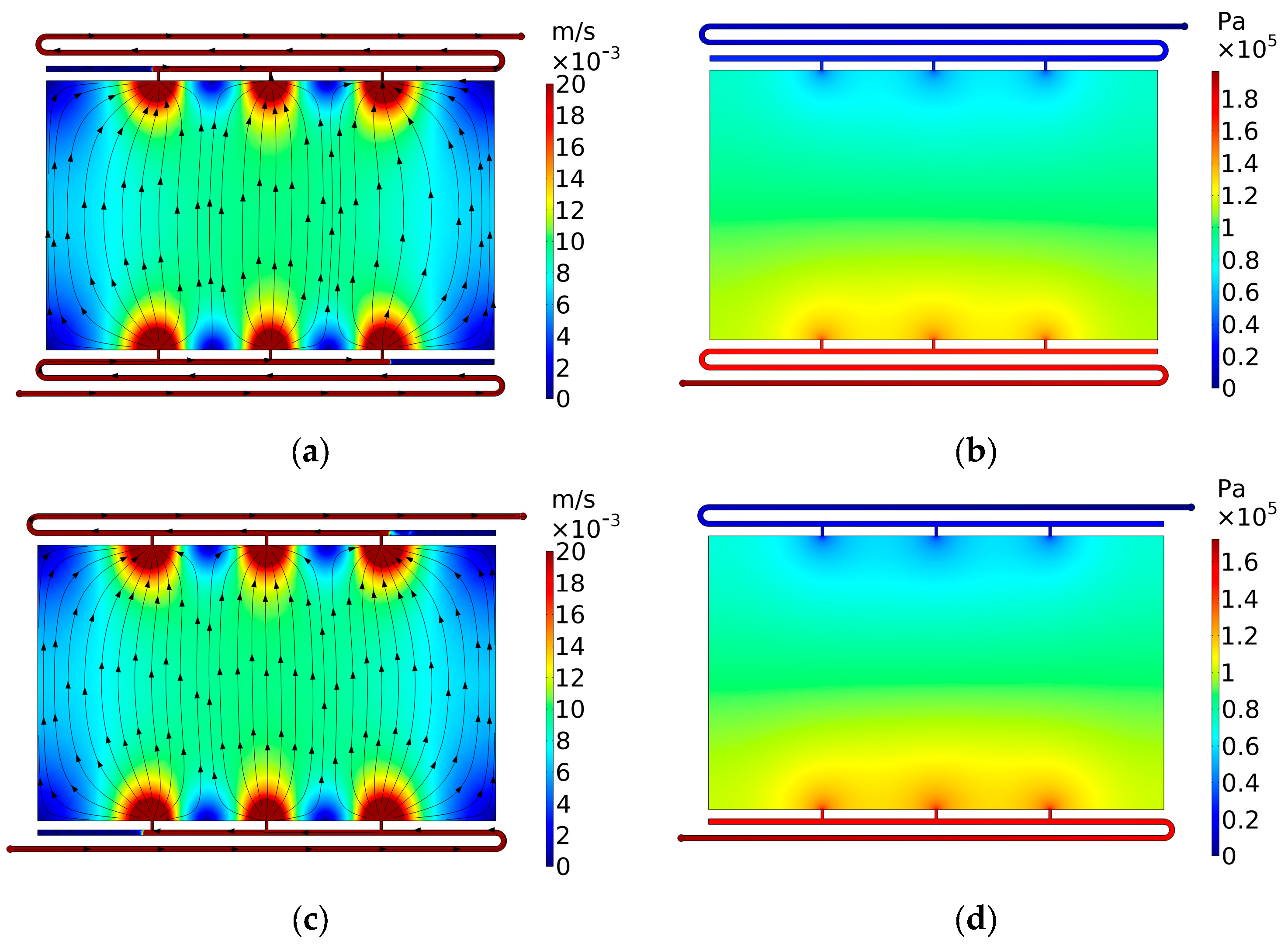
3.2.1. Case 2.1: Horizontal Channels
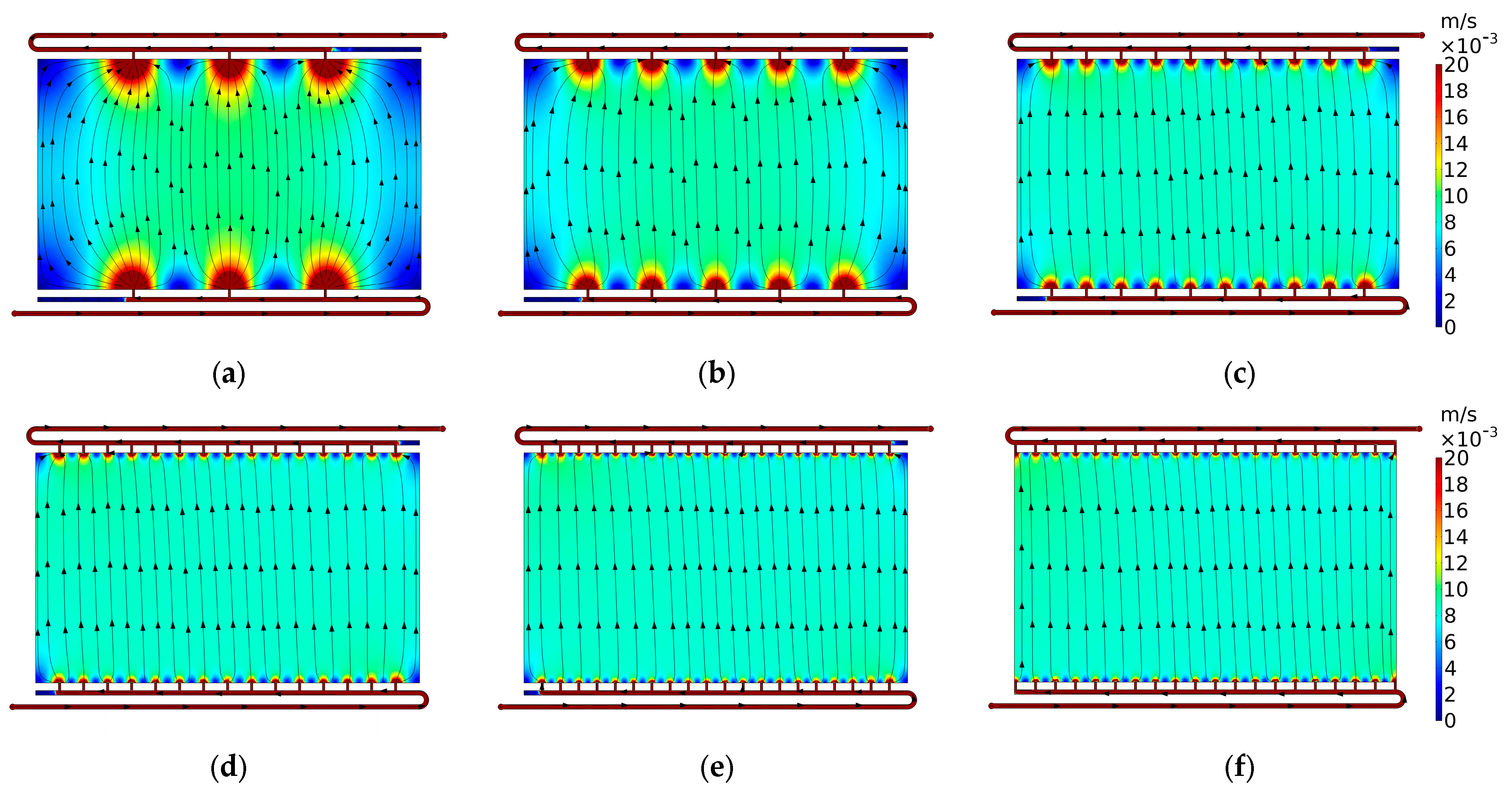
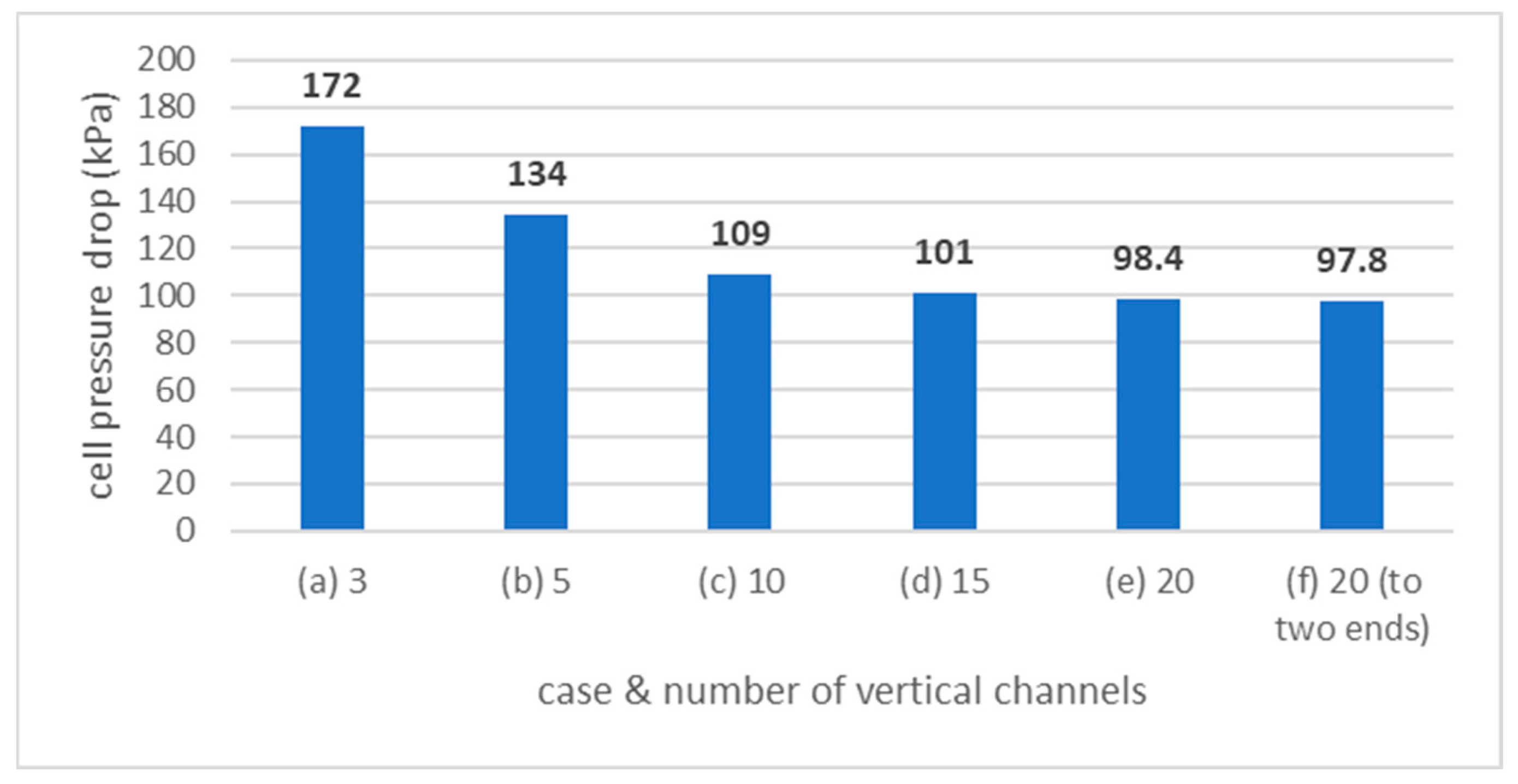
3.2.2. Case 2.2: Vertical Channels
3.2.3. Case 2.3: Secondary Manifold
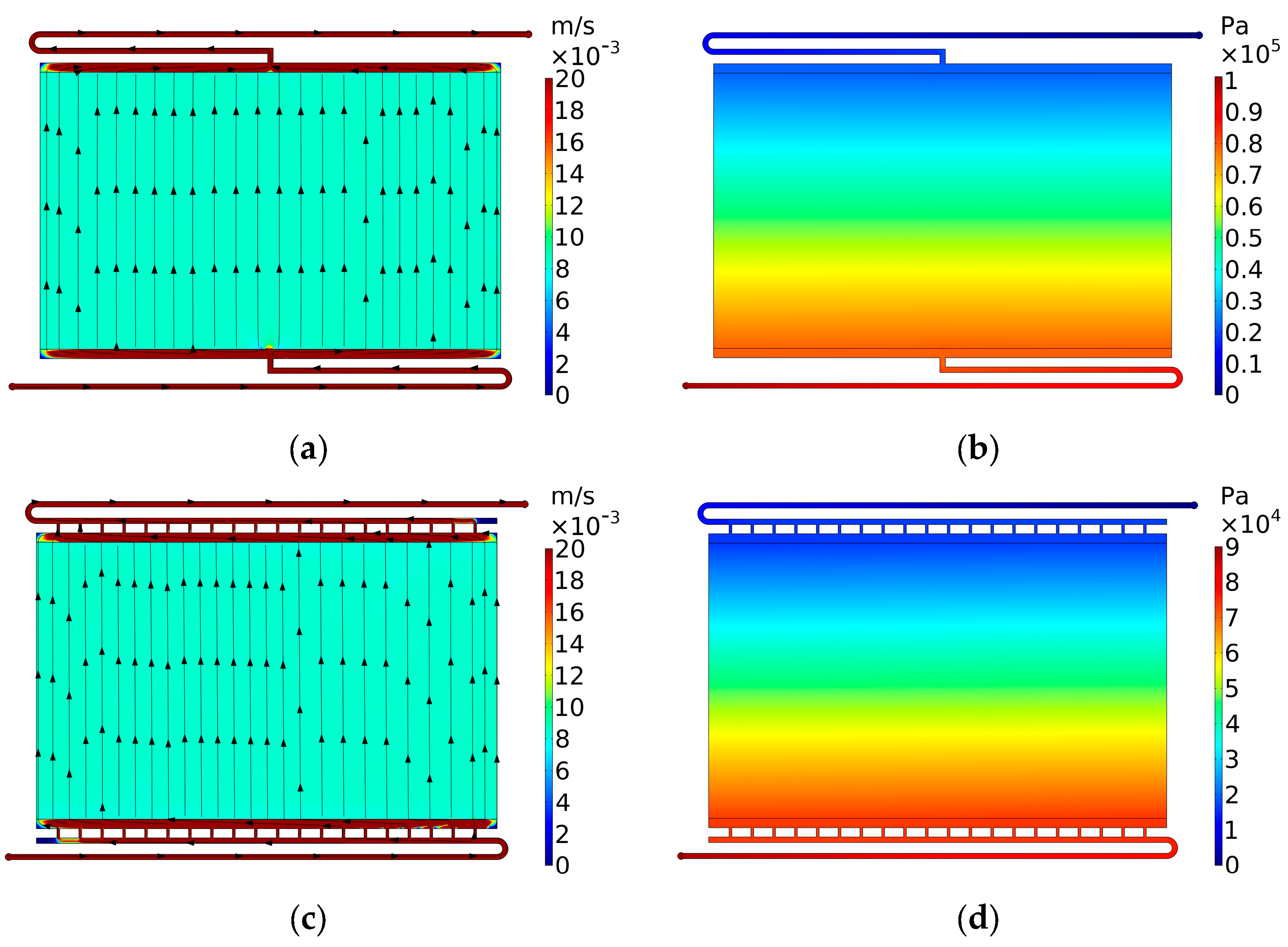
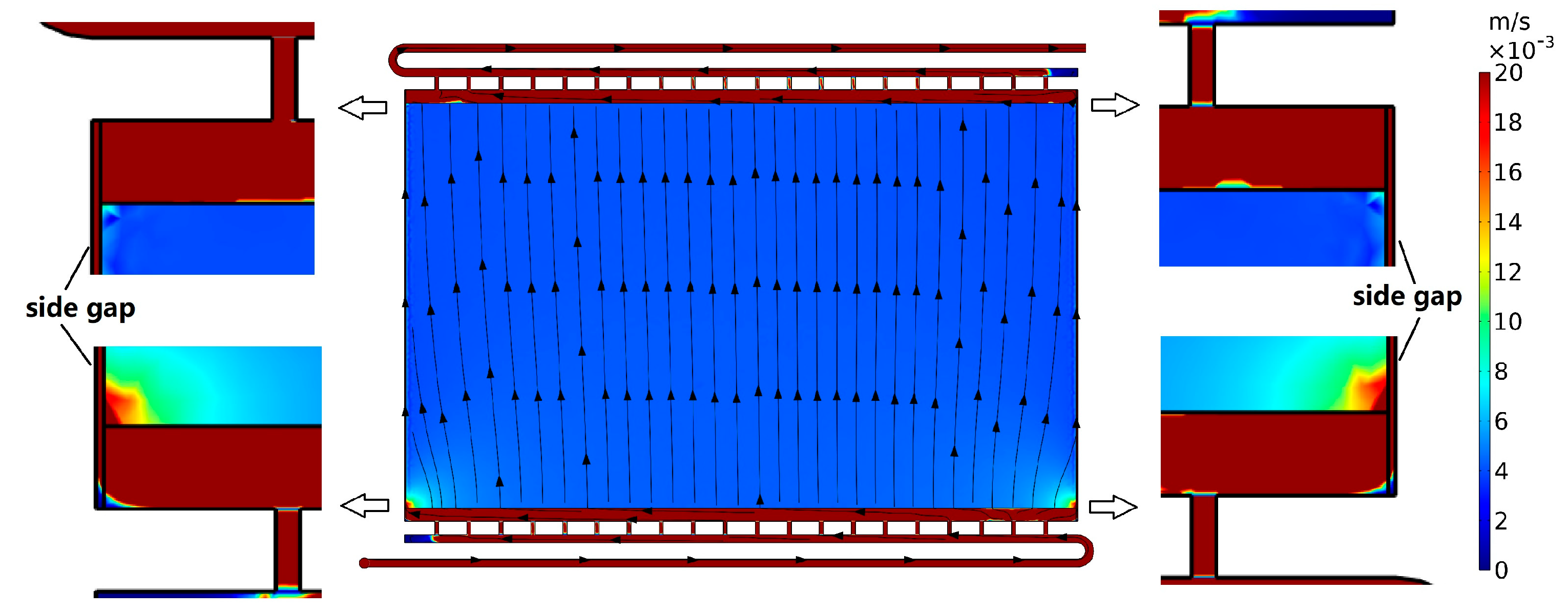
3.3. Case 3: Side Gaps
3.3.1. Case 3.1: Side Gaps on Flow Frame
3.3.2. Case 3.2: Countermeasures against the Side Gaps
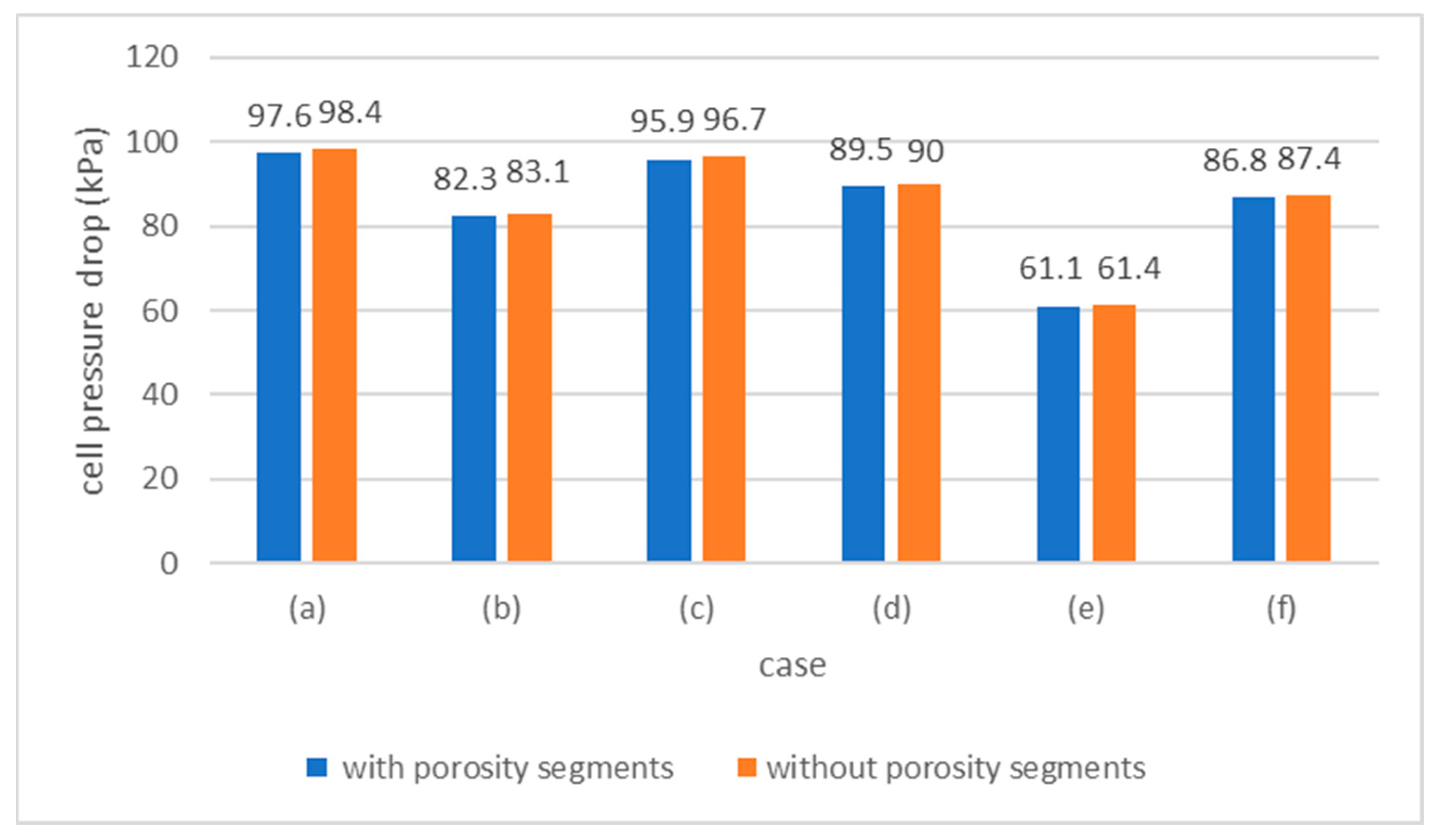
3.4. Case 4: Porosity Segments
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tang, A.; Bao, J.; Skyllas-Kazacos, M. Studies on Pressure Losses and Flow Rate Optimization in Vanadium Redox Flow Battery. J. Power Sources 2014, 248, 154–162. [Google Scholar] [CrossRef]
- Kear, G.; Shah, A.A.; Walsh, F.C. Development of the All-Vanadium Redox Flow Battery for Energy Storage: A Review of Technological, Financial and Policy Aspects. Int. J. Energy Res. 2012, 36, 1105–1120. [Google Scholar] [CrossRef]
- Shigematsu, T. Redox Flow Battery for Energy Storage. SEI Tech. Rev. 2011, 73, 13. [Google Scholar]
- Menictas, C.; Skyllas-Kazacos, M. Next-Generation Vanadium Flow Batteries. Flow Batter. Fundam. Appl. 2023, 2, 673–687. [Google Scholar]
- Aluko, A.; Knight, A. A Review on Vanadium Redox Flow Battery Storage Systems for Large-Scale Power Systems Application. IEEE Access 2023, 11, 13773–13793. [Google Scholar] [CrossRef]
- Barton, J.L.; Brushett, F.R. A One-Dimensional Stack Model for Redox Flow Battery Analysis and Operation. Batteries 2019, 5, 25. [Google Scholar] [CrossRef]
- Mourouga, G.; Schaerer, R.P.; Yang, X.; Janoschka, T.; Schmidt, T.J.; Schumacher, J.O. Physics-Based 0D-U-I-SoC Cell Performance Model for Aqueous Organic Redox Flow Batteries. Electrochim. Acta 2022, 415, 140185. [Google Scholar] [CrossRef]
- Tsehaye, M.T.; Mourouga, G.; Schmidt, T.J.; Schumacher, J.O.; Velizarov, S.; Van der Bruggen, B.; Alloin, F.; Iojoiu, C. Towards Optimized Membranes for Aqueous Organic Redox Flow Batteries: Correlation between Membrane Properties and Cell Performance. Renew. Sustain. Energy Rev. 2023, 173, 113059. [Google Scholar] [CrossRef]
- Shah, A.A.; Watt-Smith, M.J.; Walsh, F.C. A Dynamic Performance Model for Redox-Flow Batteries Involving Soluble Species. Electrochim. Acta 2008, 53, 8087–8100. [Google Scholar] [CrossRef]
- Al-Fetlawi, H.; Shah, A.A.; Walsh, F.C. Non-Isothermal Modelling of the All-Vanadium Redox Flow Battery. Electrochim. Acta 2009, 55, 78–89. [Google Scholar] [CrossRef]
- Shah, A.A.; Al-Fetlawi, H.; Walsh, F.C. Dynamic Modelling of Hydrogen Evolution Effects in the All-Vanadium Redox Flow Battery. Electrochim. Acta 2010, 55, 1125–1139. [Google Scholar] [CrossRef]
- Al-Fetlawi, H.; Shah, A.A.; Walsh, F.C. Modelling the Effects of Oxygen Evolution in the All-Vanadium Redox Flow Battery. Electrochim. Acta 2010, 55, 3192–3205. [Google Scholar] [CrossRef]
- Shah, A.A.; Tangirala, R.; Singh, R.; Wills, R.G.A.; Walsh, F.C. A Dynamic Unit Cell Model for the All-Vanadium Flow Battery. J. Electrochem. Soc. 2011, 158, A671. [Google Scholar] [CrossRef]
- You, D.; Zhang, H.; Chen, J. A Simple Model for the Vanadium Redox Battery. Electrochim. Acta 2009, 54, 6827–6836. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, H.; Xing, F. A Three-Dimensional Model for Negative Half Cell of the Vanadium Redox Flow Battery. Electrochim. Acta 2011, 58, 238–246. [Google Scholar] [CrossRef]
- Gurieff, N.; Timchenko, V.; Menictas, C. Variable Porous Electrode Compression for Redox Flow Battery Systems. Batteries 2018, 4, 53. [Google Scholar] [CrossRef]
- Gurieff, N.; Cheung, C.Y.; Timchenko, V.; Menictas, C. Performance Enhancing Stack Geometry Concepts for Redox Flow Battery Systems with Flow through Electrodes. J. Energy Storage 2019, 22, 219–227. [Google Scholar] [CrossRef]
- Darling, R.M.; Shiau, H.-S.; Weber, A.Z.; Perry, M.L. The Relationship between Shunt Currents and Edge Corrosion in Flow Batteries. J. Electrochem. Soc. 2017, 164, E3081–E3091. [Google Scholar] [CrossRef]
- Zhang, B.W.; Lei, Y.; Bai, B.F.; Xu, A.; Zhao, T.S. A Two-Dimensional Mathematical Model for Vanadium Redox Flow Battery Stacks Incorporating Nonuniform Electrolyte Distribution in the Flow Frame. Appl. Therm. Eng. 2019, 151, 495–505. [Google Scholar] [CrossRef]
- Viswanathan, V.V.; Crawford, A.J.; Thomsen, E.C.; Shamim, N.; Li, G.; Huang, Q.; Reed, D.M. An Overview of the Design and Optimized Operation of Vanadium Redox Flow Batteries for Durations in the Range of 4–24 Hours. Batteries 2023, 9, 221. [Google Scholar] [CrossRef]
- Puleston, T.; Clemente, A.; Costa-Castelló, R.; Serra, M. Modelling and Estimation of Vanadium Redox Flow Batteries: A Review. Batteries 2022, 8, 121. [Google Scholar] [CrossRef]
- Esan, O.C.; Shi, X.; Pan, Z.; Huo, X.; An, L.; Zhao, T.S. Modeling and Simulation of Flow Batteries. Adv. Energy Mater. 2020, 10, 2000758. [Google Scholar] [CrossRef]
- Aramendia, I.; Fernandez-Gamiz, U.; Martinez-San-vicente, A.; Zulueta, E.; Lopez-Guede, J.M. Vanadium Redox Flow Batteries: A Review Oriented to Fluid-Dynamic Optimization. Energies 2021, 14, 176. [Google Scholar] [CrossRef]
- Aaron, D.S.; Liu, Q.; Tang, Z.; Grim, G.M.; Papandrew, A.B.; Turhan, A.; Zawodzinski, T.A.; Mench, M.M. Dramatic Performance Gains in Vanadium Redox Flow Batteries through Modified Cell Architecture. J. Power Sources 2012, 206, 450–453. [Google Scholar] [CrossRef]
- Messaggi, M.; Canzi, P.; Mereu, R.; Baricci, A.; Inzoli, F.; Casalegno, A.; Zago, M. Analysis of Flow Field Design on Vanadium Redox Flow Battery Performance: Development of 3D Computational Fluid Dynamic Model and Experimental Validation. Appl. Energy 2018, 228, 1057–1070. [Google Scholar] [CrossRef]
- Wu, H.-W.; Zeng, Y.-K. Effect of Baffles in Flow Channel on the Performance of Vanadium Redox Flow Battery. Processes 2023, 11, 523. [Google Scholar] [CrossRef]
- Xiong, B.; Li, Y.; Ding, Y.; Wang, J.; Wei, Z.; Zhao, J.; Ai, X.; Fang, J. Numerical Analysis of Vanadium Redox Flow Batteries Considering Electrode Deformation under Various Flow Fields. J. Power Sources 2023, 564, 232814. [Google Scholar] [CrossRef]
- Huang, Z.; Mu, A.; Wu, L.; Wang, H. Vanadium Redox Flow Batteries: Flow Field Design and Flow Rate Optimization. J. Energy Storage 2022, 45, 103526. [Google Scholar] [CrossRef]
- Prumbohm, E.; Becker, M.; Flaischlen, S.; Wehinger, G.D.; Turek, T. Flow Field Designs Developed by Comprehensive CFD Model Decrease System Costs of Vanadium Redox-Flow Batteries. J. Flow Chem. 2021, 11, 461–481. [Google Scholar] [CrossRef]
- He, Q.; Yu, J.; Guo, Z.; Sun, J.; Zhao, S.; Zhao, T.; Ni, M. Modeling of Vanadium Redox Flow Battery and Electrode Optimization with Different Flow Fields. e-Prime-Adv. Electr. Eng. Electron. Energy 2021, 1, 100001. [Google Scholar] [CrossRef]
- Xu, Q.; Zhao, T.S.; Leung, P.K. Numerical Investigations of Flow Field Designs for Vanadium Redox Flow Batteries. Appl. Energy 2013, 105, 47–56. [Google Scholar] [CrossRef]
- Xu, Q.; Zhao, T.S.; Zhang, C. Performance of a Vanadium Redox Flow Battery with and without Flow Fields. Electrochim. Acta 2014, 142, 61–67. [Google Scholar] [CrossRef]
- Kumar, S.; Jayanti, S. Effect of Flow Field on the Performance of an All-Vanadium Redox Flow Battery. J. Power Sources 2016, 307, 782–787. [Google Scholar] [CrossRef]
- Maurya, S.; Nguyen, P.T.; Kim, Y.S.; Kang, Q.; Mukundan, R. Effect of Flow Field Geometry on Operating Current Density, Capacity and Performance of Vanadium Redox Flow Battery. J. Power Sources 2018, 404, 20–27. [Google Scholar] [CrossRef]
- Tomadakis, M.M.; Robertson, T.J. Viscous Permeability of Random Fiber Structures: Comparison of Electrical and Diffusional Estimates with Experimental and Analytical Results. J. Compos. Mater. 2005, 39, 163–188. [Google Scholar] [CrossRef]
- Skyllas-Kazacos, M.; Kasherman, D.; Hong, D.R.; Kazacos, M. Characteristics and Performance of 1 KW UNSW Vanadium Redox Battery. J. Power Sources 1991, 35, 399–404. [Google Scholar] [CrossRef]
- Fink, H.; Remy, M. Shunt Currents in Vanadium Flow Batteries: Measurement, Modelling and Implications for Efficiency. J. Power Sources 2015, 284, 547–553. [Google Scholar] [CrossRef]
- Park, S.K.; Shim, J.; Yang, J.H.; Jin, C.S.; Lee, B.S.; Lee, Y.S.; Shin, K.H.; Jeon, J.D. The Influence of Compressed Carbon Felt Electrodes on the Performance of a Vanadium Redox Flow Battery. Electrochim. Acta 2014, 116, 447–452. [Google Scholar] [CrossRef]



| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| number of cells in stack | 1 | ||
| inlet vertical channel length | 10 | mm | |
| vertical channel width | 3 | mm | |
| horizontal channel width | 6 | mm | |
| channel depth | 2 | mm | |
| total length of inlet manifold | 38 | mm | |
| manifold diameter | 8 | mm | |
| porous electrode thickness | 3 | mm | |
| porous electrode height | 0.3 | m | |
| porous electrode width | 0.5 | m | |
| electrode porosity (for 25% compression felt) | 0.88 | ||
| (if applicable) secondary manifold height | 1 | cm | |
| (if applicable) side gap width | 1 | mm | |
| (if applicable) dimple radius | 2 | mm | |
| fluid density | 1354 | kg m−3 | |
| fluid dynamic viscosity | 4.928 | mPa s | |
| charging current | 120 | A | |
| current density | i | 80 | mA cm−2 |
| flow factor | FlowFactor | 2 | |
| total vanadium concentration | 2 | mol L−1 | |
| SOCupper limit of charging process | 0.9 | ||
| fibre diameter | 17.6 | μm | |
| Kozeny–Carman constant | 4.28 | ||
| temperature | 293 | K |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, X.; Skyllas-Kazacos, M.; Menictas, C. A Three-Dimensional Hydraulic Stack Model for Redox Flow Batteries Considering Porosity Variations in Porous Felt Electrodes and Bypass Flow in Side Gaps. Batteries 2023, 9, 359. https://doi.org/10.3390/batteries9070359
Guan X, Skyllas-Kazacos M, Menictas C. A Three-Dimensional Hydraulic Stack Model for Redox Flow Batteries Considering Porosity Variations in Porous Felt Electrodes and Bypass Flow in Side Gaps. Batteries. 2023; 9(7):359. https://doi.org/10.3390/batteries9070359
Chicago/Turabian StyleGuan, Xinjie, Maria Skyllas-Kazacos, and Chris Menictas. 2023. "A Three-Dimensional Hydraulic Stack Model for Redox Flow Batteries Considering Porosity Variations in Porous Felt Electrodes and Bypass Flow in Side Gaps" Batteries 9, no. 7: 359. https://doi.org/10.3390/batteries9070359
APA StyleGuan, X., Skyllas-Kazacos, M., & Menictas, C. (2023). A Three-Dimensional Hydraulic Stack Model for Redox Flow Batteries Considering Porosity Variations in Porous Felt Electrodes and Bypass Flow in Side Gaps. Batteries, 9(7), 359. https://doi.org/10.3390/batteries9070359








