State of Charge Estimation for Lithium-Ion Battery Based on Unscented Kalman Filter and Long Short-Term Memory Neural Network
Abstract
:1. Introduction
- This paper proposes a novel framework for a parallel estimation of the SOC that combines UKF and LSTM methods and achieves an accurate estimation through a secondary estimation, which effectively combines the robustness of the model-based method with the accuracy of the data-driven method.
- In this method, the ECM adopted fixed parameters, which avoids frequent changes in model parameters, and effectively reduces the amount of calculation.
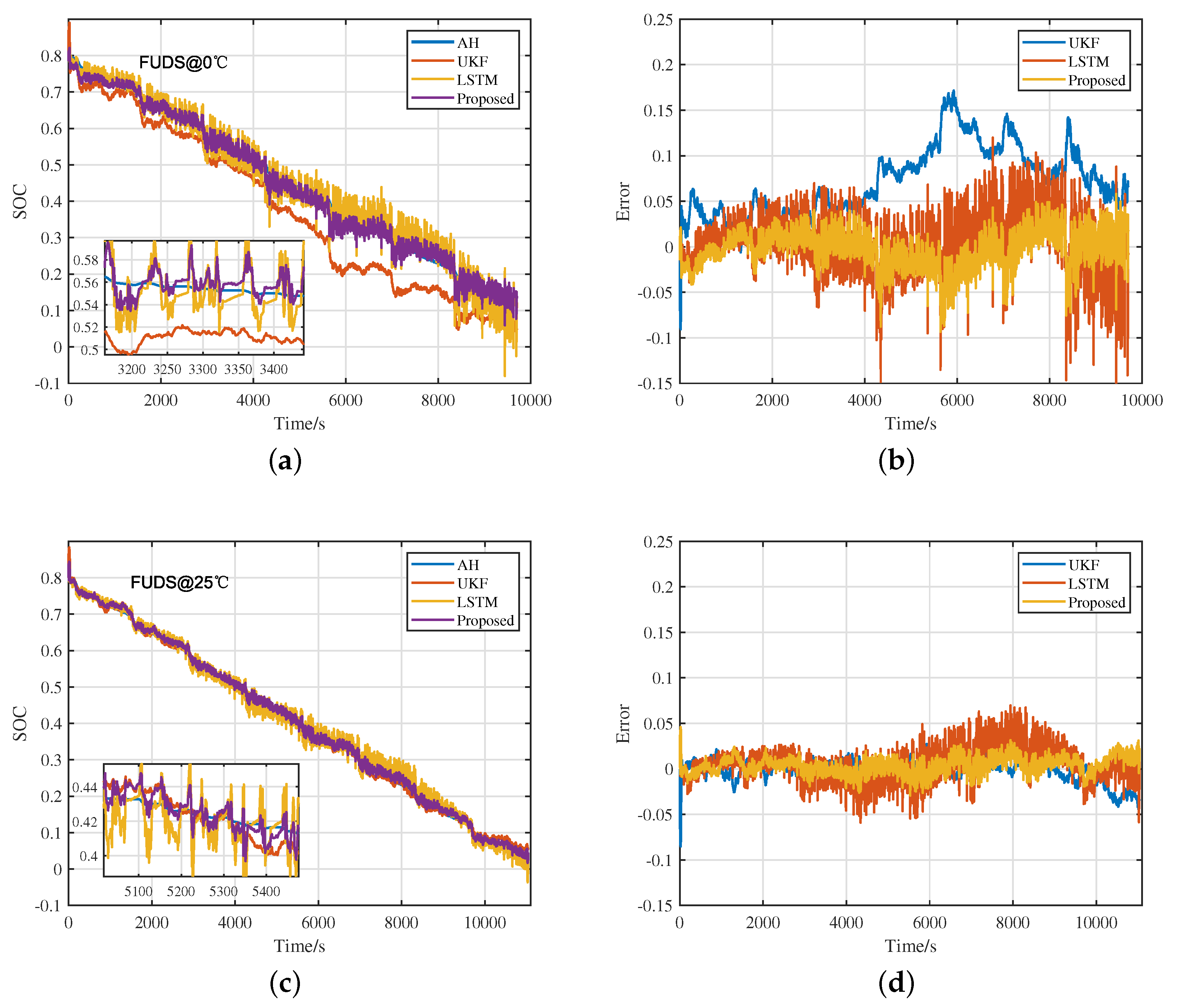
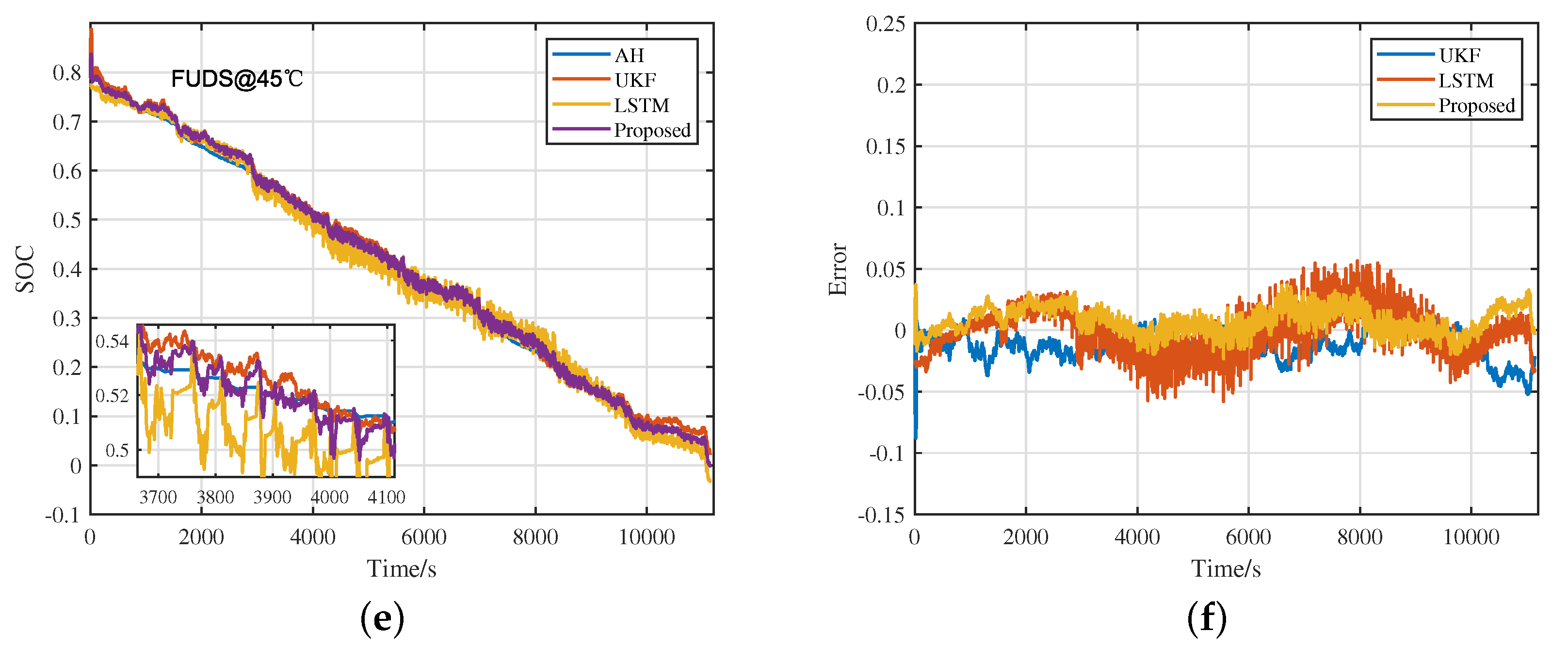
- Experiments are carried out at 0 °C, 25 °C and 45 °C under DST, BJDST, and FUDS conditions, and verified on different kinds of batteries and charging data, which proves the accuracy, robustness, and universality of the proposed method.
2. Theoretical Knowledge of the Proposed Method
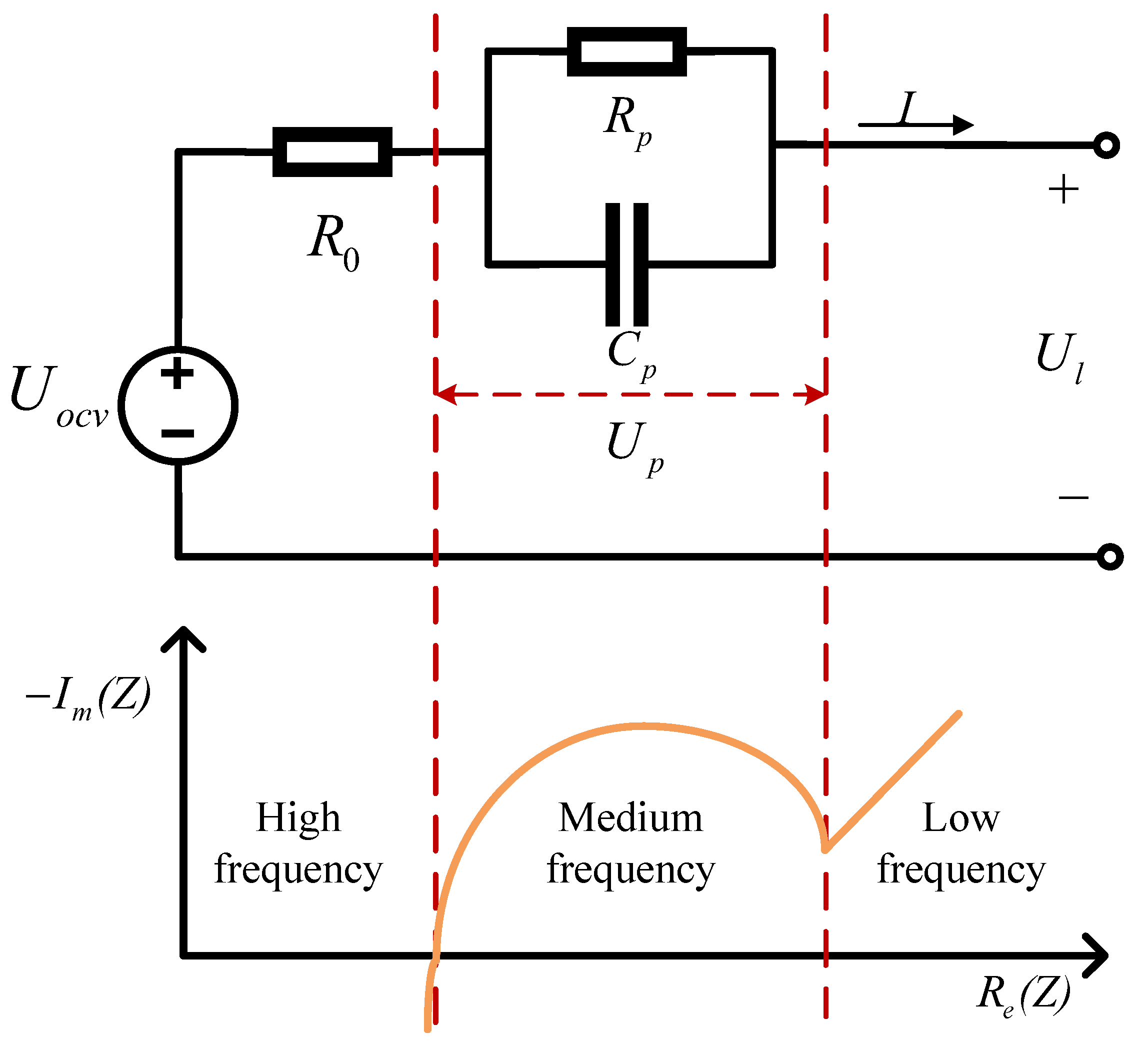
2.1. Battery Model
2.1.1. Parameter Identification Method
2.1.2. Model-Based SOC Estimation Method
- Symmetric sampling:,,.
- Calculate the corresponding weight of sigma points:,,.
- Calculate the mean and covariance of :,.
- Obtain sigma points () through UT; calculate the predicted value of the state variable: .
- Mean value of the predicted value of state variable: .
- Variance in state-predicted value: .
- Update the sampling points and calculate the observation prediction value: .
- Mean value of observed predicted value: .
- Variance in observed predicted value: .
- Covariance of state variable and observation: .
- Update Kalman filter gain: .
- Update status variables: .
- Update covariance of state variables: .
2.2. Data-Driven SOC Estimation Method
2.3. The Method Framework
3. Experiment
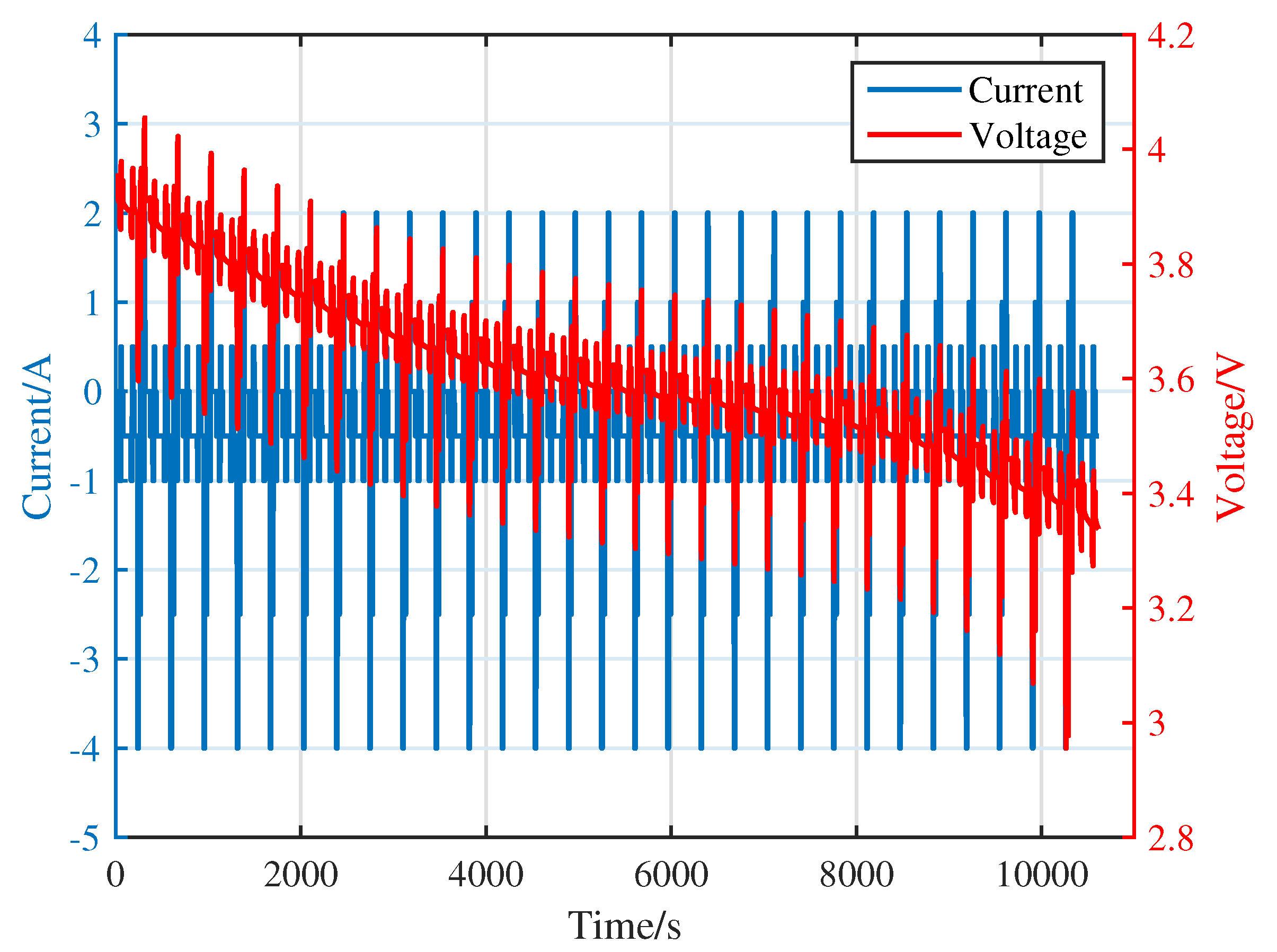
3.1. Experimental Platform and Data
3.2. Experiment Results and Analysis
4. Verification and Discussion
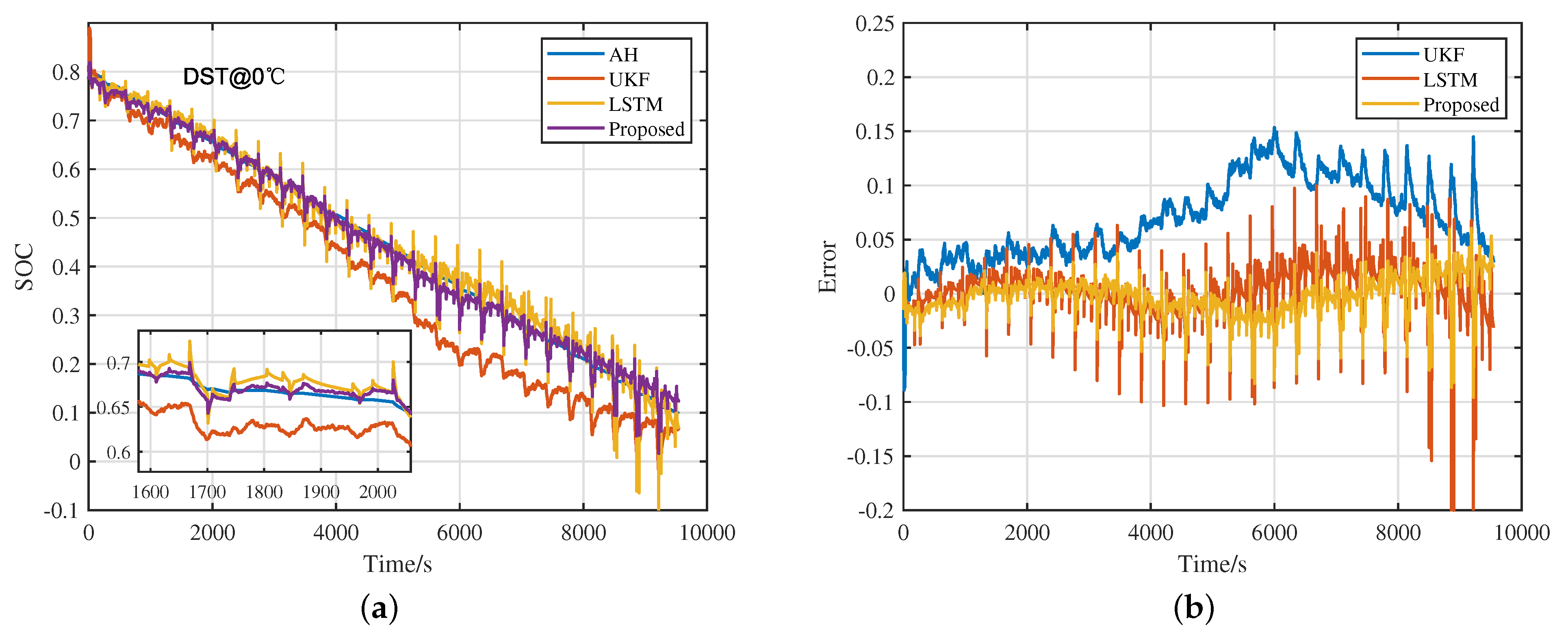
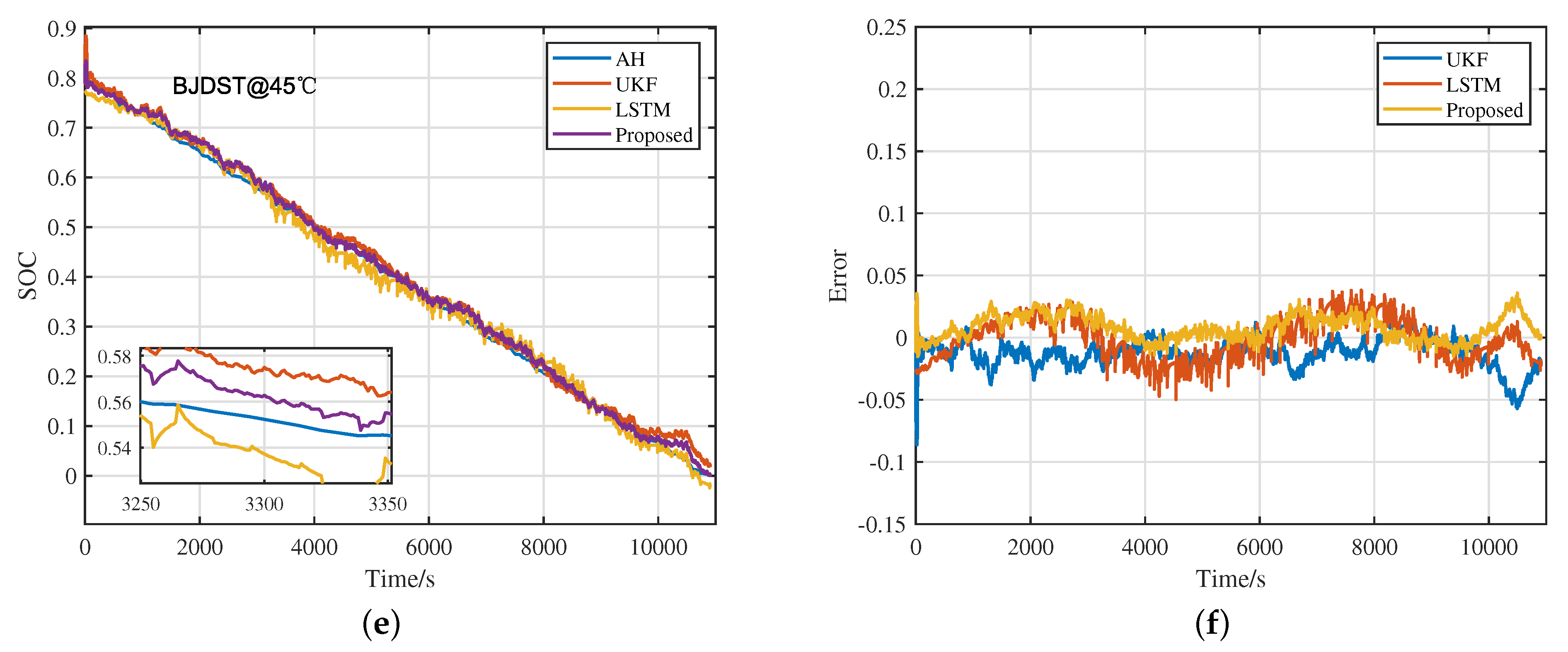
4.1. Verify under Different Working Conditions
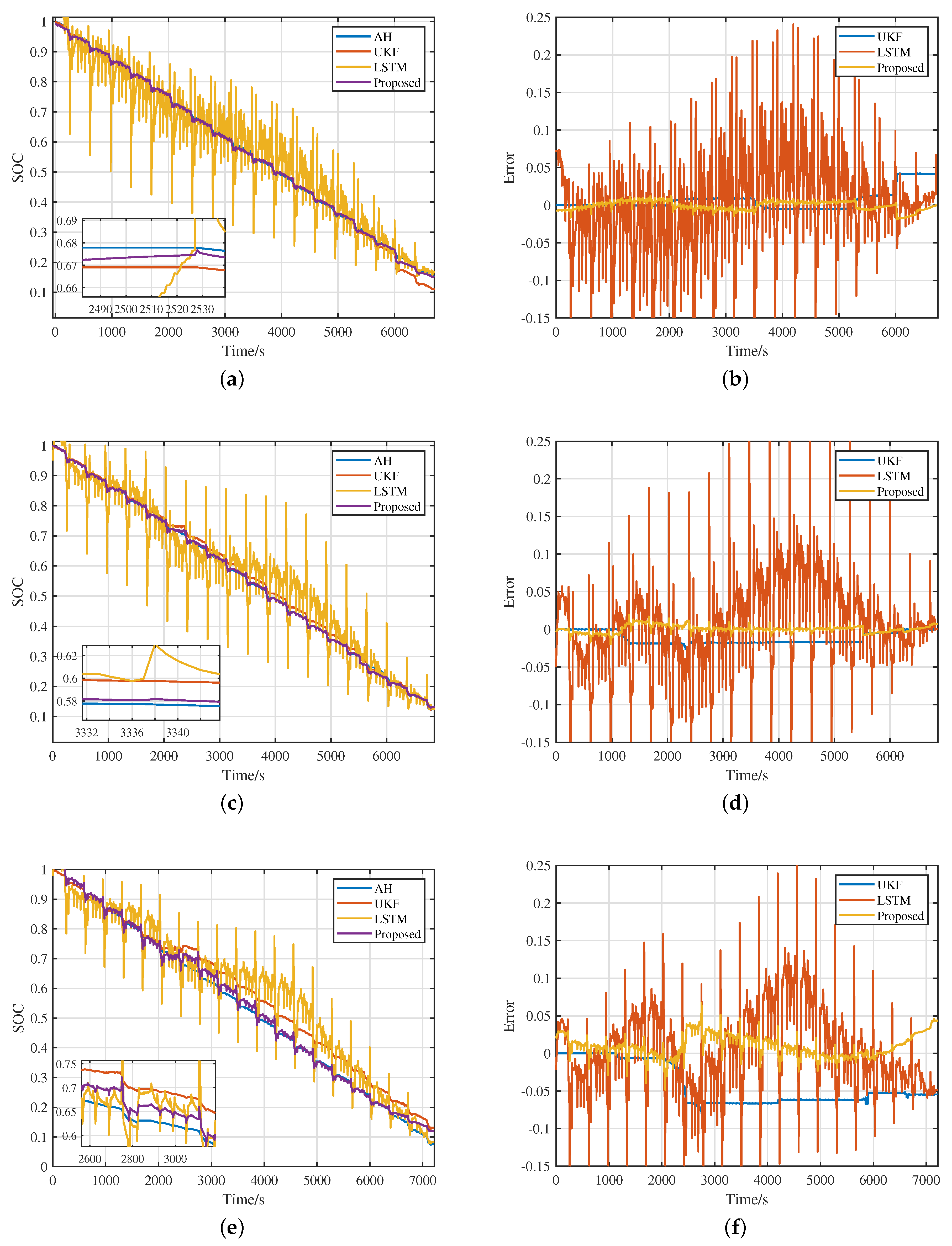
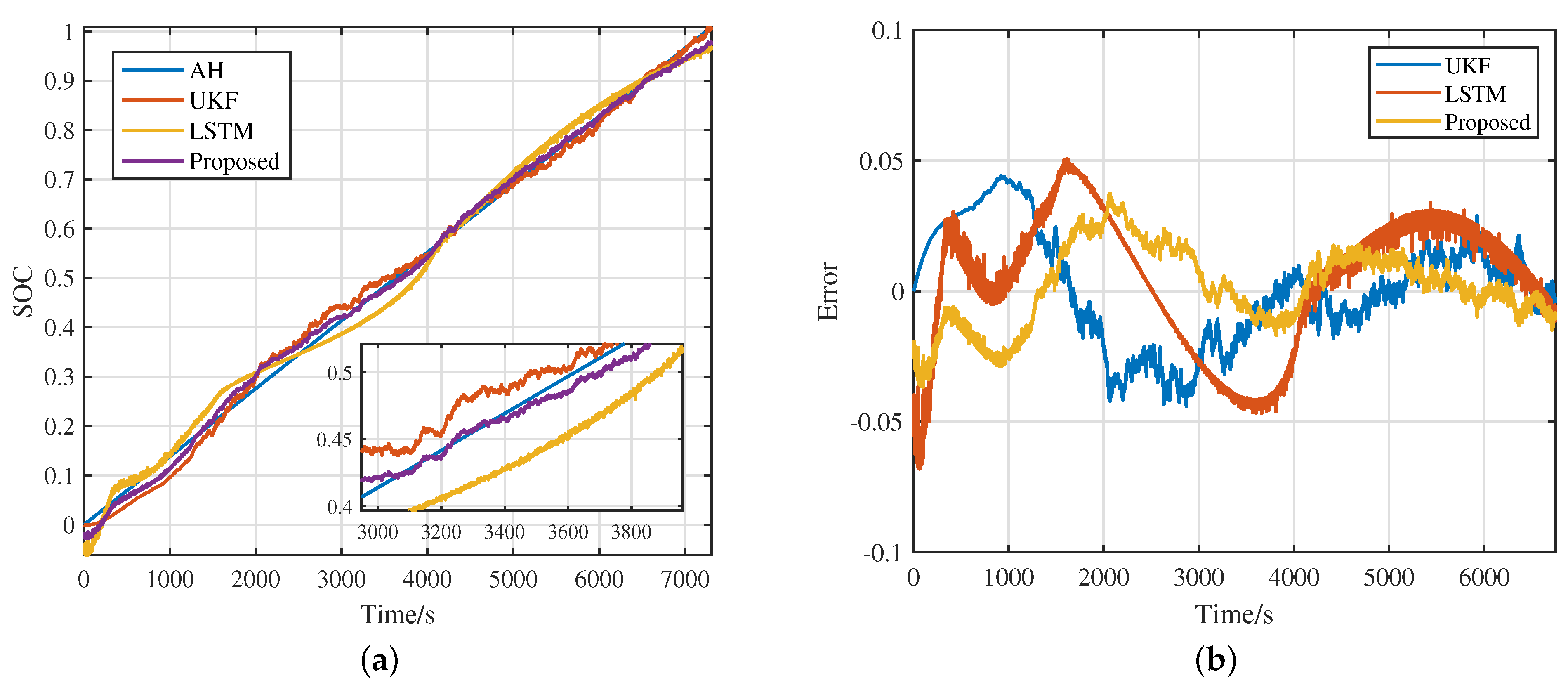
4.2. Verify Universality
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AH | Ampere-hour counting |
| BJDST | Beijing dynamic stress test |
| DST | Dynamic stress test |
| ECM | Equivalent circuit model |
| EKF | Extended Kalman filter |
| FUDS | Federal urban driving schedule |
| KF | Kalman filter |
| LS | Least square |
| LSTM | Long short-term memory |
| MAE | Mean absolute error |
| MHLSTM | Multi-hidden layer long short-term memory |
| OCV | Open circuit voltage |
| RLS | Recursive least squares |
| RMSE | Root mean square error |
| RNN | Recurrent neural network |
| SFEKF | Suboptimal fading extended Kalman filtering |
| SOC | State of charge |
| UKF | Unscented Kalman filter |
| UT | Unscented transformation |
References
- Du, X.; Meng, J.; Peng, J. Hybrid Pseudorandom Sequence for Broadband Impedance Measurements of Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2023, 70, 6856–6864. [Google Scholar] [CrossRef]
- Semeraro, C.; Caggiano, M.; Olabi, A.G.; Dassisti, M. Battery monitoring and prognostics optimization techniques: Challenges and opportunities. Energy 2022, 255, 124538. [Google Scholar] [CrossRef]
- Zhao, X.; Qian, X.; Xuan, D.; Jung, S. State of charge estimation of lithium-ion battery based on multi-input extreme learning machine using online model parameter identification. J. Energy Storage 2022, 56, 105796. [Google Scholar] [CrossRef]
- Takyi-Aninakwa, P.; Wang, S.; Zhang, H.; Yang, X.; Fernandez, C. A hybrid probabilistic correction model for the state of charge estimation of lithium-ion batteries considering dynamic currents and temperatures. Energy 2023, 273, 127231. [Google Scholar] [CrossRef]
- Gong, Z.; Kachura, A.; Assadi, S.A.; Cusimano, N.; Piruzza, J.; Xu, J.; Trescases, O. An EV-Scale Demonstration of In-Situ Battery Electrochemical Impedance Spectroscopy and BMS-Limited Pack Performance Analysis. IEEE Trans. Ind. Electron. 2023, 70, 9112–9122. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Y.; Yu, M.; Zhou, Z.; Zhang, Q.; Duan, B.; Shang, Y.; Zhang, C. Variable fractional order - A comprehensive evaluation indicator of lithium-ion batteries. J. Power Sources 2020, 448, 227411. [Google Scholar] [CrossRef]
- Shrivastava, P.; Naidu, P.A.; Sharma, S.; Panigrahi, B.K.; Garg, A. Review on technological advancement of lithium-ion battery states estimation methods for electric vehicle applications. J. Energy Storage 2023, 64, 107159. [Google Scholar] [CrossRef]
- Xiao, R.; Hu, Y.; Zhang, W.; Chen, Z. A novel approach to estimate the state of charge for lithium-ion battery under different temperatures incorporating open circuit voltage online identification. J. Energy Storage 2023, 67, 107509. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.I.B.; Mekhilef, S.; Adnan, S.B.R.S. Comprehensive co-estimation of lithium-ion battery state of charge, state of energy, state of power, maximum available capacity, and maximum available energy. J. Energy Storage 2022, 56, 106049. [Google Scholar] [CrossRef]
- Luan, Z.; Qin, Y.; Hu, B.; Zhao, W.; Wang, C. Estimation of state of charge for hybrid unmanned aerial vehicle Li-ion power battery for considering rapid temperature change. J. Energy Storage 2023, 59, 106479. [Google Scholar] [CrossRef]
- Li, S.; Li, Y.; Zhao, D.; Zhang, C. Adaptive state of charge estimation for lithium-ion batteries based on implementable fractional-order technology. J. Energy Storage 2020, 32, 101838. [Google Scholar] [CrossRef]
- Wu, C.; Hu, W.; Meng, J.; Xu, X.; Huang, X.; Cai, L. State-of-charge estimation of lithium-ion batteries based on MCC-AEKF in non-Gaussian noise environment. Energy 2023, 274, 127316. [Google Scholar] [CrossRef]
- Zhou, W.; Zheng, Y.; Pan, Z.; Lu, Q. Review on the Battery Model and SOC Estimation Method. Processes 2021, 9, 1685. [Google Scholar] [CrossRef]
- Wu, S.; Pan, W.; Zhu, M. A Collaborative Estimation Scheme for Lithium-Ion Battery State of Charge and State of Health Based on Electrochemical Model. J. Electrochem. Soc. 2022, 169, 090516. [Google Scholar] [CrossRef]
- Li, N.; Zhang, Y.; He, F.; Zhu, L.; Zhang, X.; Ma, Y.; Wang, S. Review of lithium-ion battery state of charge estimation. Glob. Energy Interconnect. 2021, 4, 619–630. [Google Scholar] [CrossRef]
- Lian, G.; Ye, M.; Wang, Q.; Wei, M.; Ma, Y. Noise-immune state of charge estimation for lithium-ion batteries based on optimized dynamic model and improved adaptive unscented Kalman filter under wide temperature range. J. Energy Storage 2023, 64, 107223. [Google Scholar] [CrossRef]
- Hou, J.; Liu, J.; Chen, F.; Li, P.; Zhang, T.; Jiang, J.; Chen, X. Robust lithium-ion state-of-charge and battery parameters joint estimation based on an enhanced adaptive unscented Kalman filter. Energy 2023, 271, 126998. [Google Scholar] [CrossRef]
- Yu, M.; Li, Y.; Podlubny, I.; Gong, F.; Sun, Y.; Zhang, Q.; Shang, Y.; Duan, B.; Zhang, C. Fractional-order modeling of lithium-ion batteries using additive noise assisted modeling and correlative information criterion. J. Adv. Res. 2020, 25, 49–56. [Google Scholar] [CrossRef]
- Wang, M.; Wang, G.; Xiao, Z.; Sun, Y.; Zheng, Y. State of Charge Estimation of LiFePO4 in Various Temperature Scenarios. Batteries 2023, 9, 43. [Google Scholar] [CrossRef]
- Ragone, M.; Yurkiv, V.; Ramasubramanian, A.; Kashir, B.; Mashayek, F. Data driven estimation of electric vehicle battery state-of-charge informed by automotive simulations and multi-physics modeling. J. Power Sources 2021, 483, 229108. [Google Scholar] [CrossRef]
- Ma, L.; Zhang, T. Deep learning-based battery state of charge estimation: Enhancing estimation performance with unlabelled training samples. J. Energy Chem. 2023, 80, 48–57. [Google Scholar] [CrossRef]
- Hao, X.; Wang, S.; Fan, Y.; Xie, Y.; Fernandez, C. An improved forgetting factor recursive least square and unscented particle filtering algorithm for accurate lithium-ion battery state of charge estimation. J. Energy Storage 2023, 59, 106478. [Google Scholar] [CrossRef]
- Wang, C.; Li, Q.; Tang, A.; Zhang, Z. A comparative study of state of charge estimation methods of ultracapacitors for electric vehicles considering temperature characteristics. J. Energy Storage 2023, 63, 106908. [Google Scholar] [CrossRef]
- El Fallah, S.; Kharbach, J.; Hammouch, Z.; Rezzouk, A.; Ouazzani Jamil, M. State of charge estimation of an electric vehicle’s battery using Deep Neural Networks: Simulation and experimental results. J. Energy Storage 2023, 62, 106904. [Google Scholar] [CrossRef]
- Liu, X.; Li, Q.; Wang, L.; Lin, M.; Wu, J. Data-Driven State of Charge Estimation for Power Battery With Improved Extended Kalman Filter. IEEE Trans. Instrum. Meas. 2023, 72, 1–10. [Google Scholar] [CrossRef]
- Wadi, A.; Abdel-Hafez, M.F.; Hussein, A.A.; Alkhawaja, F. Alleviating Dynamic Model Uncertainty Effects for Improved Battery SOC Estimation of EVs in Highly Dynamic Environments. IEEE Trans. Veh. Technol. 2021, 70, 6554–6566. [Google Scholar] [CrossRef]
- Zhang, X.; Hou, J.; Wang, Z.; Jiang, Y. Study of SOC Estimation by the Ampere-Hour Integral Method with Capacity Correction Based on LSTM. Batteries 2022, 8, 170. [Google Scholar] [CrossRef]
- Moulik, B.; Dubey, A.K.; Ali, A.M. A Battery Modeling Technique Based on Fusion of Hybrid and Adaptive Algorithms for Real-Time Applications in Pure EVs. IEEE Trans. Intell. Transp. Syst. 2023, 24, 2760–2771. [Google Scholar] [CrossRef]
- Takyi-Aninakwa, P.; Wang, S.; Zhang, H.; Yang, X.; Fernandez, C. An optimized long short-term memory-weighted fading extended Kalman filtering model with wide temperature adaptation for the state of charge estimation of lithium-ion batteries. Appl. Energy 2022, 326, 120043. [Google Scholar] [CrossRef]
- Bai, W.; Zhang, X.; Gao, Z.; Xie, S.; Chen, Y.; He, Y.; Zhang, J. State of charge estimation for lithium-ion batteries under varying temperature conditions based on adaptive dual extended Kalman filter. Electr. Power Syst. Res. 2022, 213, 108751. [Google Scholar] [CrossRef]
- Liu, X.; Yang, J.; Wang, L.; Wu, J. Bayesian information criterion based data-driven state of charge estimation for lithium-ion battery. J. Energy Storage 2022, 55, 105669. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, S.; Zhang, G.; Fan, Y.; Fernandez, C.; Blaabjerg, F. Optimized multi-hidden layer long short-term memory modeling and suboptimal fading extended Kalman filtering strategies for the synthetic state of charge estimation of lithium-ion batteries. Appl. Energy 2023, 336, 120866. [Google Scholar] [CrossRef]
- Xu, S.; Zhou, F.; Liu, Y. A Hybrid Method for Lithium-Ion Batteries State-of-Charge Estimation Based on Gated Recurrent Unit Neural Network and an Adaptive Unscented Kalman Filter. J. Electrochem. Energy Convers. Storage 2022, 19, 031005. [Google Scholar] [CrossRef]
- Cui, Z.; Kang, L.; Li, L.; Wang, L.; Wang, K. A combined state-of-charge estimation method for lithium-ion battery using an improved BGRU network and UKF. Energy 2022, 259, 124933. [Google Scholar] [CrossRef]
- Cui, X.; Xu, B. State of Charge Estimation of Lithium-Ion Battery Using Robust Kernel Fuzzy Model and Multi-Innovation UKF Algorithm Under Noise. IEEE Trans. Ind. Electron. 2022, 69, 11121–11131. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Hossain, M.; Haque, M.E.; Arif, M.T. Online Model Parameter and State of Charge Estimation of Li-Ion Battery Using Unscented Kalman Filter Considering Effects of Temperatures and C-Rates. IEEE Trans. Energy Convers. 2022, 37, 2498–2511. [Google Scholar] [CrossRef]
- Quan, R.; Liu, P.; Li, Z.; Li, Y.; Chang, Y.; Yan, H. A multi-dimensional residual shrinking network combined with a long short-term memory network for state of charge estimation of Li-ion batteries. J. Energy Storage 2023, 57, 106263. [Google Scholar] [CrossRef]





| Brand | Type | Nominal Voltage | Nominal Capacity | Cut-Off Voltages |
|---|---|---|---|---|
| Samsung | INR-18650-20R | 3.6 V | 2 Ah | 2.5 V/4.2 V |
| Condition | Temperature | |||
|---|---|---|---|---|
| DST | 25 °C | 0.0715 | 0.0223 | 996.2 |
| Temperature | Data | Method | MAE | RMSE |
|---|---|---|---|---|
| DST data | UKF | 0.0702 | 0.0789 | |
| Training set | LSTM | 0.0148 | 0.0192 | |
| 0 °C | proposed | 0.0114 | 0.0150 | |
| Verification set | LSTM | 0.0182 | 0.0268 | |
| proposed | 0.0208 | 0.0226 | ||
| DST data | UKF | 0.0093 | 0.0122 | |
| Training set | LSTM | 0.0110 | 0.0155 | |
| 25 °C | proposed | 0.0057 | 0.0076 | |
| Verification set | LSTM | 0.0179 | 0.0232 | |
| proposed | 0.0080 | 0.0106 | ||
| DST data | UKF | 0.0147 | 0.0186 | |
| Training set | LSTM | 0.0156 | 0.0183 | |
| 45 °C | proposed | 0.0083 | 0.0097 | |
| Verification set | LSTM | 0.0153 | 0.0184 | |
| proposed | 0.0109 | 0.0129 |
| Condition | Temperature | MAE | RMSE | ||||
|---|---|---|---|---|---|---|---|
| UKF | LSTM | Proposed | UKF | LSTM | Proposed | ||
| BJDST | 0 °C | 0.0800 | 0.0226 | 0.0175 | 0.0898 | 0.0323 | 0.0224 |
| 25 °C | 0.0091 | 0.0147 | 0.0083 | 0.0127 | 0.0190 | 0.0104 | |
| 45 °C | 0.0137 | 0.0143 | 0.0100 | 0.0172 | 0.0166 | 0.0127 | |
| FUDS | 0 °C | 0.0715 | 0.0217 | 0.0161 | 0.0809 | 0.0286 | 0.0206 |
| 25 °C | 0.0091 | 0.0147 | 0.0079 | 0.0123 | 0.0189 | 0.0098 | |
| 45 °C | 0.0134 | 0.0147 | 0.0105 | 0.0168 | 0.0179 | 0.0131 |
| Brand | Material | Nominal Voltage | Nominal Capacity | Cut-Off Voltages |
|---|---|---|---|---|
| A123 | LiFePO | 3.3 V | 1.1 Ah | 2.0 V/3.6 V |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Y.; Li, Y.; Yang, T. State of Charge Estimation for Lithium-Ion Battery Based on Unscented Kalman Filter and Long Short-Term Memory Neural Network. Batteries 2023, 9, 358. https://doi.org/10.3390/batteries9070358
Zeng Y, Li Y, Yang T. State of Charge Estimation for Lithium-Ion Battery Based on Unscented Kalman Filter and Long Short-Term Memory Neural Network. Batteries. 2023; 9(7):358. https://doi.org/10.3390/batteries9070358
Chicago/Turabian StyleZeng, Yi, Yan Li, and Tong Yang. 2023. "State of Charge Estimation for Lithium-Ion Battery Based on Unscented Kalman Filter and Long Short-Term Memory Neural Network" Batteries 9, no. 7: 358. https://doi.org/10.3390/batteries9070358
APA StyleZeng, Y., Li, Y., & Yang, T. (2023). State of Charge Estimation for Lithium-Ion Battery Based on Unscented Kalman Filter and Long Short-Term Memory Neural Network. Batteries, 9(7), 358. https://doi.org/10.3390/batteries9070358










