State of Charge and Temperature Joint Estimation Based on Ultrasonic Reflection Waves for Lithium-Ion Battery Applications
Abstract
1. Introduction
2. Mechanisms
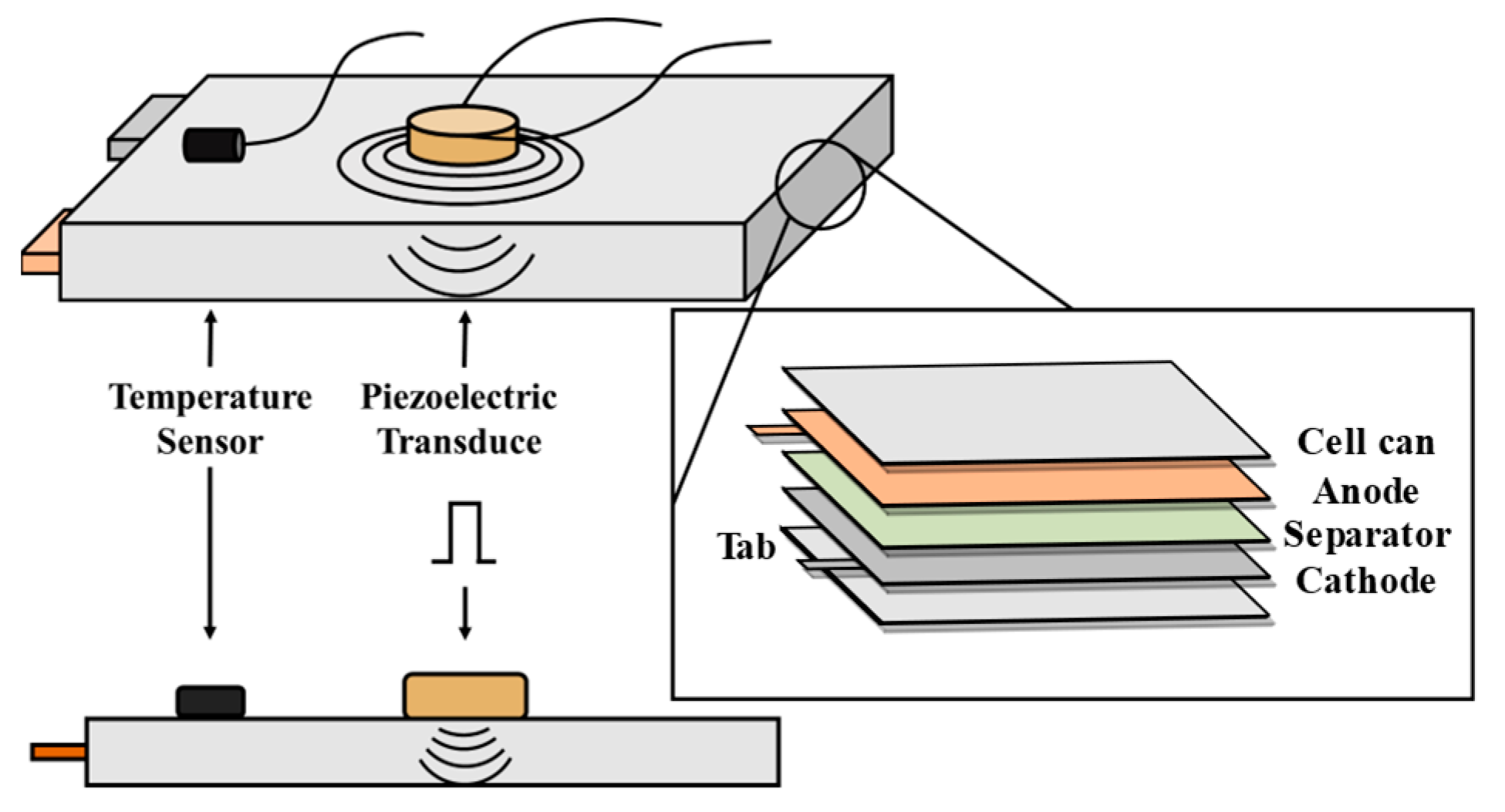
2.1. Ultrasonic Transmission Mechanism
2.2. Relationship between Ultrasonic Signal and Battery States
3. Methods
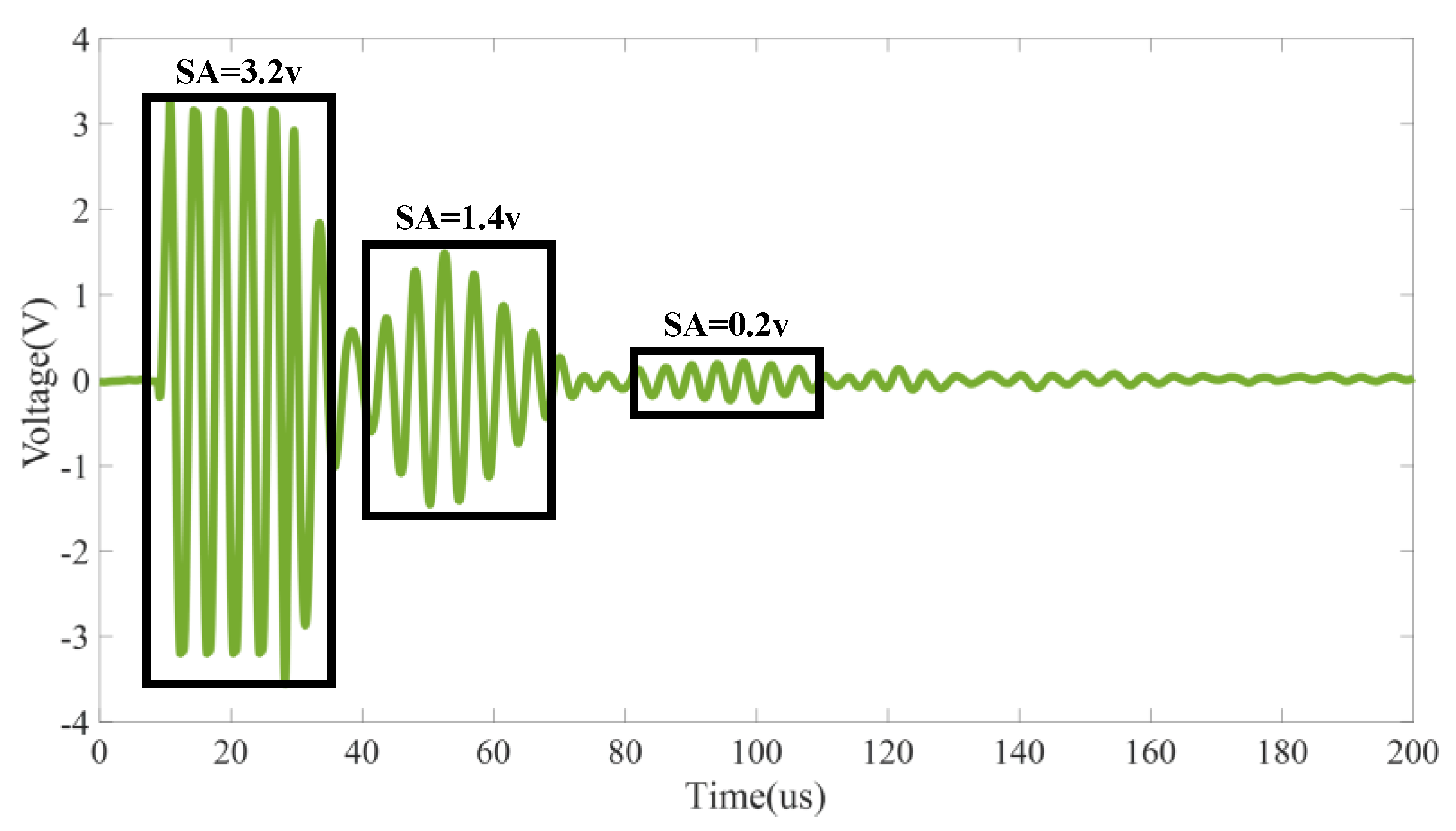
3.1. Feature Indicators of the Ultrasonic Signal
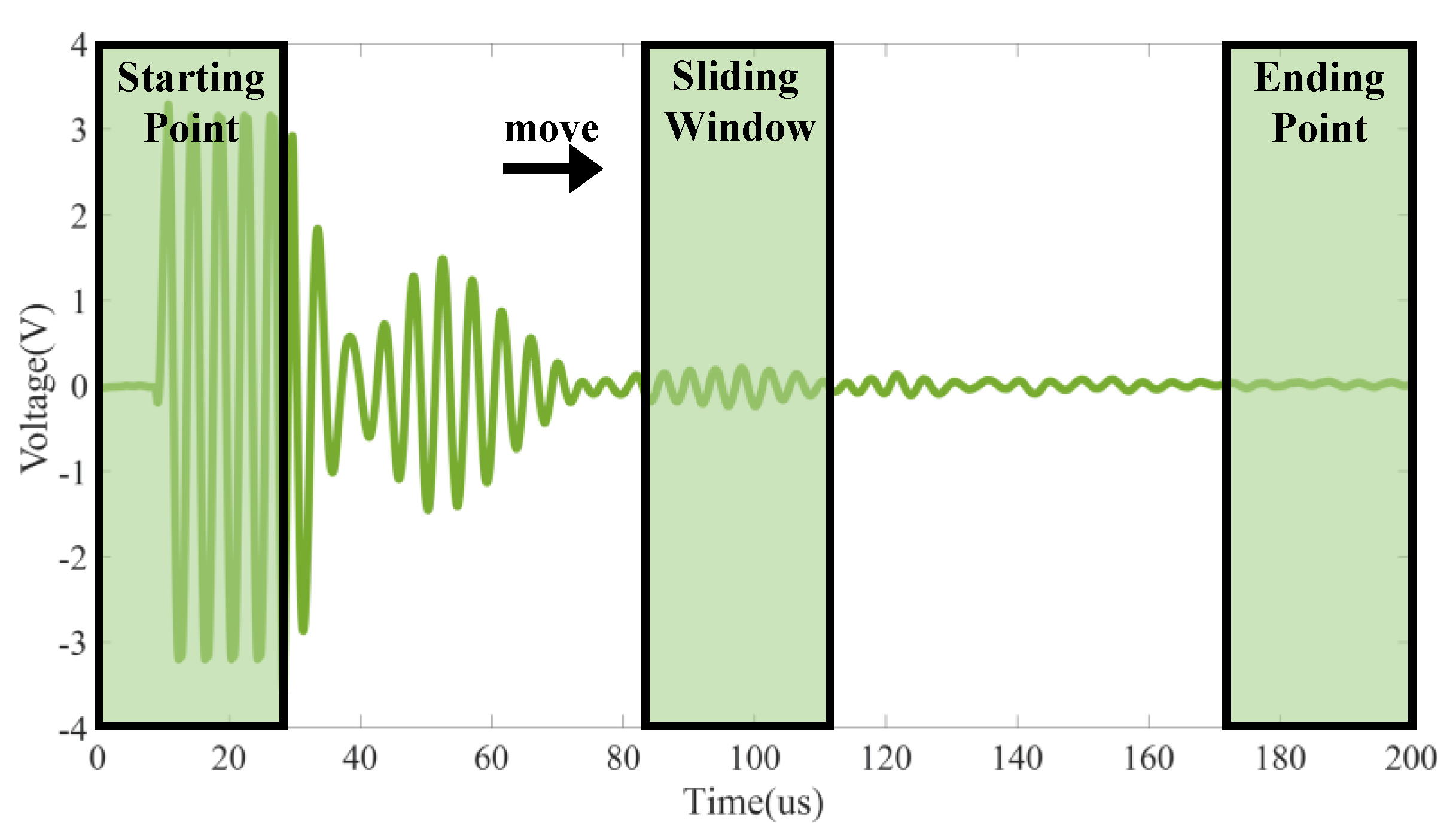
3.2. The Optimal Intervals of the Signal
3.3. Virtual Sample Generation
3.4. BP Neural Network Model
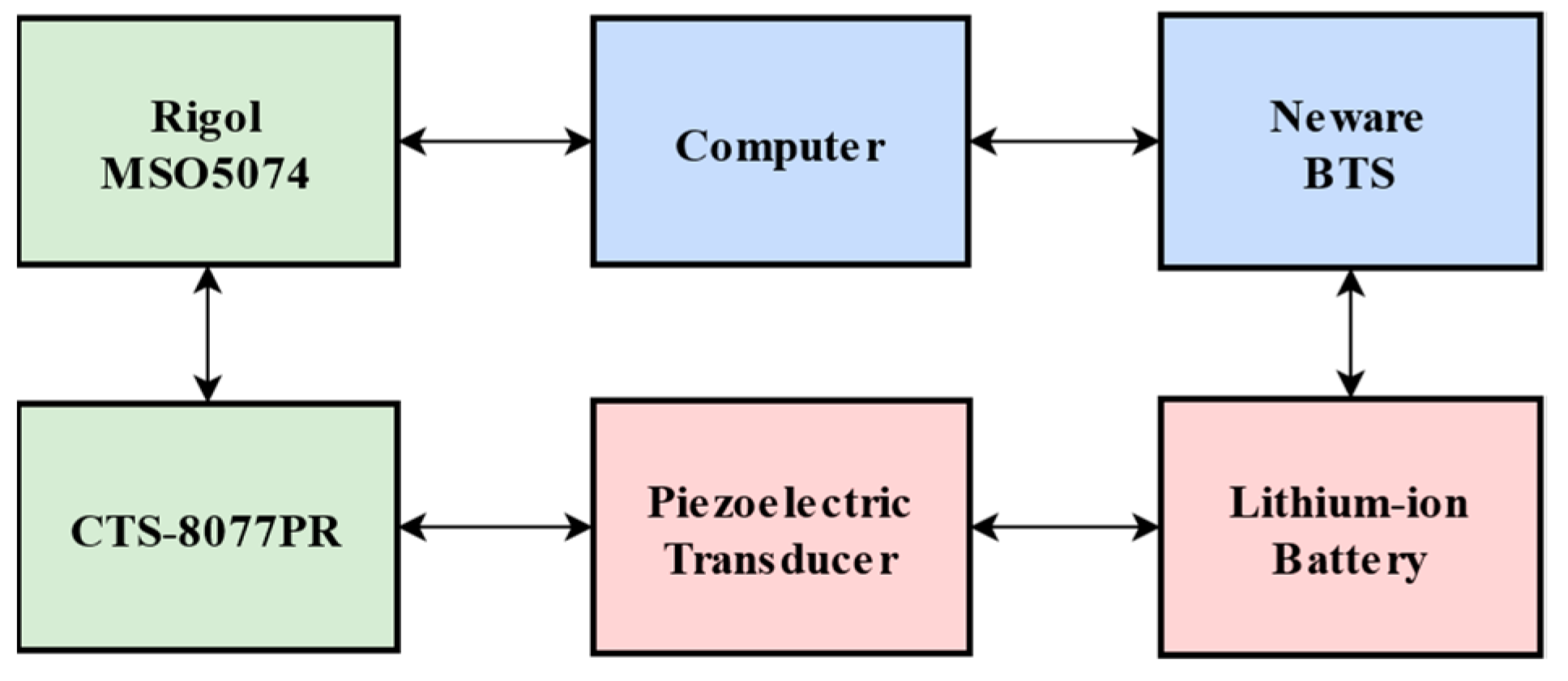
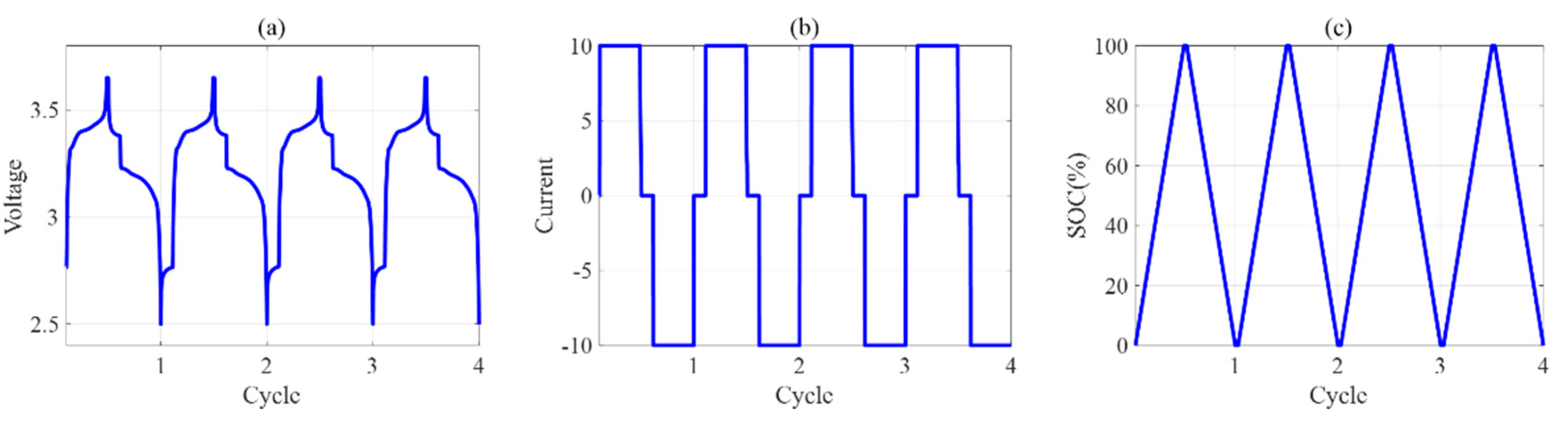
4. Experiments
5. Results and Discussion
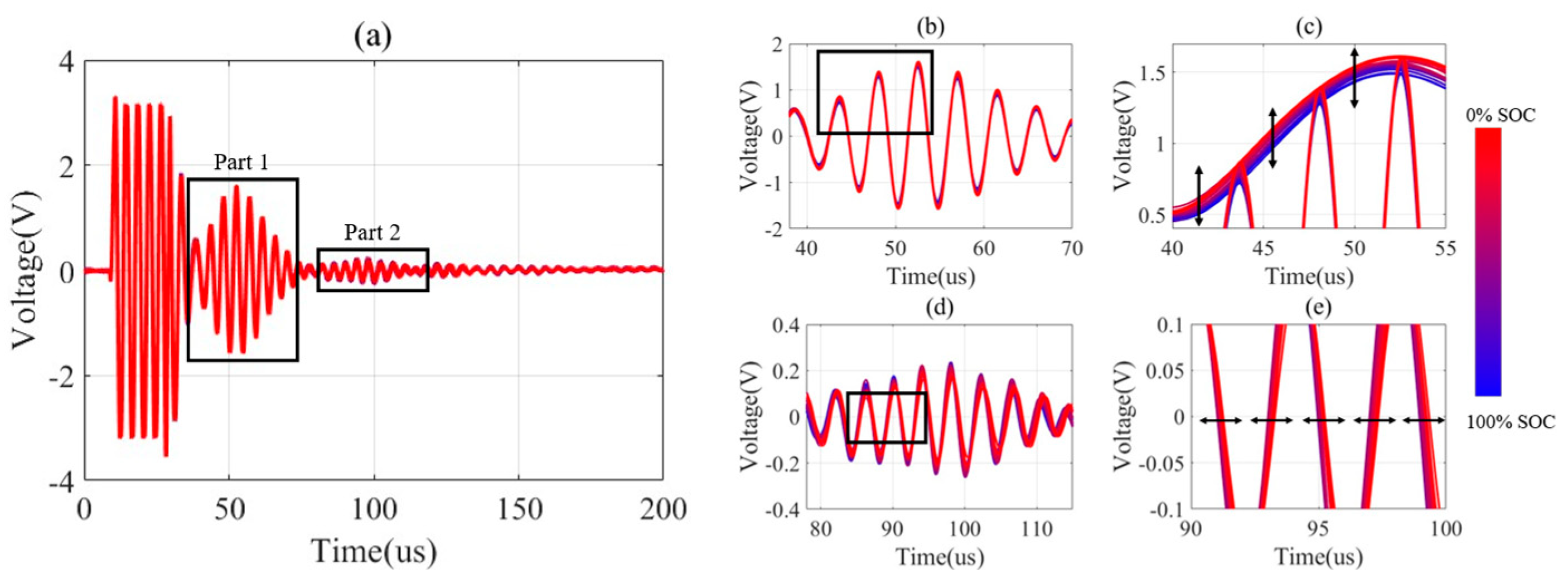
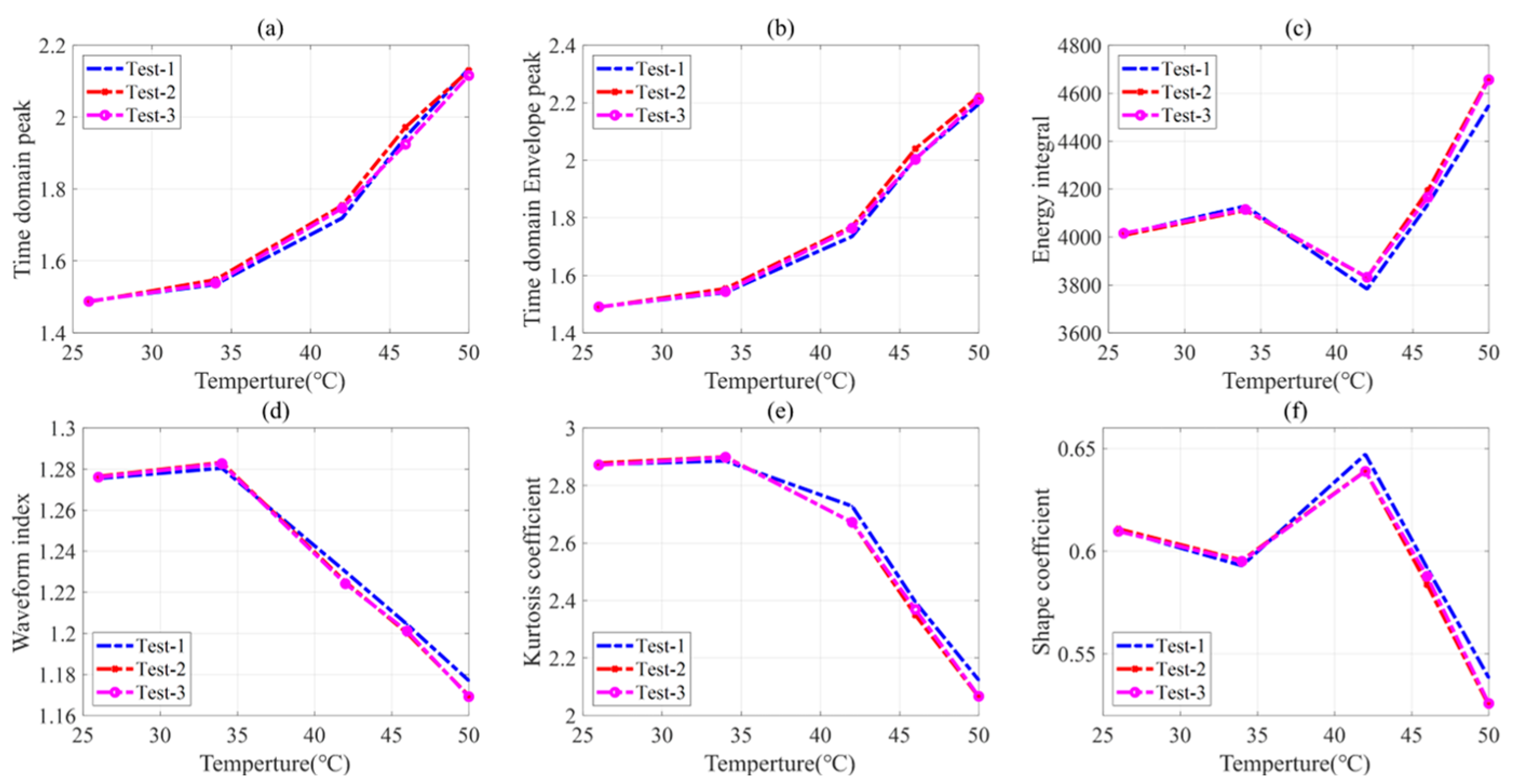
5.1. Influence of Battery States on the Ultrasonic Signal
5.2. Optimal Ultrasonic Signal Application Range
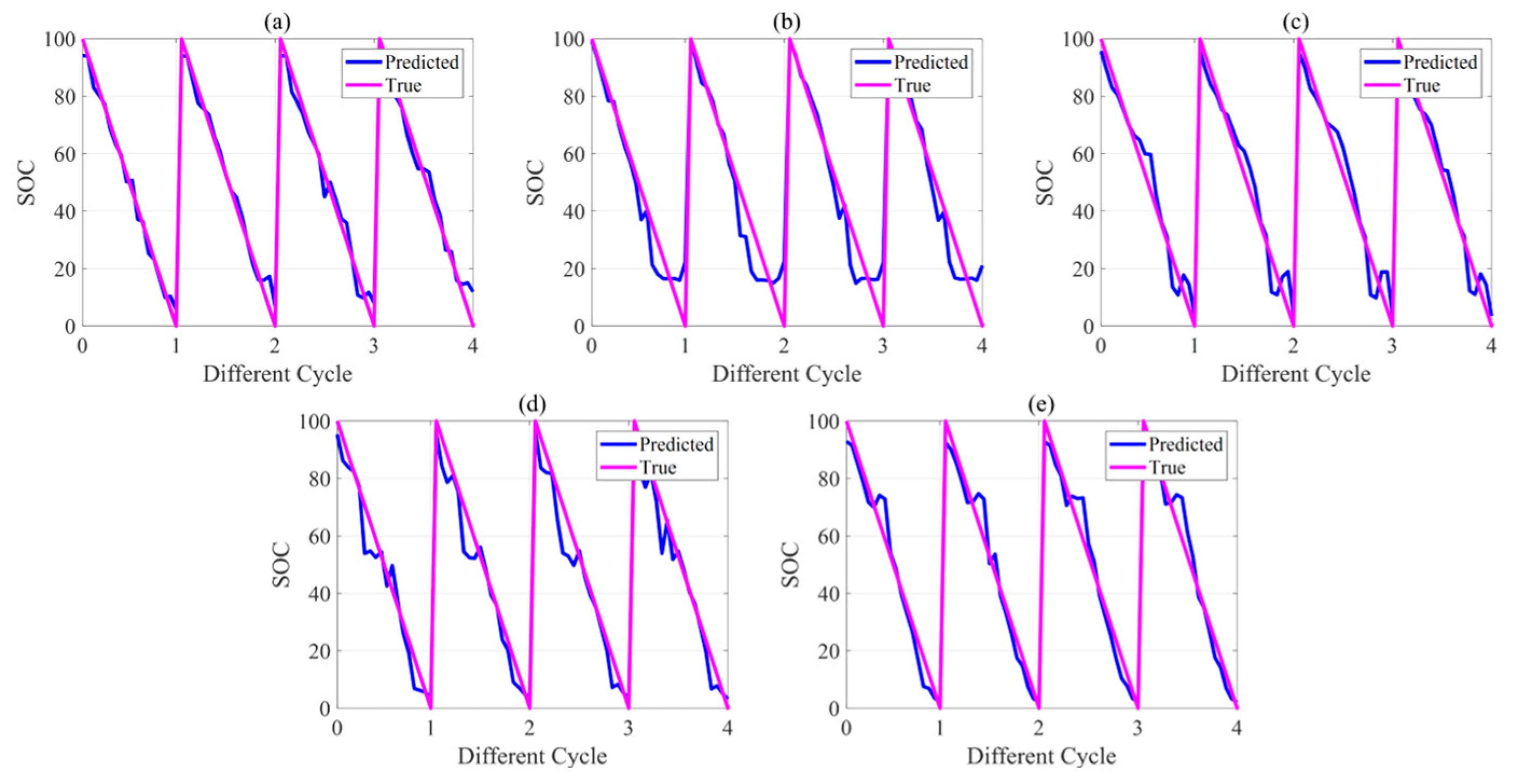
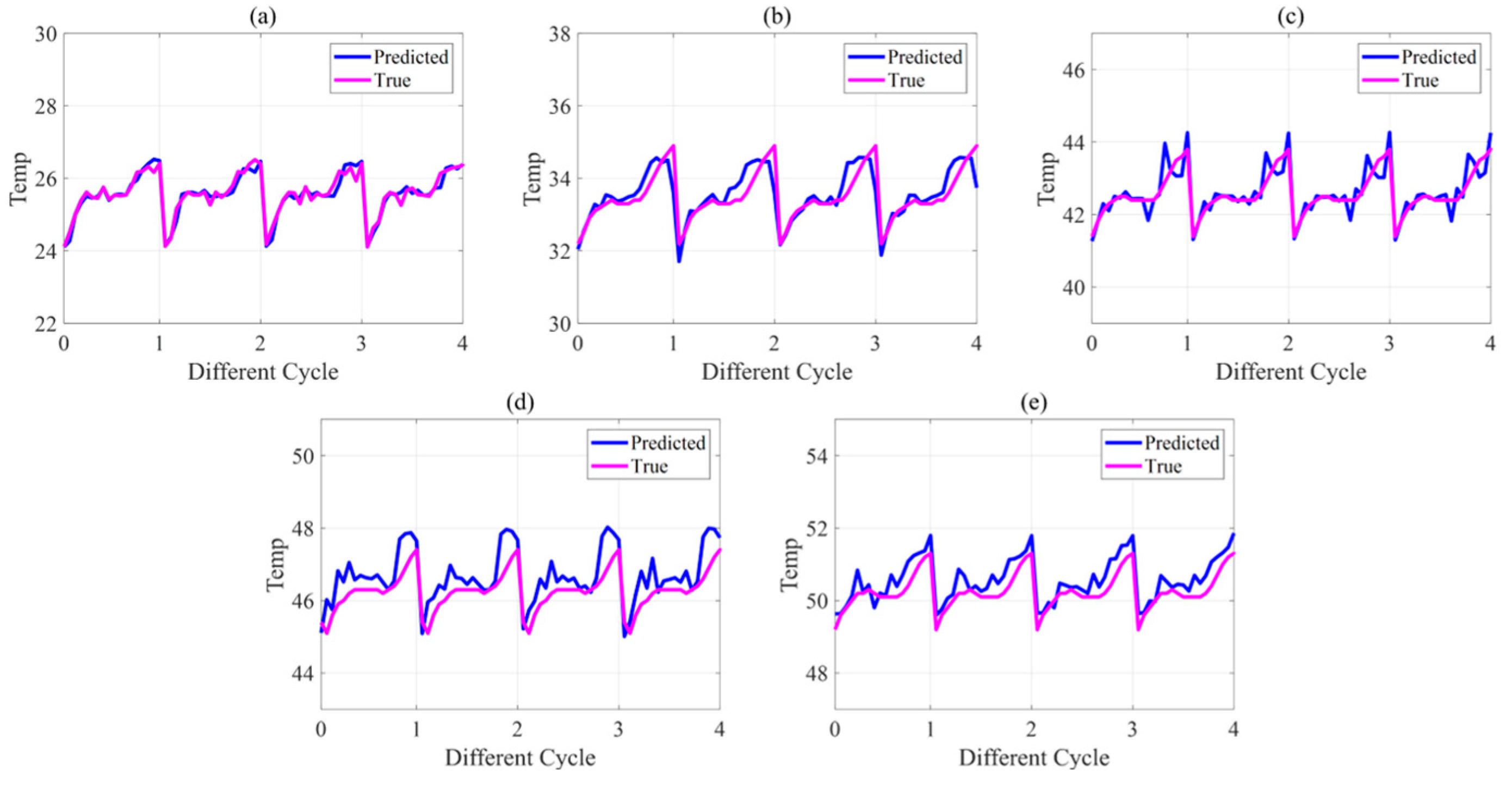
5.3. Battery State Estimation Results
5.4. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sun, F. Green Energy and Intelligent Transportation—Promoting Green and Intelligent Mobility. Green Energy Intell. Transp. 2022, 1, 100017. [Google Scholar] [CrossRef]
- Xiong, R.; Kim, J.; Shen, W.; Lv, C.; Li, H.; Zhu, X.; Zhao, W.; Gao, B.; Guo, H.; Zhang, C.; et al. Key Technologies for Electric Vehicles. Green Energy Intell. Transp. 2022, 1, 100041. [Google Scholar] [CrossRef]
- Sparber, W.; Grotto, A.; Zambelli, P.; Vaccaro, R.; Zubaryeva, A. Evaluation of Different Scenarios to Switch the Whole Regional Bus Fleet of an Italian Alpine Region to Zero-Emission Buses. World Electr. Veh. J. 2023, 14, 91. [Google Scholar] [CrossRef]
- Fahim, K.E.; De Silva, L.C.; Hussain, F.; Shezan, S.K.A.; Yassin, H. An Evaluation of ASEAN Renewable Energy Path to Carbon Neutrality. Sustainability 2023, 15, 6961. [Google Scholar] [CrossRef]
- Song, K.; Lan, Y.; Zhang, X.; Jiang, J.; Sun, C.; Yang, G.; Yang, F.; Lan, H. A Review on Interoperability of Wireless Charging Systems for Electric Vehicles. Energies 2023, 16, 1653. [Google Scholar] [CrossRef]
- Zhao, H.; Guo, S.; Zhao, H. Comprehensive Performance Assessment on Various Battery Energy Storage Systems. Energies 2018, 11, 2841. [Google Scholar] [CrossRef]
- Lyu, P.; Liu, X.; Qu, J.; Zhao, J.; Huo, Y.; Qu, Z.; Rao, Z. Recent Advances of Thermal Safety of Lithium Ion Battery for Energy Storage. Energy Storage Mater. 2020, 31, 195–220. [Google Scholar] [CrossRef]
- Fioravanti, R.; Kumar, K.; Nakata, S.; Chalamala, B.; Preger, Y. Predictive-Maintenance Practices: For Operational Safety of Battery Energy Storage Systems. IEEE Power Energy Mag. 2020, 18, 86–97. [Google Scholar] [CrossRef]
- Zhang, Y.; Jiang, M.; Zhou, Y.; Zhao, S.; Yuan, Y. Towards High-Safety Lithium-Ion Battery Diagnosis Methods. Batteries 2023, 9, 63. [Google Scholar] [CrossRef]
- Li, X.; Huang, Z.; Hua, W.; Rao, L.; Tian, Y.; Tian, J. Mechanical Vibration Modeling and Characterization of a Plastic-Cased Lithium-Ion Battery. Green Energy Intell. Transp. 2022, 1, 100006. [Google Scholar] [CrossRef]
- Zappen, H.; Fuchs, G.; Gitis, A.; Sauer, D. In-Operando Impedance Spectroscopy and Ultrasonic Measurements during High-Temperature Abuse Experiments on Lithium-Ion Batteries. Batteries 2020, 6, 25. [Google Scholar] [CrossRef]
- Xu, J.; Sun, C.; Ni, Y.; Lyu, C.; Wu, C.; Zhang, H.; Yang, Q.; Feng, F. Fast Identification of Micro-Health Parameters for Retired Batteries Based on a Simplified P2D Model by Using Padé Approximation. Batteries 2023, 9, 64. [Google Scholar] [CrossRef]
- Zhou, M.; Wei, K.; Wu, X.; Weng, L.; Su, H.; Wang, D.; Zhang, Y.; Li, J. Fractional-Order Sliding-Mode Observers for the Estimation of State-of-Charge and State-of-Health of Lithium Batteries. Batteries 2023, 9, 213. [Google Scholar] [CrossRef]
- Yang, X.; Ma, B.; Xie, H.; Wang, W.; Zou, B.; Liang, F.; Hua, X.; Liu, X.; Chen, S. Lithium-Ion Battery State of Health Estimation with Multi-Feature Collaborative Analysis and Deep Learning Method. Batteries 2023, 9, 120. [Google Scholar] [CrossRef]
- Li, Z.; Shen, S.; Zhou, Z.; Cai, Z.; Gu, W.; Zhang, F. Novel Method for Modelling and Adaptive Estimation for SOC and SOH of Lithium-Ion Batteries. J. Energy Storage 2023, 62, 106927. [Google Scholar] [CrossRef]
- Jasiūnienė, E.; Mažeika, L.; Samaitis, V.; Cicėnas, V.; Mattsson, D. Ultrasonic Non-Destructive Testing of Complex Titanium/Carbon Fibre Composite Joints. Ultrasonics 2019, 95, 13–21. [Google Scholar] [CrossRef] [PubMed]
- Hu, S.; Shi, W.; Lu, C.; Chen, Y.; Chen, G.; Shen, G. Rapid Detection of Cracks in the Rail Foot by Ultrasonic B-Scan Imaging Using a Shear Horizontal Guided Wave Electromagnetic Acoustic Transducer. NDT E Int. 2021, 120, 102437. [Google Scholar] [CrossRef]
- Ying, K.-N.; Ni, C.-Y.; Dai, L.-N.; Yuan, L.; Kan, W.-W.; Shen, Z.-H. Multi-Mode Laser-Ultrasound Imaging Using Time-Domain Synthetic Aperture Focusing Technique (T-SAFT). Photoacoustics 2022, 27, 100370. [Google Scholar] [CrossRef]
- Sood, M.B.; Osterman, M.; Pecht, M. Health monitoring of lithium-ion batteries. In Proceedings of the 2013 IEEE Symposium on Product Compliance Engineering (ISPCE), Austin, TX, USA, 7–9 October 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Hsieh, A.G.; Bhadra, S.; Hertzberg, B.J.; Gjeltema, P.J.; Goy, A.; Fleischer, J.W.; Steingart, D.A. Electrochemical-Acoustic Time of Flight: In Operando Correlation of Physical Dynamics with Battery Charge and Health. Energy Environ. Sci. 2015, 8, 1569–1577. [Google Scholar] [CrossRef]
- Gold, L.; Bach, T.; Virsik, W.; Schmitt, A.; Müller, J.; Staab, T.E.M.; Sextl, G. Probing Lithium-Ion Batteries’ State-of-Charge Using Ultrasonic Transmission—Concept and Laboratory Testing. J. Power Sources 2017, 343, 536–544. [Google Scholar] [CrossRef]
- Ladpli, P.; Kopsaftopoulos, F.; Chang, F.-K. Estimating State of Charge and Health of Lithium-Ion Batteries with Guided Waves Using Built-in Piezoelectric Sensors/Actuators. J. Power Sources 2018, 384, 342–354. [Google Scholar] [CrossRef]
- Copley, R.J.; Cumming, D.; Wu, Y.; Dwyer-Joyce, R.S. Measurements and Modelling of the Response of an Ultrasonic Pulse to a Lithium-Ion Battery as a Precursor for State of Charge Estimation. J. Energy Storage 2021, 36, 102406. [Google Scholar] [CrossRef]
- Zhao, G.; Liu, Y.; Liu, G.; Jiang, S.; Hao, W. State-of-Charge and State-of-Health Estimation for Lithium-Ion Battery Using the Direct Wave Signals of Guided Wave. J. Energy Storage 2021, 39, 102657. [Google Scholar] [CrossRef]
- Sun, H.; Muralidharan, N.; Amin, R.; Rathod, V.; Ramuhalli, P.; Belharouak, I. Ultrasonic Nondestructive Diagnosis of Lithium-Ion Batteries with Multiple Frequencies. J. Power Sources 2022, 549, 232091. [Google Scholar] [CrossRef]
- Galiounas, E.; Tranter, T.G.; Owen, R.E.; Robinson, J.B.; Shearing, P.R.; Brett, D.J.L. Battery State-of-Charge Estimation Using Machine Learning Analysis of Ultrasonic Signatures. Energy AI 2022, 10, 100188. [Google Scholar] [CrossRef]
- Li, X.; Hua, W.; Wu, C.; Zheng, S.; Tian, Y.; Tian, J. State Estimation of a Lithium-Ion Battery Based on Multi-Feature Indicators of Ultrasonic Guided Waves. J. Energy Storage 2022, 56, 106113. [Google Scholar] [CrossRef]
- Schmerr, L.W. Fundamentals of Ultrasonic Nondestructive Evaluation: A Modeling Approach; Springer Series in Measurement Science and Technology; Springer International Publishing: Cham, Switzerland, 2016; ISBN 978-3-319-30461-8. [Google Scholar]
- Feng, Y. Research on Casing Detection in Mixed Media Based on Ultrasonic Wave; Harbin Institute of Technology: Harbin, China, 2013. [Google Scholar]
- Zhang, Q. Study on Attenuation Characteristics of Ultrasonic Propagation in Non-Uniform Medium; Shenyang University of Technology: Shenyang, China, 2015. [Google Scholar]
- Swallow, J.G.; Woodford, W.H.; McGrogan, F.P.; Ferralis, N.; Chiang, Y.-M.; Van Vliet, K.J. Effect of Electrochemical Charging on Elastoplastic Properties and Fracture Toughness of LiXCoO2. J. Electrochem. Soc. 2014, 161, F3084–F3090. [Google Scholar] [CrossRef]
- Meng, X.; Zheng, P.; Wu, J. Experimental measurement of viscosity and density of dimethyl carbonate. J. Engi-Neering Thermophys. 2009, 30, 26–30. [Google Scholar]
- Li, D.-C.; Wu, C.-S.; Tsai, T.-I.; Lina, Y.-S. Using Mega-Trend-Diffusion and Artificial Samples in Small Data Set Learning for Early Flexible Manufacturing System Scheduling Knowledge. Comput. Oper. Res. 2007, 34, 966–982. [Google Scholar] [CrossRef]
- Tian, Y.; Dong, Q.; Tian, J.; Li, X.; Li, G.; Mehran, K. Capacity Estimation of Lithium-Ion Batteries Based on Optimized Charging Voltage Section and Virtual Sample Generation. Appl. Energy 2023, 332, 120516. [Google Scholar] [CrossRef]
- Jin, D.; Lin, S. (Eds.) Advances in Computer Science and Information Engineering: Volume 2; Advances in Intelligent and Soft Computing; Springer: Berlin/Heidelberg, Germany, 2012; Volume 169, ISBN 978-3-642-30222-0. [Google Scholar]




| Pressure\Temperature | Density ρ (kg·m3) | |||
|---|---|---|---|---|
| 20 °C | 30 °C | 40 °C | 50 °C | |
| 0.1 MPa | 1068.60 | 1054.90 | 1041.48 | 1029.87 |
| 4.56 MPa | 1072.27 | 1059.30 | 1045.90 | 1032.93 |
| 9.58 MPa | 1077.09 | 1064.35 | 1050.35 | 1038.48 |
| Pressure\Temperature | Viscosity η (mPa·s) | |||
|---|---|---|---|---|
| 20 °C | 30 °C | 40 °C | 50 °C | |
| 0.1 MPa | 0.619 | 0.547 | 0.491 | 0.438 |
| 4.56 MPa | 0.637 | 0.561 | 0.503 | 0.448 |
| 9.58 MPa | 0.659 | 0.581 | 0.513 | 0.463 |
| Indicator | Equation | Implication |
|---|---|---|
| Time domain peak | Maximum amplitude of time domain waveform | |
| Time domain envelope peak | Maximum amplitude of time domain waveform envelope | |
| Energy integral | Energy of the signal time domain waveform | |
| Waveform index | Degree of fluctuation of the signal time domain waveform | |
| Kurtosis coefficient | Sharpness of the peak of the signal time domain waveform | |
| Shape coefficient | Distribution range of the signal time domain waveform on the time axis |
| Indicator | Optimal Interval | Optimal Interval Correlation | Part 1 Correlation | Part 2 Correlation |
|---|---|---|---|---|
| Time domain peak (Pt) | 1750:3500 | −0.95 | −0.95 | 0.56 |
| Time domain envelope peak (Pet) | 1750:3500 | −0.95 | −0.95 | 0.56 |
| Energy integral (E) | 1050:3500 | −0.99 | −0.99 | 0.38 |
| Waveform index (W) | 1050:2750 | 0.93 | 0.63 | 0.86 |
| Kurtosis coefficient (K) | 1050:2750 | 0.98 | 0.77 | 0.82 |
| Shape coefficient (S) | 1050:3500 | 0.99 | 0.99 | −0.38 |
| Parameters | Value |
|---|---|
| Layers | 6 |
| Input shape | 6 |
| Output shape | 2 |
| Epochs | 300 |
| Batch size | 256 |
| Group 1 | |||||
| RMSE | 26 °C | 34 °C | 42 °C | 46 °C | 50 °C |
| SOC (%) | 8.60 | 6.50 | 7.53 | 10.22 | 10.04 |
| TEMP (°C) | / | / | / | / | / |
| Group 2 | |||||
| RMSE | 26 °C | 34 °C | 42 °C | 46 °C | 50 °C |
| SOC (%) | 7.74 | 6.58 | 9.63 | 9.25 | 11.98 |
| TEMP (°C) | 0.80 | 0.83 | 1.08 | 1.26 | 0.94 |
| Group 3 | |||||
| RMSE | 26 °C | 34 °C | 42 °C | 46 °C | 50 °C |
| SOC (%) | 6.11 | 9.20 | 6.89 | 7.80 | 6.76 |
| TEMP (°C) | 0.29 | 0.40 | 0.31 | 0.56 | 0.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Li, X.; Sun, C.; Yang, S.; Tian, Y.; Tian, J. State of Charge and Temperature Joint Estimation Based on Ultrasonic Reflection Waves for Lithium-Ion Battery Applications. Batteries 2023, 9, 335. https://doi.org/10.3390/batteries9060335
Zhang R, Li X, Sun C, Yang S, Tian Y, Tian J. State of Charge and Temperature Joint Estimation Based on Ultrasonic Reflection Waves for Lithium-Ion Battery Applications. Batteries. 2023; 9(6):335. https://doi.org/10.3390/batteries9060335
Chicago/Turabian StyleZhang, Runnan, Xiaoyu Li, Chuanyu Sun, Songyuan Yang, Yong Tian, and Jindong Tian. 2023. "State of Charge and Temperature Joint Estimation Based on Ultrasonic Reflection Waves for Lithium-Ion Battery Applications" Batteries 9, no. 6: 335. https://doi.org/10.3390/batteries9060335
APA StyleZhang, R., Li, X., Sun, C., Yang, S., Tian, Y., & Tian, J. (2023). State of Charge and Temperature Joint Estimation Based on Ultrasonic Reflection Waves for Lithium-Ion Battery Applications. Batteries, 9(6), 335. https://doi.org/10.3390/batteries9060335









