A K-Value Dynamic Detection Method Based on Machine Learning for Lithium-Ion Battery Manufacturing
Abstract
:1. Introduction
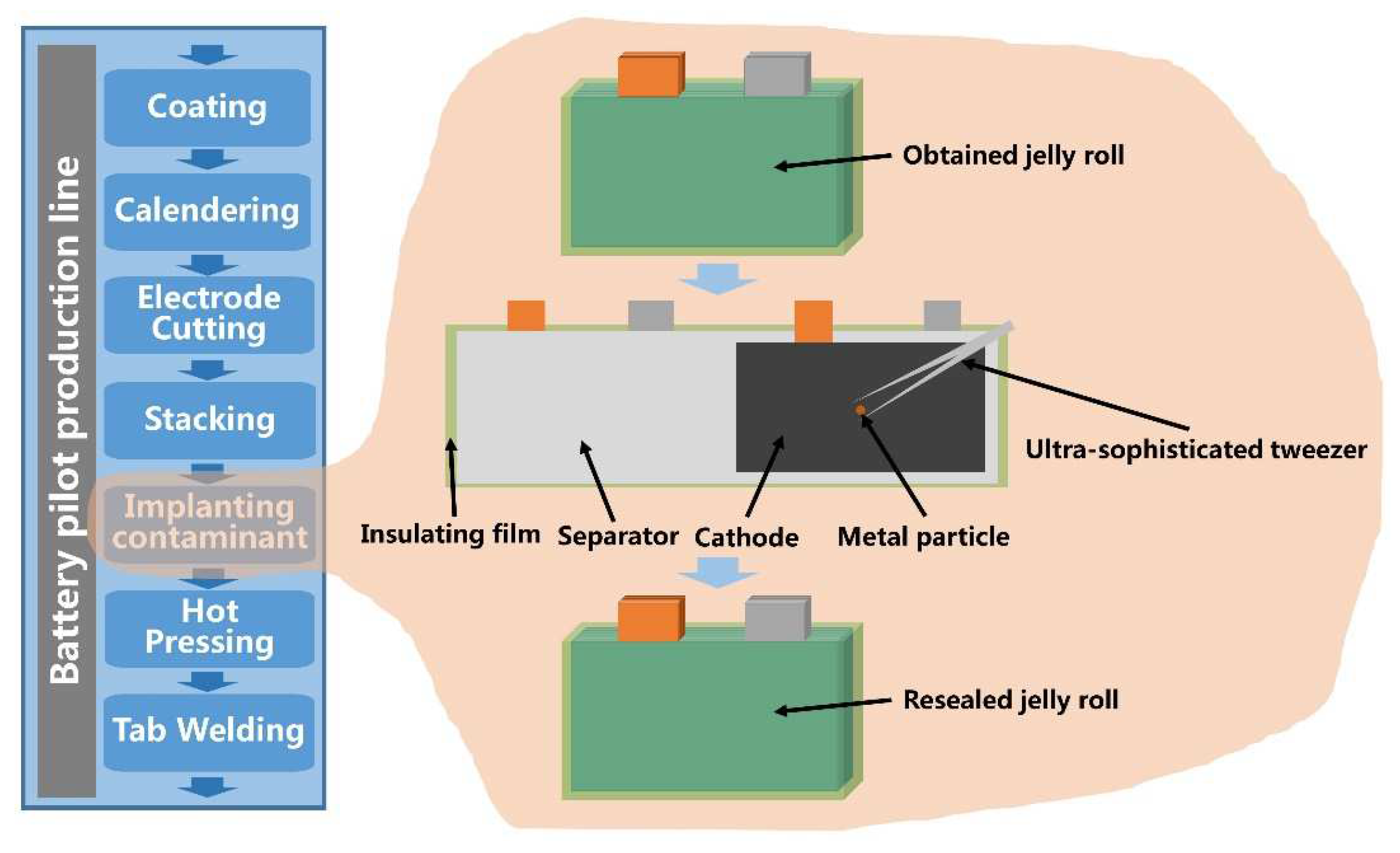
2. Foreign Matter Defect and K-Value Test
2.1. Relationship between Foreign Matter Defect and K-Value
2.2. Disadvantages of Traditional K-Value Test
3. Performance of Different Anomaly Detection Algorithms
3.1. Algorithm Description
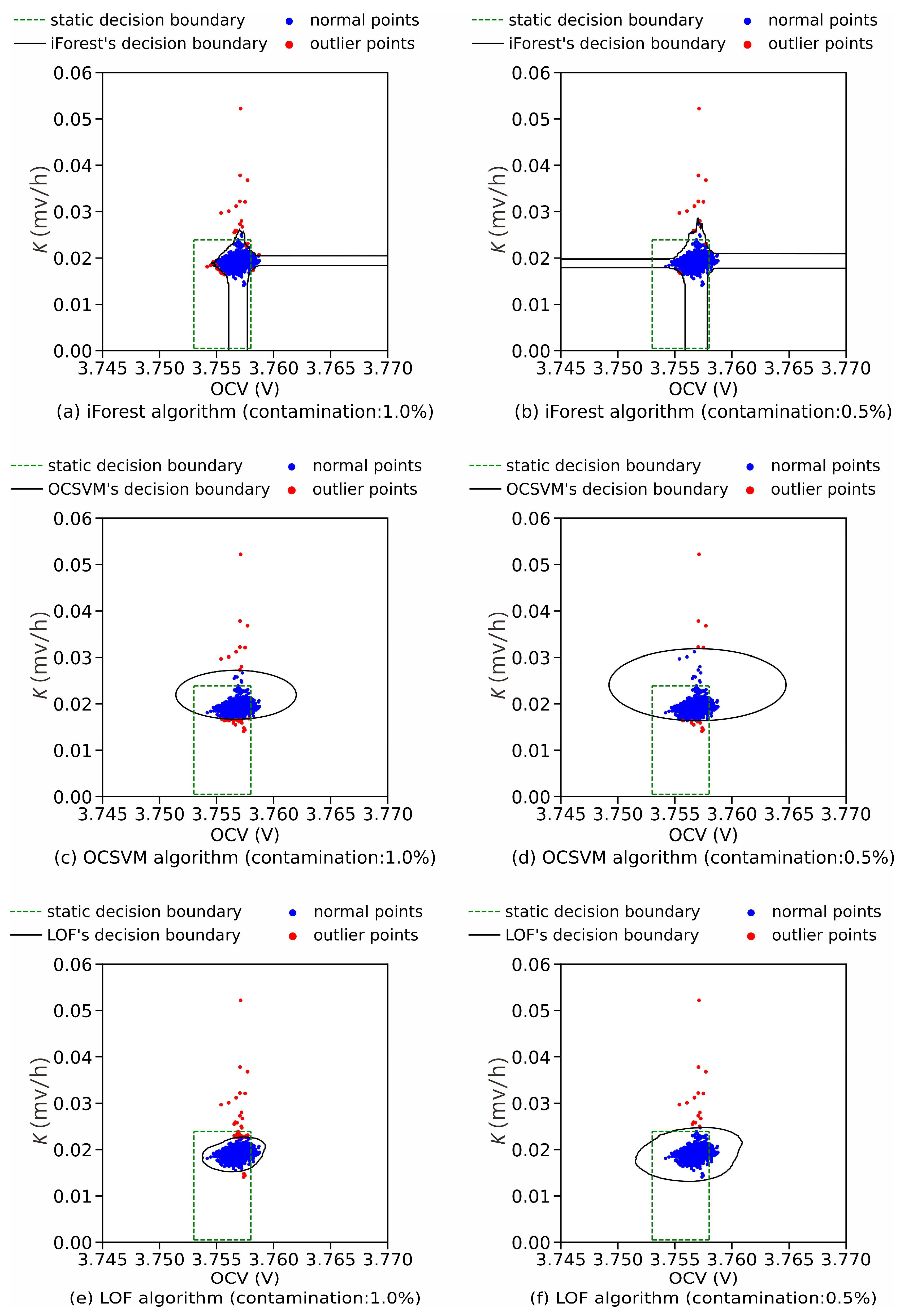
3.1.1. Isolation Forest Algorithm
- Step 1 Training dataset
- Step 2 Computing anomaly score
- Step 3 Identifying the outlier point based on the threshold
3.1.2. One-Class Support Vector Machine Algorithm
- Step 1 Training dataset
- Step 2 Identifying the outlier points
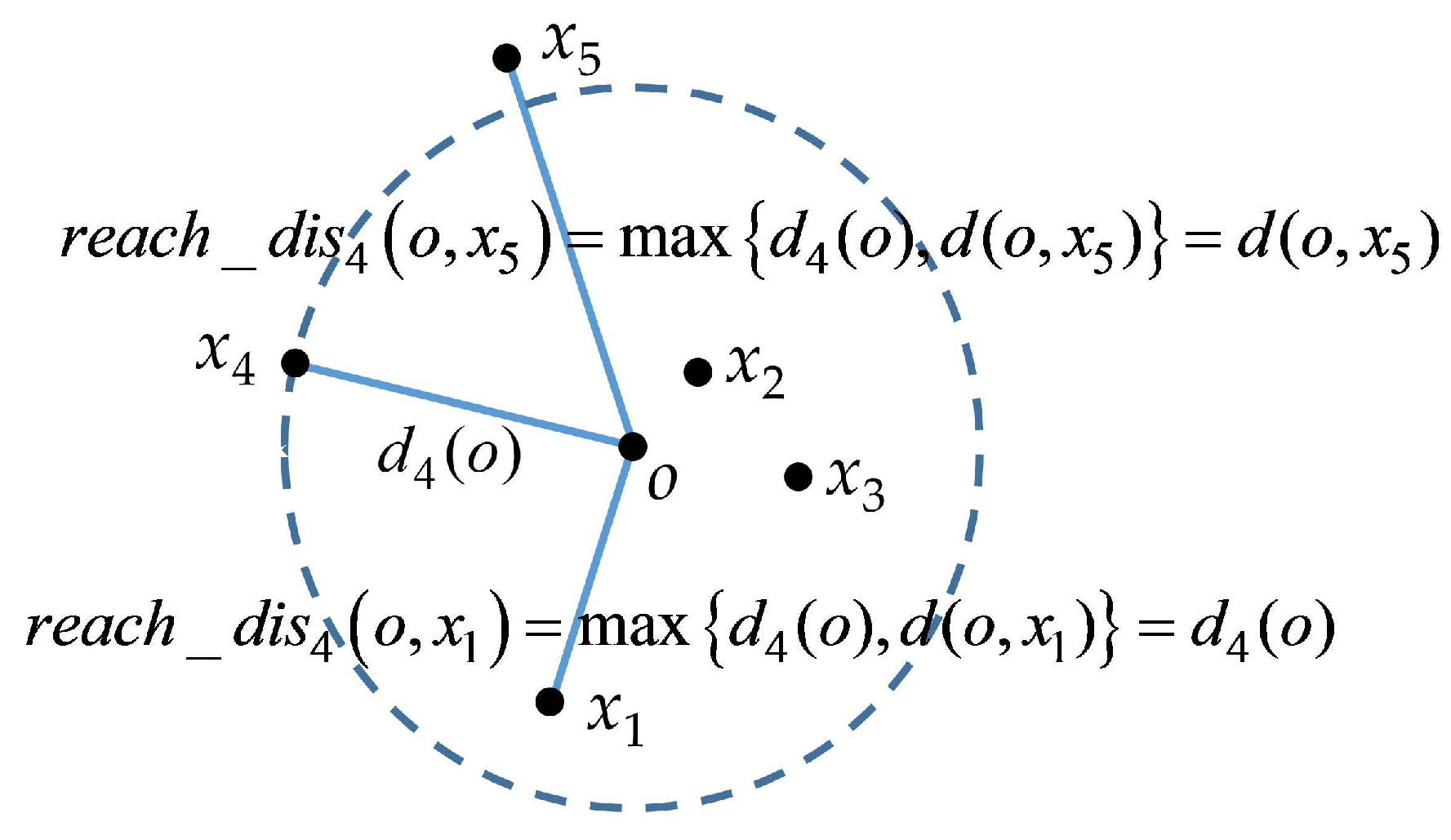
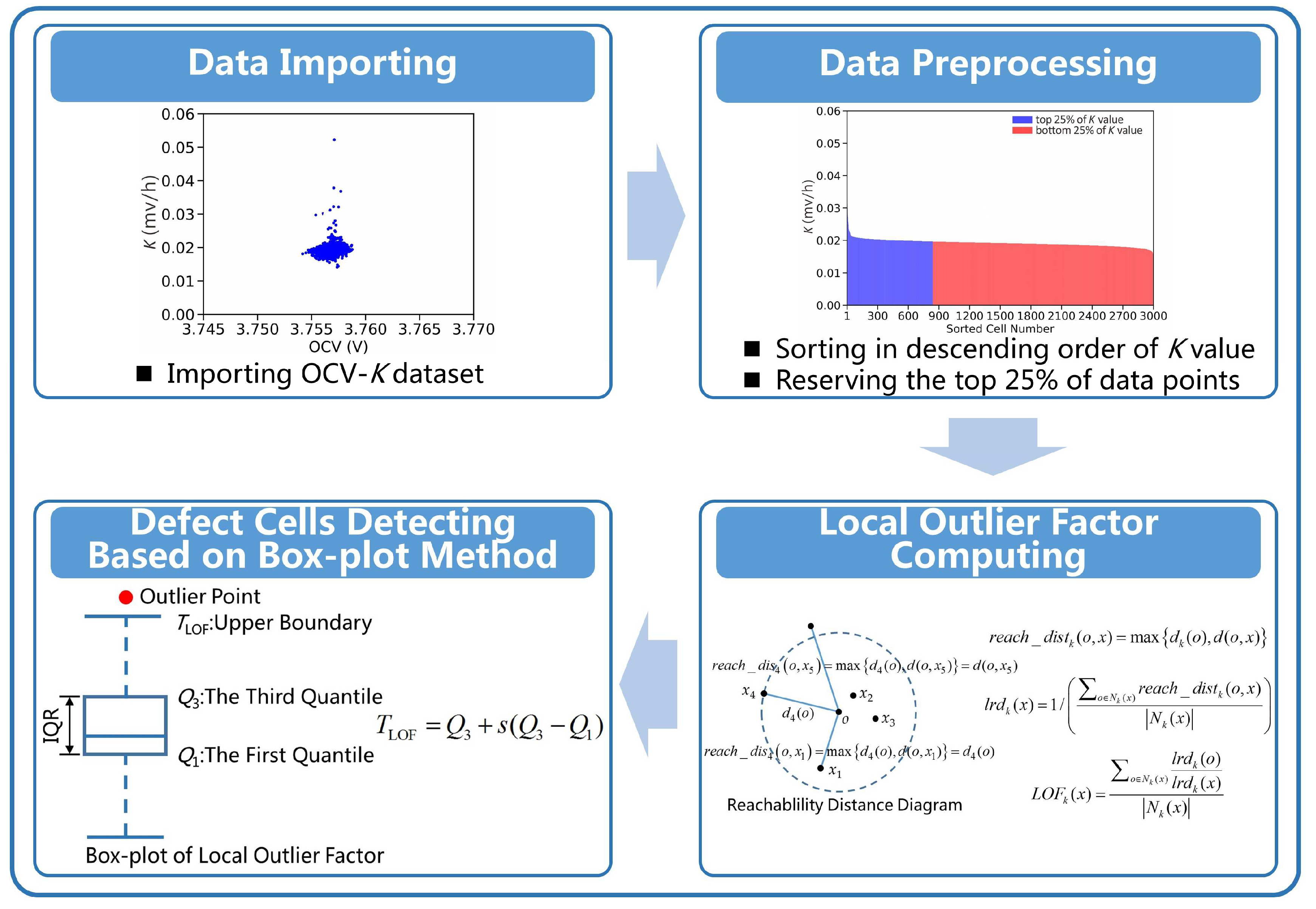
3.1.3. Local Outlier Factor Algorithm
- Step 1 Computing the local reachability density
- Step 2 Computing the local outlier factor
- Step 3 Identifying the outlier point based on the threshold
3.2. Comparison of Different Algorithms’ Performance
4. K-Value Dynamic Detection Method Based on LOF
4.1. Description of K-Value Dynamic Detection Method
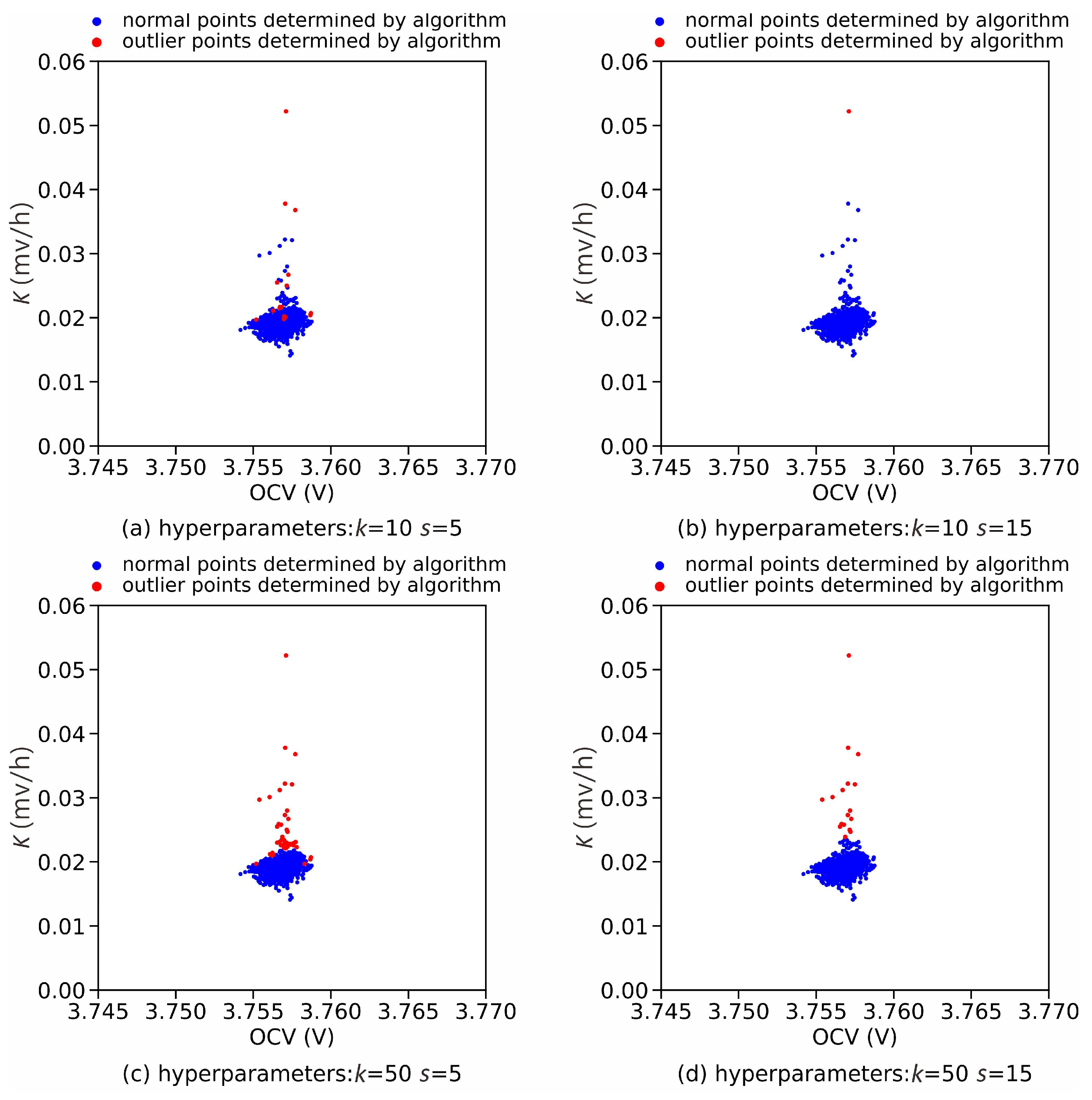
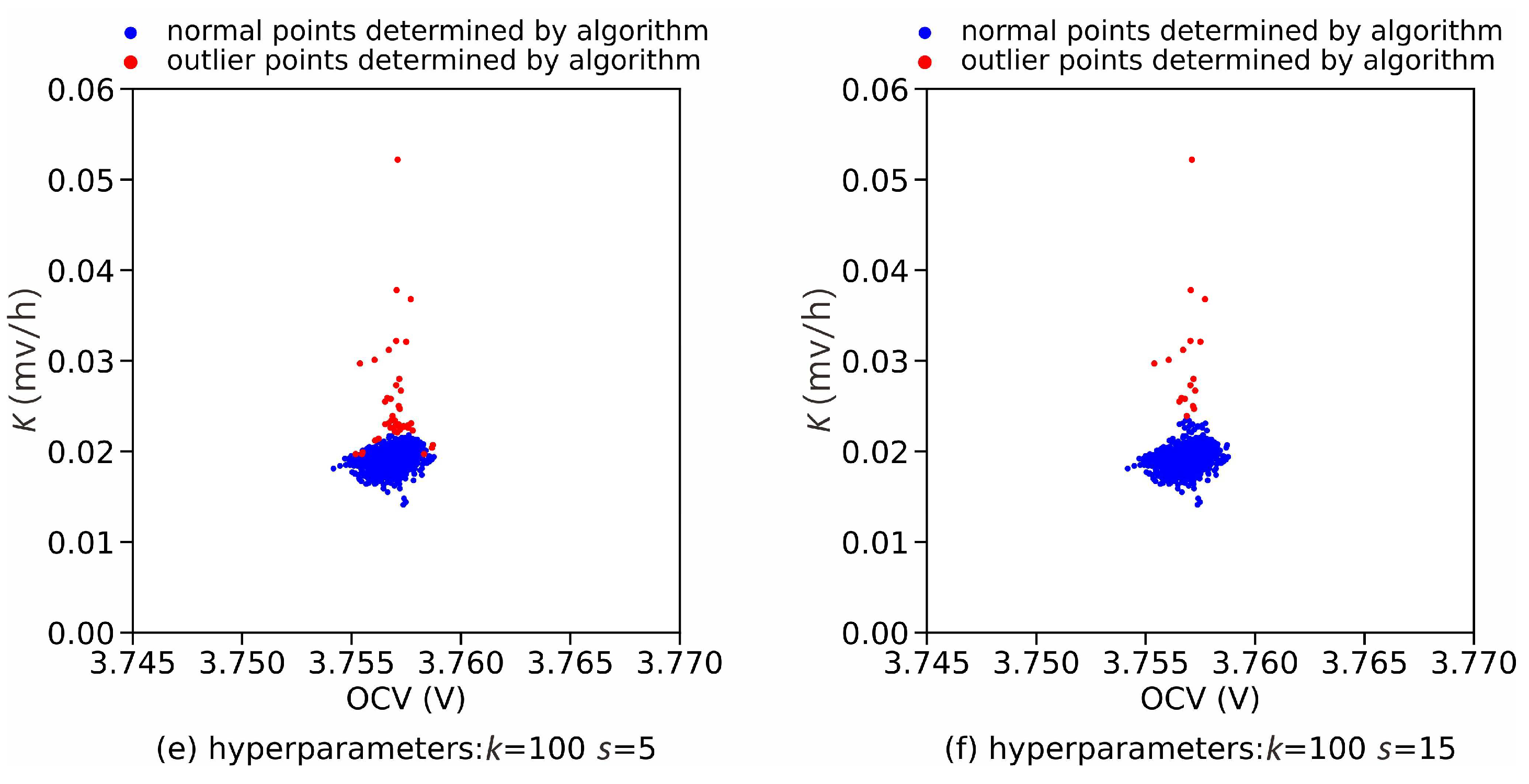
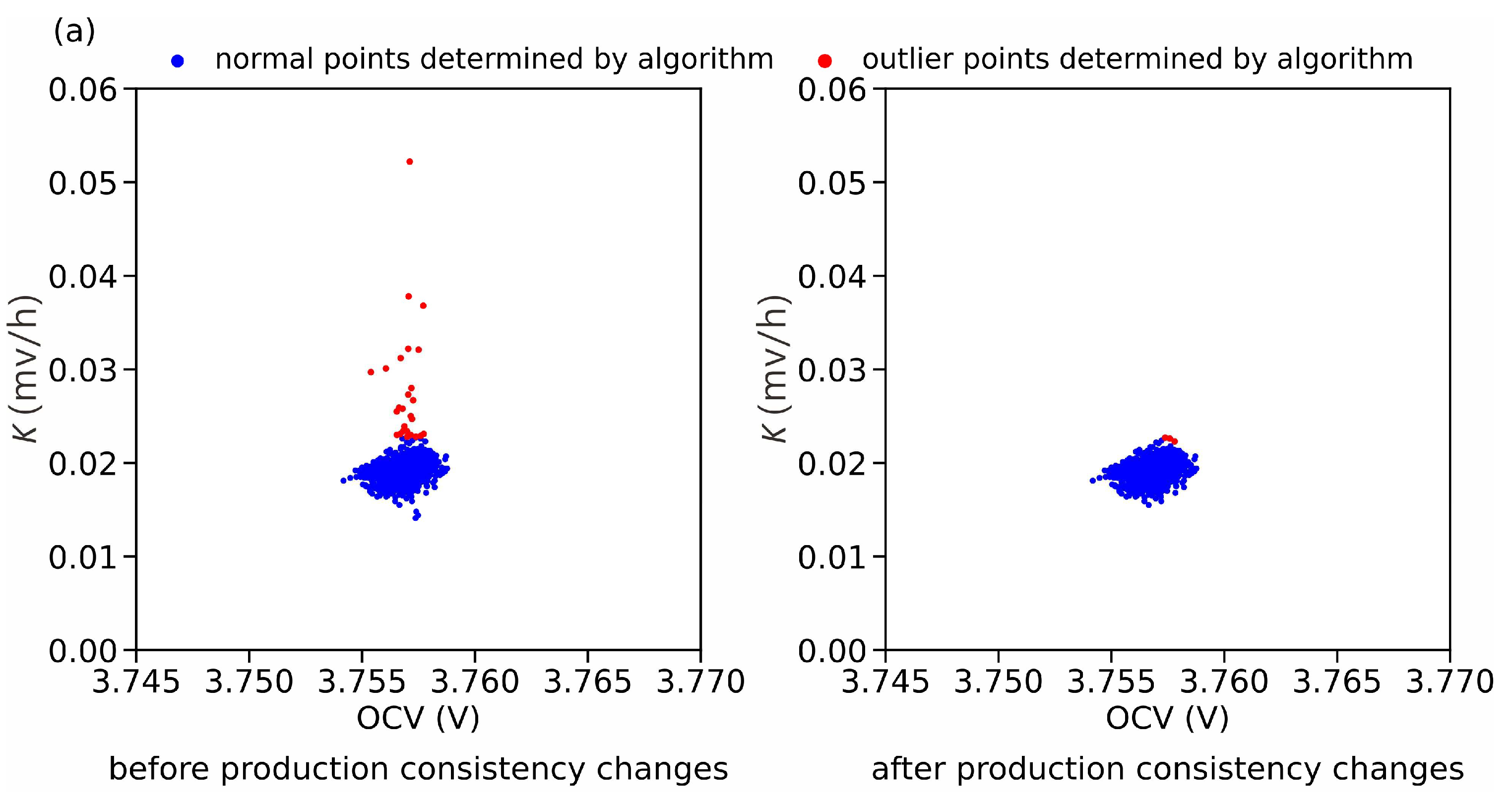
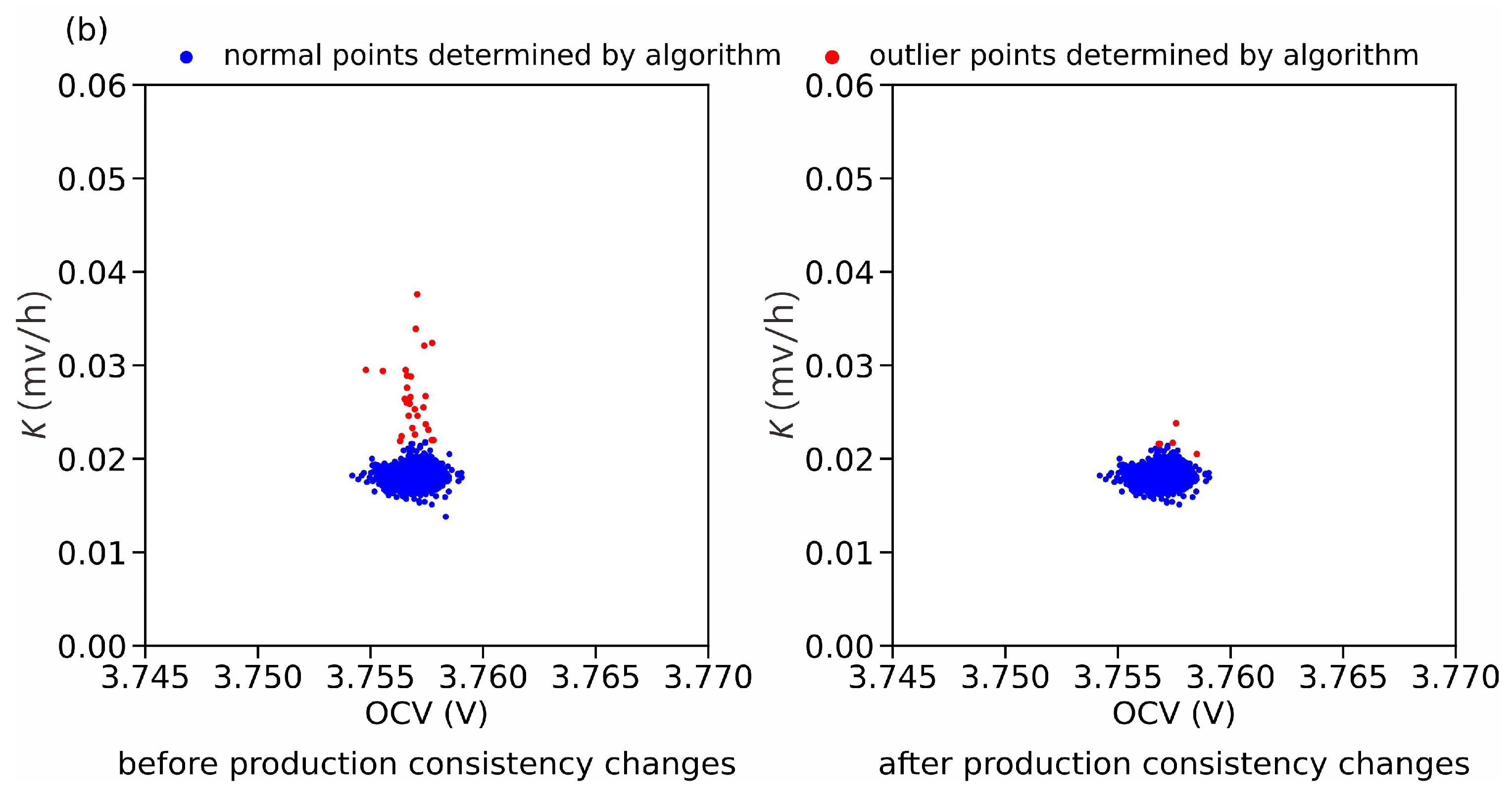
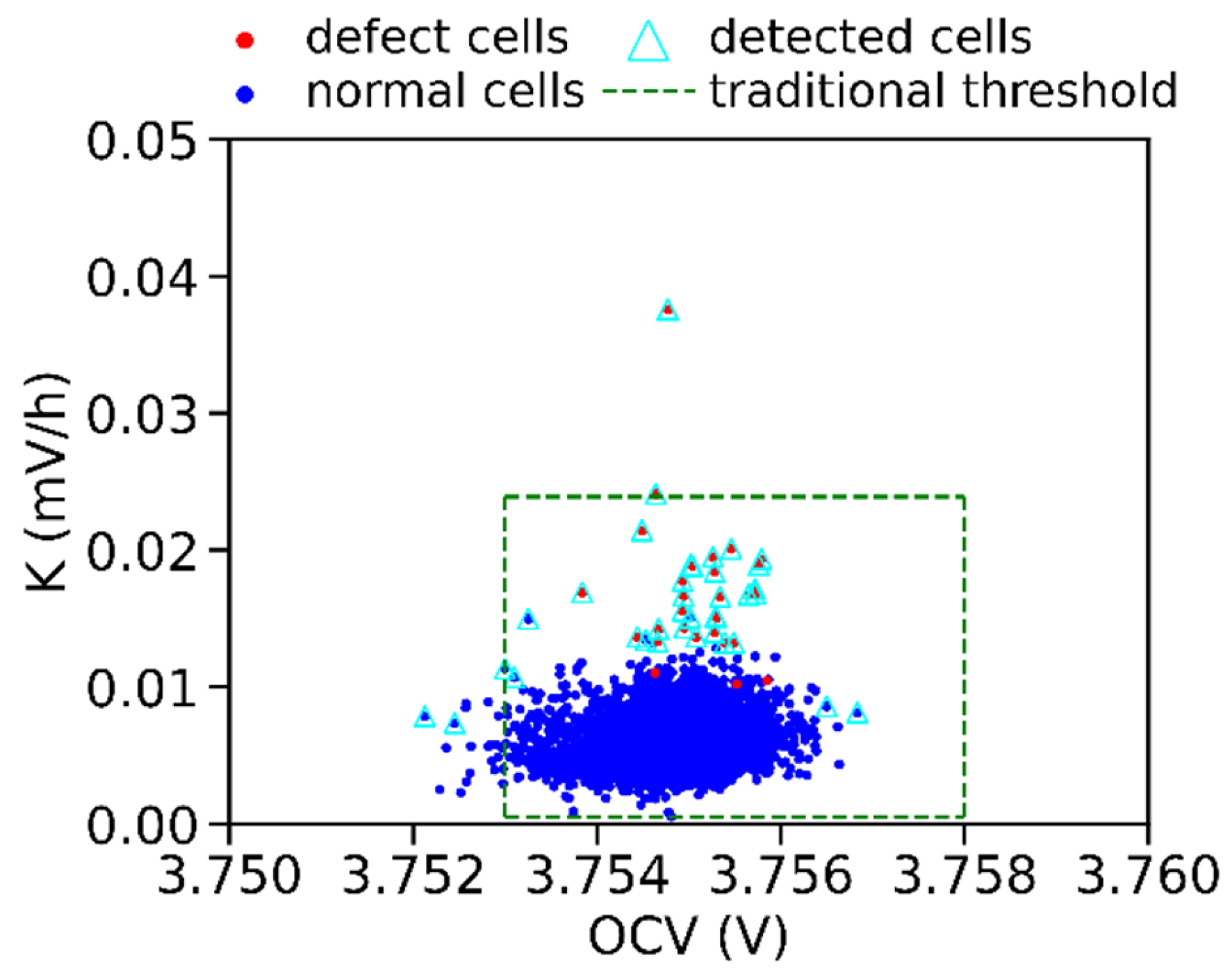
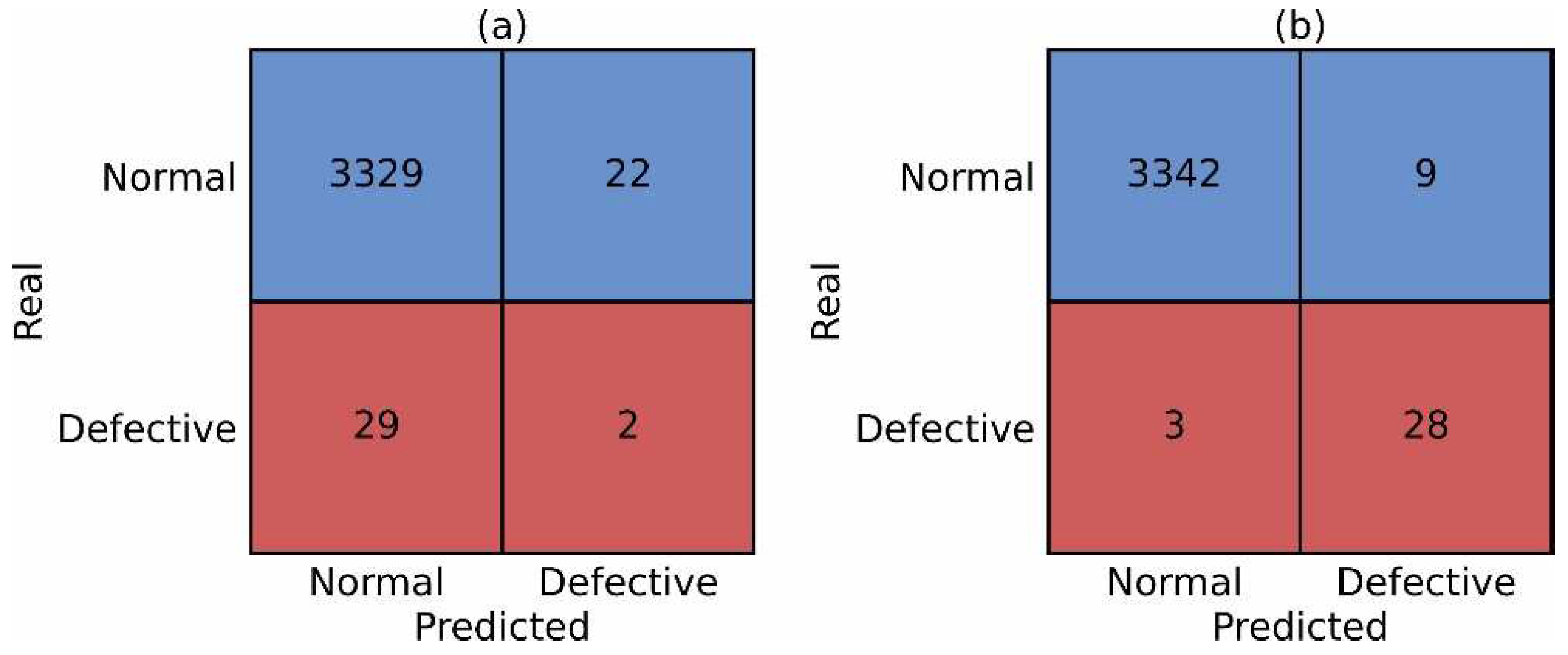
4.2. Performance Analysis of K-Value Dynamic Detection Method
4.3. Experimental Validation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kong, D.; Wang, G.; Ping, P.; Wen, J. A Coupled Conjugate Heat Transfer and CFD Model for the Thermal Runaway Evolution and Jet Fire of 18650 Lithium-Ion Battery under Thermal Abuse. eTransportation 2022, 12, 100157. [Google Scholar] [CrossRef]
- Hu, G.; Huang, P.; Bai, Z.; Wang, Q.; Qi, K. Comprehensively Analysis the Failure Evolution and Safety Evaluation of Automotive Lithium Ion Battery. eTransportation 2021, 10, 100140. [Google Scholar] [CrossRef]
- Wang, H.; Xu, H.; Zhang, Z.; Wang, Q.; Jin, C.; Wu, C.; Xu, C.; Hao, J.; Sun, L.; Du, Z.; et al. Fire and Explosion Characteristics of Vent Gas from Lithium-Ion Batteries after Thermal Runaway: A Comparative Study. eTransportation 2022, 13, 100190. [Google Scholar] [CrossRef]
- Held, M.; Tuchschmid, M.; Zennegg, M.; Figi, R.; Schreiner, C.; Mellert, L.D.; Welte, U.; Kompatscher, M.; Hermann, M.; Nachef, L. Thermal Runaway and Fire of Electric Vehicle Lithium-Ion Battery and Contamination of Infrastructure Facility. Renew. Sustain. Energy Rev. 2022, 165, 112474. [Google Scholar] [CrossRef]
- Wang, Q.; Mao, B.; Stoliarov, S.I.; Sun, J. A Review of Lithium Ion Battery Failure Mechanisms and Fire Prevention Strategies. Prog. Energy Combust. Sci. 2019, 73, 95–131. [Google Scholar] [CrossRef]
- Lai, X.; Yao, J.; Jin, C.; Feng, X.; Wang, H.; Xu, C.; Zheng, Y. A Review of Lithium-Ion Battery Failure Hazards: Test Standards, Accident Analysis, and Safety Suggestions. Batteries 2022, 8, 248. [Google Scholar] [CrossRef]
- Peiyan, Q.I.; Jie, Z.M.; Da, J.; Kai, Y.; Jianling, L.; Yilin, L.; Fei, G.; Hao, L. Combustion Characteristics of Lithium–Iron–Phosphate Batteries with Different Combustion States. eTransportation 2022, 11, 100148. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhou, X.; Cao, B.; Yang, L.; Liew, K.M. Investigating the Relationship between Heating Temperature and Thermal Runaway of Prismatic Lithium-Ion Battery with LiFePO4 as Cathode. Energy 2022, 256, 124714. [Google Scholar] [CrossRef]
- Jones, C.; Li, B.; Tomar, V. Determining the Effects of Non-Catastrophic Nail Puncture on the Operational Performance and Service Life of Small Soft Case Commercial Li-Ion Prismatic Cells. eTransportation 2021, 8, 100109. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Bai, J. Influences of Multi Factors on Thermal Runaway Induced by Overcharging of Lithium-Ion Battery. J. Energy Chem. 2022, 70, 531–541. [Google Scholar] [CrossRef]
- Kong, X.; Lu, L.; Yuan, Y.; Sun, Y.; Feng, X.; Yang, H.; Zhang, F.; Zhang, J.; Liu, X.; Han, X.; et al. Foreign Matter Defect Battery and Sudden Spontaneous Combustion. eTransportation 2022, 12, 100170. [Google Scholar] [CrossRef]
- David, L.; Ruther, R.E.; Mohanty, D.; Meyer, H.M.; Sheng, Y.; Kalnaus, S.; Daniel, C.; Wood, D.L. Identifying Degradation Mechanisms in Lithium-Ion Batteries with Coating Defects at the Cathode. Appl. Energy 2018, 231, 446–455. [Google Scholar] [CrossRef]
- Qian, G.; Monaco, F.; Meng, D.; Lee, S.-J.; Zan, G.; Li, J.; Karpov, D.; Gul, S.; Vine, D.; Stripe, B.; et al. The Role of Structural Defects in Commercial Lithium-Ion Batteries. Cell Rep. Phys. Sci. 2021, 2, 100554. [Google Scholar] [CrossRef]
- Choudhary, N.; Clever, H.; Ludwigs, R.; Rath, M.; Gannouni, A.; Schmetz, A.; Hülsmann, T.; Sawodny, J.; Fischer, L.; Kampker, A.; et al. Autonomous Visual Detection of Defects from Battery Electrode Manufacturing. Adv. Intell. Syst. 2022, 4, 2200142. [Google Scholar] [CrossRef]
- Li, Y.; Fu, X.; Wang, Y.; Zhong, W.-H.; Li, R. “See” the Invisibles: Inspecting Battery Separator Defects via Pressure Drop. Energy Storage Mater. 2019, 16, 589–596. [Google Scholar] [CrossRef]
- Kim, N.; Byun, S.; Jin, D.; Dzakpasu, C.B.; Park, S.H.; Lee, H.; Hong, S.-T.; Lee, Y.M. Electrode Alignment: Ignored but Important Design Parameter in Assembling Coin-Type Full Lithium-Ion Cells. J. Electrochem. Soc. 2022, 169, 023502. [Google Scholar] [CrossRef]
- Zhang, G. Internal Short Circuit Mechanisms, Experimental Approaches and Detection Methods of Lithium-Ion Batteries for Electric Vehicles: A Review. Renew. Sustain. Energy Rev. 2021, 141, 110790. [Google Scholar] [CrossRef]
- Nakajima, H.; Kitahara, T. Diagnosis Method to Detect the Incorporation of Metallic Particles in a Lithium Ion Battery. ECS Trans. 2015, 68, 59–74. [Google Scholar] [CrossRef]
- Grabow, J.; Klink, J.; Benger, R.; Hauer, I.; Beck, H.-P. Particle Contamination in Commercial Lithium-Ion Cells—Risk Assessment with Focus on Internal Short Circuits and Replication by Currently Discussed Trigger Methods. Batteries 2022, 9, 9. [Google Scholar] [CrossRef]
- Sun, Y.; Yuan, Y.; Lu, L.; Han, X.; Kong, X.; Wang, H.; Ouyang, M.; Gao, P.; Zheng, H.; Wang, K. A Comprehensive Research on Internal Short Circuits Caused by Copper Particle Contaminants on Cathode in Lithium-Ion Batteries. eTransportation 2022, 13, 100183. [Google Scholar] [CrossRef]
- Mohanty, D.; Hockaday, E.; Li, J.; Hensley, D.K.; Daniel, C.; Wood, D.L. Effect of Electrode Manufacturing Defects on Electrochemical Performance of Lithium-Ion Batteries: Cognizance of the Battery Failure Sources. J. Power Source 2016, 312, 70–79. [Google Scholar] [CrossRef] [Green Version]
- Yuan, H. Early Stage Internal Short Circuit Fault Diagnosis for Lithium-Ion Batteries Based on Local-Outlier Detection. J. Energy Storage 2023, 57, 106196. [Google Scholar] [CrossRef]
- Feng, X. Detecting the Internal Short Circuit in Large-Format Lithium-Ion Battery Using Model-Based Fault-Diagnosis Algorithm. J. Energy Storage 2018, 18, 26–39. [Google Scholar] [CrossRef]
- Chen, A.; Zhang, W.; Zhang, C.; Wang, Z.; Fan, X. A Novel Al–Cu Internal Short Circuit Detection Method for Lithium-Ion Batteries Based on on-Board Signal Processing. J. Energy Storage 2022, 52, 104748. [Google Scholar] [CrossRef]
- Kong, L.; Aalund, R.; Alipour, M.; Stoliarov, S.I.; Pecht, M. Evaluating the Manufacturing Quality of Lithium Ion Pouch Batteries. J. Electrochem. Soc. 2022, 169, 040541. [Google Scholar] [CrossRef]
- McGovern, M.E.; Bruder, D.D.; Huemiller, E.D.; Rinker, T.J.; Bracey, J.T.; Sekol, R.C.; Abell, J.A. A Review of Research Needs in Nondestructive Evaluation for Quality Verification in Electric Vehicle Lithium-Ion Battery Cell Manufacturing. J. Power Source 2023, 561, 232742. [Google Scholar] [CrossRef]
- Yi, M.; Jiang, F.; Lu, L.; Hou, S.; Ren, J.; Han, X.; Huang, L. Ultrasonic Tomography Study of Metal Defect Detection in Lithium-Ion Battery. Front. Energy Res. 2021, 9, 806929. [Google Scholar] [CrossRef]
- Fink, K.E.; Polzin, B.J.; Vaughey, J.T.; Major, J.J.; Dunlop, A.R.; Trask, S.E.; Jeka, G.T.; Spangenberger, J.S.; Keyser, M.A. Influence of Metallic Contaminants on the Electrochemical and Thermal Behavior of Li-Ion Electrodes. J. Power Source 2022, 518, 230760. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, P.; Wang, Z.; Zhang, L.; Hong, J. Fault and Defect Diagnosis of Battery for Electric Vehicles Based on Big Data Analysis Methods. Appl. Energy 2017, 207, 354–362. [Google Scholar] [CrossRef]
- Jiang, J.; Li, T.; Chang, C.; Yang, C.; Liao, L. Fault Diagnosis Method for Lithium-Ion Batteries in Electric Vehicles Based on Isolated Forest Algorithm. J. Energy Storage 2022, 50, 104177. [Google Scholar] [CrossRef]
- Samanta, A.; Chowdhuri, S.; Williamson, S.S. Machine Learning-Based Data-Driven Fault Detection/Diagnosis of Lithium-Ion Battery: A Critical Review. Electronics 2021, 10, 1309. [Google Scholar] [CrossRef]
- Liu, Z.; He, H.; Xie, J.; Wang, K.; Huang, W. Self-Discharge Prediction Method for Lithium-Ion Batteries Based on Improved Support Vector Machine. J. Energy Storage 2022, 55, 105571. [Google Scholar] [CrossRef]
- Zimmerman, A.H. Self-Discharge Losses in Lithium-Ion Cells. IEEE Aerosp. Electron. Syst. Mag. 2004, 19, 19–24. [Google Scholar] [CrossRef]
- Shan, H.; Cao, H.; Xu, X.; Xiao, T.; Hou, G.; Cao, H.; Tang, Y.; Zheng, G. Investigation of Self-Discharge Properties and a New Concept of Open-Circuit Voltage Drop Rate in Lithium-Ion Batteries. J. Solid State Electrochem. 2022, 26, 163–170. [Google Scholar] [CrossRef]
- Liu, F.T.; Ting, K.M.; Zhou, Z.-H. Isolation-Based Anomaly Detection. ACM Trans. Knowl. Discov. Data 2012, 6, 3. [Google Scholar] [CrossRef]
- Tao, X.; Peng, Y.; Zhao, F.; Zhao, P.; Wang, Y. A Parallel Algorithm for Network Traffic Anomaly Detection Based on Isolation Forest. Int. J. Distrib. Sens. Netw. 2018, 14, 155014771881447. [Google Scholar] [CrossRef] [Green Version]
- Chabchoub, Y.; Togbe, M.U.; Boly, A.; Chiky, R. An In-Depth Study and Improvement of Isolation Forest. IEEE Access 2022, 10, 10219–10237. [Google Scholar] [CrossRef]
- Mahadevan, S.; Shah, S.L. Fault Detection and Diagnosis in Process Data Using One-Class Support Vector Machines. J. Process Control 2009, 19, 1627–1639. [Google Scholar] [CrossRef]
- Schölkopf, B.; Platt, J.C.; Shawe-Taylor, J.; Smola, A.J.; Williamson, R.C. Estimating the Support of a High-Dimensional Distribution. Neural Comput. 2001, 13, 1443–1471. [Google Scholar] [CrossRef]
- Huang, G.; Chen, J.; Liu, L. One-Class SVM Model-Based Tunnel Personnel Safety Detection Technology. Appl. Sci. 2023, 13, 1734. [Google Scholar] [CrossRef]
- Breunig, M.M.; Kriegel, H.-P.; Ng, R.T.; Sander, J. LOF: Identifying Density-Based Local Outliers. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 15–18 May 2000; pp. 93–104. [Google Scholar] [CrossRef]
- Fan, Z.; Zi-xuan, X.; Ming-hu, W. Fault Diagnosis Method for Lithium-Ion Batteries in Electric Vehicles Using Generalized Dimensionless Indicator and Local Outlier Factor. J. Energy Storage 2022, 52, 104963. [Google Scholar] [CrossRef]
- Morales, C.; Giraldo, R.; Torres, M. Boxplot Fences in Proficiency Testing. Accredit. Qual. Assur. 2021, 26, 193–200. [Google Scholar] [CrossRef]



| Parameters | Values |
|---|---|
| Nominal capacity (Ah) | 114 |
| Cathode material | NCM |
| Anode material | Graphite |
| Charging cutoff voltage (V) | 4.2 |
| Discharging cutoff voltage (V) | 2.8 |
| Energy density (Wh/kg) | 227 |
| Length/Height/Thickness (mm) | 147.5/105.8/2.3 |
| The Diameter of the Metal Particle | 150 μm | 200 μm | 250 μm | 300 μm |
|---|---|---|---|---|
| Number of defect cells | 8 | 8 | 8 | 7 |
| Number of detected defect cells | 6 | 8 | 8 | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Kong, X.; Yuan, Y.; Hua, J.; Han, X.; Lu, L.; Li, Y.; Zhou, X.; Ouyang, M. A K-Value Dynamic Detection Method Based on Machine Learning for Lithium-Ion Battery Manufacturing. Batteries 2023, 9, 346. https://doi.org/10.3390/batteries9070346
Zhang H, Kong X, Yuan Y, Hua J, Han X, Lu L, Li Y, Zhou X, Ouyang M. A K-Value Dynamic Detection Method Based on Machine Learning for Lithium-Ion Battery Manufacturing. Batteries. 2023; 9(7):346. https://doi.org/10.3390/batteries9070346
Chicago/Turabian StyleZhang, Hekun, Xiangdong Kong, Yuebo Yuan, Jianfeng Hua, Xuebing Han, Languang Lu, Yihui Li, Xiaoyi Zhou, and Minggao Ouyang. 2023. "A K-Value Dynamic Detection Method Based on Machine Learning for Lithium-Ion Battery Manufacturing" Batteries 9, no. 7: 346. https://doi.org/10.3390/batteries9070346
APA StyleZhang, H., Kong, X., Yuan, Y., Hua, J., Han, X., Lu, L., Li, Y., Zhou, X., & Ouyang, M. (2023). A K-Value Dynamic Detection Method Based on Machine Learning for Lithium-Ion Battery Manufacturing. Batteries, 9(7), 346. https://doi.org/10.3390/batteries9070346







