High-Precision and Robust SOC Estimation of LiFePO4 Blade Batteries Based on the BPNN-EKF Algorithm
Abstract
1. Introduction
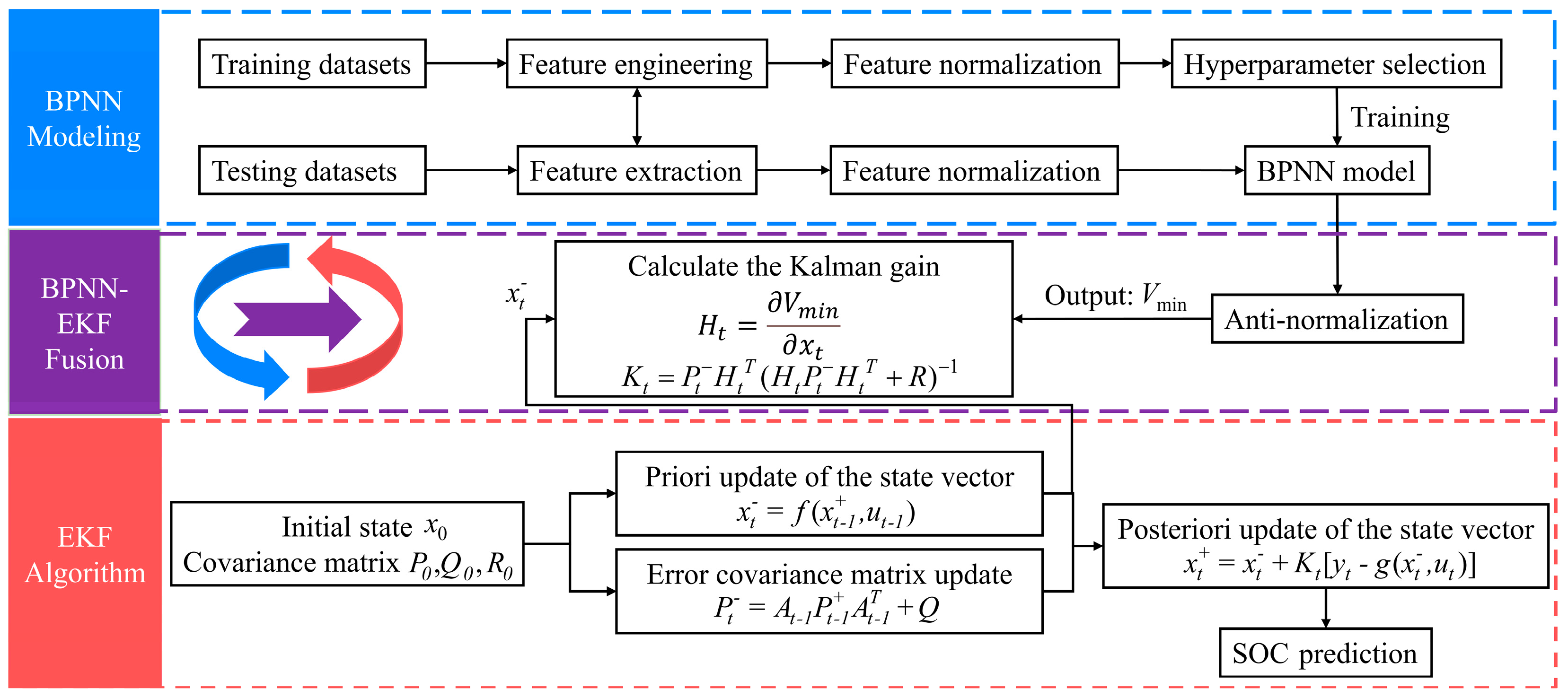
2. BPNN-EKF Algorithm
2.1. Training of the BPNN Model
2.1.1. Dataset Construction
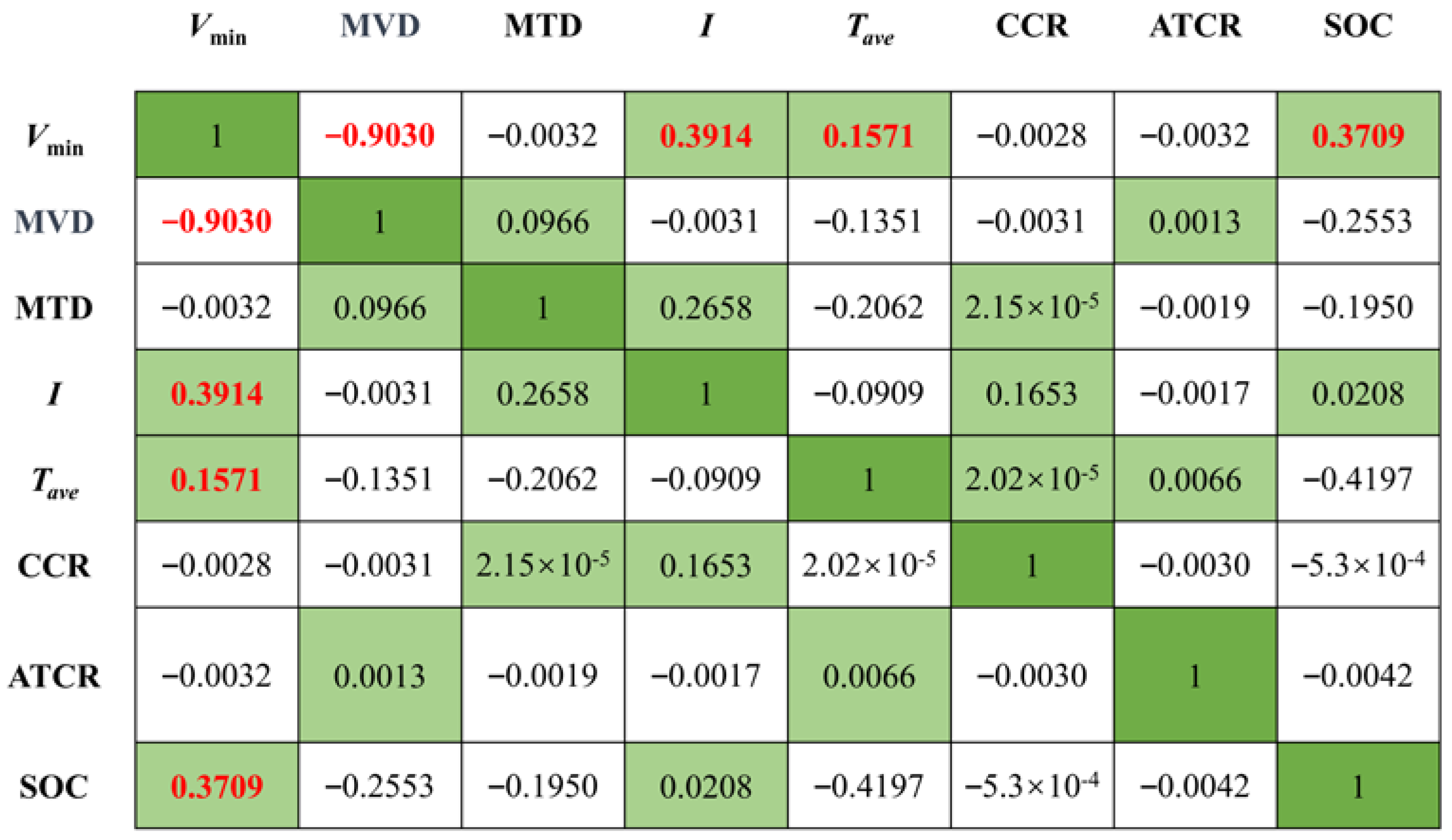
2.1.2. Feature Selection
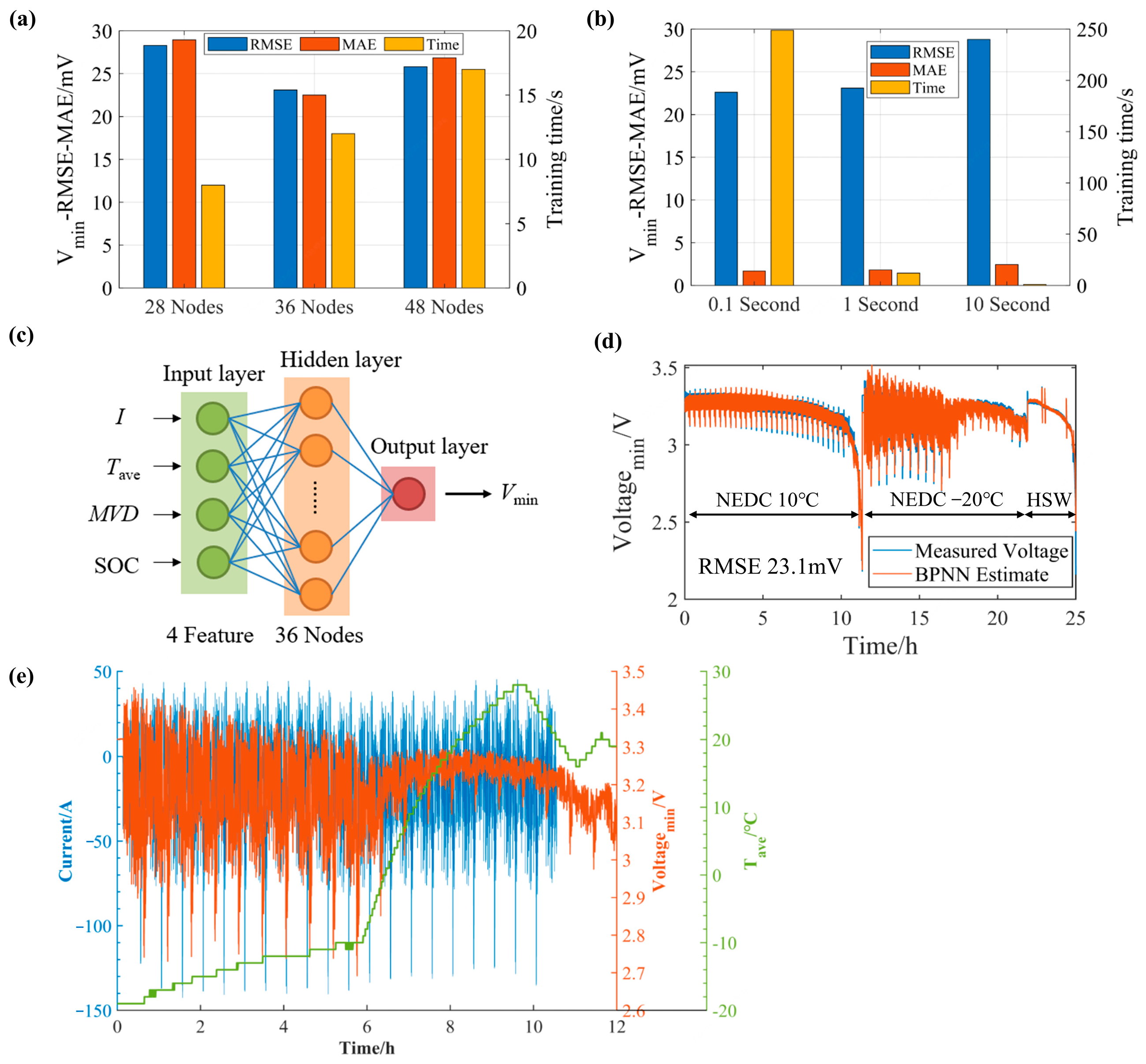
2.1.3. BPNN Training
2.2. BPNN-EKF Algorithm
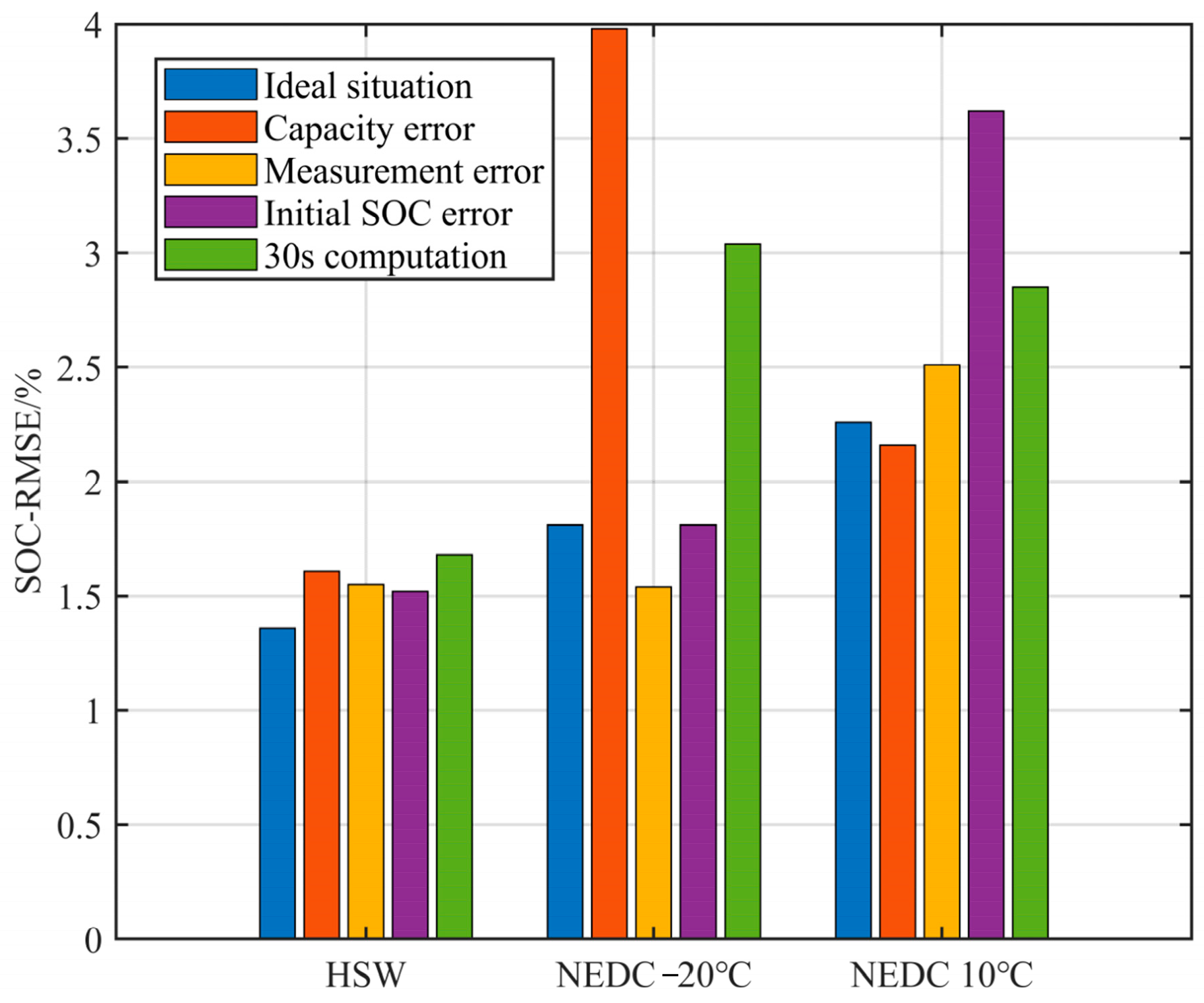
3. SOC Estimation Results
3.1. Ideal Situation
3.2. Algorithm Robustness Verification
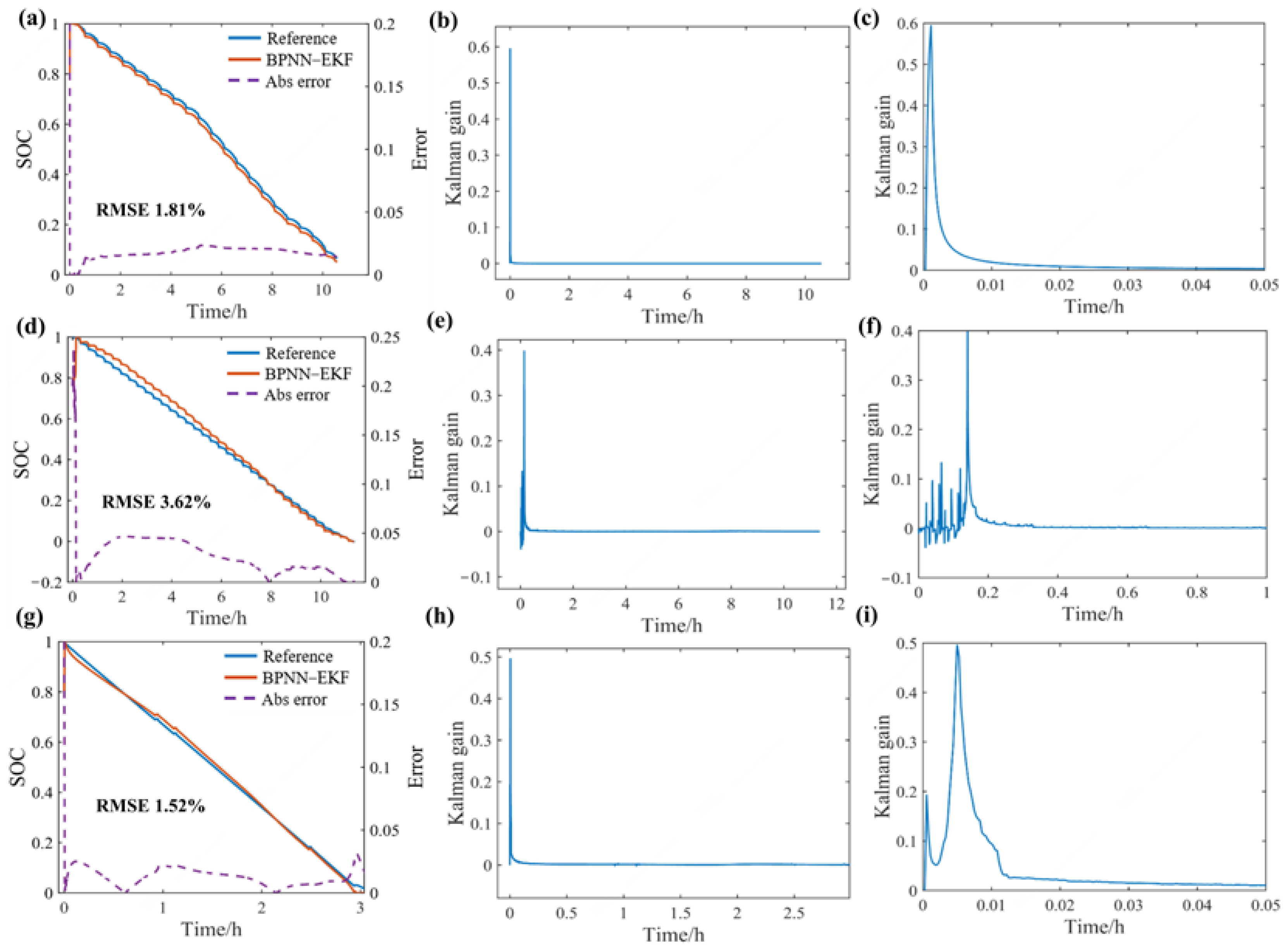
3.2.1. Capacity Error
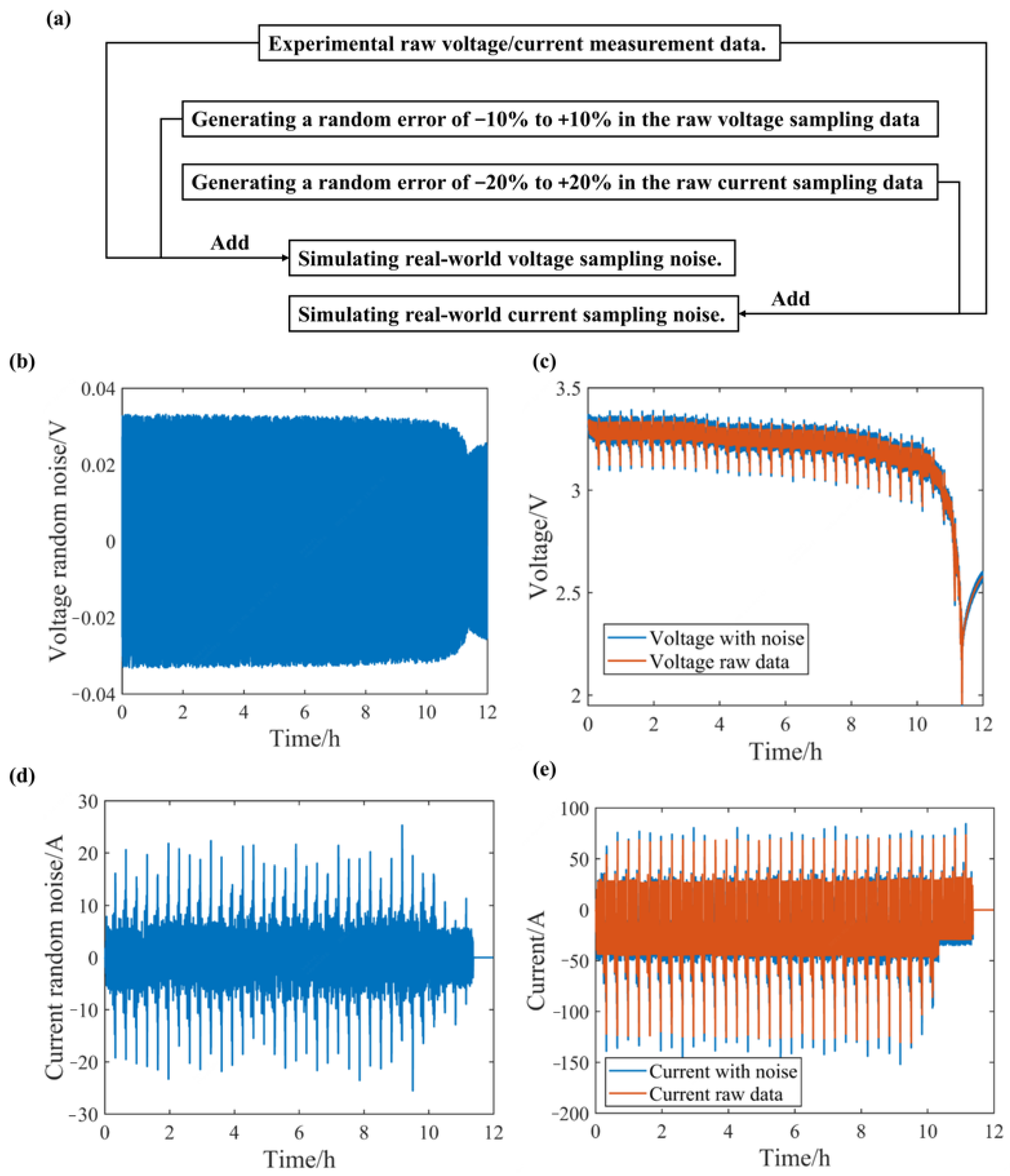
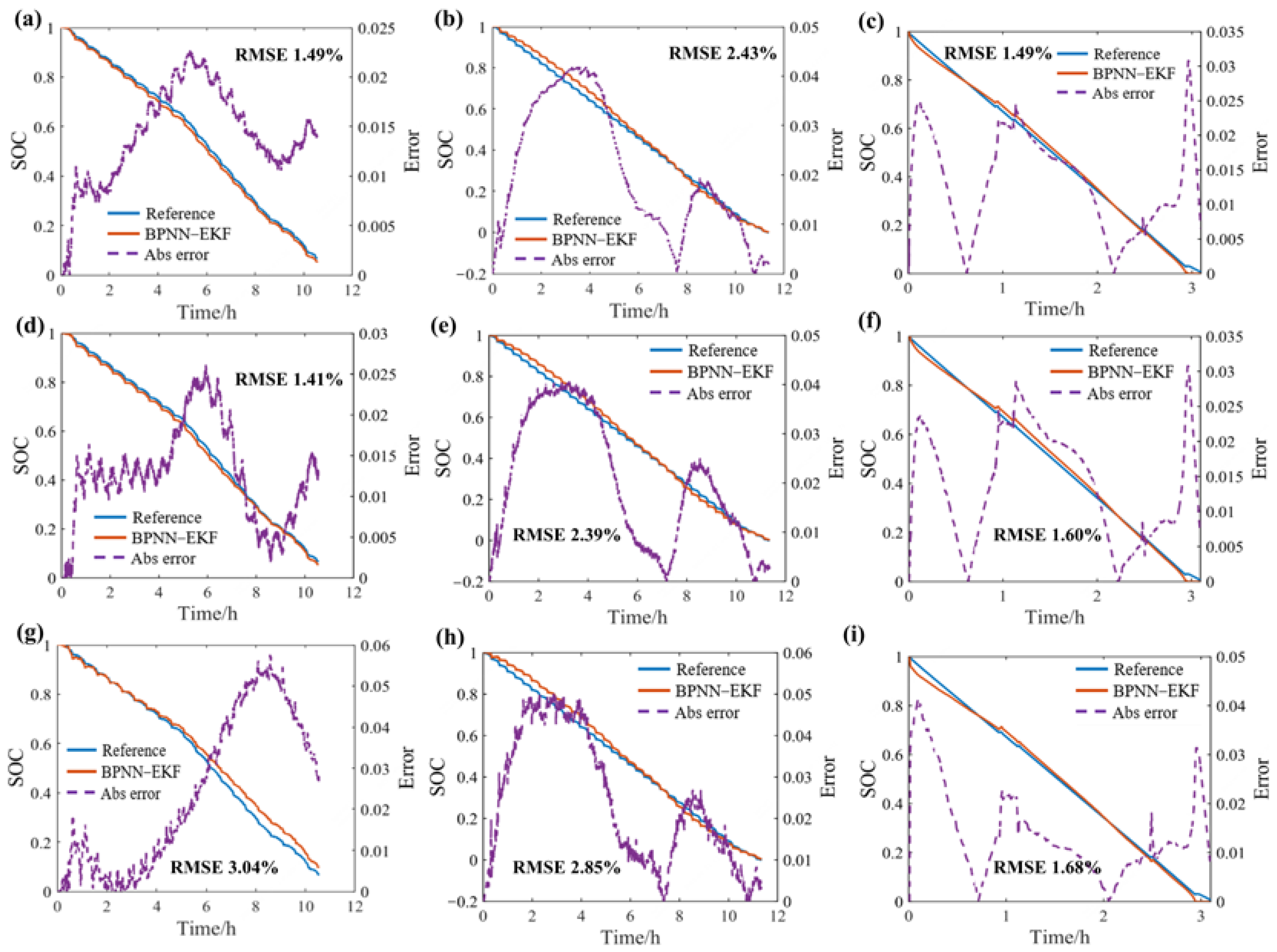
3.2.2. Current and Voltage Sampling Error
3.2.3. Initial SOC Error
3.2.4. Interval Calculation of SOC
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviation
| LiFePO4 | Lithium iron phosphate |
| BMS | Battery management system |
| SOC | State of charge |
| OCV | Open circuit voltage |
| ECMs | Equivalent circuit models |
| SP | Single particle |
| EKF | Extended Kalman filter |
| UKF | Unscented Kalman filter |
| CKF | Cubature Kalman filter |
| NN | Neural network |
| LSTM | Long short term memory |
| RNN | Recurrent neural network |
| BPNN | backpropagation neural network |
| NEDC | New European driving cycle |
| HSW | High-speed working |
| PCC | Pearson correlation coefficient |
| MVD | Maximum voltage difference |
| MTD | Maximum temperature difference |
| I | Current |
| Tave | Average temperature |
| CCR | Current change rate |
| ATCR | Average temperature change rate |
| RMSE | Root mean square error |
| MAE | Mean absolute error |
| NCM | Nickel-cobalt-manganese |
References
- Li, Y.; Wei, Y.; Zhu, F.; Du, J.; Zhao, Z.; Ouyang, M. The path enabling storage of renewable energy toward carbon neutralization in China. Etransportation 2023, 16, 100226. [Google Scholar] [CrossRef]
- Dixon, J.; Bukhsh, W.; Bell, K.; Brand, C. Vehicle to grid: Driver plug-in patterns, their impact on the cost and carbon of charging, and implications for system flexibility. Etransportation 2022, 13, 100180. [Google Scholar] [CrossRef]
- Hu, G.; Huang, P.; Bai, Z.; Wang, Q.; Qi, K. Comprehensively analysis the failure evolution and safety evaluation of automotive lithium ion battery. Etransportation 2021, 10, 100140. [Google Scholar] [CrossRef]
- Wang, X.; Wei, X.; Zhu, J.; Dai, H.; Zheng, Y.; Xu, X.; Chen, Q. A review of modeling, acquisition, and application of lithium-ion battery impedance for onboard battery management. Etransportation 2021, 7, 100093. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, C.; Jiang, J.; Zhang, L.; Zhang, W.; Wang, L.Y. Deduction of the transformation regulation on voltage curve for lithium-ion batteries and its application in parameters estimation. Etransportation 2022, 12, 100164. [Google Scholar] [CrossRef]
- Liu, W.; Hu, X.; Lin, X.; Yang, X.-G.; Song, Z.; Foley, A.M.; Couture, J. Toward high-accuracy and high-efficiency battery electrothermal modeling: A general approach to tackling modeling errors. Etransportation 2022, 14, 100195. [Google Scholar] [CrossRef]
- Mao, S.; Han, M.; Han, X.; Lu, L.; Feng, X.; Su, A.; Wang, D.; Chen, Z.; Lu, Y.; Ouyang, M. An Electrical–Thermal Coupling Model with Artificial Intelligence for State of Charge and Residual Available Energy Co-Estimation of LiFePO4 Battery System under Various Temperatures. Batteries 2022, 8, 140. [Google Scholar] [CrossRef]
- Song, Z.; Yang, X.-G.; Yang, N.; Delgado, F.P.; Hofmann, H.; Sun, J. A study of cell-to-cell variation of capacity in parallel-connected lithium-ion battery cells. Etransportation 2021, 7, 100091. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Z.; Zhang, J.; Su, L.; Ge, H. Accurate and efficient estimation of lithium-ion battery state of charge with alternate adaptive extended Kalman filter and ampere-hour counting methods. Energies 2019, 12, 757. [Google Scholar] [CrossRef]
- Xiong, X.; Wang, S.L.; Fernandez, C.; Yu, C.M.; Zou, C.Y.; Jiang, C. A novel practical state of charge estimation method: An adaptive improved ampere-hour method based on composite correction factor. Int. J. Energy Res. 2020, 44, 11385–11404. [Google Scholar] [CrossRef]
- Xiao, T.; Shi, X.; Zhou, B.; Wang, X. Comparative Study of EKF and UKF for SOC Estimation of Lithium-ion Batteries. In Proceedings of the 2019 IEEE Innovative Smart Grid Technologies-Asia (ISGT Asia), Chengdu, China, 21–24 May 2019; pp. 1570–1575. [Google Scholar]
- Yu, Q.; Huang, Y.; Tang, A.; Wang, C.; Shen, W. OCV-SOC-Temperature Relationship Construction and State of Charge Estimation for a Series–Parallel Lithium-Ion Battery Pack. IEEE Trans. Intell. Transp. Syst. 2023, 24, 6362–6371. [Google Scholar] [CrossRef]
- Fan, K.; Wan, Y.; Wang, Z.; Jiang, K. Time-efficient identification of lithium-ion battery temperature-dependent OCV-SOC curve using multi-output Gaussian process. Energy 2023, 268, 126724. [Google Scholar] [CrossRef]
- Dreyer, W.; Jamnik, J.; Guhlke, C.; Huth, R.; Moškon, J.; Gaberšček, M. The thermodynamic origin of hysteresis in insertion batteries. Nat. Mater. 2010, 9, 448–453. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. J. Electrochem. Soc. 1993, 140, 1526. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J. Simplification of physics-based electrochemical model for lithium ion battery on electric vehicle. Part I: Diffusion simplification and single particle model. J. Power Sources 2015, 278, 802–813. [Google Scholar] [CrossRef]
- Hu, X.; Feng, F.; Liu, K.; Zhang, L.; Xie, J.; Liu, B. State estimation for advanced battery management: Key challenges and future trends. Renew. Sustain. Energy Rev. 2019, 114, 109334. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Wang, L.; Han, J.; Liu, C.; Li, G. State of charge estimation of lithium-ion based on VFFRLS-noise adaptive CKF algorithm. Ind. Eng. Chem. Res. 2022, 61, 7489–7503. [Google Scholar] [CrossRef]
- Anton, J.C.A.; Nieto, P.J.G.; Gonzalo, E.G.; Pérez, J.C.V.; Vega, M.G.; Viejo, C.B. A new predictive model for the state-of-charge of a high-power lithium-ion cell based on a PSO-optimized multivariate adaptive regression spline approach. IEEE Trans. Veh. Technol. 2015, 65, 4197–4208. [Google Scholar] [CrossRef]
- Yao, J.; Ding, J.; Cheng, Y.; Feng, L. Sliding mode-based H-infinity filter for SOC estimation of lithium-ion batteries. Ionics 2021, 27, 5147–5157. [Google Scholar] [CrossRef]
- How, D.N.T.; Hannan, M.A.; Lipu, M.S.H.; Ker, P.J. State of charge estimation for lithium-ion batteries using model-based and data-driven methods: A review. IEEE Access 2019, 7, 136116–136136. [Google Scholar] [CrossRef]
- Fu, B.; Wang, W.; Li, Y.; Peng, Q. An improved neural network model for battery smarter state-of-charge estimation of energy-transportation system. Green Energy Intell. Transp. 2023, 2, 100067. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y.; Wu, J.; Cheng, W.; Zhu, Q. SOC estimation for lithium-ion battery using the LSTM-RNN with extended input and constrained output. Energy 2023, 262, 125375. [Google Scholar] [CrossRef]
- Ren, Z.; Du, C. A review of machine learning state-of-charge and state-of-health estimation algorithms for lithium-ion batteries. Energy Rep. 2023, 9, 2993–3021. [Google Scholar] [CrossRef]
- Wang, W.; Ma, B.; Hua, X.; Zou, B.; Zhang, L.; Yu, H.; Yang, K.; Yang, S.; Liu, X. End-Cloud Collaboration Approach for State-of-Charge Estimation in Lithium Batteries Using CNN-LSTM and UKF. Batteries 2023, 9, 114. [Google Scholar] [CrossRef]
- Kumar, C.; Zhu, R.; Buticchi, G.; Liserre, M. Sizing and SOC management of a smart-transformer-based energy storage system. IEEE Trans. Ind. Electron. 2017, 65, 6709–6718. [Google Scholar] [CrossRef]
- Hong, J.; Wang, Z.; Chen, W.; Wang, L.-Y.; Qu, C. Online joint-prediction of multi-forward-step battery SOC using LSTM neural networks and multiple linear regression for real-world electric vehicles. J. Energy Storage 2020, 30, 101459. [Google Scholar] [CrossRef]
- Jiao, M.; Wang, D.; Qiu, J. A GRU-RNN based momentum optimized algorithm for SOC estimation. J. Power Sources 2020, 459, 228051. [Google Scholar] [CrossRef]
- Lopes, E.D.R.; Soudre, M.M.; Llanos, C.H.; Ayala, H.V.H. Nonlinear receding-horizon filter approximation with neural networks for fast state of charge estimation of lithium-ion batteries. J. Energy Storage 2023, 68, 107677. [Google Scholar] [CrossRef]
- Srinivasan, V.; Newman, J. Existence of path-dependence in the LiFePO4 electrode. Electrochem. Solid-State Lett. 2006, 9, A110. [Google Scholar] [CrossRef]
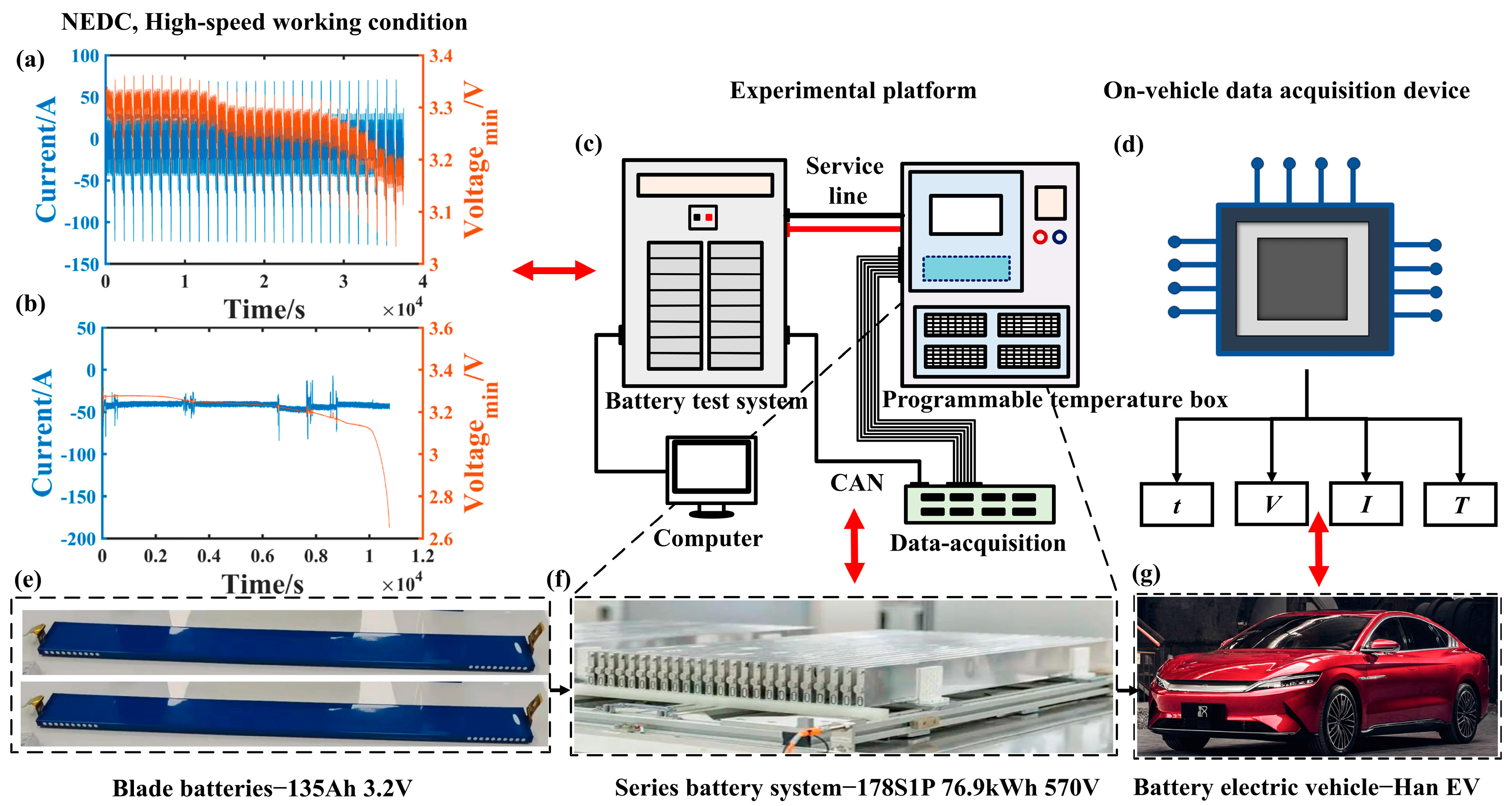
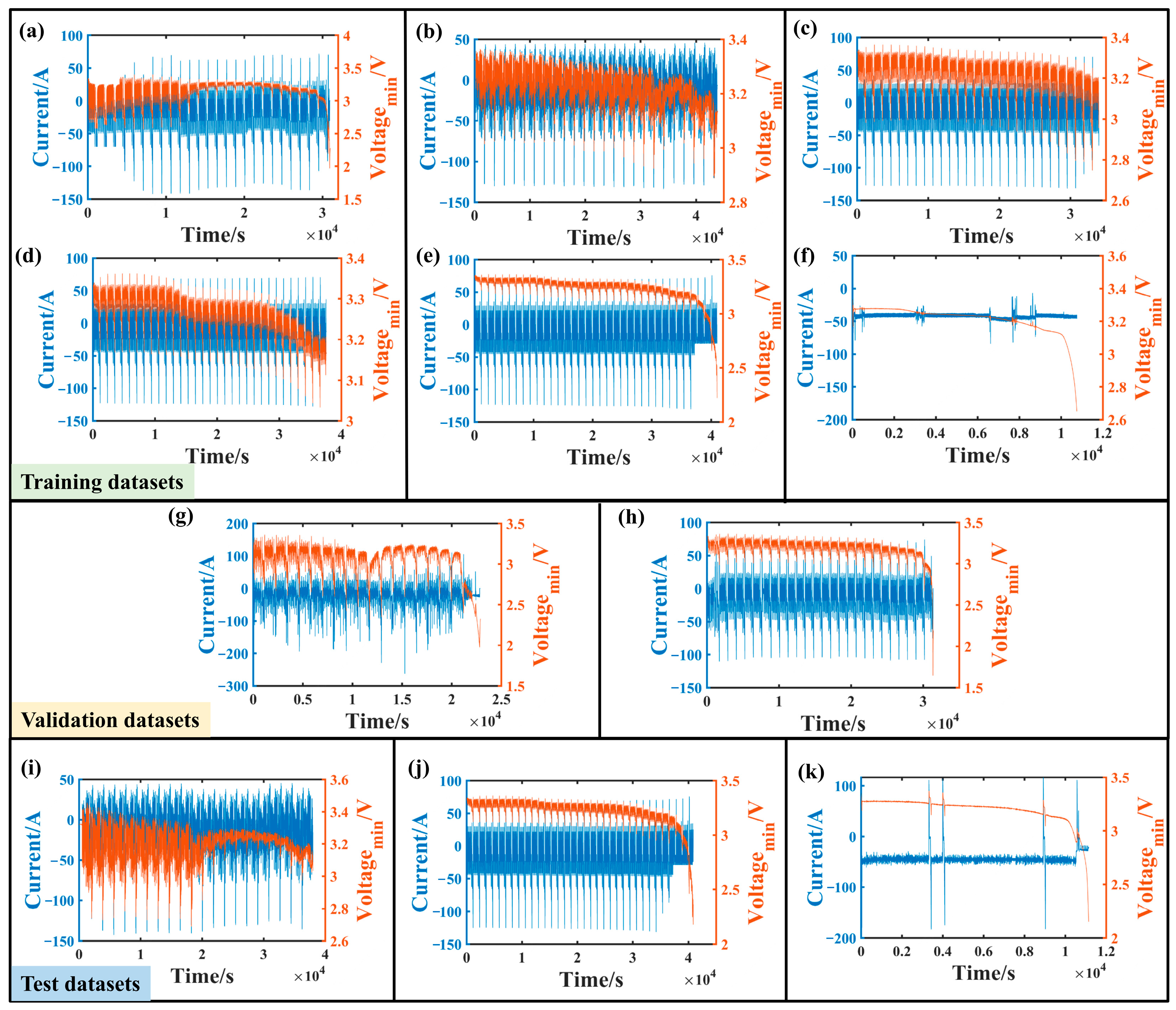

| Battery Cell | Specification |
|---|---|
| Cathode material | LiFePO4 |
| Anode material | Graphite |
| Nominal capacity | 135 Ah |
| Nominal voltage | 3.2 V |
| Charging cutoff voltage | 3.8 V |
| Discharging cutoff voltage | 2.0 V |
| Battery System | Specification |
|---|---|
| Configuration | 178S1P |
| Nominal voltage | 570 V |
| Nominal capacity | 135 Ah |
| Nominal energy capacity | 76.9 kWh |
| Feature Name | Description |
|---|---|
| Maximum voltage difference (MVD) | The difference between the highest and lowest voltage of individual cells within the series-connected blade battery system. |
| Maximum temperature difference (MTD) | The difference between the highest temperature sampling data and the lowest temperature sampling data within the series-connected blade battery pack. |
| Current (I) | The current flowing through the series-connected blade battery pack, with positive value indicating charging. |
| Average temperature (Tave) | The average value of temperature sampling data within the series-connected blade battery pack. |
| Current change rate (CCR) | The difference in current between two sampling intervals. |
| Average temperature change rate (ATCR) | The difference in average temperature between two sampling intervals. |
| State of charge (SOC) | The available capacity of the battery divided by its nominal capacity (135 Ah). |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Chen, S.; Lu, L.; Han, X.; Li, Y.; Chen, S.; Wang, H.; Lian, Y.; Ouyang, M. High-Precision and Robust SOC Estimation of LiFePO4 Blade Batteries Based on the BPNN-EKF Algorithm. Batteries 2023, 9, 333. https://doi.org/10.3390/batteries9060333
Zhang Z, Chen S, Lu L, Han X, Li Y, Chen S, Wang H, Lian Y, Ouyang M. High-Precision and Robust SOC Estimation of LiFePO4 Blade Batteries Based on the BPNN-EKF Algorithm. Batteries. 2023; 9(6):333. https://doi.org/10.3390/batteries9060333
Chicago/Turabian StyleZhang, Zhihang, Siliang Chen, Languang Lu, Xuebing Han, Yalun Li, Siqi Chen, Hewu Wang, Yubo Lian, and Minggao Ouyang. 2023. "High-Precision and Robust SOC Estimation of LiFePO4 Blade Batteries Based on the BPNN-EKF Algorithm" Batteries 9, no. 6: 333. https://doi.org/10.3390/batteries9060333
APA StyleZhang, Z., Chen, S., Lu, L., Han, X., Li, Y., Chen, S., Wang, H., Lian, Y., & Ouyang, M. (2023). High-Precision and Robust SOC Estimation of LiFePO4 Blade Batteries Based on the BPNN-EKF Algorithm. Batteries, 9(6), 333. https://doi.org/10.3390/batteries9060333








