AdaBoost.Rt-LSTM Based Joint SOC and SOH Estimation Method for Retired Batteries

Abstract

Achieving accurate retired battery state of health (SOH) and state of charge (SOC) estimation is a safe prerequisite for securing the battery secondary utilization and thus effectively improving the energy utilization efficiency. The data-driven approach is efficient and accurate, and does not rely on accurate battery models, which is a hot direction in battery state estimation research. However, the huge number of retired batteries and obvious consistency differences bring bottleneck problems such as long learning time and low model updating efficiency to the traditional data-driven algorithm. In view of this, this paper proposes an integrated learning algorithm based on AdaBoost. Rt-LSTM to realize the joint estimation of SOC and SOH of retired lithium batteries, which relies on the LSTM neural network model and completes the correlation adaption in the spatio-temporal dimension of the whole life cycle sample data. The LSTM model is used as the base learner to construct the AdaBoost. Rt-LSTM strong learning model. The LSTM weak predictor is combined with weights to form a strong predictor, which greatly solves the problem of low accuracy of state estimation due to the large number and variability of retired batteries. Simulation and experimental comparison show that the integrated algorithm proposed in this paper is suitable for improving the SOC and SOH prediction accuracy and the generalization performance of the model.

1. Introduction

Due to the widespread popularity of electric vehicles in recent years, the amount of retired power batteries will also increase rapidly [1]. Among the retired power batteries, many still have high residual capacity (70% to 80% of the rated capacity of the battery), and these batteries can potentially be used in scenarios such as energy storage in power grids and backup in communication base stations to realize the secondary utilization of power batteries [2,3]. However, since the state of power batteries is usually unknown when they are retired, it is necessary to accurately estimate the State of Health (SOH) of the batteries before the batteries are used in the secondary process, so that the batteries with a greater degree of aging can be eliminated in time and the batteries with different aging states can enter the step-up environment in the corresponding stage. At the same time, the accurate estimation of State of Charge (SOC) in the process of step-up utilization can improve the utilization efficiency of retired batteries.

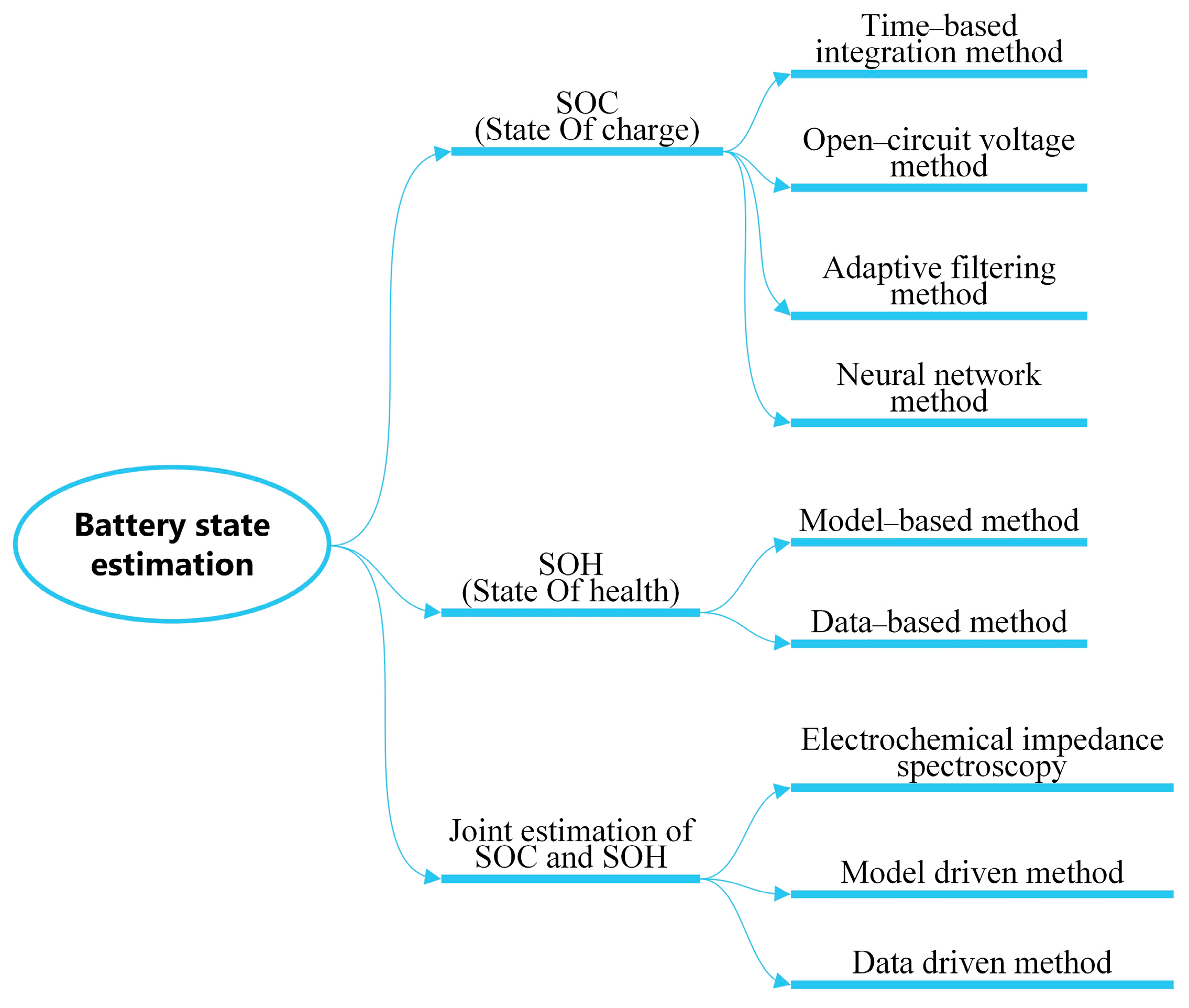
The existing SOC estimation methods mainly include time integration method [4], open circuit voltage method [5], adaptive filtering method [6] and neural network method [7]. Among them, the time-integral method discretely sums the current flowing through the battery, and obtains the SOC value through simple division [8]. The open-circuit voltage method is to measure the open-circuit voltage of the battery and obtain the charge state according to the correspondence between the open-circuit voltage and the charge state [9]. Adaptive filtering method is an optimal estimation of battery system in the sense of minimum variance, and is a model-based SOC estimation method [10]. The neural network algorithm does not need to deeply understand the electrochemical mechanism inside the battery, nor does it need to establish additional complex physical and chemical models. Instead, it only needs to extract features by using the physical quantities measured during the battery charging and discharging process, and then use the features to train the model and establish a mapping model between the battery data features and SOC [11].

SOH estimation algorithms mainly contain model-based methods [12] and data-based methods [13]. The research of model-based methods focuses on identifying and analyzing the main aging mechanisms of lithium-ion batteries and estimating the SOH values of batteries based on their correlation with model parameters. The commonly used models are generally classified into two main categories:physical models and equivalent circuit models. Usually, the parameters of the model are obtained by analyzing the performance of the battery, and then the SOH of the battery under different operating conditions can be obtained by analyzing the parameters of the model [14]; the data-driven algorithm can learn the health condition and external characteristics of the battery autonomously and determine the nonlinear relationship between them, without understanding the working mechanism of the battery or establishing a clear battery The data-driven algorithm can estimate the battery health status by relying only on the aging data of the battery [15]. Data-driven algorithms are increasingly used in battery state estimation due to their superiority.

The above algorithms are all single estimates of the battery SOC or SOH. However, in actual battery use, the effect of SOC estimation will be affected by the different degree of battery aging, while inaccurate SOC estimation will also affect SOH correction. And this situation becomes more obvious in the estimation of retired batteries because the aging degree of retired batteries varies with the actual operating environment they are in during their service. A fast prediction method for SOC and SOH of battery based on electrochemical impedance spectroscopy (EIS) was proposed in literature [16], but this method achieved SOH prediction by comparing the difference of SOC with the discharge of constant current in a short time. In literature [17], based on the DP-Thevenin model and least square parameter estimation method, the DP-Thevenin model was updated with time-varying parameters, and the improved extended Kalman filter algorithm was combined to complete the online collaborative prediction of SoC SOH for lithium ion batteries. 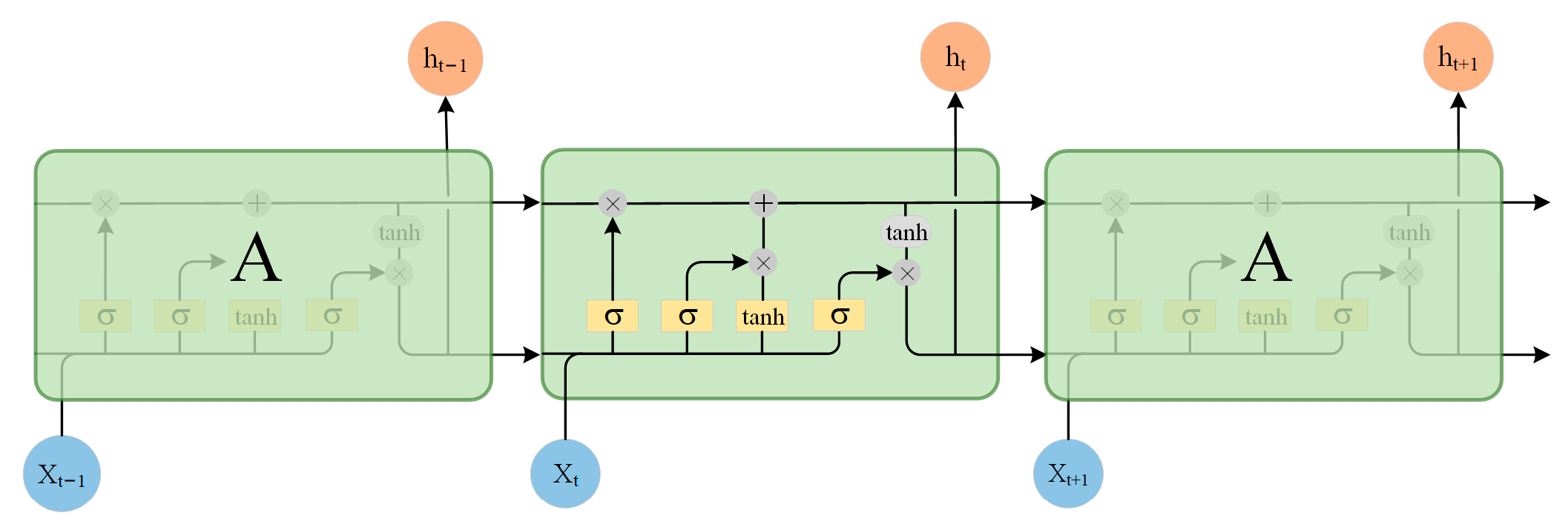However, the above methods have high requirements on the accuracy of the battery equivalent circuit model, so literature [18] adopts a data-driven method to jointly predict the SOC and SOH of lithium batteries by constructing two recurrent neural networks (RNN). However, RNN can only store part of the sequence, which is not suitable for dealing with long sequence dependent problems, such as the estimation of the health state of lithium batteries. It is easy to produce large errors. Therefore, LSTM-RNN method was adopted in literature [19] to predict battery remaining service life (RUL). Literature [20] uses LSTM neural network combined with empirical mode decomposition to reduce the influence of capacity self-recovery effect and improve the prediction accuracy. Reference [21] proposes a variant LSTM structure that includes a constant error turntable to reduce estimation errors. Literature [22] analyzed the coupling relationship between battery SOC and SOH, and co-predicted SOC and SOH through LSTM deep learning network. Figure 1 shows a breakdown of the battery state estimates.

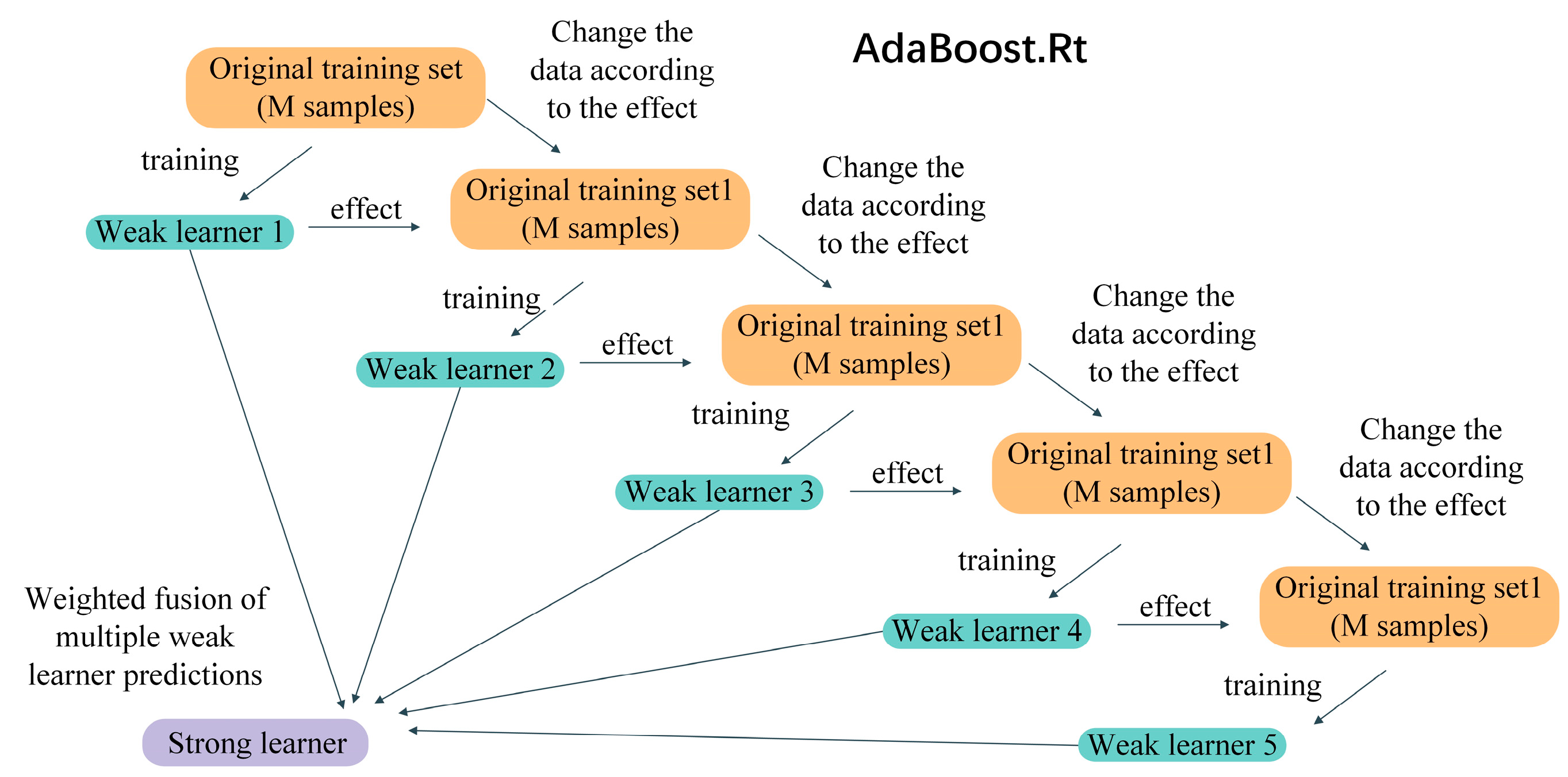
The above literature shows that data-driven algorithmic models have considerable potential and application prospects in joint battery estimation, but the large number of retired battery samples makes the previous data-driven algorithms face problems such as long learning time and low model update efficiency.AdaBoost, as one of the most typical Boosting algorithms, breaks the distribution law of the original samples by resampling. AdaBoost, as a typical Boosting algorithm, breaks the distribution of the original samples by resampling, so that the learning machine focuses more on the hard-to-learn samples, thus making Boosting an integrated algorithm with real practical value. The AdaBoost. RT algorithm, as one of the AdaBoost algorithm family, improves the AdaBoost algorithm by introducing a threshold constant, which transforms the regression problem into a simple binary classification problem, and combined with a specific weak learning machine, it can effectively achieve the prediction of time series, which greatly enhances the practicality of the AdaBoost algorithm and improves the learning efficiency of the algorithm as well as the model accuracy of the estimation [23].

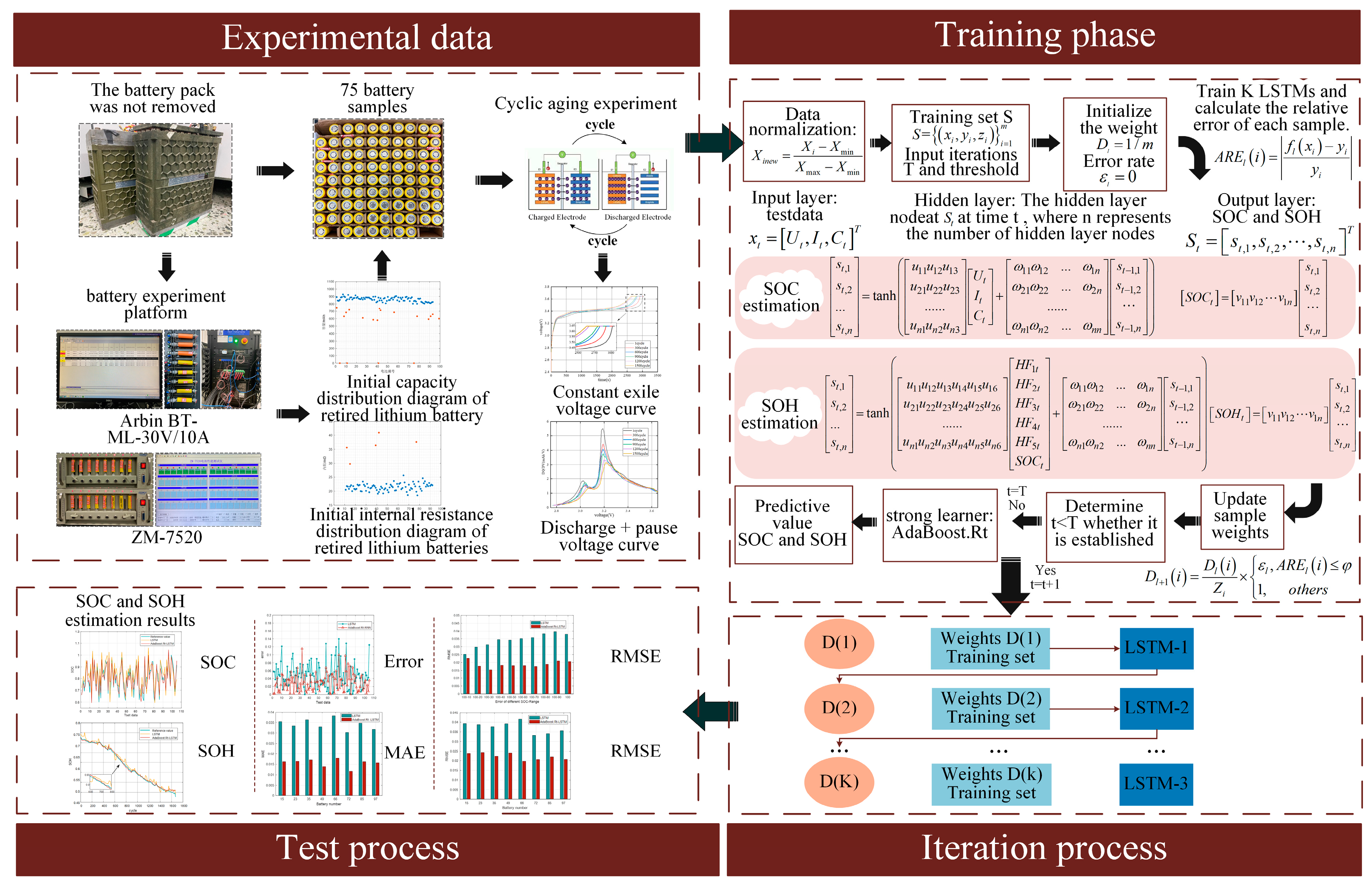
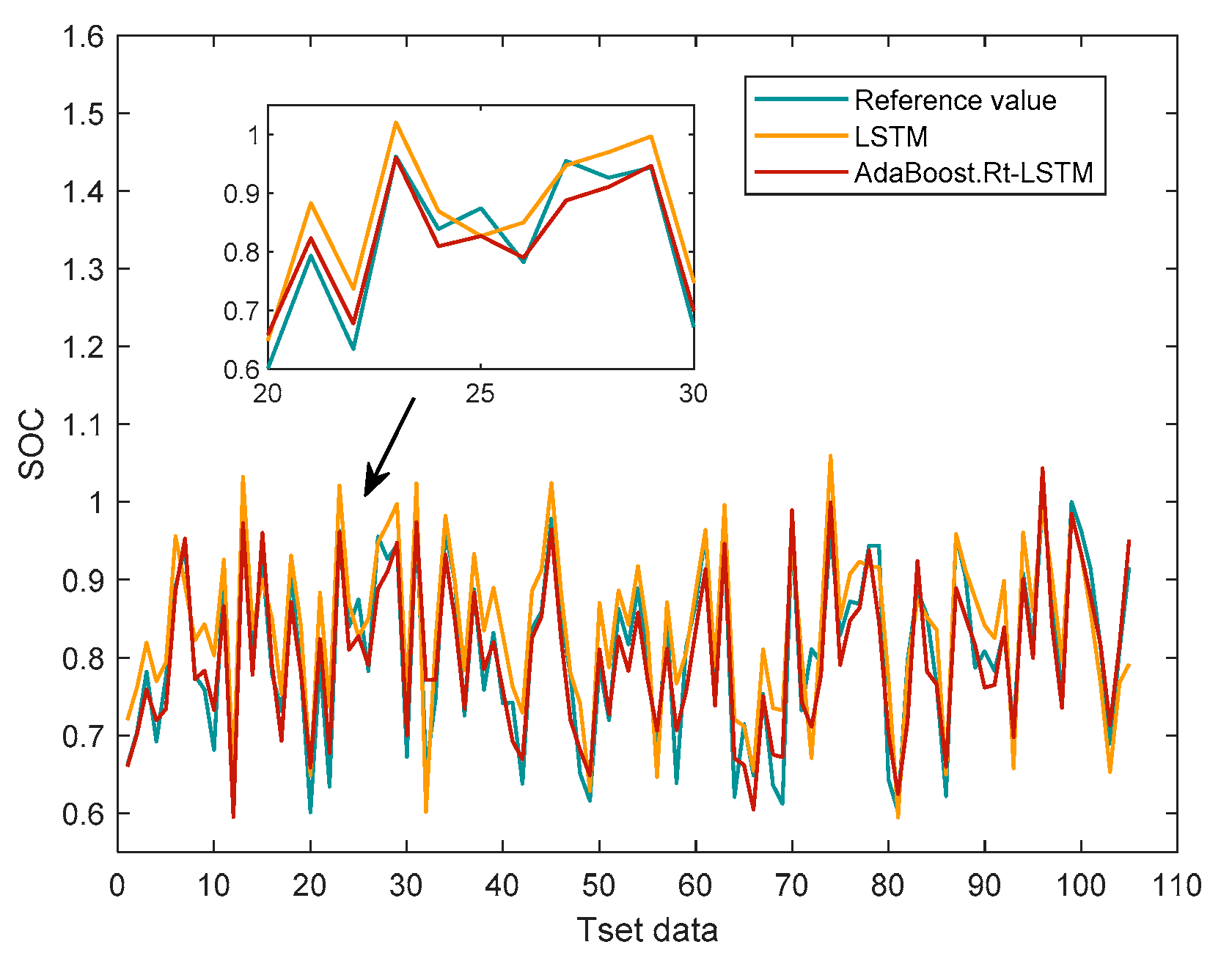
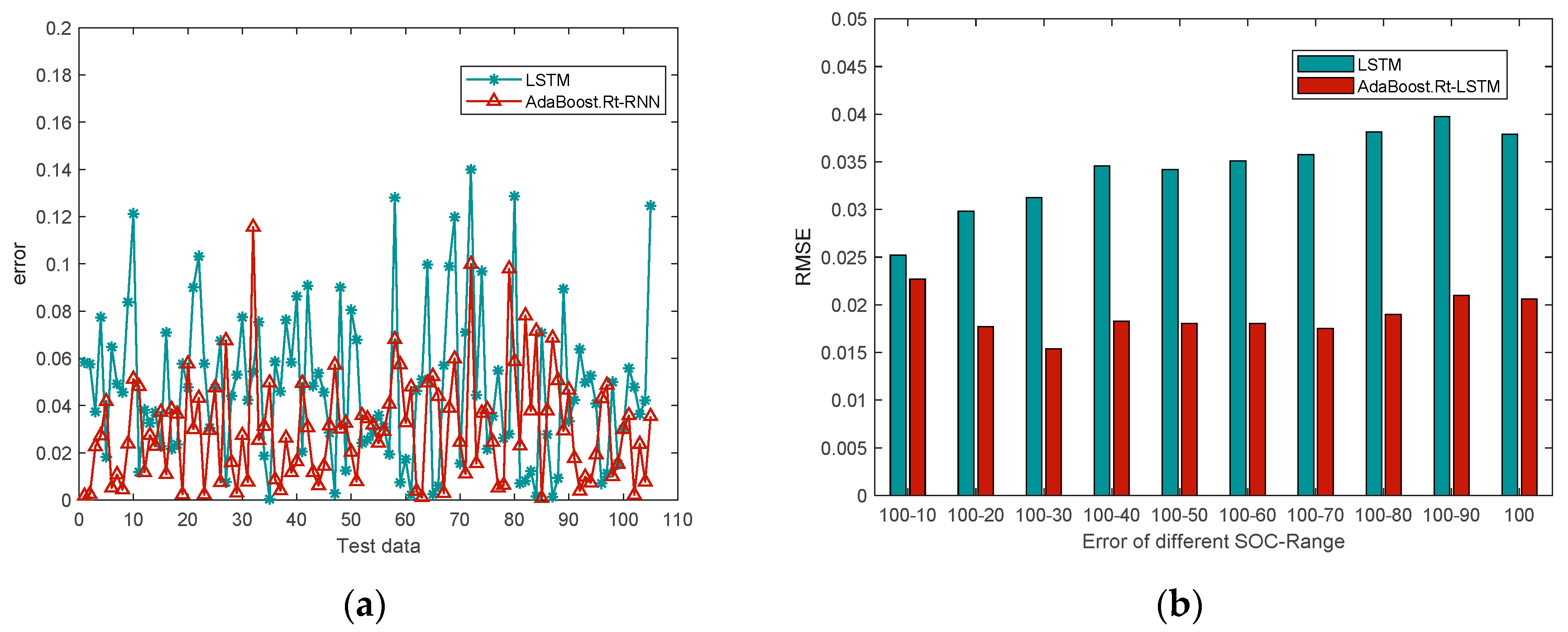
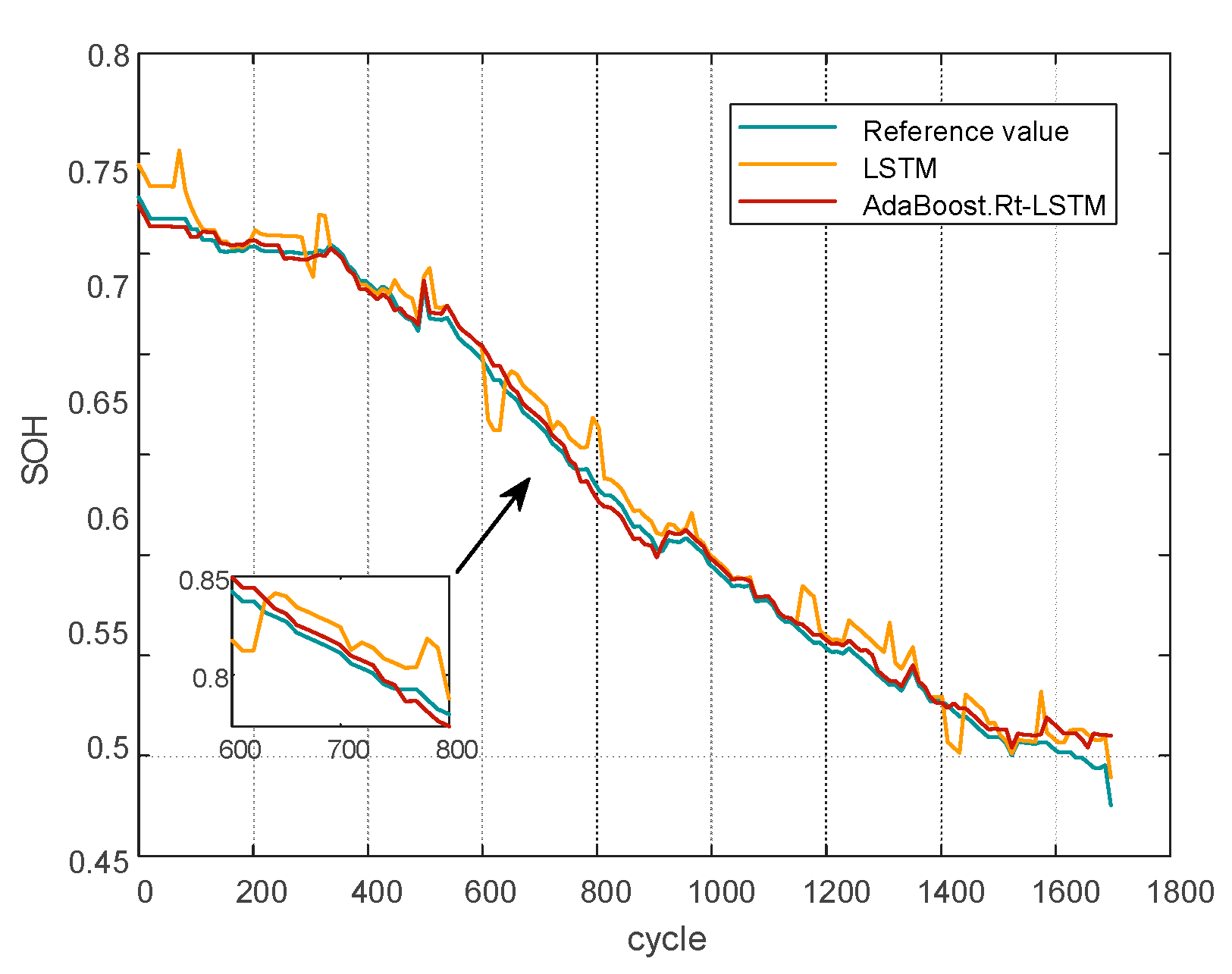
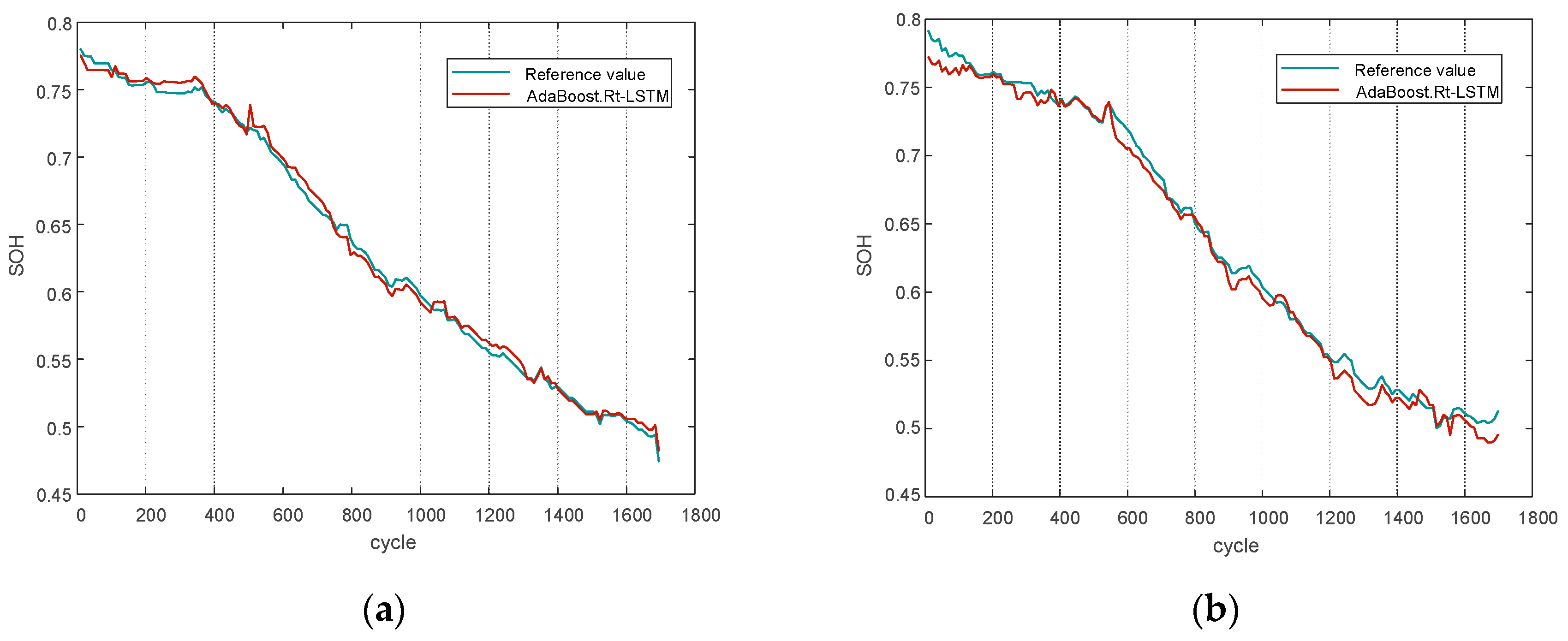
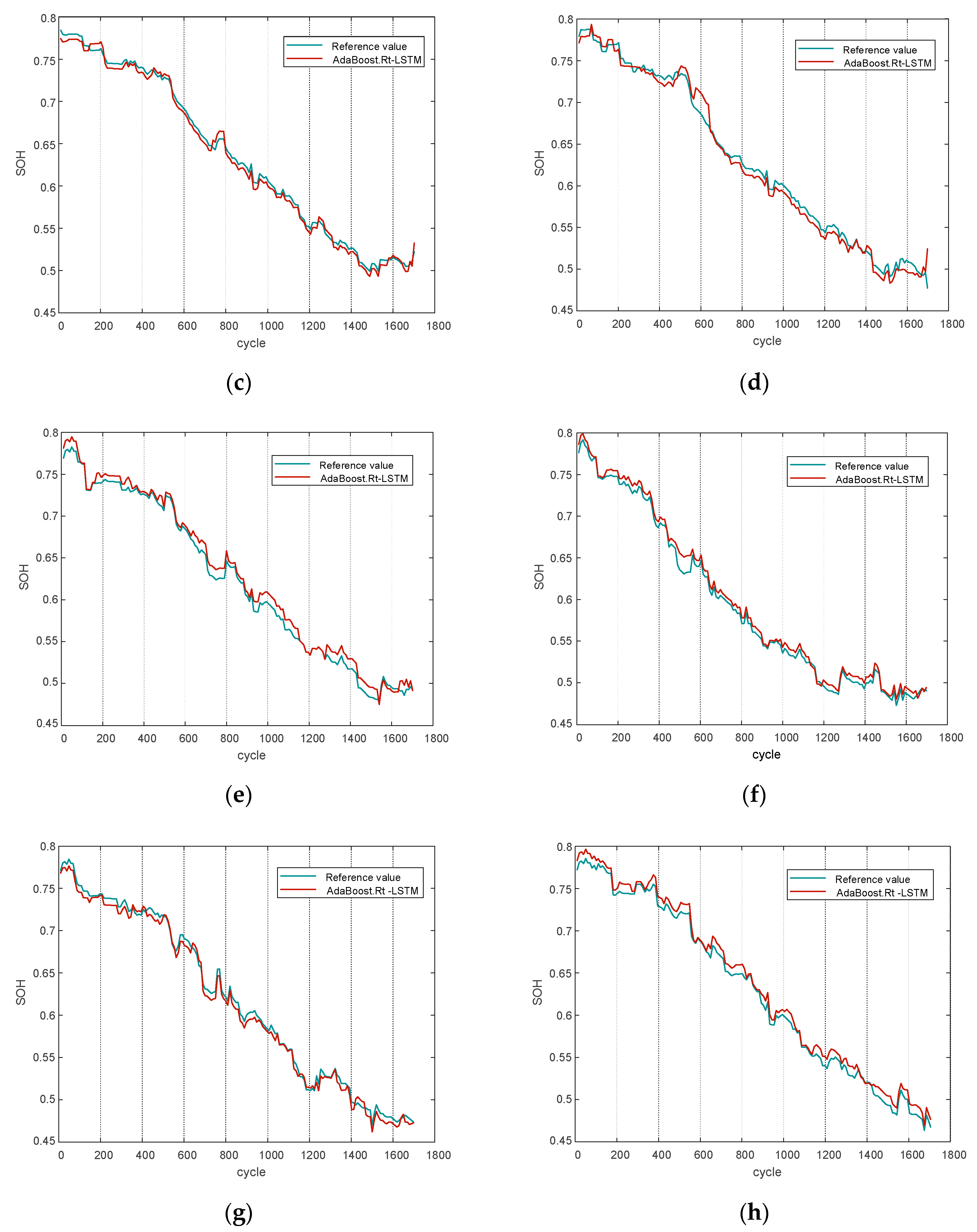
In summary, the data-driven battery estimation algorithm is simple and reliable and does not depend on the establishment of an accurate battery model, but most of the existing data-driven algorithms rely on the life cycle experimental data of a few batteries in the laboratory to estimate the SOH of the remaining battery cells, while in practice, the retired batteries are widely sourced and large in number, and the SOH estimation model established based on the laboratory environment has high accuracy but poor generalization The SOH estimation model based on the laboratory environment has high accuracy but poor generalization capability. Therefore, in this paper, an improved AdaBoost.Rt-LSTM battery SOC and SOH joint estimation method is proposed in a data-driven framework. The same batch of retired lithium battery packs are selected, and after screening and performance testing, 75 lithium iron phosphate batteries with good appearance and can be reused are finally obtained, five health characteristics of retired lithium batteries are extracted, and the correlation between health characteristics and capacity is analyzed using Pearson correlation coefficient, and the AdaBoost.Rt-LSTM model is used to jointly realize the retired lithium battery charge state and health state estimation. The long and short-term memory neural network used in this method not only has the advantages of recurrent neural network, but also can solve the problems of gradient disappearance and gradient explosion. The AdaBoost.Rt integration algorithm, which combines the LSTM weak predictors with weights to form a strong predictor, greatly solves the problem of low accuracy of state estimation due to the large number of retired batteries and large variability. Simulation and experimental comparison show that the proposed AdaBoost.Rt-LSTM algorithm can jointly estimate the SOC and SOH of Li-ion batteries, ensuring the prediction accuracy and generalization performance of the model.

2. Principle of AdaBoost.Rt-LSTM Algorithm

2.1. LSTM (Long Short Term Memory) Algorithm Principle

Long Short Term Memory (LSTM) is a temporal recurrent neural network that effectively solves the gradient disappearance and gradient explosion problems of recurrent neural networks (RNNs) when processing long time series data by invoking a “gating” device. Figure 2 shows the principle structure of LSTM algorithm.

The order of information transmission in LSTM is that it first passes through the input gate to decide the input of information, then the forgetting gate selects whether to forget the information of the neuron, and finally it passes through the output gate to determine whether to output the information at this moment.

(1)

Input Gate

Input gate for updating cell status. When the switch is turned on, the information is input through the sigmoid activation function and multiplied (×) with the information through the double tangent activation function (tanh) to input a new ${\overline{C}}_t$ into the “memory”. The input gate calculation formula is shown in Equations (1) and (2).

$$i_t=\sigma (W_i[h_{t-1},X_t]+b_i)$$

(1)

$${\overline{C}}_t=\tanh (W_c[h_{t-1},X_t]+b_c)$$

(2)

where $i_t$ is the input gate at the moment $t$, $\sigma$ is the sigmoid activation function, ${\overline{C}}_t$ is the cell state, $h_{t-1}$ is the information of the hidden layer at the previous moment $t-1$, and $X_t$ is the input information at the moment $t$.

(2)

Forgetting Gate

At each moment, the value in the “memory” undergoes a process of forgetting or not, which is controlled by the forgetting gate. By reading the information from the hidden layer $h_{t-1}$ and the input $x_t$ of the previous moment, the information forgotten at that moment is determined and a value between 0–1 is output to the neuron, which indicates the degree of forgetting of the information. The forgetting gate calculation formula is shown in Equation (3).

$$f_t=\sigma (W_f[h_{t-1},X_t]+b_f)$$

(3)

where: $f_t$ is the forgetting gate at the moment $t$.

(3)

Output Gate

The output gate determines whether there is information from the “memory” output at each moment. The input information of the gate is passed through the sigmoid activation function and multiplied (×) with the “memory” updated by the tanh activation function to obtain the output value, as shown in Equations (4) and (5).

$$o_t=\sigma (W_o[h_{t-1},X_t]+b_o)$$

(4)

$$h_t=o_t\ast \tanh (C_t)$$

(5)

where: $o_t$ is the output gate at the time of $t$.

In summary, the sigmoid layer determines the output cell state, and the tanh function processes the cell state, compresses it between [−1, 1] and multiplies it with the output of the sigmoid gate to finally output the desired fraction.

2.2. AdaBoost.Rt Integration Algorithm Principle

In the training process of machine learning algorithm models, usually we can only get multiple models with different preferences, and integration learning is the combination of these weak learners to seek a better and more stable strong learning model. The Adaboost integration algorithm is an adaptive and iterative algorithm based on the idea of boost. The main idea of the algorithm is to continuously recombine and adjust the training samples according to the prediction effect of the base learner, so that the samples with poor prediction effect of the previous base learner receive more attention in the following, and then retrain the next base learner according to the recombined samples. The iteration is not stopped until the pre-specified maximum number of iterations or error rate is reached or below. The specific implementation is shown in Figure 3.

The computational procedure of the AdaBoost.Rt algorithm is as follows:

• Given a training set $m$ of $S$ samples, determine the number of iterations $T$ and the threshold $\phi$.

  $$S=\left\{\left(x_1,y_1\right),\left(x_2,y_2\right),\cdots ,\left(x_m,y_m\right)\right\}$$

  (6)
• Initialize the sample weights $D_t(i)=1/m$, where $i$ is the number of training sets and $t$ is the number of current iterations; error rate ${\epsilon }_t=0$.
• According to the weight distribution $D_t$, the original sample set is sampled and the weak learning machine is invoked for training to build the regression model $f_t(x)\to y$. Accordingly, the relative error of each sample is calculated.

  $$AR{E}_t\left(i\right)=\left|\frac{f_t\left(x_i\right)-y_i}{y_i}\right|$$

  (7)
• Calculate the error rate ${\epsilon }_t={\displaystyle \sum _{i}D\left(i\right)},i:AR{E}_t\left(i\right)>\phi$.
• Update the sample weights as follows.

  $$D_{t+1}\left(i\right)=\frac{D_t\left(i\right)}{Z_t}\times \left\{\begin{array}{l}{\epsilon }_t,AR{E}_t\left(i\right)\le \phi \\ 1,\mathrm{Others}\end{array}\right.$$

  (8)

  where: $Z_t$ is a normalization factor to ensure that the updated $D_{t+1}$ is a distribution.
• Determine whether the stopping condition is satisfied: if $t<T$, make $t=t+1$, and go to step 3, otherwise output the final strong learner.

3. Joint Estimation of SOC and SOH for Lithium Batteries Based on Adaboost.Rt-LSTM Model

3.1. Joint Estimation Model Construction Based on LSTM Algorithm

In order to improve the accuracy of the SOC and SOH estimation results of Li-ion batteries, this paper adopts an integrated learning model with LSTM as the weak predictor to jointly estimate the SOC and SOH of Li-ion batteries. The specific joint estimation process is shown below.

• Initialize the LSTM model with the relevant parameters $k$ (Hidden state dimensions), $L_1$ ($L_1$ regularization), $L_2$ ($L_2$ regularization) and $I_r$ (Learning rate).
• Set the maximum number of iterations $T_{\max }$ and the prediction error accuracy ${\epsilon }_t$.
• The voltage $U_t$, current $I_t$ and capacity $C_t$ at the moment $t$ are input to the LSTM model and the charge state $SO{C}_t$ at the moment $t$ is estimated as the output.

  $$X_t^1=[U_t,I_t,C_t]$$

  (9)

  $$Y_t^1=[SO{C}_t]$$

  (10)
• 5 health features and $SO{C}_t$ are input to the LSTM model to estimate the health state $SO{H}_t$ at the moment $t$, and finally the joint estimation result $Y_t$ of SOC and SOH at the moment $t$ is obtained.

  $$X_t^2=[H{F}_1,H{F}_2,H{F}_3,H{F}_4,H{F}_5,SO{C}_t]$$

  (11)

  $$Y_t^2=[SO{H}_t]$$

  (12)

  $$Y_t=[SO{C}_t,SO{H}_t]$$

  (13)
• Determine whether the termination iteration condition is reached. If the number of iterations reaches the preset value $T_{\max }$, stop the iteration and finally output the SOC and SOH estimation results of the lithium battery.

3.2. Adaboost.Rt Reinforcement Learning Modeling Approach

In this paper, Adaboost.Rt-LSTM model is used to estimate the SOC and SOH of lithium batteries. Firstly, the experimental data of decommissioned batteries are preprocessed, and unqualified battery data are proposed. Then, the preprocessed battery data set is input into the model, and the weak learner is trained according to the initial weight, and the learning error rate of the learner is calculated. At the same time, the weights of all training samples are updated and iterated until all weak learners are obtained. Finally, all the weak learners are combined into one strong learner to achieve SOC estimation of lithium batteries. The SOC estimation results and five health characteristics at the same time are used as input parameters to jointly estimate the SOH of lithium batteries, and finally achieve the joint estimation of lithium battery SOC and SOH. The specific estimation process is as follows.

• Initialize the relevant parameters of $K$ LSTM model.
• Adaboost.Rt-LSTM model training. Input sample training set $X_t^1$ and $X_t^2$. Initialize the initial weights of the sample training set, train the weak predictor LSTM1 and calculate the relative error, update the weights of the training samples according to the error results, and iterate continuously until the weights $D$ of the $K$ weak predictor LSTM are determined. combine with the independent evaluation dataset $P$, aggregate the $K$ LSTM models by AdaBoost.Rt, and finally constitute the AdaBoost.Rt-LSTM model.
• Input the voltage $U_t$, current $I_t$ and capacity $C_t$ at the current moment into the model and estimate the state of charge at that moment as the output.
• 5 health characteristics and $SO{C}_t$ are jointly used as input parameters of health state to estimate the health state of current moment $SO{H}_t$.
• The final results of SOC and SOH prediction for Li-ion batteries are obtained.

Figure 4 shows the overall structure of the proposed Adaboost.Rt-LSTM lithium battery state estimation method in this paper.

4. Simulation Test and Result Analysis

4.1. Experimental Data Pre-Processing

4.1.1. Experimental Protocol Design

In this paper, the same batch of retired lithium battery packs were selected, and after disassembly, grinding, appearance screening and performance testing, 100 lithium iron phosphate batteries with good appearance and able to be reused were finally obtained, and their model number was LR18650EH. The samples of retired lithium batteries used in the experiments are shown in Figure 5. The specific parameters and specifications of the lithium batteries are shown in

Table 1. Experimental battery specific parameters and specifications information.

Sequence	Parameters	Specification
1	Weight	40 ± 2.0 g
2	Rated capacity	1100 mAh
3	Rated voltage	3.65 V
4	Rated current	1 C
5	Operating voltage range	2.5~3.65 V
6	Operating temperature range	−20~60 °C

.

The experimental data in this paper come from: Arbin BT-ML-30 V/10 A power tester produced by Arbin USA and ZM-7520 battery performance tester produced by Harbin Zimu. Figure 6 shows the experimental test platform of retired lithium battery.

In this paper, the capacity and ohmic internal resistance of retired lithium batteries are tested by Hybrid Pulse Power Charasteristic (HPPC) condition test with Arbin BT-ML-30 V/10 A power tester. This method requires simple experimental equipment, simple operation, short experiment time and accurate measurement results. The internal resistance of the battery under different SOC can be obtained by establishing the relationship between the response voltage and current during discharge, resting and charging. The specific experimental steps are shown in

Table 2. Steps of HPPC experiments on retired lithium batteries.

Steps	Rules	End Conditions
1	1 C constant current charging	Voltage up to 3.65 V
2	3.65 V constant voltage charging	Current up to 0.05 C
3	Resting	60 min
4	1 C constant current discharge	10% decrease in SOC
5	Resting	60 min
6	Cycle (step 1–5)	Voltage up to 2.5 V

.

According to the actual test data of 100 batteries retired from the same batch obtained from the experiment for capacity and internal resistance testing, the capacity and internal resistance distribution of single cells are shown in Figure 7. The batteries numbered 4, 11, 41, and 75 have been severely damaged and cannot be charged; the batteries numbered 1, 8, 10, 13, 26, 36, 40, 42, 43, 56, 78, 89, 91, 93, 95, and 99 have lower capacities and differ significantly from other retired batteries; the batteries numbered 2, 5, 29, 32, and 67 have ohmic internal resistance significantly higher than the average. Therefore, these batteries will not be used as the research object of this paper.

After eliminating the unqualified batteries, the remaining 75 batteries were subjected to cyclic aging experiments. The aging test of retired lithium batteries is conducted by ZM-7520 battery performance tester with two 16-channel channels, and the experimental steps are shown in

Table 3. Aging experiment steps for retired lithium batteries.

Steps	Rules	End Conditions
1	1 C constant current charging	Voltage up to 3.65 V
2	3.65 V constant voltage charging	Current up to 0.05 C
3	Resting	20 min
4	1 C constant current discharge	Voltage up to 2.5 V
5	Resting	20 min
6	Cycle (step 1–5)	1700 times

.

4.1.2. Eigenvalue Extraction

In this paper, the health characteristics of retired lithium batteries are selected based on the important parameters affecting the health status of lithium batteries obtained from the analysis of the basic structure and characteristics of lithium batteries in the previous paper, and the mapping relationship between the health status of retired lithium batteries and experimental data is established on this basis. The charge/discharge aging experiment of Li-ion battery can obtain the relevant parameters of its whole life cycle, such as voltage, current, internal resistance and cycle capacity at each moment. These parameters can directly predict the SOH of Li-ion battery, but the large amount of data increases its computational effort and cannot be estimated online. In addition, the capacity increment curve as the health characteristic of Li-ion battery is more effective in predicting its SOH, but the original IC curve data of Li-ion battery needs to be filtered before estimation. In summary, in this paper, five health features (HF), denoted as HF₁~HF₅, are selected based on the charge/discharge voltage curves of retired lithium batteries to improve the computational rate of the SOH prediction process of retired lithium batteries with more efficient and concise features.

Figure 8 shows the voltage curves of Li-ion battery under different SOH with constant current discharge and pause. As can be seen from the figure, there is a large gap between the discharge voltage curves of Li-ion battery under different SOH. Therefore, in this paper, five health characteristics are selected to estimate the retired Li-ion battery SOH: equal time charging voltage (HF1:charge_v), constant current charging time percentage (HF2:cc/(cc+cv)), mean value of capacity increment curve (HF3:mean_IC), maximum value of capacity increment curve (HF₄:IC_max), and variance of capacity increment curve (HF₅:area_IC). SOH values of Li-ion batteries, randomly selected sample batteries are No. 9, No. 15, No. 23, No. 35, No. 49, No. 66, No. 72, No. 85 and No. 97, and No. 9 battery is used as the validation set to test the accuracy of the AdaBoost.Rt-LSTM model.

In order to verify that the five selected health characteristics can effectively reflect the health status of retired lithium batteries, the Pearson Correlation Coefficient is used to reflect the correlation degree between health characteristics and SOH.

The Pearson correlation coefficient method can respond to the degree of linear correlation between two variables. For the two data sets $X=\{X_1,X_2,\cdots ,X_n\}$ and $Y=\{Y_1,Y_2,\cdots ,Y_n\}$, the correlation coefficient is calculated as shown below.

$${\rho }_{XY}=\frac{Cov(X,Y)}{{\sigma }_X{\sigma }_Y}=\frac{n{\displaystyle \sum _{i=1}^n{X}_i{Y}_i-}{\displaystyle \sum _{i=1}^n{X}_i}{\displaystyle \sum _{i=1}^n{Y}_i}}{\sqrt{n{{\displaystyle \sum _{i=1}^n{X}_i{}^2-\left({\displaystyle \sum _{i=1}^n{X}_i}\right)}}^2}\sqrt{n{{\displaystyle \sum _{i=1}^n{Y}_i{}^2-\left({\displaystyle \sum _{i=1}^n{Y}_i}\right)}}^2}}$$

(14)

where: ${\sigma }_X$ and ${\sigma }_Y$ are the standard deviations of $X$ and $Y$ respectively, which are calculated as shown in Equation (15).

$${\sigma }_X=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{(X_i-E(X))}^2}}$$

(15)

The closer the absolute value of $\rho$ is to 1, the stronger the correlation between its health characteristics and lithium SOH; conversely, the closer the absolute value of $\rho$ is to 0, the less correlated they are.

From the results in

Table 4. Correlation between SOH and health characteristics of sample cells.

Categories	HF1	HF2	HF3	HF4	HF5
Pearson	−0.95	0.93	0.9	0.92	0.96

, it can be seen that the absolute values of Pearson correlation coefficients between the five health features and SOH of the retired lithium battery of sample No. 9 are all greater than 0.9. This result indicates that there is a strong linear and monotonic correlation between the five selected health features and SOH of the lithium battery. Therefore, in this paper, the above five health features are selected as the input of Adaboost.Rt-LSTM model to improve its training efficiency and prediction accuracy.

Finally, the minimum-maximum (min-max) normalization method is used to normalize the data to speed up the solution and improve the prediction accuracy, and the results fall in interval $[0,1]$, as shown in Equation (16).

$$X_{inew}=\frac{X_i-X_{\min }}{X_{\max }-X_{\min }}$$

(16)

4.2. Experimental Results and Comparative Analysis

For the experimentally obtained dataset, half of the entire lithium battery dataset is used as the training set and the remaining half is used as the test set to verify the accuracy of the model. Following the experimental steps described in Section 3.2, the experimental data from the retired Li-ion battery No. 9 described above is fed into the single LSTM model and the Ada-boost.Rt-LSTM model so as to perform the estimation of SOC and SOH.

It can be seen from Figure 9 that the SOC estimates of the AdaBoost.Rt-LSTM model are closer to the reference value than the estimates of the single LSTM model. The absolute error values of the two models for the lithium battery SOC estimation are shown in (a) of Figure 10. It can be seen that the AdaBoost.Rt-LSTM algorithm model has less error in the prediction of Li-ion battery SOC compared to the single LSTM estimation algorithm. In order to more accurately describe the dispersion of the Li-ion battery SOC error, the RMSE values predicted by the two models under different SOCs were compared, and the comparison results are shown in Figure 10b. It can be seen from the figure that the RMSE values of the AdaBoost.Rt-LSTM model are smaller than those of the single LSTM model regardless of the SOC state of the battery, which reflects the generalizability of the proposed algorithm to a certain extent. A comparison of the SOC estimation error results of retired lithium batteries with different algorithms is shown in

Table 5. Comparison of SOC estimation error results of different algorithms.

Model	MAE	RMSE
LSTM	0.0306	0.0374
RNN [24]	0.0302	0.0378
XGBoost [24]	0.0235	0.0304
SMO [25]	0.01536	0.02663
AdaBoost.Rt-LSTM	0.0154	0.0215

. From the specific values in Table 5, it can be seen that the MAE values of the SOC estimation results of the single LSTM model and the Adaboost.Rt-LSTM model are 3.02% and 1.58%, respectively. Their RMSE values are 3.78% and 2.05%, respectively. And compared with the rest of the battery SOC estimation methods such as RNN(Recurrent Neural Network) [24], XGBoost(Extreme Gradient Boosting) [24], SMO(Sliding Mode Observer) [25]. Adaboost.Rt-LSTM model estimation is improved. In summary, the results show that the estimation results of the lithium battery SOC prediction model based on AdaBoost.Rt-LSTM are closer to the real value and have a strong feasibility compared to the single LSTM prediction model.

For the SOH prediction results, it can be seen from Figure 11 that the SOH prediction results of the Adaboost.Rt- LSTM model are closer to the real values compared to the single LSTM model. A comparison of the SOH estimation error results for decommissioned lithium batteries with different algorithms is shown in

Table 6. Comparison of SOH estimation error results of different algorithms.

Model	MAE	RMSE
LSTM	0.0315	0.0357
SMO [25]	0.0267	0.0523
FNN [26]	0.0253	0.0316
CNN [26]	0.239	0.0332
AdaBoost.Rt-LSTM	0.0148	0.0202

. From the specific values in Table 6, it can be seen that the MAE values of the SOH estimation results of the single LSTM model and the Adaboost.Rt-LSTM model are 3.17% and 1.47%, respectively. Their RMSE values are 3.52% and 2.09% respectively. We also compare the results of SMO (Sliding Mode Observer) [25], FNN(Feedforward Neural Network) [26], CNN(Convolutional Neural Network) [26]. The algorithms described in this paper have improved in prediction accuracy. The above results show that the Adaboost.Rt integrated model based on LSTM optimization has higher prediction accuracy and is more feasible.

The following AdaBoost.Rt-LSTM model algorithm is used to estimate the health status of the above randomly selected remaining eight retired lithium batteries. Due to the differences caused by the changes in the aging process of the eight batteries due to prolonged charging and discharging, their SOH change patterns also differ slightly as shown in Figure 12 for the simulation results.

As can be seen from Figure 12, the prediction results of the health status of all eight sample retired lithium batteries are good, which verifies the feasibility and accuracy of the Adaboost.Rt-LSTM model proposed in this paper, and the values of its MAE and RMSE are shown in

Table 7. SOH estimation error results for retired lithium battery samples.

Battery Number	Model	MAE	RMSE
No. 15	LSTM	0.0354	0.0393
	AdaBoost.Rt-LSTM	0.0162	0.0237
No. 23	LSTM	0.0334	0.0387
	AdaBoost.Rt-LSTM	0.0164	0.0244
No. 35	LSTM	0.0363	0.0376
	AdaBoost.Rt-LSTM	0.0171	0.0223
No. 49	LSTM	0.0329	0.0392
	AdaBoost.Rt-LSTM	0.0139	0.0241
No. 66	LSTM	0.0382	0.0416
	AdaBoost.Rt-LSTM	0.0179	0.0197
No. 72	LSTM	0.0302	0.0332
	AdaBoost.Rt-LSTM	0.0117	0.0206
No. 85	LSTM	0.0347	0.0341
	AdaBoost.Rt-LSTM	0.0162	0.0219
No. 97	LSTM	0.0317	0.0356
	AdaBoost.Rt-LSTM	0.0157	0.0207

. Among all the prediction results, the prediction effect of battery No. 72 is relatively good, with the MAE and RMSE values of 1.17% and 2.06%, respectively. the prediction effect of battery No. 23 is relatively poor, with the MAE and RMSE values of 1.64% and 2.44%, respectively, but it also meets the accuracy requirement of binning. Therefore, the SOH results of 75 retired lithium batteries estimated by the AdaBoost.Rt -LSTM model in this paper all achieve more satisfactory results. The comparison of the SOH estimation error results of the sample retired lithium batteries is shown in Figure 13.

5. Conclusions

Accurate estimation of lithium battery status can effectively reduce the risk and loss caused by failure when decommissioned batteries are reused. Therefore, based on the improved Adaboost.Rt-LSTM state prediction model, the SOC and SOH of decommissioned batteries are jointly estimated in this paper, which provides strong data support for the subsequent reuse of decommissioned batteries. Aiming at the problems of narrow application range, weak genetic ability and low accuracy of traditional neural network battery estimation method, this paper adopts LSTM recurrent neural network model algorithm and calls “gating” device to effectively solve the problem of gradient disappearance and gradient explosion caused by recurrent neural network when processing long time series data. Rt integrated learning algorithm was used to combine several LSTM weak learners into strong learners according to their weights, and the prediction model established significantly improved the estimation accuracy of SOC and SOH of decommissioned batteries. According to the analysis of simulation and experimental results, the average absolute error of SOC and SOH prediction results of Adaboost.Rt-LSTM is 1.54% and 1.48%, and the root-mean-square error is 2.15% and 2.02%, respectively. This shows that the Adaboost.Rt-LSTM algorithm model still has high estimation accuracy and good convergence when there is a large amount of decommissioned battery data, which verifies the feasibility of the Adaboost.Rt-LSTM model in the state estimation of decommissioned lithium batteries.