Transfer Learning Based on Transferability Measures for State of Health Prediction of Lithium-Ion Batteries

Abstract

Lithium-ion (Li-ion) batteries are considered to be one of the ideal energy sources for automotive and electronic products due to their size, high levels of charge, higher energy density, and low maintenance. When Li-ion batteries are used in harsh environments or subjected to poor charging habits, etc., their degradation will be accelerated. Thus, online state of health (SOH) estimation becomes a hot research topic. In this study, normalized capacity is considered as SOH for the estimation and calculation of remaining useful lifetime (RUL). A multi-step look-ahead forecast-based deep learning model is proposed to obtain SOH estimates. A total of six batteries, including three as source datasets and three as target datasets, are used to validate the deep learning model with a transfer learning approach. Transferability measures are used to identify source and target domains by accounting for cell-to-cell differences in datasets. With regard to the SOH estimation, the root mean square errors (RMSEs) of the three target batteries are 0.0070, 0.0085, and 0.0082, respectively. Concerning RUL prediction performance, the relative errors of the three target batteries are obtained as 2.82%, 1.70%, and 0.98%, respectively. In addition, all 95% prediction intervals of RUL on the three target batteries include the end-of-life (EOL) value (=0.8). These results indicate that our method can be applied to battery SOH estimation and RUL prediction.

1. Introduction

Recently, there have been major breakthroughs in battery energy technology. Investment in technologies that support mass vehicle electrification is expected to increase in adoption as the government sets a deadline to end sales of fossil fuel-powered vehicles. A total of 10.5 million new battery and plug-in hybrid vehicle deliveries took place in 2022, a 55% increase compared to 2021 [1]. Lithium-ion (Li-ion) batteries have high energy density, low self-discharge rate, and low maintenance that are superior to other energy storage systems such as NiMH batteries, lead-acid batteries, and supercapacitors [2]. Li-ion batteries are used as energy storage devices in electric vehicles (EVs). Therefore, Li-ion batteries need to be managed properly.

Estimating the state of health (SOH), state of charge (SOC), and remaining useful life (RUL) of a battery is useful information in a smart battery management system (BMS) [3]. In an RUL prediction study, the decision to replace a degraded battery can be made before the battery reaches its end-of-life (EOL) or 80% of the initial capacity [4]. Both SOH estimation and RUL prediction are getting increasing attention because accurate prediction provides useful information for proper battery health management. Three main categories, model-based methods, data-driven methods, and hybrid methods, are widely used to predict the RUL of Li-ion batteries [5,6]. A model-based method, such as one based on a physical degradation model, is applied to describe the internal electrochemical reactions of Li-ion batteries. However, modeling this type of method under different workloads and operating conditions is a challenging task. Whereas data-driven methods or hybrid methods have been shown in many studies in the literature to provide better RUL predictions.

While data-driven methods are more popular than model-based methods, the need for large amounts of data and specialized skills to guarantee accurate predictive performance is a drawback. Transfer learning is able to train a predictive model using a source dataset and transfer the learned parameters to a predictive model on a target dataset [7,8].

Previous studies on SOH estimation and RUL prediction mostly use offline methods. Regarding those offline methods, model training, and estimation verification are performed on known samples, and then the model is used for multi-step prediction. These predicted values cannot reflect the whole capacity degradation. Therefore, accurate prediction is a challenging task for the wide application of intelligent BMS. Transfer learning (TL) can reuse a pre-trained model for another dataset, reducing the time and data required to train a different predictive model. Although transfer learning has been applied to Li-ion battery RUL prediction, most of the previously published papers did not discuss the training starting point or choose a random starting point for model training [9]. A deep learning model such as the bidirectional long short-term memory and attention mechanism (Bi-LSTM-AM) model is successfully achieved online Li-ion RUL prediction [10]. Therefore, we propose a method based on Bi-LSTM-AM and a transfer learning technique called Bi-LSTM-AM-TR, expecting accurate SOH prediction.

The specific objectives of this article are: (1) to show how transfer learning can be applied to alleviate data shortage by transferring pre-trained model weights from source data to target data, and (2) to apply a sliding window approach to obtain multi-step-ahead predictions of SOH. Section 2 reviews related research on SOH and RUL prediction and transfer learning. Section 3 introduces our proposed method, including the sliding window method, transferability measure, BiLSTM-AM model, and evaluation metrics. The results of Bi-LSTM-AM-TR with other LSTM-based models for Li-ion batteries are presented in Section 4. Finally, in conclusion, we state that the prediction results of our proposed Bi-LSTM-AM-TR method are suitable for online RUL prediction.

2. Related Works

In this study, the SOH is given by:

$${\mathrm{S}\mathrm{O}\mathrm{H}}_{\mathrm{i}}=\frac{{\mathrm{Q}}_{\mathrm{i}}}{{\mathrm{Q}}_{\mathrm{r}}}\times 100\%$$

(1)

where SOH_i is a normalized discharge capacity at the ith cycle, ${\mathrm{Q}}_{\mathrm{i}}$ is the measured capacity based on discharging process at cycle number i, and ${\mathrm{Q}}_{\mathrm{r}}$ is the initial capacity.

In addition, RUL is defined as the cycle life between the current cycle number and EOL, which is defined as:

$${\mathrm{R}\mathrm{U}\mathrm{L}}_{\mathrm{T}\mathrm{S}}={\mathrm{t}}_{\mathrm{E}\mathrm{O}\mathrm{L}}-\mathrm{T}\mathrm{S}$$

(2)

where ${\mathbf{R}\mathbf{U}\mathbf{L}}_{\mathbf{T}\mathbf{S}}$ is the remaining life after the start cycle number of the predicted RUL, TS is the start cycle number of the RUL prediction, and ${\mathbf{t}}_{\mathbf{E}\mathbf{O}\mathbf{L}}$ is the end of life.

2.1. Remaining Useful Life Prediction

Online RUL and SOH estimation studies can be used to improve battery management systems. Research methods can be divided into three categories: methods based on adaptive filters, methods based on artificial intelligence (AI), and mathematical models such as stochastic processes [11]. Adaptive filters contain the Kalman filter [12], particle filter (PF) [4], and improved particle filter [13]. For example, Chen et al. [4] used PF and grey model to build an RUL prediction framework. Dong et al. [14] proposed a method consisting of PF and support vector regression (SVR) for SOH recording and RUL prediction. Peng et al. [15] developed a multivariate degradation model using batch particle filters.

AI-based methods include artificial neural networks (ANNs), support vector machine (SVM), random forest (RF) and extreme gradient boosting (XGB), recurrent neural networks (RNNs) such as LSTM and gated recurrent unit (GRU), and convolutional neural networks (CNNs). Liu et al. [16] studied an ensemble prediction method based on LSTM and Bayesian model averaging (BMA) for RUL prediction. Ungurean et al. [17] applied a GRU model to online SOH prediction.

Mathematical models include the equivalent circuit model, the Gaussian process regression (GPR) model [18,19,20], and the Wiener process model [21,22]. Xu et al. [21] used the Wiener process with useful time for regeneration for RUL prediction. Shen et al. [22] presented a two-stage Wiener process model to quantify the capacity difference between different degradation stages and an unscented particle filter (UPF) algorithm was used for RUL prediction. Jia et al. [23] used the voltage, current, and temperature during the charging process as health indicators, and a GPR model with a probability approach was used to predict short-term SOH.

A hybrid approach integrates multiple predictive models and can achieve better predictive results than a single model. Wu et al. [24] studied a hybrid approach combining neural networks and bat-based particle filters for Li-ion battery RUL prediction. Li et al. [25] proposed an Elman-LSTM model for battery RUL prediction. Gou et al. [26] used an ensemble approach based on random vector function linking (RVFL) and extreme learning machines (ELM) to predict SOH and RUL. Table 1 summarizes the pros and cons of numerous prediction methods.

Table 1. The summary of different RUL prediction methods.

Techniques	Pros	Cons
AI-based [16,17,18]	No mathematical model required Easy implementing Suitable for nonlinear systems	Need a lot of data Regardless of uncertainties
Filter-based [4,13,14,15]	Simple method Good for nonlinear and non-Gaussian estimation	Need more forecast periods Require intensive computing
Mathematical models [18,19,20,21,22,23]	Applied to any state space model Support for uncertainty calculation Suitable for nonlinear systems	Difficulty building models Requires difficult calculation
Hybrid Approaches [24,25,26]	Combining strengths of different individual models Improved prediction accuracy	A high level of research is required Require intensive computing

2.2. Transfer Learning on SOH and RUL Prediction

Che et al. [27] applied the GPR model to optimize the health indicators and used a gated recurrent neural network with transfer learning for predicting RUL. Chehade and Hussein [28,29] used the GPR model to analyze the capacity degradation trend and investigated a multi-output convolutional Gaussian process to decompose the capacity trend of multiple Li-ion cells into a latent function to forecast the capacity trend.

Many researchers have proposed transfer learning to improve SOH estimation. El-Dalahmeh et al. [30] introduced multi-domain feature time-frequency image (TFI) analysis and TL to effectively improve SOH estimation accuracy. Li and Tao [31] proposed a CNN-based architecture with TL for automatic feature extraction and online SOH estimation. Shen et al. [32] proposed a deep CNN with a transfer learning approach for online capacity estimation. Shen et al. [33] presented Deep CNN with ensemble and transfer learning called DCNN-ETL for online capacity estimation. Jia et al. [34] used the transfer component analysis (TCA) with the ELM model for the SOH estimation. Kim et al. [7] proposed the LSTM-TL model to predict SOH by using three types of batteries; one as a source dataset and the other two as target datasets. Ye and Yu [35] proposed a deep domain adversarial network (DDAN) to address the distribution difference between training and testing datasets in SOH estimation.

Health feature extraction plays a major role in SOH estimation. Kong et al. [36] developed an extraction approach for voltage-temperature health features and these features are input to a battery degradation model for RUL prediction. Table 2 provides a summary of some studies on Li-ion battery SOH and RUL prediction.

Table 2. Summary of previously published studies on Li-ion battery SOH and RUL prediction.

Authors	Input Data for the Model	Model Used	Dataset	PHM	Metric	Estimation Error
Che et al. [27]	V	TL-FT-GRNN	Toyota	RUL	AE	24
Li and Tao [31]	I, V	CNN-TL	SONY US18650VTC6 & FST-2000	SOH	RMSE	0.32%
Shen et al. [32]	V, I, Q	DCNN-TL	Medtronic & NASA	Capacity estimation	RMSE	1.22%
Shen et al. [33]	V, I, Q	DCNN-ETL	Medtronic & NASA	Capacity estimation	RMSE	1.50%
Jia et al. [34]	V	TCA-ELM	NASA & Oxford	SOH	RMSE	2.84%
Tan and Zhao [37]	V	LSTM-FC-TL	NASA & CACLE	SOH	RMSE	1.65%
Chen et al. [38]	Q	SDDL	NASA & CALCE	RUL	RMSE	1.17% 1.08%
Our study	Normalized Q	Bi-LSTM-AM-TR	Toyota	SOH RUL	RMSE RE	0.70% 0.98%

Note: V = Voltage, I = Current, Q = Capacity, DCNN-TL = Deep convolutional neural network-transfer learning, DCNN-ETL = Deep convolutional neural network with ensemble learning and transfer learning, LSTM-FC-TL = LSTM-fully connected-transfer learning, TCA-ELM = Transfer component analysis-extreme learning machine, TL-FT-GRNN = Transfer learning-fine tuning-gated recurrent neural network, and SDDL = Sequence decomposition and deep learning, Bi-LSTM-AM-TR = Bi-LSTM attention mechanism with transfer learning.

3. Proposed Method

Our proposed method framework, Bi-LSTM-AM with the transfer learning technique, for capacity prediction and RUL prediction is shown in Figure 1. The knee point is used as the start cycle number of the RUL prediction. We use the Bi-LSTM-AM model from the source data to obtain a pre-trained model. We then tune the pre-trained model by freezing the BI-LSTM-AM layers and fully connected (FC) layers. This fine-tuning step will help the pre-trained model transfer weights. Finally, the fine-tuned model will be used to predict the capacity of the target data.

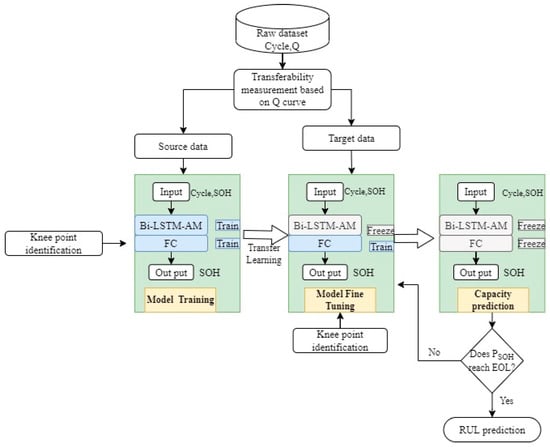
Figure 1. The proposed method framework.

An LSTM unit has 3 gates (Input, Output, and Forget Gate) to protect and control the cell state and add necessary information to the current state. There are 3 inputs to an LSTM unit, i.e., previous cell state, previous unit output, and input event at the time t. Whereas it has two outputs, i.e., current cell state, and current output.

Bi-LSTM is a variation of LSTM that flows input in both the direction to preserve future and past information. The forward LSTM reads the input visit sequence from x₁ to x_t and calculates a sequence of forward hidden states. The backward LSTM reads the visit sequence in reverse order. By concatenating the forward hidden state and the backward one, we can obtain the final latent vector representation as shown in Figure 2. Forward LSTM hidden-state ($\overrightarrow{{\mathrm{h}}_{\mathrm{t}}}$) and backward LSTM hidden-state ($\overleftarrow{{\mathrm{h}}_{\mathrm{t}}}$) are calculated simultaneously at each time step t [39].

$$\overrightarrow{{\mathrm{h}}_{\mathrm{t}}}=\mathrm{L}\left({\mathrm{x}}_{\mathrm{t}},{\overrightarrow{\mathrm{h}}}_{\mathrm{t}-1}\right),$$

(3)

$$\overleftarrow{{\mathrm{h}}_{\mathrm{t}}}=\mathrm{L}\left({\mathrm{x}}_{\mathrm{t}},{\overleftarrow{\mathrm{h}}}_{\mathrm{t}-1}\right),$$

(4)

$${\mathrm{S}}_{\mathrm{t}}={\mathrm{W}}_{\overrightarrow{\mathrm{h}}}\overrightarrow{{\mathrm{h}}_{\mathrm{t}}}+{\mathrm{W}}_{\overleftarrow{\mathrm{h}}}\overleftarrow{{\mathrm{h}}_{\mathrm{t}}}+\mathrm{b},$$

(5)

where ${\mathrm{W}}_{\overrightarrow{\mathrm{h}}}$, ${\mathrm{W}}_{\overleftarrow{\mathrm{h}}}$, and b are the forward LSTMs’ weight, the backward LSTM weight, and the output layer bias, respectively.

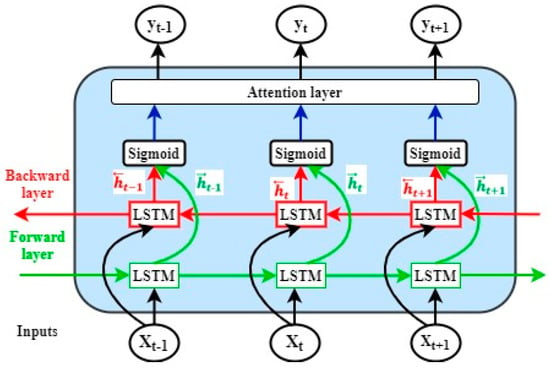
Figure 2. The Bi-LSTM-AM model.

Regarding the attention layer, the vector M_i is calculated by a weighted sum of the states (S_t), which is given by

$${\mathrm{M}}_{\mathrm{i}}={\sum }_{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{a}}_{\mathrm{i}\mathrm{j}}{\mathrm{S}}_{\mathrm{j}}$$

(6)

where $a_{ij}=\frac{\mathrm{e}\mathrm{x}\mathrm{p}\left(e_{ij}\right)}{\sum _{k=1}^n\mathrm{e}\mathrm{x}\mathrm{p}\left(e_{ik}\right)}$ and $e_{ij}$ is the output score of a feedforward neural network described by the function a that attempts to capture the alignment between input at j and output at i.

In the RUL prediction process, the sliding window approach can remove random fluctuations and noise disturbance of the dataset. In the sliding window process, the window with size L, slides over the time series data, and for each sliding step, the model will approximate the data inside the window. The output of the first step will be input for the next step of the model.

To determine the predicted RUL, a multi-step-ahead prediction approach is performed through iterative one-step ahead prediction in which every iteration generates one prediction value and then passes to Bi-LSTM-AM as the subsequent window input data. One-step-ahead predictions are iteratively made until the predicted SOH reaches its end of life (${\widehat{\mathrm{s}\mathrm{o}\mathrm{h}}}_{\mathrm{E}\mathrm{o}\mathrm{L}}$).

A long-term prediction sequence is obtained by iteratively implementing the one-step-ahead prediction approach. Let us suppose the current cycle number is $\mathrm{i}$. In the proposed sliding window prediction, the next cycle number $\mathrm{i}+1$ will be the starting point for the one-step-ahead prediction. In this prediction process, there will be a measured sequence of SOH with $i$ observations (${\mathrm{S}\mathrm{O}\mathrm{H}}_{1:\mathrm{i}}={\left[{\mathrm{s}\mathrm{o}\mathrm{h}}_1,{\mathrm{s}\mathrm{o}\mathrm{h}}_2,...,{\mathrm{s}\mathrm{o}\mathrm{h}}_{\mathrm{i}}\right]}^{\mathrm{T}}$), and a predicted sequence of os SOH (${\widehat{\mathrm{S}\mathrm{O}\mathrm{H}}}_{1+\mathrm{i}:\mathrm{E}\mathrm{o}\mathrm{L}}={\left[{\widehat{\mathrm{s}\mathrm{o}\mathrm{h}}}_{\mathrm{i}+1},{\widehat{\mathrm{s}\mathrm{o}\mathrm{h}}}_{\mathrm{i}+2},...,{\widehat{\mathrm{s}\mathrm{o}\mathrm{h}}}_{\mathrm{E}\mathrm{o}\mathrm{L}}\right]}^{\mathrm{T}}$). The first predicted sequence value will be:

$${\widehat{\mathrm{s}\mathrm{o}\mathrm{h}}}_{\mathrm{i}+1}=\mathrm{f}({\mathrm{s}\mathrm{o}\mathrm{h}}_{{\mathrm{i}-\mathrm{L}}_{}+1},{\mathrm{s}\mathrm{o}\mathrm{h}}_{{\mathrm{i}-\mathrm{L}}_{}+2},...{\mathrm{s}\mathrm{o}\mathrm{h}}_{\mathrm{i}})$$

(7)

In this equation, $L_{}$ is the sliding window length at cycle number $\mathrm{i}+1$, while $\mathrm{f}(.)$ is Bi-LSTM-AT based prediction function. After finding the first predicted SOH value, we can obtain the second prediction value, where ${\widehat{\mathrm{s}\mathrm{o}\mathrm{h}}}_{\mathrm{i}+1}$ is the first predicted SOH value at cycle number $\mathrm{i}+1$.

$${\widehat{\mathrm{s}\mathrm{o}\mathrm{h}}}_{\mathrm{i}+2}=\mathrm{f}({\mathrm{s}\mathrm{o}\mathrm{h}}_{{\mathrm{i}-\mathrm{L}}_{}+2},{\mathrm{s}\mathrm{o}\mathrm{h}}_{{\mathrm{i}-\mathrm{L}}_{}+3},...{\widehat{\mathrm{s}\mathrm{o}\mathrm{h}}}_{\mathrm{i}+1})$$

(8)

The alternative prediction process will continue until the predicted SOH value reaches EOL, as indicated in Equation (9) below.

$${\widehat{\mathrm{s}\mathrm{o}\mathrm{h}}}_{\mathrm{E}\mathrm{o}\mathrm{L}}=\mathrm{f}({\widehat{\mathrm{s}\mathrm{o}\mathrm{h}}}_{{\mathrm{E}\mathrm{o}\mathrm{L}-\mathrm{L}}_{}},...,{\widehat{\mathrm{s}\mathrm{o}\mathrm{h}}}_{\mathrm{E}\mathrm{o}\mathrm{L}-2},{\widehat{\mathrm{s}\mathrm{o}\mathrm{h}}}_{\mathrm{E}\mathrm{o}\mathrm{L}-1})$$

(9)

The illustration of the entire prediction process is provided in Figure 3.

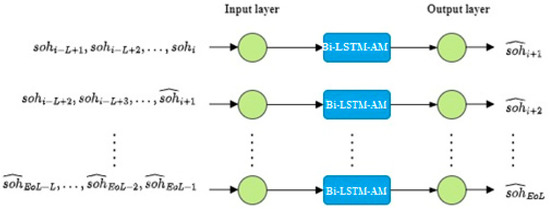
Figure 3. Illustration of iterative prediction of Bi-LSTM-AM with sliding window approach.

4. Transferability Measures for Source and Target Batteries Selection

In transfer learning, the data distribution similarity between the source and target data plays a vital role in the model’s training and prediction performance. Therefore, instead of randomly choosing the source data and the target data, a transferable sample selection approach [40] is used in this study. The four-step transferability measures are based on the curve shapes, the rate of long-term degradation, based on the life span concentration at the end of the test, and the distance between the degradation curves. The Toyota battery dataset [41] has a total of 124 cells that tested under fast charging policies with a cycle life ranging from 150 to 2300 cycles. As a transferability measurement, we apply the following two steps to select the source and target data.

Step 1: As the first step, we select batteries with a cycle life greater than 400. Batteries with unknown EOL values and those with cycle life less than 400 will be removed. Therefore, batteries with long and medium cycle life span will be selected for the next selection step.

Step 2: After identifying the batteries with long and medium cycle life, the degradation curves are grouped into three regions as shown in Figure 4, where the capacity values are the actual capacity values from the dataset.

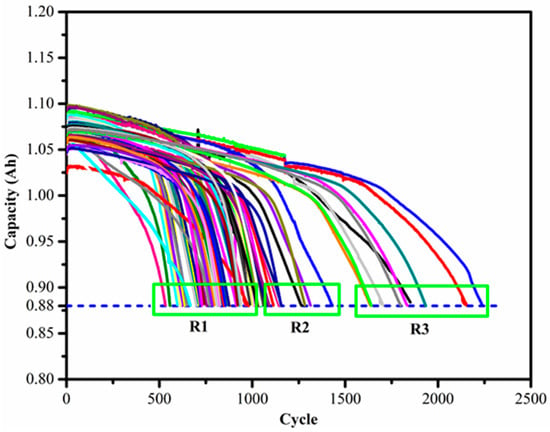
Figure 4. Grouping of the batteries based on cycle life.

The selection of the source and target data from these regions has its advantages and disadvantages.

Option 1: Use batteries at region 3 as the source battery and at region 1 as the target battery. This will help to have more training data but may result in negative transfer because of the difference in the shape of the degradation curves.

Option 2: Use batteries at region 2 as the source battery and batteries at region 1 as the target battery. The degradation curve similarity is better than the first option, but this will result in less training data.

Option 3: Use batteries from region 1 with a similar curve shape and minimum Chebyshev distance as the source battery and the target battery. It provides better similarity between source data and target data.

Therefore, considering the merits and demerits of the above three options, one source and one target dataset are selected from each region based on the Chebyshev distance between curves. The equation for Chebyshev distance is given as:

$$DCheb(k,l)=max\left(\right|k_i-l_i\left|\right)$$

(10)

where $k$ and $l$ are two vectors,$k_i$ and $l_i$ are standard coordinates on the curve, and $DCheb(k,l)$ is the Chebyshev distance between points $k$ and $l$.

Finally, three source batteries and three target batteries are selected for our proposed method validation as shown in Table 3 and Figure 5.

Table 3. Description of cells in the source and target domain.

	Battery #	Charging Policy	Cell Barcode	Cycle Life	Region
Source battery	1_1	3.6C(80%)-3.6C	EL150800460623	2235	R3
	2_1	5.3C(54%)-4C	EL150800737378	1314	R2
	3_1	5.3C(36%)-4C	EL150800737320	858	R1
Target battery	1_2	3.6C(80%)-3.6C	EL150800460486	2158	R3
	2_2	5C(67%)-4C	EL150800737304	1283	R2
	3_2	5.6C(54%)-4.3C	EL150800737251	850	R1

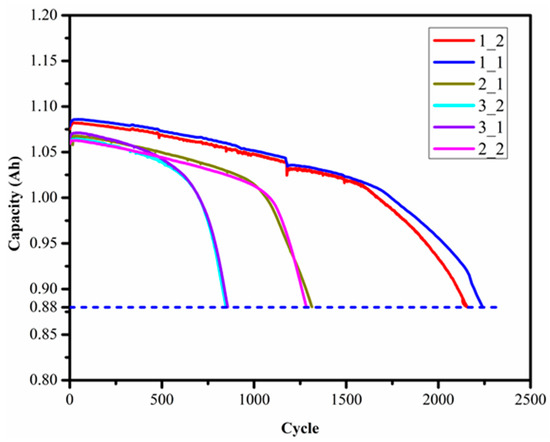
Figure 5. The six batteries used as the source and target dataset.

The root mean square error (RMSE) is used as a performance evaluation metric in this study to compare different model performances for SOH prediction and is given by:

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\frac{1}{\mathrm{n}}{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{S}\mathrm{O}\mathrm{H}}_{\mathrm{i}}-{\widehat{\mathrm{S}\mathrm{O}\mathrm{H}}}_{\mathrm{i}}\right)}^2}$$

(11)

where ${\mathrm{S}\mathrm{O}\mathrm{H}}_{\mathrm{i}}$ and ${\widehat{\mathrm{S}\mathrm{O}\mathrm{H}}}_{\mathrm{i}}$ denote the observed SOH and the predicted SOH for cycle number i.

For testing the RUL prediction performance of the proposed model, absolute error (AE) and relative error (RE) measures are used as indicated in Equations (12) and (13).

$$\mathrm{A}\mathrm{E}=\left|{\mathrm{R}\mathrm{U}\mathrm{L}}_{\mathrm{a}}-\widehat{\mathrm{R}\mathrm{U}\mathrm{L}}\right|$$

(12)

$$\mathrm{R}\mathrm{E}\left(\mathrm{\%}\right)=\frac{\left|{\mathrm{R}\mathrm{U}\mathrm{L}}_{\mathrm{a}}-\widehat{\mathrm{R}\mathrm{U}\mathrm{L}}\right|}{{\mathrm{R}\mathrm{U}\mathrm{L}}_{\mathrm{a}}}\times 100\mathrm{\%}$$

(13)

where $\widehat{\mathrm{R}\mathrm{U}\mathrm{L}}$ denotes the predicted RUL and ${\mathrm{R}\mathrm{U}\mathrm{L}}_{\mathrm{a}}$ denotes the actual RUL.

Here, the 95% prediction interval of SOH is derived by:

$${\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}_{\mathrm{S}\mathrm{O}\mathrm{H}}\pm 1.96\ast \sqrt{{{\mathsf{\eta }}_1}^2+{{\mathsf{\eta }}_2}^2}$$

(14)

where pred_SOH is the predicted SOH, ${\mathsf{\eta }}_1$ is obtained by using the MC dropout approach, and ${\mathsf{\eta }}_2$ is based on the inherent noise. The details of this approach can be found in [10].

5. Analysis Results

We discuss the performance of two prediction methods (without and with transfer learning), where four LSTM-based models including LSTM, LSTM-AM, Bi-LSTM, and Bi-LSTM-AM are considered. All analyses were carried out on a desktop computer equipped with Intel Core (TM) i9-9900K (3.60 GHz) CPU, NVIDIA GeForce GX 1060, and Microsoft Operating System (Windows NTx64). The Python code runs under Spyder 3.7.3 environment with PyTorch library.

In the proposed method, different cells are selected as the source domain and target domain using transferability measures analysis. The Bi-LSTM-AM model is used to train batteries 1_1, 2_1, and 3_1, respectively, as the pre-trained model. Then batteries 1_2, 2_2, and 3_2 used the fine-tuning approach for the pre-trained model by freezing the Bi-LSTM-AM layer and the fully connected (FC) layer. Finally, we use the fine-tuned model to predict the future SOH.

The Bi-LSTM-AM-TR model hyperparameters need to be assigned first. Finding the optimal parameters of a deep learning model is a challenging task. Therefore, iterative optimization is followed by assigning preset values for the model hyperparameters to improve performance. From the model hyperparameters, the number of epochs, the number of lookbacks, the number of neurons, batch size, and dropout rate affect the model prediction performance. Table 4 provides the hyperparameters used for all batteries to obtain the SOH prediction results.

Table 4. Hyperparameters used in SOH predictions.

Battery	Epochs	Lookbacks	Neurons	Batch Size	Dropout Rate
1_1	200	4	80	24	0.01
1_2	200	4	80	24	0.01
2_1	500	6	60	20	0.001
2_2	500	6	60	20	0.001
3_1	300	6	60	18	0.001
3_2	300	6	60	18	0.001

The SOH prediction results using different LSTM-based models using without/with transfer learning are shown in Table 5 and Table 6. The RMSE values displayed in both tables are for the test data on the target batteries. The comparison results of the four LSTM-based models (LSTM, LSTM-AM, Bi-LSTM, and Bi-LSTM-AM) without transfer learning for the three source batteries are shown in Table 5. Using transfer learning, the comparison results of Bi-LSTM-AM-TR with the other four models are shown in Table 6. The weights from the source batteries are transferred to train the corresponding target battery. Accordingly, the trained weights are transferred from source battery 1_1 to target battery 1_2, from source battery 2_1 to target battery 2_2, and from source battery 3_1 to target battery 3_2.

Table 5. SOH prediction results of the three target batteries without transfer learning.

Battery	TS	EOL	RMSE
			LSTM	LSTM-AM	Bi-LSTM	Bi-LSTM-AM
1_2	1624	2158	0.2595	0.4121	0.1383	0.1218
2_2	1088	1283	0.2198	0.3348	0.2258	0.2002
3_2	675	850	0.3016	0.3499	0.2139	0.2015

Table 6. SOH prediction results of the three target batteries with transfer learning.

Battery	TS	EOL	RMSE
			LSTM	LSTM-AM	Bi-LSTM	Bi-LSTM-AM	Bi-LSTM-AM-TR
1_2	1624	2158	0.0272	0.0375	0.0180	0.0128	0.0070
2_2	1088	1283	0.0242	0.0307	0.0200	0.0190	0.0085
3_2	675	850	0.0324	0.0452	0.0217	0.0226	0.0082

The hyperparameters used for both target and source batteries are the same in the transfer learning process. We use a constant length of 500 cycles as the training length; for the test data, use the point from the start of RUL prediction (knee point) to EOL. As we can see from the table results, our proposed transfer learning model provides the lowest RMSE compared to the other models. The computational time is also significantly reduced for the target batteries since we transfer the trained weights to the Bi-LSTM-AM-TR model, which will save time for training the model again. The prediction results for the target batteries are shown in Figure 6. We can see from the figures that our proposed Bi-LSTM-AM-TR model has the best performance in all three target datasets, while the LSTM_AM model has the worst performance.

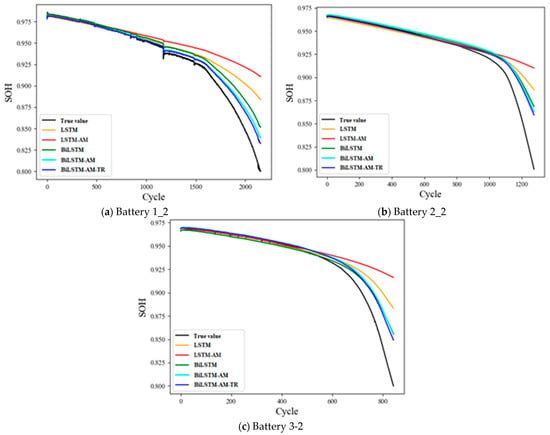
Figure 6. Comparison results of SOH prediction for the three target batteries.

The computational time for the comparative models is also shown in Table 7. We can observe from the comparison results that the computational time is also significantly reduced for the target batteries since we transfer the trained weights to the Bi-LSTM-AM-TR model, which will save time for training the model again.

Table 7. Computational time of different models for the six batteries (unit = second).

Battery	LSTM	LSTM-AM	Bi-LSTM	Bi-LSTM-AM	Bi-LSTM-AM-TR
1_1	888.25	886.33	894.21	906.54	-
2_1	1293.34	1293.66	1295.71	1311.20	-
3_1	1115.17	1117.21	1202.65	1216.73	-
1_2	860.16	855.65	877.53	879.63	127.82
2_2	1147.46	1163.35	1188.39	1231.75	166.37
3_2	1095.17	1103.37	1125.95	1198.84	147.45

The comparison results of different models on SOH for the three target batteries are shown in Figure 6. These prediction results indicate that our proposed method has the best performance in terms of RMSE and computational time. The Bi-LSTM-AM model is the second-best in tracking the capacity degradation curve of the three target batteries. On the other hand, the LSTM-AM model has the worst performance in tracking the capacity degradation curve of the three target batteries. It can be seen from the model comparison graph that with the increase in the three target battery cycle times, the predicted value of the LSTM-AM model deviates from the actual value. Before the degradation curve reaches the TS point, all five models’ prediction values are closer to the actual value. However, as the cycle number increases (especially between the TS point to EOL), the prediction performance of the other models deviates from the actual value. In this regard, our proposed model performs better than the other models. That is, our proposed model can capture the real capacity degradation curves from TS to EOL for the three target batteries as the number of cycles increases.

The RUL prediction of the three source batteries and three target batteries is discussed here. All batteries used in the RUL prediction are considered to reach their EOL when the capacity value drops below 80 % of their rated capacity. The training length for all six batteries keeps constant with 500 data points prior to the prediction starting point. The sliding window with the transfer learning approach is used to predict the unknown test dataset. In this approach, the data points from the training starting point to the EOL are considered unknown.

The hyperparameter values used in computing the RUL of both the source and target batteries are indicated in Table 8. The hyperparameters for the source and target dataset have to be the same for possible weight transfer from the source to the target dataset.

Table 8. Hyperparameters used in computing the predicted RUL.

Battery	Batch Size	Sequence Length	Hidden Size	Dropout Rate
1_2	12	3	120	0.01
1_1	12	3	120	0.01
2_1	6	9	105	0.001
2_2	6	9	105	0.001
3_1	8	10	100	0.001
3_2	8	10	100	0.001

The RUL prediction results for the target batteries using the proposed method are shown in Table 9. The training starting point (TS) and prediction starting point (TSP) are indicated in the table, all batteries have the same training length of 500. The predicted RUL with 95 % PI is also shown in the table. As we can see from the table, the maximum absolute error (AE) value is 10 and the relative error (RE) value is less than 9%. The RE values for the target batteries 1_2, 2_2, and 3_2 are 2.82%, 1.70%, and 0.98%, respectively. Figure 7 shows the RUL prediction plot for the target batteries with upper and lower 95% prediction intervals using the Monte Carlo approach.

Table 9. RUL prediction results for the target batteries.

Battery	TS	TSP	Actual RUL	Predicted RUL [95% PI on SOH]	AE	RE (%)
1_2	1304	1804	354	344 [0.797, 0.802]	10	2.82
2_2	548	1048	235	231 [0.793, 0.801]	4	1.70
3_2	146	646	204	206 [0.794, 0.802]	2	0.98

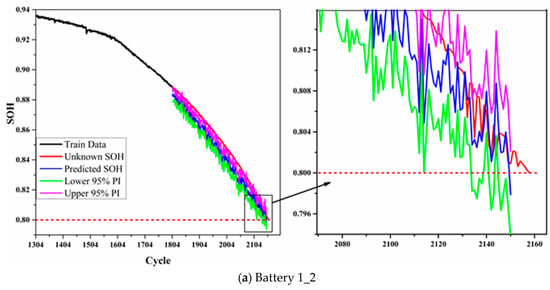
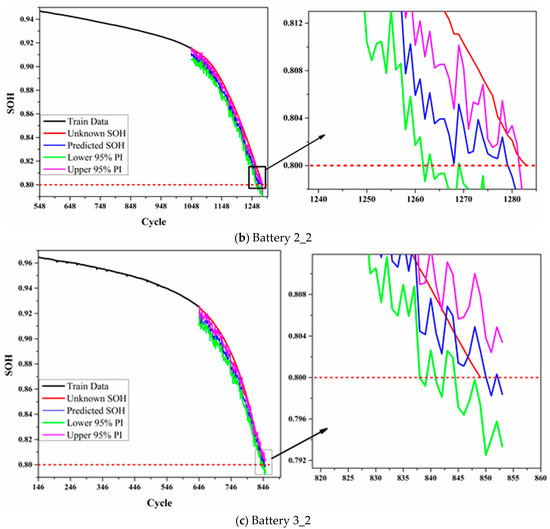
Figure 7. RUL prediction with prediction intervals for the three target batteries.

Figure 7 shows the RUL prediction plot for the target battery. The upper and lower 95% prediction intervals are obtained by using the Monte Carlo dropout method. The black curve is the train data, the red curve is the actual (unknown) SOH value, and the blue curve is the predicted SOH. The green and pink curves are the lower and upper bounds of the 95% prediction interval values. The dashed red line represents the EOL point of the three batteries which is indicated as 80 % of the SOH value. The SOH of 88% is used as the prediction starting point, while the training starting point is the knee point of the respective batteries. For battery 1_2, our proposed model predicted the RUL before its actual RUL, while for batteries 2_2 and 3_2, the model predicted the RUL was beyond the actual RUL point. The AE values of the three target batteries are 10, 4, and 2, respectively. The RE percentage values of the three target batterie are 2.82%, 1.70%, and 0.98%, respectively. In addition, all 95% prediction intervals of RUL on the three target batteries include the EOL value (=0.8). These results show that the proposed RUL prediction method can be applied to battery health management with uncertainty.

6. Conclusions

Accurate prediction is a challenging task for the wide application of intelligent BMS. Transfer learning can reuse a pre-trained model in another related task, reducing the time and data required to train a different predictive model. Although transfer learning has been applied to Li-ion battery RUL prediction, most of the previously published papers did not discuss the training starting point or choose a random starting point for model training.

We propose a method based on Bi-LSTM-AM and a transfer learning technique called Bi-LSTM-AM-TR, where normalized capacity is considered as SOH. The EOL of the battery is given as SOH = 0.8. Three source and three target batteries using a transferable sample selection approach were selected for model validation. Our proposed method achieves better prediction results than the other LSTM-based models.

For this study, the relative error values of the target battery using the proposed method on the three target batteries are 2.82%, 1.70%, and 0.98%, respectively. These prediction results show that our proposed method is very suitable for online RUL prediction.

For the proposed transfer learning approach, the weights from the three trained source batteries are transferred to the corresponding three target batteries, and SOH is predicted using the transferred weights. The transfer learning approach gives a better result compared to LSTM-based models without transfer learning and saves a significant amount of training time, making it suitable for online prediction.

Further research will extend our proposed model to predict multiple target cells from multiple source cells. In addition, the impact of different prediction starting points and training lengths on model prediction performance can be considered.