Battery Test Profile Generation Framework for Electric Vehicles
Abstract
1. Introduction
2. Dynamics Model Considering Regenerative Braking
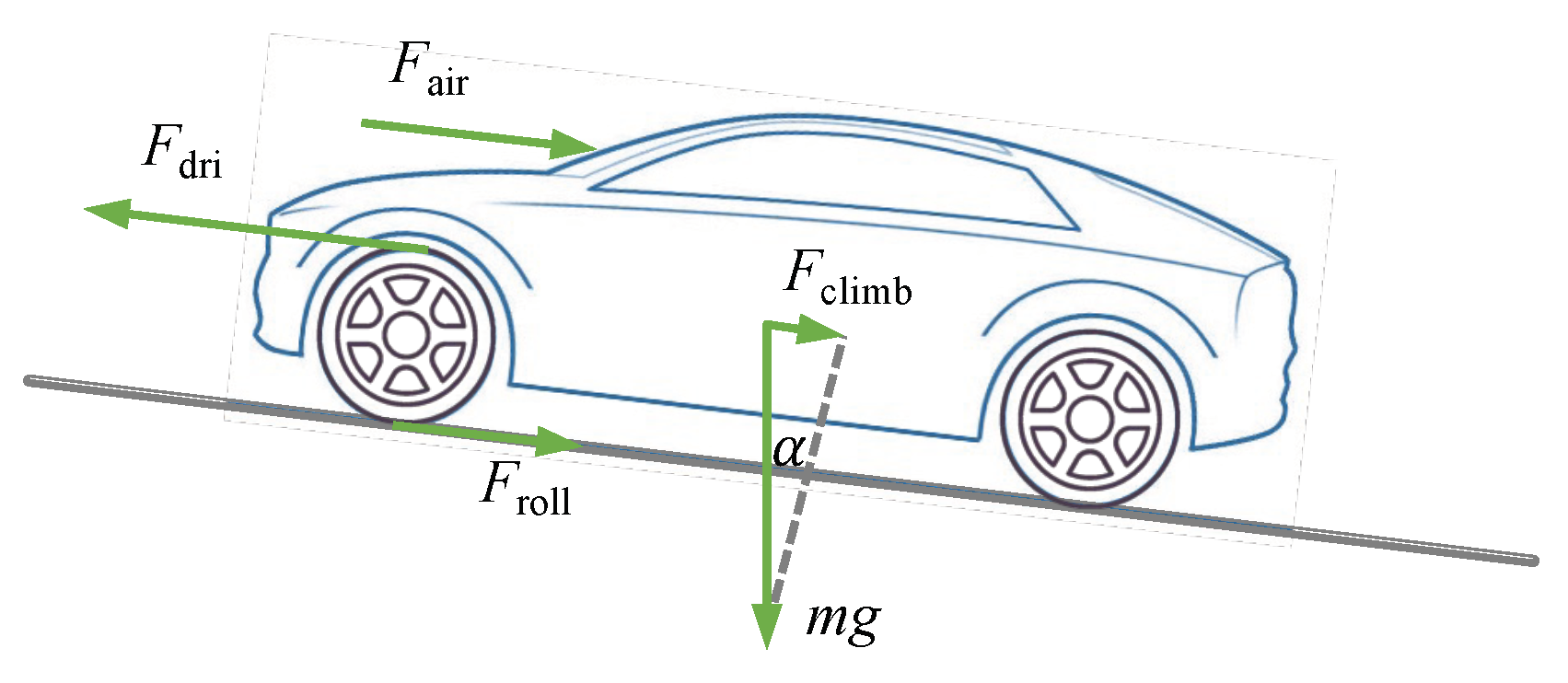
2.1. Simplified Longitudinal Dynamics Model
- Rolling resistance: Equal to the product of rolling resistance coefficient f and wheel load. The rolling resistance can be directly expressed as follows, since the climbing resistance has been ignored.where m is the mass in running order, g is the gravitational acceleration, and f is the rolling resistance coefficient.
- Aerodynamic drag: Proportional to the dynamic pressure of the relative velocity of the air flow.where is the density of air, is the aerodynamic drag coefficient, is the cross-sectional area, and v is the velocity of the electric vehicle.
- Acceleration resistance: is commonly used as the conversion coefficient of vehicle rotating mass after taking into account the inertia force for the electric vehicle [20]. Therefore, the acceleration resistance can be expressed aswhere is the factor for rotational masses, is the accelerated speed.
2.2. Power Load Profile Considering Regenerative Braking
3. Experiments
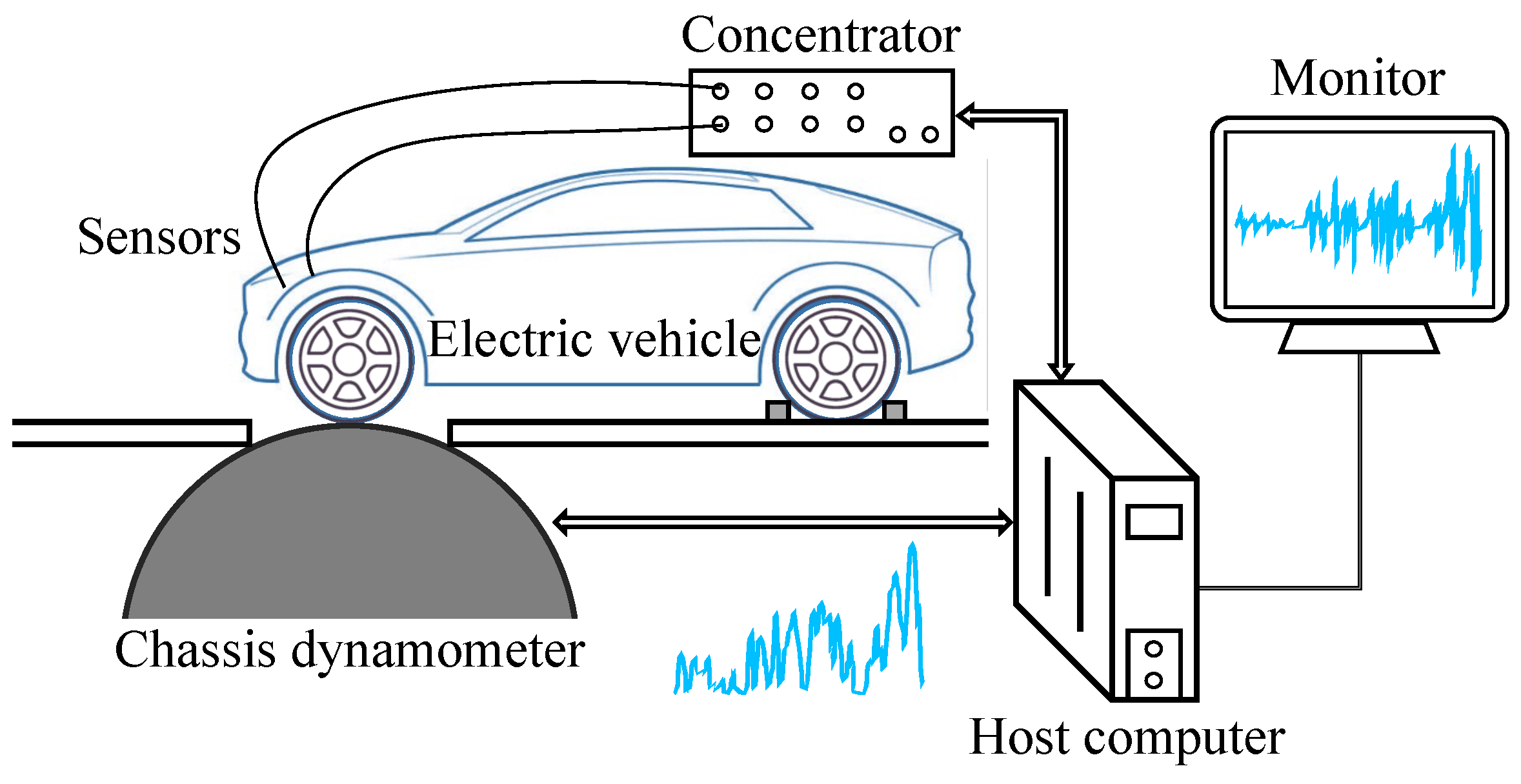
3.1. Experimental Configurations
3.2. Experimental Procedures
- 1.
- Power off the electric vehicle and install the voltage and current sensors on the direct current (DC) bus of the battery system.
- 2.
- Fix the electric vehicle on the chassis dynamometer. The front wheels of the vehicle are placed directly above the dynamometer and the rear wheels are locked, as shown in Figure 2.
- 3.
- Power on the electric vehicle and confirm that the vehicle is in a good status.
- 4.
- Power on the chassis dynamometer and the data acquisition system and confirm that they are in a good status.
- 5.
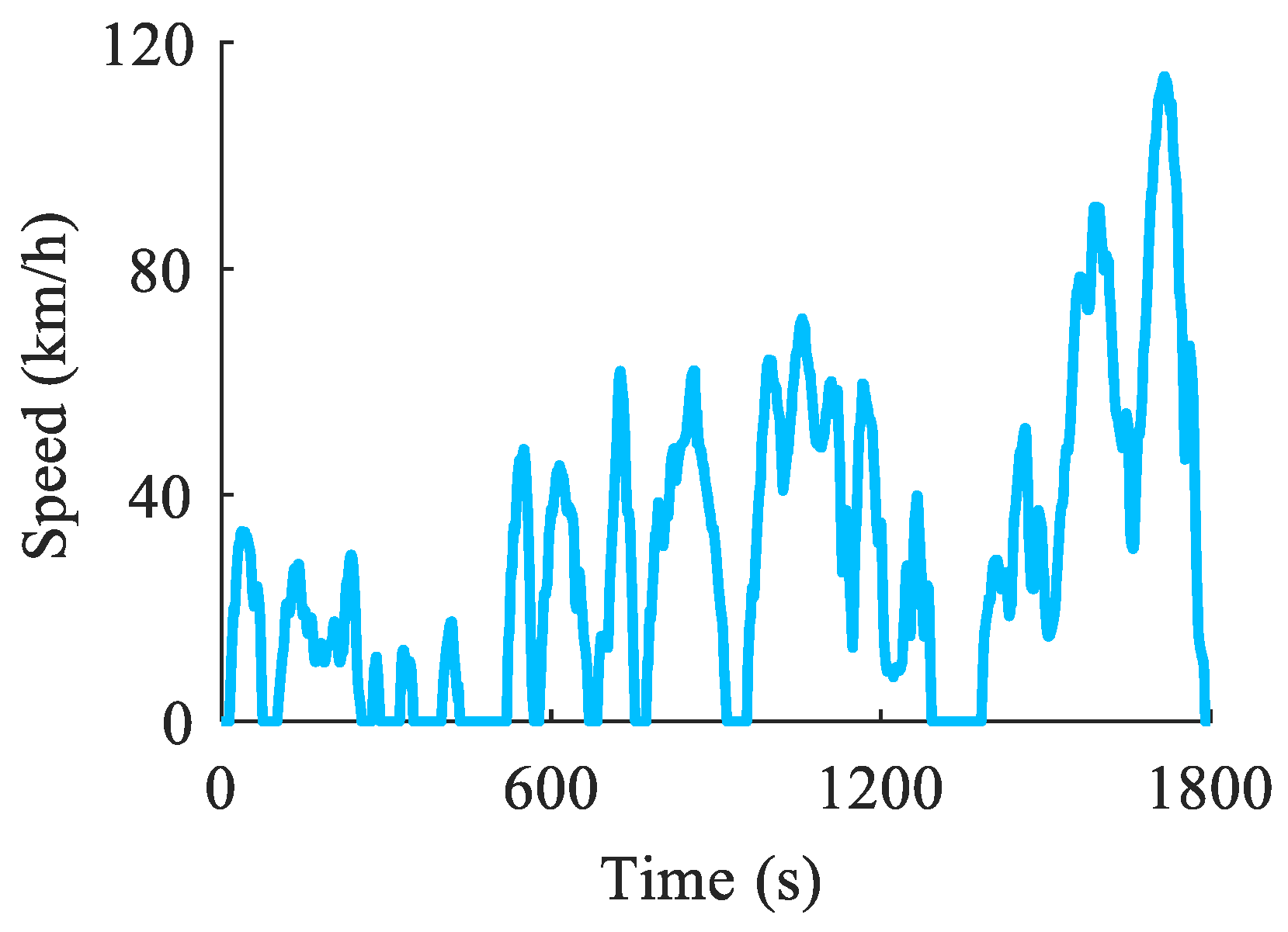
- Drive the vehicle according to the specified test profile. In this experiment, the CLTC-P is used as the test profile, as shown in Figure 4.
4. Results and Discussions
4.1. Repeatability of the Vehicle Test Profile on the Chassis Dynamometer
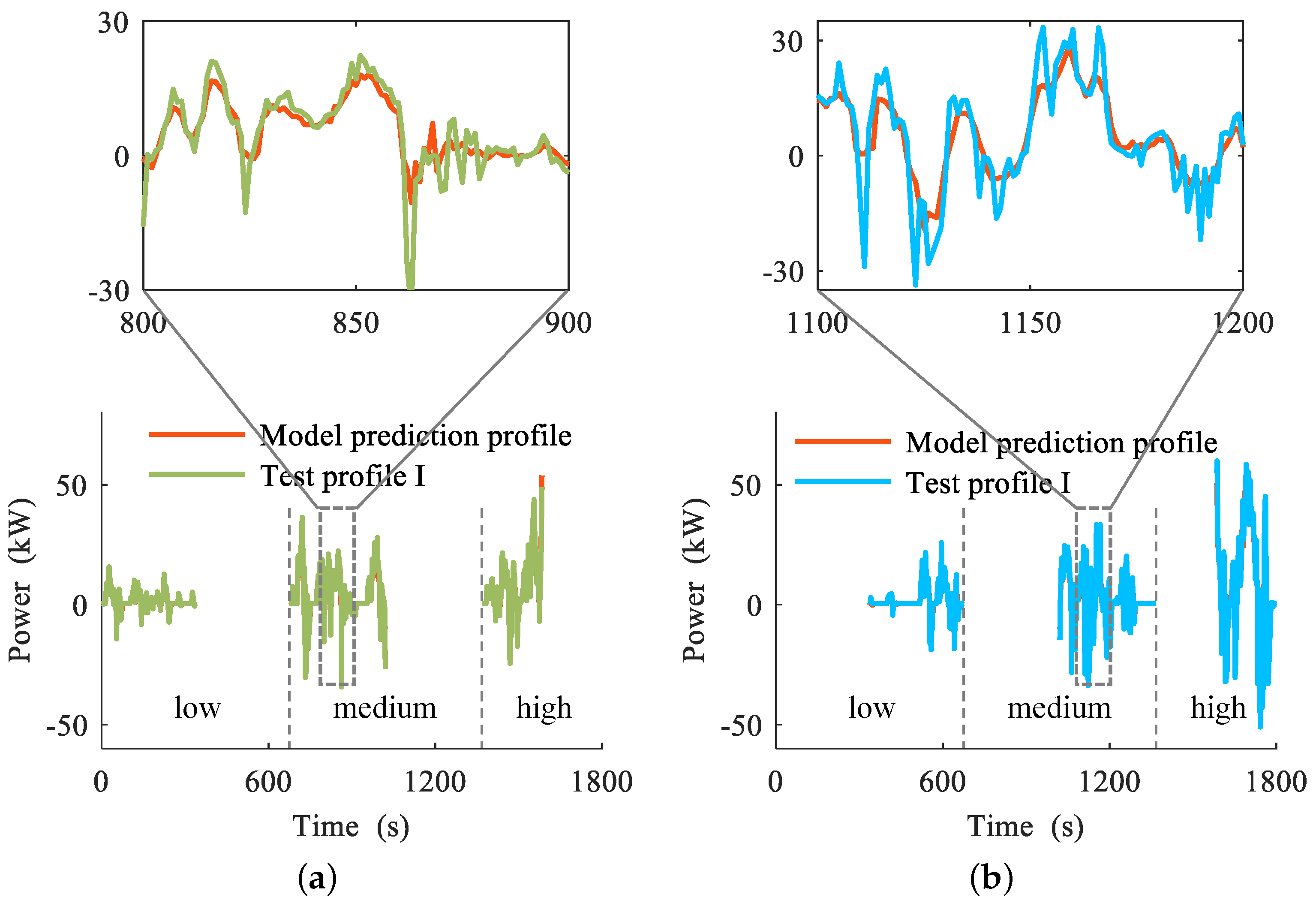
4.2. Verification of the Simplified Vehicle Longitudinal Dynamics Model
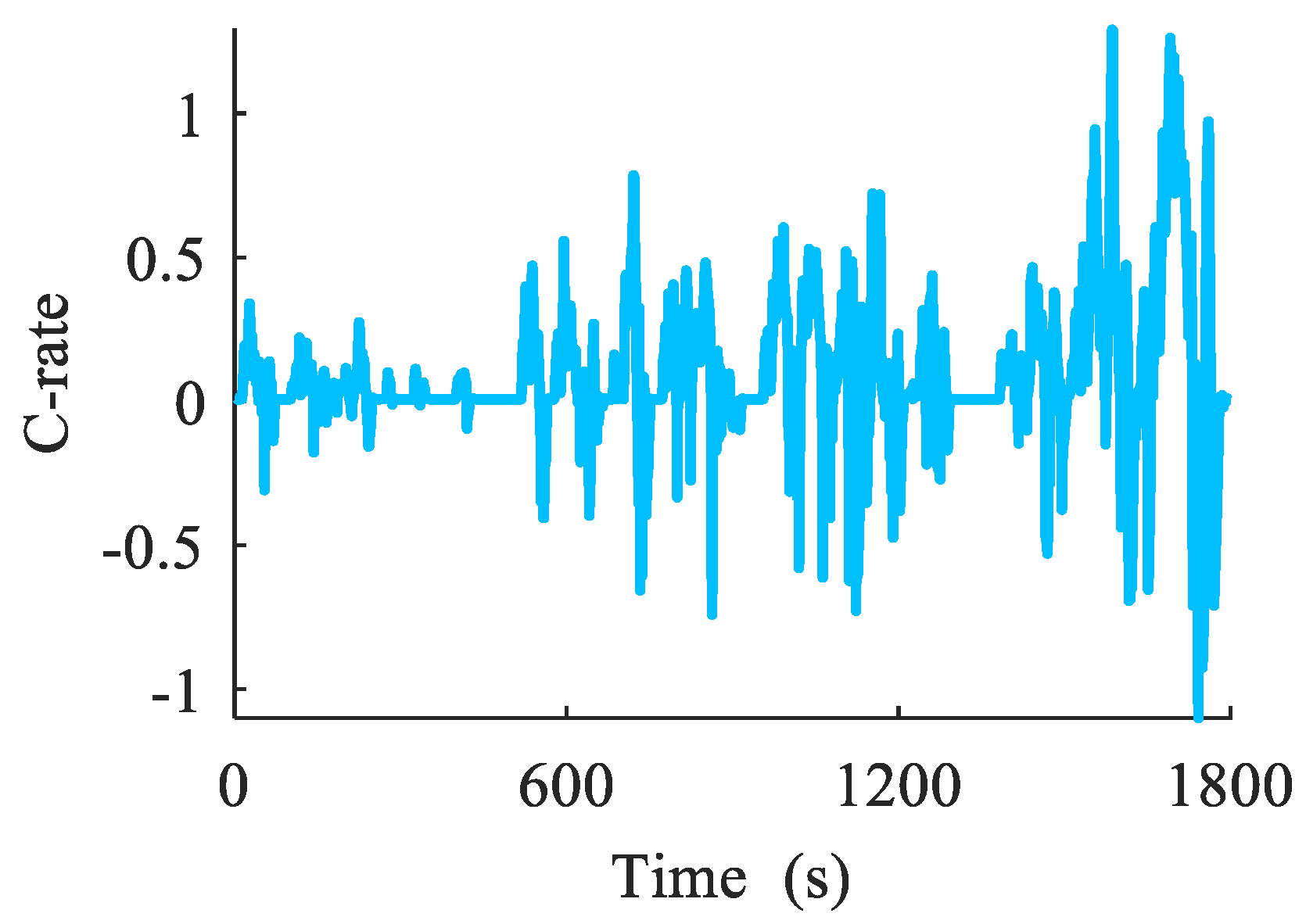
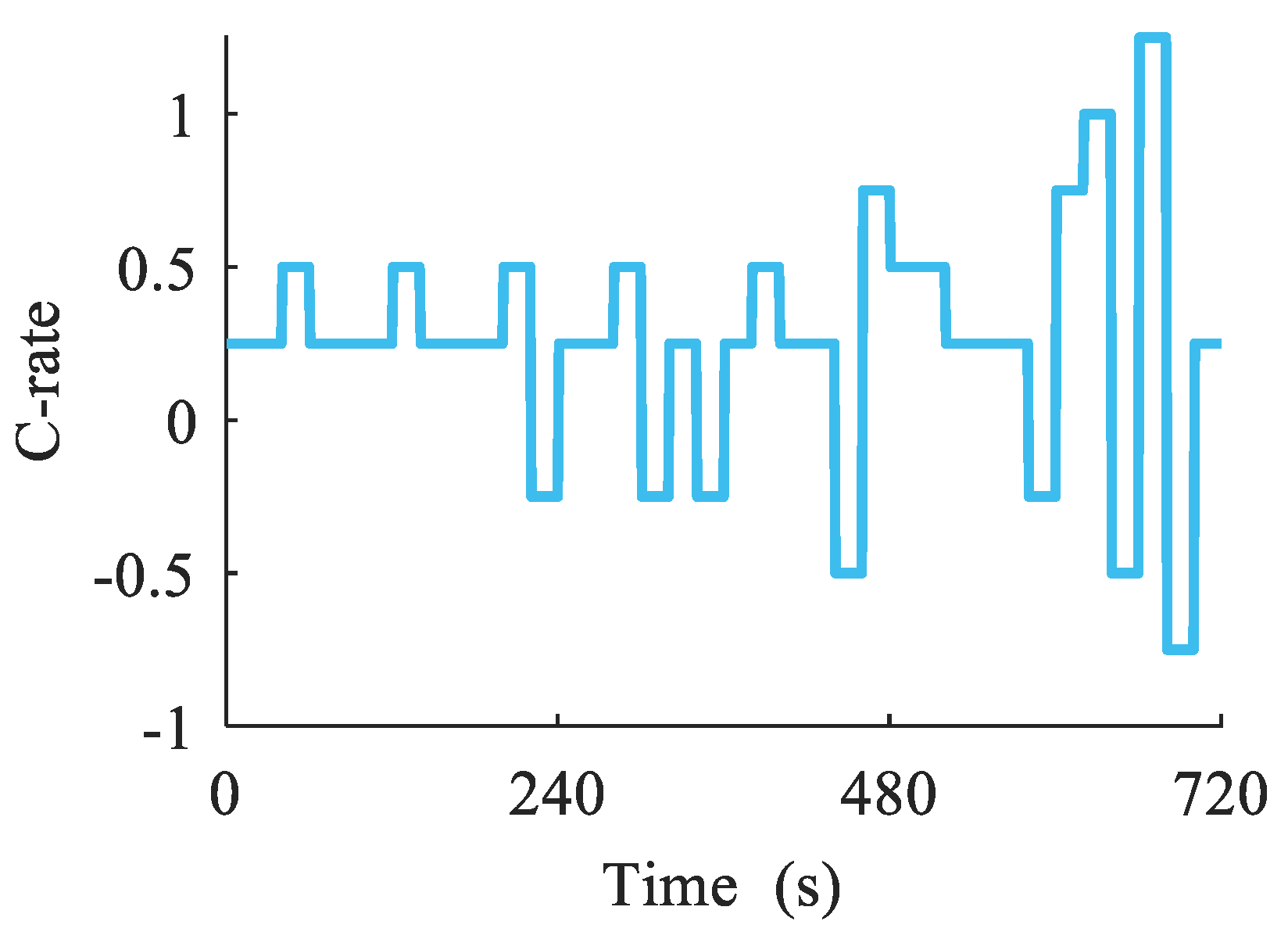
4.3. Accelerated Battery Aging Profile Results
4.4. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CATARC | China Automotive Technology & Research Center |
| CHTC | China heavy-duty commercial vehicle test cycle |
| CHTC-B | China heavy-duty commercial vehicle test cycle-bus |
| CHTC-C | China heavy-duty commercial vehicle test cycle-coach |
| CHTC-D | China heavy-duty commercial vehicle test cycle-dump |
| CHTC-HT | China heavy-duty commercial vehicle test cycle-truck (GVW > 5500 kg) |
| CHTC-LT | China heavy-duty commercial vehicle test cycle-truck (GVW ≤ 5500 kg) |
| CHTC-S | China heavy-duty commercial vehicle test cycle-semitrailer |
| CLTC | China light-duty vehicle test cycle |
| CLTC-C | China light-duty vehicle test cycle-commercial car |
| CLTC-P | China light-duty vehicle test cycle-passenger car |
| DC | Direct current |
| GVW | Gross vehicle weight |
| MAE | Mean absolute error |
| NEDC | New European driving cycle |
| RMSE | Root mean square error |
| WLTC | Worldwide harmonized light vehicles test cycle |
References
- Wang, X.; Wei, X.; Zhu, J.; Dai, H.; Zheng, Y.; Xu, X.; Chen, Q. A review of modeling, acquisition, and application of lithium-ion battery impedance for onboard battery management. eTransportation 2020, 7, 100093. [Google Scholar] [CrossRef]
- Kovachev, G.; Ellersdorfer, C.; Gstrein, G.; Hanzu, I.; Wilkening, H.M.R.; Werling, T.; Schauwecker, F.; Sinz, W. Safety assessment of electrically cycled cells at high temperatures under mechanical crush loads. eTransportation 2020, 6, 100087. [Google Scholar] [CrossRef]
- Kim, J.; Kowal, J. Development of a Matlab/Simulink Model for Monitoring Cell State-of-Health and State-of-Charge via Impedance of Lithium-Ion Battery Cells. Batteries 2022, 8, 8. [Google Scholar] [CrossRef]
- Singh, S.; Weeber, M.; Birke, K.P. Implementation of Battery Digital Twin: Approach, Functionalities and Benefits. Batteries 2021, 7, 78. [Google Scholar] [CrossRef]
- Farmann, A.; Waag, W.; Marongiu, A.; Sauer, D.U. Critical review of on-board capacity estimation techniques for lithium-ion batteries in electric and hybrid electric vehicles. J. Power Sources 2015, 281, 114–130. [Google Scholar] [CrossRef]
- Farmann, A.; Sauer, D.U. Comparative study of reduced order equivalent circuit models for on-board state-of-available-power prediction of lithium-ion batteries in electric vehicles. Appl. Energy 2018, 225, 1102–1122. [Google Scholar] [CrossRef]
- Feng, X.; Li, J.; Lu, L.; Hua, J.; Xu, L.; Ouyang, M. Research on a battery test profile based on road test data from hybrid fuel cell buses. J. Power Sources 2012, 209, 30–39. [Google Scholar] [CrossRef]
- Liaw, B.Y.; Dubarry, M. From driving cycle analysis to understanding battery performance in real-life electric hybrid vehicle operation. J. Power Sources 2007, 174, 76–88. [Google Scholar] [CrossRef]
- Devie, A.; Vinot, E.; Pelissier, S.; Venet, P. Real-world battery duty profile of a neighbourhood electric vehicle. Transp. Res. Part C Emerg. Technol. 2012, 25, 122–133. [Google Scholar] [CrossRef]
- Sun, F.; Meng, X.; Lin, C.; Wang, Z. Dynamic stress test profile of power battery for electric vehicle. Trans. Beijing Inst. Technol. 2010, 30, 297–301. [Google Scholar] [CrossRef]
- Panchal, S.; Mcgrory, J.; Kong, J.; Fraser, R.; Fowler, M.; Dincer, I.; Agelin-Chaab, M. Cycling degradation testing and analysis of a LiFePO4 battery at actual conditions. Int. J. Energy Res. 2017, 41, 2565–2575. [Google Scholar] [CrossRef]
- Zhao, X.; Zhao, X.; Yu, Q.; Ye, Y.; Yu, M. Development of a representative urban driving cycle construction methodology for electric vehicles: A case study in Xi’an. Transp. Res. Part D Transp. Environ. 2020, 81, 102279. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Liu, P.; Zhang, Z.; Li, X.; Qu, C. Driving cycles construction for electric vehicles considering road environment: A case study in Beijing. Appl. Energy 2019, 253, 113514. [Google Scholar] [CrossRef]
- Tao, L.; Cheng, Y.; Lu, C.; Su, Y.; Chong, J.; Jin, H.; Lin, Y.; Noktehdan, A. Lithium-ion battery capacity fading dynamics modelling for formulation optimization: A stochastic approach to accelerate the design process. Appl. Energy 2017, 202, 138–152. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, F.; Hao, H.; Chen, K.; Liu, Z.; Babiker, H.; Amer, A.A. From NEDC to WLTP: Effect on the Energy Consumption, NEV Credits, and Subsidies Policies of PHEV in the Chinese Market. Sustainability 2020, 12, 5747. [Google Scholar] [CrossRef]
- Ma, R.; He, X.; Zheng, Y.; Zhou, B.; Lu, S.; Wu, Y. Real-world driving cycles and energy consumption informed by large-sized vehicle trajectory data. J. Clean. Prod. 2019, 223, 564–574. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, Z.X.; Zhou, H.; Zheng, H.; Yu, N.; An, X.P.; Li, J.Y.; Li, M.L. Development of China Light-Duty Vehicle Test Cycle. Int. J. Automot. Technol. 2020, 21, 1233–1246. [Google Scholar] [CrossRef]
- Guo, D.; Yang, G.; Feng, X.; Lu, L.; Ouyang, M. Accelerated aging profile generation method for lithium-Ion batteries considering aging path. Trans. China Electrotech. Soc. 2022, 37, 4788–4797. [Google Scholar] [CrossRef]
- Miceli, R.; Viola, F. Designing a sustainable university recharge area for electric vehicles: Technical and economic analysis. Energies 2017, 10, 1604. [Google Scholar] [CrossRef]
- Park, G.; Lee, S.; Jin, S.; Kwak, S. Integrated modeling and analysis of dynamics for electric vehicle powertrains. Expert Syst. Appl. 2014, 41, 2595–2607. [Google Scholar] [CrossRef]
- Keil, P.; Jossen, A. Aging of lithium-ion batteries in electric vehicles: Impact of regenerative braking. World Electr. Veh. J. 2015, 7, 41–51. [Google Scholar] [CrossRef]
- Keil, P.; Jossen, A. Impact of dynamic driving loads and regenerative braking on the aging of lithium-ion batteries in electric vehicles. J. Electrochem. Soc. 2017, 164, A3081. [Google Scholar] [CrossRef]
- Lu, Y.; Li, K.; Han, X.; Feng, X.; Chu, Z.; Lu, L.; Huang, P.; Zhang, Z.; Zhang, Y.; Yin, F.; et al. A method of cell-to-cell variation evaluation for battery packs in electric vehicles with charging cloud data. eTransportation 2020, 6, 100077. [Google Scholar] [CrossRef]
- Schindler, M.; Sturm, J.; Ludwig, S.; Schmitt, J.; Jossen, A. Evolution of initial cell-to-cell variations during a three-year production cycle. eTransportation 2021, 8, 100102. [Google Scholar] [CrossRef]
- Wildfeuer, L.; Lienkamp, M. Quantifiability of inherent cell-to-cell variations of commercial lithium-ion batteries. eTransportation 2021, 9, 100129. [Google Scholar] [CrossRef]
- Hu, G.; Huang, P.; Bai, Z.; Wang, Q.; Qi, K. Comprehensively analysis the failure evolution and safety evaluation of automotive lithium ion battery. eTransportation 2021, 10, 100140. [Google Scholar] [CrossRef]
- Su, L.; Wu, M.; Li, Z.; Zhang, J. Cycle life prediction of lithium-ion batteries based on data-driven methods. eTransportation 2021, 10, 100137. [Google Scholar] [CrossRef]
- López-Ibarra, J.A.; Goitia-Zabaleta, N.; Herrera, V.I.; Camblong, H. Battery aging conscious intelligent energy management strategy and sensitivity analysis of the critical factors for plug-in hybrid electric buses. eTransportation 2020, 5, 100061. [Google Scholar] [CrossRef]
- Yang, H.; Wang, P.; An, Y.; Shi, C.; Sun, X.; Wang, K.; Zhang, X.; Wei, T.; Ma, Y. Remaining useful life prediction based on denoising technique and deep neural network for lithium-ion capacitors. eTransportation 2020, 5, 100078. [Google Scholar] [CrossRef]
- Guo, D.; Yang, G.; Han, X.; Feng, X.; Lu, L.; Ouyang, M. Parameter identification of fractional-order model with transfer learning for aging lithium-ion batteries. Int. J. Energy Res. 2021, 45, 12825–12837. [Google Scholar] [CrossRef]
- Christopher Frey, H.; Patil, S.R. Identification and review of sensitivity analysis methods. Risk Anal. 2002, 22, 553–578. [Google Scholar] [CrossRef]
- Lai, X.; Meng, Z.; Wang, S.; Han, X.; Zhou, L.; Sun, T.; Li, X.; Wang, X.; Ma, Y.; Zheng, Y. Global parametric sensitivity analysis of equivalent circuit model based on Sobol’method for lithium-ion batteries in electric vehicles. J. Clean. Prod. 2021, 294, 126246. [Google Scholar] [CrossRef]
- Nossent, J.; Elsen, P.; Bauwens, W. Sobol’ sensitivity analysis of a complex environmental model. Environ. Model. Softw. 2011, 26, 1515–1525. [Google Scholar] [CrossRef]



| Symbol | Description (Unit) | Value |
|---|---|---|
| g | Gravitational acceleration () | 9.81 |
| f | Rolling resistance coefficient (-) | 0.010∼0.020 |
| Air density () | 1.2 | |
| Factor for rotational masses (-) | 1.04 |
| Symbol | Description (Unit) | Value |
|---|---|---|
| m | Mass in running order () | 2206 |
| Aerodynamic drag coefficient (-) | 0.346 | |
| Cross-sectional area () | 2.6 | |
| Drivetrain efficiency (-) | 81.2% | |
| Regenerative braking efficiency (-) | 76.9% | |
| Energy conversion efficiency (-) | 97.6% | |
| Auxiliary power consumption () | 300 |
| Term (Unit) | Value |
|---|---|
| Maximum sampling frequency () | 2 M |
| Voltage range () | 0∼2000 |
| Current range () | 0∼500 |
| Voltage accuracy (%) | 0.15 |
| Current accuracy (%) | 0.3 |
| Evaluation Index | Identification Error | Prediction Error |
|---|---|---|
| MAE | ||
| RMSE |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, D.; Ren, H.; Feng, X.; Han, X.; Lu, L.; Ouyang, M. Battery Test Profile Generation Framework for Electric Vehicles. Batteries 2023, 9, 256. https://doi.org/10.3390/batteries9050256
Guo D, Ren H, Feng X, Han X, Lu L, Ouyang M. Battery Test Profile Generation Framework for Electric Vehicles. Batteries. 2023; 9(5):256. https://doi.org/10.3390/batteries9050256
Chicago/Turabian StyleGuo, Dongxu, Hailong Ren, Xuning Feng, Xuebing Han, Languang Lu, and Minggao Ouyang. 2023. "Battery Test Profile Generation Framework for Electric Vehicles" Batteries 9, no. 5: 256. https://doi.org/10.3390/batteries9050256
APA StyleGuo, D., Ren, H., Feng, X., Han, X., Lu, L., & Ouyang, M. (2023). Battery Test Profile Generation Framework for Electric Vehicles. Batteries, 9(5), 256. https://doi.org/10.3390/batteries9050256






