Fractional-Order Sliding-Mode Observers for the Estimation of State-of-Charge and State-of-Health of Lithium Batteries
Abstract
1. Introduction
- (1)
- The accuracy of estimation for SoC and SoH is enhanced without utilizing the LPF. Owing to the fractional-order sliding manifolds, the control signals of the observers are smoothed by the α + 1 order integrator, which can be directly used to estimate SoC and SoH.
- (2)
- The accuracy of the data is improved. The proposed FOSMOs adopt the data of measured voltage and current to estimate the significant data, which will be used in the next development of FOSMOs.
2. Preliminary
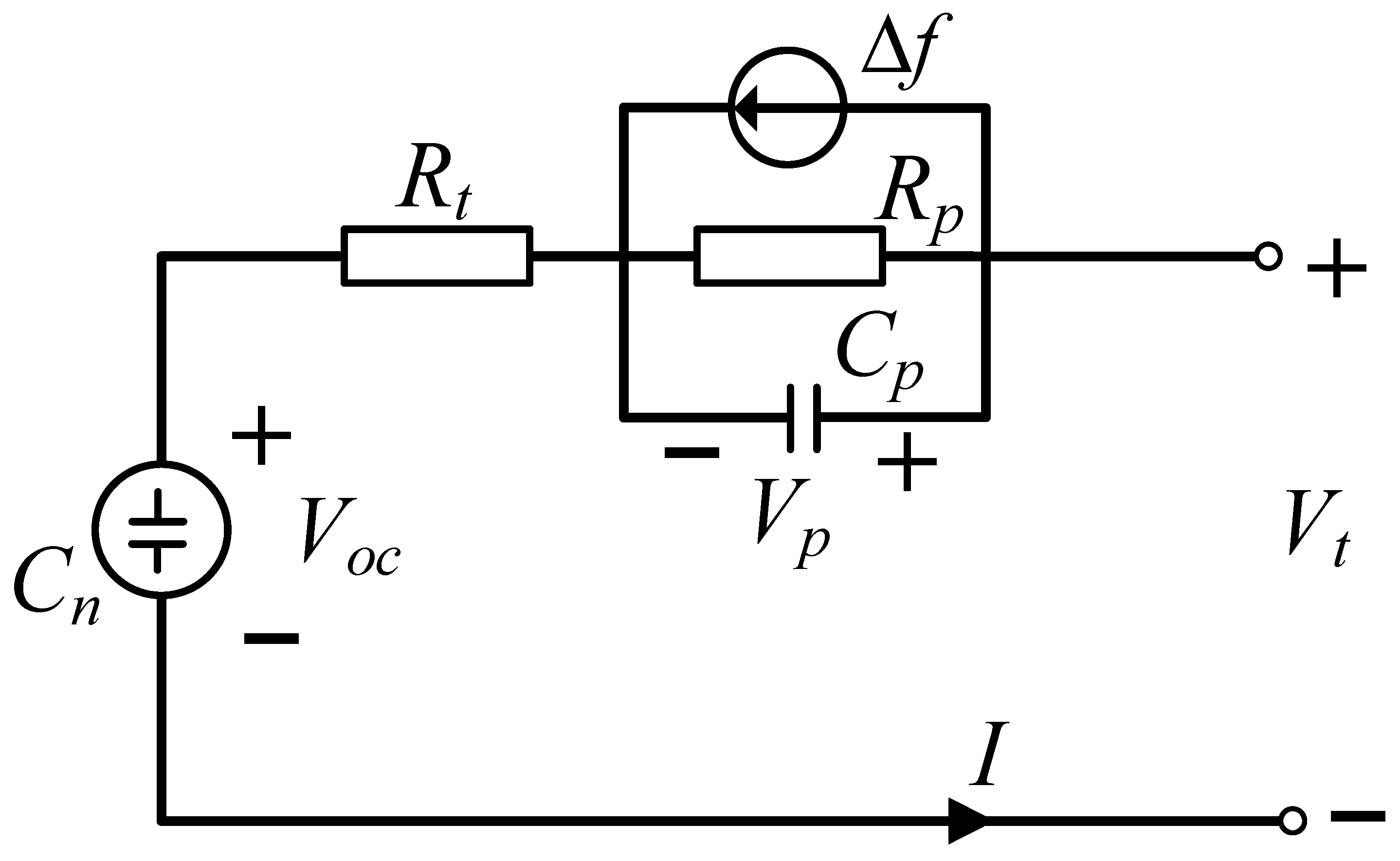
2.1. The Mathematical Model of the Battery
2.2. High Order Sliding-Mode Observer
3. The Estimation Method for SoC
- (1)
- The electric quantity perspective-based definition is given as [35]:where Cs and CN are the discharge quantity and rated capacity of the lithium battery, is(t) is the discharge current, and ηs is the discharge efficiency factor.
- (2)
- The energy perspective-based definition is shown by [37]:where Ws and WN are the released energy and total energy of the lithium battery, and V(t) is the terminal voltage.
3.1. Terminal Voltage Observer
3.2. Open-Circuit Voltage Observer
3.3. Polarization Voltage Observer
3.4. Calculation of SoC
4. The Estimation Method for SoH
- (1)
- The capacity-based definition is shown by [36]:where Cn and Cnom are the actual capacity and nominal capacity of the lithium battery.
- (2)
- The internal resistance-based definition is given as [38]:where Rt and Rnom are the actual and nominal resistance, and REoL is the resistance at the end of life [39]. In the SoH estimation, the capacity and resistance are monotonically changing with aging, environmental temperature, magnitude of current, and depth of discharge. The observer control signals can be viewed as continuous. Therefore, the following assumptions can be given:whereandare the estimation value, and Fc, Fcn, Ft, and Frt are all known positive constants.
4.1. Battery Capacity Observer
4.2. Battery Inner Resistance Observer
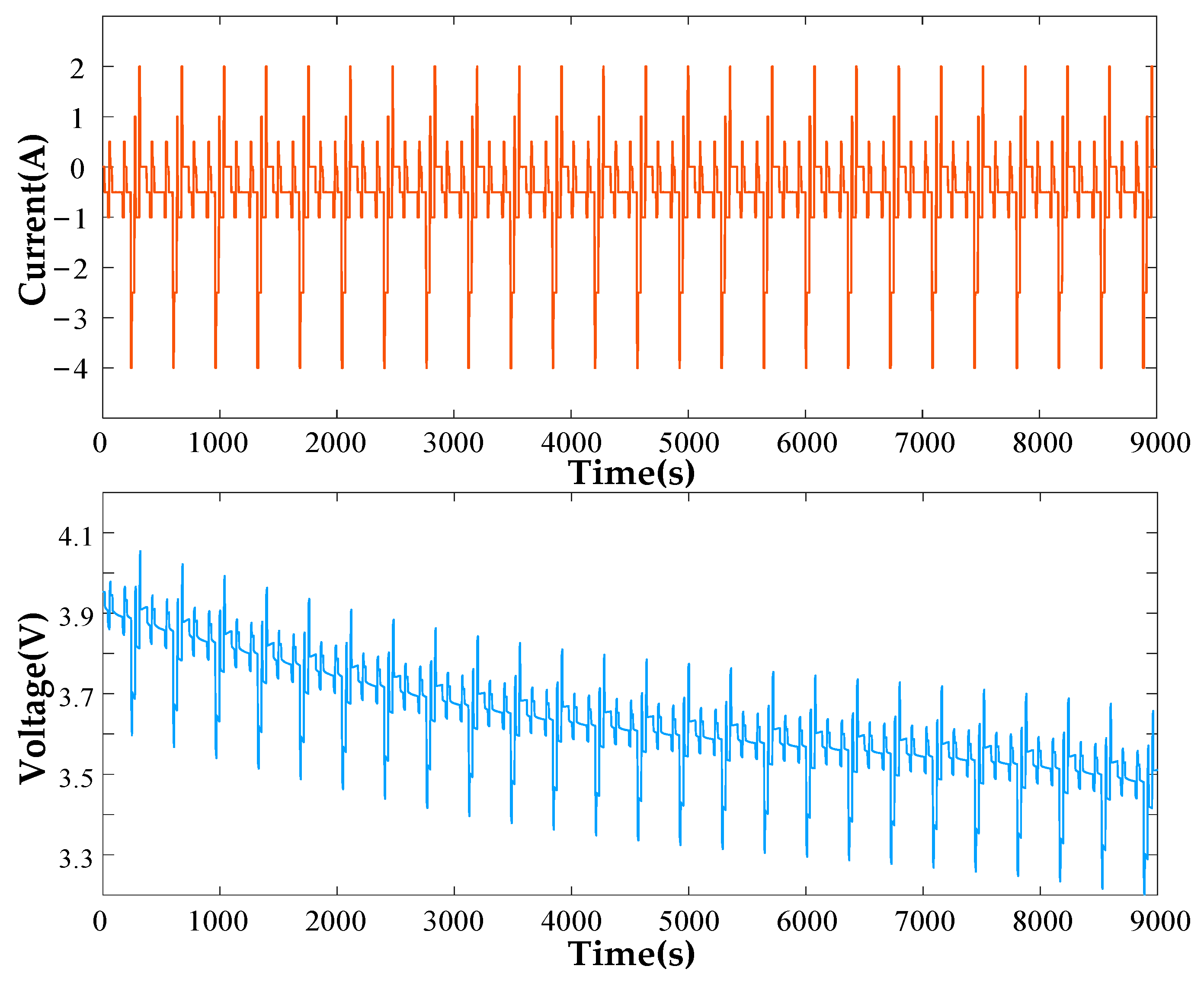
5. Experiments
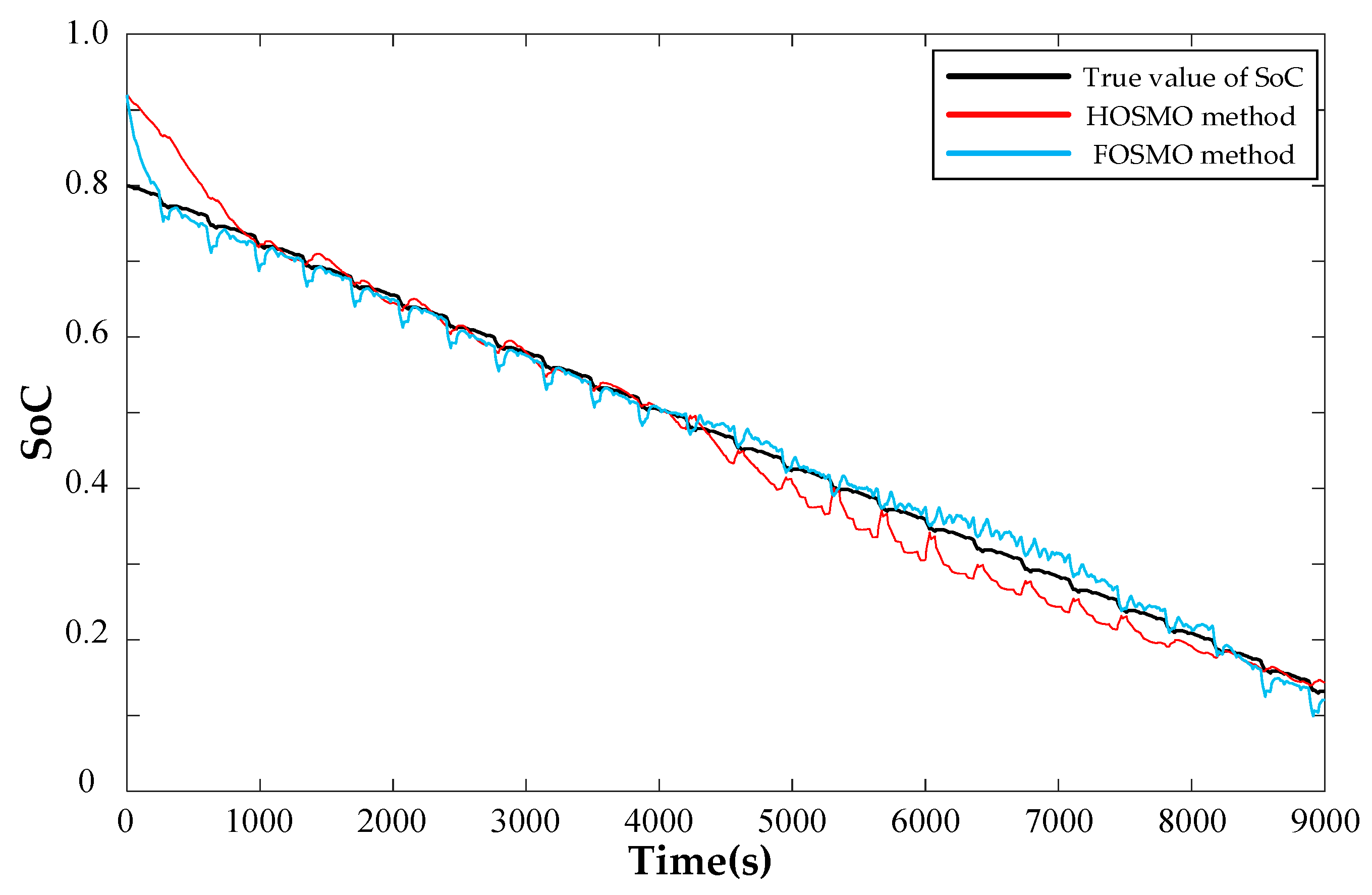
5.1. SoC-Estimation
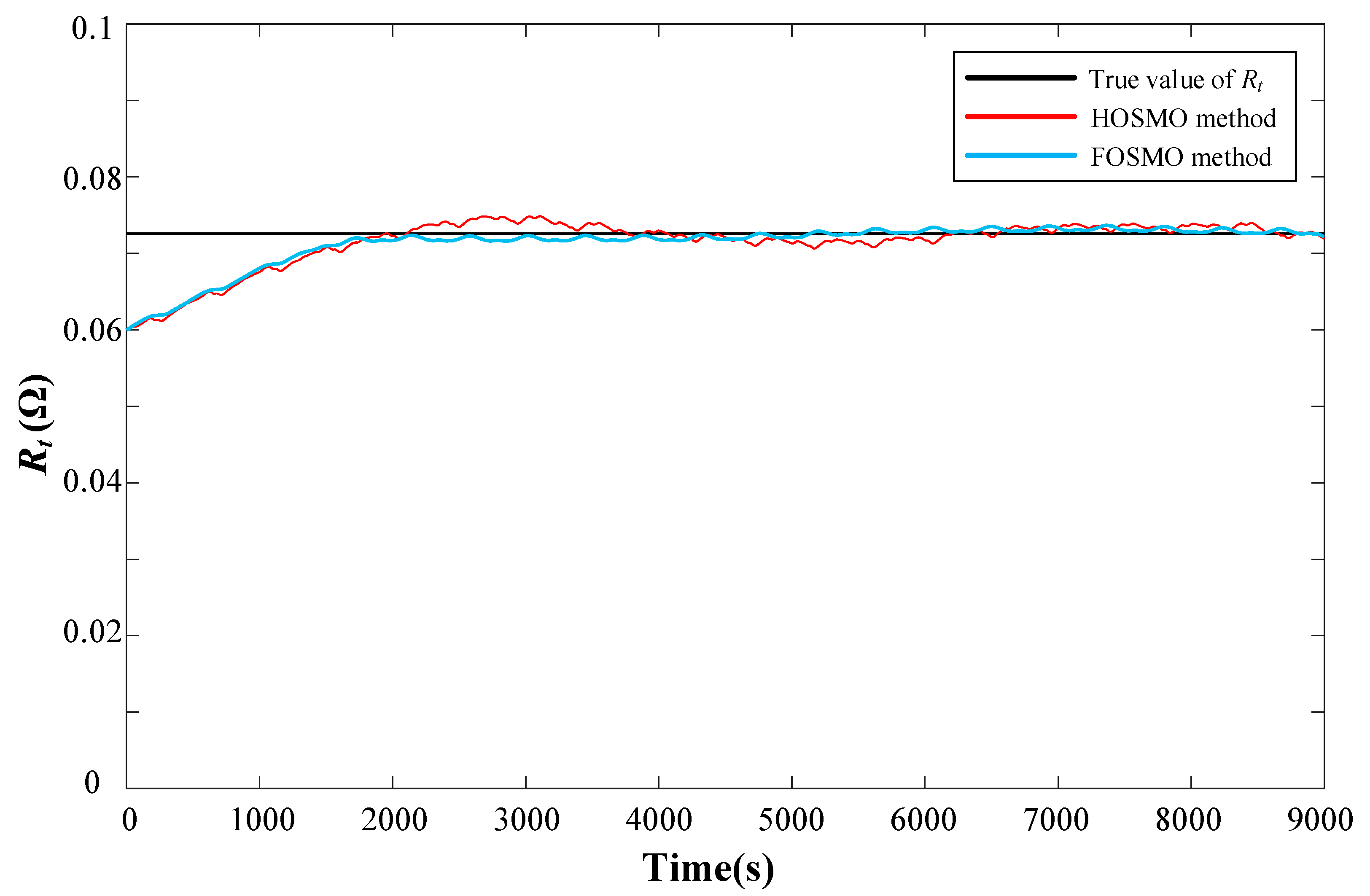
5.2. SoH-Estimation
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Voc | Open-circuit voltage |
| Vt | Terminal voltage |
| Vp | Polarization voltage |
| Vn | Nominal voltage |
| Rt | Ohmic resistance |
| Rp | Polarization resistance |
| Cp | Polarization capacitance |
| Cnom | Nominal capacity |
| Cn | Rated capacity if battery |
| Δf | Uncertainties disturbance |
| REoL | Resistance at the end of life |
| A | Fractional-order parameter |
| Estimate of open-circuit voltage | |
| Estimate of polarization voltage | |
| Estimate of terminal voltage | |
| Estimate of ohmic resistance |
Appendix A
References
- Yang, H.; Wang, P.L.; An, Y.B.; Shi, C.L.; Sun, X.Z.; Wang, K.; Zhang, X. Remaining useful life prediction based on denoising technique and deep neural network for lithium-ion capacitors. eTransportation 2020, 5, 1168–2590. [Google Scholar] [CrossRef]
- Jamal, H.; Khan, F.; Si, H.R.; Kim, J.H. Enhanced compatibility of a polymer-based electrolyte with Li-metal for stable and dendrite-free all-solid-state Li-metal batteries. J. Mater. Chem. A 2021, 9, 27304–27319. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, L.; Wang, L.; Liao, C.; Zhang, Y. Joint state-of-charge and state-of-available-power estimation based on the online parameter identification of lithium-ion battery model. IEEE Trans. Ind. Electron. 2022, 69, 3677–3688. [Google Scholar] [CrossRef]
- Bhat, C.; Channegowda, J.; Chaudhari, S.; Naraharisetti, K. Accurate equivalent circuit parameter estimation using electrochemical battery modelling for pulsed load applications. In Proceedings of the 2021 IEEE Mysore Sub Section International Conference (MysuruCon), Hassan, India, 24–25 October 2021. [Google Scholar]
- Feng, W.; Joseph, Y.; Kaushini, S.W.; William, M.; Javad, S.; Emanuel, T. Epitaxial Al-InAs heterostructures as platform for Josephson junction field-effect transistor logic devices. IEEE Trans. Electron Devices 2021, 68, 1524–1529. [Google Scholar]
- Wang, Y.J.; Wang, L.; Li, M.; Chen, Z.H. A review of key issues for control and management in battery and ultra-capacitor hybrid energy storage systems. eTransportation 2020, 4, 1168–2590. [Google Scholar] [CrossRef]
- Khan, F.; Oh, M.; Kim, J.H. N-functionalized graphene quantum dots: Charge transporting layer for high-rate and durable Li4Ti5O12-based Li-ion battery. Chem. Eng. J. 2019, 369, 1024–1033. [Google Scholar] [CrossRef]
- Siddhartha, R.S.R.; Feng, W.; Ravi, P.; Vivek, D.; Jaydeep, P.K. High noise margin, digital logic design using josephson junction field-effect transistors for cryogenic computing. IEEE Trans. Appl. Superconduct. 2021, 31, 1–5. [Google Scholar]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.I.B.; Mekhilef, S.; Adnan, S.B.R.S. Combined state of charge and state of energy estimation of lithium-ion battery using dual forgetting factor-based adaptive extended lalman filter for electric vehicle applications. IEEE Trans. Veh. Technol. 2021, 70, 1200–1215. [Google Scholar] [CrossRef]
- Feng, Y.; Xue, C.; Han, Q.; Han, F.; Du, J. Robust estimation for state-of-charge and state-of-health of lithium-ion batteries using integral-type terminal sliding-mode observers. IEEE Trans. Ind. Electron. 2020, 67, 4013–4023. [Google Scholar] [CrossRef]
- Wei, Z.; Dong, G.; Zhang, X.; Pou, J.; Quan, Z.; He, H. Model identification and state-of-charge estimation for lithium-ion battery using bilinear parameterization. IEEE Trans. Ind. Electron. 2021, 68, 312–323. [Google Scholar] [CrossRef]
- Tanvir, R.T.; Eric, J.D.; Lee, K.W.; Chinh, D.H. Advanced diagnostics to evaluate heterogeneity in lithium-ion battery modules. eTransportation 2020, 3, 1168–2590. [Google Scholar]
- Lorenzo, M.F.; Bhonsle, S.P.; Arena, C.B.; Davalos, R.V. Rapid impedance spectroscopy for monitoring tissue impedance, temperature, and treatment outcome during electroporation-based therapies. IEEE Trans. Biomed. Eng. 2021, 68, 1536–1546. [Google Scholar] [CrossRef]
- Madani, S.S.; Soghrati, R.; Ziebert, C. A regression-based technique for capacity estimation of lithium-ion batteries. Batteries 2022, 8, 31. [Google Scholar] [CrossRef]
- Yang, G.; Song, K.; Huang, X.; Wang, C.; Huang, X.; Li, J.; Zhu, C. Improved interoperability evaluation method for wireless charging systems based on interface impedance. IEEE Trans. Power Electron. 2021, 36, 8588–8592. [Google Scholar] [CrossRef]
- Haus, B.; Mercorelli, P. Polynomial augmented extended Kalman filter to estimate the state of charge of lithium-ion batteries. IEEE Trans. Veh. Technol. 2020, 69, 1452–1463. [Google Scholar] [CrossRef]
- He, L.; Guo, D.; Zhang, J.; Li, W.; Zheng, Y. A threshold extend Kalman filter algorithm for state of charge estimation of lithium-ion batteries in electric vehicles. IEEE J. Emerg. Select. Top. Ind. Electron. 2020, 3, 190–198. [Google Scholar] [CrossRef]
- Galushkin, N.E.; Yazvinskaya, N.N.; Galushkin, D.N. Investigation of the temperature dependence of parameters in the generalized peukert equation used to estimate the residual capacity of traction lithium-ion batteries. Batteries 2022, 8, 280. [Google Scholar] [CrossRef]
- Kopp, M.; Ströbel, M.; Fill, A.; Pross-Brakhage, J.; Birke, K.P. Artificial feature extraction for estimating state-of-temperature in lithium-ion-cells using various long short-term memory architectures. Batteries 2022, 8, 36. [Google Scholar] [CrossRef]
- Doostmohammadian, M. Single-bit consensus with finite-time convergence: Theory and applications. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3332–3338. [Google Scholar] [CrossRef]
- Kim, I.S. A Technique for Estimating the State of Health of Lithium Batteries through a Dual-Sliding-Mode Observer. IEEE Trans. Power Electron. 2010, 25, 1013–1022. [Google Scholar]
- Alexander, B.; Anderson, H.; Joshua, T. Study on the effect of solar irradiance intermittency mitigation on electric vehicle battery lifetime. In Proceedings of the IEEE Conference on Technologies for Sustainability, Portland, OR, USA, 1–2 August 2013; pp. 262–267. [Google Scholar]
- Mukhopadhyay, S.; Usman, H.M.; Rehman, H. Real time li-ion battery bank parameters estimation via universal adaptive stabilization. IEEE Open J. Control Syst. 2022, 1, 268–293. [Google Scholar] [CrossRef]
- Alexander, P.S.; Matthias, B.; Árpád, W.I. Model-based distinction and quantification of capacity loss and rate capability fade in Li-ion batteries. J. Power Sources 2020, 195, 7634–7638. [Google Scholar]
- Domenico, D.; Stefanopoulou, A.; Fiengo, G. Lithium-ion battery state of charge and critical surface charge estimation using an electrochemical model-based extended Kalman filter. J. Dyn. Syst. Meas. Control 2020, 132, 061302. [Google Scholar] [CrossRef]
- Anudeep, M.; Kim, J.Y.; Carney, K.; DuBois, P. Modeling extreme deformations in lithium batteries. eTransportation 2020, 4, 1168–2590. [Google Scholar]
- Feng, X.N.; Merla, Y.; Weng, C.H.; Ouyang, M.G.; He, X.M.; Liaw, B.Y.; Santhanagopalan, S.; Li, X.M. A reliable approach of differentiating discrete sampled data for battery diagnosis. eTransportation 2020, 3, 1168–2590. [Google Scholar] [CrossRef]
- Morstyn, T.; Savkin, A.V.; Hredzak, B.; Agelidis, V.G. Multi-agent sliding mode control for state of charge balancing between battery energy storage systems distributed in a dc microgrid. IEEE Trans. Smart Grid. 2018, 9, 4735–4743. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, K.; Zhu, C.; Zhang, X.; Zhang, D. Co-estimation of state-of-charge and state-of-health for lithium-ion batteries using an enhanced electrochemical model. IEEE Trans. Ind. Electron. 2022, 69, 2684–2696. [Google Scholar] [CrossRef]
- Levant, A.; Alelishvili, L. Integral High-Order Sliding Modes. IEEE Trans. Autom. Control 2007, 52, 1278–1282. [Google Scholar] [CrossRef]
- Obeid, H.; Laghrouche, S.; Fridman, L.; Chitour, Y.; Harmouche, M. Barrier function-based adaptive super-twisting controller. IEEE Trans. Autom. Control 2020, 65, 4928–4933. [Google Scholar] [CrossRef]
- Obeid, H.; Petrone, R.; Chaoui, H.; Gualous, H. Higher order sliding-mode observers for state-of-charge and state-of-health estimation of lithium-ion batteries. IEEE Trans. Veh. Technol. 2022. [Google Scholar] [CrossRef]
- Tang, Y.G.; Zhang, X.Y.; Zhang, D.L.; Zhao, G.; Guan, X.P. Fractional order sliding mode controller design for antilock braking systems. Neurocomputing 2013, 111, 122–130. [Google Scholar] [CrossRef]
- Feng, Y.; Han, F.L.; Yu, X.H. Chattering free full-order sliding-mode control. Automatica 2014, 50, 1310–1314. [Google Scholar] [CrossRef]
- Zhao, X.B. Research on On-Line State-of-Charge Estimation Technology of Lithium-Ion Battery; Nanjing University of Aeronautics and Astronaut: Nanjing, China, 2016; pp. 45–48. [Google Scholar]
- He, Z.; Yang, Z.; Cui, X.; Li, E. A method of state-of-charge estimation for EV power lithium-ion battery using a novel adaptive extended Kalman filter. IEEE Trans. Veh. Technol. 2020, 69, 14618–14630. [Google Scholar] [CrossRef]
- Lin, C.; Tang, A.H.; Xing, J. Evaluation of electrochemical models-based battery state-of-charge estimation approaches for electric vehicles. Appl. Energy 2017, 207, 394–404. [Google Scholar] [CrossRef]
- Zou, Y.; Hu, X.; Ma, H.; Li, S.E. Combined state of charge and state of health estimation over lithium-ion battery cell cycle lifespan for electric vehicles. J. Power Sources 2015, 273, 793–803. [Google Scholar] [CrossRef]
- Goh, T.; Park, M.; Koo, G.; Seo, M.; Kim, S.W. State-of-health estimation algorithm of Li-ion battery using impedance at low sampling rate. In Proceedings of the IEEE PES Asia-Pacifific Power and Energy Engineering Conference, Xi’an, China, 25–28 October 2016. [Google Scholar]





| Symbol | Mean | Value |
|---|---|---|
| Vn | Nominal voltage | 3.6 V |
| Cnom | Nominal capacity | 2A h |
| Vup | Upper cut-off voltage | 2.5 V |
| Vlow | Lower cut-off voltage | 4.2 V |
| Rp | Polarization resistance | 0.0276 Ω |
| Cp | Polarization capacitance | 1435.2 F |
| Rt | Ohmic resistance | 0.0726 Ω |
| Operating Condition | Method | Mean Absolute Error (MAE) | Root Mean Squared Error (RMSE) | Mean Relative Error (MRE) |
|---|---|---|---|---|
| DST | HOSMO | 0.01536 | 0.02663 | 3.698% |
| FOSMO | 0.01042 | 0.01475 | 2.126% | |
| FUDST | HOSMO | 0.01436 | 0.01843 | 4.088% |
| FOSMO | 0.01018 | 0.01438 | 2.424% |
| Test | Method | Mean Absolute Error (MAE) | Root Mean Squared Error (RMSE) | Mean Relative Error (MRE) |
|---|---|---|---|---|
| Cn | HOSMO | 16.42 F | 149.2 F | 0.2582% |
| FOSMO | 12.49 F | 109.6 F | 0.1739% | |
| Rt | HOSMO | 0.001938 Ω | 0.003795 Ω | 2.969% |
| FOSMO | 0.001576 Ω | 0.003108 Ω | 2.073% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, M.; Wei, K.; Wu, X.; Weng, L.; Su, H.; Wang, D.; Zhang, Y.; Li, J. Fractional-Order Sliding-Mode Observers for the Estimation of State-of-Charge and State-of-Health of Lithium Batteries. Batteries 2023, 9, 213. https://doi.org/10.3390/batteries9040213
Zhou M, Wei K, Wu X, Weng L, Su H, Wang D, Zhang Y, Li J. Fractional-Order Sliding-Mode Observers for the Estimation of State-of-Charge and State-of-Health of Lithium Batteries. Batteries. 2023; 9(4):213. https://doi.org/10.3390/batteries9040213
Chicago/Turabian StyleZhou, Minghao, Kemeng Wei, Xiaogang Wu, Ling Weng, Hongyu Su, Dong Wang, Yuanke Zhang, and Jialin Li. 2023. "Fractional-Order Sliding-Mode Observers for the Estimation of State-of-Charge and State-of-Health of Lithium Batteries" Batteries 9, no. 4: 213. https://doi.org/10.3390/batteries9040213
APA StyleZhou, M., Wei, K., Wu, X., Weng, L., Su, H., Wang, D., Zhang, Y., & Li, J. (2023). Fractional-Order Sliding-Mode Observers for the Estimation of State-of-Charge and State-of-Health of Lithium Batteries. Batteries, 9(4), 213. https://doi.org/10.3390/batteries9040213







