Experimental Investigation on Reversible Swelling Mechanisms of Lithium-Ion Batteries under a Varying Preload Force
Abstract
1. Introduction
2. Materials and Methods
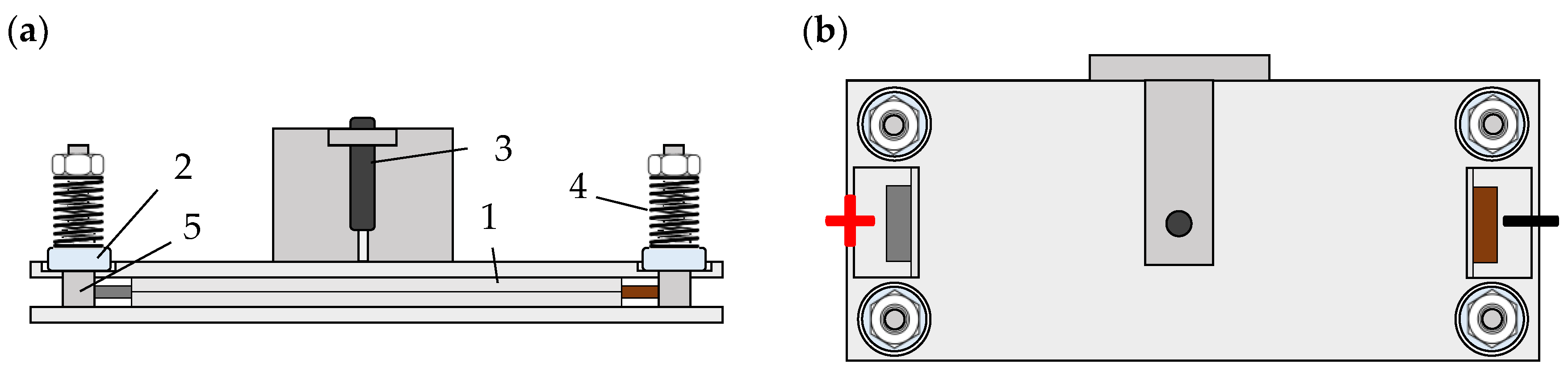
2.1. Specimen
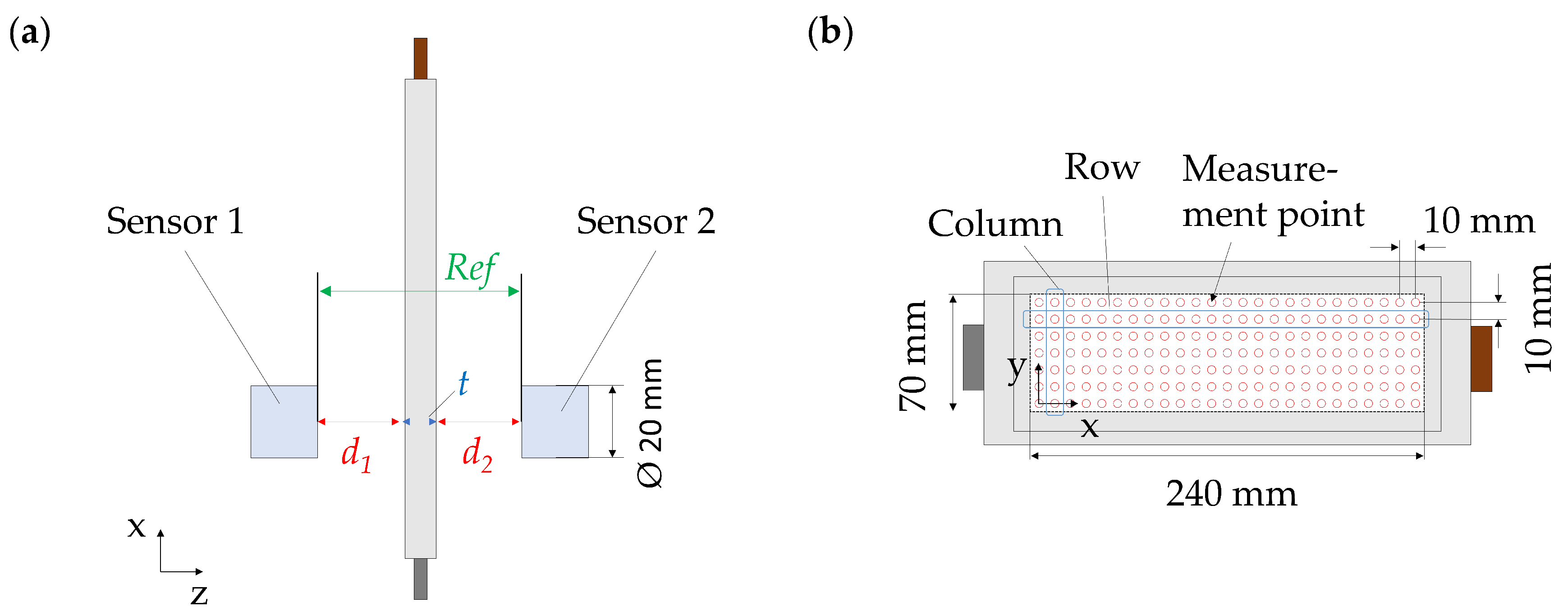
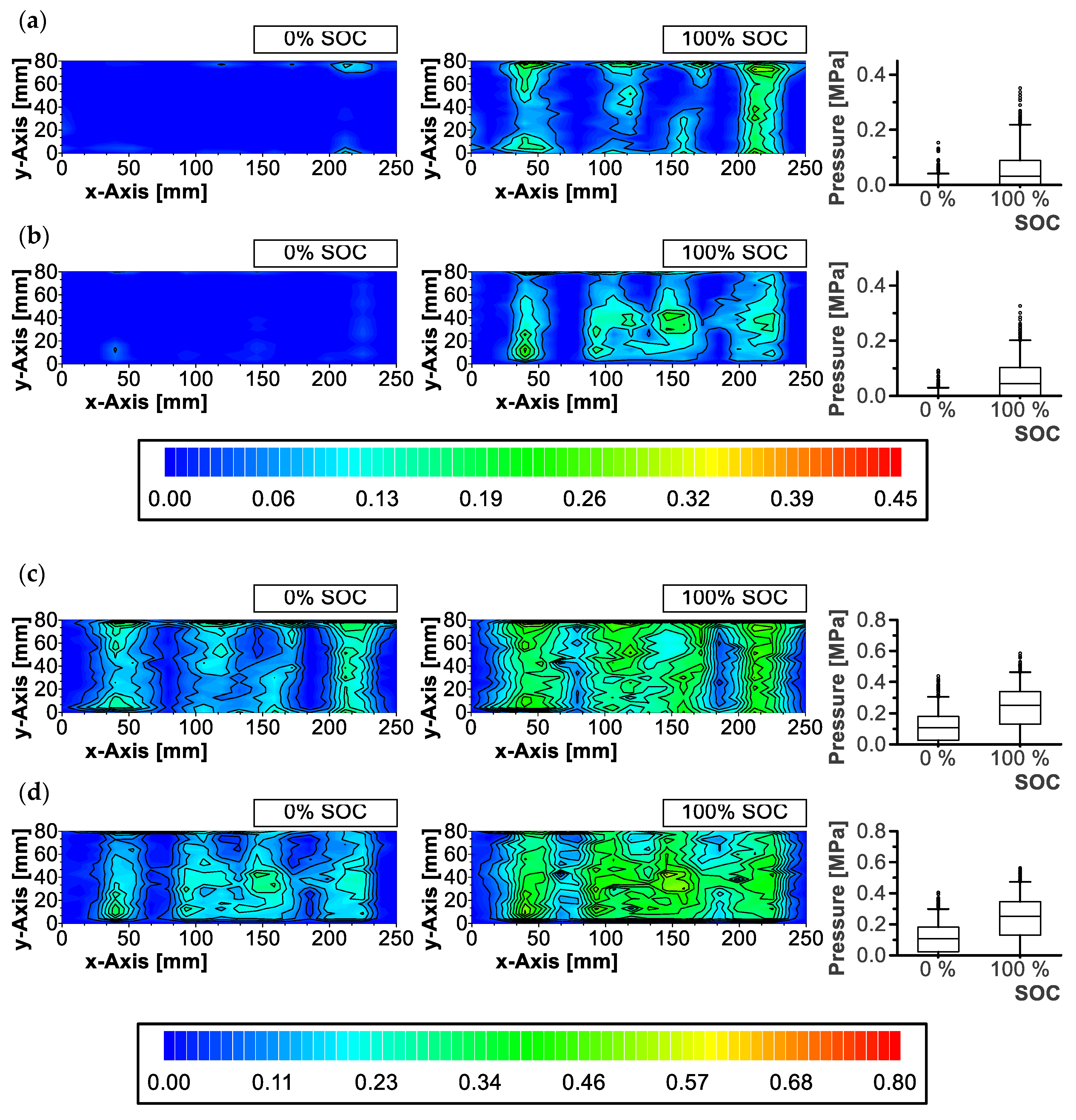
2.2. Pressure Distribution
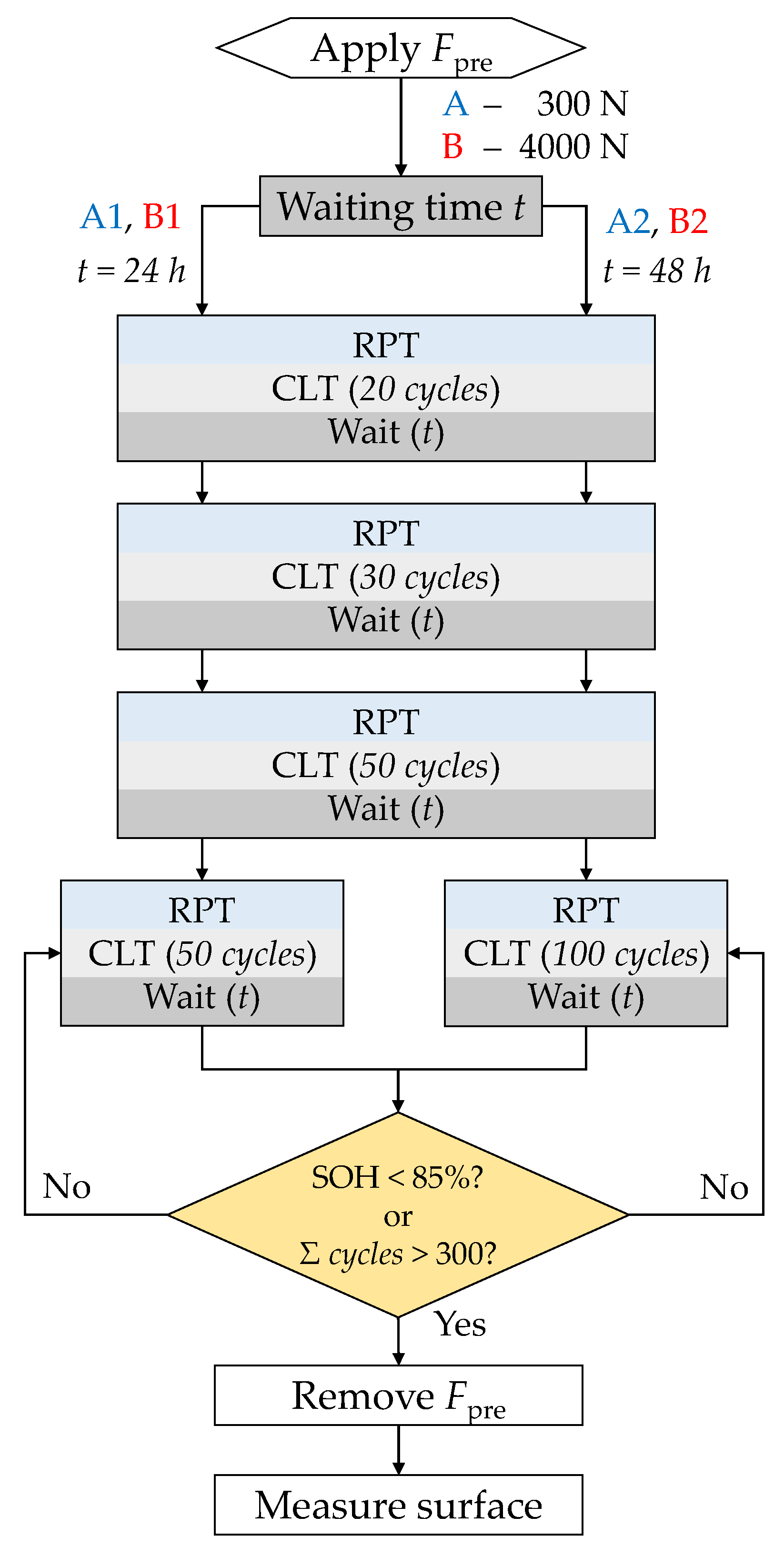
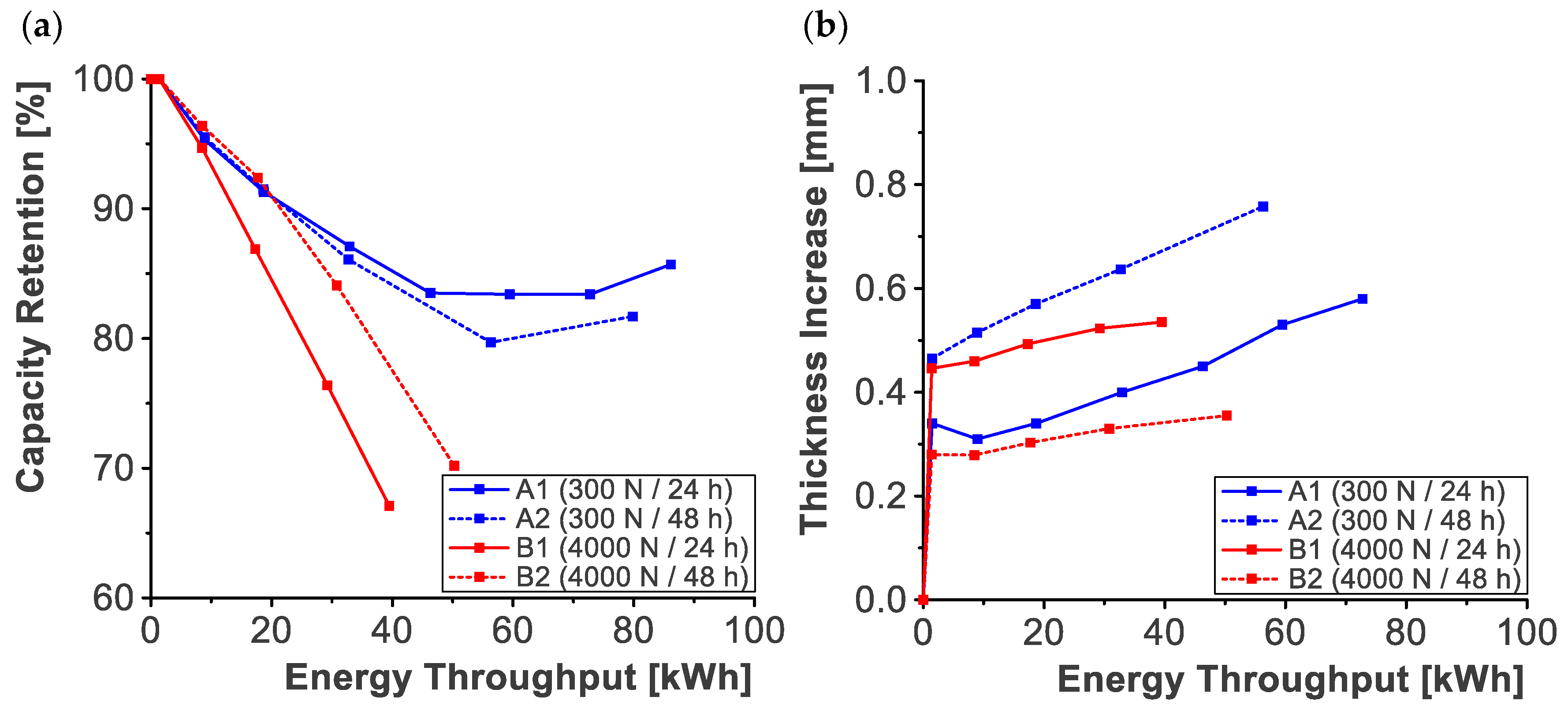
2.3. Aging Procedure
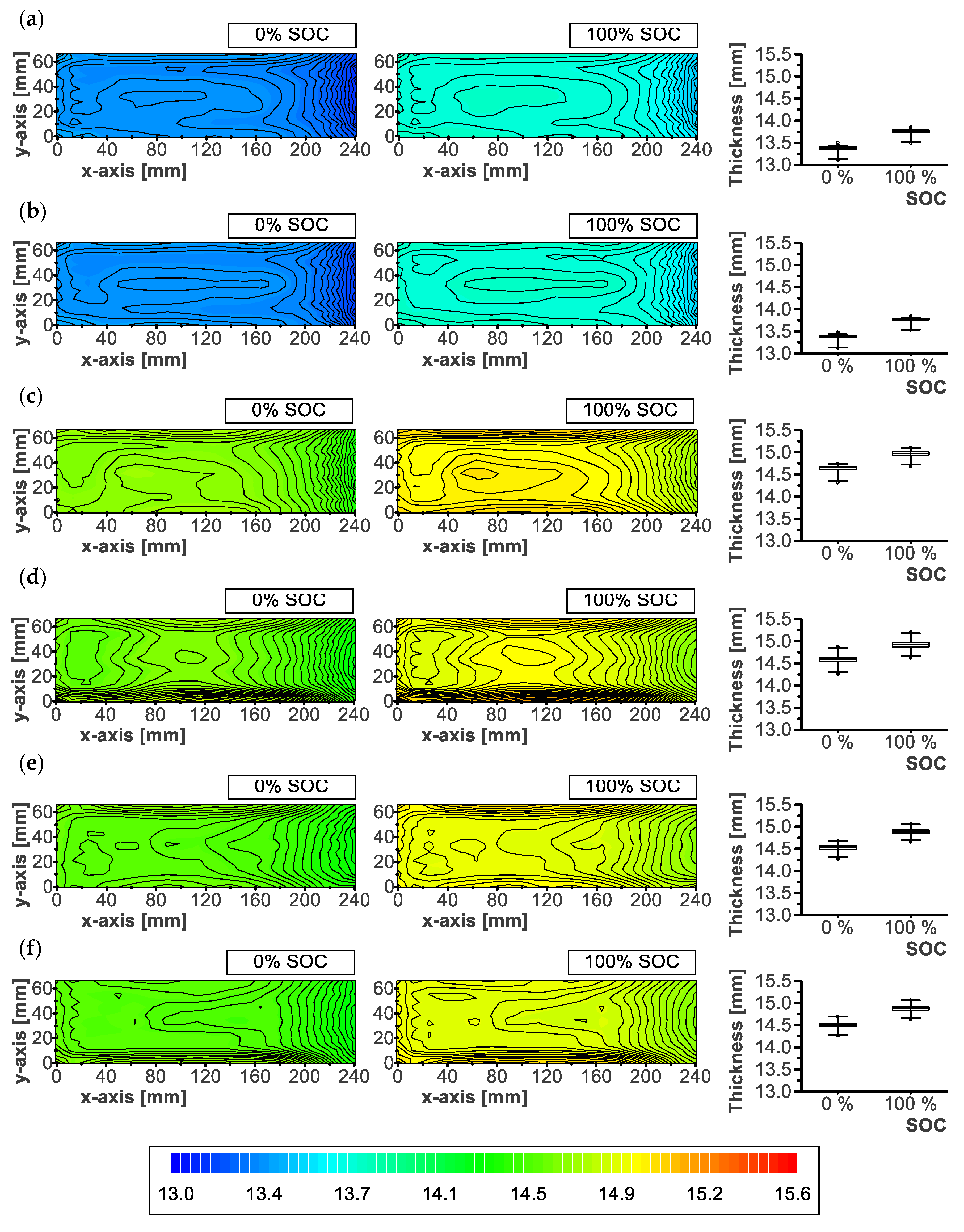
2.4. Local Thickness
3. Results and Discussion
3.1. Pressure Distribution
3.2. Aging Procedure
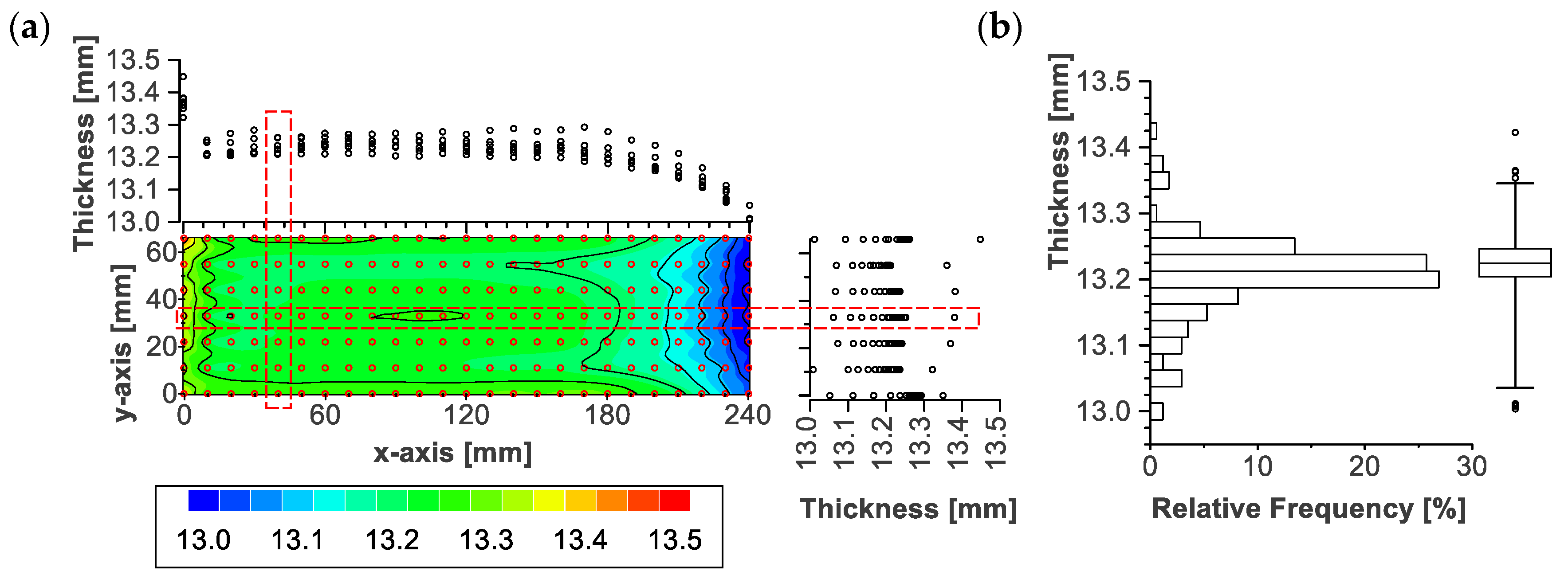
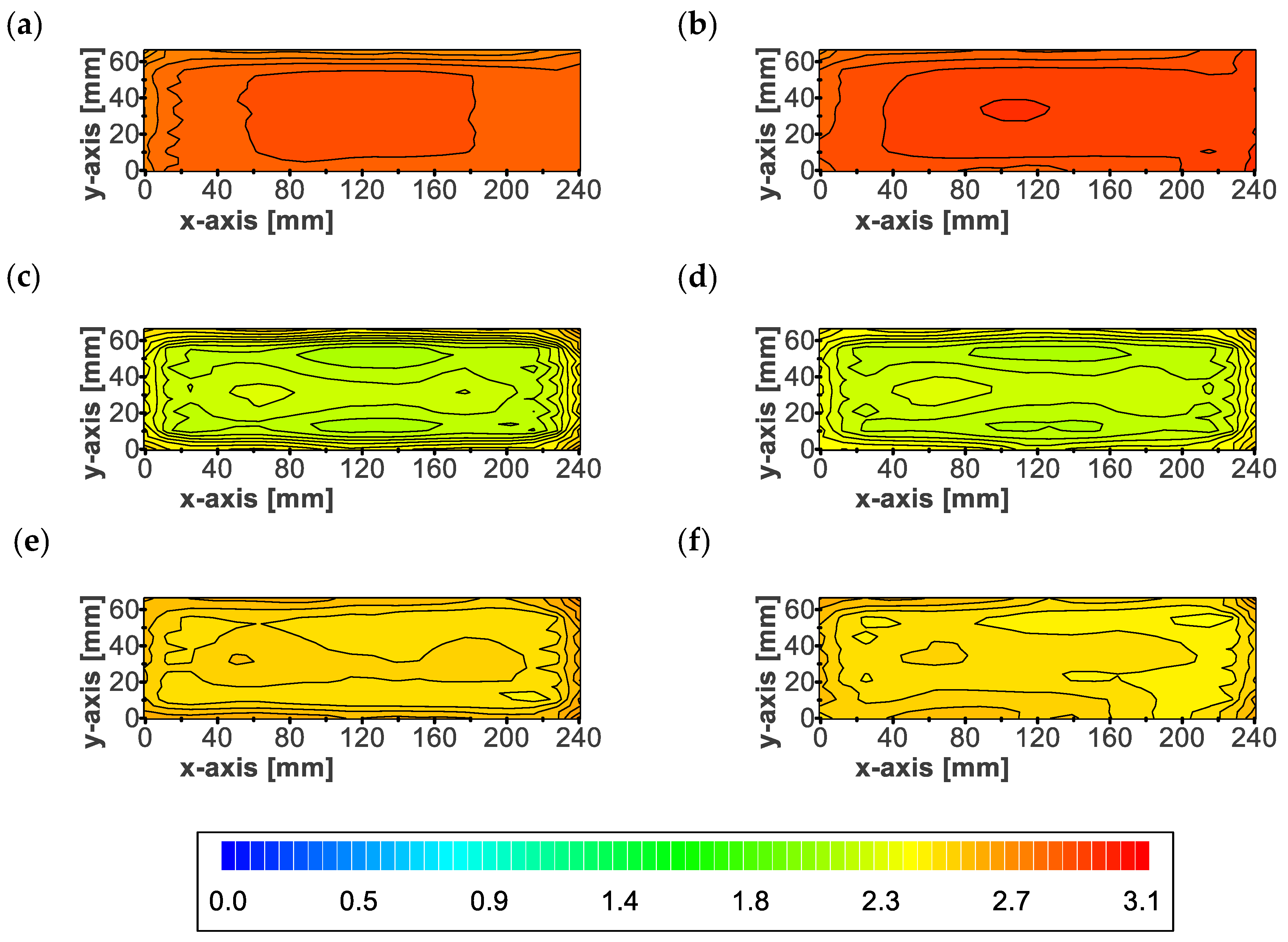
3.3. Local Thickness
3.4. Limitations
4. Conclusions
- Thickness variations related to reversible swelling were conditioned by aging. An aged cell was characterized by a smaller increase in thickness and a different distribution.
- The inhomogeneous irreversible thickness increase did not depend on the level of initial preload force and is expected to be dependent on pressure gradients during aging.
- Positions with higher pressure were prone to irreversible thickness increase. In the case of the investigated pouch cells, these positions were along the edges and in the central area.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CC-CV | Constant current–constant voltage |
| CLT | Cycle life test |
| EV | Electric vehicle |
| LLI | Loss of lithium inventory |
| LIB | Lithium-ion battery |
| RPT | Reference performance test |
| SOC | State of charge |
| SOH | State of health |
Appendix A
Appendix A.1
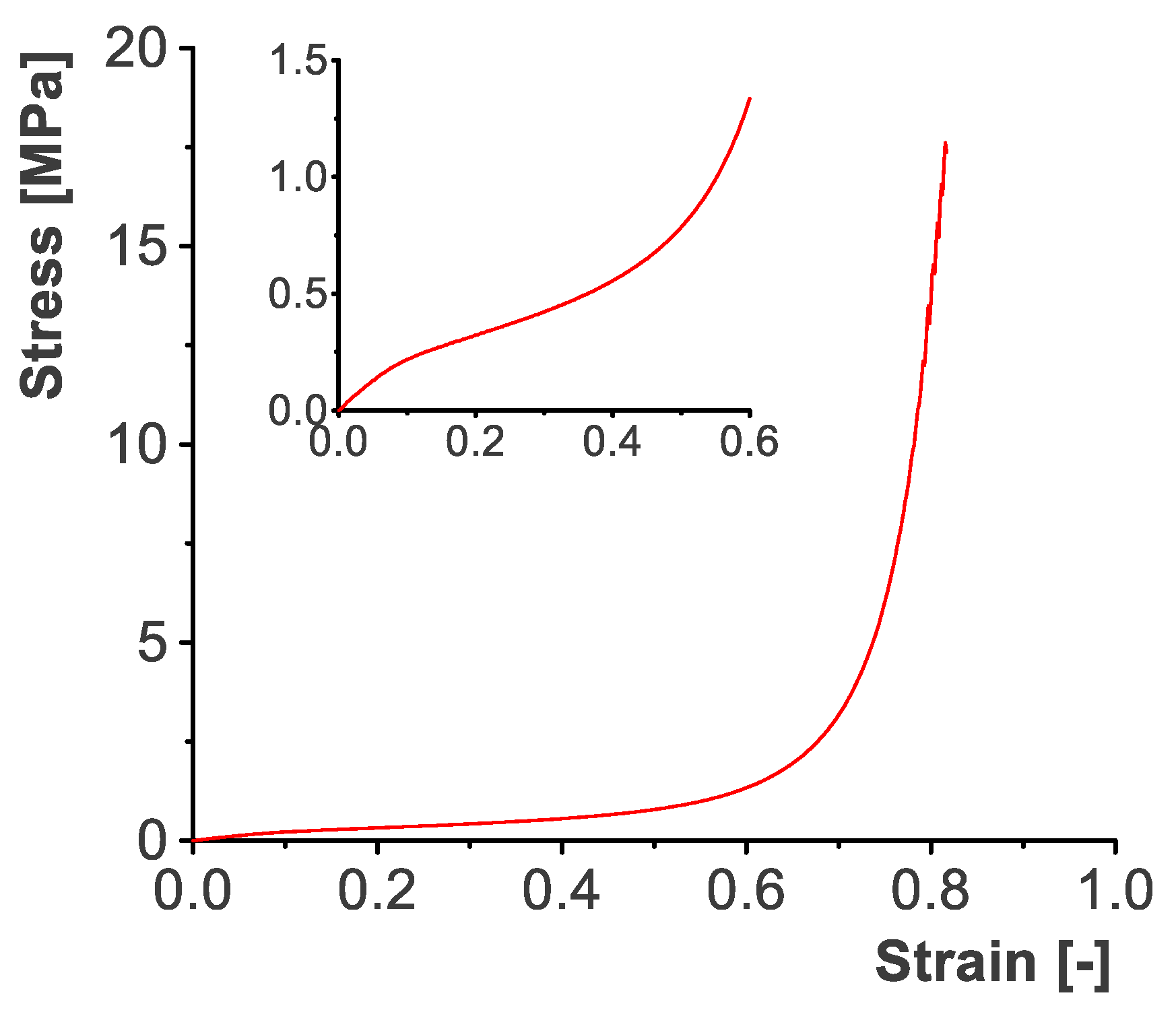
Appendix A.2
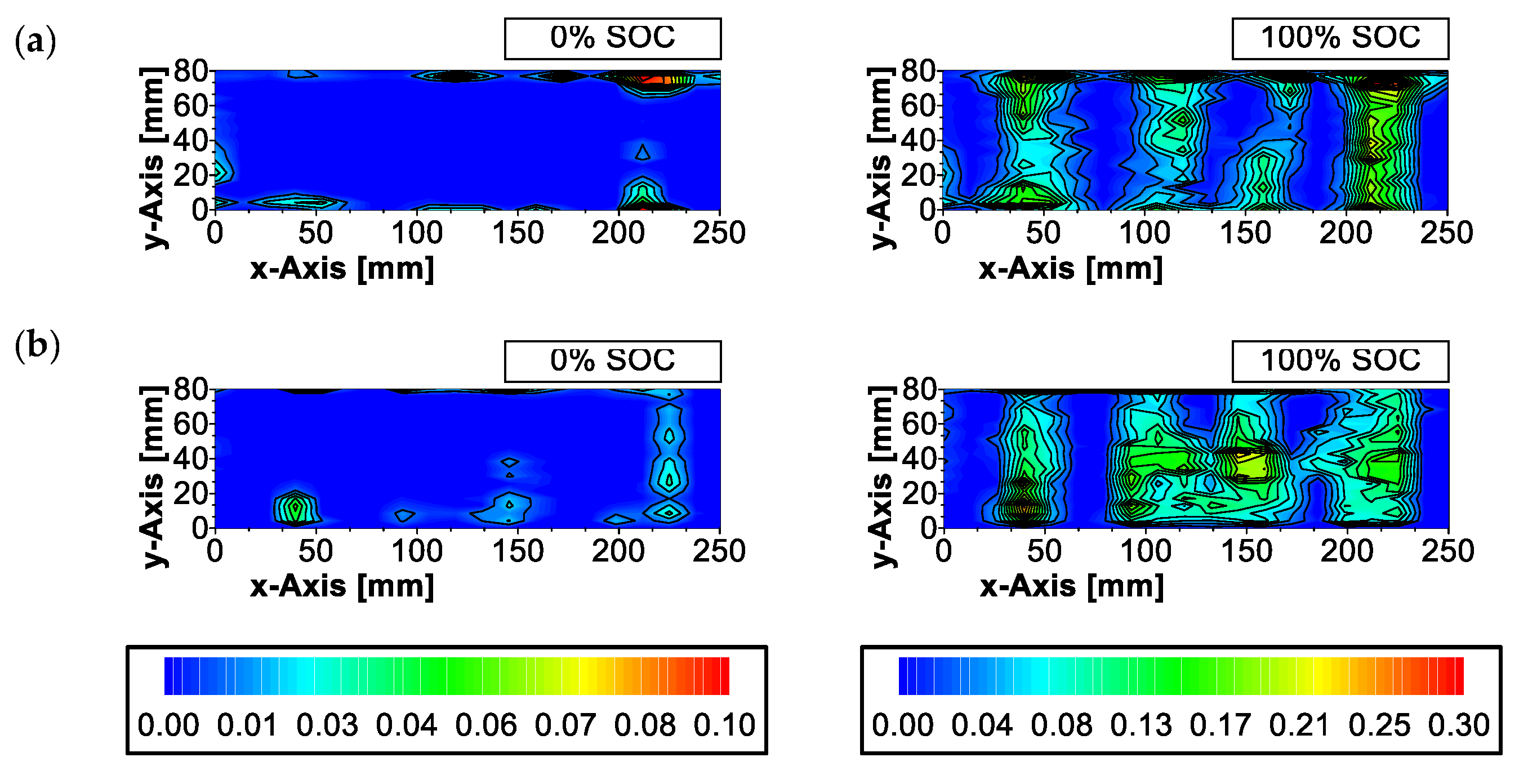
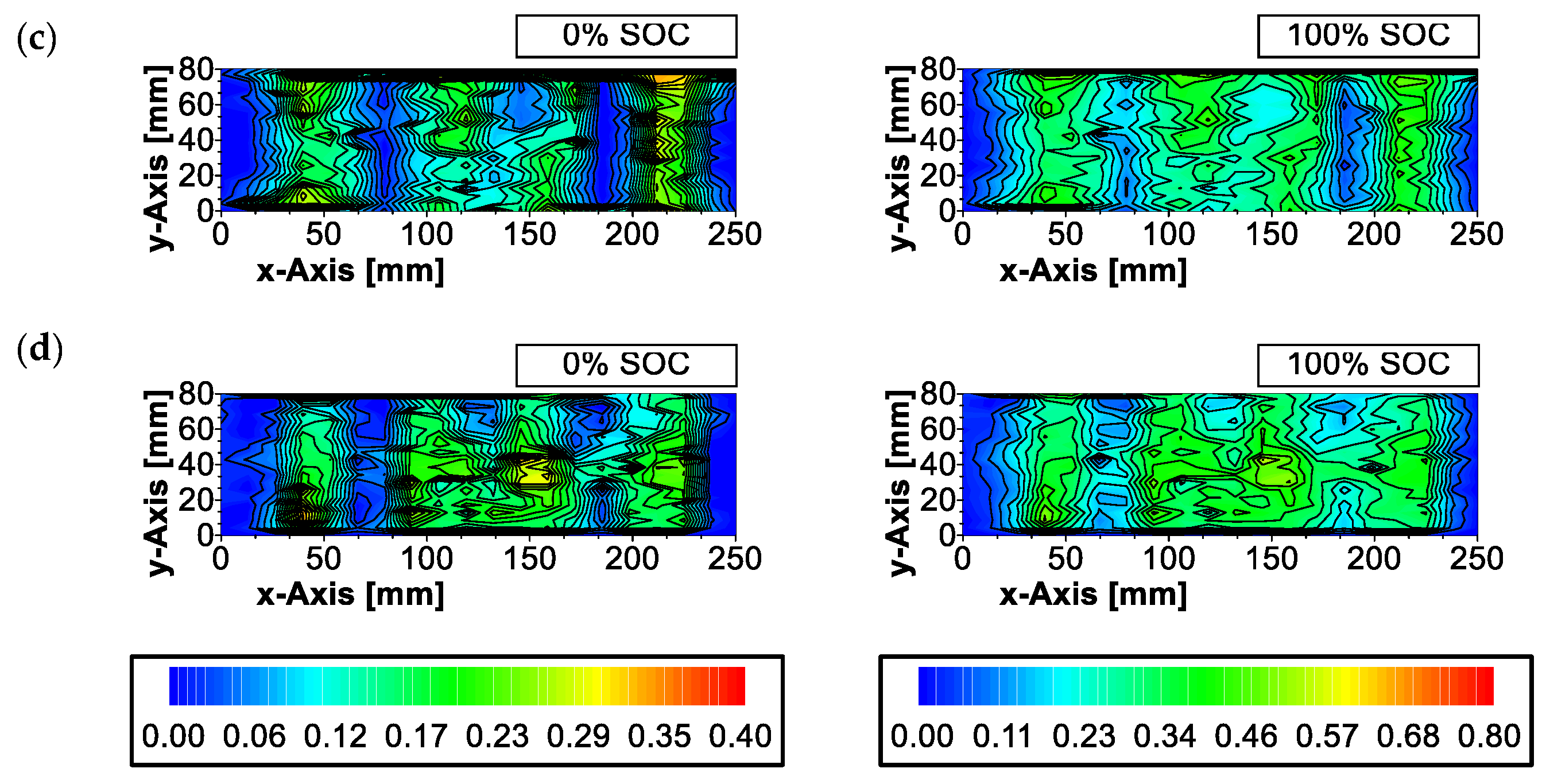
References
- IEA. Global EV Outlook 2022; IEA: Paris, France, 2022. [Google Scholar]
- Feng, X.; Ouyang, M.; Liu, X.; Lu, L.; Xia, Y.; He, X. Thermal runaway mechanism of lithium ion battery for electric vehicles: A review. Energy Storage Mater. 2018, 10, 246–267. [Google Scholar] [CrossRef]
- Ouyang, D.; Chen, M.; Huang, Q.; Weng, J.; Wang, Z.; Wang, J. A Review on the Thermal Hazards of the Lithium-Ion Battery and the Corresponding Countermeasures. Appl. Sci. 2019, 9, 2483. [Google Scholar] [CrossRef]
- Chen, Y.; Kang, Y.; Zhao, Y.; Wang, L.; Liu, J.; Li, Y.; Liang, Z.; He, X.; Li, X.; Tavajohi, N.; et al. A review of lithium-ion battery safety concerns: The issues, strategies, and testing standards. J. Energy Chem. 2021, 59, 83–99. [Google Scholar] [CrossRef]
- Duan, J.; Tang, X.; Dai, H.; Yang, Y.; Wu, W.; Wei, X.; Huang, Y. Building safe lithium-ion batteries for electric vehicles: A review. Electrochem. Energy Rev. 2020, 3, 1–42. [Google Scholar] [CrossRef]
- Höschele, P.; Heindl, S.F.; Erker, S.; Ellersdorfer, C. Influence of reversible swelling and preload force on the failure behavior of a lithium-ion pouch cell tested under realistic boundary conditions. J. Energy Storage, 2023; in press. [Google Scholar]
- Bach, T.C.; Schuster, S.F.; Fleder, E.; Müller, J.; Brand, M.J.; Lorrmann, H.; Jossen, A.; Sextl, G. Nonlinear aging of cylindrical lithium-ion cells linked to heterogeneous compression. J. Energy Storage 2016, 5, 212–223. [Google Scholar] [CrossRef]
- Barai, A.; Tangirala, R.; Uddin, K.; Chevalier, J.; Guo, Y.; McGordon, A.; Jennings, P. The effect of external compressive loads on the cycle lifetime of lithium-ion pouch cells. J. Energy Storage 2017, 13, 211–219. [Google Scholar] [CrossRef]
- Daubinger, P.; Ebert, F.; Hartmann, S.; Giffin, G.A. Impact of electrochemical and mechanical interactions on lithium-ion battery performance investigated by operando dilatometry. J. Power Sources 2021, 488, 229457. [Google Scholar] [CrossRef]
- Klett, M.; Eriksson, R.; Groot, J.; Svens, P.; Ciosek Högström, K.; Lindström, R.W.; Berg, H.; Gustafson, T.; Lindbergh, G.; Edström, K. Non-uniform aging of cycled commercial LiFePO4//graphite cylindrical cells revealed by post-mortem analysis. J. Power Sources 2014, 257, 126–137. [Google Scholar] [CrossRef]
- Li, R.; Li, W.; Singh, A.; Ren, D.; Hou, Z.; Ouyang, M. Effect of external pressure and internal stress on battery performance and lifespan. Energy Storage Mater. 2022, 52, 395–429. [Google Scholar] [CrossRef]
- Rieger, B.; Erhard, S.V.; Rumpf, K.; Jossen, A. A New Method to Model the Thickness Change of a Commercial Pouch Cell during Discharge. J. Electrochem. Soc. 2016, 163, A1566–A1575. [Google Scholar] [CrossRef]
- Zhao, Y.; Patel, Y.; Hunt, I.A.; Kareh, K.M.; Holland, A.A.; Korte, C.; Dear, J.P.; Yue, Y.; Offer, G.J. Preventing lithium ion battery failure during high temperatures by externally applied compression. J. Energy Storage 2017, 13, 296–303. [Google Scholar] [CrossRef]
- Zhou, Y. External pressure: An overlooked metric in evaluating next-generation battery performance. Curr. Opin. Electrochem. 2022, 31, 100916. [Google Scholar] [CrossRef]
- Zhao, J.; Hong, M.; Ju, Z.; Yan, X.; Gai, Y.; Liang, Z. Durable Lithium Metal Anodes Enabled by Interfacial Layers Based on Mechanically Interlocked Networks Capable of Energy Dissipation. Angew. Chem. 2022, 61, e202214386. [Google Scholar] [CrossRef]
- Xu, W.; Wang, J.; Ding, F.; Chen, X.; Nasybulin, E.; Zhang, Y.; Zhang, J.G. Lithium metal anodes for rechargeable batteries. Energy Environ. Sci. 2014, 7, 513–537. [Google Scholar] [CrossRef]
- Cannarella, J.; Arnold, C.B. Ion transport restriction in mechanically strained separator membranes. J. Power Sources 2013, 226, 149–155. [Google Scholar] [CrossRef]
- Cannarella, J.; Arnold, C.B. The Effects of Defects on Localized Plating in Lithium-Ion Batteries. J. Electrochem. Soc. 2015, 162, A1365–A1373. [Google Scholar] [CrossRef]
- Fuchs, G.; Willenberg, L.; Ringbeck, F.; Sauer, D.U. Post-Mortem Analysis of Inhomogeneous Induced Pressure on Commercial Lithium-Ion Pouch Cells and Their Effects. Sustainability 2019, 11, 6738. [Google Scholar] [CrossRef]
- Mohanty, D.; Hockaday, E.; Li, J.; Hensley, D.K.; Daniel, C.; Wood, D.L. Effect of electrode manufacturing defects on electrochemical performance of lithium-ion batteries: Cognizance of the battery failure sources. J. Power Sources 2016, 312, 70–79. [Google Scholar] [CrossRef]
- Spingler, F.B.; Friedrich, S.; Kücher, S.; Schmid, S.; López-Cruz, D.; Jossen, A. The Effects of Non-Uniform Mechanical Compression of Lithium-Ion Cells on Local Current Densities and Lithium Plating. J. Electrochem. Soc. 2021, 168, 110515. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, S.; Li, R.; Ren, D.; Yi, M.; Xu, C.; Han, X.; Lu, L.; Friess, B.; Offer, G.; et al. Inhomogeneous degradation induced by lithium plating in a large-format lithium-ion battery. J. Power Sources 2022, 542, 231753. [Google Scholar] [CrossRef]
- Arunachala, R.; Parthasarathy, C.; Jossen, A.; Garche, J. Inhomogeneities in Large Format Lithium Ion Cells: A Study by Battery Modelling Approach. ECS Trans. 2016, 73, 201–212. [Google Scholar] [CrossRef]
- Galatro, D.; Al-Zareer, M.; Da Silva, C.; Romero, D.A.; Amon, C.H. Thermal behavior of lithium-ion batteries: Aging, heat generation, thermal management and failure. Front. Heat Mass Transf. 2020, 14, 17. [Google Scholar] [CrossRef]
- Ren, D.; Feng, X.; Liu, L.; Hsu, H.; Lu, L.; Wang, L.; He, X.; Ouyang, M. Investigating the relationship between internal short circuit and thermal runaway of lithium-ion batteries under thermal abuse condition. Energy Storage Mater. 2021, 34, 563–573. [Google Scholar] [CrossRef]
- Lin, X.; Khosravinia, K.; Hu, X.; Li, J.; Lu, W. Lithium Plating Mechanism, Detection, and Mitigation in Lithium-Ion Batteries. Prog. Energy Combust. Sci. 2021, 87, 100953. [Google Scholar] [CrossRef]
- Zhao, X.; Yin, Y.; Hu, Y.; Choe, S.Y. Electrochemical-thermal modeling of lithium plating/stripping of Li(Ni0.6Mn0.2Co0.2)O2/Carbon lithium-ion batteries at subzero ambient temperatures. J. Power Sources 2019, 418, 61–73. [Google Scholar] [CrossRef]
- Bitzer, B.; Gruhle, A. A new method for detecting lithium plating by measuring the cell thickness. J. Power Sources 2014, 262, 297–302. [Google Scholar] [CrossRef]
- Bauer, M.; Wachtler, M.; Stöwe, H.; Persson, J.V.; Danzer, M.A. Understanding the dilation and dilation relaxation behavior of graphite-based lithium-ion cells. J. Power Sources 2016, 317, 93–102. [Google Scholar] [CrossRef]
- Epding, B.; Rumberg, B.; Jahnke, H.; Stradtmann, I.; Kwade, A. Investigation of significant capacity recovery effects due to long rest periods during high current cyclic aging tests in automotive lithium ion cells and their influence on lifetime. J. Energy Storage 2019, 22, 249–256. [Google Scholar] [CrossRef]
- Lewerenz, M.; Dechent, P.; Sauer, D.U. Investigation of capacity recovery during rest period at different states-of-charge after cycle life test for prismatic Li(Ni1/3Mn1/3Co1/3)O2-graphite cells. J. Energy Storage 2019, 21, 680–690. [Google Scholar] [CrossRef]
- Tang, M.; Albertus, P.; Newman, J. Two-Dimensional Modeling of Lithium Deposition during Cell Charging. J. Electrochem. Soc. 2009, 156, A390. [Google Scholar] [CrossRef]
- Spingler, F.B.; Naumann, M.; Jossen, A. Capacity Recovery Effect in Commercial LiFePO4/Graphite Cells. J. Electrochem. Soc. 2020, 167, 040526. [Google Scholar] [CrossRef]
- Liu, X.M.; Arnold, C.B. Effects of Cycling Ranges on Stress and Capacity Fade in Lithium-Ion Pouch Cells. J. Electrochem. Soc. 2016, 163, A2501–A2507. [Google Scholar] [CrossRef]
- Fu, R.; Xiao, M.; Choe, S.Y. Modeling, validation and analysis of mechanical stress generation and dimension changes of a pouch type high power Li-ion battery. J. Power Sources 2013, 224, 211–224. [Google Scholar] [CrossRef]
- Grimsmann, F.; Brauchle, F.; Gerbert, T.; Gruhle, A.; Knipper, M.; Parisi, J. Hysteresis and current dependence of the thickness change of lithium-ion cells with graphite anode. J. Energy Storage 2017, 12, 132–137. [Google Scholar] [CrossRef]
- Sauerteig, D.; Hanselmann, N.; Arzberger, A.; Reinshagen, H.; Ivanov, S.; Bund, A. Electrochemical-mechanical coupled modeling and parameterization of swelling and ionic transport in lithium-ion batteries. J. Power Sources 2018, 378, 235–247. [Google Scholar] [CrossRef]
- Zhao, Y.; Spingler, F.B.; Patel, Y.; Offer, G.J.; Jossen, A. Localized Swelling Inhomogeneity Detection in Lithium Ion Cells Using Multi-Dimensional Laser Scanning. J. Electrochem. Soc. 2019, 166, A27–A34. [Google Scholar] [CrossRef]
- Kovachev, G.; Ellersdorfer, C.; Gstrein, G.; Hanzu, I.; Wilkening, H.M.R.; Werling, T.; Schauwecker, F.; Sinz, W. Safety assessment of electrically cycled cells at high temperatures under mechanical crush loads. eTransportation 2020, 6, 100087. [Google Scholar] [CrossRef]
- Dahn, J.R.; Fong, R.; Spoon, M.J. Suppression of staging in lithium-intercalated carbon by disorder in the host. Phys. Rev. Condens. Matter 1990, 42, 6424–6432. [Google Scholar] [CrossRef]
- Yabuuchi, N.; Ohzuku, T. Novel lithium insertion material of LiCo1/3Ni1/3Mn1/3O2 for advanced lithium-ion batteries. J. Power Sources 2003, 119-121, 171–174. [Google Scholar] [CrossRef]
- Li, R.; Ren, D.; Guo, D.; Xu, C.; Fan, X.; Hou, Z.; Lu, L.; Feng, X.; Han, X.; Ouyang, M. Volume Deformation of Large-Format Lithium Ion Batteries under Different Degradation Paths. J. Electrochem. Soc. 2019, 166, A4106–A4114. [Google Scholar] [CrossRef]
- Sturm, J.; Spingler, F.B.; Rieger, B.; Rheinfeld, A.; Jossen, A. Non-Destructive Detection of Local Aging in Lithium-Ion Pouch Cells by Multi-Directional Laser Scanning. J. Electrochem. Soc. 2017, 164, A1342–A1351. [Google Scholar] [CrossRef]
- Choi, Y.H.; Lim, H.K.; Seo, J.H.; Shin, W.J.; Choi, J.H.; Park, J.H. Development of Standardized Battery Pack for Next-Generation PHEVs in Considering the Effect of External Pressure on Lithium-Ion Pouch Cells. SAE Int. J. Altern. Powertrains 2018, 7, 195–205. [Google Scholar] [CrossRef]
- Cannarella, J.; Arnold, C.B. Stress evolution and capacity fade in constrained lithium-ion pouch cells. J. Power Sources 2014, 245, 745–751. [Google Scholar] [CrossRef]
- Cannarella, J.; Arnold, C.B. State of health and charge measurements in lithium-ion batteries using mechanical stress. J. Power Sources 2014, 269, 7–14. [Google Scholar] [CrossRef]
- Deich, T.; Hahn, S.L.; Both, S.; Birke, K.P.; Bund, A. Validation of an actively-controlled pneumatic press to simulate automotive module stiffness for mechanically representative lithium-ion cell aging. J. Energy Storage 2020, 28, 101192. [Google Scholar] [CrossRef]
- Hahn, S.; Theil, S.; Kroggel, J.; Birke, K.P. Pressure Prediction Modeling and Validation for Lithium-Ion Pouch Cells in Buffered Module Assemblies. J. Energy Storage 2021, 40, 102517. [Google Scholar] [CrossRef]
- Mohan, S.; Kim, Y.; Siegel, J.B.; Samad, N.A.; Stefanopoulou, A.G. A Phenomenological Model of Bulk Force in a Li-Ion Battery Pack and Its Application to State of Charge Estimation. J. Electrochem. Soc. 2014, 161, A2222–A2231. [Google Scholar] [CrossRef]
- Oh, K.Y.; Epureanu, B.I.; Siegel, J.B.; Stefanopoulou, A.G. Phenomenological force and swelling models for rechargeable lithium-ion battery cells. J. Power Sources 2016, 310, 118–129. [Google Scholar] [CrossRef]
- Sauerteig, D.; Ivanov, S.; Reinshagen, H.; Bund, A. Reversible and irreversible dilation of lithium-ion battery electrodes investigated by in-situ dilatometry. J. Power Sources 2017, 342, 939–946. [Google Scholar] [CrossRef]
- Deich, T.; Storch, M.; Steiner, K.; Bund, A. Effects of module stiffness and initial compression on lithium-ion cell aging. J. Power Sources 2021, 506, 230163. [Google Scholar] [CrossRef]
- Müller, V.; Scurtu, R.G.; Richter, K.; Waldmann, T.; Memm, M.; Danzer, M.A.; Wohlfahrt-Mehrens, M. Effects of Mechanical Compression on the Aging and the Expansion Behavior of Si/C-Composite|NMC811 in Different Lithium-Ion Battery Cell Formats. J. Electrochem. Soc. 2019, 166, A3796–A3805. [Google Scholar] [CrossRef]
- Mussa, A.S.; Klett, M.; Lindbergh, G.; Lindström, R.W. Effects of external pressure on the performance and ageing of single-layer lithium-ion pouch cells. J. Power Sources 2018, 385, 18–26. [Google Scholar] [CrossRef]
- Peabody, C.; Arnold, C.B. The role of mechanically induced separator creep in lithium-ion battery capacity fade. J. Power Sources 2011, 196, 8147–8153. [Google Scholar] [CrossRef]
- Aufschläger, A.; Kücher, S.; Kraft, L.; Spingler, F.; Niehoff, P.; Jossen, A. High precision measurement of reversible swelling and electrochemical performance of flexibly compressed 5 Ah NMC622/graphite lithium-ion pouch cells. J. Energy Storage 2023, 59, 106483. [Google Scholar] [CrossRef]
- Agubra, V.A.; Fergus, J.W. The formation and stability of the solid electrolyte interface on the graphite anode. J. Power Sources 2014, 268, 153–162. [Google Scholar] [CrossRef]
- Blazek, P.; Westenberger, P.; Erker, S.; Brinek, A.; Zikmund, T.; Rettenwander, D.; Wagner, N.P.; Keckes, J.; Kaiser, J.; Kazda, T.; et al. Axially and radially inhomogeneous swelling in commercial 18650 Li-ion battery cells. J. Energy Storage 2022, 52, 104563. [Google Scholar] [CrossRef]
- Jaumann, T.; Balach, J.; Langklotz, U.; Sauchuk, V.; Fritsch, M.; Michaelis, A.; Teltevskij, V.; Mikhailova, D.; Oswald, S.; Klose, M.; et al. Lifetime vs. rate capability: Understanding the role of FEC and VC in high-energy Li-ion batteries with nano-silicon anodes. Energy Storage Mater. 2017, 6, 26–35. [Google Scholar] [CrossRef]
- Li, R.; Ren, D.; WANG, S.; XIE, Y.; Hou, Z.; LU, L.; Ouyang, M. Non-destructive local degradation detection in large format lithium-ion battery cells using reversible strain heterogeneity. J. Energy Storage 2021, 40, 102788. [Google Scholar] [CrossRef]
- Maranchi, J.P.; Hepp, A.F.; Evans, A.G.; Nuhfer, N.T.; Kumta, P.N. Interfacial Properties of the a Si Cu: Active–Inactive Thin-Film Anode System for Lithium-Ion Batteries. J. Electrochem. Soc. 2006, 153, A1246. [Google Scholar] [CrossRef]
- Matadi, B.P.; Geniès, S.; Delaille, A.; Waldmann, T.; Kasper, M.; Wohlfahrt-Mehrens, M.; Aguesse, F.; Bekaert, E.; Jiménez-Gordon, I.; Daniel, L.; et al. Effects of Biphenyl Polymerization on Lithium Deposition in Commercial Graphite/NMC Lithium-Ion Pouch-Cells during Calendar Aging at High Temperature. J. Electrochem. Soc. 2017, 164, A1089–A1097. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Sheldon, B.W. Deformation and stress in electrode materials for Li-ion batteries. Prog. Mater. Sci. 2014, 63, 58–116. [Google Scholar] [CrossRef]
- Wünsch, M.; Kaufman, J.; Sauer, D.U. Investigation of the influence of different bracing of automotive pouch cells on cyclic liefetime and impedance spectra. J. Energy Storage 2019, 21, 149–155. [Google Scholar] [CrossRef]
- Xu, Z.; Rahman, M.M.; Mu, L.; Liu, Y.; Lin, F. Chemomechanical behaviors of layered cathode materials in alkali metal ion batteries. J. Mater. Chem. 2018, 6, 21859–21884. [Google Scholar] [CrossRef]
- Yan, P.; Zheng, J.; Gu, M.; Xiao, J.; Zhang, J.G.; Wang, C.M. Intragranular cracking as a critical barrier for high-voltage usage of layer-structured cathode for lithium-ion batteries. Nat. Commun. 2017, 8, 14101. [Google Scholar] [CrossRef]
- Zhang, N.; Tang, H. Dissecting anode swelling in commercial lithium-ion batteries. J. Power Sources 2012, 218, 52–55. [Google Scholar] [CrossRef]
- Gupta, A.; Kazyak, E.; Craig, N.; Christensen, J.; Dasgupta, N.P.; Sakamoto, J. Evaluating the Effects of Temperature and Pressure on Li/PEO-LiTFSI Interfacial Stability and Kinetics. J. Electrochem. Soc. 2018, 165, A2801–A2806. [Google Scholar] [CrossRef]
- Louli, A.J.; Genovese, M.; Weber, R.; Hames, S.G.; Logan, E.R.; Dahn, J.R. Exploring the Impact of Mechanical Pressure on the Performance of Anode-Free Lithium Metal Cells. J. Electrochem. Soc. 2019, 166, A1291–A1299. [Google Scholar] [CrossRef]
- Mao, Z.; Farkhondeh, M.; Pritzker, M.; Fowler, M.; Chen, Z. Calendar Aging and Gas Generation in Commercial Graphite/NMC-LMO Lithium-Ion Pouch Cell. J. Electrochem. Soc. 2017, 164, A3469–A3483. [Google Scholar] [CrossRef]
- Müller, V.; Scurtu, R.G.; Memm, M.; Danzer, M.A.; Wohlfahrt-Mehrens, M. Study of the influence of mechanical pressure on the performance and aging of Lithium-ion battery cells. J. Power Sources 2019, 440, 227148. [Google Scholar] [CrossRef]
- Wang, M.J.; Choudhury, R.; Sakamoto, J. Characterizing the Li-Solid-Electrolyte Interface Dynamics as a Function of Stack Pressure and Current Density. Joule 2019, 3, 2165–2178. [Google Scholar] [CrossRef]
- Weber, R.; Genovese, M.; Louli, A.J.; Hames, S.; Martin, C.; Hill, I.G.; Dahn, J.R. Long cycle life and dendrite-free lithium morphology in anode-free lithium pouch cells enabled by a dual-salt liquid electrolyte. Nat. Energy 2019, 4, 683–689. [Google Scholar] [CrossRef]
- Wilkinson, D.P.; Blom, H.; Brandt, K.; Wainwright, D. Effects of physical constraints on Li cyclability. J. Power Sources 1991, 36, 517–527. [Google Scholar] [CrossRef]
- Yin, X.; Tang, W.; Im Jung, D.; Phua, K.C.; Adams, S.; Lee, S.W.; Zheng, G.W. Insights into morphological evolution and cycling behaviour of lithium metal anode under mechanical pressure. Nano Energy 2018, 50, 659–664. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, Q.J.; Harrison, K.L.; Jungjohann, K.; Boyce, B.L.; Roberts, S.A.; Attia, P.M.; Harris, S.J. Rethinking How External Pressure Can Suppress Dendrites in Lithium Metal Batteries. J. Electrochem. Soc. 2019, 166, A3639–A3652. [Google Scholar] [CrossRef]
- Zhong, X.; Yang, L.; Li, N.; Chu, Z.; Chen, J.; Zhu, S.; Song, W.L.; Ai, S.; Chen, H.S. In-situ characterizations and mechanism analysis of mechanical inhomogeneity in a prismatic battery module. J. Power Sources 2022, 548, 232053. [Google Scholar] [CrossRef]
- Von Kessel, O.; Deich, T.; Hahn, S.; Brauchle, F.; Vrankovic, D.; Soczka-Guth, T.; Birke, K.P. Mechanical impedance as a tool for electromechanical investigation and equivalent modeling of lithium-ion batteries. J. Power Sources 2021, 508, 230337. [Google Scholar] [CrossRef]
- USABC. Electric Vehicle Battery Test Procedures Manual: Revision 2; Lockheed Idaho Technologies Company: Idaho Falls, ID, USA, 1996. [Google Scholar]
- Sun, T.; Shen, T.; Zheng, Y.; Ren, D.; Zhu, W.; Li, J.; Wang, Y.; Kuang, K.; Rui, X.; Wang, S.; et al. Modeling the inhomogeneous lithium plating in lithium-ion batteries induced by non-uniform temperature distribution. Electrochim. Acta 2022, 425, 140701. [Google Scholar] [CrossRef]
- Zhu, Y.; Yan, F.; Kang, J.; Du, C.; Zhang, C.; Turkson, R.F. Fading analysis of the Li(NiCoMn)O2 battery under different SOC cycle intervals. Ionics 2017, 23, 1383–1390. [Google Scholar] [CrossRef]
- Preger, Y.; Barkholtz, H.M.; Fresquez, A.; Campbell, D.L.; Juba, B.W.; Romàn-Kustas, J.; Ferreira, S.R.; Chalamala, B. Degradation of Commercial Lithium-Ion Cells as a Function of Chemistry and Cycling Conditions. J. Electrochem. Soc. 2020, 167, 120532. [Google Scholar] [CrossRef]
- Sommer, L.W.; Kiesel, P.; Ganguli, A.; Lochbaum, A.; Saha, B.; Schwartz, J.; Bae, C.J.; Alamgir, M.; Raghavan, A. Fast and slow ion diffusion processes in lithium ion pouch cells during cycling observed with fiber optic strain sensors. J. Power Sources 2015, 296, 46–52. [Google Scholar] [CrossRef]
- Lee, J.H.; Lee, H.M.; Ahn, S. Battery dimensional changes occurring during charge/discharge cycles—Thin rectangular lithium ion and polymer cells. J. Power Sources 2003, 119–121, 833–837. [Google Scholar] [CrossRef]
- Li, X.; Zeng, T.; Qin, H.; Huo, R.; Liu, Y.; Wei, D.; Ding, X. Investigation of inhomogeneous degradation in large-format lithium-ion batteries. J. Energy Storage 2021, 42, 103113. [Google Scholar] [CrossRef]
- Hu, D.; Chen, L.; Tian, J.; Su, Y.; Li, N.; Chen, G.; Hu, Y.; Dou, Y.; Chen, S.; Wu, F. Research Progress of Lithium Plating on Graphite Anode in Lithium—Ion Batteries. Chin. J. Chem. 2021, 39, 165–173. [Google Scholar] [CrossRef]
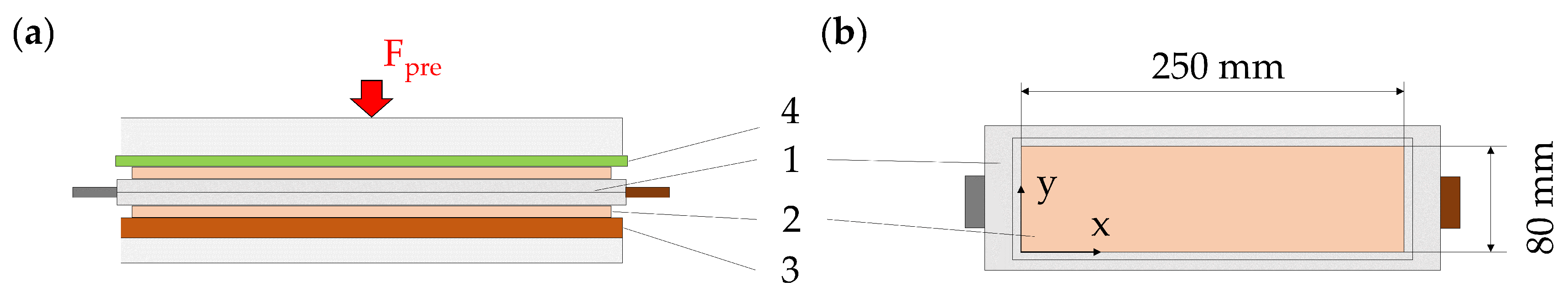
| Parameter | Value | |
|---|---|---|
| Nominal capacity | 60 | |
| Dimension | 300 × 110 × 14.5 | |
| Cathode/anode material | NMC622/graphite | |
| Min. voltage | 2.5 | |
| Max. voltage | 4.2 | |
| Anode thickness | 208 | |
| Cathode thickness | 172 | |
| Separator thickness | 15 | |
| Layers of cathodes/anodes | 31/32 | |
| Cell | Initial Capacity under | No. of Cycles | Capacity Retention | |
|---|---|---|---|---|
| () | (Ah) | (-) | (%) | |
| A1 | 300 | 59.5 | 331 | 85.7 |
| A2 | 300 | 59.7 | 323 | 81.7 |
| B1 | 4000 | 58.1 | 169 | 67.1 |
| B2 | 4000 | 58.0 | 219 | 70.2 |
| Cell | Average | ||
|---|---|---|---|
| (mm) | (mm) | ||
| Fresh | F1 | 13.36 | 13.37 |
| F2 | 13.37 | ||
| Aged | A1 | 14.59 | 14.56 |
| A2 | 14.63 | ||
| B1 | 14.52 | ||
| B2 | 14.51 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michelini, E.; Höschele, P.; Heindl, S.F.; Erker, S.; Ellersdorfer, C. Experimental Investigation on Reversible Swelling Mechanisms of Lithium-Ion Batteries under a Varying Preload Force. Batteries 2023, 9, 218. https://doi.org/10.3390/batteries9040218
Michelini E, Höschele P, Heindl SF, Erker S, Ellersdorfer C. Experimental Investigation on Reversible Swelling Mechanisms of Lithium-Ion Batteries under a Varying Preload Force. Batteries. 2023; 9(4):218. https://doi.org/10.3390/batteries9040218
Chicago/Turabian StyleMichelini, Emanuele, Patrick Höschele, Simon Franz Heindl, Simon Erker, and Christian Ellersdorfer. 2023. "Experimental Investigation on Reversible Swelling Mechanisms of Lithium-Ion Batteries under a Varying Preload Force" Batteries 9, no. 4: 218. https://doi.org/10.3390/batteries9040218
APA StyleMichelini, E., Höschele, P., Heindl, S. F., Erker, S., & Ellersdorfer, C. (2023). Experimental Investigation on Reversible Swelling Mechanisms of Lithium-Ion Batteries under a Varying Preload Force. Batteries, 9(4), 218. https://doi.org/10.3390/batteries9040218









