Electrical Modeling and Impedance Spectra of Lithium-Ion Batteries and Supercapacitors
Abstract
1. Introduction
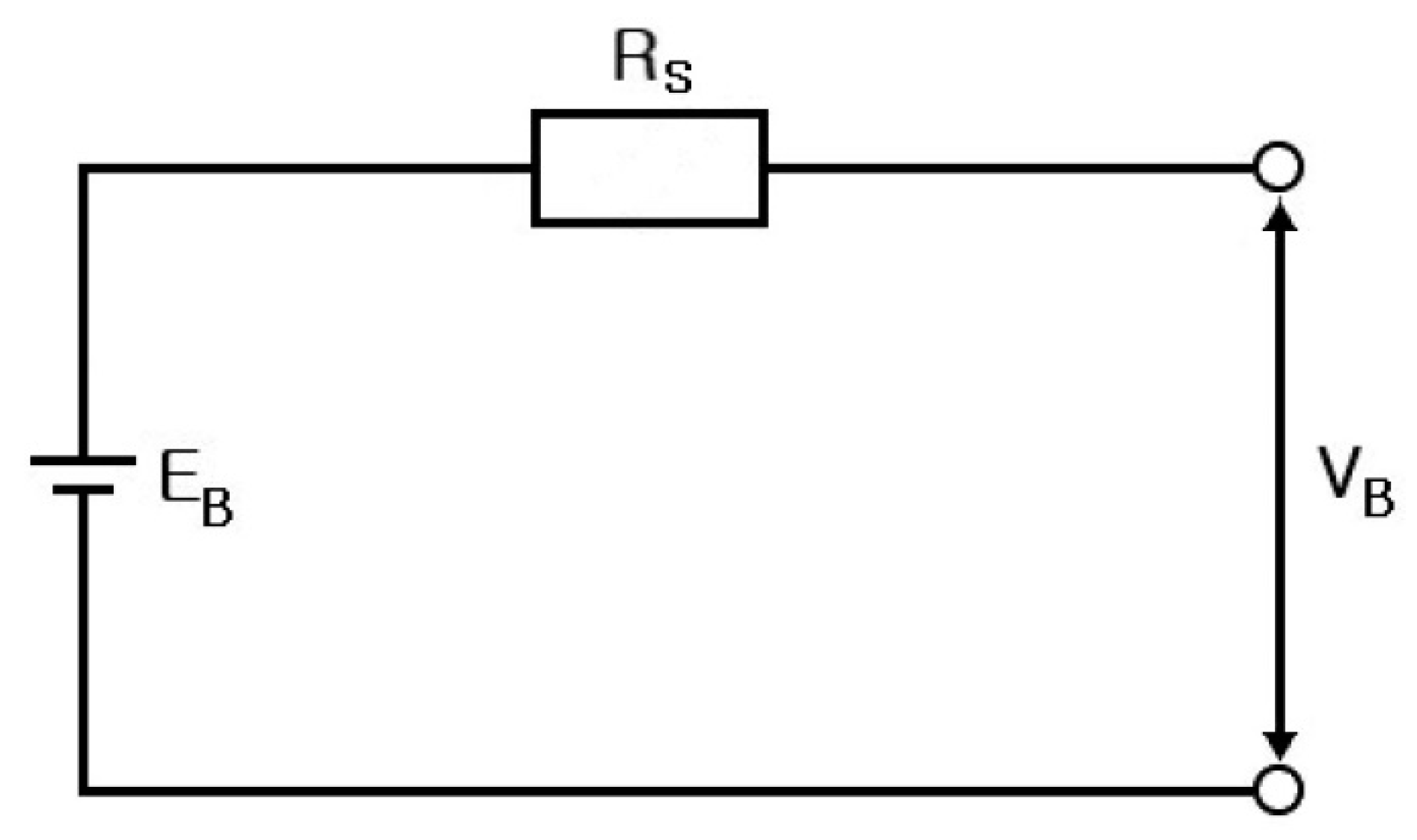
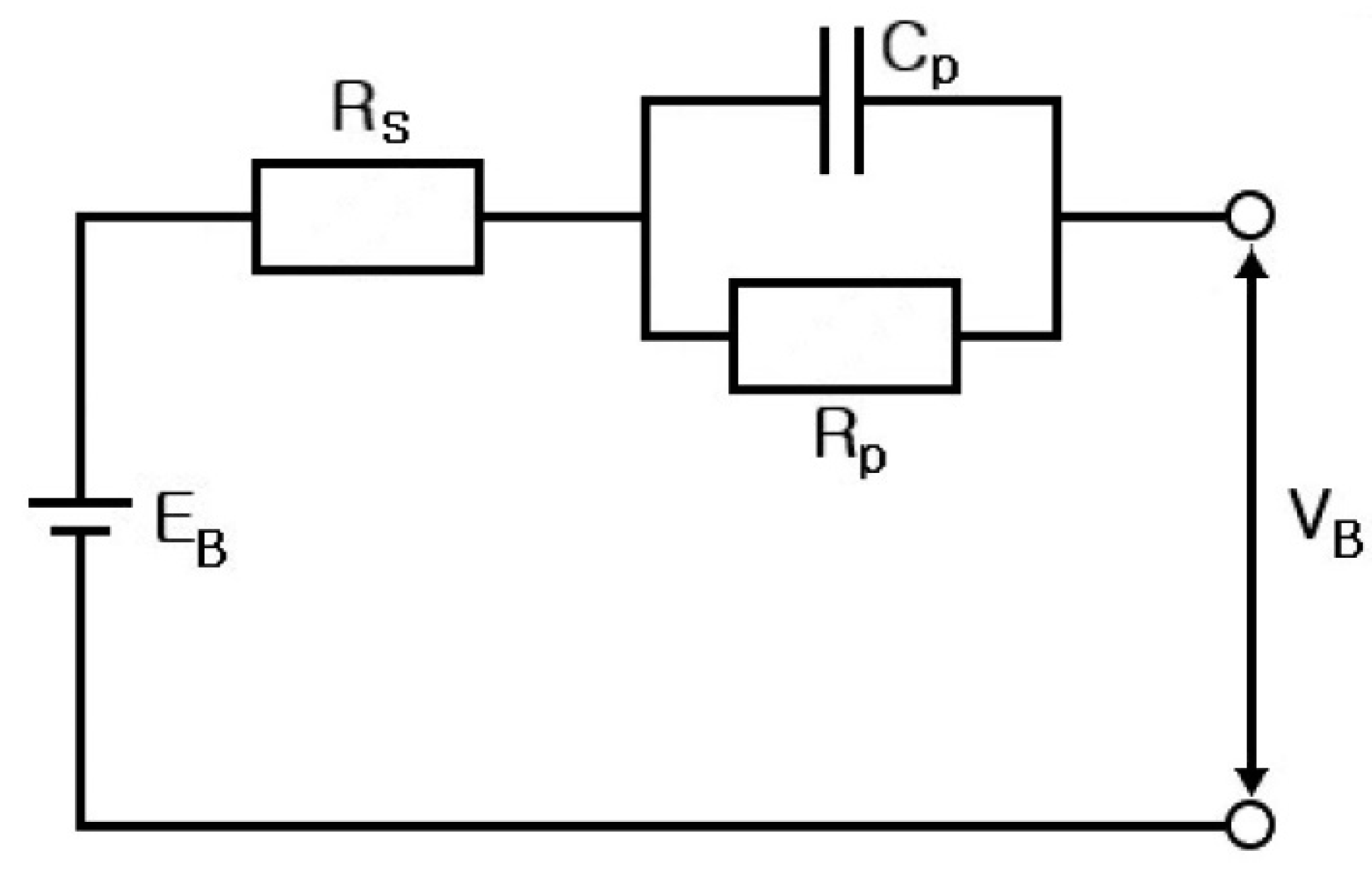
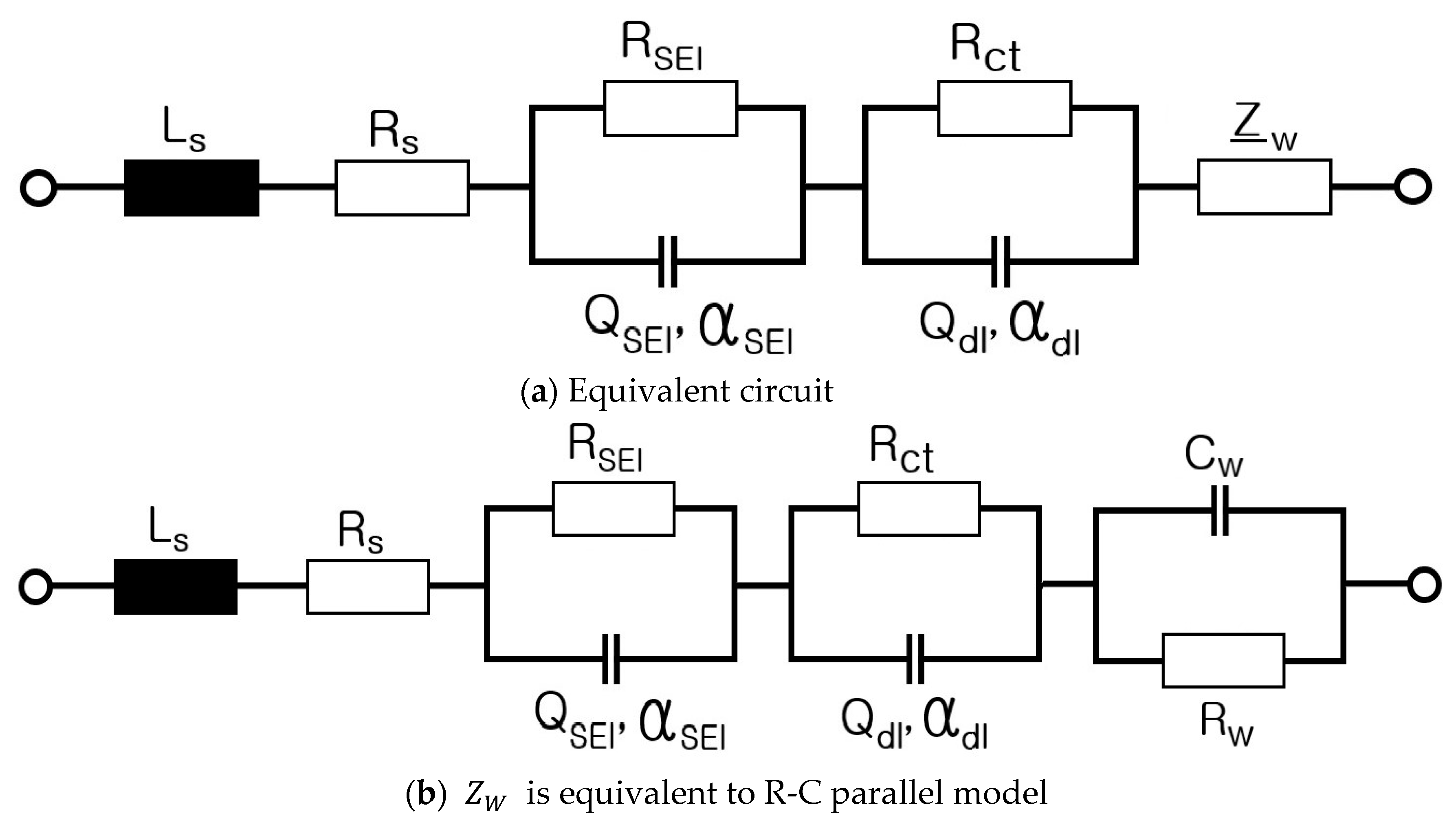
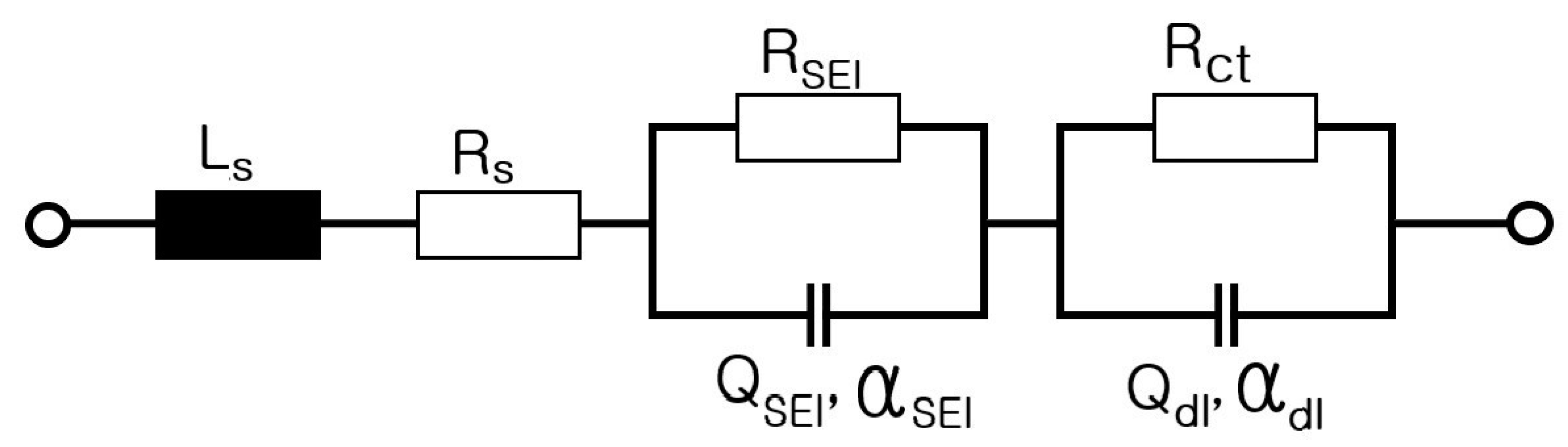
2. Electrical Modeling of Cylindrical Li-Ion Batteries
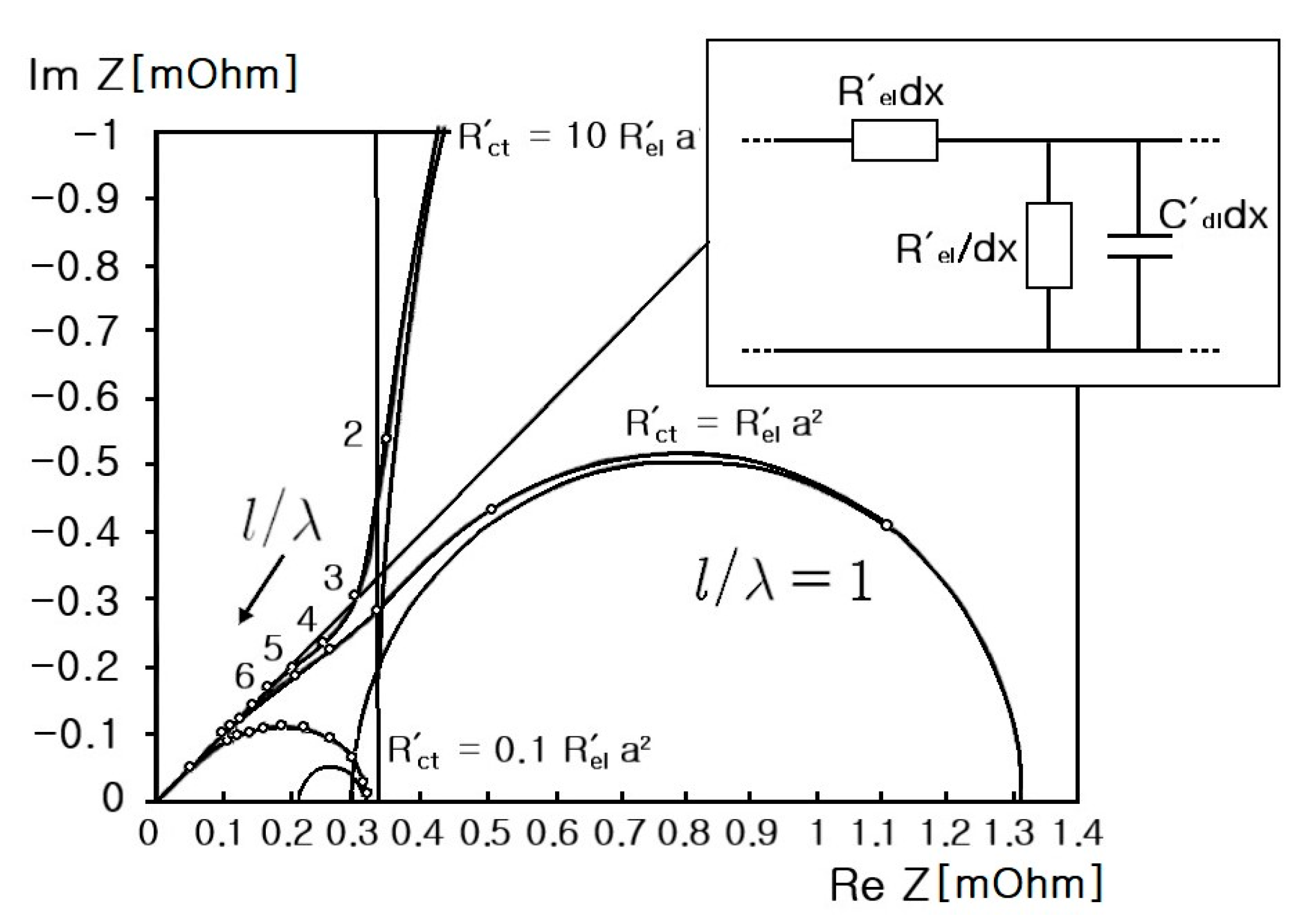
3. Electrical Modeling of Pouch-Type Li-Ion Batteries
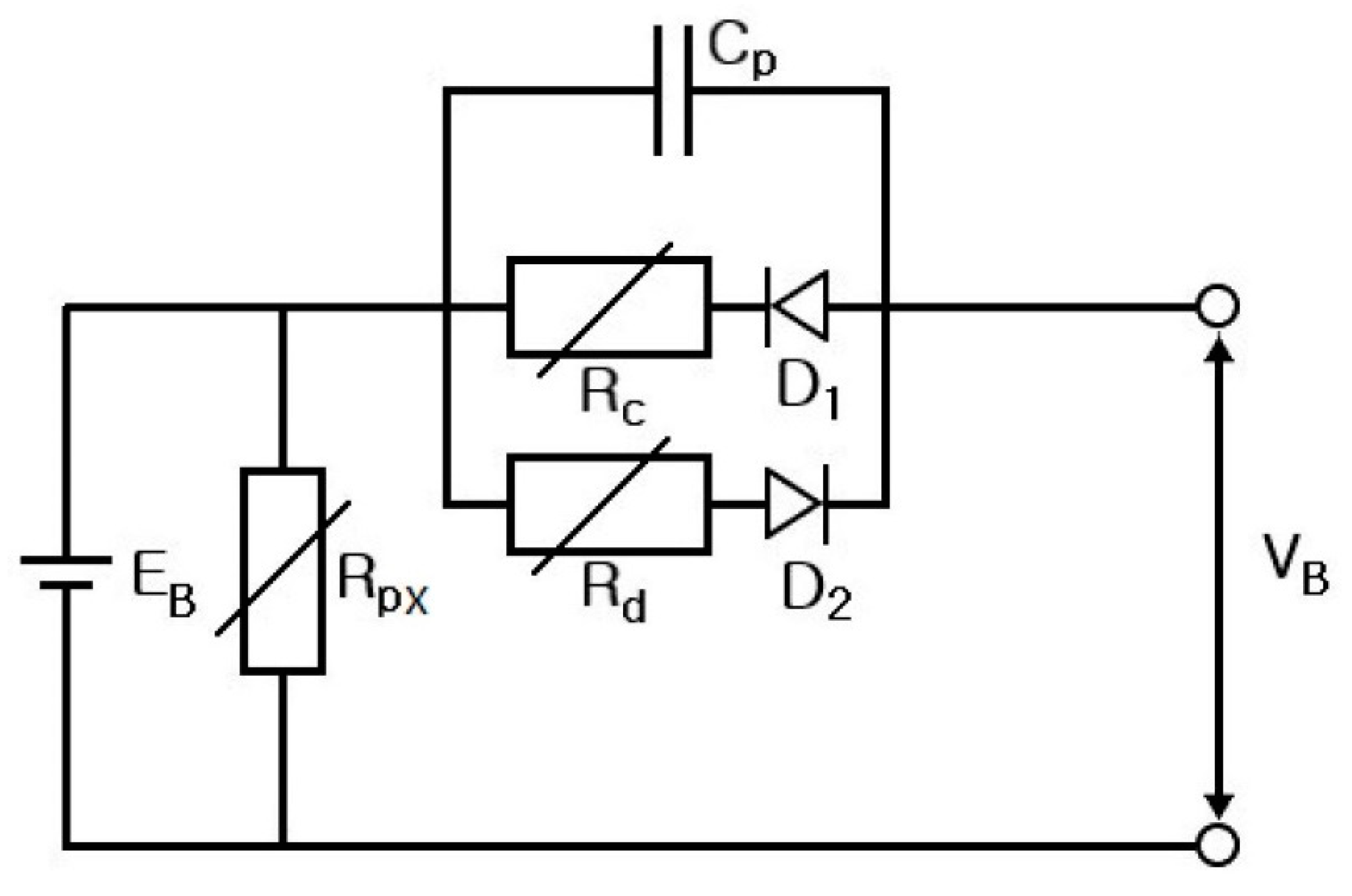
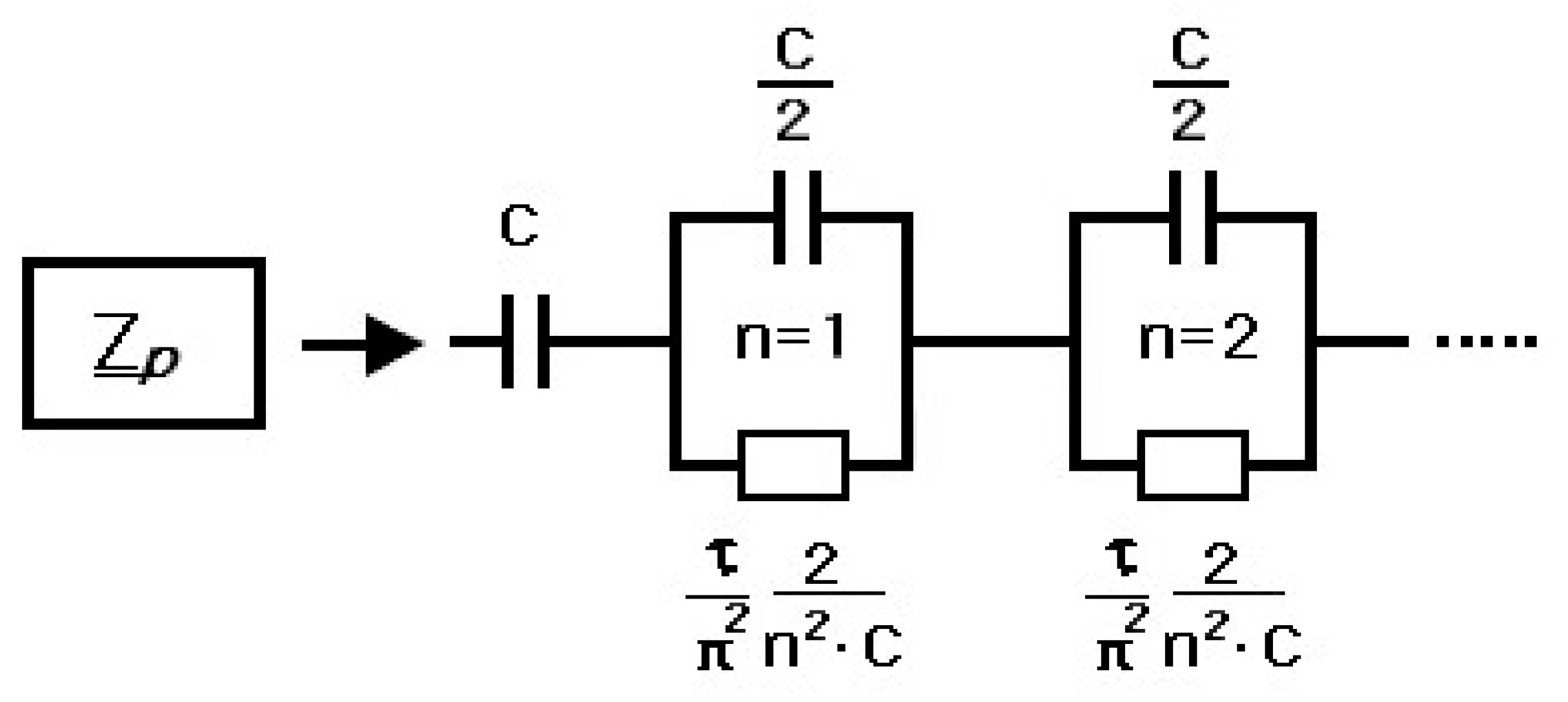
4. Electrical Modeling of Supercapacitors
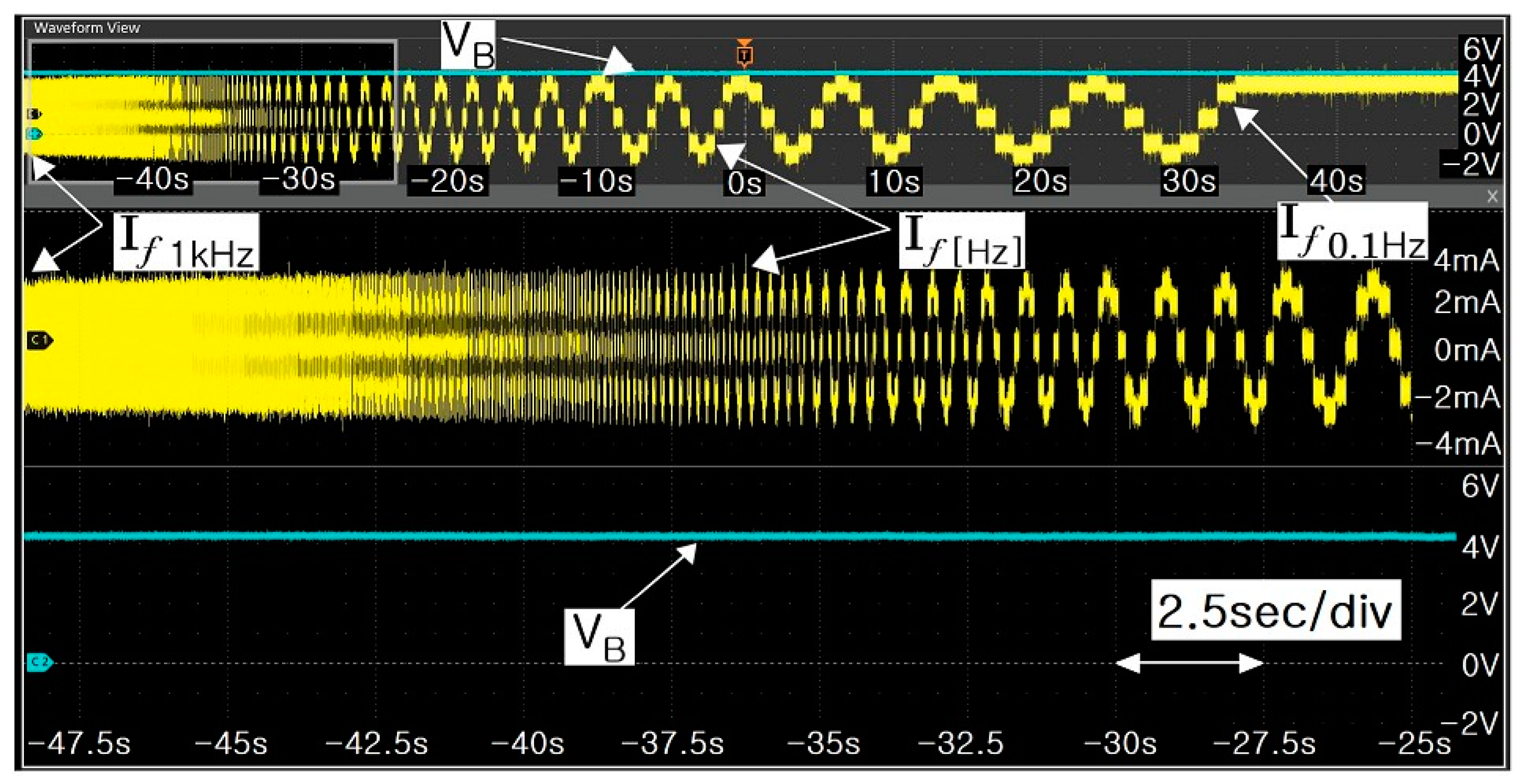
5. Experimental Equipment and System
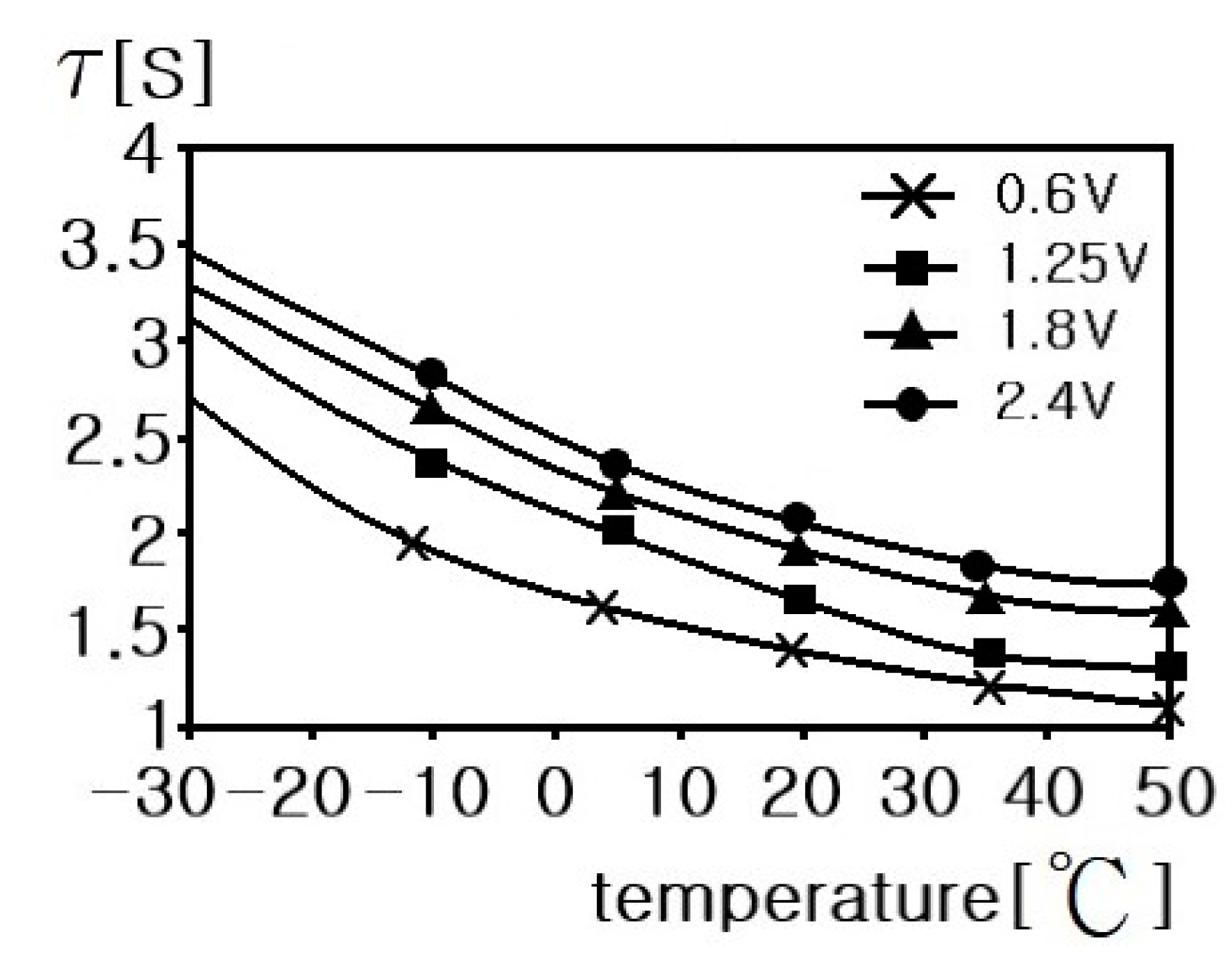
6. Experimental Results
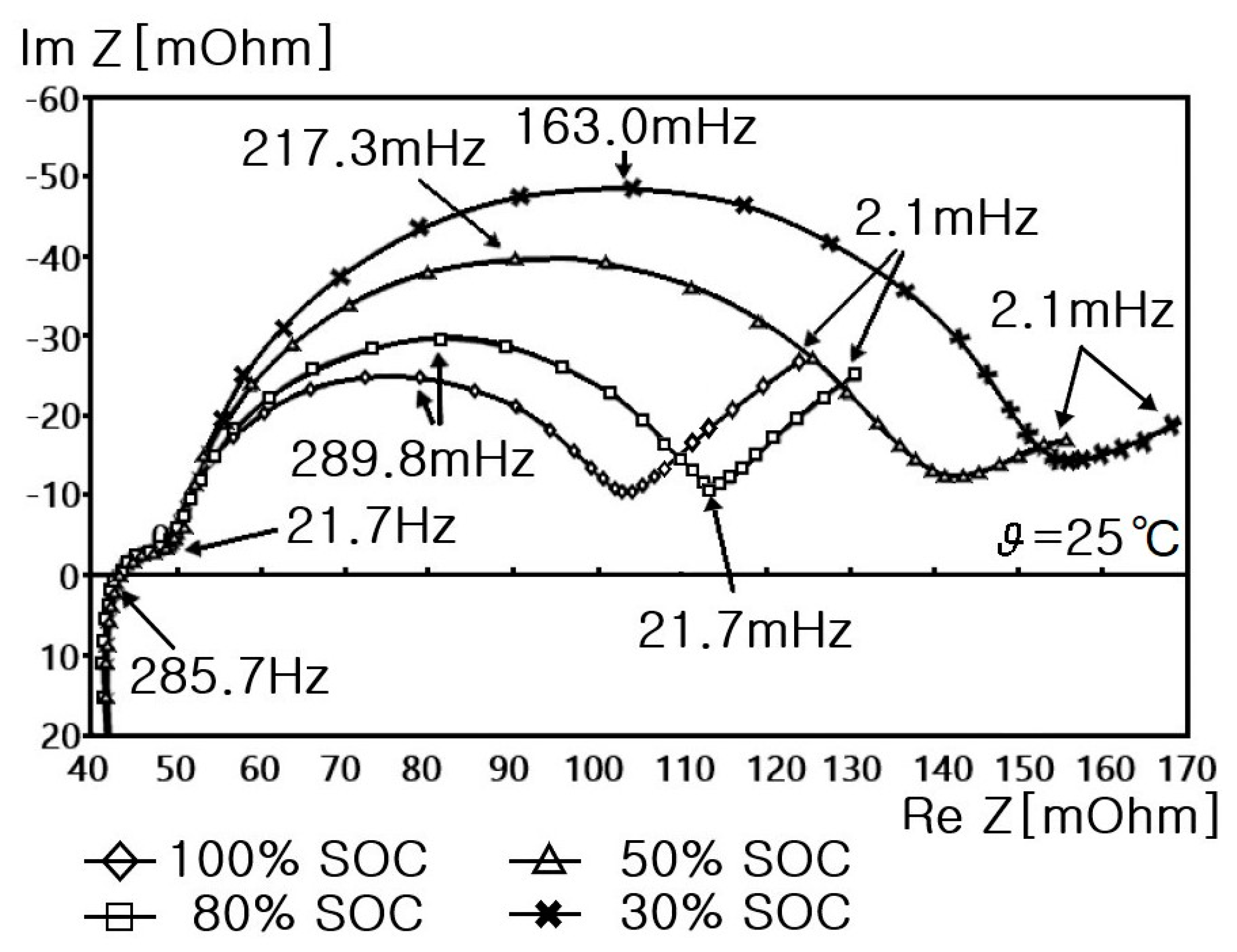
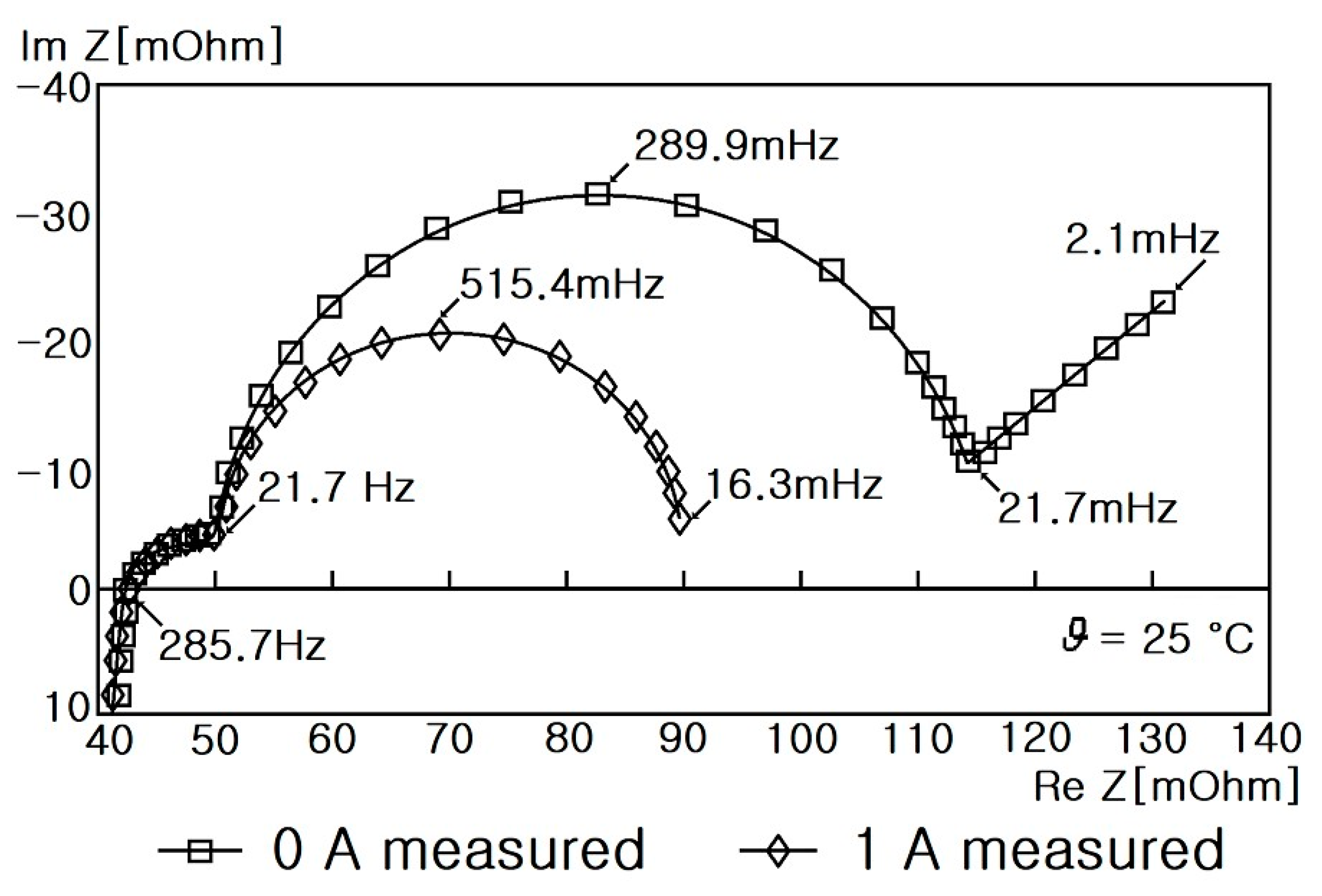
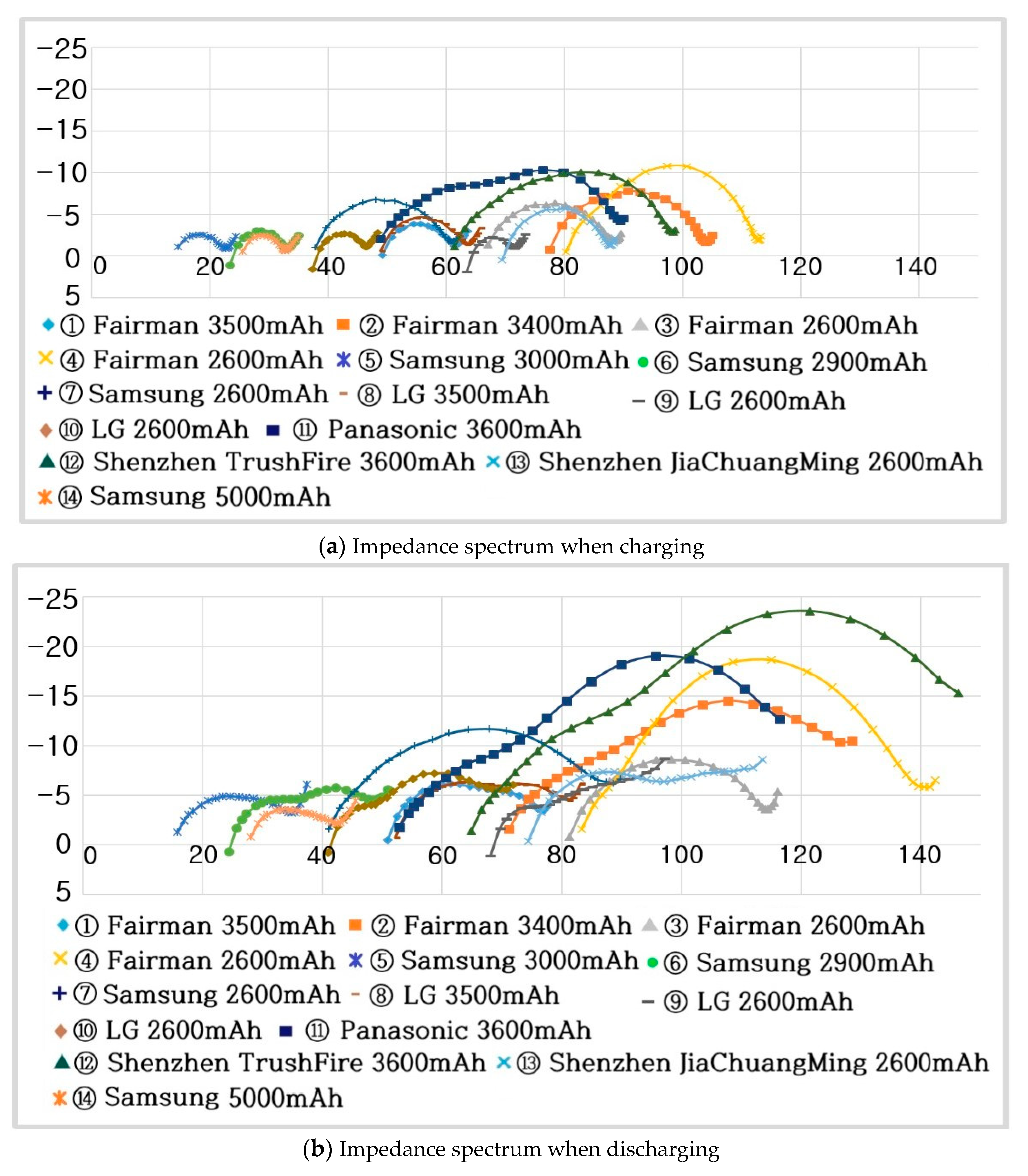
6.1. Impedance Spectra of Cylindrical Li-Ion Batteries
- -
- Step 1: Cylindrical pouch-type Li-ion batteries and supercapacitors were prepared (Figure 14).
- -
- Step 2: A chamber was used to keep the temperature constant at 25 °C. This is because the characteristics of batteries are temperature sensitive (Figure 15).
- -
- Step 3: A sine wave frequency in the range of 1 kHz to 0.1 Hz was injected into the battery, through the impedance spectrum equipment (BRS Ltd.).
- -
- Step 4: The impedance spectrum equipment acquired the following information from a reflected wave of the sinusoidal signal supplied: (1) injection frequency value (f), (2) RMS current value (I), and (3) RMS voltage value (V). The data were analyzed by shifting their frequency from 1 kHz to 0.1 Hz. The above data were graphed by dividing f.
- -
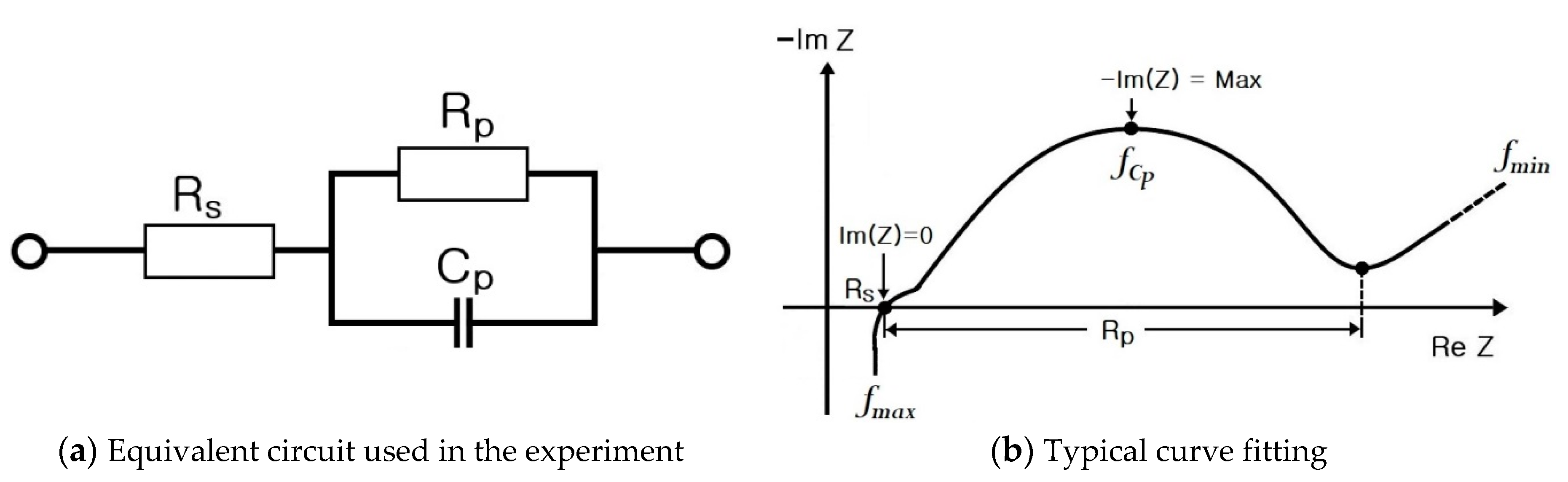
- Step 5: The change in the parameters R, XL, XC, L, and C of the battery, with the battery frequency, was obtained from the following expressions:
- -
- Step 6: The values of R, XL, XC, L, and C, at frequencies from 1 kHz to 0.1 Hz, were determined, and graphs were drawn using the data.
- -
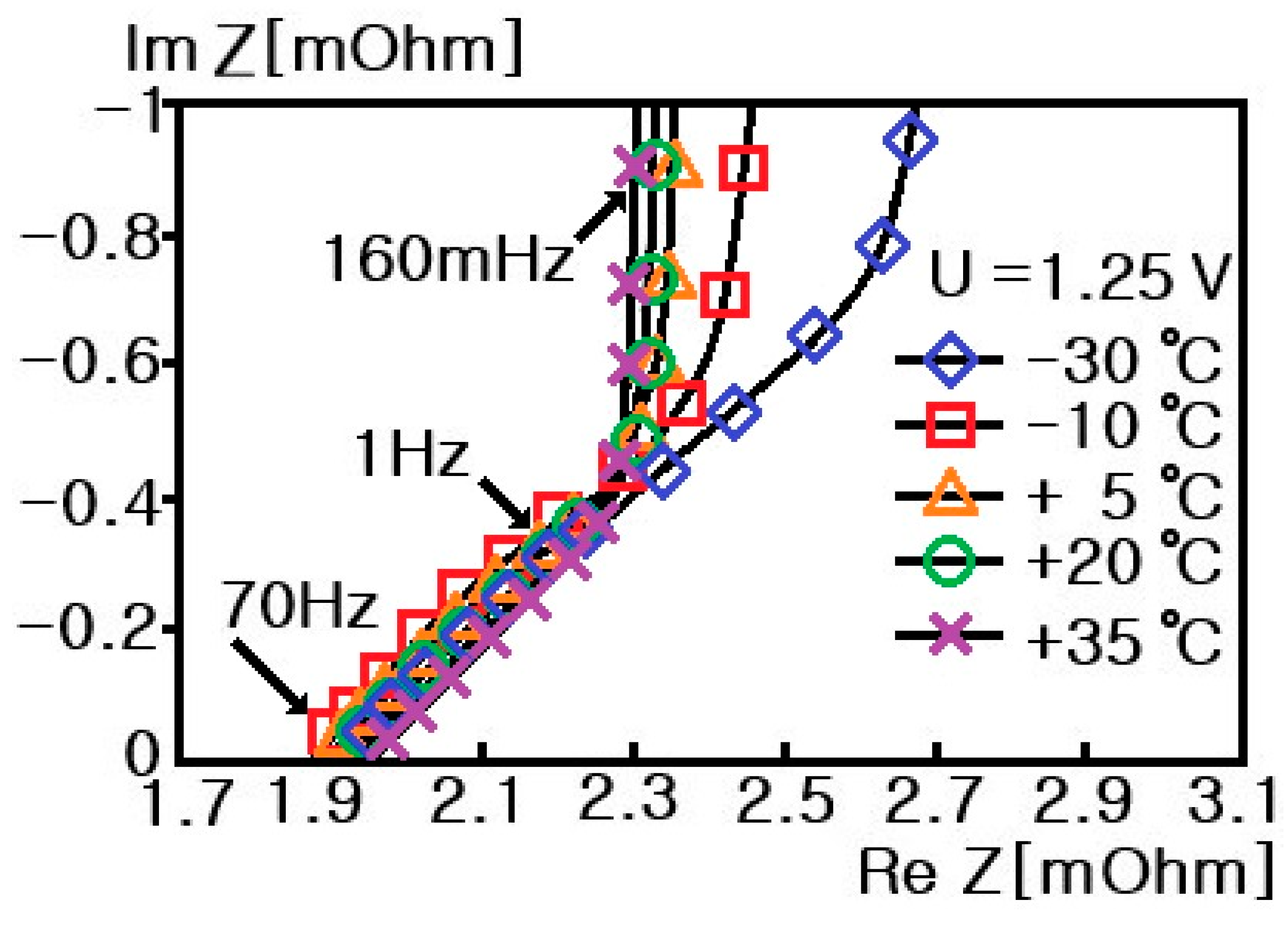
- Step 7: RS, RP, and CP are shown in Figure 17 and measured on the basis of the above data. Thus, the results in Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23 and Figure 24 are experimental data, obtained by injecting a sine wave into a real battery, and based on the injection frequency, RMS current value (I), and RMS voltage value (V). In Figure 18, Figure 19, Figure 20, Figure 21, Figure 22, Figure 23 and Figure 24, the units of the x-axis and y-axis are mΩ.
- -
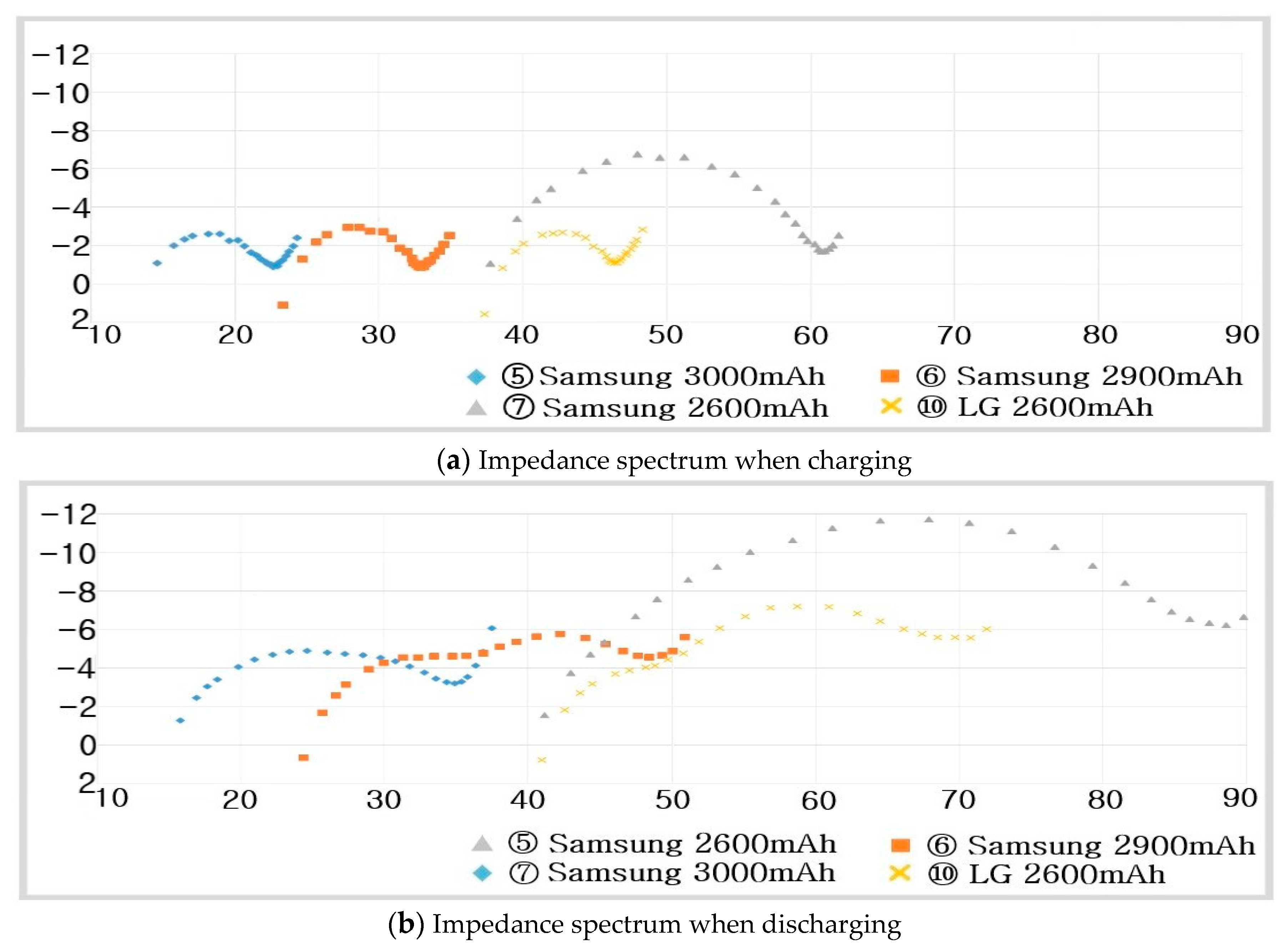
- ⑤ Samsung :
- -
- ⑥ Samsung :
- -
- ⑦ Samsung :
- -
- ⑩ LG :
- -
- ⑦ Samsung :
- -
- ⑩ LG :
- -
- ⑤ Samsung :
- -
- ⑥ Samsung :
- -
- ⑦ Samsung :
- -
- ⑩ LG :
- -
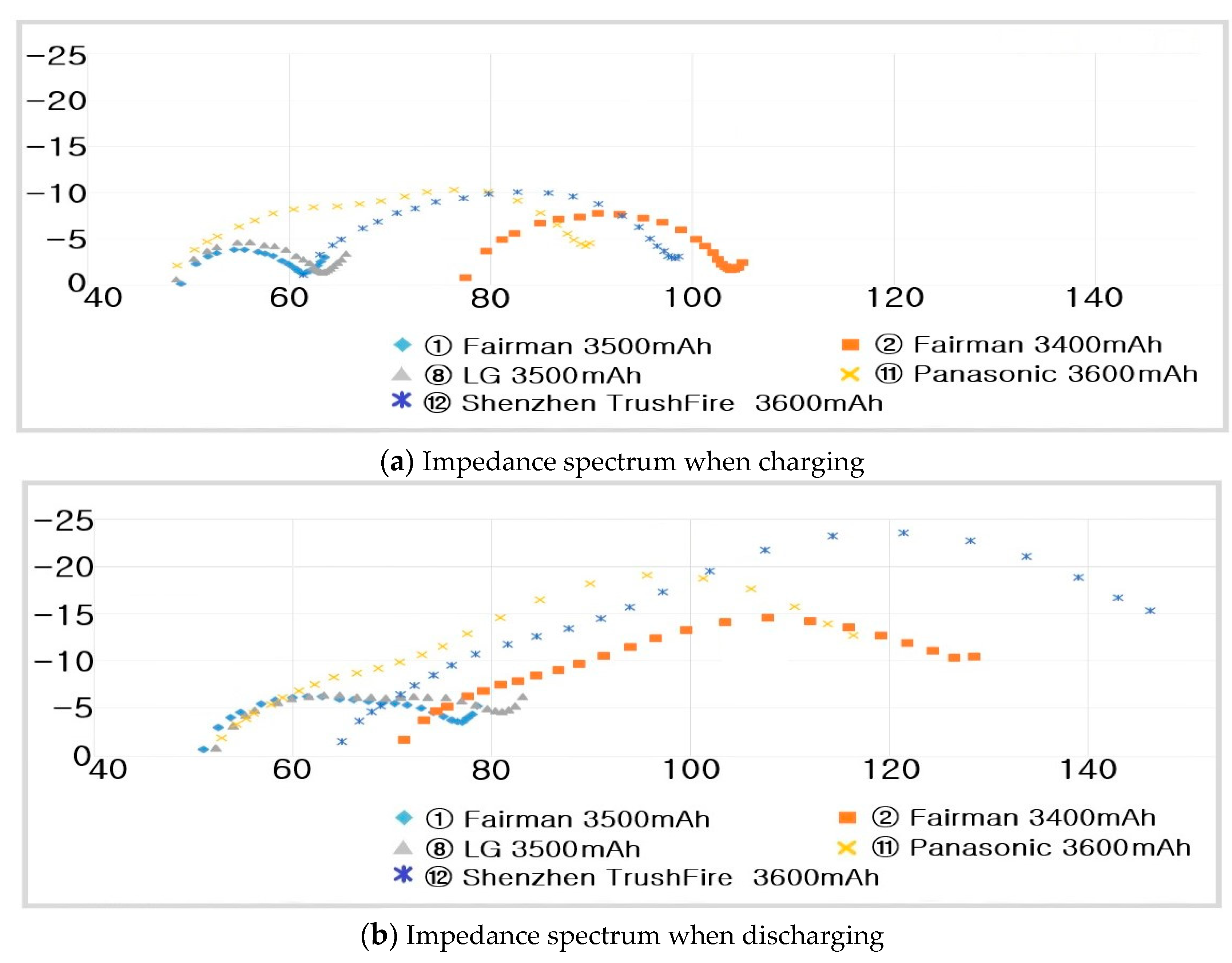
- ⑧ LG :
- -
- ⑪ Panasonic :
- -
- ① Fairman :
- -
- ⑫ Shenzhen TrushFire :
- -
- ② Fairman :
- -
- ⑧ LG :
- -
- ⑪ Panasonic :
- -
- ① Fairman :
- -
- ⑧ LG :
- -
- ⑪ Panasonic :
- -
- ① Fairman :
- -
- ⑫ Shenzhen TrushFire :
- -
- ② Fairman :
- -
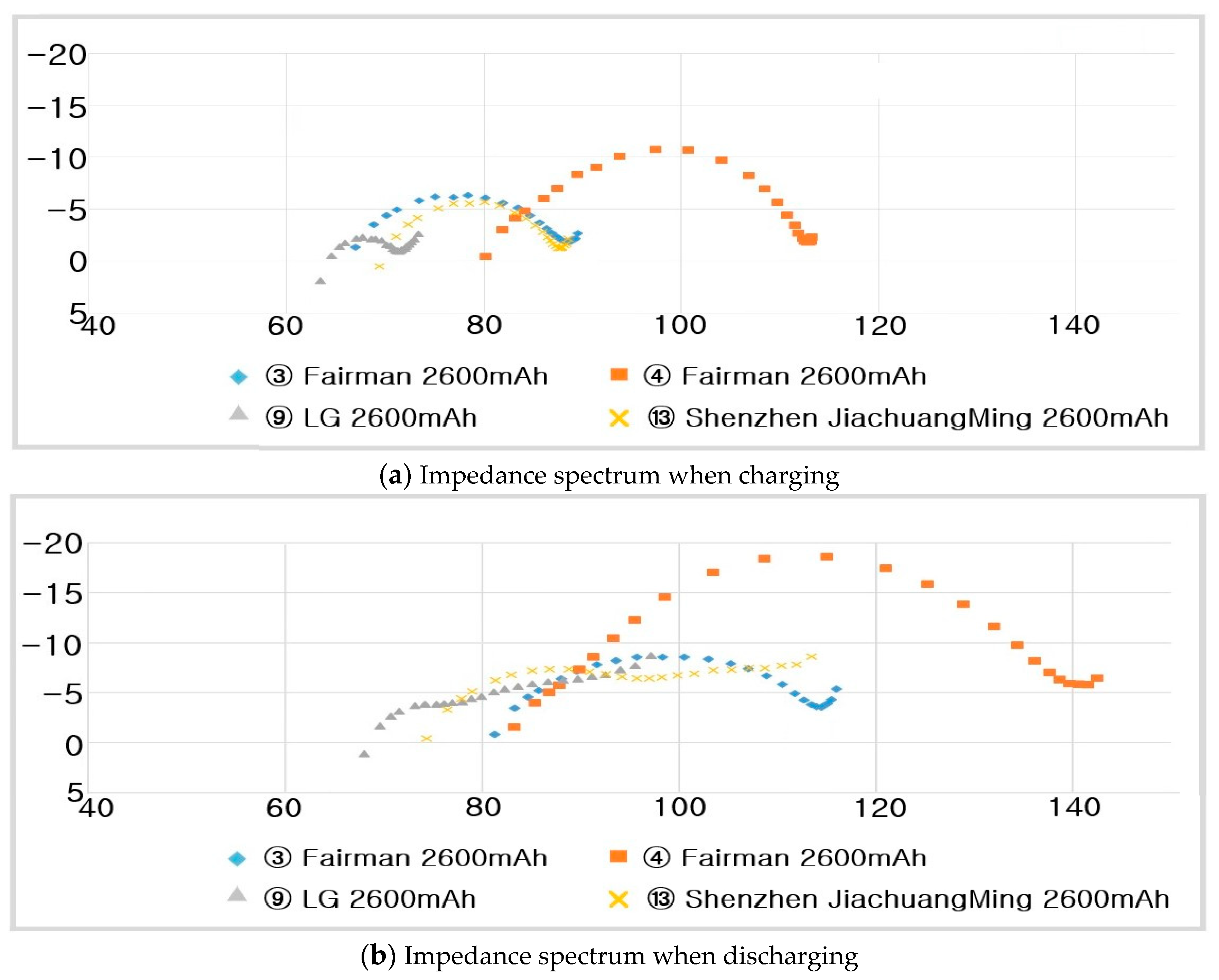
- ⑨ LG :
- -
- ③ Fairman :
- -
- ④ Fairman :
- -
- ⑬ Shenzhen JiaChuangMing :
- -
- (Charging) Samsung :
- -
- (Discharging) Samsung :
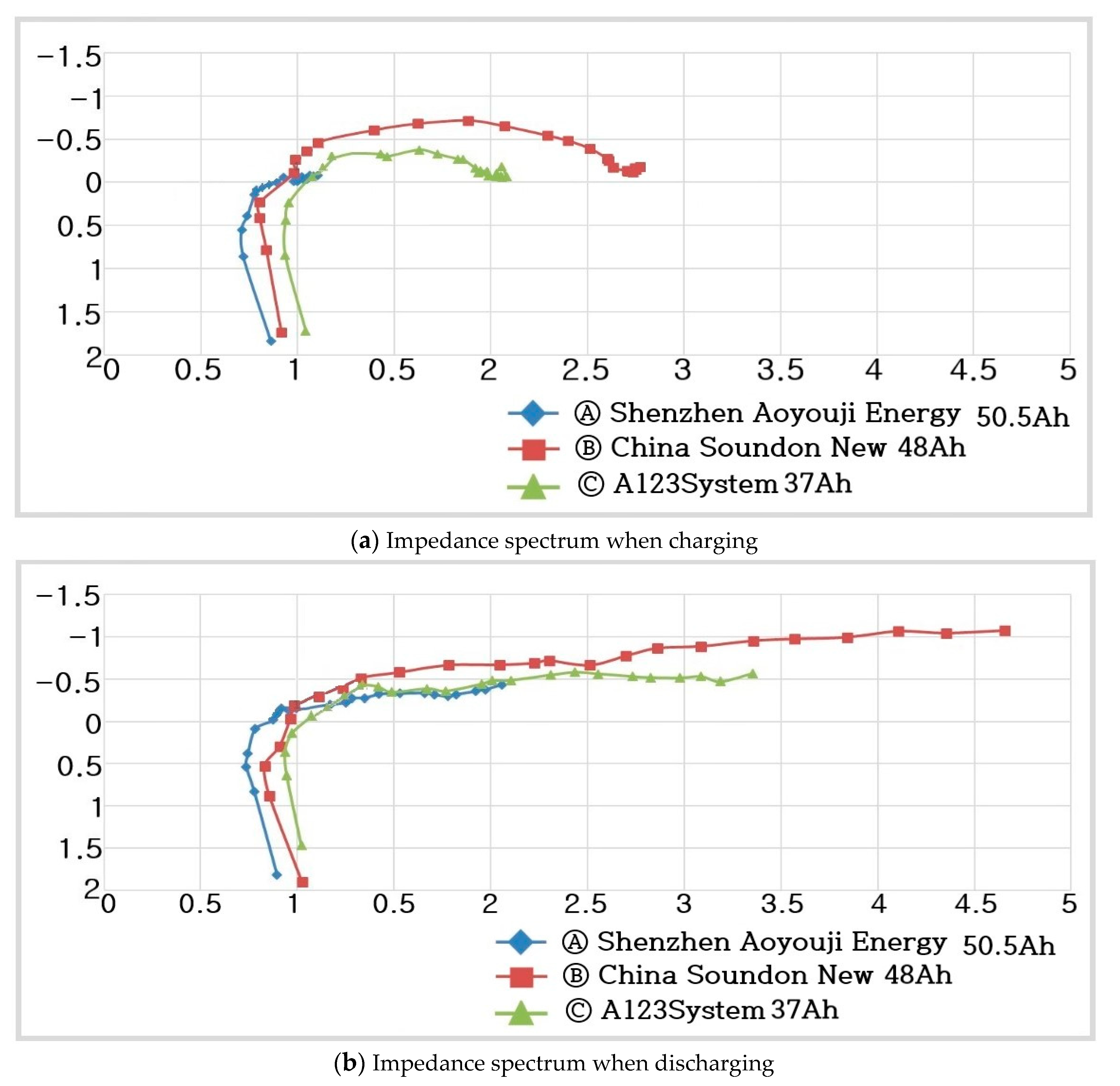
6.2. Impedance Spectra of Pouch-Type Li-Ion Batteries
- -
- Ⓐ Shenzhen Aoyou vji Energy :
- -
- Ⓑ China Soundon New Energy :
- -
- Ⓒ A123System :
- -
- Ⓐ-1 Shenzhen Aoyou vji Energy 50.5 Ah charging range of : 0.722–1.181
- -
- Ⓐ-2 Shenzhen Aoyou vji Energy 50.5 Ah discharging range of : 0.725–2.021
- -
- Ⓑ-1 China Soundon New Energy 48 Ah charging range of : 0.728–2.758
- -
- Ⓑ-2 China Soundon New Energy 48 Ah discharging range of : 0.729–4.199
- -
- Ⓒ-1 A123System 37 Ah charging range of : 0.921–2.174
- -
- Ⓒ-2 A123System 37 Ah discharging range of : 0.923–3.328
- -
- 18,650 Cylindrical Li-Ion Battery (protected):
- -
- 18,650 Cylindrical Li-Ion Battery (protected):
- -
- 18,650 Cylindrical Li-Ion Battery (unprotected):
- -
- 21,700 Cylindrical Li-Ion Battery (protected):
- -
- Pouch-type Li-Ion Battery (unprotected):
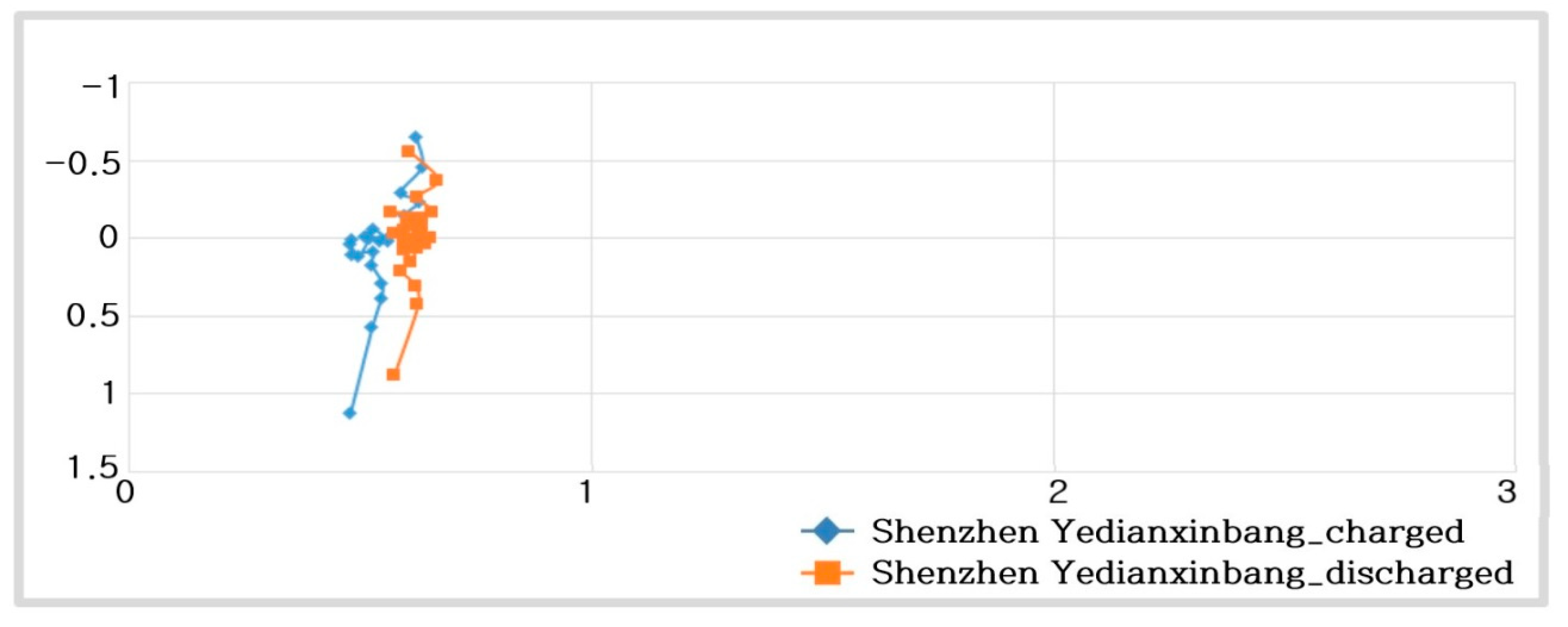
6.3. Impedance Spectrum of a Supercapacitor
- -
- (Charging) Shenzhen Yedianxinbang 500:
- -
- (Discharging) Shenzhen Yedianxinbang 500 F:
- The value decreases in the following order: 18650-type cylindrical Li-ion battery > 21700-type cylindrical Li-ion battery > pouch-type Li-ion battery > supercapacitor.
- A cylindrical Li-ion battery with the smallest , , and values exhibits the best characteristics.
- A cylindrical Li-ion battery exhibits a semicircular shape due to the oxidation and reduction reactions of Li ions, which increases with a slope of 45° in the complex plane due to the generated by Li ion diffusion.
- For a pouch-type Li-ion battery, a part of the semicircle shape appears due to the oxidation and reduction reactions of Li ions, but the afforded by Li ion diffusion does not appear.
- For a supercapacitor, no oxidation or reduction reactions of ions are observed, and the caused by Li ion diffusion hardly occurs, and its characteristics are similar to those of an ideal capacitor.
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chan, H.L.; Sutanto, D. A New Battery Model for use with Battery Energy Storage Systems and Electric Vehicles Power Systems. In Proceedings of the IEEE Power Engineering Society Conference, Singapore, 23–27 January 2000; pp. 470–475. [Google Scholar] [CrossRef]
- Sims, R.I.; Carnes, J.C.; Dzieciuch, M.A.; Fenton, J.E. Computer Modeling of Automotive Lead Acid Batteries; Ford Research Laboratories Technical Report; 1990; SR-90-154. [Google Scholar]
- Ziyad, M.S.; Margaret, A.C.; William, A.L. A Mathematical Model for Lead-Acid Batteries. IEEE Trans. Energy Con. 1992, 7, 93–98. [Google Scholar] [CrossRef]
- Margaret, A.C.; Ziyad, M.S. Determination of Lead-Acid Battery Capacity Via Mathematical Modeling Techniques. IEEE Trans. Energy Con. 1992, 7, 442–446. [Google Scholar] [CrossRef]
- Buller, S.; Thele, M.; Doncker, R.W.D.; Karden, E. Impedance-Based Simulation Models of Supercapacitors and Li-Ion Batteries for Power Electronic Applications. IEEE Trans. Ind. App. 2005, 41, 742–747. [Google Scholar] [CrossRef]
- Buller, S.; Karden, E.; Kok, D.; Doncker, R.W.D. Modeling the Dynamic Behavior of Supercapacitors Using Impedance Spectroscopy. IEEE Trans. Ind. App. 2002, 38, 1622–1626. [Google Scholar] [CrossRef]
- Stroe, D.I.; Swierczynski, M.; Stan, A.I.; Knap, V.; Teodorescu, R.; Andreasen, S.J. Diagnosis of Lithium-Ion Batteries State-of-Health based on Electrochemical Impedance Spectroscopy Technique. In Proceedings of the IEEE Transactions on Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 4576–4582. [Google Scholar] [CrossRef]
- Oldenburger, M.; Bedürftig, B.; Gruhle, A.; Grimsmann, F.; Richter, E.; Findeisen, R.; Hintennach, A. Investigation of the Low Frequency Warburg Impedance of Li-Ion Cells by Frequency Domain Measurements. J. Energy Storage 2019, 21, 272–280. [Google Scholar] [CrossRef]
- Samuel, C.M.; Paul, G. An Impedance Model Based on a Transmission Line Circuit and a Frequency Dispersion Warburg Component for the Study of EIS in Li-Ion Batteries. J. Electroanal. Chem. 2020, 871, 114305. [Google Scholar] [CrossRef]
- Maheshwari, A.; Heck, M.; Santarelli, M. Cycle Aging Studies of Lithium Nickel Manganese Cobalt Oxide-Based Batteries Using Electrochemical Impedance Spectroscopy. Electrochim. Acta 2018, 273, 335–348. [Google Scholar] [CrossRef]
- Karden, E.; Buller, S.; Doncker, R.W.D. A Frequency-Domain Approach to Dynamical Modeling of Electrochemical Power Sources. Electrochim. Acta 2002, 47, 2347–2356. [Google Scholar] [CrossRef]
- Buller, S.; Thele, M.; Karden, E.; Doncker, R.W.D. Impedance-Based Non-Linear Dynamic Battery Modeling for Automotive Applications. J. Power Source 2003, 113, 422–430. [Google Scholar] [CrossRef]
- Chen, M.; Rincón-Mora, G.A. Accurate Electrical Battery Model Capable of Predicting Runtime and I–V Performance. IEEE Trans. Energy Con. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Lee, J.M.; Nam, O.Y.; Cho, B.H. Li-ion Battery SOC Estimation Method Based on the Reduced Order Extended Kalman Filtering. J. Power Source 2007, 174, 9–15. [Google Scholar] [CrossRef]
- Kim, J.H.; Shin, J.W.; Chun, C.Y.; Cho, B.H. Stable Configuration of a Li-Ion Series Battery Pack Based on a Screening Process for Improved Voltage/SOC Balancing. IEEE Trans. Power Electron. 2012, 27, 411–424. [Google Scholar] [CrossRef]
- Deng, Z.; Zhang, Z.; Lai, Y.; Liu, J.; Li, J.; Liu, Y. Electrochemical Impedance Spectroscopy Study of a Lithium/Sulfur Battery: Modeling and Analysis of Capacity Fading. J. Electrochem. Soc. 2013, 160, A553–A558. [Google Scholar] [CrossRef]
- Bugryniec, P.J.; Davidson, J.N.; Brown, S.F. Advanced Abuse Modelling of Li-ion Cells—A Novel Description of Cell Pressurisation and Simmering Reactions. J. Power Source 2020, 474, 228396. [Google Scholar] [CrossRef]
- Abada, S.; Marlair, G.; Lecocq, A.; Petit, M.; Sauvant-Moynot, V.; Huet, F. Safety Focused Modeling of Lithium-Ion Batteries: A Review. J. Power Source 2016, 306, 178–192. [Google Scholar] [CrossRef]
- Gauchia, L.; Castaño, S.; Sanz, J. New Approach to Supercapacitor Testing and Dynamic Modelling. In Proceedings of the IEEE, Vehicle Power and Propulsion Conference, Lille, France, 1–3 September 2010; pp. 1–5. [Google Scholar] [CrossRef]
- Mahon, P.J.; Paul, G.L.; Keshishian, S.M.; Vassallo, A.M. Measurement and Modelling of the High-Power Performance of Carbon-Based Supercapacitors. J. Power Source 2000, 91, 68–76. [Google Scholar] [CrossRef]
- Du, Y.; Mo, Y.; Chen, Y. Effects of Fe Impurities on Self-Discharge Performance of Carbon-Based Supercapacitors. Materials 2021, 14, 1908. [Google Scholar] [CrossRef] [PubMed]
- Himanshu; Rao, S.S.; Punnoose, D.; Sathishkumar, P.; Gopi, C.V.V.M.; Bandari, N.; Durga, I.K.; Krishna, T.N.V.; Kim, H.J. Development of Novel and Ultra-High-Performance Supercapacitor Based on a Four Layered Unique Structure. Electronics 2018, 7, 121. [Google Scholar] [CrossRef]
- Huang, Z.; Qin, C.; Wang, J.; Cao, L.; Ma, Z.; Yuan, Q.; Lin, Z.; Zhang, P. Research on High-Value Utilization of Carbon Derived from Tobacco Waste in Supercapacitors. Materials 2021, 14, 1714. [Google Scholar] [CrossRef]
- Yuan, Y.; Sun, Y.; Feng, Z.; Li, X.; Yi, R.; Sun, W.; Zhao, C.; Yang, L. Nitrogen-doped hierarchical porous activated carbon derived from paddy for high-performance supercapacitors. Materials 2021, 14, 318. [Google Scholar] [CrossRef]
- Khalid, S.; Cao, C.; Naveed, M.; Younas, W. 3D hierarchical MnO2 microspheres: A prospective material for high performance supercapacitors and lithium-ion batteries. Sustain. Energy Fuels 2017, 1, 1795–1804. [Google Scholar] [CrossRef]
- Bi, S.; Banda, H.; Chen, M.; Niu, L.; Chen, M.; Wu, T.; Wang, J.; Wang, R.; Feng, J.; Chen, T.; et al. Molecular understanding of charge storage and charging dynamics in supercapacitors with MOF electrodes and ionic liquid electrolytes. Nat. Mater. 2020, 19, 552–558. [Google Scholar] [CrossRef]
- Stroe, D.I.; Knap, V.; Swierczynski, M.; Schaltz, E. Electrochemical Impedance Spectroscopy-based Electric Circuit Modeling of Lithium-Sulfur Batteries during Discharging State. IEEE Trans. Ind. Appl. 2019, 55, 631–637. [Google Scholar] [CrossRef]
- Lee, J.H.; Choi, W.J. Novel State-of-Charge Estimation Method for Lithium Polymer Batteries Using Electrochemical Impedance Spectroscopy. J. Power Electron. 2011, 11, 237–243. [Google Scholar] [CrossRef]
- Sihvo, J.; Stroe, D.I.; Messo, T.; Roinila, T. A Fast Approach for Battery Impedance Identification Using Pseudo Random Sequence (PRS) Signals. IEEE Trans. Power Electron. 2020, 35, 2548–2557. [Google Scholar] [CrossRef]
- Santoni, F.; Angelis, A.D.; Moschitta, A.; Carbone, P. Digital Impedance Emulator for Battery Measurement System Calibration. Senors 2021, 21, 7377. [Google Scholar] [CrossRef] [PubMed]
- Islam, S.M.R.; Park, S.Y.; Balasingam, B. Unification of Internal Resistance Estimation Methods for Li-Ion Batteries Using Hysteresis-Free Equivalent Circuit Models. Batteries 2020, 6, 32. [Google Scholar] [CrossRef]
- Ovejas, V.J.; Cuadras, A. Impedance Characterization of an LCO-NMC/Graphite Cell: Ohmic Conduction, SEI Transport and Charge-Transfer Phenomenon. Batteries 2018, 4, 43. [Google Scholar] [CrossRef]
- Gheem, E.V.; Pintelon, R.; Vereecken, J.; Schoukens, J.; Hubin, A.; Verboven, P.; Blajiev, O. Electro-Chemical Impedance Spectroscopy in the Presence of Nonlinear Distortions and Non-Stationary Behaviour Part I: Theory and Validation. Electrochim. Acta 2004, 49, 4753–4762. [Google Scholar] [CrossRef]
- Kim, J.H.; Kowal, J. Development of a Matlab/Simulink Model for Monitoring Cell State-of-Health and State-of-Charge via Impedance of Lithium-Ion Battery Cells. Batteries 2022, 8, 8. [Google Scholar] [CrossRef]
- Heinrich, M.; Wolff, N.; Seitz, S.; Krewer, U. Identifying Anode and Cathode Contributions in Li-Ion Full-Cell Impedance Spectra. Batteries 2022, 8, 40. [Google Scholar] [CrossRef]
- Goldammer, E.; Kowal, J. Determination of the Distribution of Relaxation Times by Means of Pulse Evaluation for Offline and Online Diagnosis of Lithium-Ion Batteries. Batteries 2021, 7, 36. [Google Scholar] [CrossRef]
- Macdonald, J.R. Impedance Spectroscopy. Ann. Biomed. Eng. 1992, 20, 289–305. [Google Scholar] [CrossRef] [PubMed]
- Choi, W.S.; Shin, H.C.; Kim, J.M.; Choi, J.Y.; Yoon, W.S. Modeling and Applications of Electrochemical Impedance Spectroscopy (EIS) for Lithium-ion Batteries. J. Electrochem. Sci. Technol 2020, 11, 1–13. [Google Scholar] [CrossRef]
- Olarte, J.; Ilarduya, J.M.; Zulueta, E.; Ferret, R.; Fernández-Gámiz, U.; Lopez-Guede, J.M. A Battery Management System with EIS Monitoring of Life Expectancy for Lead–Acid Batteries. Electronics 2021, 10, 1228. [Google Scholar] [CrossRef]
- Franke-Lang, R.; Kowa, J. Analysis of Electrochemical Impedance Spectroscopy on Zinc-Air Batteries Using the Distribution of Relaxation Times. Batteries 2021, 7, 56. [Google Scholar] [CrossRef]
- Podias, A.; Pfrang, A.; Persio, F.D.; Kriston, A.; Bobba, S.; Mathieux, F.; Messagie, M.; Boon-Brett, L. Sustainability Assessment of Second Use Applications of Automotive Batteries: Ageing of Li-Ion Battery Cells in Automotive and Grid-Scale Applications. World Electr. Veh. J. 2018, 9, 24. [Google Scholar] [CrossRef]
- Hasan, R.; Scott, J. Impedance Measurement of Batteries under load. In Proceedings of the IEEE International Instrumentation and Measurement Technology Conference(I2MTC), Auckland, New Zealand, 20–23 May 2019. [Google Scholar] [CrossRef]
- Ray, A.; Saruhan, B. Application of Ionic Liquids for Batteries and Supercapacitors. Materials 2021, 14, 2942. [Google Scholar] [CrossRef]
- Yang, G.; Song, Y.; Wang, Q.; Zhang, L.; Deng, L. Review of ionic liquids containing, polymer/inorganic hybrid electrolytes for lithium metal batteries. Mater. Des. 2020, 190, 108563. [Google Scholar] [CrossRef]
- Karuppasamy, K.; Theerthagiri, J.; Vikraman, D.; Yim, C.J.; Hussain, S.; Sharma, R.; Maiyalagan, T.; Qin, J.; Kim, H.S. Ionic liquid-based electrolytes for energy storage devices: A brief review on their limits and applications. Polymers 2020, 12, 918. [Google Scholar] [CrossRef]
- Zhang, R.; Xia, B.; Li, B.; Cao, L.; Lai, Y.; Zheng, W.; Wang, H.; Wang, W. State of the Art of Lithium-Ion Battery SOC Estimation for Electrical Vehicles. Energies 2018, 11, 1820. [Google Scholar] [CrossRef]
- Rivera-Barrera, J.P.; Muñoz-Galeano, N.; Sarmiento-Maldonado, H.O. SoC Estimation for Lithium-ion Batteries: Review and Future Challenges. Electronics 2017, 6, 102. [Google Scholar] [CrossRef]
- Hahn, M.; Schindler, S.; Triebs, L.C.; Danzer, M.A. Optimized Process Parameters for a Reproducible Distribution of Relaxation Times Analysis of Electrochemical Systems. Batteries 2019, 5, 43. [Google Scholar] [CrossRef]






| Device Type of Energy Storage | Company | Quantity | Value | |
|---|---|---|---|---|
| Cylindrical Li-ion battery | 18650 | ① Fairman (Kor.) | Capacity | 3500 mAh |
| Type | Built-in protection device | |||
| Color | Yellow | |||
| ② Fairman (Kor.) | Capacity | 3400 mAh | ||
| Type | Built-in protection device | |||
| Color | Orange | |||
| ③ Fairman (Kor.) | Capacity | 2600 mAh | ||
| Type | Built-in protection device | |||
| Color | Blue | |||
| ④ Fairman (Kor.) | Capacity | 2600 mAh | ||
| Type | Built-in protection device | |||
| Color | Dark pink | |||
| ⑤ Samsung (Kor.) | Capacity | 3000 mAh | ||
| Type | Non-protection device | |||
| Color | Pink | |||
| ⑥ Samsung (Kor.) | Capacity | 2900 mAh | ||
| Type | Non-protection device | |||
| Color | Blue | |||
| ⑦ Samsung (Kor.) | Capacity | 2600 mAh | ||
| Type | Non-protection device | |||
| Color | Pink | |||
| ⑧ LG (Kor.) | Capacity | 3500 mAh | ||
| Type | Built-in protection device | |||
| Color | Yellow/Black | |||
| ⑨ LG (Kor.) | Capacity | 2600 mAh | ||
| Type | Built-in protection device | |||
| Color | Green | |||
| ⑩ LG (Kor.) | Capacity | 2600 mAh | ||
| Type | Non-protection device | |||
| Color | Purple | |||
| ⑪ Panasonic (Jap.) | Capacity | 3600 mAh | ||
| Type | Built-in protection device | |||
| Color | Green | |||
| ⑫ Shenzhen TrushFire Tech. (Chi.) | Capacity | 3600 mAh | ||
| Type | Built-in protection device | |||
| Color | Black | |||
| ⑬ Shenzhen JiaChuangMing Tech. (Chi.) | Capacity | 2600 mAh | ||
| Type | Built-in protection device | |||
| Color | Pink | |||
| 21700 | ⑭ Samsung (Kor.) | Capacity | 5000 mAh | |
| Type | Built-in protection device | |||
| Color | Black | |||
| Pouch-type Li-ion battery | Ⓐ Shenzhen Aoyouji Energy Electronics (Chi.) | Capacity | 50.5 Ah | |
| Type | Non-protection device | |||
| Color | BEV battery | |||
| Ⓑ China Soundon New Energy (Chi.) | Capacity | 48 Ah | ||
| Type | Non-protection device | |||
| Color | BEV battery | |||
| Ⓒ A123System LLC (Chi.) | Capacity | 37 Ah | ||
| Type | Non-protection device | |||
| Color | PHEV battery | |||
| Supercapacitor | Shenzhen Yedianxinbang Tech. (Chi.) | Capacity | 600 F | |
| Rated voltage | DC 2.7 V | |||
| Cell Type | Charging 4.1–4.2 V | Charging 2.5–3.0 V | ||||||
|---|---|---|---|---|---|---|---|---|
| RS[mΩ] | RP[mΩ] | CP[F] | RS[mΩ] | RP[mΩ] | CP[F] | |||
| C Y L I N D R E R | 18650 | ① Fairman 3500 mAh Built-in protection | 49.2132 | 12.1129 | 0.4140 | 50.9349 | 26.0793 | 0.5439 |
| 18650 | ② Fairman 3400 mAh Built-in protection | 77.4560 | 26.3065 | 0.4286 | 71.1773 | 55.2958 | 7.2934 | |
| 18650 | ③ Fairman 2600 mAh Built-in protection | 66.9574 | 21.5832 | 0.5269 | 81.2983 | 33.1674 | 0.8552 | |
| 18650 | ④ Fairman 2600 mAh Built-in protection | 80.1501 | 32.5909 | 0.6811 | 83.2599 | 58.2183 | 0.8534 | |
| 18650 | ⑤ Samsung 3000 mAh Non-protection | 14.5825 | 8.0615 | 0.4300 | 15.7654 | 19.1020 | 0.9763 | |
| 18650 | ⑥ Samsung 2900 mAh Non-protection | 23.2917 | 9.5717 | 0.3764 | 24.3366 | 24.0597 | 12.5382 | |
| 18650 | ⑦ Samsung 2600 mAh Non-protection | 37.7485 | 22.9729 | 0.3525 | 41.1192 | 47.4514 | 1.9968 | |
| 18650 | ⑧ LG 3500 mAh Built-in protection | 48.7836 | 14.5156 | 0.3427 | 52.2040 | 28.7976 | 0.5290 | |
| 18650 | ⑨ LG 2600 mAh Built-in protection | 63.4390 | 8.0161 | 0.6920 | 68.0641 | 29.1099 | 182.175 | |
| 18650 | ⑩ LG 2600 mAh Non-protection | 37.3298 | 9.0120 | 0.6067 | 40.9606 | 29.8173 | 6.6918 | |
| 18650 | ⑪ Panasonic 3600 mAh Built-in protection | 48.8667 | 40.5615 | 4.6757 | 52.8348 | 63.5486 | 12.2790 | |
| 18650 | ⑫ Shenzhen TrushFire Tech. 3600 mAh Built-in protection | 61.4019 | 36.9122 | 1.5803 | 64.9093 | 81.3262 | 9.9237 | |
| 18650 | ⑬ Shenzhen JiaChuangMing Tech. 2600 mAh Built-in protection | 69.4137 | 18.2993 | 0.5883 | 74.3780 | 22.6098 | 0.4537 | |
| 21700 | ⑭ Samsung 5000 mAh Built-in protection | 25.4537 | 7.2190 | 0.2645 | 28.0604 | 14.0903 | 0.4479 | |
| P O U C H | Ⓐ Shenzhen Aoyouji Energy 50.5 Ah Non-protection | 0.8625 | - | 41.2273 | 0.8941 | - | 3694.40 | |
| Ⓑ China Soundon New Energy 48 Ah Non-protection | 0.9151 | - | 14.6219 | 1.0247 | - | 1480.24 | ||
| Ⓒ A123System 37 Ah Non-protection | 1.0420 | - | 19.6525 | 1.0209 | - | 2746.89 | ||
| Supercapacitor Shenzhen Yedianxinbang 600 F | 0.4779 | - | 2427.99 | 0.5737 | - | 2855.31 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bae, J.-Y. Electrical Modeling and Impedance Spectra of Lithium-Ion Batteries and Supercapacitors. Batteries 2023, 9, 160. https://doi.org/10.3390/batteries9030160
Bae J-Y. Electrical Modeling and Impedance Spectra of Lithium-Ion Batteries and Supercapacitors. Batteries. 2023; 9(3):160. https://doi.org/10.3390/batteries9030160
Chicago/Turabian StyleBae, Jin-Yong. 2023. "Electrical Modeling and Impedance Spectra of Lithium-Ion Batteries and Supercapacitors" Batteries 9, no. 3: 160. https://doi.org/10.3390/batteries9030160
APA StyleBae, J.-Y. (2023). Electrical Modeling and Impedance Spectra of Lithium-Ion Batteries and Supercapacitors. Batteries, 9(3), 160. https://doi.org/10.3390/batteries9030160