Defect Chemistry in Zn3V4(PO4)6
Abstract
1. Introduction
2. Computational Methods
3. Results and Discussion
3.1. Crystal Structure of Zn3V4(PO4)6
3.2. Intrinsic Defect Properties
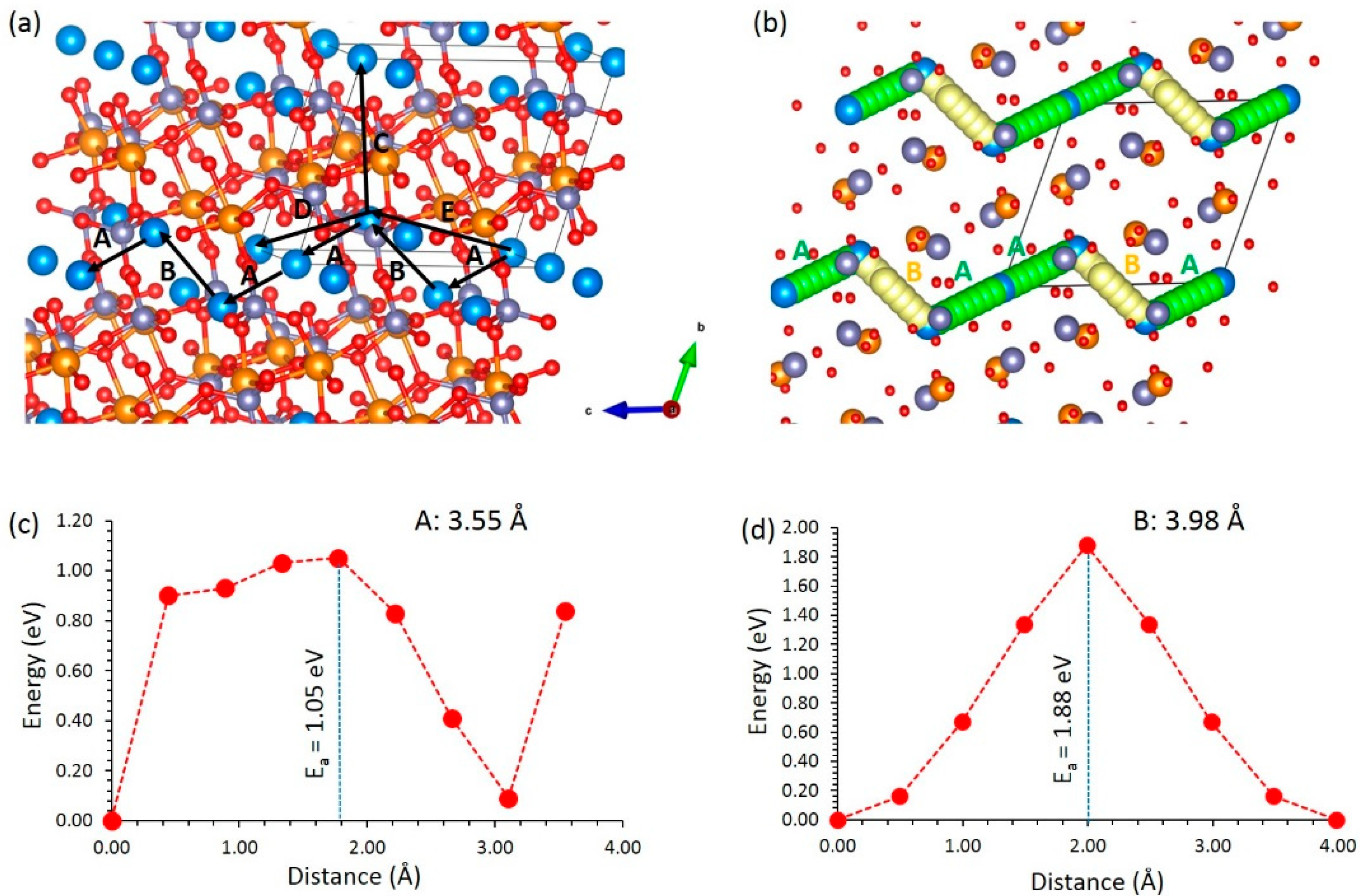
3.3. Diffusion of Zn2+ Ions
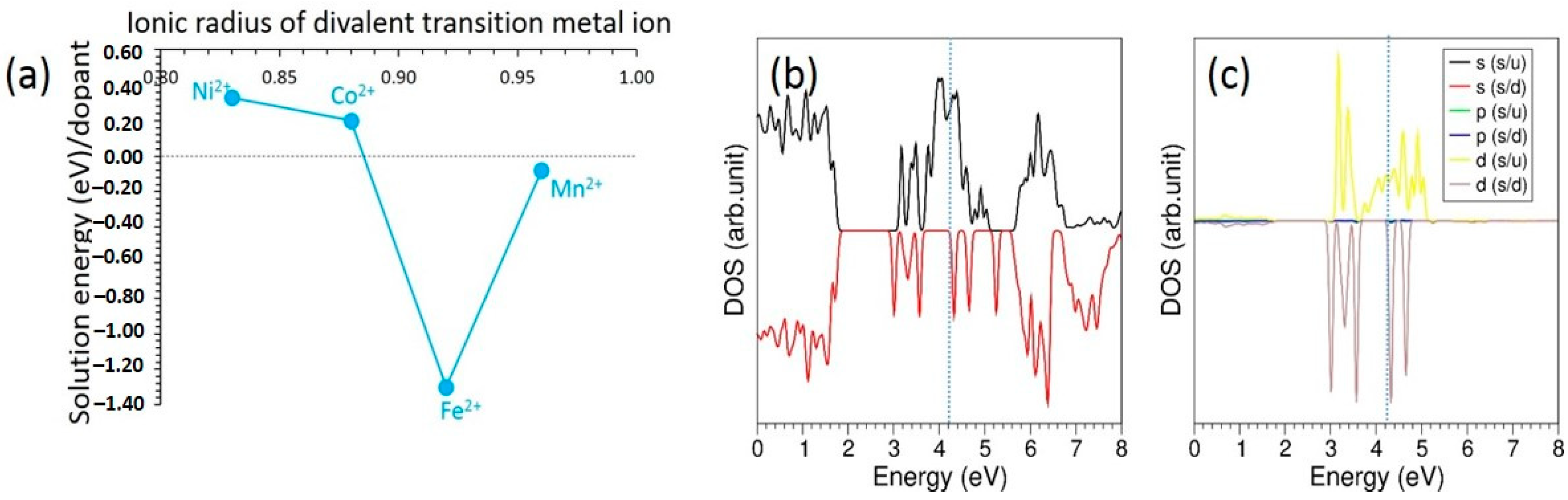
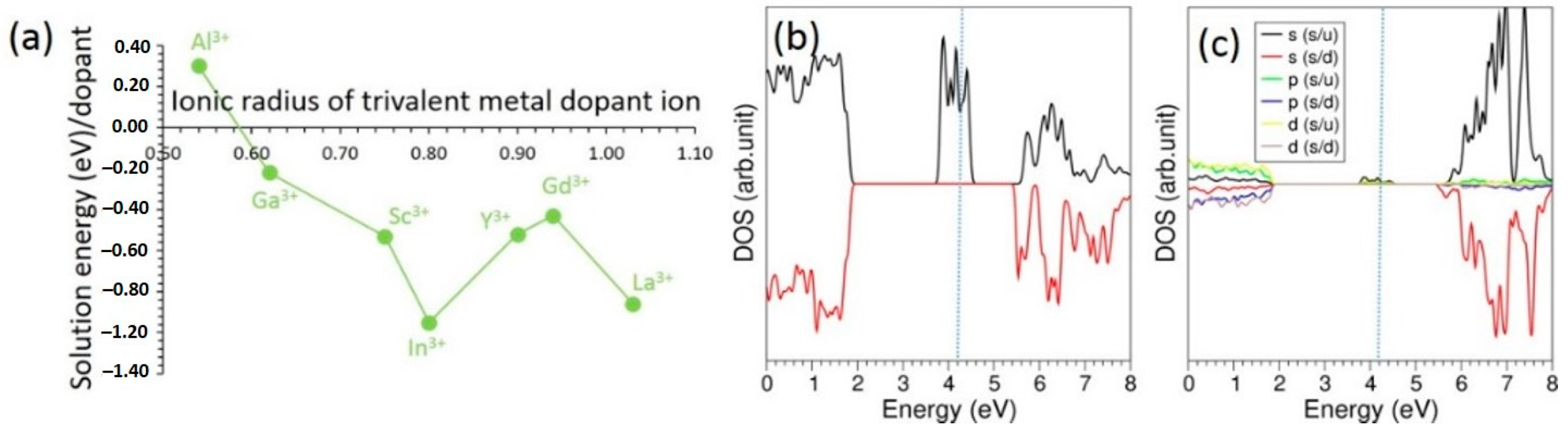
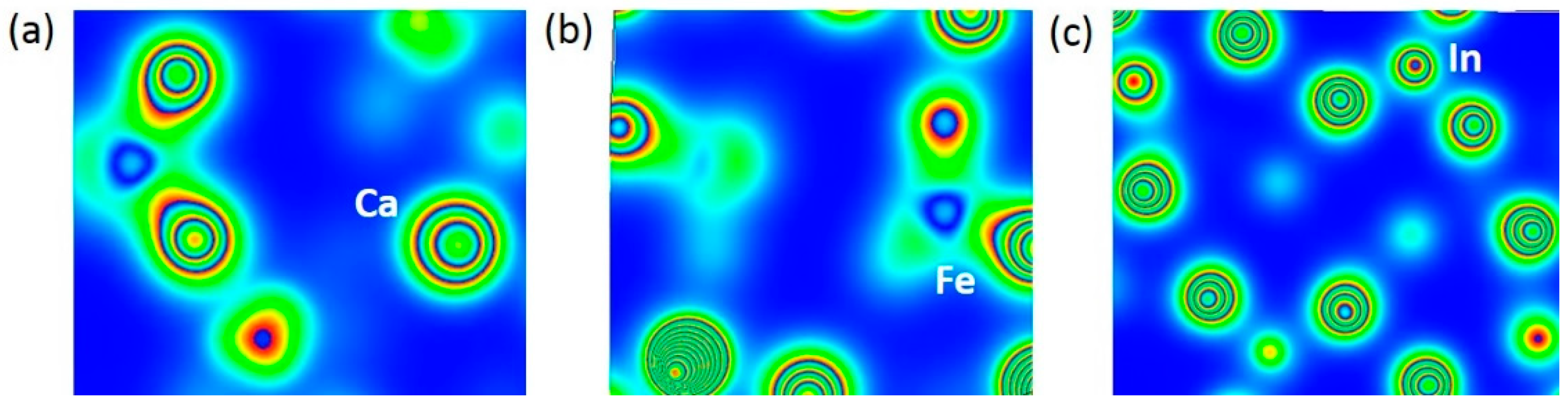
3.4. Solution of Dopants
3.5. Synthetic Routes for the Formation of Zn3V4(PO4)6
4. Conclusions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Goodenough, J.B.; Park, K.-S. The Li-Ion Rechargeable Battery: A Perspective. J. Am. Chem. Soc. 2013, 135, 1167–1176. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Wang, J.; Tian, J.; Lu, J.; Xiong, R. Application of Digital Twin in Smart Battery Management Systems. Chin. J. Mech. Eng. 2021, 34, 57. [Google Scholar] [CrossRef]
- Sun, Y.-K. Promising All-Solid-State Batteries for Future Electric Vehicles. ACS Energy Lett. 2020, 5, 3221–3223. [Google Scholar] [CrossRef]
- Manthiram, A. An Outlook on Lithium Ion Battery Technology. ACS Central Sci. 2017, 3, 1063–1069. [Google Scholar] [CrossRef] [PubMed]
- Kim, T.; Song, W.; Son, D.-Y.; Ono, L.K.; Qi, Y. Lithium-ion batteries: Outlook on present, future, and hybridized technologies. J. Mater. Chem. A 2019, 7, 2942–2964. [Google Scholar] [CrossRef]
- Grey, C.P.; Hall, D.S. Prospects for lithium-ion batteries and beyond—A 2030 vision. Nat. Commun. 2020, 11, 6279. [Google Scholar] [CrossRef]
- Nitta, N.; Wu, F.; Lee, J.T.; Yushin, G. Li-ion battery materials: Present and future. Mater. Today 2014, 18, 252–264. [Google Scholar] [CrossRef]
- Blomgren, G.E. The Development and Future of Lithium Ion Batteries. J. Electrochem. Soc. 2016, 164, A5019–A5025. [Google Scholar] [CrossRef]
- Edge, J.S.; O’Kane, S.; Prosser, R.; Kirkaldy, N.D.; Patel, A.N.; Hales, A.; Ghosh, A.; Ai, W.; Chen, J.; Yang, J.; et al. Lithium ion battery degradation: What you need to know. Phys. Chem. Chem. Phys. 2021, 23, 8200–8221. [Google Scholar] [CrossRef]
- Palomares, V.; Serras, P.; Villaluenga, I.; Hueso, K.B.; Carretero-González, J.; Rojo, T. Na-ion batteries, recent advances and present challenges to become low cost energy storage systems. Energy Environ. Sci. 2012, 5, 5884–5901. [Google Scholar] [CrossRef]
- Abraham, K.M. How Comparable Are Sodium-Ion Batteries to Lithium-Ion Counterparts? ACS Energy Lett. 2020, 5, 3544–3547. [Google Scholar] [CrossRef]
- Anoopkumar, V.; John, B.; Mercy, T.D. Potassium-Ion Batteries: Key to Future Large-Scale Energy Storage? ACS Appl. Energy Mater. 2020, 3, 9478–9492. [Google Scholar]
- Min, X.; Xiao, J.; Fang, M.; Wang, W.; Zhao, Y.; Liu, Y.; Abdelkader, A.M.; Xi, K.; Kumar, R.V.; Huang, Z. Potassium-ion batteries: Outlook on present and future technologies. Energy Environ. Sci. 2021, 14, 2186–2243. [Google Scholar] [CrossRef]
- You, C.; Wu, X.; Yuan, X.; Chen, Y.; Liu, L.; Zhu, Y.; Fu, L.; Wu, Y.; Guo, Y.-G.; van Ree, T. Advances in rechargeable Mg batteries. J. Mater. Chem. A 2020, 8, 25601–25625. [Google Scholar] [CrossRef]
- Lu, D.; Liu, H.; Huang, T.; Xu, Z.; Ma, L.; Yang, P.; Qiang, P.; Zhang, F.; Wu, D. Magnesium ion based organic secondary batteries. J. Mater. Chem. A 2018, 6, 17297–17302. [Google Scholar] [CrossRef]
- Hosein, I.D. The Promise of Calcium Batteries: Open Perspectives and Fair Comparisons. ACS Energy Lett. 2021, 6, 1560–1565. [Google Scholar] [CrossRef]
- Gummow, R.J.; Vamvounis, G.; Kannan, M.B.; He, Y. Calcium-Ion Batteries: Current State-of-the-Art and Future Perspectives. Adv. Mater. 2018, 30, e1801702. [Google Scholar] [CrossRef]
- Li, G.; Huang, Z.; Chen, J.; Yao, F.; Liu, J.; Li, O.L.; Sun, S.; Shi, Z. Rechargeable Zn-ion batteries with high power and energy densities: A two-electron reaction pathway in birnessite MnO2 cathode materials. J. Mater. Chem. A 2019, 8, 1975–1985. [Google Scholar] [CrossRef]
- Fang, G.; Zhou, J.; Pan, A.; Liang, S. Recent Advances in Aqueous Zinc-Ion Batteries. ACS Energy Lett. 2018, 3, 2480–2501. [Google Scholar] [CrossRef]
- Zampardi, G.; La Mantia, F. Open challenges and good experimental practices in the research field of aqueous Zn-ion batteries. Nat. Commun. 2022, 13, 687. [Google Scholar] [CrossRef]
- Mallick, S.; Raj, C.R. Aqueous Rechargeable Zn-ion Batteries: Strategies for Improving the Energy Storage Performance. Chemsuschem 2021, 14, 1987–2022. [Google Scholar] [CrossRef]
- Blanc, L.E.; Kundu, D.; Nazar, L.F. Scientific Challenges for the Implementation of Zn-Ion Batteries. Joule 2020, 4, 771–799. [Google Scholar] [CrossRef]
- Lahiri, A.; Yang, L.; Li, G.; Endres, F. Mechanism of Zn-Ion Intercalation/Deintercalation in a Zn–Polypyrrole Secondary Battery in Aqueous and Bio-Ionic liquid Electrolytes. ACS Appl. Mater. Interfaces 2019, 11, 45098–45107. [Google Scholar] [CrossRef] [PubMed]
- Xu, S.; Sun, M.; Wang, Q.; Wang, C. Recent progress in organic electrodes for zinc-ion batteries. J. Semicond. 2020, 41, 091704. [Google Scholar] [CrossRef]
- Du, H.; Zheng, Y.; Dou, Z.; Zhan, H. Zn-Doped LiNi1/3Co1/3Mn1/3O2 Composite as Cathode Material for Lithium Ion Battery: Preparation, Characterization, and Electrochemical Properties. J. Nanomater. 2015, 2015, 867618. [Google Scholar] [CrossRef]
- Wang, L.; Huang, K.-W.; Chen, J.; Zheng, J. Ultralong cycle stability of aqueous zinc-ion batteries with zinc vanadium oxide cathodes. Sci. Adv. 2019, 5, eaax4279. [Google Scholar] [CrossRef]
- Shen, H.; Liu, B.; Nie, Z.; Li, Z.; Jin, S.; Huang, Y.; Zhou, H. A comparison study of MnO2 and Mn2O3 as zinc-ion battery cathodes: An experimental and computational investigation. RSC Adv. 2021, 11, 14408–14414. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Liu, Z.; Wu, X.; Wen, Y.; Chen, H.; Ni, X.; Liu, G.; Huang, J.; Peng, S. MnO2 cathode materials with the improved stability via nitrogen doping for aqueous zinc-ion batteries. J. Energy Chem. 2021, 64, 23–32. [Google Scholar] [CrossRef]
- Venkatesan, R.; Bauri, R.; Mayuranathan, K.K. Zinc Vanadium Oxide Nanobelts as High-Performance Cathodes for Rechargeable Zinc-Ion Batteries. Energy Fuels 2022, 36, 7854–7864. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, J.; Hu, Q.; Hao, T.; Cao, H.; Huang, X.; Liu, Y.; Zhang, Y.; Lin, D.; Tang, Y.; et al. Prussian blue analogs cathodes for aqueous zinc ion batteries. Mater. Today Energy 2022, 29, 101095. [Google Scholar] [CrossRef]
- Cai, K.; Luo, S.; Feng, J.; Wang, J.; Zhan, Y.; Wang, Q.; Zhang, Y.; Liu, X. Recent Advances on Spinel Zinc Manganate Cathode Materials for Zinc-Ion Batteries. Chem. Rec. 2021, 22, e202100169. [Google Scholar] [CrossRef] [PubMed]
- Kundu, D.; Oberholzer, P.; Glaros, C.; Bouzid, A.; Tervoort, E.; Pasquarello, A.; Niederberger, M. Organic Cathode for Aqueous Zn-Ion Batteries: Taming a Unique Phase Evolution toward Stable Electrochemical Cycling. Chem. Mater. 2018, 30, 3874–3881. [Google Scholar] [CrossRef]
- Li, X.; Chen, Z.; Yang, Y.; Liang, S.; Lu, B.; Zhou, J. The phosphate cathodes for aqueous zinc-ion batteries. Inorg. Chem. Front. 2022, 9, 3986–3998. [Google Scholar] [CrossRef]
- Li, G.; Yang, Z.; Jiang, Y.; Jin, C.; Huang, W.; Ding, X.; Huang, Y. Towards polyvalent ion batteries: A zinc-ion battery based on NASICON structured Na3V2(PO4)3. Nano Energy 2016, 25, 211–217. [Google Scholar] [CrossRef]
- Zhao, H.B.; Hu, C.J.; Cheng, H.; Fang, J.H.; Xie, Y.P.; Fang, W.Y.; Doan, T.N.L.; Hoang, T.K.A.; Xu, J.Q.; Chen, P. Novel Rechargeable M3V2(PO4)3//Zinc (M = Li, Na) Hybrid Aqueous Batteries with Excellent Cycling Performance. Sci. Rep. 2016, 6, 25809. [Google Scholar] [CrossRef]
- Li, W.; Wang, K.; Cheng, S.; Jiang, K. A long-life aqueous Zn-ion battery based on Na3V2(PO4)2F3 cathode. Energy Storage Mater. 2018, 15, 14–21. [Google Scholar] [CrossRef]
- Yesibolati, N.; Umirov, N.; Koishybay, A.; Omarova, M.; Kurmanbayeva, I.; Zhang, Y.; Zhao, Y.; Bakenov, Z. High Performance Zn/LiFePO4 Aqueous Rechargeable Battery for Large Scale Applications. Electrochim. Acta 2015, 152, 505–511. [Google Scholar] [CrossRef]
- Verma, V.; Kumar, S.; Manalastas, W.J.; Zhao, J.; Chua, R.; Meng, S.; Kidkhunthod, P.; Srinivasan, M. Layered VOPO4 as a Cathode Material for Rechargeable Zinc-Ion Battery: Effect of Polypyrrole Intercalation in the Host and Water Concentration in the Electrolyte. ACS Appl. Energy Mater. 2019, 2, 8667–8674. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhu, Y.; Liu, S.; Liu, Y.; He, T.; Jiang, X.; Yang, X.; Feng, K.; Hu, J. Zn3V4(PO4)6: A New Rocking-Chair-Type Cathode Material with High Specific Capacity Derived from Zn2+/H+ Cointercalation for Aqueous Zn-Ion Batteries. ACS Appl. Mater. Interfaces 2022, 14, 32066–32074. [Google Scholar] [CrossRef]
- Morando, C.; Cofrancesco, P.; Tealdi, C. Zn ion diffusion in spinel-type cathode materials for rechargeable batteries: The role of point defects. Mater. Today Commun. 2020, 25, 101478. [Google Scholar] [CrossRef]
- Fisher, C.A.J.; Prieto, V.M.H.; Islam, M.S. Lithium Battery Materials LiMPO4 (M = Mn, Fe, Co, and Ni): Insights into Defect Association, Transport Mechanisms, and Doping Behavior. Chem. Mater. 2008, 20, 5907–5915. [Google Scholar] [CrossRef]
- Kuganathan, N.; Chroneos, A. Na3V(PO4)2 cathode material for Na ion batteries: Defects, dopants and Na diffusion. Solid State Ion. 2019, 336, 75–79. [Google Scholar] [CrossRef]
- Kuganathan, N.; Chroneos, A. Defect Chemistry and Na-Ion Diffusion in Na3Fe2(PO4)3 Cathode Material. Materials 2019, 12, 1348. [Google Scholar] [CrossRef]
- Kuganathan, N.; Rushton, M.J.D.; Grimes, R.W.; Kilner, J.A.; Gkanas, E.I.; Chroneos, A. Self-diffusion in garnet-type Li7La3Zr2O12 solid electrolytes. Sci. Rep. 2021, 11, 451. [Google Scholar] [CrossRef]
- Reischl, B.R.; Raiteri, P.; Gale, J.D.; Rohl, A.L. Atomistic Simulation of Atomic Force Microscopy Imaging of Hydration Layers on Calcite, Dolomite, and Magnesite Surfaces. J. Phys. Chem. C 2019, 123, 14985–14992. [Google Scholar] [CrossRef]
- Gale, J.D.; Rohl, A.L. The General Utility Lattice Program (GULP). Mol. Simul. 2003, 29, 291–341. [Google Scholar] [CrossRef]
- Lewis, G.V.; Catlow, C.R.A. Potential models for ionic oxides. J. Phys. C Solid State Phys. 1985, 18, 1149–1161. [Google Scholar] [CrossRef]
- Kuganathan, N.; Ganeshalingam, S.; Chroneos, A. Defects, Dopants and Lithium Mobility in Li9V3(P2O7)3(PO4)2. Sci. Rep. 2018, 8, 8140. [Google Scholar] [CrossRef] [PubMed]
- Gale, J.D. GULP: A computer program for the symmetry-adapted simulation of solids. J. Chem. Soc. Faraday Trans. 1997, 93, 629–637. [Google Scholar] [CrossRef]
- Mott, N.F.; Littleton, M.J. Conduction in polar crystals. I. Electrolytic conduction in solid salts. Trans. Faraday Soc. 1938, 34, 485–499. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2005, 36, 354–360. [Google Scholar] [CrossRef]
- Boudin, S.; Grandin, A.; LeClaire, A.; Borel, M.; Raveau, B. The Original Structure of Zn3V4(PO4)6 Involving Bioctahedral V2O10 Units and ZnO5 Trigonal Bipyramids. J. Solid State Chem. 1995, 115, 140–145. [Google Scholar] [CrossRef]
- Kröger, F.A.; Vink, H.J. Relations between the Concentrations of Imperfections in Crystalline Solids. In Solid State Physics; Seitz, F., Turnbull, D., Eds.; Academic Press: Cambridge, MA, USA, 1956; Volume 3, pp. 307–435. [Google Scholar]
- Lee, J.S.; Adams, S.; Maier, J. Defect chemistry and transport characteristics of β-AgI. J. Phys. Chem. Solids 2000, 61, 1607–1622. [Google Scholar] [CrossRef]
- Wærnhus, I.; Grande, T.; Wiik, K. Electronic properties of polycrystalline LaFeO3. Part II: Defect modelling including Schottky defects. Solid State Ion. 2005, 176, 2609–2616. [Google Scholar] [CrossRef]
- Chen, H.; Millis, A. Antisite defects at oxide interfaces. Phys. Rev. B 2016, 93, 104111. [Google Scholar] [CrossRef]
- Saloaro, M.; Liedke, M.O.; Angervo, I.; Butterling, M.; Hirschmann, E.; Wagner, A.; Huhtinen, H.; Paturi, P. Exploring the anti-site disorder and oxygen vacancies in Sr2FeMoO6 thin films. J. Magn. Magn. Mater. 2021, 540, 168454. [Google Scholar] [CrossRef]
- Dey, U.; Chatterjee, S.; Taraphder, A. Antisite-disorder engineering in La-based oxide heterostructures via oxygen vacancy control. Phys. Chem. Chem. Phys. 2018, 20, 17871–17880. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.-L.; Holber, J.; Paudel, H.P.; Sorescu, D.C.; Senor, D.J.; Duan, Y. Density functional theory study of the point defect energetics in γ-LiAlO2, Li2ZrO3 and Li2TiO3 materials. J. Nucl. Mater. 2018, 511, 375–389. [Google Scholar] [CrossRef]
- Oba, F.; Choi, M.; Togo, A.; Tanaka, I. Point defects in ZnO: An approach from first principles. Sci. Technol. Adv. Mater. 2011, 12, 034302. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Choe, M.-J.; Enrique, R.A.; Orvañanos, B.; Zhou, L.; Liu, T.; Thornton, K.; Grey, C.P. Effects of Antisite Defects on Li Diffusion in LiFePO4 Revealed by Li Isotope Exchange. J. Phys. Chem. C 2017, 121, 12025–12036. [Google Scholar] [CrossRef]
- Devaraju, M.K.; Truong, Q.D.; Hyodo, H.; Sasaki, Y.; Honma, I. Synthesis, characterization and observation of antisite defects in LiNiPO4 nanomaterials. Sci. Rep. 2015, 5, 11041. [Google Scholar] [CrossRef]
- Armstrong, A.R.; Kuganathan, N.; Islam, M.S.; Bruce, P.G. Structure and Lithium Transport Pathways in Li2FeSiO4 Cathodes for Lithium Batteries. J. Am. Chem. Soc. 2011, 133, 13031–13035. [Google Scholar] [CrossRef]
- Islam, M.S.; Driscoll, D.J.; Fisher, C.A.J.; Slater, P.R. Atomic-Scale Investigation of Defects, Dopants, and Lithium Transport in the LiFePO4 Olivine-Type Battery Material. Chem. Mater. 2005, 17, 5085–5092. [Google Scholar] [CrossRef]
- Nishimura, S.-I.; Kobayashi, G.; Ohoyama, K.; Kanno, R.; Yashima, M.; Yamada, A. Experimental visualization of lithium diffusion in LixFePO4. Nat. Mater. 2008, 7, 707–711. [Google Scholar] [CrossRef]
- Morkhova, Y.A.; Rothenberger, M.; Leisegang, T.; Adams, S.; Blatov, V.A.; Kabanov, A.A. Computational Search for Novel Zn-Ion Conductors—A Crystallochemical, Bond Valence, and Density Functional Study. J. Phys. Chem. C 2021, 125, 17590–17599. [Google Scholar] [CrossRef]
- Bin, D.; Huo, W.; Yuan, Y.; Huang, J.; Liu, Y.; Zhang, Y.; Dong, F.; Wang, Y.; Xia, Y. Organic-Inorganic-Induced Polymer Intercalation into Layered Composites for Aqueous Zinc-Ion Battery. Chem 2020, 6, 968–984. [Google Scholar] [CrossRef]
- Huang, J.; Li, Y.; Xie, R.; Li, J.; Tian, Z.; Chai, G.; Zhang, Y.; Lai, F.; He, G.; Liu, C.; et al. Structural engineering of cathodes for improved Zn-ion batteries. J. Energy Chem. 2021, 58, 147–155. [Google Scholar] [CrossRef]
- Fan, Y.; Yu, X.; Feng, Z.; Hu, M.; Zhang, Y. Synthesis of Zn2+-Pre-Intercalated V2O5·nH2O/rGO Composite with Boosted Electrochemical Properties for Aqueous Zn-Ion Batteries. Molecules 2022, 27, 5387. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Sheng, H.; Wu, X.-W.; Fu, L.; Liu, Z.; Zhou, C.; Holze, R.; Wu, Y. Improving electrochemical properties by sodium doping for lithium-rich layered oxides. ACS Appl. Energy Mater. 2020, 3, 8953–8959. [Google Scholar] [CrossRef]
- Park, J.S.; Kim, Y.-B.; An, J.; Prinz, F.B. Oxygen diffusion across the grain boundary in bicrystal yttria stabilized zirconia. Solid State Commun. 2012, 152, 2169–2171. [Google Scholar] [CrossRef]
- Gao, Y.; Xiong, K.; Zhang, H.; Zhu, B. Effect of Ru Doping on the Properties of LiFePO4/C Cathode Materials for Lithium-Ion Batteries. ACS Omega 2021, 6, 14122–14129. [Google Scholar] [CrossRef]



| Interaction | A/eV | ρ/Å | C/eV·Å6 | Y/e | K/eV·Å–2 |
|---|---|---|---|---|---|
| Zn2+ − O2− | 499.6 | 0.3595 | 0.00 | 2.00 | 99,999 |
| V3+ − O2− | 1410.82 | 0.3117 | 16.00 | 2.04 | 196.3 |
| P5+ − O2− | 897.2648 | 0.3577 | 0.00 | 5.000 | 99,999 |
| O2 − O2− | 22,764.30 | 0.1490 | 27.89 | −2.80 | 74.92 |
| Parameter | Calculated | Experiment [57] | |∆| (%) | ||
|---|---|---|---|---|---|
| Classical | DFT | Classical | DFT | ||
| a (Å) | 6.172 | 6.393 | 6.349 | 2.79 | 0.69 |
| b (Å) | 7.960 | 7.975 | 7.869 | 1.16 | 1.35 |
| c (Å) | 9.208 | 9.391 | 9.324 | 1.24 | 0.78 |
| α (°) | 105.43 | 105.45 | 105.32 | 0.10 | 0.12 |
| β (°) | 108.31 | 107.20 | 108.66 | 0.33 | 1.34 |
| γ (°) | 102.35 | 101.97 | 101.23 | 1.11 | 0.73 |
| Atom | Bader Charge (e) |
|---|---|
| Zn | +1.43 |
| V | +2.10 |
| P | +5.00 |
| O | −1.78 |
| Hop | Distance (Å) | Activation Energy (eV) |
|---|---|---|
| A | 3.55 | 1.05 |
| B | 3.98 | 1.88 |
| C | 5.87 | 3.48 |
| D | 5.94 | 3.62 |
| E | 6.24 | 3.80 |
| Interaction | A (eV) | ρ (Å) | C (eV·Å6) | Y (e) | K (eV·Å−2) |
|---|---|---|---|---|---|
| Mg+ − O2− | 946.627 | 0.31813 | 0.000 | 2.000 | 99,999 |
| Ca2+ − O2− | 1090.40 | 0.3372 | 0.000 | 1.260 | 34.00 |
| Sr2+ − O2− | 776.84 | 0.35867 | 0.000 | 1.526 | 11.406 |
| Ba2+ − O2− | 931.79 | 0.3949 | 0.000 | 1.460 | 14.78 |
| Ni2+ − O2− | 683.5 | 0.3332 | 0.000 | 2.000 | 8.77 |
| Co2+ − O2− | 696.3 | 0.3362 | 0.000 | 2.000 | 10.74 |
| Fe2+ − O2− | 1207.6 | 0.3084 | 0.000 | 2.000 | 99,999 |
| Mn2+ − O2− | 715.80 | 0.3464 | 0.000 | 3.000 | 81.20 |
| Al3+ − O2− | 1725.20 | 0.28971 | 0.000 | 3.000 | 99,999 |
| Ga3+ − O2− | 2901.12 | 0.2742 | 0.000 | 3.000 | 99,999 |
| Sc3+ − O2− | 1575.85 | 0.3211 | 0.000 | 3.000 | 99,999 |
| In3+ − O2− | 1495.65 | 0.3327 | 4.33 | 3.000 | 99,999 |
| Y3+ − O2− | 1766.40 | 0.33849 | 19.43 | 3.000 | 99,999 |
| Gd3+ − O2− | 1885.75 | 0.3399 | 20.34 | 3.000 | 99,999 |
| La3+ − O2− | 2088.79 | 0.3460 | 23.25 | 3.000 | 99,999 |
| Reaction Number | Reaction | Reaction Energy (eV) |
|---|---|---|
| 1 | 3 ZnO + 2 V2O3 + 3P2O5 → Zn3V4(PO4)6 | −6.27 |
| 2 | 3 ZnO + 4 VPO4 + P2O5 → Zn3V4(PO4)6 | −3.12 |
| 3 | 1.5 Zn2(P2O7) + 2 V2O3 + 1.5 P2O5 → Zn3V4(PO4)6 | −2.30 |
| 4 | 3 ZnO + V4(P2O7)3 → Zn3V4(PO4)6 | −1.72 |
| 5 | 3 Zn(PO3)2 + 2 V2O3 → Zn3V4(PO4)6 | −1.10 |
| 6 | Zn3(PO4)2 + 4 VPO4 → Zn3V4(PO4)6 | −0.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuganathan, N. Defect Chemistry in Zn3V4(PO4)6. Batteries 2023, 9, 5. https://doi.org/10.3390/batteries9010005
Kuganathan N. Defect Chemistry in Zn3V4(PO4)6. Batteries. 2023; 9(1):5. https://doi.org/10.3390/batteries9010005
Chicago/Turabian StyleKuganathan, Navaratnarajah. 2023. "Defect Chemistry in Zn3V4(PO4)6" Batteries 9, no. 1: 5. https://doi.org/10.3390/batteries9010005
APA StyleKuganathan, N. (2023). Defect Chemistry in Zn3V4(PO4)6. Batteries, 9(1), 5. https://doi.org/10.3390/batteries9010005






