Abstract
Renewable energy sources have been a topic of ever-increasing interest, not least due to escalating environmental changes. The significant rise of research into energy harvesting and storage over the years has yielded a plethora of approaches and methodologies, and associated reviews of individual aspects thereof. Here, we aim at highlighting a rather new avenue within the field of batteries, the (noaqueous) all-organic redox-flow battery, albeit seeking to provide a comprehensive and wide-ranging overview of the subject matter that covers all associated aspects. This way, subject matter on a historical perspective, general types of redox-flow cells, electrolyte design and function, flow kinetics, and cell design are housed within one work, providing perspective on the all-organic redox-flow battery in a broader sense.
1. Introduction
Humankind has experienced many boosts in quality of life over the course of its existence, paired with unprecedented technological advances. Arguably, the harnessing of energy has been pivotal to our growth, as is the ability to collect and store energy for on-demand use [1,2]. Although the dominant source of energy over the past century has originated from fossil fuels, a switch towards renewable energy sources is imminent [3]. As the collection of solar, wind, and hydroelectric energy is well-developed, the bottleneck for now lies in the storage thereof, as the demand is often not synchronized with the energy production. Redox flow batteries (RFBs) offer a scalable technological and economical solution to the intrinsic intermittency of renewable energy sources [4,5,6,7]. The unique feature of this technology is that energy storage and energy conversion are decoupled, in effect requiring a scale-up of the electrolyte volume only in order to increase the energy storage capacity [8]. This promising application was first conceptualized in the early 1970s when the first prototype from NASA was built and patented [9], though early hints of modern flow batteries were observed in 1949 when Kangro identified liquid redox electrolytes for possible energy storage [10]. A concept introduced in 1986 [11] and the related patent registered for all-vanadium redox-flow batteries in 1988 [12] by Skyllas-Kazacos were, arguably, a clear indication of its true potential.
The scrupulous development of vanadium redox systems jump-started modern RFB technology [13,14,15,16], which is nowadays in full pursuit of viable alternatives with fast responsiveness, a high output energy density, low costs, and a long lifetime [17]. Despite the ubiquity of vanadium redox systems, the electrochemical core of the technology remains modular, and therefore, the possibility of other redox chemistries commercially replacing them is looming [18]. The challenges in replacing vanadium can be divided into those physical (e.g., hydrostatics, compressed air, and high-speed flywheels) or chemical in nature (e.g., electrical double layers, solution/membrane resistance, and electron transfer kinetics) [19,20]. Among other candidates, organic systems preoccupy a special place due to an almost infinite combinatorial diversity of organic structures, limited only by one’s imagination and the framework of contemporary organic synthesis [21]. The design flexibility grants a two-fold advantage: the battery-relevant properties of target redox molecules can be modified in various manners, and the influence of said properties in the context of operating conditions can be better understood [22]. The dynamic nature of the flow cell necessitates such flexibility, as favorable physicochemical properties of redox electrolytes and compatibility of the cell components with the molecular system (electrolyte, solvent, supporting electrolyte, membrane, electrode) are key to their overall performance [6,16,18]. At the current stage of research and development, however, the main challenge for redox electrolytes is the charge/discharge cycling stability, defining the longevity of resulting battery prototypes.
This review addresses aspects of various kinds, covering cell designs, electrolyte design principles and their operating conditions, and the influences of cell components on the battery system. Our goal is to provide an overview that offers insights into the many aspects affecting the overall battery performance all at once, hoping it may not only prove useful as a general starting guide, but that this work will also alert seasoned battery researchers to promising methodologies or sources of performance failure.
2. Description of General Redox-Flow Cell Types
Due to the complex diversity of redox-flow cells with respect to their chemistries, and their different setups, it is difficult to categorize and relate them to and distinguish them from comparable energy storage devices (e.g., fuel cells; see Figure 1A) [23,24,25,26]. In this section, a general definition of flow batteries will be given, along with general descriptions of flow cell types regarding their terminology and their manifold setups.
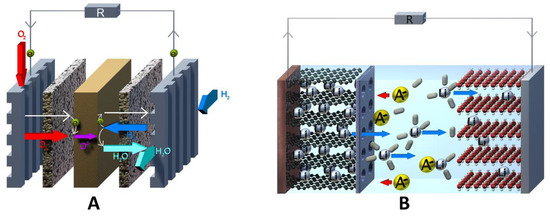
Figure 1.
(A) Schematic of a hydrogen fuel cell with irreversible gas electrodes and (B) a lithium-ion battery (LIB).
2.1. General Definition of a Redox-Flow Cell
For a general comparison, we emphasize a definition for redox-flow cell setup types as follows. Therefore, an energy storage device can be called a flow cell if:
(A) At least one reversible redox process takes place. Accordingly, a hydrogen fuel cell is not a redox-flow cell in the “classic” high-temperature solid-oxide fuel cell (SOFC) [27,28] or the “classic” low-temperature proton-exchange-membrane fuel cell (PEMFC) setups [29], since their conversion of hydrogen and oxygen to water is irreversible. However, there are exceptions: unitized reversible fuel cells (URFC) or reversible regenerative fuel cells (RFC) are capable of operating both as fuel cells and as electrolyzers, and could therefore be categorized as redox-flow cells of a special type. A more detailed description will be given in Section 2.3. (hybrid redox-flow cells) [30].
(B) One or more fluid transport systems to and from an external storage compartment have to be present in order to enable a separation between energy storage and energy conversion (charge and discharge of the cell). For example, a lithium-ion battery (see Figure 1B) is not a flow cell because all battery components (electrolyte, active material, current collector, separator) are confined in the cell housing without any interaction with an outside cell tank.
(C) At least one redox active species (RAS) has to be dissolved or dispersed in a liquid carrier.
2.2. Definition and Terminology of Possible Redox-Flow-Cell Setups
Despite the above-mentioned delimitation, a large number of different cell setups have been introduced. Related to organic catholyte, anolyte, and bipolar electrolytes (see Section 3), these can be in general divided in the first place into aqueous (AqRFBs) and non-aqueous or all-organic redox-flow batteries (AORFBs). Furthermore, depending on their transport medium, on the given fluid mechanics, and on the nature of the electrodes, redox-flow cells can be divided into four basic types: all-liquid redox-flow batteries (ALRFBs), semi-solid redox-flow batteries (SSRFBs), hybrid redox-flow batteries (HRFBs), and single-flow batteries (SFB). These four basic types can be further classified by their cell separation techniques and membrane setups. They range from having no separation membrane to having up to three separation membranes in parallel (Figure 2) [31]. As shown later, more than three membranes cannot be recommended, as no additional positive effects occur.
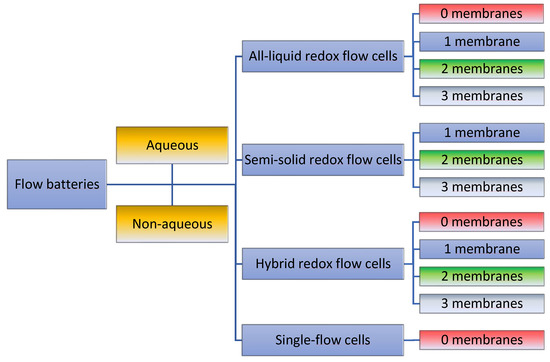
Figure 2.
Overview and terminology over general flow cell setups for both aqueous and non-aqueous RFBs, classified by the cell setup and the number of used membranes.
2.3. General Cell Types
All-liquid redox-flow cell
The ALRFB cell [32] represents the most widely used and widespread cell design. This setup consists of a cell in which the anolyte and catholyte sides are either not separated (see single flow cell below), or physically separated from each other by one or more (up to three) separating membrane. On both sides of the membrane, all electrolyte components—charged and discharged redox-active species and supporting electrolytes—are completely dissolved in the selected solvent. The anolyte or catholyte sides can each have one or two separate storage tanks, depending on whether separation of the oxidized and reduced forms of anolyte and catholyte is necessary. However, since the redox species are completely dissolved €n the electrolyte, cross-contamination through the membrane separator can be a major challenge, and several strategies have been devised to overcome this problem [33,34,35,36,37]. A schematic representation of an all-liquid redox-flow cell is shown in Figure 3A. The most well-known design is the all-vanadium RFB with its many iterations to improve energy density and longevity over the years [11,38,39,40,41,42,43,44,45,46].
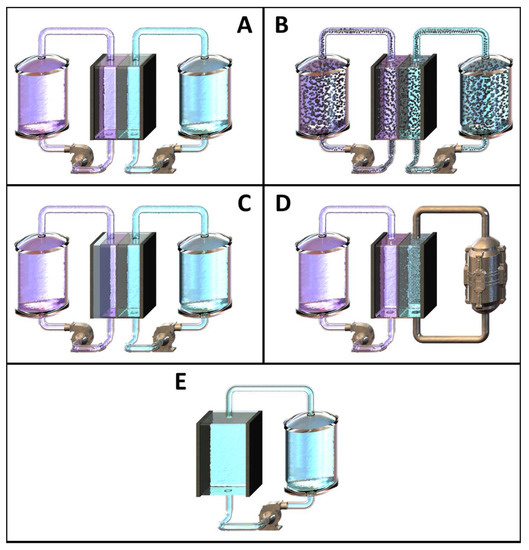
Figure 3.
Different flow cell types: (A) all-liquid redox-flow battery (ALRFB) with separated anolyte and catholyte; (B) semi-solid redox-flow battery (SSRFB) consisting of an anolyte and a catholyte with solid active material particle dispersions; (C) hybrid redox-flow battery (HRFB) with solid anode; (D) HRFB with gas conversion cathode; (E) a single flow battery (SFB) with insoluble charged active material plated on cathode and anode. Anolyte and catholyte have the same composition.
Semi-solid redox-flow cell
A possible approach to minimize or even completely avoid the above-mentioned cross contamination problem is to use redox active particle dispersions within the anolyte and/or the catholyte formulation. In this case, the anolyte and the catholyte compartments are separated from each other by a well-defined size exclusion separator with significantly smaller pore diameters compared to the particles. This special setup is known as the SSRFB and can also be connected to one or two storage tanks for the anolyte and catholyte dispersion, respectively. A graphical representation is shown in Figure 3B. This cell design allows easy adaptation of other energy storage technologies, e.g., the lithium-ion battery. Cathode materials such as lithium iron phosphate (LFP), LiCoO2 (LCO), and LiNi0.33Co0.33Mn0.33O2 (NMC111); and anode materials such as graphite, Li4Ti5O12 (LTO), and silicon (Li/Si) are used in combination with separators (e.g., Celgard© 2022) [47,48,49,50,51]. In addition to redox-active inorganic particle dispersions, low-molecular and polymer dispersions are also used in combination with, for example, dialysis membranes for size separation. Exemplary systems are polyhydroquinones and polyimides dispersed in water and 10-methylphenothiazines (MPT) and thioxanthones (THA) dispersed in acetonitrile [52,53]. However, in addition to the benefit of reducing or suppressing cross-contamination, the semi-solid flow system faces other challenges. These include high viscosities of the electrolyte dispersions, limited redox kinetics resulting from slow charge transport from the interior of the particles to the surface, partial deposition of particle agglomerates in the storage tanks during long storage, and clogging of the membrane surface [52,54,55]. The influence of these challenges will be discussed in more detail in Section 4.
Hybrid redox-flow cell
In contrast to the two full flow cell types mentioned above, HRFCs consist partly of a redox-flow cell and partly of a different energy storage technology. Additionally, they allow for easy adaptation, as explained for semi-solid redox-flow cells above. In general, two types are possible: solid reversible anode/cathode (Figure 3C) and reversible gas cathode/anode (Figure 3D) [31]. In the latter one, hydrogen is mainly used as an energy storage medium, and as mentioned at the beginning of this section, this type of hybrid redox-flow cell is also called a regenerative fuel cell (RFC). While hydrogen can be reversibly converted on the cathode side, inorganic and organic redox species are utilized in the anolyte compositions. Known examples of such anolyte compositions contain vanadium, iron, manganese, cerium, and bromine as inorganic redox species, or, e.g., 1,2-dihydrobenzoquinone-3,5-disulfonic acid as the organic redox species (BQDS, see Scheme 1) [56,57,58,59,60,61]. Hydrogen-based RFCs enable very high energy densities. For example, Rubio-Garcia et al. were able to achieve an energy density of 45 W h L−1 in an H2/V hybrid redox-flow system [62].

Scheme 1.
Reversible redox reaction of 1,2−dihydrobenzoquinone−3,5−disulfonic acid (BQDS) as the anolyte component in redox-flow [61].
Overall, HRFCs with gas cathode are a clever combination of the fuel cell and the redox flow concept, enabling the use of the high-energy storage medium hydrogen and gaseous energy storage media in general. However, this concept also bears major drawbacks: Some of these include the use of platinum, rhodium, or palladium as catalysts, which makes cell construction more expensive and more dependent on rare materials. Then, the conversion and storage of hydrogen poses a significant safety risk, especially for grid-connected large-scale stationary plants.
HRFCs with solid anodes can be generally divided into two types, namely, HRFCs with a solid anode where the metal is plated and redox-targeting HRFCs where an active material is present as a stationary solid in a storage tank. In the case of HRFCs with classic solid anodes, zinc metal anodes with Ce3+|Ce4+ and Fe2+|Fe3+, and lithium metal in combination with the Fe2+|Fe3+ redox couple, are widely investigated in the literature, leading to high energy densities [63,64,65]. A combination of both types is presented by Zhu et al. He introduced a concept which utilized Li metal as the anode and LFP as the cathode. The LFP is present as the stationary solid in the storage tank and is reversibly oxidized and reduced by the two-stage redox mediator 2,3,5,6-tetramethyl-p-phenylenediamine (TMPD) dissolved in the catholyte solution flowing through the cell. A theoretical energy density of 1023 Wh L−1 is possible with a given porosity of the LFP of about 50%. Additionally, a Coulombic efficiency close to 100% was achieved [66].
In general, HRFCs with solid anodes offer the advantage that the anolyte, and the catholyte, being present and applicable in solid form in at least one oxidation state. This therefore minimizes the need for high solubility of both oxidation states in the catholyte and in the anolyte composition to achieve high energy densities, up to 500 W h L−1 [67,68,69,70].
However, redox processes inevitably use redox mediators. These often have low solubility, and therefore, large volumes of electrolyte must be pumped through the cell for complete redox conversion. Considering the energy consumption of the pumps during charge and discharge, this leads to a significant reduction in the overall efficiency of the system, especially if a high flow rate is used. Zou and co-workers investigated the influence of pump loss on a 35 kW all vanadium redox-flow battery system. They found that the energy efficiency of the stack increases continuously with the increase in flow, but with an increase in flow, the required power consumption of the pump also increases quadratically [71]. Therefore, selecting the right flow rate can effectively reduce the energy loss. Furthermore, HRFC with solid anodes also have the disadvantage that they do not represent a complete decoupling of conversion cell and storage. Therefore, a separate scaling of energy and power, which normally is the unique selling point of the redox-flow technology, is only possible to a limited extent.
Single flow cell
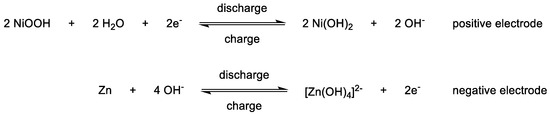
In order to simplify a redox-flow cell to a minimum of components, membrane-less cell concepts with one common electrolyte have been developed, also known as single flow cells (Figure 3E). The single flow cell concept can be realized if both redox-active species are insoluble in their charged states, deposited on current collectors, and afterwards provide electronic conductivity. The most investigated system is based on the nickel-hydroxide‖zinc alkaline flow battery (Scheme 2) [72,73,74].
Scheme 2.
Redox reactions of the nickel−hydroxide‖zinc−alkaline−flow−system for the positive electrode in the anolyte compartment (above) and the negative electrode in the catholyte compartment (below).
Turney et al. showed that energy densities of up to 20.9 W h L−1 can be achieved with the abovementioned nickel-hydroxide‖zinc-alkaline-system [75].
Another method to realize the SFB concept is to use a multiphase liquid electrolyte. This consists of an emulsion whose non-aqueous phase (e.g., finely dispersed droplets of an organic solvent) contains in high concentrations the other redox-active species in their charged forms. At equilibrium, the aqueous phase provides only very low concentrations of the charged form, which significantly reduces its activity within the electrolyte and thus largely reduces crossover. This concept was investigated by Naar et al. and involves in their case a zinc metal anode and a graphite current collector on the cathode side [76]. In addition, an electrolyte emulsion was used consisting of 95% water and 5% polybromide. The aqueous phase contains zinc bromide as a zinc source and supporting conducting salt, and the polybromide phase consists of bromine and N-ethyl-N-methyl pyrrolidinium bromide (MEP) as a bromine complexing agent (BCA).
In the aqueous phase, the bromine concentration ranges from 37–85 mM/L, depending on the overall bromine concentration, and therefore, zinc corrosion is largely reduced. An additional side effect is the mitigated formation of zinc dendrites [76].
In general, the concept of the SFB features involves easy and low-cost setup with one common electrolyte, one circular pump system with one tank, and no membranes. However, it is rarely found in the literature. A couple of examples are the PbO2‖Zn and the I2‖Zn system [77,78].
Aside from the above-mentioned advantages of the SFB, the single flow battery faces a big disadvantage. As described earlier for the hybrid redox-flow cells, separate scaling of energy and power for single flow systems with one solid electrode is only possible to a limited extent.
2.4. Cell Separation Techniques and Membrane Configurations
The above-mentioned flow cell types can be built without separation membranes and with one or more separation membrane, depending on the cell chemistry and cell geometry [79]. All possible separation techniques and membrane setups are displayed in Figure 4A–D using a “modified” Daniell-cell model. In this section, only charge-exclusion membranes are discussed and not size-exclusion separators (see Section 4.1.3), as the latter has no beneficial effects in a multi-membrane setup.
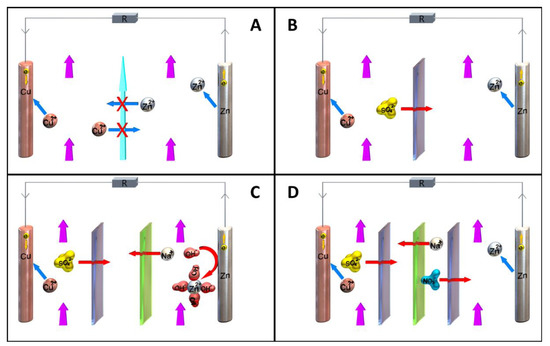
Figure 4.
Different numbers of ion exchange membranes and their functionality explained on a Danielle-cell-like model during discharge: (A) Setup with no membranes, realized by laminar flow, which prevents cross-stream diffusion, and therefore, intermixing of the anolyte and the catholyte. (B) Setup with one ion exchange membrane (here an anion exchange membrane (AEM)). This represents the most common setup. (C) Setup with two membranes. One AEM und one CEM. This setup is used when the electrolyte compositions of the anolyte and catholyte are different and the non-redox active counter-ions each have opposite charges. (D) Setup with three membranes with a symmetrical membrane arrangement (either AEM/CEM/AEM or CEM/AEM/CEM). This setup is used to highly suppress crossover of the RAS.
Zero membrane configuration
A “zero-membrane” configuration can be realized when either only one electrolyte composition is present, as in the single flow cell example (see Section 2.3), or when the geometric cell setup creates a laminar flow with cross-stream diffusion of the anolyte and catholyte; see Figure 4A [80]. To enable laminar flow in the cell, several conditions must be fulfilled:
The flow velocities of analyte and the catholyte must be as equal as possible. Furthermore, the flow rate must be slow and uniform. Point-like turbulent spots that always grow in size with downstream movement and finally merge to form a continuously turbulent region should be prevented [81]. Therefore, particle dispersions, as described for the semi-solid redox-flow type, are not suitable for a zero-membrane setup. Additionally, surfaces inside the cell and the pipe system should be smooth and without hard edges. This setup requires very precise cells, and also requires at all-times a constant flow through the cell to maintain separation by laminar flow.
Single-membrane configuration
In the single-membrane configuration, anolyte and catholyte are separated by one membrane (see Figure 4B), be it a size-exclusion or charge-exclusion membrane [79]. For cation exchange membranes (CEMs), the most known example is the all-vanadium redox-flow cell, where derivatives of polystyrene sulfonic acid cation exchange membranes are used [11,12,82].
For anion exchange membranes (AEMs), which are frequently used in AORFBs, the most common membranes are based on Nafion [83,84,85]. Next to that, micro- and meso-porous membranes consisting of polymer networks or metal organic frameworks (MOFs) [86] are often utilized as size-exclusion membranes for redox active polymer solutions and dispersions [87]. In the case of the above-mentioned Daniell-cell model, one RAS is reduced and plated to the electrode, whereas the other will be oxidized and dissolved. The common counterion (in this case the sulfate anion) migrates through the AEM to ensure charge balance in the anolyte and the catholyte compartment.
Dual-membrane configuration
In dual-membrane configuration, the anolyte and the catholyte are separated by two membranes, which in turn are separated by a third flow chamber; see Figure 4C [79]. The cell is designed with one anion exchange membrane and one cation exchange membrane. For the third chamber, a non-redox-active electrolyte is required, which has its own tank and pumping system.
This setup is used when the electrolyte compositions of the anolyte and catholyte are different and the non-redox active counter-ions each have opposite charges. To illustrate it using the Daniell cell setup, a tetrahydroxyzincate-based ([Zn(OH)4]2−) electrolyte is used on the cathode side, which contains Na+ as non-redox active counter-ion (Figure 4C). If the cell is discharged, [Zn(OH)4]2− is formed, and the remaining Na+ ions diffuse through the cation exchange membrane in the center chamber. On the anion side, Cu is plated during the discharge process, and the remaining sulfate ion diffuses through the anion exchange membrane into the center chamber. Both processes increase the concentration of NaSO4 in the third non-redox active electrolyte.
This setup highly suppresses crossover of the RAS, due to a third chamber, and it allows a very strong pH gradient between the anolyte and the catholyte. The latter can lead to a large increase in cell voltage. A typical example is given by the zincate-cerium RFB [79]. Redox reactions in the anolyte and catholyte compartment are shown in Figure 5. It shows an exceptionally high cell voltage (3.08 V), a high voltage efficiency (91%), and high Coulombic efficiency (98%) at 5 mA/cm2. In general, the disadvantage of a dual-membrane configuration is the utilization of an expensive double membrane system using an additional tank and pumping system. Furthermore, double membrane systems exhibit a huge ohmic drop; therefore, the above-mentioned system show a round-trip energy efficiency of 89% at 5 mA cm−2 charge–discharge current density [79].
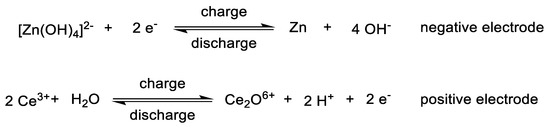
Figure 5.
Reactions of the zincate-cerium redox-flow system for the negative electrode in the catholyte compartment (above) and the positive electrode in the anolyte compartment (below).
Triple-membrane configuration
In the triple-membrane configuration, a symmetric membrane arrangement is used. The setup can either be AEM/CEM/AEM or CEM/AEM/CEM (e.g., arrangement AEM/CEM/AEM; see Figure 4D) [79]. A particularly outstanding feature of the two above-mentioned configurations is that they can be used universally. The anolyte and the catholyte can each consist of positively charged redox active ions and their negatively charged non-redox active counter-ions or vice versa. A combination of positively and negatively charged RAS is also possible. All combinations are illustrated in Figure 6A–D, exemplified by the triple membrane configuration AEM/CEM/AEM. A similar scheme can be constructed for the triple-membrane combination CEM/AEM/CEM. Another feature of the triple-membrane configuration is the ability to separate redox-pairs and their counter ions from each other. In the example of the Daniell cell model in Figure 4D, the sulfate anion and the nitrate anion also remain separate from each other. In all cases, these configurations are able to suppress crossover of the RAS. However, examples are rarely shown in the literature, and none of them are commercially used due to the high cost of two additional membranes and two additional pumping circuits. Furthermore, two additional membranes represent two additional resistances, as can be noted for every multi-membrane system that is connected in series with the total resistance of the cell, and these negatively affect the kinetics of the entire cell.
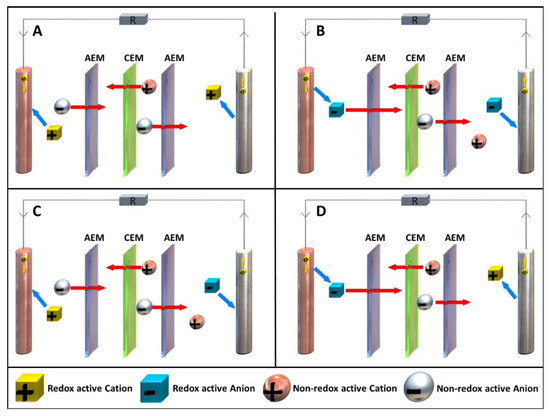
Figure 6.
Overview of all possible redox pair combinations, exemplified by the triple membrane configuration AEM/CEM/AEM, during the discharge process (anolyte on the right and catholyte on the left, respectively). The redox active ions are shown as cubes and non-redox active ions as spheres. (A): the RAS are positively charged in the anolyte and in the catholyte; (B): the RAS are negatively charged in the anolyte and in the catholyte; (C): the RAS within the anolyte is positively charged and that within the catholyte, negatively charged; (D): the RAS within the anolyte is negatively charged and within the catholyte, positively charged.
2.5. Summary
A variety of cell setups and special configurations are possible, as shown previously. The three most important factors are:
- Type and number of membranes.
- The nature, geometry, and surface area of the electrodes.
- Geometry of the cell body, which strongly affects the electrolyte flow.
The setup is largely related to the choice of anolyte and catholyte composition. Polarity, number of phases, aggregate state of individual phases to each other, solvents, conducting salts, and the nature of the RAS used. The latter will be discussed in detail in the following section.
3. Electrolytes and Electrochemical Behavior
3.1. Introduction
Over the past decade, many studies have been dedicated to overcoming the drawbacks of conventional metal-based redox-flow systems by employing all-organic substrates as an inexpensive, safe, and sustainable alternative [88]. A transfer to non-aqueous solvents enables widening of the electrochemical window, and expanding operation to sub-zero temperatures and thus potentially higher energy densities. However, although the access to organic redox-active compounds is broad, thanks to the contemporary synthetic chemist’s toolbox, we have to keep in mind that accessibility, toxicity, and durability also need to achieve widespread sustainable energy. Most notably, opening RFBs up to organics opens up to a plethora of solvents, each with its own limitations [89]. One major contributing factor to increasing theoretical energy densities is the increase in the potential stability window for many organic solvents compared to water [90]. Since the first report on the concept on non-aqueous flow batteries in 1984 [91], however, the large number of contributions seems to have converged to a select few promising organic media to consider for AORFBs, fairly independent of changes in the electrolyte structure (Figure 7).
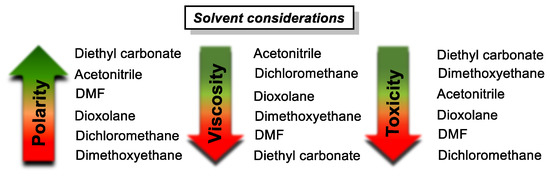
Figure 7.
General considerations for choice of solvent for application in all-organic redox-flow batteries. Other parameters that are less limiting (or irrelevant even in some of the highlighted cases) but may be considered include freezing point/boiling point temperatures, and solvent redox potentials. Toxicity was compiled from the LD50 values for rats reported in MSDSs.
Under strong consideration in general are polarity, with respect to the solubility of electrolytes and their charged states; viscosity, pertaining to the required circulation energy and mass transfer control from the electrode surfaces; and toxicity [92,93]. Another parameter one could take into consideration is the proficiency of the solvent to contribute to radical stabilization, which is related to the dipolarity/polarizability (not to be confused with polarity) of the electrolyte [94,95]. Nevertheless, although the solvent contribution can be tailored, the extent of stabilization is primarily dependent on the ionization potential of the redox events, with more stable radical ions being less sensitive to any solvent changes, making the issue more suitable for discussion in the molecular engineering of electrolytes below.
Out of these popular choices for solvent, acetonitrile is to date the most widely used, owing to its overall performance in these categories, and due to its relatively low corrosiveness and high physical resemblance to water. Nevertheless, though a fitting solvent system is essential for the durability of the RFB, ultimately, it is the electrolyte that makes up the final RFB characteristics within the solvent boundaries. Their chemical design involves several non-linearly related considerations for acquiring maximum energy density (e.g., synthetic costs, solubility of neutral and charged states, number of electrons passed, and cycling stability), making optimization a challenge, but the field as a whole open to significant advances. In this section, we provide an overview of pivotal non-aqueous organic electrolyte designs, and from them collect essential contributing strategies to aid in future electrolyte design (Figure 8).
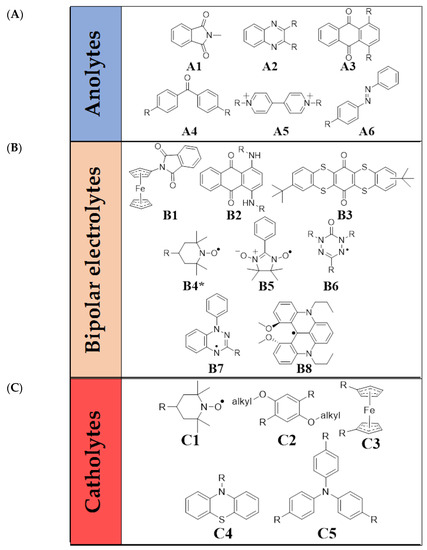
Figure 8.
Pivotal chemical structures in the domain of organic (A) anolytes, (B) bipolar electrolytes, and (C) catholytes. We note that through its widespread use in organics, and its similarity thereto, ferrocene has been included as an exception. A1 = N-methylphthalimide [96,97], A2 = quinoxaline [98], A3 = anthraquinone [99], A4 = benzophenone [100], A5 = viologen [101,102], A6 = azobenzene [103,104]. B1 = N-ferrocenylphthalimide [105], B2 = 1,4-diaminoanthraquinone [106,107], B3 = thianthrene [108], B4 * = 2,2,6,6-tetramethyl-1-piperidinyloxy (TEMPO) in ionic liquid [109], B5 = 2-phenyl-4,4,5,5-tetramethylimidazoline-1-oxyl-3-oxide [110,111], B6 = 1,5-diphenyl-3-isopropyl-6-oxo-verdazyl [36], B7 = 1,2,4-benzotriazin-4-yl [112], B8 = dimethoxyquinacridinium [113,114], C1 = 2,2,6,6-tetramethyl-1-piperidinyloxy (TEMPO) [96], C2 = dialkoxybenzene [98,115,116,117,118,119], C3 = ferrocene [120,121,122], C4 = phenothiazine [99], C5 = triarylamine [123].
A gradual shift from conventional metal-based to organic electrolytes was logically foreseen to transition through lithium-based hybrid redox-flow [124], and indeed, the advent of promising all-organic systems followed several years after in 2011. In the first work on an AORFB, N-methylphthalimide (A1) was utilized by Li and coworkers to replace lithium, providing alongside 2,2,6,6-tetramethyl-1-piperidinyloxy (TEMPO, C1) a cell potential of ≈1.60 V vs. Ag|AgCl and setting the stage for the transition to all-organic substrates [96]. Despite the quasi-reversibility in cyclic voltammetry, the coulombic efficiency of the catholyte-anolyte pair was shown to be 90% over the first 20 charge–discharge cycles in acetonitrile. The higher overall capital costs of organic solvents and supporting electrolytes, such as bis(trifluoromethylsulfonyl)imide (TFSI-) and PF6−, put the AORFB at a disadvantage to its aqueous counterpart, but increasingly, higher current densities (15–100 mA cm−2) and energy densities are being reached to achieve the set-out goal of >$100 (kW h)−1 [90]. Shortly after the pioneering work involving N-methylphthalimide and TEMPO, many alternative all-organic catholyte-anolyte pairs started to appear, along with some bipolar electrolytes (capable of both functions simultaneously [106]), showing great promise for the design of next-generation RFBs.
3.2. Catholytes
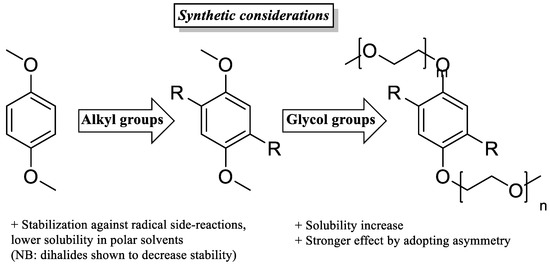
Next to its pioneering application in the first AORFB [96], TEMPO (C1) has been utilized to demonstrate other interesting conceptual advances in the field, most notably including bipolar application both upon stabilization of its reduction in ionic liquids (B4 *) [109] and by synthetic modification of the nitroxide radical (vide infra, “bipolar electrolytes”) [110,111,125], and it is a prospect for membrane-free batteries [126]. However, although membrane-free batteries could be a new avenue for redox flow, despite self-discharging arising from electron transfer at the interphase, to date there is no clear understanding of whether all-organic phases are feasible. The closest concept, having a liquid H2O separator between two organic phases, displayed volatility of the involved solvents and high Ohmic drops, causing major problems for this approach [127]. Staying with traditional AORFB setups instead—one of the quickest, and ultimately most developed, catholytes for AORFBs to follow was the dialkoxybenzene C2, owing to its modularity and chemical stability (Scheme 3).
Scheme 3.
An overview of relevant considerations for electrolyte design, with the well-studied dialkoxybenzene catholyte as an example. Notably, molecular asymmetry was shown to be beneficial to the solubility, and thus energy density of the dissolved catholyte species [119].
Shortly after ethylene glycol phenoxy-substituents were shown by Zhang et al. to exhibit superior solubility (up to 0.4 M in ethylene carbonate: methyl ethyl carbonate 3:7) during successful application as redox-shuttle for overcharge protection in a hybrid RFB [115], Brushett et al. demonstrated a cell voltage of ca. 1 V for the prototypical first dialkoxybenzene-AORFB contribution. Although it exhibited moderate Coulombic efficiency (43% on the first cycle, stabilizing over time to 70%), their screening of substitution patterns and electrolyte formulations gave valuable insights and opened up to many more works centered around the catholyte [98]. For example, they found that using typical lithium battery electrolytes based on organic carbonate solvents [128] and a lithium salt [129], and then changing from 1.2 M LiPF6 in 3:7 ethylene carbonate/ethyl methyl carbonate to 0.2 M LiBF4 in propylene carbonate, shifted the redox potential up 100 mV and increased the diffusion coefficient by 24%, showing the susceptibility of the RFB to the solvent/electrolyte system. This trend resonates with a later study by Wang and coworkers on acetonitrile/organic carbonate co-solvent effects on AORFB performance, which detailed that higher diethyl carbonate content widens the electrochemical stability window of dialkoxybenzene, whereas dimethyl carbonate does not [116]. Though lower acetonitrile contents in these co-solvents improved the alkoxybenzene solubility, it is counter-balanced by the inherent highly flammable nature of carbonate solvents and a loss in conductivity. Wei et al. had also reported on the superior conductivity of acetonitrile, and underlined a strong role of solvent in general, and in addition, the role of the supporting electrolyte in stabilizing the radical charged state against parasitic radical coupling reactions [117]. Electron spin resonance (ESR) studies showed the lowest fading rates with tetraethylammonium/bis(trifluoromethylsulfonyl)imide (TEA/TFSI) supporting electrolyte, with 1,2-dimethoxyethane as a solvent, which is known for its proficiency in radical stabilization. They also showed that tetraethylammonium salts in general lead to higher conductivities than their lithium analogues, and lower cell overvoltages.
Stabilization against radical side-reactions can also be efficiently tuned synthetically by steric shielding, as demonstrated by the frequent use of 2,5-dimethyl substituents. We note that 2,5-dihalides were shown by Kowalski and coworkers to decrease the stability of charged states despite increasing solubility and redox potentials [130]. Cycling alkyl 2,3- and 5,6-positions, meanwhile, further increases the stability of the radical cation according to Zhang et al. [118], albeit at the cost of solubility in polar solvents, accentuating the tug-of-war in design optimization. A promising development in synthetic strategy, however, was found by Huang and coworkers through varying the length of 1,4-ethylene glycol chains, ultimately creating the first liquid catholyte for non-aqueous redox-flow [119]. Importantly, though increasing the chain length improved solubility, the key to liquefying the catholyte was asymmetry in the two glycol chain lengths.
This trend was also shown for 1,1′-dimethylferrocene (C3) by Cong and coworkers in their hybrid RFB [131]. The melting point of the subtly modified ferrocene was drastically lowered to 50 °C by the introduced asymmetry, and the solubility in turn greatly increased. Although not strictly organic, ferrocene has also been a popular choice for non-aqueous RFB applications. The small molecule is often considered amidst organics and plays a pivotal role in many redox-responsive systems next to serving as a standard reference on its own, not least for their robustness [132]. Ding and coworkers were able to raise the interest even further; however, when they successfully demonstrated a ferrocene (C3) catholyte and cobaltocene anolyte non-aqueous RFB in 2017 [120]. Though the plain metallocenes already achieved a cell potential of 1.7 V, a common modification as easy as using decamethylcobaltocene instead provided a cell potential of 2.1 V, demonstrating the room for synthetic improvements. Indeed, ferrocene has shown ample synthetic flexibility since its first application in hybrid RFBs [121,122], including a recent notable AORFB contribution demonstrating the advantage of ferrocene dimers [133]. The double ferrocene, separated by a single tertiary carbon with a methyl and glycol group, profits from enhanced energy density due to both increased solubility owing to the glycol substituent, and possessing twice the electron concentration in the 1 M battery setup. While not conjugated, the proximity of the two ferrocene components causes a separation of redox events by 0.2 V, owing to the inductive electron-withdrawing effect following the first oxidation.
An inductive effect on the redox potential of ferrocene was also demonstrated by Wei et al. who showed that an alkyl quaternary amine thus raises the open circuit potential, while additionally increasing the solubility of ferrocene more than ten-fold [134]. Moreover, a study on the effects of various counter anions on performance revealed an overall most-favored solubility and stability for TFSI- and ClO4− [135]. The aforementioned studies by the group of Wang not only aptly show the relevance of the counterion and that an inductive electron-withdrawing effect can be significant (versus conjugated functionality, e.g., acetylferrocene [136]), but also were the start of a new strategy against cross-over of electrolytes in AORFBs. The permanent positive charge keeps the rejection rate by anion exchange membranes high, inspiring researchers ultimately to instill anolytes with permanent positive charges also (vide infra, “anolytes”) [134,135,137,138,139].
Another catholyte that has been widely investigated for its synthetic flexibility from the moment it was suggested as a possible overcharge protector, much like dialkoxybenzene, is phenothiazine (C4) [140,141]. Notably, although still with the aim of overcharge protection, Kaur et al. showed in 2016 that electron-withdrawing groups efficiently increase the oxidation potential, with per-fluorination of the phenothiazine, specifically, leading to upshifting by an impressive 0.8 V [142]. Relatively swift decomposition of the redox shuttles occurred in overcharge cycling tests, albeit under increased stress at 200% charging currents over 10 h periods. That same year, however, the group of Odom also provided a detailed look into the RFB performances of more phenothiazine derivatives and reported as one on the few even that are problematic—limiting the solubility of the charged species [143]. Although appending an N-ethylene glycol chain is shown to be an efficient strategy to once again increase solubility by over ten-fold, the isolated charged radical cation salt (best performed with a TFSI counter-ion [144]) was shown to limit the solubility to 0.5 M instead of the 2.0 M reported for the neutral species. While not common practice, this gives an accurate insight into the limits for RFB cycling and more of a handle to tackle bottleneck problems involving charged species that are central to the application, let alone doubly charged species.
Theoretically, the energy density could increase significantly despite a lower solubility if the second redox event is made use of, as explored by Huang et al. in a phenothiazine AORFB with anthraquinone (A3) anolyte [99]. Though the cycling performance of the RFB was hampered by a limited chemical stability, it was shown that the anthraquinone anolyte rather than the phenothiazine catholyte was the major cause. In earlier work, Kowalski and coworkers showed that 3,7-dimethoxy substituents effectively stabilize the 2-electron oxidation through electron delocalization, albeit at the cost of solubility [145]. The abovementioned N-substitution with an oligoethylene glycol chain [143], or better yet, a polyethylene glycol (PEG) chain, as shown by Chai et al. [146], could be an efficient counterbalance. The pairing of so called “PEGylated” phenothiazine with doubly PEGylated viologen (A5) by Chai et al., specifically, achieved an impressive capacity retention of 99.9% and a Coulombic efficiency of 99.7% over 300 charge/discharge cycles at a current density of 2 mA cm−2, though without stabilizing para-methoxy groups, as it was not operated with 2-electron oxidations [146]. On the other hand, simply extending the methoxy units with diethylene glycol chains was shown to be an efficient strategy to improve on solubility while retaining stability by Attayanake et al., leading to 0.5 M solutions in acetonitrile containing supporting electrolyte for both the phenothiazine radical cation and dication [141]. The resulting stability of the di-cationic species allows for overcompensation of the 1.5-fold increase in weight by doubling the storage capacity owing to the 2-electron process. Notably, the redox events are still separated by 0.6 V, leading to some charging/discharging inefficiencies that are the target of further work.
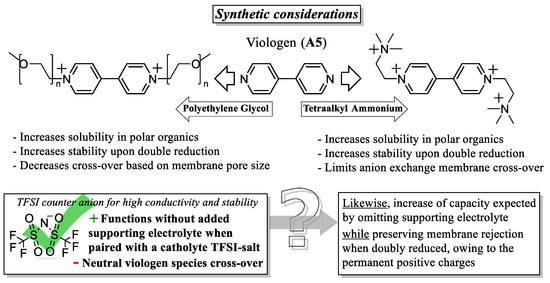
Although this separation is not smoothed out yet, an alternative synthetic strategy laid out in further work of the Odom group highlights a significant recent advance in electrolyte design. Upon introduction of a permanently charged tertiary ammonium group on the phenothiazine N-alkyl chain, Attanayake and coworkers demonstrated in very recent work that the corresponding conducting salt acts as a supporting electrolyte on its own, with ionic conductivity similar to that of TEA-TFSI [147]. Paired with a bis-TFSI viologen (A5) salt anolyte, the TFSI- anions are able to cross an anion exchange membrane in lieu of supporting electrolyte upon charging/discharging, creating the first supporting-salt-free AORFB (Figure 9). Though at 1 M, the high viscosity causes the ionic conductivity to drop, battery tests at 0.5 M electrolyte concentrations yielded a volumetric capacity of 18.3 Ah/L with only 0.90% capacity decay per day, which was most notably assigned to membrane incompatibility rather than decomposition. Though the incompatibility of the membrane caused a significant amount of active species cross-over, the battery did not suffer from the absence of supporting electrolyte in the proof of concept. This novel strategy could hold promise for increasing electrolyte concentrations, and therefore, battery capacity, in all electrolyte designs.
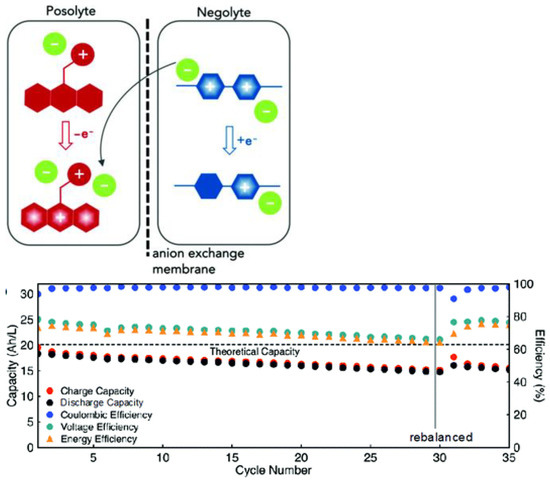
Figure 9.
(Top) Mode of charge compensation in the supporting−electrolyte−free AORFB of Attanayake et al. The TFSI−anions on a viologen anolyte and on a tetraalkylamonium-modified phenothiazine catholyte are capable of single−handedly balancing charge. (Bottom) Monitoring of the capacity of charge/discharge cycles and the Coulombic efficiency over 30 cycles (10 mA cm−2). Due to the high cross-over in lieu of a suitable membrane, both electrolyte compartments were “remixed” after cycle 30 to reset the system. Reproduced with permission from Attanayake et al. [147], copyright Royal Society of Chemistry.
Virtually just as recent, and well worth noting, is the work of Romadina et al. on optimizing battery performance for a redox-active unit that has been widely studied in a range of electrochemical and photophysical fields, the triarylamine (C5) [123,148]. The investigation of a range of (multi-)diethylene-glycol-modified triarylamines, in particular, revealed that even one glycol chain effectively turns the catholyte into a viscous liquid and increases its solubility drastically, once again underlining the positive effect of glycation on energy density (Scheme 3) [123]. Despite exhibiting high solubility (>2.2 M in acetonitrile), dimers were found to be unstable towards double oxidation in the current design. Since the authors thoroughly screened the role of electrolyte in their stability, the solution may lie in further engineering with alkyl substituents such as dimethoxybenzene [116,117]. Over prolonged cycling, the stability with NaClO4 supporting electrolyte outcompeted TBABF4 and TBAPF6, though importantly, no TFSI-based electrolytes were screened. A strong role of cross-over in capacity fading likely leaves room for improvements through membrane selection, and pairing with a low-potential phenazine anolyte has already shown to yield more substantial energy densities and a Coulombic efficiency of over 95%. Although more work is due in order to improve their stability, this exemplar study opens up the possibility for a familiar family of aryl amines (anilines, carbazoles, etc.) that are known for their synthetic modularity to potentially take the RFB stage also.
3.3. Anolytes
Although phthalimides have developed further since Li and coworkers’ pioneering use of N-methylphthalimide A1 as an AORFB anolyte [96], their poor solubility generally holds them back from competing with the state-of-the-art electrolytes. Most notably, however, Zhang et al. reported on an interesting strategy to circumvent this issue, by forming eutectics with LiTFSI and urea [149]. Although further work showed the possibility of creating bi redox-active eutectics [150], certain compositions in their earlier work yielded lower viscosities upon variation of the dilution with 1,2-dichloroethane. With a viscosity of ca. 130 mPa s at ca. 4 M of active species, ultimately posing a foreseeable issue for redox-flow circulation (versus water at 1 mPa s [151]), a viscosity of 15 mPa s upon further dilution to 1 M still demonstrates promise for this unusual approach. Notably, Daub et al. showed that the functionalization of various phthalimide derivatives revealed pyromellitic diimide as the best-performing [97]. In line with the earlier-proposed PEG-functionalization (Scheme 1), PEG chains provided high solubility in the now multi-electron reduction process, and thereby overall higher volumetric capacities of up to 24 W h L−1, making this a promising candidate for further synthetic adjustments to and incorporation into bipolar scaffolds (vide infra, “Bipolar Electrolytes”)
The first more competitive structural follow-up to phthalimides as AORFB anolytes was a series of quinoxaline derivatives in the aforementioned work of Brushett et al. [98] Quinoxaline is especially interesting, considering its high solubility in propylene carbonate (ca. 7 M) and it undergoing a 2-electron transfer. Although the cyclic voltammetry of plain quinoxaline A2 (R = H) shows poor reversibility, substitution with methyl groups α to the pyrazine nitrogens (R = CH3) resulted in both an improvement in reversibility and a further lowering of redox potentials owing to their electron donating ability. Methylation on the phenyl moiety with and without the α-methyls resulted in no significant changes, whereas introducing α-phenyl groups instead resulted in only a weak improvement over the core quinoxaline structure, suggesting that steric shielding of the redox-active site plays a role in the chemical reversibility here. Notably, introducing electron-withdrawing α-groups (e.g., dichloro and trifluoromethyl) only resulted in the disappearing of redox activity, which reflects the abovementioned trend seen for the dialkoxybenzene catholyte [130]. When a phenyl group replaces the R-groups to form a symmetric dibenzopyrazine, the so called phenazine also shows increased stability, while retaining their synthetic modularity. Romadina et al., for example, showed recently that functionalization with 2,3-di(diethylene glycol methyl ether) substituents yielded a highly soluble and stable anolyte with a record low potential for phenazines of −1.72 V vs. SCE, providing high energy densities [148].
Another structurally well-studied anolyte is anthraquinone A3. Although Huang and coworkers encountered stability issues regarding the second redox event of anthraquinone, the pairing with the phenothiazine (C4) catholyte led to a concept dual 2-electron AORFB [99]. Appending single and double 2-methoxyethoxy substituents to anthraquinone at various one-sided positions (1-, 2-, 1,2-, and 1,4-) increased their solubility and lowered their reduction potential. Interestingly, 1,4-bis(2-methoxyethoxy)anthraquinone was at upwards of 10 times more soluble than the other three derivatives, tentatively assigned to the largest molecular asymmetry in 3D space. As a structurally closely related anolyte, benzophenone (A4) also is influenced strongly by its substitution pattern [100,152], although the exact influence of asymmetry on final battery performance is yet to be explored in more detail. Nevertheless, a clear influence thereof that is observed is 3-methylbenzophenone, where the addition of a mere methyl group liquefies the benzophenone [152]. On the other hand, symmetric electron-withdrawing and donating groups were shown by Huo et al. to raise and lower the redox potential, respectively, in line with the trends for the other electrolytes above [100]. Furthermore, 4,4′-dimethoxybenzophenone was shown to have high diffusivity in acetonitrile of 1.23–1.97 × 10−5 cm2 s−1, thereby holding promise for future modification through asymmetric substitution with ethylene glycol or tertiary ammonium groups.
A well-studied anolyte that has been given much attention as of late, not least for its inherent positive charges and thus high solubility in polar solvents, is viologen (A5). The inherent charges have led to viologens playing an exemplary role in an approach to tackle one of the major design issues in AORFBs, the battle against cross-over of electrolytes. Two approaches to maximizing electrolyte localization have been shown to possess distinct advantages: considerably increasing their size to suppress electrolyte penetration through low-cost porous membranes [101,153] and adding permanent positive charges to increase anion-exchange-membrane-rejection rates (Figure 10) [134,135,137,138,139]. In terms of increasing size, although the synthetic flexibility allows for long alkyl chains [154], the introduction of ethylene glycol chains, as shown for catholytes also, yields high stability while liquefying the viologen electrolyte [146,155]. In fact, their stability alongside that of the 1-electron oxidation of phenothiazine (C4) was the basis for the abovementioned all-PEGylated phenothiazine/viologen AORFB operating at 99.9% capacity retention and 99.7% Coulombic efficiency over 300 cycles at 2 mA cm−2 [146].
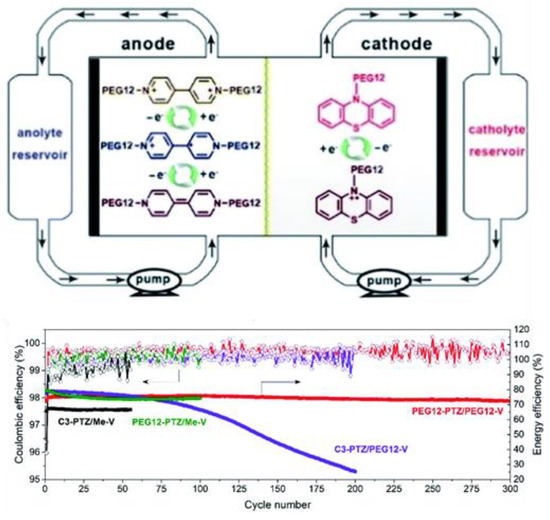
Figure 10.
(Top) Design of the all−PEGylated AORFB by Chai et al., employing viologen and PEGylated phenothiazine as anolyte and catholyte, respectively. (Bottom) Monitoring of the capacity of charge/discharge cycles and the Coulombic efficiency of the all−PEGylated AORFB over 300 cycles (2 mA cm−2). For comparison with non−PEGylated derivatives, dimethylviologen (Me−V) and N−propylphenothiazine (C3−PTZ) were also measured. Reproduced with permission from Chai et al. [146], copyright Royal Society of Chemistry.
It is worth mentioning that in more recent work on structural isomers of viologens, 2,2′-bipyridene, Antoni et al. showed how complex architecture could transform the normally 2-electron reduction process to a 4-electron one, raising the theoretical capacity of the electrolytes [156]. However, the gain by increasing electron storage capacity was unfortunately compromised by a loss in solubility, and despite the promising results, further synthetic modifications are required to make up for the poor capacity stemming from the 1 to 4 mM concentrations.
Not only have viologen polymer electrolytes played an early role in mapping possible use of porous instead of ion-exchange membranes, but the double positive charge is also well-compatible on its own with anion exchange membranes. Double reduction has been shown to be possible, provided the viologen counterion is exchanged in favor of the solubility of the neutral species, e.g., with TFSI [102]. Indeed, it was also the (TFSI)2-viologen salt that was paired with TFSI-tetraalkylammonium phenothiazine in the abovementioned supporting electrolyte-free AORFB of Attanayake et al., exhibiting sufficient charge compensation through efficient TFSI- transmembrane migration (Figure 9) [147]. However, utilizing the full 2-electron reduction yields a neutral “charged” state of the anolyte, significantly decreasing anion exchange membrane rejection and thereby the durability in the charged state. Symmetric mixed loading of catholytes and anolytes counteracts rapid cross-over, albeit it compromises the overall capacity due to limiting active species on each side [102].
A promising avenue to avoid capacity loss through cross-over while retaining stability and solubility is to build in additional charge with a quaternary ammonium group, inspired by the abovementioned tetraalkylammonium ferrocene [134]. Tetraalkyl ammonium was long ago shown to preclude transmembrane migration of viologens, showing promise for increased energy storage with one (asymmetric) or two (symmetric) additional positive charges [137]. Indeed, such viologen derivatives have been shown to provide highly efficient anolytes for aqueous RFBs already, exhibiting very low cross-over rates [138,139]. We thus foresee that additional permanent charges in viologens paired with the TFSI— counter-ion will further advance AORFB capacity and capacity retention through increasing effective concentration by omitting supporting electrolyte [147] and increasing membrane rejection rates of active species [134,135], respectively (Scheme 4).
Scheme 4.
Viologen is considered an exemplary anolyte owing to its inherent charges and modularity, providing two accessible avenues to efficient 2−electron charging. PEGylation is once again an efficient strategy to increase solubility, and thereby capacity [136,146], though there is still more room for adding permanent charges [124,125,138].
Indeed, these strategies could apply in a more general sense to, for example, small molecules that are known for their redox activity and synthetic flexibility, as shown by Makarova et al. recently [157]. We note that the introduction of PEG-groups to benzoxadiazole and benzothiadiazole scaffolds could be replaced by tetraalkyl ammonium in order to achieve higher solubilities and better membrane rejection rates, as solubilities are relatively low at 7–13 mM concentrations, and rapid cross-over of electrolyte is reported to be a major contributor to the capacity fading.
Other recent developments in anolyte design notably include a molecule that, owing to its versatility, has been ubiquitous in photochemical applications: azobenzene [158]. Their broad implementation in numerous fields was extended even further by Zhang et al. when they reported in 2020 on the feasibility for their use in RFBs [103]. The redox-potential of ca. −2.3 V vs. SCE and favorable solubility in polar organics translates to a high theoretical capacity, and solubility in acetonitrile—specifically, strongly enhanced from 1 to 4 M through mere para-methoxy substitution. Nevertheless, the authors decided to utilize DMF for its superior solubility, possibly due to the almost simultaneously reported irreversibility of the azobenzene reduction with LiTFSI in acetonitrile by Wang and coworkers [104]. Interestingly, however, Zhang et al. showed that employing Li-TFSI as a supporting electrolyte in DMF causes a seemingly favorable coordination between the radical azo-anion and lithium, contributing to the excellent cycling stability (99.992% capacity retention per cycle over 3000 cycles in DMF at a current density of 0.2 mA cm−2), though the coordination compromises the OCP by −0.8 V [103]. On the other hand, while concluding that Li-TFSI seems to be incompatible with acetonitrile, Wang et al. reported reversibility of the azobenzene reduction in acetonitrile containing tetrabutylammonium hexafluorophosphate (TBAPF) instead [104]. Although both reductions were accessed in the AORFB study, it was the unaltered azobenzene rather than the phenothiazine that suffered from proton-assisted decay mechanisms. Nevertheless, despite this anolyte being in its infancy, still, the vast synthetic flexibility and adaptability exhibited by azobenzene in a vast range of applications before substantiates its significant potential, making it likely it will come to play a significant role in the near future.
3.4. Bipolar Electrolytes
A newer development in RFBs, due to their increasing complexity and compatibility requirements, is the creation of bipolar electrolytes, i.e., electrolytes containing a catholyte and an anolyte function simultaneously [159]. Although this generally requires a larger synthetic effort and imbues the active electrolyte with one to be solubilized component that is inactive at all times, the major advantage is that it eliminates capacity loss from cross-over [106,159]. An oxidized bipolar electrolyte traversing the membrane will regain its electron, reducing energy efficiency, but will then go on to take an active part in the charging process on the other side, and vice versa. One key requirement for favorable energy density in bipolar electrolytes is that the redox events are substantially separated. The presence of two successive redox events alone, such as in viologens (A5), does not compete with state of the art when the OCP is only 0.5 V. Notably, conditions as subtle as the selected positive counterion in the supporting electrolyte can contribute significantly to the separation, as shown in an analogous pyridinium electrolyte (Figure 11) [160], ultimately having a much more crucial impact on bipolar activity than on two-electron anolyte or catholyte storage. The poor compatibility of Li+ towards retaining redox potentials was noted in the abovementioned work of Zhang et al. on azobenzene also [103], although Li+-coordination with the charged anolyte state had a stabilizing effect. On the other hand, this compensatory effect was found to be absent for Wei and coworkers, with Li+, specifically out of a range of supporting electrolytes, having a substantial destabilizing effect on the fluorenone anolyte despite functioning well on the catholyte side [117].
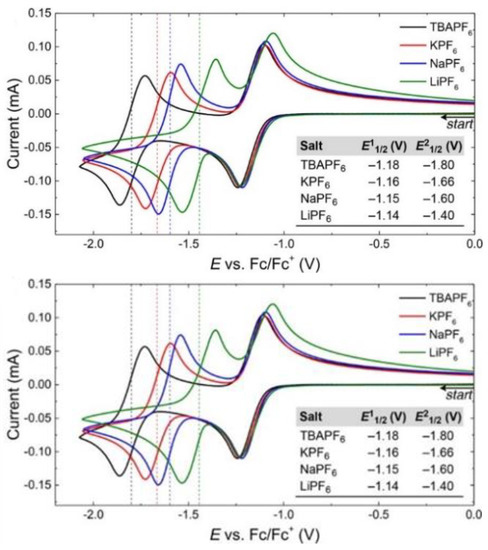
Figure 11.
(Top) Redox chemistry of 4−benzoylpyridinium. (Bottom) Cyclic voltammograms of 4−benzoylpyridinium (5.0 mM in acetonitrile, 100 mV/s scan rate) in various supporting electrolytes (0.50 M in each case). Reproduced with permission from Hendriks et al. [160], copyright American Chemical Society 2017.
One way to ensure a larger operating window is to tether a donor and an acceptor for which the redox events are known to be far apart (Figure 12, B1). As in the case of N-ferrocenylphthalimide (B1), the active electrolyte components can be relatively small and tethered with a short linker [105]. The simple hybrid design with moderate polarity was soluble up to 0.3 M in 1,3-dioxolane with 1.0 M TBABF4 and showed good chemical stability over 50 cycles with current densities ranging from 20 to 60 µA cm−2 (1.0 to 3.0 C). However, although small molecules and short linkers could instinctively reduce the need for solubilizing molecular parts that do not partake in the charging or discharging process, Li et al. showed important irregularities in chemical behavior between phenothiazine and phthalimide moieties tethered through various chain length linkers [161]. Molecular conformations arising from specific chain lengths and flexibilities are found to have a profound effect on the ability to undergo charge transfer and the molecular packing. Thus, this strategy is likely to benefit the most from a combined experimental-theoretical approach, using molecular dynamics calculations to identify promising target structures.
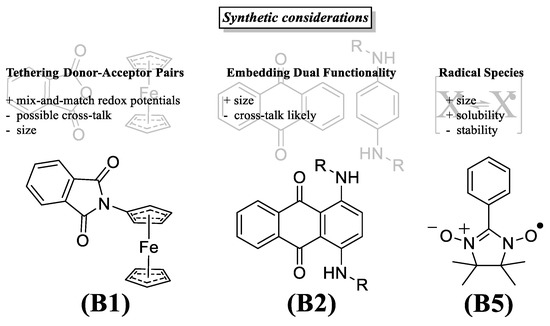
Figure 12.
Strategies to attain electrolytes capable of anolyte and catholyte function simultaneously. The assigned acronyms (B1, B2, B5) come from the structural overview of Figure 8.
Alternatively, the much more polar diaminoanthraquinone [106,107] (B2) takes away a linker component altogether, leading to a second strategy: fusing of electrolyte motifs (Figure 12, B2). A noteworthy complication that can arise during this approach is that fused moieties tend to cross-communicate more heavily due to the even closer proximity, having a pronounced effect on electron density, and thus, potentially, redox potential and chemical stability. Nevertheless, Geysens et al. demonstrated that a close structural fusion between anthraquinone and dianiline united the two-electron processes with further synthetic modularity, ultimately yielding high energy density owing to the 5 redox states and increased solubility through additional engineering [107]. Additionally, here, a substantial positive contribution of triethylene glycol substituents (Figure 12, B2, R = C2H4OC2H4OC2H4OCH3) is seen in a significant solubility increase, enabling 1 to 2 M solutions compared to isopropyl substituents (R = C3H7), only reaching 19 and 122 mM in acetonitrile and 1,2-dimethoxyethane, respectively. The glycolated bipolar electrolyte reached an average Coulombic efficiency of 99.3% over 100 cycles in DME in static symmetric charge/discharge at a current density of 2.1 mA cm−2, but the full 2-electron cycling resulted in a capacity decay, thus requiring further chemical stabilization before being able to access the higher energy densities.
Another promising and as of yet relatively unexplored fused motif is the thianthrene (B3) [108]. Etkind et al. demonstrated high open circuit potentials (OCVs) and solubilities for several derivatives while validating in static cells, although stability, and quite possibly a large influence of poor membrane rejection rates, are holding their efficiency back. As the scaffolds are relatively unexplored, the synthetic room for adjustments peripheral to the active species could go a long way in unlocking their full potential.
As a final and ideal approach, the structural design for catholyte or anolyte function is in itself capable of reaching multiple redox states already, with sufficient separation of redox potentials (Figure 12, B5). This may also mean mere stabilization of redox events in well-studied electrolytes suffices, as was done by Wylie et al. for TEMPO (C1 and B4 *) [109]. The authors made use of an ionic liquid to prevent the proton transfer side reaction of TEMPO in its reduced form, rendering the redox process reversible and thereby enabling access to both redox directions reversibly. This strategy is seemingly universal to proton transfer side reactions, as the reversibility of the para-benzoquinone reduction was on an earlier occasion also shown to be increased in ionic liquid [126]. Importantly, however, the use of ionic liquids to preclude proton interactions inevitably brings about viscosity issues, much like with eutectics [149], and presumably there is not an energy-efficiency sweet spot for having to circulate a viscous liquid (e.g., pure 1-butyl-1-methylpyrrolidinium triflate, from stabilizing TEMPO [109], has a viscosity of 158 mPas versus 1 mPas for water [151]).
In an alternative strategy, however, Duan et al. have made steps toward increased redox-stability by making structural changes to the TEMPO core, yielding a chemically reversible reduction in an imidazoline-based nitroxide radical species, 2-phenyl-4,4,5,5-tetramethylimidazoline-1-oxyl-3-oxide (B5) [110]. The AORFB exhibited good chemical stability at 0.1 M operating conditions and a moderate cell voltage of 1.73 V at a current density of 20 mA cm−2, and the detection of the nitroxide radical by FTIR highlighted an interesting and efficient method to monitor the state of charge online. The 2-phenyl-4,4,5,5-tetramethylimidazoline-1-oxyl-3-oxide exhibited significant loss in the Coulombic, voltage, and energy efficiencies (cf. ref. [162]) at 0.5 M due in part to cross-over through the porous membrane, although we expect this could also be partially counteracted with a change from a TBAPF counter-ion to, e.g., TFSI [117]. Although capacity decay occurred also at 0.1 M upon prolonged cycling (100 cycles), its intrinsic solubility (2.6 M in acetonitrile) leaves room for molecular engineering, especially on the phenyl ring, in order to tune the separation of redox events, solubility of charged states, stability, and bias for crossing over (Scheme 4). Indeed, Hagemann et al. reported on its dimer, linked by a tetraethylene glycol chain through the phenyl moiety, possessing similar RFB characteristics at higher energy densities [111]. Despite the symmetrically charged active species crashing out at 0.5 M (however, at 1.0 M of active species), the tetraethylene glycol dimer achieved a higher saturation level at 1.9 M (3.8 M of active species, versus 2.6 M by Duan et al. [110]) and at a current density of 1 mA cm−2 a lower capacity fade than the single 2-phenyl-4,4,5,5-tetramethylimidazoline-1-oxyl-3-oxide (B5). Nevertheless, relatively low energy densities at lower concentrations still limit their application, suggesting that the solubility of the charged states may be the current bottleneck.
Notably, both solubility of charged states and separation of redox-potentials can be potentially found in further nitroxyl derivatives, as the scaffold is shown to offer promising opportunities for symmetric redox flow. Charlton et al., for example, showed that verdazyl radicals have potential as bipolar electrolytes provided the OCP, capacity, and stability are increased [125], which could be achieved through synthetic adjustments. Indeed, Korshunov et al. showed that after synthetic screening, the 1,5-diphenyl-3-isopropyl-6-oxo-verdazyl (B6) is a quite capable electrolyte, exhibiting an OCV of 1.42 V and high Coulombic (>97%) and energy efficiencies over more than 100 cycles at 2.22 mA cm−2 [36]. The average 0.147 W h L−1 over 80 cycles is postulated to benefit further from synthetic modifications to increase solubility and membrane rejection rates, such as appending tetraalkyl ammonium groups.
Steen et al. show this tailoring potential for the structurally similar Blatter radical (B7) [112]. Through a series of synthetic adjustments, substitution patterns were shown to influence stability of the charged states and their redox potential, increasing both the capacity retention and the OCV. Additionally, Steen et al. showed that a polarity inversion (i.e., inverting working and counter electrode) during cycling benefitted the performance of the symmetric RFB, showing an instant partial recovery towards the initially observed capacity upon inversion at the 50th cycle. This indicates that a part of the capacity loss could be attributed to a loss in homogeneity in the anolyte and the catholyte compartment during repeated charging and discharging. Importantly, this strategy could only apply in symmetric RFBs, where the electrolyte can perform both functions at all times.
Recently, Moutet and coworkers showed that not only nitroxyl radicals, but also a helical carbenium ion, dimethoxyquinacridinium (B8), can be a promising bipolar electrolyte [113]. Their first study involved the plain carbenium ion, which is able to reduce to a neutral radical, and oxidize to a dicationic radical state with a ΔE of 2.12 V, paired with high diffusion coefficients (9.4 and 9.9 × 10−6 cm2 s−1, respectively). Although the dicationic radical of the plain carbenium could not be isolated, a follow-up study with a nitro-substituted carbenium exhibited increased stability to all redox-states, including the doubly reduced form, allowing for an impressive 3.02 V OCV (Figure 13) [114]. The updated design also yielded a large increase in solubility from 32 to 154 mM with the nitro-substituent, leading in turn to higher energy densities also (9.25 W h L−1 versus the previous 1.84 W h L−1, with 12.5 W h L−1 upon double reduction). Initial static tests in H-cell configuration show good Coulombic efficiencies at a 0.15 mA cm−2 current; the capacity faded at around the 200th cycle (Figure 7b). The carbenium electrolyte was thus proved to be a promising scaffold for further synthetic tuning. Both the N-propyl side groups also leave room for synthetic adjustments [163] to benefit the capacity, e.g., through maximizing solubility with ethylene glycol chains or a tetraalkylammonium substituent, as does pairing with potentially more suitable counter ions than TBAPF.
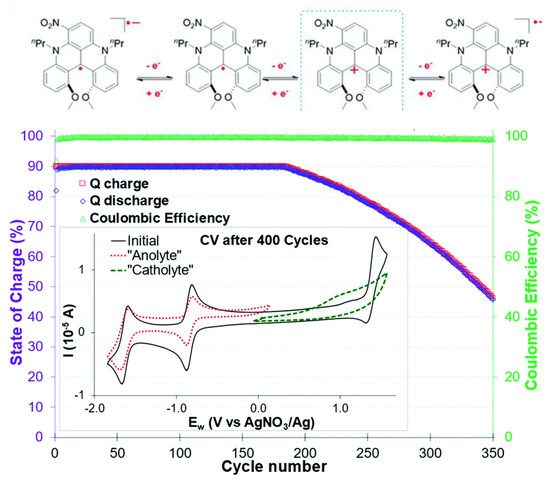
Figure 13.
(Top) Oxidation and reduction mechanism for dimethoxyquinacridinium (B8) and (bottom) monitoring of the capacity of charge/discharge cycles and the Coulombic efficiency over 350 cycles of mono−electronic exchange at a 5 mA current in a symmetric H−cell. Inset: cyclic voltammogram before and after 800 cycles (0.1 M dimethoxyquinacridinium and 0.1 M TBAPF6 supporting electrolyte in acetonitrile). Reproduced with permission from Moutet et al. [114], copyright Royal Society of Chemistry 2022.
3.5. Summary
Granted that the make-up of the RFB contains many complexly interrelated facets and that any given system may respond differently to minor changes, the trends observed above may contribute strongly to improving overall battery performance:
- Acetonitrile is the solvent of choice, given its low viscosity and toxicity, and importantly, its polar nature, which generally contributes to solubilizing charged states also.
- Generally, TFSI− and TEA+ are preferred supporting ions. Alternatively, TBAPF6 is also often applied and performs well. Li+, notably, has exhibited some incompatibility issues in the anolyte compartment.
- Electron-withdrawing substituents on catholytes and electron donating substituents on anolytes can slightly increase the system’s voltage, though a possible negative effect on stability may negate the gain in OCV.
- Appending ethylene glycol (preferably asymmetrically) or tetraalkylammonium chains substantially increases the solubility in acetonitrile and to date seems to be the most efficient way to non-invasively increase energy density.
- Imbuing both the catholyte and anolyte with permanent charge, for example, with tetraalkylammonium side-groups, enables the formation of electrolyte salts. This approach is especially promising, as it discards the need for a supporting electrolyte, since solely the counter-ion (e.g., TFSI) needs to traverse the anion exchange membrane, thereby simultaneously maximizing the concentration of active species and combating capacity decay from cross-over of electrolyte.
4. Introducing a RAS from Basic Lab-Scale Identification towards in-Flow RFB Measurements
Due to the steeply increasing interest in RFBs in recent years, improvements have been made not only in cell setup (Section 2) and electrolyte chemistry (Section 3), but also in the field of RFB cell composition and operating to minimize efficiency-loss. As described in the previous sections, in the field of RFBs, only a limited distinction can be made between cell setup and electrolytes, but both these areas must be thought of. If optimal cell efficiency is to be achieved, cell setup and electrolyte must be tuned with each other. For this, computational tools and simulations are of huge interest, as they can give deep insights into RAS and RFB functionalities. However, since this section focuses on practical handling and investigation of AORFBs, we would like to refer the reader to a recent review that covers the computational aspect in detail [164]. In this section, we describe the different compartments of the cell setup and their influence, and we recommend a practical step-by-step guide on how to recognize these effects when introducing an RAS into an RFB, and their theoretical background.
4.1. Main RFB-Cell Components
4.1.1. Reference Electrode
The implementation of reference electrodes enables monitoring of either the anolyte or the catholyte compartment during galvanostatic battery charge and discharge (see Section 4.2.) [165,166,167,168]. With this, informative polarization techniques can be made, as they touch the limits of any redox electrolyte [169]. Ultimately, measuring an accurate cell voltage is highly important to guarantee a safe and reversible electrochemical reaction, as many efficiency-lowering processes are due to overpotential-induced decomposition side reactions. Therefore, the reference electrode has to be placed in the opposite half-cell of the current-applying electrode.
4.1.2. Current Collector, Flow Field, and Bipolar Plate
The differentiation within a half-cell between current collector, bipolar plate, and flow field can be misunderstood, since the respective component often fulfills multiple and mutually substitutive functions. The current collector works as an electrical connection to the circuit outside and reaction surface, and the flow field acts as a turbulent inducer to ensure good electrolyte distribution over the current collector’s entire surface [13]. The bipolar plate combines these properties, as it plays both a fluidic and an electrodynamic role, serving as a reaction surface and turbulence inducer [170]. For this, several different technical approaches have been developed, e.g., turbulent flow-through electrodes [171], “piece of pie” cell configuration [172], static mixer electrodes [173], and zero-gap cell designs [18,174]. However, the majority of research-scale RFB cell setups operate with the zero-gap approach. Here, all cell materials (i.e., conductive ground plates, carbon felts, and membrane) used are compressed by the cell to minimize distance-induced resistances. In a zero-gap configuration, conductive ground plates play a dual hydro- and electrodynamic role. The embedded flow frame guides redox electrolytes within an inner compartment of a flow cell, ultimately boosting the conversion rate and preventing an overpotential build-up over the entire electroactive surface [175]. Notably, this strategy has been subject to many computational studies over the past years [16,176,177]. On the other side, conductive plates act as current collectors, securing an electrical interfacing with external energy sources or loads [178]. To alter a diffusion regime, to extend an accessible electrochemically active area, and therefore, to ensure more effective mass conversion on the surface of current collector, a macro-porous 3D block of compressible and conductive material is normally introduced on top of the ground plate [179,180]. This configuration enables a considerably improved range of operational current densities supported by RFBs, although the range of accessible electrolyte flow rates is slightly decreased due to the pressure drop over an additional physical obstacle [181,182]. Typical choices for porous current collectors are carbon-based materials—thermally altered, chemically altered, or pristine versions of carbon/graphite felts [183,184,185] or carbon/graphite paper [186], and in some cases, well-defined reticulated vitreous carbon foams [187]. The influences of current collector geometry in regard to mass transport, charge transfer, and efficiency are discussed in Section 4.2.1.
4.1.3. Separator
A separator, sometimes called “the heart of an RFB”, effectively separates the anolyte and the catholyte compartment electrolytes and serves to selectively permeate certain species of redox electrolytes [188,189,190]. Separators are conventionally classified referring to their transport mechanisms: (cation/anion/bipolar) selective-ion exchange membranes, microporous size-exclusion separators, ion-conductive glass ceramics, or an interface of immiscible redox electrolytes. In the context of RFBs, the term “membrane” refers to solid polymer ion-selective membranes, whereas a separator uses size exclusion [34,191]. Typical cation exchange membranes (CEM) consist of fluorocarbon- or hydrocarbon-based polymers with embedded terminal sulfonic groups, providing a rigid hydrophobic exterior and hydrophilic pore, where the cationic transport occurs. In turn, typical anion exchange membranes (AEM) incorporate terminal tetraalkylammonium groups. The special case, lastly, is bipolar exchange membranes, which are multilayer combinations of anion and cation conductive polymers.
Apart from membranes, microporous (non-ionic) separators are considered for RFBs as well [192]. Inert films with a pore size of 100 nm level imbue chemical stability and a low area-specific resistance, but ionic selectivity suffers, leaving space only for a size-exclusion effect. This kind of separator is appropriate for battery prototypes, where an absolute capacity can be recuperated [193]. In practice, microporous separators are the choice for non-aqueous batteries. Ion conducting ceramics are an established separator alternative for hybrid RFB prototypes that functionality depend on a solid state electrode (normally lithium metal anode), and the solvent uptake can result in RFB failure [194]. The rare case of mutual immiscibility of redox electrolytes can be exploited for membrane-less RFB setups where no additional separating interface is necessary [195]. Even considering the limited performance of reported proof-of-concept prototypes, an idea of “ideal” membrane-less RFBs does not lose its appeal and economic advantage.
Despite the seemingly wide choice of separators, there is no universal solution for an arbitrary RFB. A scrutinized screening procedure must take place for every battery prototype, as a separator must be compatible with a redox electrolyte (chemical stability) and a set hydrodynamic regimen (mechanical stability). At the current state of research, imposed transport requirements for RFBs are rationalized empirically from a point of an “effect” rather than a “cause”, namely, from parameters affecting voltage efficiency (area-specific resistance) and Coulombic efficiency (an efficiency of separation due to prevention of cross-over) [189,193]. Making a choice of separator for a battery prototype is the “Achilles’ heel”—the limiting factor in the electrochemical performance of redox electrolytes—thus, only an intelligent approach can narrow the difficulty of selection. State-of-the-art membranes have a well-balanced trade-off among ionic conductivity, barrier properties, the ability of balancing net electrolyte transport, and chemical persistence. Therefore, we suggest a step-by-step sequence, as described in Section 4.3, to get structured and comprehensible results when introducing a new RAS species to a RFB.
4.2. Practical Difficulties of RAS Transversion and Their Theoretical Background
Introducing a new RAS into the area of redox flow brings about several new challenges. Compared to first fundamental investigations of the electrochemical behavior in a classical three-electrode setup, transferring to a RFB setup (i) changes electrode geometry and size, (ii) adds a separator between electrodes, and (iii) adds fluid-related mechanical effects, such as viscosity. The concurrent introduction of fluid mechanics during in-flow RFB cycling intensifies additional effects of mass transport and iR drop, leading to further changes in electron transfer kinetics during cycling. Simplified, these effects can be summarized in additional overpotentials in electrochemical measurements. As overpotentials have a huge impact on the reversibility, stability, and durability on long-term battery cycling, it is important to identify these. For this, an easy and fast technique such as cyclic voltammetry (CV) can be used. In this review, we suggest a step-by-step sequence to obtain comprehensible and stringent information on the reversibility and stability of electrochemical measurements should be performed: (1) proof-of-concept electrochemical measurements; (2) stationary RFB measurements; (3) in-flow RFB measurements. For easier discussions, Table 1 summarizes the most important cycling parameters and performance variables:

Table 1.
Most important electrochemical cycling parameters and cell-performance variables [196].
4.2.1. Cell Setup and Processing Impacts on Mass Transport, Conversion, and Overpotential
In initial proof-of-concept electrochemical measurements, a classic three-electrode CV measurement should be performed to identify the RAS redox potential under “ideal” conditions. Additionally, this stage should be used to identify further important RAS specific characteristics, such as reversibility (basically peak-to-peak separation), diffusional coefficient D0, standard rate constant k0, or charge-transfer coefficient α [197,198]. Herein, it is recommended to investigate different electrolyte combinations to find a suitable RAS-supporting-electrolyte–solvent combination (see Section 3).
When changing from proof-of-concept electrochemical to static RFB measurements, two main points change: the electrode surface size, and often also material, and the introduction of a separator (see also Section 4.1.2 and Section 4.2.2) between the working electrode and the counter and reference electrode. In terms of the electrode surface area for a classical disc macro-electrode, a linear semi-infinite diffusion model is assumed, where the peak-to-peak separation for reversible systems is equal to 2.218 RT/F [199]. However, if a macroscopically structured electrode material (e.g., carbon nanotubes, carbon foams, or graphite plates) is studied, the diffusion model changes. Tichter et al. have classified different ideal electrode structures: 1D planar finite (layered porous electrodes), 2D cylindrical finite external (cylindrical electrode felts) and internal (cylindrical electrode tube network) and 3D spherical internal finite (electrode foam) [200]. For static potentiodynamic studies on porous electrodes (flow rate = 0 mL min−1), e.g., for carbon felt on graphite plate zero-gap RFB setups (see also Section 4.1.2), mainly two diffusion regimes coexist: linear semi-infinite, and the predominant one, external finite cylindrical. These diffusion models can be assumed based on the structure of the pseudo-3D structured graphite field classified by Tichter et al. This change not only increases the maximum peak current due to the increase in surface area, but also leads to an increase in CV peak-to-peak potential, as also shown by Tichter et al. in further studies [201]. Since the electrochemical conversion takes place at the electrode surface, the resulting peak is representative for the homogeneity of the surface. The more inhomogeneous electrode surface leads to a more inhomogeneous electrochemical reaction, reflected in the cyclic voltammogram by a broader peak. Thus, an overall increase in the maximum peak current, peak-to-peak separation, and peak broadening take place when switching from the classical CV three-electrode setup to CV measurements in the static RFB setup. For the time being, this can give the impression that an RAS, performing electrochemically reversibly in the first proof-of-concept step, appears to be performing irreversibly in the RFB cell. However, this can be attributed to the effects of the cell-setup changes. Furthermore, the static measurements are primarily used to monitor the functionality of the membrane (e.g., permeating of charge balancing ions), tracing charge balancing over time. As described in Section 4.1.3, the membrane and electrolyte play crucial roles in the RFB efficiency, and thus, mismatches should be avoided at all times. Often, H-cell setups are also used for such tests. This, however, requires an additional cell setup, which in turn causes different overpotentials than the later RFB setup (as can be seen in the previous section also). When switching from the static second step towards the in-flow third step, deliberate induction of bulk convection in an analyzed electrolyte system adds a hydrodynamic transport component and helps apparent redox properties of electrolytes to further approach battery-like properties. “In-flow” overvoltage is a function of potential sweep rate and efficiency of mass convection under mass transfer limiting conditions, which contributes to the final performance of any RFB system. By changing from static to in-flow measurements, the flow of redox electrolyte through porous hydrodynamic electrodes significantly reshapes the 3-dimensional distribution of redox material concentration. This reduces the diffusive mass transport fraction towards the direct electrode surface region only. An effective flux of the redox material nearby the electrode surface aids to step beyond Fickian limits, enabling higher current densities [7]. In summary, these enhancements in mass transport reduce the previously explained overpotential-induced peak-to-peak separation and further increase the peak intensities. Since for in-flow potentiodynamic measurements, the diffusive mass transport at the electrode surface is now superimposed by convection, the peak-limiting current of the CV measurement no longer is achieved by mass transport but by high SOC. The scan rate must be selected so low that the volume current ensures complete circulation of the electrolyte within 59 mV. As a higher SOC must be achieved for these measurements, both the stability of the RAS and the prevention of crossover of the RAS can be tested easily and quickly.
In order to quantify the influence of electrochemical transversion efficiency, Yin et al. emphasized a dimensionless number called stoich, which indicates the ratio of input RAS to the already consumed ones at a certain current [202]. They have shown that at a low stoich (i.e., low rate of conversion), the mass transport by convection and diffusion are the dominating factors for performance, whereas at high stoich (i.e., high rate of conversion), factors such as electrode reactivity and reactive surface area are rate-limiting. By applying different flow rates to a vanadium RFB (VRFB), Ma et al. have shown that with increasing flow rate the Coulombic efficiency decreases, but due to an increase in voltage efficiency, the overall energy efficiency increases with higher flow rates [203]. Additionally, to analyze the overall battery system efficiency, they introduced the power consumption of the pumps to the assessment. By this, they have shown that the overall system efficiency, contrary to the energy efficiency, decreases at higher flow rates.
4.2.2. Membrane’s Impacts on Mass Transport, Conversion, and Overpotential
In order for the anolyte and catholyte compartment reactions to take place independently, a separator needs to be used. A semipermeable membrane, ideally, allows for passage of only the charge balancing ions, and not the RAS themselves [204]. To achieve this, one of two different mechanisms are applied: (i) charge exclusion or (ii) size exclusion [205,206]. In both cases, the separator is, in the electrochemical sense, an additional resistor in the system, as the crossing of charge-balancing species requires a certain activation energy [189]. For size exclusion, this mainly originates from the limited mass transport in the direct area of the membrane surface by Fickian’s law. For charge exclusion, specifically, coulombic repulsion additionally takes place, so that overall the introduced resistance is higher than that of a size exclusion separator [146,206]. For multiple separator setups, this resistance increases with every additional separator. Zhao et al. and Yuan et al. have investigated the VE and CE depending on the pore size and membrane thickness [207,208]. The VE increases with thinner membranes and bigger pore size due to lower membrane resistance, whereas the CE is decreased regarding easier cross-over. Summarizing, in RFB setups the overall resulting resistance induced by a separator is reflected in further overpotentials at constant current measurements or in a higher peak-to-peak separation in static RFB CVs.
4.2.3. Viscosity’s Impacts on Mass Transport, Conversion, and Overpotential
In addition to the electrochemical changes described in the previous section, fluid mechanics play a large role in energy efficiency in-flow, largely effected by the porosity of the electrode and viscosity of the electrolyte solution [209,210]. A distinction can be made between the viscosity influence at the macroscopic level (I) and the atomic level (II). At the macroscopic level (I), viscosity acts like a force working against the flowing electrolyte, demanding more pump energy to maintain a constant volume flow with increasing viscosities [211]. Simplified, this can be described for a homogeneous Newtonian fluid in a straight pipe by the Hagen–poiseuille equation (see Table 2), with the volume flow being inversely proportional to the viscosity.

Table 2.
Summary of viscosity-influencing equations for RFB electrolytes.
At the atomic level (II), the Stokes–Einstein equation can be used for better understanding of the viscosity’s impact. Here, the diffusion coefficient, which is representative of the molecule’s mobility and therefor, mass transport, is also inversely proportional to the viscosity [212,213]. This means that by an increase in viscosity, the molecular mobility decreases. As described in the previous section, diffusive mass transport is particularly important in the direct region of the electrode surface (Helmholtz layer), so that a higher viscosity directly acts as additional resistance, and thus overvoltage, from an electrochemical perspective. Not only does this phenomenon reduce the RAS’ mobility, but also that of the charge balancing molecules of the supporting electrolyte, thereby decreasing electrolyte conductivity. This, again, can be seen as an additional resistance resulting in an overpotential [210]. Since the charge of the RAS is changed during the charge/discharge process, the Nernst–Einstein relationship must also be considered. Here, too, the diffusion coefficient is reciprocal to the charge of the charge carrier [206]. Thus, if the charge on the RAS changes during the electrochemical conversion, the molecule’s mobility also changes. In summary, this viscosity impact on the atomic level can be seen as having two additional overpotential origins: first from RAS mobility at the electrode surface, and second, as an adverse effect on electrolyte conductivity. As Ma et al. has introduced system efficiency for flow rates, this model can similarly be used for the electrolyte viscosity [203]. Furthermore, at a certain electrolyte viscosity, induced by a higher concentration of RAS, the additional gain in capacity no longer outweighs the energy loss due to the increase in viscosity [210]. In fact, Zhang et al. have recommended an ideal RAS and supporting electrolyte concentration for a given RFB chemistry at which the efficiency and the concentration are in ideal balance [214]. For quantification, they recommended limits for poor conductivities (<5 mS cm−1) and high viscosities (>10 cP) for small neutral redox-active organic molecules.
4.3. Summary
While moving towards in-flow RFB measurements, a phased approach of introducing the RAS to the RFB allows a stepwise identification of effects such as diffusional and convectional mass transport, Coulombic repulsion, and fluid mechanical changes, such as viscosity. This causes overpotentials and an iR drop. These effects are highly dependent on electrolyte composition and RFB setup and therefore, the optimum varies from RFB to RFB (electrolyte composition, type of membrane, flow rate, current density, type and geometry of electrode). For this, we emphasize the step-by-step transferring sequence to better understand the transitioning effects and their intensity: (1) proof-of-concept electrochemical measurements with classic CV three-electrode setup; (2) stationary RFB CV measurements; (3) in-flow RFB CV measurements. In the first part, the basic functionality of a RAS should be validated (i.e., redox potential, reversibility). In the second step, the impacts of RFB cell, electrode type, and membrane on the results obtained in the first part are evaluated. Finally, in the third step, the impact of volume flow is investigated, along with the minimization of cross-over. The results of this step-by-step sequence can then be used to define optimum charge-discharge parameters and cut-off criteria in order to obtain the most stable, safe, and durable RFB settings.
5. Conclusions
Although AORFBs are still at their infancy, the great advances in cost efficiency and energy capacity that can be realized by utilizing the organic-synthetic toolbox hold great promise. In this review, we covered the various aspects that impact RFB performance, ranging from current cell designs to promising electrolyte strategies; cell components to cell operation. Ultimately, our aim was to provide an aid for the reader to systematically tackle both the battery cell and molecular design, and outline the (stepwise) experimental road towards discovering the next generation of flow-based energy storage systems.
Author Contributions
Conceptualization, L.K., M.G., A.K. and I.C.-L.; investigation, A.K. and S.F.; writing—original draft preparation, L.K., M.G., A.K. and S.F.; writing—review and editing, I.C.-L. and M.W.; visualization, M.G.; supervision, M.G. and I.C.-L.; funding acquisition, creation of a local RFB program and its R&D directions, M.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the German Federal Ministry of Education and Research and by the Ministry of Arts and Science of the state of North Rhine-Westphalia in the framework of the core funding for Juelich Research Centre. This research was funded by the Ministry of Economic Affairs, Innovation, Digitalization and Energy of the State of North Rhine-Westphalia in the framework of the “GrEEn” project, grant number 313-W044A.
Data Availability Statement
No SI will be submitted.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dühnen, S.; Betz, J.; Kolek, M.; Schmuch, R.; Winter, M.; Placke, T. Toward Green Battery Cells: Perspective on Materials and Technologies. Small Methods 2020, 4, 2000039. [Google Scholar] [CrossRef]
- Winter, M.; Barnett, B.; Xu, K. Before Li Ion Batteries. Chem. Rev. 2018, 118, 11433–11456. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Wang, S. A review on energy management, operation control and application methods for grid battery energy storage systems. CSEE JPES 2019, 7, 1026–1040. [Google Scholar] [CrossRef]
- Alotto, P.; Guarnieri, M.; Moro, F. Redox flow batteries for the storage of renewable energy: A review. Renew. Sustain. Energy Rev. 2014, 29, 325–335. [Google Scholar] [CrossRef]
- Darling, R.M.; Gallagher, K.G.; Kowalski, J.A.; Ha, S.; Brushett, F.R. Pathways to low-cost electrochemical energy storage: A comparison of aqueous and nonaqueous flow batteries. Energy Environ. Sci. 2014, 7, 3459–3477. [Google Scholar] [CrossRef]
- Noack, J.; Roznyatovskaya, N.; Herr, T.; Fischer, P. The Chemistry of Redox-Flow Batteries. Angew. Chem. Int. Ed. 2015, 54, 9776–9809. [Google Scholar] [CrossRef] [PubMed]
- Arenas, L.F.; Ponce de León, C.; Walsh, F.C. Redox flow batteries for energy storage: Their promise, achievements and challenges. Curr. Opin. Electrochem. 2019, 16, 117–126. [Google Scholar] [CrossRef]
- Sánchez-Díez, E.; Ventosa, E.; Guarnieri, M.; Trovò, A.; Flox, C.; Marcilla, R.; Soavi, F.; Mazur, P.; Aranzabe, E.; Ferret, R. Redox flow batteries: Status and perspective towards sustainable stationary energy storage. J. Power Sources 2021, 481, 228804. [Google Scholar] [CrossRef]
- Thaller, L. Energy Storage System. 1976. Available online: https://patents.google.com/patent/US3996064A/en (accessed on 15 December 2022).
- Kangro, W. Method for Storing Electrical Energy. Available online: https://patents.google.com/patent/DE914264C/en (accessed on 15 December 2022).
- Skyllas-Kazacos, M.; Rychcik, M.; Robins, R.G.; Fane, A.G.; Green, M.A. New All-Vanadium Redox Flow Cell. J. Electrochem. Soc. 1986, 133, 1057–1058. [Google Scholar] [CrossRef]
- Skyllas-Kazacos, M.; Rychick, M.; Robins, R. All-Vanadium Redox Battery. U.S. Patent 4786567, 22 November 1988. [Google Scholar]
- Ke, X.; Prahl, J.M.; Alexander, J.I.D.; Wainright, J.S.; Zawodzinski, T.A.; Savinell, R.F. Rechargeable redox flow batteries: Flow fields, stacks and design considerations. Chem. Soc. Rev. 2018, 47, 8721–8743. [Google Scholar] [CrossRef]
- Lucas, A.; Chondrogiannis, S. Smart grid energy storage controller for frequency regulation and peak shaving, using a vanadium redox flow battery. Int. J. Electr. Power Energy Syst. 2016, 80, 26–36. [Google Scholar] [CrossRef]
- Kear, G.; Shah, A.A.; Walsh, F.C. Development of the all-vanadium redox flow battery for energy storage: A review of technological, financial and policy aspects. Int. J. Energy Res. 2012, 36, 1105–1120. [Google Scholar] [CrossRef]
- Aramendia, I.; Fernandez-Gamiz, U.; Martinez-San-Vicente, A.; Zulueta, E.; Lopez-Guede, J.M. Vanadium Redox Flow Batteries: A Review Oriented to Fluid-Dynamic Optimization. Energies 2021, 14, 176. [Google Scholar] [CrossRef]
- Gür, T.M. Review of electrical energy storage technologies, materials and systems: Challenges and prospects for large-scale grid storage. Energy Environ. Sci. 2018, 11, 2696–2767. [Google Scholar] [CrossRef]
- Arenas, L.F.; Ponce de León, C.; Walsh, F.C. Engineering aspects of the design, construction and performance of modular redox flow batteries for energy storage. J. Energy Storage 2017, 11, 119–153. [Google Scholar] [CrossRef]
- Hameer, S.; van Niekerk, J.L. A review of large-scale electrical energy storage. Int. J. Energy Res. 2015, 39, 1179–1195. [Google Scholar] [CrossRef]
- Wang, W.; Luo, Q.; Li, B.; Wei, X.; Li, L.; Yang, Z. Recent Progress in Redox Flow Battery Research and Development. Adv. Funct. Mater. 2013, 23, 970–986. [Google Scholar] [CrossRef]
- Leung, P.; Shah, A.A.; Sanz, L.; Flox, C.; Morante, J.R.; Xu, Q.; Mohamed, M.R.; Ponce de León, C.; Walsh, F.C. Recent developments in organic redox flow batteries: A critical review. J. Power Sources 2017, 360, 243–283. [Google Scholar] [CrossRef]
- Cao, J.; Tian, J.; Xu, J.; Wang, Y. Organic Flow Batteries: Recent Progress and Perspectives. Energy Fuels 2020, 34, 13384–13411. [Google Scholar] [CrossRef]
- Xu, F.; Li, H.; Liu, Y.; Jing, Q. Advanced redox flow fuel cell using ferric chloride as main catalyst for complete conversion from carbohydrates to electricity. Sci. Rep. 2017, 7, 5142. [Google Scholar] [CrossRef]
- Winter, M.; Brodd, R.J. What are batteries, fuel cells, and supercapacitors? Chem. Rev. 2004, 104, 4245–4269. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Gong, Y.; Tricker, A.; Wu, G.; Liu, C.; Chao, Z.; Deng, Y. Fundamental Study toward Improving the Performance of a High-Moisture Biomass-Fueled Redox Flow Fuel Cell. Ind. Eng. Chem. Res. 2020, 59, 4817–4828. [Google Scholar] [CrossRef]
- Cho, K.T.; Tucker, M.C.; Weber, A.Z. A Review of Hydrogen/Halogen Flow Cells. Energy Technol. 2016, 4, 655–678. [Google Scholar] [CrossRef]
- Lyu, Y.; Xie, J.; Wang, D.; Wang, J. Review of cell performance in solid oxide fuel cells. J. Mater. Sci. 2020, 55, 7184–7207. [Google Scholar] [CrossRef]
- Brett, D.J.L.; Atkinson, A.; Brandon, N.P.; Skinner, S.J. Intermediate temperature solid oxide fuel cells. Chem. Soc. Rev. 2008, 37, 1568–1578. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Ruiz Diaz, D.F.; Chen, K.S.; Wang, Z.; Adroher, X.C. Materials, technological status, and fundamentals of PEM fuel cells—A review. Mater. Today 2020, 32, 178–203. [Google Scholar] [CrossRef]
- Mitlitsky, F.; Myers, B.; Weisberg, A.H.; Molter, T.M.; Smith, W.F. Reversible (unitised) PEM fuel cell devices. Fuel Cells Bull. 1999, 2, 6–11. [Google Scholar] [CrossRef]
- Soloveichik, G.L. Flow Batteries: Current Status and Trends. Chem. Rev. 2015, 115, 11533–11558. [Google Scholar] [CrossRef]
- Hamelet, S.; Tzedakis, T.; Leriche, J.-B.; Sailler, S.; Larcher, D.; Taberna, P.-L.; Simon, P.; Tarascon, J.-M. Non-Aqueous Li-Based Redox Flow Batteries. J. Electrochem. Soc. 2012, 159, A1360–A1367. [Google Scholar] [CrossRef]
- Chakrabarti, M.H.; Dryfe, R.; Roberts, E. Evaluation of electrolytes for redox flow battery applications. Electrochim. Acta 2007, 52, 2189–2195. [Google Scholar] [CrossRef]
- Shin, S.-H.; Yun, S.-H.; Moon, S.-H. A review of current developments in non-aqueous redox flow batteries: Characterization of their membranes for design perspective. RSC Adv. 2013, 3, 9095. [Google Scholar] [CrossRef]
- Noh, C.; Shin, M.; Kwon, Y. A strategy for lowering cross-contamination of aqueous redox flow batteries using metal-ligand complexes as redox couple. J. Power Sources 2022, 520, 230810. [Google Scholar] [CrossRef]
- Korshunov, A.; Milner, M.J.; Grünebaum, M.; Studer, A.; Winter, M.; Cekic-Laskovic, I. An oxo-verdazyl radical for a symmetrical non-aqueous redox flow battery. J. Mater. Chem. A 2020, 8, 22280–22291. [Google Scholar] [CrossRef]
- Sikukuu Nambafu, G. Organic molecules as bifunctional electroactive materials for symmetric redox flow batteries: A mini review. Electrochem. Commun. 2021, 127, 107052. [Google Scholar] [CrossRef]
- Rychcik, M.; Skyllas-Kazacos, M. Evaluation of electrode materials for vanadium redox cell. J. Power Sources 1987, 19, 45–54. [Google Scholar] [CrossRef]
- Rychcik, M.; Skyllas-Kazacos, M. Characteristics of a new all-vanadium redox flow battery. J. Power Sources 1988, 22, 59–67. [Google Scholar] [CrossRef]
- Kaneko, H.; Nozaki, K.; Wada, Y.; Aoki, T.; Negishi, A.; Kamimoto, M. Vanadium redox reactions and carbon electrodes for vanadium redox flow battery. Electrochim. Acta 1991, 36, 1191–1196. [Google Scholar] [CrossRef]
- Mohammadi, T.; Kazacos, M. Modification of anion-exchange membranes for vanadium redox flow battery applications. J. Power Sources 1996, 63, 179–186. [Google Scholar] [CrossRef]
- Zhao, P.; Zhang, H.; Zhou, H.; Chen, J.; Gao, S.; Yi, B. Characteristics and performance of 10kW class all-vanadium redox-flow battery stack. J. Power Sources 2006, 162, 1416–1420. [Google Scholar] [CrossRef]
- Liao, J.B.; Lu, M.Z.; Chu, Y.Q.; Wang, J.L. Ultra-low vanadium ion diffusion amphoteric ion-exchange membranes for all-vanadium redox flow batteries. J. Power Sources 2015, 282, 241–247. [Google Scholar] [CrossRef]
- Jia, C.; Liu, J.; Yan, C. A significantly improved membrane for vanadium redox flow battery. J. Power Sources 2010, 195, 4380–4383. [Google Scholar] [CrossRef]
- Jiang, Y.; Liu, Z.; Lv, Y.; Tang, A.; Dai, L.; Wang, L.; He, Z. Perovskite enables high performance vanadium redox flow battery. Chem. Eng. J. 2022, 443, 136341. [Google Scholar] [CrossRef]
- Xu, W.; Long, J.; Liu, J.; Luo, H.; Duan, H.; Zhang, Y.; Li, J.; Qi, X.; Chu, L. A novel porous polyimide membrane with ultrahigh chemical stability for application in vanadium redox flow battery. Chem. Eng. J. 2022, 428, 131203. [Google Scholar] [CrossRef]
- Duduta, M.; Ho, B.; Wood, V.C.; Limthongkul, P.; Brunini, V.E.; Carter, W.C.; Chiang, Y.-M. Semi-Solid Lithium Rechargeable Flow Battery. Adv. Energy Mater. 2011, 1, 511–516. [Google Scholar] [CrossRef]
- Chen, H.; Lu, Y.-C. A High-Energy-Density Multiple Redox Semi-Solid-Liquid Flow Battery. Adv. Energy Mater. 2016, 6, 1502183. [Google Scholar] [CrossRef]
- Biendicho, J.J.; Flox, C.; Sanz, L.; Morante, J.R. Static and Dynamic Studies on LiNi1/3 Co1/3 Mn1/3 O2 -Based Suspensions for Semi-Solid Flow Batteries. ChemSusChem 2016, 9, 1938–1944. [Google Scholar] [CrossRef]
- Hamelet, S.; Larcher, D.; Dupont, L.; Tarascon, J.-M. Silicon-Based Non Aqueous Anolyte for Li Redox-Flow Batteries. J. Electrochem. Soc. 2013, 160, A516–A5202013. [Google Scholar] [CrossRef]
- Guillon, O. (Ed.) Advanced Ceramics for Energy Conversion and Storage; Elsevier: Amsterdam, The Netherlands; Kidlington, UK; Oxford, UK; Cambridge, MA, USA, 2020; ISBN 978-0081027264. [Google Scholar]
- Yan, W.; Wang, C.; Tian, J.; Zhu, G.; Ma, L.; Wang, Y.; Chen, R.; Hu, Y.; Wang, L.; Chen, T.; et al. All-polymer particulate slurry batteries. Nat. Commun. 2019, 10, 2513. [Google Scholar] [CrossRef]
- Xing, X.; Liu, Q.; Li, J.; Han, Z.; Wang, B.; Lemmon, J.P. A nonaqueous all organic semisolid flow battery. Chem. Commun. 2019, 55, 14214–14217. [Google Scholar] [CrossRef]
- Wang, X.; Chai, J.; Jiang, J. Redox flow batteries based on insoluble redox-active materials. A review. Nano Mater. Sci. 2021, 3, 17–24. [Google Scholar] [CrossRef]
- Hatzell, K.B.; Boota, M.; Gogotsi, Y. Materials for suspension (semi-solid) electrodes for energy and water technologies. Chem. Soc. Rev. 2015, 44, 8664–8687. [Google Scholar] [CrossRef] [PubMed]
- Yufit, V.; Hale, B.; Matian, M.; Mazur, P.; Brandon, N.P. Development of a Regenerative Hydrogen-Vanadium Fuel Cell for Energy Storage Applications. J. Electrochem. Soc. 2013, 160, A856–A861. [Google Scholar] [CrossRef]
- Alon, M.; Blum, A.; Peled, E. Feasibility study of hydrogen/iron redox flow cell for grid-storage applications. J. Power Sources 2013, 240, 417–420. [Google Scholar] [CrossRef]
- Cho, K.T.; Ridgway, P.; Weber, A.Z.; Haussener, S.; Battaglia, V.; Srinivasan, V. High Performance Hydrogen/Bromine Redox Flow Battery for Grid-Scale Energy Storage. J. Electrochem. Soc. 2012, 159, A1806–A1815. [Google Scholar] [CrossRef]
- Rubio-Garcia, J.; Kucernak, A.; Zhao, D.; Li, D.; Fahy, K.; Yufit, V.; Brandon, N.; Gomez-Gonzalez, M. Hydrogen/manganese hybrid redox flow battery. J. Phys. Energy 2019, 1, 15006. [Google Scholar] [CrossRef]
- Hewa Dewage, H.; Wu, B.; Tsoi, A.; Yufit, V.; Offer, G.; Brandon, N. A novel regenerative hydrogen cerium fuel cell for energy storage applications. J. Mater. Chem. A 2015, 3, 9446–9450. [Google Scholar] [CrossRef]
- Rubio-Garcia, J.; Kucernak, A.; Parra-Puerto, A.; Liu, R.; Chakrabarti, B. Hydrogen/functionalized benzoquinone for a high-performance regenerative fuel cell as a potential large-scale energy storage platform. J. Mater. Chem. A 2020, 8, 3933–3941. [Google Scholar] [CrossRef]
- Rubio-Garcia, J.; Cui, J.; Parra-Puerto, A.; Kucernak, A. Hydrogen/Vanadium Hybrid Redox Flow Battery with enhanced electrolyte concentration. Energy Storage Mater. 2020, 31, 1–10. [Google Scholar] [CrossRef]
- Walsh, F.C.; Ponce de Léon, C.; Berlouis, L.; Nikiforidis, G.; Arenas-Martínez, L.F.; Hodgson, D.; Hall, D. The Development of Zn-Ce Hybrid Redox Flow Batteries for Energy Storage and Their Continuing Challenges. ChemPlusChem 2015, 80, 288–311. [Google Scholar] [CrossRef]
- Jeena, C.B.; Elsa, P.J.; Moly, P.P.; Ambily, K.J.; Joy, V.T. A dendrite free Zn-Fe hybrid redox flow battery for renewable energy storage. Energy Storage 2022, 4, e275. [Google Scholar] [CrossRef]
- Wang, Y.; He, P.; Zhou, H. Li-Redox Flow Batteries Based on Hybrid Electrolytes: At the Cross Road between Li-ion and Redox Flow Batteries. Adv. Energy Mater. 2012, 2, 770–779. [Google Scholar] [CrossRef]
- Zhu, Y.G.; Du, Y.; Jia, C.; Zhou, M.; Li, F.; Wang, X.; Wang, Q. Unleashing the Power and Energy of LiFePO4-Based Redox Flow Lithium Battery with a Bifunctional Redox Mediator. J. Am. Chem. Soc. 2017, 139, 6286–6289. [Google Scholar] [CrossRef] [PubMed]
- Nariyama, H.; Ito, S.; Okada, Y.; Inatomi, Y.; Ichikawa, K.; Masumoto, Y.; Fujimoto, M. High energy density 3V-class redox flow battery using LiFePO4 and graphite with organic bifunctional redox mediators. Electrochim. Acta 2022, 409, 139915. [Google Scholar] [CrossRef]
- Jia, C.; Pan, F.; Zhu, Y.G.; Huang, Q.; Lu, L.; Wang, Q. High-energy density nonaqueous all redox flow lithium battery enabled with a polymeric membrane. Sci. Adv. 2015, 1, e15008862. [Google Scholar] [CrossRef]
- Pan, F.; Yang, J.; Huang, Q.; Wang, X.; Huang, H.; Wang, Q. Batteries: Redox Targeting of Anatase TiO2 for Redox Flow Lithium-Ion Batteries. Adv. Energy Mater. 2014, 4, 1400567. [Google Scholar] [CrossRef]
- Huang, Q.; Li, H.; Grätzel, M.; Wang, Q. Reversible chemical delithiation/lithiation of LiFePO4: Towards a redox flow lithium-ion battery. Phys. Chem. Chem. Phys. 2013, 15, 1793–1797. [Google Scholar] [CrossRef]
- Zou, T.; Shi, X.; Yu, L. Study on energy loss of 35 kW all vanadium redox flow battery energy storage system under closed-loop flow strategy. J. Power Sources 2021, 490, 229514. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, L.; Yang, Y.-S.; Wen, Y.-H.; Cao, G.-P.; Wang, X.-D. Preliminary study of single flow zinc–nickel battery. Electrochem. Commun. 2007, 9, 2639–2642. [Google Scholar] [CrossRef]
- Im, Y.; Kim, J.; Park, K.S.; Cho, T.W.; Jeon, J.; Chung, K.; Eguchi, K.; Kang, M. Influence of small amount of Mg incorporated into hexagonal ZnO crystal on cell performance in membrane free Zinc–Nickel redox battery. J. Ind. Eng. Chem. 2018, 64, 318–327. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhang, H.; Lai, Q.; Li, X.; Zheng, Q.; Xi, X.; Ding, C. Effect of temperature on the performances and in situ polarization analysis of zinc–nickel single flow batteries. J. Power Sources 2014, 249, 435–439. [Google Scholar] [CrossRef]
- Turney, D.E.; Shmukler, M.; Galloway, K.; Klein, M.; Ito, Y.; Sholklapper, T.; Gallaway, J.W.; Nyce, M.; Banerjee, S. Development and testing of an economic grid-scale flow-assisted zinc/nickel-hydroxide alkaline battery. J. Power Sources 2014, 264, 49–58. [Google Scholar] [CrossRef]
- Amit, L.; Naar, D.; Gloukhovski, R.; La O’, G.J.; Suss, M.E. A Single-Flow Battery with Multiphase Flow. ChemSusChem 2021, 14, 1068–1073. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Wen, Y.; Cheng, J.; Pan, J.; Bai, S.; Yang, Y. Evaluation of substrates for zinc negative electrode in acid PbO2–Zn single flow batteries. Chin. J. Chem. Eng. 2016, 24, 529–534. [Google Scholar] [CrossRef]
- Xie, C.; Liu, Y.; Lu, W.; Zhang, H.; Li, X. Highly stable zinc–iodine single flow batteries with super high energy density for stationary energy storage. Energy Environ. Sci. 2019, 12, 1834–1839. [Google Scholar] [CrossRef]
- Gu, S.; Gong, K.; Yan, E.Z.; Yan, Y. A multiple ion-exchange membrane design for redox flow batteries. Energy Environ. Sci. 2014, 7, 2986–2998. [Google Scholar] [CrossRef]
- Bamgbopa, M.O.; Almheiri, S.; Sun, H. Prospects of recently developed membraneless cell designs for redox flow batteries. Renew. Sustain. Energy Rev. 2017, 70, 506–518. [Google Scholar] [CrossRef]
- Von Doenhoff, A.E.; Braslow, A.L. The effect of distributed surface roughness on laminar flow. In Boundary Layer and Flow Control; Lachmann, G.V., Ed.; Elsevier Science: Amsterdam, The Netherlands, 1961; pp. 657–681. ISBN 9781483213231. [Google Scholar]
- Skyllas-Kazacos, M.; Grossmith, F. Efficient Vanadium Redox Flow Cell. J. Electrochem. Soc. 1987, 134, 2950–2953. [Google Scholar] [CrossRef]
- Schulte, D.; Drillkens, J.; Schulte, B.; Sauer, D.U. Nafion Hybrid Membranes for Use in Vanadium Redox Flow Batteries. ECS Trans. 2010, 25, 247–255. [Google Scholar] [CrossRef]
- Jiang, B.; Wu, L.; Yu, L.; Qiu, X.; Xi, J. A comparative study of Nafion series membranes for vanadium redox flow batteries. J. Membr. Sci. 2016, 510, 18–26. [Google Scholar] [CrossRef]
- Maghsoudy, S.; Rahimi, M.; Dehkordi, A.M. Investigation on various types of ion-exchange membranes in vanadium redox flow batteries: Experiment and modeling. J. Energy Storage 2022, 54, 105347. [Google Scholar] [CrossRef]
- Peng, S.; Zhang, L.; Zhang, C.; Ding, Y.; Guo, X.; He, G.; Yu, G. Gradient-Distributed Metal-Organic Framework-Based Porous Membranes for Nonaqueous Redox Flow Batteries. Adv. Energy Mater. 2018, 8, 1802533. [Google Scholar] [CrossRef]
- Hendriks, K.H.; Robinson, S.G.; Braten, M.N.; Sevov, C.S.; Helms, B.A.; Sigman, M.S.; Minteer, S.D.; Sanford, M.S. High-Performance Oligomeric Catholytes for Effective Macromolecular Separation in Nonaqueous Redox Flow Batteries. ACS Cent. Sci. 2018, 4, 189–196. [Google Scholar] [CrossRef]
- Chen, R. Redox flow batteries for energy storage: Recent advances in using organic active materials. Curr. Opin. Electrochem. 2020, 21, 40–45. [Google Scholar] [CrossRef]
- Gong, K.; Fang, Q.; Gu, S.; Li, S.F.Y.; Yan, Y. Nonaqueous redox-flow batteries: Organic solvents, supporting electrolytes, and redox pairs. Energy Environ. Sci. 2015, 8, 3515–3530. [Google Scholar] [CrossRef]
- Tang, L.; Leung, P.; Xu, Q.; Mohamed, M.R.; Dai, S.; Zhu, X.; Flox, C.; Shah, A.A. Future perspective on redox flow batteries: Aqueous versus nonaqueous electrolytes. Curr. Opin. Chem. Eng. 2022, 37, 100833. [Google Scholar] [CrossRef]
- Singh, P. Application of non-aqueous solvents to batteries. J. Power Sources 1984, 11, 135–142. [Google Scholar] [CrossRef]
- Reichardt, C.; Welton, T. Solvents and Solvent Effects in Organic Chemistry, 4th ed.; Wiley-VCH: Weinheim, Germany, 2011; ISBN 9783527324736. [Google Scholar]
- Smallwood, I. Handbook of Organic Solvent Properties; Elsevier Science: Burlington, MA, USA, 1996; ISBN 0340645784. [Google Scholar]
- Jonsson, M.; Houmam, A.; Jocys, G.; Wayner, D.D.M. Solvent effects on redox properties of radical ions 1. J. Chem. Soc. Perkin Trans. 1999, 2, 425–430. [Google Scholar] [CrossRef]
- Catalán, J. Toward a generalized treatment of the solvent effect based on four empirical scales: Dipolarity (SdP, a new scale), polarizability (SP), acidity (SA), and basicity (SB) of the medium. J. Phys. Chem. B 2009, 113, 5951–5960. [Google Scholar] [CrossRef]
- Li, Z.; Li, S.; Liu, S.; Huang, K.; Fang, D.; Wang, F.; Peng, S. Electrochemical Properties of an All-Organic Redox Flow Battery Using 2,2,6,6-Tetramethyl-1-Piperidinyloxy and N-Methylphthalimide. Electrochem. Solid State Lett. 2011, 14, A171. [Google Scholar] [CrossRef]
- Daub, N.; Janssen, R.A.J.; Hendriks, K.H. Imide-Based Multielectron Anolytes as High-Performance Materials in Nonaqueous Redox Flow Batteries. ACS Appl. Energy Mater. 2021, 4, 9248–9257. [Google Scholar] [CrossRef]
- Brushett, F.R.; Vaughey, J.T.; Jansen, A.N. An All-Organic Non-aqueous Lithium-Ion Redox Flow Battery. Adv. Energy Mater. 2012, 2, 1390–1396. [Google Scholar] [CrossRef]
- Huang, J.; Yang, Z.; Vijayakumar, M.; Duan, W.; Hollas, A.; Pan, B.; Wang, W.; Wei, X.; Zhang, L. A Two-Electron Storage Nonaqueous Organic Redox Flow Battery. Adv. Sustain. Syst. 2018, 2, 1700131. [Google Scholar] [CrossRef]
- Huo, Y.; Xing, X.; Zhang, C.; Wang, X.; Li, Y. An all organic redox flow battery with high cell voltage. RSC Adv. 2019, 9, 13128–13132. [Google Scholar] [CrossRef] [PubMed]
- Nagarjuna, G.; Hui, J.; Cheng, K.J.; Lichtenstein, T.; Shen, M.; Moore, J.S.; Rodríguez-López, J. Impact of redox-active polymer molecular weight on the electrochemical properties and transport across porous separators in nonaqueous solvents. J. Am. Chem. Soc. 2014, 136, 16309–16316. [Google Scholar] [CrossRef]
- Hu, B.; Liu, T.L. Two electron utilization of methyl viologen anolyte in nonaqueous organic redox flow battery. J. Energy Chem. 2018, 27, 1326–1332. [Google Scholar] [CrossRef]
- Zhang, L.; Qian, Y.; Feng, R.; Ding, Y.; Zu, X.; Zhang, C.; Guo, X.; Wang, W.; Yu, G. Reversible redox chemistry in azobenzene-based organic molecules for high-capacity and long-life nonaqueous redox flow batteries. Nat. Commun. 2020, 11, 3843. [Google Scholar] [CrossRef]
- Wang, X.; Chai, J.; Lashgari, A.; Jiang, J.J. Azobenzene-Based Low-Potential Anolyte for Nonaqueous Organic Redox Flow Batteries. ChemElectroChem 2021, 8, 83–89. [Google Scholar] [CrossRef]
- Hwang, S.; Kim, H.; Ryu, J.H.; Oh, S.M. N-ferrocenylphthalimide; A single redox couple formed by attaching a ferrocene moiety to phthalimide for non-aqueous flow batteries. J. Power Sources 2018, 395, 60–65. [Google Scholar] [CrossRef]
- Potash, R.A.; McKone, J.R.; Conte, S.; Abruña, H.D. On the Benefits of a Symmetric Redox Flow Battery. J. Electrochem. Soc. 2016, 163, A338–A344. [Google Scholar] [CrossRef]
- Geysens, P.; Li, Y.; Vankelecom, I.; Fransaer, J.; Binnemans, K. Highly Soluble 1,4-Diaminoanthraquinone Derivative for Nonaqueous Symmetric Redox Flow Batteries. ACS Sustain. Chem. Eng. 2020, 8, 3832–3843. [Google Scholar] [CrossRef]
- Etkind, S.I.; Lopez, J.; Zhu, Y.G.; Fang, J.-H.; Ong, W.J.; Shao-Horn, Y.; Swager, T.M. Thianthrene-Based Bipolar Redox-Active Molecules Toward Symmetric All-Organic Batteries. ACS Sustain. Chem. Eng. 2022, 10, 11739–11750. [Google Scholar] [CrossRef]
- Wylie, L.; Blesch, T.; Freeman, R.; Hatakeyama-Sato, K.; Oyaizu, K.; Yoshizawa-Fujita, M.; Izgorodina, E.I. Reversible Reduction of the TEMPO Radical: One Step Closer to an All-Organic Redox Flow Battery. ACS Sustain. Chem. Eng. 2020, 8, 17988–17996. [Google Scholar] [CrossRef]
- Duan, W.; Vemuri, R.S.; Milshtein, J.D.; Laramie, S.; Dmello, R.D.; Huang, J.; Zhang, L.; Hu, D.; Vijayakumar, M.; Wang, W.; et al. A symmetric organic-based nonaqueous redox flow battery and its state of charge diagnostics by FTIR. J. Mater. Chem. A 2016, 4, 5448–5456. [Google Scholar] [CrossRef]
- Hagemann, T.; Winsberg, J.; Häupler, B.; Janoschka, T.; Gruber, J.J.; Wild, A.; Schubert, U.S. A bipolar nitronyl nitroxide small molecule for an all-organic symmetric redox-flow battery. NPG Asia Mater. 2017, 9, e340. [Google Scholar] [CrossRef]
- Steen, J.S.; Nuismer, J.L.; Eiva, V.; Wiglema, A.E.T.; Daub, N.; Hjelm, J.; Otten, E. Blatter Radicals as Bipolar Materials for Symmetrical Redox-Flow Batteries. J. Am. Chem. Soc. 2022, 144, 5051–5058. [Google Scholar] [CrossRef]
- Moutet, J.; Veleta, J.M.; Gianetti, T.L. Symmetric, Robust, and High-Voltage Organic Redox Flow Battery Model Based on a Helical Carbenium Ion Electrolyte. ACS Appl. Energy Mater. 2021, 4, 9–14. [Google Scholar] [CrossRef]
- Moutet, J.; Mills, D.; Hossain, M.M.; Gianetti, T.L. Increased performance of an all-organic redox flow battery model via nitration of the [4]helicenium DMQA ion electrolyte. Mater. Adv. 2022, 3, 216–223. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Z.; Redfern, P.C.; Curtiss, L.A.; Amine, K. Molecular engineering towards safer lithium-ion batteries: A highly stable and compatible redox shuttle for overcharge protection. Energy Environ. Sci. 2012, 5, 8204. [Google Scholar] [CrossRef]
- Wang, X.; Xing, X.; Huo, Y.; Zhao, Y.; Li, Y. A systematic study of the co-solvent effect for an all-organic redox flow battery. RSC Adv. 2018, 8, 24422–24427. [Google Scholar] [CrossRef]
- Wei, X.; Xu, W.; Huang, J.; Zhang, L.; Walter, E.; Lawrence, C.; Vijayakumar, M.; Henderson, W.A.; Liu, T.; Cosimbescu, L.; et al. Radical Compatibility with Nonaqueous Electrolytes and Its Impact on an All-Organic Redox Flow Battery. Angew. Chem. Int. Ed. Engl. 2015, 54, 8684–8687. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, Z.; Shkrob, I.A.; Assary, R.S.; Tung, S.O.; Silcox, B.; Duan, W.; Zhang, J.; Su, C.C.; Hu, B.; et al. Annulated Dialkoxybenzenes as Catholyte Materials for Non-aqueous Redox Flow Batteries: Achieving High Chemical Stability through Bicyclic Substitution. Adv. Energy Mater. 2017, 7, 1701272. [Google Scholar] [CrossRef]
- Huang, J.; Cheng, L.; Assary, R.S.; Wang, P.; Xue, Z.; Burrell, A.K.; Curtiss, L.A.; Zhang, L. Liquid Catholyte Molecules for Nonaqueous Redox Flow Batteries. Adv. Energy Mater. 2015, 5, 1401782. [Google Scholar] [CrossRef]
- Ding, Y.; Zhao, Y.; Li, Y.; Goodenough, J.B.; Yu, G. A high-performance all-metallocene-based, non-aqueous redox flow battery. Energy Environ. Sci. 2017, 10, 491–497. [Google Scholar] [CrossRef]
- Park, K.; Cho, J.H.; Shanmuganathan, K.; Song, J.; Peng, J.; Gobet, M.; Greenbaum, S.; Ellison, C.J.; Goodenough, J.B. New battery strategies with a polymer/Al2O3 separator. J. Power Sources 2014, 263, 52–58. [Google Scholar] [CrossRef]
- Zhao, Y.; Ding, Y.; Song, J.; Li, G.; Dong, G.; Goodenough, J.B.; Yu, G. Sustainable electrical energy storage through the ferrocene/ferrocenium redox reaction in aprotic electrolyte. Angew. Chem. Int. Ed. Engl. 2014, 53, 11036–11040. [Google Scholar] [CrossRef]
- Romadina, E.I.; Volodin, I.A.; Stevenson, K.J.; Troshin, P.A. New highly soluble triarylamine-based materials as promising catholytes for redox flow batteries. J. Mater. Chem. A 2021, 9, 8303–8307. [Google Scholar] [CrossRef]
- Armand, M.; Tarascon, J.-M. Building better batteries. Nature 2008, 451, 652–657. [Google Scholar] [CrossRef]
- Charlton, G.D.; Barbon, S.M.; Gilroy, J.B.; Dyker, C.A. A bipolar verdazyl radical for a symmetric all-organic redox flow-type battery. J. Energy Chem. 2019, 34, 52–56. [Google Scholar] [CrossRef]
- Navalpotro, P.; Sierra, N.; Trujillo, C.; Montes, I.; Palma, J.; Marcilla, R. Exploring the Versatility of Membrane-Free Battery Concept Using Different Combinations of Immiscible Redox Electrolytes. ACS Appl. Mater. Interfaces 2018, 10, 41246–41256. [Google Scholar] [CrossRef]
- Peljo, P.; Bichon, M.; Girault, H.H. Ion transfer battery: Storing energy by transferring ions across liquid-liquid interfaces. Chem. Commun. 2016, 52, 9761–9764. [Google Scholar] [CrossRef]
- Cekic-Laskovic, I.; von Aspern, N.; Imholt, L.; Kaymaksiz, S.; Oldiges, K.; Rad, B.R.; Winter, M. Synergistic Effect of Blended Components in Nonaqueous Electrolytes for Lithium Ion Batteries. In Electrochemical Energy Storage; Eichel, R.-A., Ed.; Springer International Publishing: Cham, Switzerland, 2019; pp. 1–64. ISBN 978-3-030-26128-3. [Google Scholar]
- Von Aspern, N.; Röschenthaler, G.-V.; Winter, M.; Cekic-Laskovic, I. Fluorine and Lithium: Ideal Partners for High-Performance Rechargeable Battery Electrolytes. Angew. Chem. Int. Ed. 2019, 58, 15978–16000. [Google Scholar] [CrossRef] [PubMed]
- Kowalski, J.A.; Carney, T.J.; Huang, J.; Zhang, L.; Brushett, F.R. An investigation on the impact of halidization on substituted dimethoxybenzenes. Electrochim. Acta 2020, 335, 135580. [Google Scholar] [CrossRef]
- Cong, G.; Zhou, Y.; Li, Z.; Lu, Y.-C. A Highly Concentrated Catholyte Enabled by a Low-Melting-Point Ferrocene Derivative. ACS Energy Lett. 2017, 2, 869–875. [Google Scholar] [CrossRef]
- Astruc, D. Why is Ferrocene so Exceptional? Eur. J. Inorg. Chem. 2017, 2017, 6–29. [Google Scholar] [CrossRef]
- Chen, H.; Niu, Z.; Ye, J.; Zhang, C.; Zhang, X.; Zhao, Y. Multicore Ferrocene Derivative as a Highly Soluble Cathode Material for Nonaqueous Redox Flow Batteries. ACS Appl. Energy Mater. 2021, 4, 855–861. [Google Scholar] [CrossRef]
- Wei, X.; Cosimbescu, L.; Xu, W.; Hu, J.Z.; Vijayakumar, M.; Feng, J.; Hu, M.Y.; Deng, X.; Xiao, J.; Liu, J.; et al. Towards High-Performance Nonaqueous Redox Flow Electrolyte Via Ionic Modification of Active Species. Adv. Energy Mater. 2015, 5, 1400678. [Google Scholar] [CrossRef]
- Cosimbescu, L.; Wei, X.; Vijayakumar, M.; Xu, W.; Helm, M.L.; Burton, S.D.; Sorensen, C.M.; Liu, J.; Sprenkle, V.; Wang, W. Anion-Tunable Properties and Electrochemical Performance of Functionalized Ferrocene Compounds. Sci. Rep. 2015, 5, 14117. [Google Scholar] [CrossRef]
- Kim, H.; Yoon, T.; Kim, Y.; Hwang, S.; Ryu, J.H.; Oh, S.M. Increase of both solubility and working voltage by acetyl substitution on ferrocene for non-aqueous flow battery. Electrochem. Commun. 2016, 69, 72–75. [Google Scholar] [CrossRef]
- Tricot, Y.M.; Porat, Z.; Manassen, J. Photoinduced and redox-induced transmembrane processes with vesicle-stabilized colloidal cadmium sulfide and multicharged viologen derivatives. J. Phys. Chem. 1991, 95, 3242–3248. [Google Scholar] [CrossRef]
- DeBruler, C.; Hu, B.; Moss, J.; Liu, X.; Luo, J.; Sun, Y.; Liu, T.L. Designer Two-Electron Storage Viologen Anolyte Materials for Neutral Aqueous Organic Redox Flow Batteries. Chem 2017, 3, 961–978. [Google Scholar] [CrossRef]
- Liu, Y.; Goulet, M.-A.; Tong, L.; Liu, Y.; Ji, Y.; Wu, L.; Gordon, R.G.; Aziz, M.J.; Yang, Z.; Xu, T. A Long-Lifetime All-Organic Aqueous Flow Battery Utilizing TMAP-TEMPO Radical. Chem 2019, 5, 1861–1870. [Google Scholar] [CrossRef]
- Buhrmester, C.; Moshurchak, L.; Wang, R.L.; Dahn, J.R. Phenothiazine Molecules. J. Electrochem. Soc. 2006, 153, A288. [Google Scholar] [CrossRef]
- Attanayake, N.H.; Kowalski, J.A.; Greco, K.V.; Casselman, M.D.; Milshtein, J.D.; Chapman, S.J.; Parkin, S.R.; Brushett, F.R.; Odom, S.A. Tailoring Two-Electron-Donating Phenothiazines to Enable High-Concentration Redox Electrolytes for Use in Nonaqueous Redox Flow Batteries. Chem. Mater. 2019, 31, 4353–4363. [Google Scholar] [CrossRef]
- Kaur, A.P.; Casselman, M.D.; Elliott, C.F.; Parkin, S.R.; Risko, C.; Odom, S.A. Overcharge protection of lithium-ion batteries above 4 V with a perfluorinated phenothiazine derivative. J. Mater. Chem. A 2016, 4, 5410–5414. [Google Scholar] [CrossRef]
- Milshtein, J.D.; Kaur, A.P.; Casselman, M.D.; Kowalski, J.A.; Modekrutti, S.; Zhang, P.L.; Harsha Attanayake, N.; Elliott, C.F.; Parkin, S.R.; Risko, C.; et al. High current density, long duration cycling of soluble organic active species for non-aqueous redox flow batteries. Energy Environ. Sci. 2016, 9, 3531–3543. [Google Scholar] [CrossRef]
- Ergun, S.; Casselman, M.D.; Kaur, A.P.; Attanayake, N.H.; Parkin, S.R.; Odom, S.A. Improved synthesis of N -ethyl-3,7-bis(trifluoromethyl)phenothiazine. N. J. Chem. 2020, 44, 11349–11355. [Google Scholar] [CrossRef]
- Kowalski, J.A.; Casselman, M.D.; Kaur, A.P.; Milshtein, J.D.; Elliott, C.F.; Modekrutti, S.; Attanayake, N.H.; Zhang, N.; Parkin, S.R.; Risko, C.; et al. A stable two-electron-donating phenothiazine for application in nonaqueous redox flow batteries. J. Mater. Chem. A 2017, 5, 24371–24379. [Google Scholar] [CrossRef]
- Chai, J.; Lashgari, A.; Wang, X.; Williams, C.K.; Jiang, J. All-PEGylated redox-active metal-free organic molecules in non-aqueous redox flow battery. J. Mater. Chem. A 2020, 8, 15715–15724. [Google Scholar] [CrossRef]
- Attanayake, N.H.; Liang, Z.; Wang, Y.; Kaur, A.P.; Parkin, S.R.; Mobley, J.K.; Ewoldt, R.H.; Landon, J.; Odom, S.A. Dual function organic active materials for nonaqueous redox flow batteries. Mater. Adv. 2021, 2, 1390–1401. [Google Scholar] [CrossRef]
- Romadina, E.I.; Komarov, D.S.; Stevenson, K.J.; Troshin, P.A. New phenazine based anolyte material for high voltage organic redox flow batteries. Chem. Commun. 2021, 57, 2986–2989. [Google Scholar] [CrossRef]
- Zhang, C.; Niu, Z.; Ding, Y.; Zhang, L.; Zhou, Y.; Guo, X.; Zhang, X.; Zhao, Y.; Yu, G. Highly Concentrated Phthalimide-Based Anolytes for Organic Redox Flow Batteries with Enhanced Reversibility. Chem 2018, 4, 2814–2825. [Google Scholar] [CrossRef]
- Zhang, C.; Qian, Y.; Ding, Y.; Zhang, L.; Guo, X.; Zhao, Y.; Yu, G. Biredox Eutectic Electrolytes Derived from Organic Redox-Active Molecules: High-Energy Storage Systems. Angew. Chem. Int. Ed. Engl. 2019, 58, 7045–7050. [Google Scholar] [CrossRef] [PubMed]
- Biso, M.; Mastragostino, M.; Montanino, M.; Passerini, S.; Soavi, F. Electropolymerization of poly(3-methylthiophene) in pyrrolidinium-based ionic liquids for hybrid supercapacitors. Electrochim. Acta 2008, 53, 7967–7971. [Google Scholar] [CrossRef]
- Xing, X.; Liu, Q.; Wang, B.; Lemmon, J.P.; Xu, W.Q. A low potential solvent-miscible 3-methylbenzophenone anolyte material for high voltage and energy density all-organic flow battery. J. Power Sources 2020, 445, 227330. [Google Scholar] [CrossRef]
- Montoto, E.C.; Nagarjuna, G.; Moore, J.S.; Rodríguez-López, J. Redox Active Polymers for Non-Aqueous Redox Flow Batteries: Validation of the Size-Exclusion Approach. J. Electrochem. Soc. 2017, 164, A1688–A1694. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, S.; Zhu, Y.; Qian, Y.; Niu, Z.; Ye, J.; Zhao, Y.; Zhang, X. Pyridyl group design in viologens for anolyte materials in organic redox flow batteries. RSC Adv. 2018, 8, 18762–18770. [Google Scholar] [CrossRef]
- Chai, J.; Lashgari, A.; Cao, Z.; Williams, C.K.; Wang, X.; Dong, J.; Jiang, J.J. PEGylation-Enabled Extended Cyclability of a Non-aqueous Redox Flow Battery. ACS Appl. Mater. Interfaces 2020, 12, 15262–15270. [Google Scholar] [CrossRef]
- Antoni, P.W.; Golz, C.; Hansmann, M.M. Organic Four-Electron Redox Systems Based on Bipyridine and Phenanthroline Carbene Architectures. Angew. Chem. Int. Ed. Engl. 2022, 61, e202203064. [Google Scholar] [CrossRef]
- Makarova, M.V.; Akkuratov, A.V.; Sideltsev, M.E.; Stevenson, K.J.; Romadina, E.I. Novel Ethylene Glycol Substituted Benzoxadiazole and Benzothiadiazole as Anolytes for Nonaqueous Organic Redox Flow Batteries. ChemElectroChem 2022, 9, e202200483. [Google Scholar] [CrossRef]
- Pianowski, Z.L. Recent Implementations of Molecular Photoswitches into Smart Materials and Biological Systems. Chem. Eur. J. 2019, 25, 5128–5144. [Google Scholar] [CrossRef]
- Li, M.; Case, J.; Minteer, S.D. Bipolar Redox-Active Molecules in Non-Aqueous Organic Redox Flow Batteries: Status and Challenges. ChemElectroChem 2021, 8, 1215–1232. [Google Scholar] [CrossRef]
- Hendriks, K.H.; Sevov, C.S.; Cook, M.E.; Sanford, M.S. Multielectron Cycling of a Low-Potential Anolyte in Alkali Metal Electrolytes for Nonaqueous Redox Flow Batteries. ACS Energy Lett. 2017, 2, 2430–2435. [Google Scholar] [CrossRef]
- Li, M.; Agarwal, G.; Shkrob, I.A.; VanderLinden, R.T.; Case, J.; Prater, M.; Rhodes, Z.; Assary, R.S.; Minteer, S.D. Critical role of structural order in bipolar redox-active molecules for organic redox flow batteries. J. Mater. Chem. A 2021, 9, 23563–23573. [Google Scholar] [CrossRef]
- Meister, P.; Jia, H.; Li, J.; Kloepsch, R.; Winter, M.; Placke, T. Best Practice: Performance and Cost Evaluation of Lithium Ion Battery Active Materials with Special Emphasis on Energy Efficiency. Chem. Mater. 2016, 28, 7203–7217. [Google Scholar] [CrossRef]
- Herse, C.; Bas, D.; Krebs, F.C.; Bürgi, T.; Weber, J.; Wesolowski, T.; Laursen, B.W.; Lacour, J. A highly configurationally stable [4]heterohelicenium cation. Angew. Chem. Int. Ed. Engl. 2003, 42, 3162–3166. [Google Scholar] [CrossRef]
- Esan, O.C.; Shi, X.; Pan, Z.; Huo, X.; An, L.; Zhao, T.S. Modeling and Simulation of Flow Batteries. Adv. Energy Mater. 2020, 10, 2000758. [Google Scholar] [CrossRef]
- Langner, J.; Melke, J.; Ehrenberg, H.; Roth, C. Determination of Overpotentials in All Vanadium Redox Flow Batteries. ECS Trans. 2014, 58, 1–7. [Google Scholar] [CrossRef]
- Ventosa, E.; Skoumal, M.; Vázquez, F.J.; Flox, C.; Morante, J.R. Operando studies of all-vanadium flow batteries: Easy-to-make reference electrode based on silver–silver sulfate. J. Power Sources 2014, 271, 556–560. [Google Scholar] [CrossRef]
- Cecchetti, M.; Casalegno, A.; Zago, M. Local potential measurement through reference electrodes in vanadium redox flow batteries: Evaluation of overpotentials and electrolytes imbalance. J. Power Sources 2018, 400, 218–224. [Google Scholar] [CrossRef]
- Huang, Q.; Li, B.; Song, C.; Jiang, Z.; Platt, A.; Fatih, K.; Bock, C.; Jang, D.; Reed, D. In Situ Reliability Investigation of All-Vanadium Redox Flow Batteries by a Stable Reference Electrode. J. Electrochem. Soc. 2020, 167, 160541. [Google Scholar] [CrossRef]
- Amini, K.; Pritzker, M.D. In situ polarization study of zinc–cerium redox flow batteries. J. Power Sources 2020, 471, 228463. [Google Scholar] [CrossRef]
- Duan, Z.; Qu, Z.; Ren, Q.; Zhang, J. Review of Bipolar Plate in Redox Flow Batteries: Materials, Structures, and Manufacturing. Electrochem. Energy Rev. 2021, 4, 718–756. [Google Scholar] [CrossRef]
- Ressel, S.; Laube, A.; Fischer, S.; Chica, A.; Flower, T.; Struckmann, T. Performance of a vanadium redox flow battery with tubular cell design. J. Power Sources 2017, 355, 199–205. [Google Scholar] [CrossRef]
- Gurieff, N.; Keogh, D.F.; Baldry, M.; Timchenko, V.; Green, D.; Koskinen, I.; Menictas, C. Mass Transport Optimization for Redox Flow Battery Design. Appl. Sci. 2020, 10, 2801. [Google Scholar] [CrossRef]
- Percin, K.; Rommerskirchen, A.; Sengpiel, R.; Gendel, Y.; Wessling, M. 3D-printed conductive static mixers enable all-vanadium redox flow battery using slurry electrodes. J. Power Sources 2018, 379, 228–233. [Google Scholar] [CrossRef]
- Ye, R.; Henkensmeier, D.; Yoon, S.J.; Huang, Z.; Kim, D.K.; Chang, Z.; Kim, S.; Chen, R. Redox Flow Batteries for Energy Storage: A Technology Review. J. Electrochem. Energy Convers. Storage 2018, 15. [Google Scholar] [CrossRef]
- Arenas, L.F.; de León, C.P.; Walsh, F.C. Mass transport and active area of porous Pt/Ti electrodes for the Zn-Ce redox flow battery determined from limiting current measurements. Electrochim. Acta 2016, 221, 154–166. [Google Scholar] [CrossRef]
- Cervantes-Alcalá, R.; Miranda-Hernández, M. Flow distribution and mass transport analysis in cell geometries for redox flow batteries through computational fluid dynamics. J. Appl. Electrochem. 2018, 48, 1243–1254. [Google Scholar] [CrossRef]
- Kumar, S.; Jayanti, S. Effect of flow field on the performance of an all-vanadium redox flow battery. J. Power Sources 2016, 307, 782–787. [Google Scholar] [CrossRef]
- Houser, J.; Pezeshki, A.; Clement, J.T.; Aaron, D.; Mench, M.M. Architecture for improved mass transport and system performance in redox flow batteries. J. Power Sources 2017, 351, 96–105. [Google Scholar] [CrossRef]
- Agar, E.; Dennison, C.R.; Knehr, K.W.; Kumbur, E.C. Identification of performance limiting electrode using asymmetric cell configuration in vanadium redox flow batteries. J. Power Sources 2013, 225, 89–94. [Google Scholar] [CrossRef]
- Aguiló-Aguayo, N.; Drozdzik, T.; Bechtold, T. The role of electrode orientation to enhance mass transport in redox flow batteries. Electrochem. Commun. 2020, 111, 106650. [Google Scholar] [CrossRef]
- Tang, A.; Bao, J.; Skyllas-Kazacos, M. Studies on pressure losses and flow rate optimization in vanadium redox flow battery. J. Power Sources 2014, 248, 154–162. [Google Scholar] [CrossRef]
- Zhou, X.L.; Zhao, T.S.; An, L.; Zeng, Y.K.; Wei, L. Critical transport issues for improving the performance of aqueous redox flow batteries. J. Power Sources 2017, 339, 1–12. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, Q.; Lv, Y.; Li, Y.; Zhou, X. Binder-free carbon nano-network wrapped carbon felt with optimized heteroatom doping for vanadium redox flow batteries. J. Mater. Chem. A 2019, 7, 25132–25141. [Google Scholar] [CrossRef]
- Cecchetti, M.; Messaggi, M.; Donazzi, A.; Facibeni, A.; Russo, V.; Casari, C.S.; Bassi, A.L.; Casalegno, A.; Zago, M. A combined morphological and electrochemical characterization of carbon electrodes in vanadium redox flow batteries: Insights into positive and negative electrode performance. Electrochim. Acta 2020, 329, 135143. [Google Scholar] [CrossRef]
- Goulet, M.-A.; Habisch, A.; Kjeang, E. In Situ Enhancement of Flow-through Porous Electrodes with Carbon Nanotubes via Flowing Deposition. Electrochim. Acta 2016, 206, 36–44. [Google Scholar] [CrossRef]
- Dennison, C.R.; Agar, E.; Akuzum, B.; Kumbur, E.C. Enhancing Mass Transport in Redox Flow Batteries by Tailoring Flow Field and Electrode Design. J. Electrochem. Soc. 2016, 163, A5163–A5169. [Google Scholar] [CrossRef]
- Friedrich, J.M.; Ponce-de-León, C.; Reade, G.W.; Walsh, F.C. Reticulated vitreous carbon as an electrode material. J. Electroanal. Chem. 2004, 561, 203–217. [Google Scholar] [CrossRef]
- Crothers, A.R.; Darling, R.M.; Kushner, D.I.; Perry, M.L.; Weber, A.Z. Theory of Multicomponent Phenomena in Cation-Exchange Membranes: Part III. Transport in Vanadium Redox-Flow-Battery Separators. J. Electrochem. Soc. 2020, 167, 13549. [Google Scholar] [CrossRef]
- Darling, R.; Gallagher, K.; Xie, W.; Su, L.; Brushett, F. Transport Property Requirements for Flow Battery Separators. J. Electrochem. Soc. 2016, 163, A5029–A5040. [Google Scholar] [CrossRef]
- You, D.; Zhang, H.; Sun, C.; Ma, X. Simulation of the self-discharge process in vanadium redox flow battery. J. Power Sources 2011, 196, 1578–1585. [Google Scholar] [CrossRef]
- Schwenzer, B.; Zhang, J.; Kim, S.; Li, L.; Liu, J.; Yang, Z. Membrane development for vanadium redox flow batteries. ChemSusChem 2011, 4, 1388–1406. [Google Scholar] [CrossRef] [PubMed]
- Gubler, L. Membranes and separators for redox flow batteries. Curr. Opin. Electrochem. 2019, 18, 31–36. [Google Scholar] [CrossRef]
- Perry, M.L.; Saraidaridis, J.D.; Darling, R.M. Crossover mitigation strategies for redox-flow batteries. Curr. Opin. Electrochem. 2020, 21, 311–318. [Google Scholar] [CrossRef]
- Takechi, K.; Kato, Y.; Hase, Y. A highly concentrated catholyte based on a solvate ionic liquid for rechargeable flow batteries. Adv. Mater. 2015, 27, 2501–2506. [Google Scholar] [CrossRef]
- Bamgbopa, M.O.; Shao-Horn, Y.; Hashaikeh, R.; Almheiri, S. Cyclable membraneless redox flow batteries based on immiscible liquid electrolytes: Demonstration with all-iron redox chemistry. Electrochim. Acta 2018, 267, 41–50. [Google Scholar] [CrossRef]
- Yao, Y.; Lei, J.; Shi, Y.; Ai, F.; Lu, Y.-C. Assessment methods and performance metrics for redox flow batteries. Nat. Energy 2021, 6, 582–588. [Google Scholar] [CrossRef]
- Wang, H.; Sayed, S.Y.; Luber, E.J.; Olsen, B.C.; Shirurkar, S.M.; Venkatakrishnan, S.; Tefashe, U.M.; Farquhar, A.K.; Smotkin, E.S.; McCreery, R.L.; et al. Redox Flow Batteries: How to Determine Electrochemical Kinetic Parameters. ACS Nano 2020, 14, 2575–2584. [Google Scholar] [CrossRef]
- Li, M.; Odom, S.A.; Pancoast, A.R.; Robertson, L.A.; Vaid, T.P.; Agarwal, G.; Doan, H.A.; Wang, Y.; Suduwella, T.M.; Bheemireddy, S.R.; et al. Experimental Protocols for Studying Organic Non-aqueous Redox Flow Batteries. ACS Energy Lett. 2021, 6, 3932–3943. [Google Scholar] [CrossRef]
- Streeter, I.; Wildgoose, G.G.; Shao, L.; Compton, R.G. Cyclic voltammetry on electrode surfaces covered with porous layers: An analysis of electron transfer kinetics at single-walled carbon nanotube modified electrodes. Sens. Actuators B Chem. 2008, 133, 462–466. [Google Scholar] [CrossRef]
- Tichter, T.; Schneider, J.; Andrae, D.; Gebhard, M.; Roth, C. Universal Algorithm for Simulating and Evaluating Cyclic Voltammetry at Macroporous Electrodes by Considering Random Arrays of Microelectrodes. Chemphyschem 2020, 21, 428–441. [Google Scholar] [CrossRef] [PubMed]
- Tichter, T.; Andrae, D.; Mayer, J.; Schneider, J.; Gebhard, M.; Roth, C. Theory of cyclic voltammetry in random arrays of cylindrical microelectrodes applied to carbon felt electrodes for vanadium redox flow batteries. Phys. Chem. Chem. Phys. 2019, 21, 9061–9068. [Google Scholar] [CrossRef] [PubMed]
- Yin, C.; Gao, Y.; Guo, S.; Tang, H. A coupled three dimensional model of vanadium redox flow battery for flow field designs. Energy 2014, 74, 886–895. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, H.; Sun, C.; Zou, Y.; Zhang, T. An optimal strategy of electrolyte flow rate for vanadium redox flow battery. J. Power Sources 2012, 203, 153–158. [Google Scholar] [CrossRef]
- Liang, Z.; Attanayake, N.H.; Greco, K.V.; Neyhouse, B.J.; Barton, J.L.; Kaur, A.P.; Eubanks, W.L.; Brushett, F.R.; Landon, J.; Odom, S.A. Comparison of Separators vs Membranes in Nonaqueous Redox Flow Battery Electrolytes Containing Small Molecule Active Materials. ACS Appl. Energy Mater. 2021, 4, 5443–5451. [Google Scholar] [CrossRef]
- Machado, C.A.; Brown, G.O.; Yang, R.; Hopkins, T.E.; Pribyl, J.G.; Epps, T.H. Redox Flow Battery Membranes: Improving Battery Performance by Leveraging Structure–Property Relationships. ACS Energy Lett. 2021, 6, 158–176. [Google Scholar] [CrossRef]
- Yuan, J.; Pan, Z.-Z.; Jin, Y.; Qiu, Q.; Zhang, C.; Zhao, Y.; Li, Y. Membranes in non-aqueous redox flow battery: A review. J. Power Sources 2021, 500, 229983. [Google Scholar] [CrossRef]
- Yuan, J.; Zhang, C.; Zhen, Y.; Zhao, Y.; Li, Y. Enhancing the performance of an all-organic non-aqueous redox flow battery. J. Power Sources 2019, 443, 227283. [Google Scholar] [CrossRef]
- Zhao, Y.; Yuan, Z.; Lu, W.; Li, X.; Zhang, H. The porous membrane with tunable performance for vanadium flow battery: The effect of charge. J. Power Sources 2017, 342, 327–334. [Google Scholar] [CrossRef]
- Barton, J.L.; Milshtein, J.D.; Hinricher, J.J.; Brushett, F.R. Quantifying the impact of viscosity on mass-transfer coefficients in redox flow batteries. J. Power Sources 2018, 399, 133–143. [Google Scholar] [CrossRef]
- Barton, J.L.; Milshtein, J.D.; Brushett, F.R. Impact of Electrolyte Viscosity on Redox Flow Battery Performance. Meet. Abstr. 2017, MA2017-02, 560. [Google Scholar] [CrossRef]
- Song, Y.; Li, X.; Yan, C.; Tang, A. Unraveling the viscosity impact on volumetric transfer in redox flow batteries. J. Power Sources 2020, 456, 228004. [Google Scholar] [CrossRef]
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 1905, 322, 549–560. [Google Scholar] [CrossRef]
- Von Smoluchowski, M. Zur kinetischen Theorie der Brownschen Molekularbewegung und der Suspensionen. Ann. Phys. 1906, 326, 756–780. [Google Scholar] [CrossRef]
- Zhang, J.; Corman, R.E.; Schuh, J.K.; Ewoldt, R.H.; Shkrob, I.A.; Zhang, L. Solution Properties and Practical Limits of Concentrated Electrolytes for Nonaqueous Redox Flow Batteries. J. Phys. Chem. C 2018, 122, 8159–8172. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).