Abstract
Lithium-ion (Li-ion) batteries with Ni-based cathodes are leading storage technology in the fields of electric vehicles and power-grid applications. NCA (LiNiCoAlO2) batteries are known for their troublesome degradation tendencies, and this susceptibility to degradation raises questions regarding the safety of their usage. Hence, it is of vital importance to analyse the degradation of NCA batteries via methods which are applicable to onboard systems, so that the changes in the battery’s state of health can be addressed accordingly. For this purpose, it is crucial to study batteries stressed by various conditions which might induce degradation of different origins or magnitudes. Methods such as electrochemical impedance spectroscopy (EIS), galvanostatic intermittent titration technique (GITT), and incremental capacity analysis (ICA) have been used in battery research for years, however, there is a lack of published studies which would analyse the degradation of NCA batteries by simultaneous usage of these methods, which is essential for a comprehensive and confirmatory understanding of battery degradation. This study intends to fill this research gap by analysing the degradation of NCA batteries via simultaneous usage of EIS, GITT, and ICA methods for common stress-inducing operating conditions (over-charge, over-discharge, and high-current charging).
1. Introduction
Lithium-ion batteries have garnered a great deal of attention as an integral component of energy storage systems for consumer electronics, electric vehicles, power grids, and solar, wind, and geothermal power plants [1,2,3,4]. In 2019, the European Commission identified batteries as a strategic value chain [5]. For transport and power grid applications, Ni-based cathode materials are widely considered to be the most promising, due to their high specific capacity and high discharge voltage [6,7,8]. Another advantage of Ni-based (mainly Ni-rich) batteries is the reduction of used cobalt, which is expensive and has a controversial and unstable supply chain [9]. NMC (LiNiMnCoO2) and NCA (LiNiCoAlO2) batteries are already dominating in electric vehicles and plug-in hybrid vehicles, while they are being manufactured by several “Battery giants”, such as CATL, Samsung SDI, and Panasonic [10,11,12].
Aside from their obvious advantages, NCA-based batteries are prone to degradation, which leads to capacity and power fade upon cycling. Various usage protocols can lead to various sources of degradation, making NCA batteries overly sensitive to undesirable operating conditions [6,7]. Because of that, it is necessary to understand and monitor their degradation, so it can be addressed accordingly by battery management system (BMS) protocols, in order to further improve the usage of NCA batteries [13,14,15]. This degradation can be elevated by various stress conditions, such as over-charging, over-discharging, high-current charging (or fast-charging), and operating outside of the recommended temperature window [16,17]. Aside from post mortem analysis, it is equally important to study degradation and its footprints via methods of non-destructive electrochemical analysis, to learn about the behaviour of NCA-based batteries under various stress conditions. Techniques such as electrochemical impedance spectroscopy (EIS), incremental capacity analysis (ICA), and galvanostatic intermittent titration technique (GITT) are suitable methods for the non-destructive on-board analysis of ongoing battery degradation, implementable in advanced BMSs [18,19,20,21,22]. These techniques are also important for State of Health (SoH) analysis of batteries prior to their possible secondary utilization (second-life applications) [23].
In the area of electrochemical characterization and analysis of NCA batteries, many noteworthy studies have been published. In 2018, Cabañero et al. [24] demonstrated the applicability of the GITT for the analysis of Li+ diffusion of commercial batteries, including NCA. In 2021, Su et al. [25] used GITT-like measurements to study the effects of a wide range of conditions such as various charge/discharge currents, cut-off voltages, and ambient temperatures. In 2020, Sebastian et al. [26] compared GITT and EIS for a study of the impact of fast-charging protocols on the battery’s SoH and performance. In 2016, Devie and Dubarry [27] demonstrated simulation-based ICA for the first time for the analysis of footprints of degradation modes for NCA batteries, and in 2020, Zhang [28] used this technique together with EIS, to study the influence of high-current charging. Over-charge conditions have been studied by EIS by Kong et al. [29] and Togasaki et al. [30]. SoH for both over-charge and over-discharge scenarios was analysed by EIS by Li et al. [31]. The influence of depth of discharge (DoD) on the degradation of NCA batteries was studied by Preger et al. [32] using cyclic tests, by Watanabe et al. [33] by EIS, and by Pastor-Fernández et al. [34] by EIS and ICA. There are other notable studies on NCA batteries that used the EIS [35,36], GITT [37,38], or ICA [39,40] methods. Each of these techniques provides a distinct approach to battery analysis, providing a unique set of information about the battery’s condition, yet the singular use of one of these methods does not provide an extensive or confirmatory degradation analysis of the studied battery. The thesis of this work is to demonstrate that only simultaneous usage of these methods can lead to a comprehensive and more profound understanding of ongoing degradation processes. Moreover, this study shows that to avoid making assumptions arising from two-electrode measurements of full-cell batteries, and to determine the correct origin of degradation with confidence, several complementary methods of characterisation should be used. To the best of our knowledge, this is the first work that provides a comprehensive degradation analysis of full-cell NCA batteries (NCR18650B) via EIS, GITT, and ICA methods for various stress-inducing scenarios (over-charge, over-discharge, and high-current charging).
2. Degradation of NCA Cathode Material
As was mentioned above, Ni-based batteries, especially NCA batteries, are prone to degradation upon cycling, while various operating conditions can elevate these undesirable processes. Prior to the experiment, it is important to define common degradation scenarios, which may occur in NCA batteries. Dominant sources of NCA cathode degradation are cationic mixing, phase transition, residual lithium compounds, and microcracks [41,42]. Cationic mixing represents Ni2+/Li+ mixing, meaning that the Ni2+ can migrate and occupy the location of the Li+ in the layered NCA structure. The Ni2+ migration occurs during delithiation when Li+ leaves its position in the NCA structure, which can be easily occupied by similar-radii Ni2+, causing NCA lattice distortion, and preventing Li+ to return to its original position during subsequent lithiation [43]. This leads to an irreversible phase transition (formation of a NiO-like phase) accompanied by an evolution of Li2O and O2 [42,43,44]. This phase transition occurs especially on the cathode/electrolyte interface and in electrolyte-filled microcracks, where reactions between oxygen intermediates and electrolyte solvents take place. The NiO-like phase is not ionic conductive, hence its increase results in a decrease in charge-transfer [42]. Cationic mixing and NCA phase transition lead to capacity loss and a decrease in fast Li+ diffusion paths [42,43].
Residual lithium compounds refer mainly to the reversible Li2CO3 layer formed on the surface of the NCA cathode. Its formation occurs during storage [42] and discharging [26] conditions, according to Equations (1) and (2) [42,43,44,45]. This layer also forms as a result of a reaction between Li2O with CO2, following Equation (3) [46]. Its decomposition occurs when the cathode is being delithiated, thus during battery charging. This process is high-voltage [42] and high-current [26] sensitive, where along Li2CO3 decomposition occurs also gas evolution [41], following Equation (4) [42].
Volumetric changes in NCA cathodes caused by cyclic intercalation/deintercalation lead to mechanical stress and structural microcracking. Microcracking leads to a decrease in the active cathode material [42,43]. Moreover, these microcracks allow electrolytes to enter deeper into the bulk of the NCA cathode, resulting in an increase in reaction zones for parasitic reactions [47]. Watanabe et al. [33] demonstrated in their study that microcracking is not assignable to operation in a specific voltage region which corresponds to either low or high SOC, but that microcracking elevates with wide regions of DOD, especially for DOD 100%.
3. Experimental
For the purposes of the experiments, commercially successful NCR 18650B batteries by Panasonic were chosen. These LiNiCoAlO2/Graphite batteries have a nominal capacity of 3350 mAh. Other electrical parameters of these batteries are presented in Table 1. Prior to all experiments, fresh batteries were fully charged and fully discharged by a current corresponding to 0.5 C (repeated 5 times). One hour of relaxation was allowed between these initial charge and discharge procedures. This procedure allowed batteries to undergo additional initialisation (aside from battery formation that is being performed by manufacturers). Aside from initialisation, it also allowed us to inspect battery quality and cell-to-cell variation, and to discard batch-deviating cells, to ensure the representativeness of the results. All measurements were performed by potentiostat Gamry Interface 5000P. Measurements were performed in a faradaic cage and under the ambient temperature of the laboratory.

Table 1.
Specifications of NCR 18650B battery by Panasonic.
In these experiments, three different scenarios of cyclic degradation were studied, labelled as “High-Current Charging Scenario”, “Over-Charge Scenario”, and “Under-Charge Scenario”. The fourth set of measurements was carried out by the maximum allowed charging-discharging parameters of studied batteries for comparison purposes, labelled as Reference Scenario. The High-Current Charging Scenario was based on charging with the above-recommended current, corresponding to 1 C. The Over-Charge Scenario charges the battery up to 4.3 V, instead of the recommended 4.2 V. The Under-Charge Scenario discharges the battery to 2.3 V instead of 2.5 V. The Reference Scenario maintains the recommended voltage window, charges the battery with the maximum allowed 0.7 C, and discharges with 1 C. Between all degradation cycles, 10 min of relaxation was allowed. After each 7th degradation cycle, the battery was charged by 0.7 C and relaxed for 1 h, followed by EIS. After each 2nd EIS, GITT discharging took place (after each 14th degradation cycle). EIS was performed between and GITT discharging by C/20, ton = 10 min, and trest = 10 min. Full experiment protocols are presented in Table 2.

Table 2.
Experiment protocols and settings of testing procedures for individual stress scenarios.
4. Results and Discussion
4.1. Cyclic Degradation
Figure 1 shows capacity as a function of an increasing number of degradation cycles. Stabilisation cycles and GITT measurements are not displayed in this plot, to allow a clearer representation of degradation. For all studied scenarios, the same sequence of EIS and GITT measurements was performed, therefore the same effect of such measurements on the battery degradation is assumed, which allows the omission of this influence from the analysis.
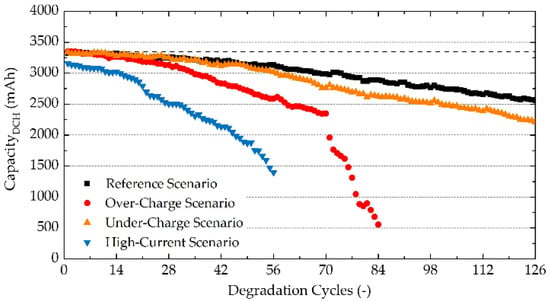
Figure 1.
Discharge capacity of the studied NCA 18650B batteries for an increasing number of degradation cycles.
Generally, three phases of degradation are recognised across the literature when analysing capacity fade: sudden capacity drop, linear capacity fade, and rapid capacity fade [32]. A sudden capacity drop represents a decrease in lithium inventory during the initial formation of the SEI layer. Nonetheless, these commercial cells undergo SEI formation in the factory and initialisation at the beginning of each experiment, which results in already finished SEI formation, hence sudden capacity drop is not present in the presented data.
For the Reference Scenario, only a slow linear decline of capacity is observed. This decrease cannot be linked to the singular source of degradation based solely on the capacity fade. It can have several origins, such as the reduction of the electrolyte, SEI thickening, or degradation of cathode active material [30]. All batteries were being discharged to DoD 100%, while it is known that NCA batteries are sensitive to high DoD, therefore this can be considered as an explanation for decreasing capacity in the Reference Scenario measurements [32,33,34]. It is also noteworthy to mention that charging with the maximum allowed current might have a negative effect on the battery’s SoH as well. The Under-Charge Scenario shows a high capacity overlap with the Reference Scenario for the first ~50 cycles, followed by slightly lower capacity values, but still resembling the same linear trend. This higher degradation is induced by higher DoD. For the Over-Charge Scenario, capacity fade occurs in two stages. The first stage consists of a more profound linear capacity decrease when compared with the Reference Scenario. The second stage occurs after the 70th degradation cycle, where a rapid capacity fade is observed, corresponding to the failing of the battery [32]. This second stage rapid capacity fade leading to battery failure was observed only for the Over-Charge Scenario. Consequently, charging to 4.3 V can be considered as a cause of this second-stage degradation. The High-Current Charging Scenario has a lower capacity from the first degradation cycle (~180 mAh less), which is in agreement with Peukert’s law [48]. It can be seen that moderate capacity fade turns into a massive quasi-linear capacity loss after only a few degradation cycles (around the 15th cycle). It is clear that high-current charging resulted in severe degradation, which is in accordance with the high-current sensitivity of NCA batteries [26].
4.2. Electrochemical Impedance Spectroscopy (EIS)
The EIS is an advantageous method for the comprehensive analysis of electrochemical systems and their behaviour. This technique was thoroughly discussed in a recent review by Wang et al. [49] with a focus on measurements, modelling, and its onboard implementation. Various parts of the EIS spectra represent different components and events in the battery cell. To distinguish individual features, analysis via an equivalent electric circuit is used (Figure 2). This circuit is commonly used for the analysis of NCA batteries, its parameters can be ascribed to physical features, and it provides a satisfactory fit with negligible errors [3,34]. The circuit consists of a serial inductor (L0), serial resistor (ROHM), in series connected to two serial-parallel combinations of a resistor and constant phase element (RSEIIICPESEI and RCHTIICPECHT), and Warburg element (W). The model used enables us to fit, parametrise, and analyse EIS data consisting of induction tail for the high-frequency region (below x-axis region), two deformed semi-circles (for higher and lower frequency regions), diffusion tail for the low-frequency region, and of course, x-axis offset [31,50].
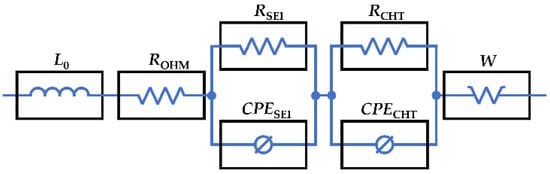
Figure 2.
The equivalent electric circuit used for EIS data analysis in this study.
Ohmic Resistance (ROHM) represents the combined resistances of the current collectors, binders, electrolyte, and separator [14]. ROHM is used to model the corrosion of current collectors and changes in electrolyte composites due to side reactions. These processes result in conductivity loss (CL) [22,34].
Solid Electrolyte Interface Resistance (RSEI) describes the formation, growth, and decomposition of the surface film formed between the electrolyte and electrode [5,22,34]. Formation and thickening of the SEI layer lead to irreversible Li+ consumption, hence loss of lithium inventory (LLI) [26,34]. Degradation of electrodes (e.g., particle cracking) and electrolyte (e.g., electrolyte decomposition) may lead to SEI thickening, showing that LLI is interlinked with the loss of active materials (LAM) and CL [22,34,50].
Charge-Transfer Resistance (RCHT) represents the amount of intercalation and deintercalation reactions, where a charge-transfer decrease indicates a decrease in Li+ that is capable of being intercalated/deintercalated [22]. The increase in RCHT is caused by kinetic and electrochemical changes in surface films and electrodes and LLI [22,31,50]. The SEI layer negatively affects the charge-transfer, showing mutual connection and interaction between RCH and RSEI [34].
The Warburg coefficient (W) is associated with the diffusion of lithium ions [50]. This diffusion can be understood as a movement of charged and uncharged particles in order to balance the concentration gradient [22]. The Li+ diffusion is dependent on the effective diffusion path length, which is strongly related to morphological changes in active materials, and therefore, the Li+ diffusion decrease can be ascribed primarily to LAM [34]. The decrease in Li+ diffusion can have several root causes, such as graphite exfoliation, dissolution and deposition of transition metals, and structural disordering [22].
Inductance (L0) is often used to model the positive imaginary part of the impedance data. This segment is generally ascribed to the inductive behaviour of current collectors and measuring cables [22,51].
4.3. Resulting Nyquist Plots
Figure 3 shows the results of the EIS measurements plotted as Nyquist plots. For this representation, plots of significant importance were selected for comparison purposes. Black lines represent initial cycles. Green lines represent 56 cycles, which is decisive for the High-Current Charging Scenario since the last EIS measured for this scenario before the battery’s death was after 56 degradation cycles. Likewise, the blue line represents 84 cycles for the last EIS for the Over-Charge Scenario. Red lines represent measurements after 126 degradation cycles, which are the last EIS measurements recorded before experiment termination. From the visual analysis of these Nyquist plots, it can be seen that impedance development for the Reference Scenario (Figure 3a) and the Under-Charge Scenario (Figure 3c) show the same shifting pattern, while the charge-transfer semicircle develops at a slightly higher rate. On the contrary, the High-Current Charging Scenario (Figure 3b) and the Over-Charge Scenario (Figure 3d) led to a much faster increase in the second semicircle and higher x-axis offset, while from the comparison of the green 56 cycles plots it is clear that high-current charging led to a more severe increase in x-axis offset, pointing to the rapid increase in the battery’s serial resistance.
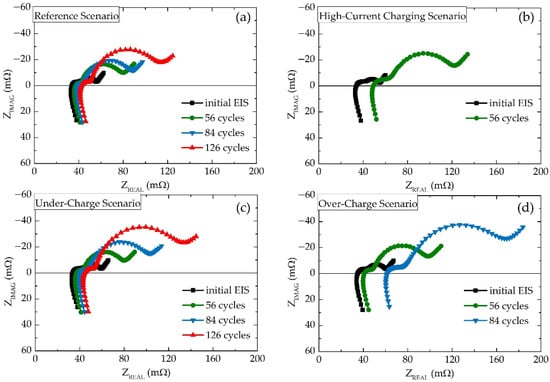
Figure 3.
Results of the EIS measurements represented as Nyquist plots for (a) Reference Scenario, (b) High-Current Charging Scenario, (c) Under-Charge Scenario, and (d) Over-Charge Scenario.
4.4. Equivalent Electric Circuit Fitting
The results of the fitting of the EIS data via the equivalent electric circuit are displayed in Figure 4. Data fitting was performed in Gamry Echem Analyst.
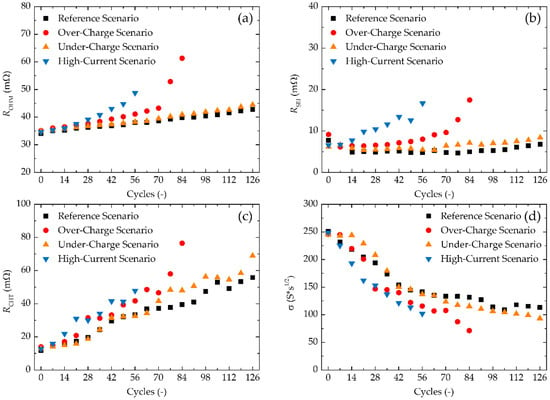
Figure 4.
Results of EIS data fitting via equivalent electric circuit for all four scenarios, where (a) represents values of modelled ROHM, (b) RSEI, (c) RCHT, and (d) Warburg coefficient.
Values of ROHM obtained from EIS data by equivalent circuit fitting are shown in Figure 4a. Values for the Under-Charge Scenario are in close to absolute overlap with the Reference Scenario, both having a minor increase of their ROHM values with an increasing cycle index. The values of ROHM for the Over-Charge Scenario are increasing at a slightly higher pace up to 70 cycles, pointing to a decrease in the battery’s conductivity. Greater change occurs from the 70th cycle onwards, where ROHM increases dramatically and almost doubles its value in just 14 cycles. Values of ROHM for the High-Current Charging Scenario are gradually increasing, which might be a footprint of high-current induced gas evolution, which leads to increased internal pressure and accelerated electrolyte depletion, resulting in increased ROHM, and therefore, in conductivity loss. This is due to the Li2CO3 layer typical for NCA cathodes. This reversible surface film is periodically formed during discharging and decomposed during charging, while high-current charging can lead to the generation of CO2 and O2 gasses [26].
Figure 4b shows values for fitted RSEI. An increase in RSEI for the Reference Scenario and the Under-Charge Scenario is close to non-existent, from which it is clear that the SEI layer remains stable throughout the measurements. For the Over-Charge Scenario, RSEI is stable up to the 49th cycle, moderately increasing up to the 70th cycle, and from the 70th cycle onwards increasing quite dramatically, pointing to substantial changes in the SEI layer. For the High-Current Charging Scenario, RSEI increases quasi-linearly right from the beginning of the experiment, from which it can be concluded that high-current has a continuous negative impact on the SEI layer.
TContrary to RSEI and ROHM, values of RCHT (Figure 4c) for the Reference Scenario and the Under-Charge Scenario increase quasi-linearly for the entire duration of the experiments, suggesting that a decrease in the charge-transfer and changes in the SEI layer are not directly interlinked. A probable explanation for increasing RCHT is microstructural and/or phase changes on one or both electrodes. Since EIS was performed in a two-electrode fashion, the influence of one or the other electrode cannot be distinguished from each other solely from impedance data. For the High-Current Charging Scenario, similar behaviour is observed, although the increase in RCHT is more rapid. The same is true for the Over-Charge Scenario up to its 70th cycle. From this point onwards, RCHT increases dramatically, following the same observation for ROHM and RSEI, from which it can be concluded that the dramatic decrease of charge-transfer from the 70th cycle onwards is closely connected with the SEI layer thickening and conductivity decrease. It was previously reported by Togasaki et al. [30] and Gilbert et al. [52] that NCA cathodes are sensitive to over-charging, which may lead to the dissolution of transition metals and their deposition on the anode/electrolyte interface. This results in a decrease in the number of utilizable intercalation/deintercalation reactions (due to LAM), and in the SEI thickening caused by transition metal deposition onto the anode/electrolyte interface. This explanation is in high accordance with our results.
Warburg coefficients obtained via EIS are shown in Figure 4d. Decreasing the Warburg coefficient has a high correlation with the decrease in charge-transfer for all four scenarios. This supports the claim mentioned above, that changes in active materials are present.
It is also important to note that ∆DoD was 100% for all discharging cycles. It is generally considered that ∆DoD greater than 70–80% has a negative effect predominantly on the cathode side. This leads to more pronounced intercalation gradient strains in the active materials, resulting in solvent co-intercalation and micro- and phase-changes in the NCA cathode material [22]. This phenomenon is in agreement with cyclically decreasing charge-transfer and diffusion observed in our EIS data analysis.
4.5. Galvanostatic Intermittent Titration Technique (GITT)
This method of analysis is generally used for the characterisation of active materials, which can be used to analyse the performance and ageing of Li-ion batteries [24]. The GITT enables the calculation of the chemical diffusion coefficient of lithium ions (DLi+) and the cell’s internal resistance (IR) [26,53]. For a graphite-based anode, the Daumas-Hérold model can be applied, allowing LiXC6 for 0 ≤ x ≤ 1 to be used instead of SOC [54,55]. The GITT is realised by a series of constant current pulses (Figure 5a), where the pulse is applied for a given time period (tpulse), alternated with the relaxation phase (trelax) [53]. The GITT quantifies the quasi-equilibrium OCV of the battery [56], so it is necessary to choose suitable current magnitude, tpulse and trelax, so the cell reaches quasi-equilibrium OCV (when dE/dt ~ 0 V/s) [24,53,57]. The voltage profile of each of these steps can be divided into the polarisation-resistance influence part (ΔEPOLAR) and the ohmic-resistance influence part (ΔEOHMIC) [26]. The ΔEPOLAR, also referred to as transient state potential (ΔEt), is integral for Li+ diffusion analysis (Figure 5b). The ΔEOHMIC enables obtaining the IR of the battery as a function of the Li+ concentration (Equation (5)):
where Ipulse represents the applied constant current during pulses and the i index of individual pulses [26,56]. IR analysis enables a study of interfacial contacts between components of the battery [26].
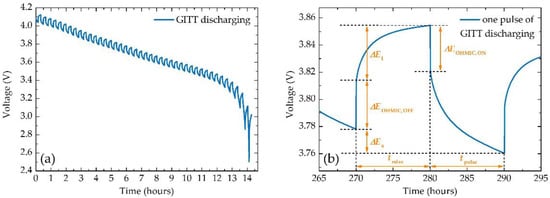
Figure 5.
(a) Voltage profile of GITT discharging of NCR18650B battery, and (b) close-up view of one GITT pulse with highlighted parameters.
To obtain DLi+ of studied active materials, it is necessary to know parameters such as diffusion length and electrode/electrolyte contact area [24,53,58]. Values of DLi+ are still to some degree estimated, since to calculate DLi+, some assumptions and approximations have to be made. For instance, particles have to be assumed one-dimensional and semi-infinite, the transport must follow Fick’s law, and DLi+ cannot vary throughout the measurement [53]. This leads to troublesome comparisons of DLi+ across the literature [24,56,58]. If these assumptions are made, required parameters are known, and condition t << L2/DLi+ is fulfilled, DLi+ can be calculated by Equation (6) [53],
where L represents characteristic diffusion length (L = Rs/3, where Rs represents a radius of spherical-like active material particles), t current pulse duration, ΔEs changes in the steady state-potential (the equilibrium voltage after the titration step) [24,53]. Another variation of this equation is Equation (7) [26,56,57].
where nm represents the number of Li+ moles (mol), Vm molar volume of the electrode (cm3 mol−1), and S represents the electrode/electrolyte interface area (cm2) [56,57]. Conveniently, when analysing battery degradation, it is not necessary to know the exact value of thediffusion coefficient but its change with cell degradation, for which purpose, solely GITT measurements are sufficient since GITT enables calculating the VR (voltage ratio) parameter, which is proportional to DLi+ [24]. This parameter is obtained via Equation (8) [24].
Despite the fact that full-cell analysis gives DLi+ of the entire cell and does not distinguish between its electrodes, according to Cabañero et al. [24], this distinguishing is still feasible. DLi+ of graphite-based anodes decreases with increasing anode lithiation [59], and that anode’s polarisation for low SOC overshadows the cathode’s influence, and on the contrary, for high SOC, the cathode’s polarisation is predominant [60]. To determine cathode- and anode-dominated regions, it is necessary to identify the peak of stage II (LiC12) of the LixC6 anode. The effect of the anode on the values of VR beyond the stage II peak is negligible due to graphite’s low and flat potential for stage II and stage I (high SOC). On the contrary, graphite’s high slope for stages V to III results in the anode’s dominancy for low SOC regions [24,31,54,56]. It is also suitable to mention the quasi-equilibrium open-circuit potential vs. Li/Li+ of the graphite anode as a function of lithiation with highlighted crystallographic phase changes of LixC6 (Figure 6) [31,54,56]. Based on the widely accepted Daumas-Hérold intercalation model [55] transitions between crystallographic phases can be ascribed to voltage plateaus of the equilibrium potential of LixC6. On the basis of the published studies concerning graphite anode and its phase transitions [54,55,56,61], the following look-up table was constructed (Table 3).
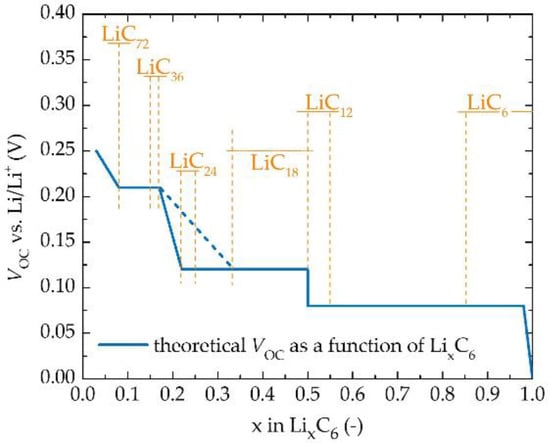
Figure 6.
VOC vs. Li/Li+ of the LixC6 (0 ≤ x ≤ 1) with highlighted crystallographic phases of LixC6 [31,54,56]. Adapted with permission from [22], Elsevier, 2011.

Table 3.
Look-up table of crystallographic phases and phase transitions of LixC6 for 0 ≤ x ≤ 1.
4.6. Results of Li+ Diffusion Analysis via GITT
Figure 7 shows VR parameters as a function of Li+ intercalation for all studied scenarios. As was discussed above, VR is proportional to DLi+, hence can be used for diffusion study, especially its change. There are five dominant local extremes which can be recognised in these plots, labelled as A–E. Cathode- and anode-dominated regions in terms of DLi+ study can be distinguished by identifying the stage II peak of the graphite electrode. For the equilibrium voltage of LixC6, the stage II peak is located at 0.50 ≤ x ≤ 0.55. From the initial GITT measurements, there is only one sharp peak in the mid-region of lithiation, with the centre at x = ~0.57. This peak is labelled as peak E. Considering the wide isolation of peak E also and the present cathode influence in the mid-region of lithiation, this peak can certainly be considered to be the stage II peak (LiC12 phase). Subsequently, peaks B and C and valleys A and D in the anode-dominant region can be studied. Valley A with its position at x = 0.08 ascribes LiC72 (Stage IV). This narrow region shows the lowest DLi+, since the d-spacing of graphite increases insignificantly during LiC72 formation, hence, it leads to hindered intercalation [56]. Peaks B and C are located at x = ~0.16 and x = ~0.22, which can be ascribed to LiC36 (Stage III) and LiC24 (Stage III/II), respectively. The phase transition from LiC72 to LiC36 is accompanied by a great increase in d-spacing, therefore DLi+ is markedly elevated (increase by ~2 × 10−4). On the contrary, the phase transition from LiC36 to LiC24 leads to a DLi+ decrease (by ~3.5 × 10−4). The reason for this decrease is a higher density of intercalated ions in the LiC24. When comparing DLi+ in a region limited by peaks C and E, a broad valley with its minimum in 0.33 ≤ x ≤ 0.36 is recognised, showing that there is not a simple direct phase transition between LiC24 and LiC12, hence it suggests the presence of another phase or coexisting phase. Referring to the work of Ohzuku et al. [62], the phase transition between LiC36 and LiC12 is accompanied by continuously varying the LiC18 phase. Contrary to this model, Allart et al. [55] in their study, did not find sufficient evidence for this phase, and they suggested that LiC24 and LiC12 coexist in the region for 0.25 ≤ x ≤ 0.50, and that phase transition occurs at different values of entropy. Park et al. [56] observed increasing DLi+ for the LiC24 → LiC12 transition. Based on the uncertain origin of valley D it was decided to leave this valley and the possible LiC18 phase from further analysis. As mentioned above, peak E was recognised as a footprint of the LiC12 phase. This peak has its maximum slightly shifted to higher values of x than it would be for LiC12 of Graphite half-cell (x = ~0.57 instead of 0.50 ≤ x ≤ 0.55). This shift is cathode-influenced since peak E lies in a superposition of both, cathode- and anode- influence regions [53].
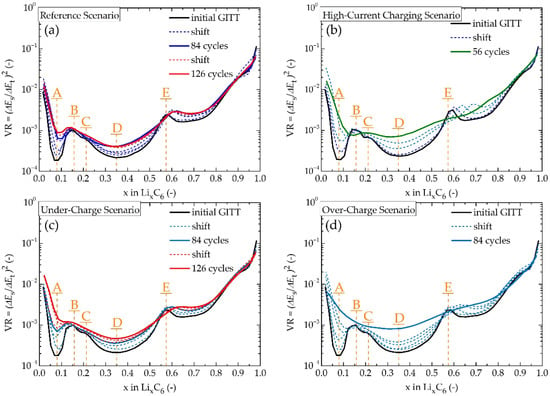
Figure 7.
VR parameters as a function of x in LixC6, where (a) refers to Reference Scenario, (b) High-Current Charging Scenario, (c) Under-Charge Scenario, and (d) Over-Charge Scenario.
In the anode-dominated region of VR, by far the most dominant change in local extreme magnitude is observed for valley A, which describes Stage IV—Phase LiC72. It is known that cyclic lithiation and delithiation of LiXC6 in the low lithiation region leads to the most severe cyclic induced structural damage of graphite electrode, primarily of its surface [61]. This phenomenon is caused by high local Li+ accumulation during the formation of LiC72, preliminarily in the surface regions of graphite’s bulk. This Li+ concentration gradient creates a high-stress disparity in the graphite’s lattice, resulting in the breaking of carbon-carbon bonds. This phenomenon gradually decreases with an increasing stage of lithiation, since more Li+ are being intercalated deeper into the electrode’s bulk, their distribution is higher across the graphite’s lattice, and therefore, stress disparity is much lower. Aside from changes in Li+ diffusion, microstructural changes in graphite lead to the cracking of the SEI layer, subsequently exposing graphite to further reactions with electrolytes, resulting in SEI thickening and Li+ consumption. Microstructural changes also lead to the formation of locally trapped Li, which cannot further participate in intercalation/deintercalation, hence it leads to a decrease in lithium inventory. As mentioned above, DLi+ decreases during LiC72 formation and subsequently increases during LiC36 formation. A decrease in the magnitude of valley A points to the decreasing influence of the LiC72 phase. This can be explained by increasing local microstructural changes in the crystallographic structure of graphite, which lead to a local increase of d-spacing for the phase of low lithiation, hence to higher DLi+. Values of the local minima of valley A for all scenarios are shown in Figure 8a. It can be seen that VR increases at the lowest rate for the Reference Scenario, although its value still quadruples in around 100 cycles. This shows that the negative influence of crystallographic phase LiC72 is being suppressed with an increasing number of cycles. The Under-Charge Scenario has only slightly higher values of the VRStage IV than the Reference Scenario, which can be assigned to more profound delithiation, which would lead to higher intercalation/deintercalation stress onto graphene layers. The VRStage IV of the High-Current Charging Scenario increases much more significantly than of the Reference Scenario, where its value quadruples in half the number of cycles. The first explanation which asks to be suggested is in high-current induced local accumulation of Li+ in the surface regions of the anode, leading to high-stress disparity and structural damage. However, for the Over-Charge Scenario, a similar VRStage IV behaviour is observed, where this local Li+ accumulation should not be an issue, therefore it might be necessary to search for another explanation, while several overlapping origins are probable.
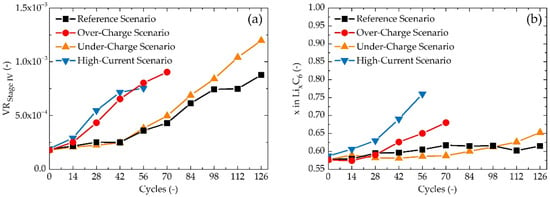
Figure 8.
(a) Analysis of Li+ diffusion for LiC72 stage (valley A) via VR parameter (b) shift of peak E.
Peaks B and C have been ascribed to the phases LiC36 and LiC24, respectively. These two peaks are easily distinguishable from each other for early cycles, but with an increasing number of cycles, the steep VR decrease between them begins to disappear, making peaks B and C appear as one deformed peak defined by local minima A and D and maximum B. This merging might be ascribed to an increase in direct transition between stages III and II [24]. Aside from that, peaks B and C remain in their position in regard to the x-axis, and their maximum value increases unimportantly. This is not the case only for the last GITT measurements for the High-Current Charging Scenario (56 cycles) and the Over-Charging Scenario (84 cycles), where these measurements were carried out on close-to-dead batteries, yielding unanalysable results. Peak E lies on the edge of anode- and cathode-dominant regions, making the analysis of the origin of its change quite difficult. Moreover, this peak is the only local maximum with a considerable shift in its position. Positions of the centres of peak E for an increasing number of cycles are shown in Figure 8b. The centres of peak E for the Reference Scenario and the Under-Charge Scenario shift towards higher values of x negligibly. This shift is more significant in the case of the Over-Charge Scenario, and even more profound for the High-Current Charging Scenario, suggesting an imbalance between anode-dominant and cathode-dominant regions, leaning towards cathode as a predominant influencer of the position of peak E for these two degradation scenarios.
4.7. Results of Internal Resistance Analysis via GITT
Contrary to VR, where the main origin of change is in Li+ concentration gradients, the main origin of IR change is in contact properties of battery components, thus these two parameters should be analysed separately. The low relation between these two parameters can also be seen in the comparison of the shape and magnitude of change, where VR contains several local extremes and the magnitude of change between the lowest and highest VR values (for initial measurement) is approx. 500-fold, compared to the U-shaped trend of IR with only a 2.5-fold value change. Figure 9 shows internal resistances as a function of SOC calculated via Ohm’s law from GITT measurements. Initial measurements show a quasi-linear decrease in IR from ~120 mΩ for SOC 0% to 50 ÷ 55 mΩ for SOC ~25%. For a region ~25% ≤ SOC ≤ ~95%, IR shows a highly stable plateau of 50 mΩ. Subsequently, IR increases for ~5 mΩ in ~95% ≤ SOC ≤ 100% region. The shape-permanence of the IR is evidence of the structural and thermodynamic stability of active materials and interfaces. An increase in overall IR without significant shape changes can be considered an indicator of decreasing State-Of-Health. The origin of the high values of the IR for SOC 0% is in the Li2CO3 layer, which is being gradually decomposed during charging, resulting in improved electric and ionic conductivity and greater interfacial reaction rate, thus the IR decrease in 0% ≤ SOC ≤ ~25% region [26].
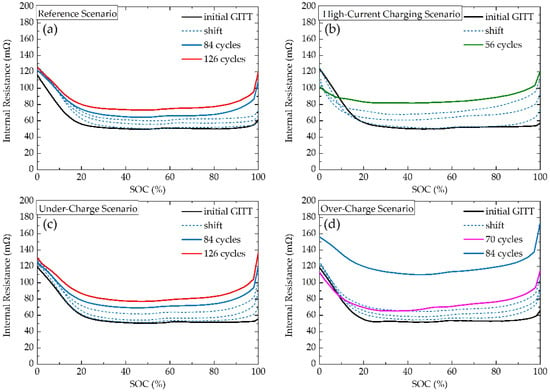
Figure 9.
Internal Resistance calculated from GITT measurements, where (a) refers to Reference Scenario, (b) High-Current Charging Scenario, (c) Under-Charge Scenario, and (d) Over-Charge Scenario.
IR of the Reference Scenario (Figure 9a) and the Under-Charge Scenario (Figure 9c) measurements yield almost the same values. The only noticeable difference is in the close-to-100% SOC region, where the Under-Charge Scenario shows slightly increasing values of IR in comparison to the Reference Scenario. The Over-Charge Scenario (Figure 9d) shows similar behaviour initially, followed by an approximately doubled increase of IR in the plateau region of SOC. This points to a severe decrease in the battery’s SOH between the 70th and 84th cycles, which correlates with a sharp capacity drop between these two cycles. The High-Current Charging Scenario (Figure 9b) shows, along with the more severe IR increase in the plateau region of SOC, a continuous drop also in IR values in the low SOC region. According to Sebastian et al. [26], this can be explained by the continuous decrease of Li2CO3 formation and decomposition, where high-current induced Li2CO3 decomposition is accompanied by CO2 and O2 generation, which leads to the increase in internal pressure, resulting in depletion of electrolyte and parasitic reactions, thus an overall IR increase.
4.8. Incremental Capacity Analysis (ICA)
The incremental capacity analysis is a non-destructive method for the characterisation of a battery’s SOH [40,63] through the identification and analysis of degradation modes at the electrode level [27,34,35,64]. To construct ICA, it is necessary to obtain a quasi-equilibrium voltage profile of the battery, where the effects of ohmic resistance and diffusion are minimised. Usually, this dataset is obtained by a very low current charge (or discharge), where any voltage alternations are suppressed. Alternatively, an envelope of the GITT data can be used for this purpose, since GITT measurements are also performed in a quasi-equilibrium fashion. From this dataset, the ICA curve is calculated by derivative equation fICA (Equation (9)) and plotted against the voltage evolution [63,64]:
where ∆Qn represents an increment of capacity and ∆V fixed voltage step. By this calculation, the two-phase transition associated with the different voltage plateaus results in a recognizable ICA peak [13]. Wide voltage plateaus lead to high increments of capacity, resulting in more pronounced peaks. Depending on the battery’s voltage profile, peaks with different locations and magnitudes are formed [16,64]. The ICA is vulnerable to a noise-caused error in these plateau regions, since these regions are subsequently differentiated, and noise is amplified [40,63,65]. It is often necessary to process the raw data by smoothening methods, for instance by Gaussian filter [63] or Savitzky-Golay filter [16].
The ICA study is realised by the identification of peaks which follow active material phase transformations [40]. In other words, the ICA peak changes are footprints of the structural changes of active materials and the formation of solid solutions over the battery’s lifetime [27,40,64]. Various changes in the peak position (shift) and magnitude (shape and area under the peak) with an increasing number of cycles provide a unique footprint for different degradation scenarios [13,27,40,64]. Degradation modes which can be studied by the ICA are loss of lithium inventory, loss of active materials, conductivity losses, and Li plating [39]. Loss of active material can be further divided by the electrode of origin (positive or negative) and by its occurrence during lithiation or delithiation into four modes: LAMliPE, LAMdePE, LAMliNE, and LAMdeNE [27]. Usage of the ICA for analysis of the degradation of full-cell batteries was pioneered by Dubarry et al. [27,66,67,68] at Hawai’i Natural Energy Institute (Honolulu, HI, USA). They have also developed an emulation tool ‘Alawa toolbox, which uses harvested data from various half-cell batteries to simulate the effect of degradation modes in full-cell batteries. In 2016, Devie and Dubarry in their study [27] analysed for the first-time, degradation mechanisms in NCA/graphite batteries by ICA and by computer simulations performed in ‘The Alawa toolbox. For NCR18650B batteries by Panasonic, up to seven ICA features can be recognised and labelled as in Figure 10 [27,40]. Individual degradation modes have their unique ICA footprints, where the shift of peak G towards higher voltages together with the disappearance of peak D is recognised as a footprint of LLI. The decrease in magnitudes of all features together with the disappearance of peak G is ascribed to LAMdePE and the decrease in magnitudes of all features together with not-disappearing peak G and magnitude of peak D decreasing at a lower rate as in LAMdePE is a footprint of LAMliPE. For the negative electrode, the shift of all features towards lower voltages together with the disappearance of peak A suggest LAMdeNE, and the shift of peak G towards higher voltages together with the decrease of peak D and separation of feature C from peak B describe LAMliNE [27,40].
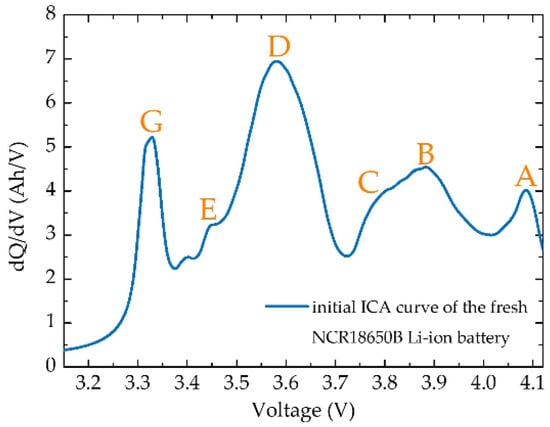
Figure 10.
ICA curve of the fresh NCR18650B battery with seven features recognised and labelled.
4.9. ICA Analysis—Results
The incremental capacity analysis of the studied batteries is shown in Figure 11. As mentioned above, up to seven features can be recognised for this type of battery. In this presented data, six features can be recognised with certainty. Peak F can be recognised only in the initial ICA of Under-Charge Scenario and Over-Charge Scenario measurements, while even in this case this peak disappears right after the initial measurements. The origin of this disappearance is in the quasi-equilibrium state of the voltage profile, which is being used for calculating ICA. Based on the work of Fly et al. [40] it can be assumed that this peak is preserved only for measurements using very low currents for obtaining the quasi-equilibrium voltage profile. For this reason, peak F is not being examined in further analysis.
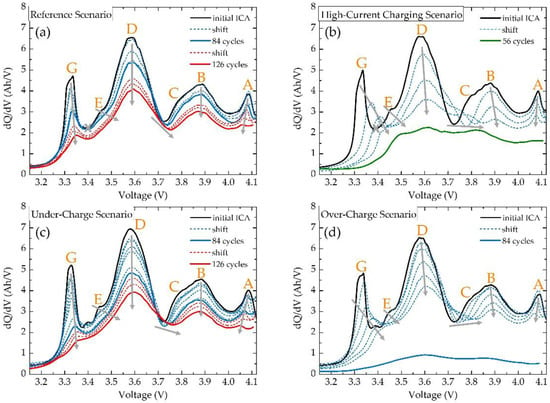
Figure 11.
Incremental capacity analysis of studied batteries, where six dominant features are recognised and studied for (a) Reference Scenario, (b) High-Current Charging Scenario, (c) Under-Charge Scenario and (d) Over-Charge Scenario.
For the Reference Scenario (Figure 11a), a decrease in the magnitudes of all features is present, while the decrease in the magnitudes of peaks D and G is the greatest. The shape and position of peak D are preserved. The maximum of peak G, however, shifts slightly from ~3.33 V (initial) to 3.35 V (126 cycles). This footprint suggests LAMliPE as the dominant source of degradation, while it is being accompanied by LLI [27]. Features C and E shift towards higher voltages, while they are being absorbed by peaks B and D, respectively. Peak A, along with its decreasing, also shifts from ~4.09 V (initial) to ~4.06 V (126 cycles). This shift of peak A is typical for LAMdeNE, although, this shift is meaningless, thus the possible occurrence of LAMdeNE would not be substantial. The ICA of the Under-Charge Scenario (Figure 11c) highly corresponds to the ICA of the Reference Scenario. The only notable differences are in a more pronounced decrease of peak D, earlier disappearance of feature C into peak B, and shift of peak A maxima from ~4.09 V (initial) to ~4.05 V (126 cycles). This shift would be expected, since under-charging can put additional stress on graphite lattice, hence LAMdeNE would be more profound. The highest degree of degradation can be seen in the ICA of the High-Current Charging Scenario (Figure 11b). Decreasing peak G shifts towards higher voltages (from an initial ~3.33 V to ~3.42 V at 42 cycles), which together with the decreasing of peak D corresponds to LLI. From the rapid decrease in the magnitude of all features, it is certain that LAMliPE takes place. From the shape of peak D, it cannot be said with certainty if peak D is collapsing into itself or rather if feature C separates itself from peak B. This separation would be a clear footprint of LAMliNE, however, this interpretation would be based on an uncertain assumption, therefore, the presence of LAMliNE solely on the ICA is not concluded. Peak A shifts from ~4.09 V (initial) to ~4.08 V (42 cycles), and since the difference of ~0.01 V can be easily caused by measuring inaccuracies, no further attention is given to this minor shift. The collapsed ICA curve for 56 degradation cycles confirms a massive level of degradation. The ICA of the Over-Charge Scenario is shown in Figure 11d. The maximum of decreasing peak G shifts from ~3.33 V (initial) to ~3.44 V (70 cycles). Similarly to the High-Current Charging Scenario, the shift and decreasing of peak G are present together with an overall magnitude decrease, hence the presence of LLI and LAMliPE is assumed. Peak A shifts from ~4.09 V (initial) to ~4.07 V (70 cycles), pointing to possible moderate LAMliNE, which could be reasonably assumed for over-charging in the same way as for under-charging. The ICA curve for 84 degradation cycles is completely collapsed, showing that the battery was essentially dead at this point.
5. Comparative Degradation Analysis of Individual Scenarios
In this section, results of the EIS, GITT, and ICA analysis for individual degradation scenarios are approached comparatively, to provide a comprehensive study of the degradation of NCR18650B batteries.
5.1. The Reference Scenario
For the Reference Scenario, a slow linear decrease in capacity was observed, where capacity decreased from an initial 3350 mAh to 2563 mAh after 126 cycles. The authors believe that this decrease was induced preliminarily by DoD 100% and by the extensive amount of analytical measurements, as discussed in the chapters above. Especially high DoD is known to lead to micro- and phase-changes of the NCA cathode material. Analysis via EIS measurements revealed that ROHM and RSEI are increasing negligibly with increasing cycle index. From this, it can be assumed that the SEI layer remains stable throughout the experiment. Quasi-stable ROHM values point to irrelevant conductivity losses, which would be otherwise caused by current collector corrosion, binder decomposition, or gas evolution and would lead to a ROHM increase. Values of RCHT are increasing quasi-linearly for the entire duration of experiments, pointing to the presence of microstructural and/or phase changes, while this change in active materials is supported also by decreasing Li+ diffusion. The disadvantage of the two-electrode EIS measurements is its inability to distinguish between the influences of individual electrodes, therefore, the origin of increasing RCHT has to be found by other methods. Analysis via GITT enabled the analysis of the behaviour of lithium-ion diffusion as a function of x in LiXC6. This analysis showed that even reference measurements lead to certain stress disparities in the graphite’s lattice, primarily in the surface region of graphite’s bulk, upon formation of Stage IV—Phase LiC72. It is assumed that the formation of this phase is being suppressed with an increasing number of cycles. The GITT also enabled the study of the internal resistance of the battery, which confirmed the thermodynamic stability of the battery. The footprint of the ICA ascribes LAMliPE as the dominant source of degradation, while mild LLI is also present. The ICA also contains a hint of a minor occurrence of LAMdeNE, which would be in accordance with the GITT study, although this mode is not considered to have an influential role in battery degradation. By combining results from ICA and GITT, it can be said that the origin of increasing RCHT is in the degradation of cathode active material. This confirms the initial hypothesis, that degradation of this battery would be induced primarily by cycling between SOC 0% and SOC 100%.
5.2. The Under-Charge Scenario
This scenario has the same capacity-decrease trend as the Reference Scenario, which has slightly lower capacity values from the ~50th cycle onwards. Higher DoD arguably induces this higher degradation due to over-discharging. Values of ROHM and RSEI obtained via EIS are in close to absolute overlap with the Reference Scenario measurements. Values of RCHT are increasing at an almost negligibly higher pace than the Reference Scenario values, hence, microstructural and/or phase changes on one or both electrodes are considered to be the dominant source of degradation. In terms of DLi+ analysis via GITT, the only notable difference is in higher VRStage IV values. As an explanation for this difference, more profound delithiation leading to higher intercalation/deintercalation stress onto graphite electrodes is suggested. A comparison of the internal resistance of the Under-Charge Scenario and the Reference Scenario points only to a single noticeable difference in the close-to-100% SOC region, where the Under-Charge Scenario shows slightly more increasing values. Analogously to the Reference Scenario, the ICA suggests primarily LAMliPE and LLI modes as dominant degradation modes. It can be argued that additional stress onto graphite lattice due to over-discharging might lead to observable LAMdeNE. Nevertheless, evidence for this degradation mode is not persuasive, hence it is not considered to have a determining effect on the battery’s state of health.
5.3. The Over-Charge Scenario
Uniquely for the Over-Charge Scenario, capacity fade occurs in two stages, where linear capacity fade occurs for the first 70 cycles, subsequently followed by a rapid capacity fade, leading to the death of the battery in just another 14 cycles. This two-stage capacity fade was observed only for this scenario, therefore, it is directly ascribed to over-charging up to 4.3 V. ROHM slowly increases up to 70 cycles, pointing to conductivity losses. Its values have almost doubled in the last 14 cycles. RSEI is stable up to the 49th cycle, and increases moderately up to the 70th cycle, from where it increases dramatically, showing gradual changes in the SEI layer. Values of RCHT initially have a similar trend as the Under-Charge Scenario, while from the 70th cycle onwards its values increase dramatically, having the same trend as ROHM and RSEI, suggesting that RCHT is connected to SEI layer changes and conductivity losses. It is known that NCA batteries are high-current and high-voltage sensitive and that the above-recommended voltages might lead to transition metal decomposition and deposition onto the SEI interface. This phenomenon is in good agreement with the presented results here. From the DLi+ study via GITT, it is clear that Stage IV—Phase LiC72 is being suppressed at a higher pace than for the reference measurements. The internal resistance of the battery develops moderately up to the 70th cycle, after which its values increase dramatically, where IR of the plateau region of SOC almost doubles its values, displaying a similar trend as ROHM. This is a clear indicator of a dying battery. The ICA suggests LLI and LAMliPE as dominant degradation modes. The shift of peak A possibly points to very moderate LAMdeNE, much the same as for under-charging.
5.4. The High-Current Charging Scenario
All analytical tools proved that this scenario led to the most severe degradation, preliminarily on the cathode side of the battery. The ICA recognizes LLI and LAMliPE as dominant and decisive degradation modes. DLi+ recognises the increasing influence of the cathode region with an increasing number of degradation cycles. Gradually increasing ROHM indicates high-current charging induced generation of CO2 and O2 gasses, leading to increased internal pressure, electrolyte depletion, and hence, conductivity loss. This is due to the reversible Li2CO3 surface film described in Section 2. The EIS measurements were performed at SOC 100%, thus ROHM values correspond to the fully charged and relaxed battery. From the internal resistance study performed via GITT, another resistance-related phenomenon was observed—decreasing resistance values for low-SOC regions. This can be attributed to the continuously decreasing pace of Li2CO3 decomposition during charging. The authors suggest that high-current charging led to disproportional Li2CO3 decomposition to Li2CO3 formation. RSEI increases quasi-linearly, suggesting the thickening of the SEI layer, which can be considered a partial source of LLI. Quasi-linearly increasing values of RCHT together with decreasing Li+ diffusion point to cationic mixing of the layered NCA structure, also resulting in LLI. All ongoing NCA degradation was strengthened by ∆DOD 100%, which leads to more intense structural microcracking, resulting in a loss of active cathode material and an increase in parasitic-reaction sites. Regarding the graphite anode, high-current charging led to more severe VRStage IV suppression than reference charging. This might have been induced by local accumulation of Li+ in the surface regions of the anode, leading to higher stress disparity and structural changes, however, similar suppression was observed for over-charging, therefore, several origins can induce this suppression. Out of all four scenarios, anode-related changes were the most profound for the High-Current Charging Scenario, nonetheless, EIS, GITT, and ICA suggest only insignificant degradation of graphite anode.
6. Conclusions
In this study, we analysed the degradation of commercial NCA batteries (NCR18650B) via methods of non-destructive electrochemical characterisation for various stress-inducing scenarios (over-charge, over-discharge, high-current charging). To the best of our knowledge, this is the first work analysing stress-induced degradation of NCA batteries simultaneously by EIS, ICA, and GITT. Comparative analysis via these methods shows that each of them provides a unique set of information about the battery’s condition, however, as we demonstrate in this work, joint usage of these methods is necessary to obtain comprehensive knowledge and a more profound understanding of the battery’s condition. Moreover, the simultaneous usage of various confirmatory techniques enables the correct assigning of the origin of degradation with certainty. Battery analysis performed in this fashion relieves the experiment of otherwise necessary assumptions arising from two-electrode measurements.
Author Contributions
Conceptualization, M.K. and M.M.; methodology, M.K. and M.M; software, M.K.; validation, M.K., M.M. and P.O.; formal analysis, M.K., P.O. and M.M.; investigation, M.K. and M.M.; resources, M.M.; data curation, M.K.; writing—original draft preparation, M.K.; writing—review and editing, M.M. and P.O.; visualization, M.K. and P.O.; supervision, M.M.; project administration, M.M.; funding acquisition, M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by Intelligent Reliability 4.0 (iRel40). iRel40 is a European co-funded innovation project that has been granted by the ECSEL Joint Undertaking (JU) under Grant 876659. The funding of the project comes from the Horizon 2020 research programme and participating countries. National funding is provided by Germany, including the Free States of Saxony and Thuringia, Austria, Belgium, Finland, France, Italy, The Netherlands, Slovakia, Spain, Sweden, and Turkey. The work was supported in part also by the grant of The Ministry of Education, Science, Research and Sport of the Slovak Republic VEGA 1/0529/20.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, L.; Li, M.; Chu, L.; Jiang, B.; Lin, R.; Zhu, X.; Cao, G. Layered ternary metal oxides: Performance degradation mechanisms as cathodes, and design strategies for high-performance batteries. Prog. Mater. Sci. 2020, 111, 100655. [Google Scholar] [CrossRef]
- Theiler, M.; Endisch, C.; Lewerenz, M. Float current analysis for fast calendar aging assessment of 18650 Li (NiCoAl) O2/graphite cells. Batteries 2021, 7, 22. [Google Scholar] [CrossRef]
- Tran, M.-K.; DaCosta, A.; Mevawalla, A.; Panchal, S.; Fowler, M. Comparative Study of Equivalent Circuit Models Performance in Four Common Lithium-Ion Batteries: LFP, NMC, LMO, NCA. Batteries 2021, 7, 51. [Google Scholar] [CrossRef]
- Nie, X.; Hou, G.; Xu, Z.; Li, J.; Li, Y.; Sun, Q.; Qiao, Y.; Li, D.; Ci, L. Lewis Acidity Organoboron-Modified Li-Rich Cathode Materials for High-Performance Lithium-Ion Batteries. Adv. Mater. Interfaces 2021, 8, 2002113. [Google Scholar] [CrossRef]
- European Commission. Report: On the Implementation of the Strategic Action Plan on Batteries: Building a Strategic Battery Value Chain in Europe. COM(2019) 176 Final, Brussels, 09. 04. 2019. Available online: https://eur-lex.europa.eu/legal-content/en/TXT/?uri=CELEX%3A52019DC0176 (accessed on 5 November 2022).
- Yang, X.; Chen, J.; Zheng, Q.; Tu, W.; Xing, L.; Liao, Y.; Xu, M.; Huang, Q.; Cao, G.; Li, W. Mechanism of cycling degradation and strategy to stabilize a nickel-rich cathode. J. Mater. Chem. A 2018, 6, 16149–16163. [Google Scholar] [CrossRef]
- Benavente-Araoz, F.; Varini, M.; Lundblad, A.; Cabrera, S.; Lindbergh, G. Effect of Partial Cycling of NCA/Graphite Cylindrical Cells in Different SOC Intervals. J. Electrochem. Soc. 2020, 167, 040529. [Google Scholar] [CrossRef]
- Jung, K.; Yim, T. Calcium- and sulfate-functionalized artificial cathode–electrolyte interphases of Ni-rich cathode materials. Rare Met. 2021, 40, 2793–2801. [Google Scholar] [CrossRef]
- Noerochim, L.; Suwarno, S.; Idris, N.H.; Dipojono, H.K. Recent Development of Nickel-Rich and Cobalt-Free Cathode Materials for Lithium-Ion Batteries. Batteries 2021, 7, 84. [Google Scholar] [CrossRef]
- Pelegov, D.V.; Pontes, J. Main drivers of battery industry changes: Electric vehicles—A market overview. Batteries 2018, 4, 65. [Google Scholar] [CrossRef]
- Blomgren, G.E. The Development and Future of Lithium Ion Batteries. J. Electrochem. Soc. 2016, 164, A5019–A5025. [Google Scholar] [CrossRef]
- Zubi, G.; Dufo-López, R.; Carvalho, M.; Pasaoglu, G. The lithium-ion battery: State of the art and future perspectives. Renew. Sustain. Energy Rev. 2018, 89, 292–308. [Google Scholar] [CrossRef]
- Xiong, R.; Li, L.; Tian, J. Towards a smarter battery management system: A critical review on battery state of health monitoring methods. J. Power Source 2018, 405, 18–29. [Google Scholar] [CrossRef]
- Berecibar, M.; Gandiaga, I.; Villarreal, I.; Omar, N.; Van Mierlo, J.; van den Bossche, P. Critical review of state of health estimation methods of Li-ion batteries for real applications. Renew. Sustain. Energy Rev. 2016, 56, 572–587. [Google Scholar] [CrossRef]
- Han, X.; Lu, L.; Zheng, Y.; Feng, X.; Li, Z.; Li, J.; Ouyang, M. A review on the key issues of the lithium ion battery degradation among the whole life cycle. eTransportation 2019, 1, 100005. [Google Scholar] [CrossRef]
- Li, Y.; Liu, K.; Foley, A.M.; Zülke, A.; Berecibar, M.; Nanini-Maury, E.; Van Mierlo, J.; Hoster, H.E. Data-driven health estimation and lifetime prediction of lithium-ion batteries: A review. Renew. Sustain. Energy Rev. 2019, 113, 109254. [Google Scholar] [CrossRef]
- Hu, X.; Xu, L.; Lin, X.; Pecht, M. Battery Lifetime Prognostics. Joule 2020, 4, 310–346. [Google Scholar] [CrossRef]
- Zheng, L.; Zhu, J.; Lu, D.D.-C.; Wang, G.; He, T. Incremental capacity analysis and differential voltage analysis based state of charge and capacity estimation for lithium-ion batteries. Energy 2018, 150, 759–769. [Google Scholar] [CrossRef]
- Ng, B.; Coman, P.T.; Mustain, W.E.; White, R.E. Non-destructive parameter extraction for a reduced order lumped electrochemical-thermal model for simulating Li-ion full-cells. J. Power Source 2019, 445, 227296. [Google Scholar] [CrossRef]
- Damay, N.; Mbeya, K.M.; Friedrich, G.; Forgez, C. Separation of the charge transfers and solid electrolyte interphase contributions to a battery voltage by modeling their non-linearities regarding current and temperature. J. Power Source 2021, 516, 230617. [Google Scholar] [CrossRef]
- Babaeiyazdi, I.; Rezaei-Zare, A.; Shokrzadeh, S. State of charge prediction of EV Li-ion batteries using EIS: A machine learning approach. Energy 2021, 223, 120116. [Google Scholar] [CrossRef]
- Pastor-Fernandez, C.; Widanage, W.D.; Marco, J.; Gama-Valdez, M.-A.; Chouchelamane, G.H. Identification and quantification of ageing mechanisms in Lithium-ion batteries using the EIS technique. In Proceedings of the 2016 IEEE Transportation Electrification Conference and Expo (ITEC), IEEE, Dearborn, MI, USA, 27–29 June 2016; pp. 1–6. [Google Scholar]
- Lai, X.; Chen, Q.; Tang, X.; Zhou, Y.; Gao, F.; Guo, Y.; Bhagat, R.; Zheng, Y. Critical review of life cycle assessment of lithium-ion batteries for electric vehicles: A lifespan perspective. eTransportation 2022, 12, 100169. [Google Scholar] [CrossRef]
- Cabañero, M.A.; Boaretto, N.; Röder, M.; Müller, J.; Kallo, J.; Latz, A. Direct Determination of Diffusion Coefficients in Commercial Li-Ion Batteries. J. Electrochem. Soc. 2018, 165, A847–A855. [Google Scholar] [CrossRef]
- Su, L.; Wu, M.; Li, Z.; Zhang, J. Cycle life prediction of lithium-ion batteries based on data-driven methods. eTransportation 2021, 10, 100137. [Google Scholar] [CrossRef]
- Sebastian, S.S.; Dong, B.; Zerrin, T.; Pena, P.A.; Akhavi, A.S.; Li, Y.; Ozkan, C.S.; Ozkan, M. Adaptive fast charging methodology for commercial Li-ion batteries based on the internal resistance spectrum. Energy Storage 2020, 2, e141. [Google Scholar] [CrossRef]
- Devie, A.; Dubarry, M. Durability and Reliability of Electric Vehicle Batteries under Electric Utility Grid Operations. Part 1: Cell-to-Cell Variations and Preliminary Testing. Batteries 2016, 2, 28. [Google Scholar] [CrossRef]
- Zhang, S.S. Identifying rate limitation and a guide to design of fast-charging Li-ion battery. InfoMat 2020, 2, 942–949. [Google Scholar] [CrossRef]
- Kong, D.; Wen, R.; Ping, P.; Peng, R.; Zhang, J.; Chen, G. Study on degradation behavior of commercial 18650 LiAlNiCoO2 cells in over-charge conditions. Int. J. Energy Res. 2019, 43, 552–567. [Google Scholar] [CrossRef]
- Togasaki, N.; Yokoshima, T.; Oguma, Y.; Osaka, T. Prediction of overcharge-induced serious capacity fading in nickel cobalt aluminum oxide lithium-ion batteries using electrochemical impedance spectroscopy. J. Power Source 2020, 461, 228168. [Google Scholar] [CrossRef]
- LI, Y.; Dong, B.; Zerrin, T.; Jauregui, E.; Wang, X.; Hau, X.; Ravichandran, D.; Shang, R.; Xie, J.; Ozkan, M.; et al. State-of-health prediction for lithium-ion batteries via electrochemical impedance spectroscopy and artificial neural networks. Energy Storage 2020, 2, 186. [Google Scholar] [CrossRef]
- Preger, Y.; Barkholtz, H.M.; Fresquez, A.; Campbell, D.L.; Juba, B.W.; Romàn-Kustas, J.; Ferreira, S.R.; Chalamala, B.R. Degradation of Commercial Lithium-Ion Cells as a Function of Chemistry and Cycling Conditions. J. Electrochem. Soc. 2020, 167, 120532. [Google Scholar] [CrossRef]
- Watanabe, S.; Kinoshita, M.; Hosokawa, T.; Morigaki, K.; Nakura, K. Capacity fade of LiAlyNi1−x−yCoxO2 cathode for lithium-ion batteries during accelerated calendar and cycle life tests (surface analysis of LiAlyNi1−x−yCoxO2 cathode after cycle tests in restricted depth of discharge ranges). J. Power Source 2014, 258, 210–217. [Google Scholar] [CrossRef]
- Pastor-Fernández, C.; Uddin, K.; Chouchelamane, G.H.; Widanage, W.D.; Marco, J. A Comparison between Electrochemical Impedance Spectroscopy and Incremental Capacity-Differential Voltage as Li-ion Diagnostic Techniques to Identify and Quantify the Effects of Degradation Modes within Battery Management Systems. J. Power Source 2017, 360, 301–318. [Google Scholar] [CrossRef]
- Wildfeuer, L.; Gieler, P.; Karger, A. Combining the Distribution of Relaxation Times from EIS and Time-Domain Data for Parameterizing Equivalent Circuit Models of Lithium-Ion Batteries. Batteries 2021, 7, 52. [Google Scholar] [CrossRef]
- Liu, W.; Delacourt, C.; Forgez, C.; Pelissier, S. Study of graphite/NCA Li-ion cell degradation during accelerated aging tests Data analysis of the SIMSTOCK project. In Proceedings of the 2011 IEEE Vehicle Power and Propulsion Conference, IEEE, Chicago, IL, USA, 6–9 September 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Shi, E.; Xia, F.; Peng, D.; Li, L.; Wang, X.; Yu, B. State-of-health estimation for lithium battery in electric vehicles based on improved unscented particle filter. J. Renew. Sustain. Energy 2019, 11, 024101. [Google Scholar] [CrossRef]
- Makimura, Y.; Sasaki, T.; Nonaka, T.; Nishimura, Y.F.; Uyama, T.; Okuda, C.; Itou, Y.; Takeuchi, Y. Factors affecting cycling life of LiNi0.8 Co0.15 Al0.05 O2 for lithium-ion batteries. J. Mater. Chem. A 2016, 4, 8350–8358. [Google Scholar] [CrossRef]
- Zhang, G.; Wei, X.; Chen, S.; Zhu, J.; Han, G.; Tang, X.; Hua, W.; Dai, H.; Ye, J. Comprehensive Investigation of a Slight Overcharge on Degradation and Thermal Runaway Behavior of Lithium-Ion Batteries. ACS Appl. Mater. Interfaces 2021, 13, 35054–35068. [Google Scholar] [CrossRef]
- Fly, A.; Chen, R. Rate dependency of incremental capacity analysis (dQ/dV) as a diagnostic tool for lithium-ion batteries. J. Energy Storage 2020, 29, 101329. [Google Scholar] [CrossRef]
- Teichert, P.; Eshetu, G.G.; Jahnke, H.; Figgemeier, E. Degradation and Aging Routes of Ni-Rich Cathode Based Li-Ion Batteries. Batteries 2020, 6, 8. [Google Scholar] [CrossRef]
- Fang, R.; Miao, C.; Nie, Y.; Wang, D. Degradation mechanism and performance enhancement strategies of LiNixCoyAl1−x−yO2 (x ≥ 0.8) cathodes for rechargeable lithium-ion batteries: A review. Ionics 2020, 26, 3199–3214. [Google Scholar] [CrossRef]
- Kim, N.Y.; Yim, T.; Song, J.H.; Yu, J.-S.; Lee, Z. Microstructural study on degradation mechanism of layered LiNi0.6Co0.2Mn0.2O2 cathode materials by analytical transmission electron microscopy. J. Power Source 2016, 307, 641–648. [Google Scholar] [CrossRef]
- Dixit, M.; Markovsky, B.; Schipper, F.; Aurbach, D.; Major, D.T. Origin of Structural Degradation During Cycling and Low Thermal Stability of Ni-Rich Layered Transition Metal-Based Electrode Materials. J. Phys. Chem. 2017, 121, 22628–22636. [Google Scholar] [CrossRef]
- Matsumoto, K.; Kuzuo, R.; Yamanaka, A. Effects of CO2 in air on Li deintercalation from LiNi1−x−yCoxAlyO. J. Power Source 1999, 81, 558–561. [Google Scholar] [CrossRef]
- Bianchini, M.; Roca-Ayats, M.; Hartmann, P.; Brezesinski, T.; Janek, J. There and back again—The journey of LiNiO2 as a cathode active material. Angew. Chem. Int. Ed. 2019, 58, 10434–10458. [Google Scholar] [CrossRef] [PubMed]
- Ryu, H.-H.; Park, K.-J.; Yoon, C.S.; Sun, Y.-K. Capacity Fading of Ni-Rich Li[NixCoyMn1–x–y]O2 (0.6 ≤ x ≤ 0.95) Cathodes for High-Energy-Density Lithium-Ion Batteries: Bulk or Surface Degradation? Chem. Mater. 2018, 30, 1155–1163. [Google Scholar] [CrossRef]
- Xie, J.; Ma, J.; Bai, K. Enhanced coulomb counting method for state-of-charge estimation of lithium-ion batteries based on peukert’s law and coulombic efficiency. J. Power Electron. 2018, 18, 910–922. [Google Scholar]
- Wang, X.; Wei, X.; Zhu, J.; Dai, H.; Zheng, Y.; Xu, X.; Chen, Q. A review of modeling, acquisition, and application of lithium-ion battery impedance for onboard battery management. eTransportation 2020, 7, 100093. [Google Scholar] [CrossRef]
- Choi, W.; Shin, H.-C.; Kim, J.M.; Choi, J.-Y.; Yoon, W.-S. Modeling and Applications of Electrochemical Impedance Spectroscopy (EIS) for Lithium-ion Batteries. J. Electrochem. Sci. Technol. 2020, 11, 1–13. [Google Scholar] [CrossRef]
- Deleebeeck, L.; Veltzé, S. Electrochemical impedance spectroscopy study of commercial Li-ion phosphate batteries: A metrology perspective. Int. J. Energy Res. 2020, 44, 7158–7182. [Google Scholar] [CrossRef]
- Gilbert, J.A.; Shkrob, I.A.; Abraham, D.P. Transition metal dissolution, ion migration, electrocatalytic reduction and capacity loss in lithium-ion full cells. J. Electrochem. Soc. 2017, 164, A389. [Google Scholar] [CrossRef]
- Capron, O.; Gopalakrishnan, R.; Jaguemont, J.; Omar, N.; Bossche, P.V.D.; Van Mierlo, J. On the Ageing of High Energy Lithium-Ion Batteries—Comprehensive Electrochemical Diffusivity Studies of Harvested Nickel Manganese Cobalt Electrodes. Materials 2018, 11, 176. [Google Scholar] [CrossRef]
- Bernardi, D.M.; GO, J.-Y. Analysis of pulse and relaxation behavior in lithium-ion batteries. J. Power Source 2011, 196, 412–427. [Google Scholar] [CrossRef]
- Allart, D.; Montaru, M.; Gualous, H. Model of Lithium Intercalation into Graphite by Potentiometric Analysis with Equilibrium and Entropy Change Curves of Graphite Electrode. J. Electrochem. Soc. 2018, 165, A380–A387. [Google Scholar] [CrossRef]
- Park, J.H.; Yoon, H.; Cho, Y.; Yoo, C.-Y. Investigation of Lithium Ion Diffusion of Graphite Anode by the Galvanostatic Intermittent Titration Technique. Materials 2021, 14, 4683. [Google Scholar] [CrossRef]
- Mendoza, I.O.S.; Vázquez-Arenas, J.; González, I.; Ramos-Sánchez, G.; Castillo-Araiza, C.O. Revisiting Electrochemical Techniques to Characterize the Solid-State Diffusion Mechanism in Lithium-Ion Batteries. Int. J. Chem. React. Eng. 2018, 17, 20180095. [Google Scholar] [CrossRef]
- Verma, A.; Smith, K.; Santhanagopalan, S.; Abraham, D.; Yao, K.P.; Mukherjee, P.P. Galvanostatic intermittent titration and performance based analysis of LiNi0.5Co0.2Mn0.3O2 cathode. J. Electrochem. Soc. 2017, 164, A3380. [Google Scholar] [CrossRef]
- Fang, W.; Kwon, O.J.; Wang, C.-Y. Electrochemical-thermal modeling of automotive Li-ion batteries and experimental validation using a three-electrode cell. Int. J. Energy Res. 2009, 34, 107–115. [Google Scholar] [CrossRef]
- Namor, E.; Torregrossa, D.; Cherkaoui, R.; Paolone, M. Parameter identification of a lithium-ion cell single-particle model through non-invasive testing. J. Energy Storage 2017, 12, 138–148. [Google Scholar] [CrossRef]
- Sethuraman, V.; Hardwick, L.; Srinivasan, V.; Kostecki, R. Surface structural disordering in graphite upon lithium intercalation/deintercalation. J. Power Source 2010, 195, 3655–3660. [Google Scholar] [CrossRef]
- Ohzuku, T.; Iwakoshi, Y.; Sawai, K. Formation of Lithium-Graphite Intercalation Compounds in Nonaqueous Electrolytes and Their Application as a Negative Electrode for a Lithium Ion (Shuttlecock) Cell. J. Electrochem. Soc. 1993, 140, 2490–2498. [Google Scholar] [CrossRef]
- Li, X.; Yuan, C.; Li, X.; Wang, Z. State of health estimation for Li-Ion battery using incremental capacity analysis and Gaussian process regression. Energy 2019, 190, 116467. [Google Scholar] [CrossRef]
- Ansean, D.; Garcia, V.M.; Gonzalez, M.; Blanco-Viejo, C.; Viera, J.C.; Pulido, Y.F.; Sanchez, L. Lithium-Ion Battery Degradation Indicators Via Incremental Capacity Analysis. IEEE Trans. Ind. Appl. 2019, 55, 2992–3002. [Google Scholar] [CrossRef]
- Weng, C.; Sun, J.; Peng, H. An Open-Circuit-Voltage Model of Lithium-Ion Batteries for Effective Incremental Capacity Analysis. In Proceedings of the Dynamic Systems and Control Conference, American Society of Mechanical Engineers 2013, Palo Alto, CA, USA, 21–23 October 2013; p. V001T05A002. [Google Scholar] [CrossRef]
- Dubarry, M.; Svoboda, V.; Hwu, R.; Liaw, B.Y. Incremental Capacity Analysis and Close-to-Equilibrium OCV Measurements to Quantify Capacity Fade in Commercial Rechargeable Lithium Batteries. Electrochem. Solid-State Lett. 2006, 9, A454–A457. [Google Scholar] [CrossRef]
- Dubarry, M.; Liaw, B.Y. Identify capacity fading mechanism in a commercial LiFePO4 cell. J. Power Source 2009, 194, 541–549. [Google Scholar] [CrossRef]
- Dubarry, M.; Truchot, C.; Liaw, B.Y. Cell degradation in commercial LiFePO4 cells with high-power and high-energy designs. J. Power Source 2014, 258, 408–419. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).