Abstract
The process chain of electrode production includes calendering as a crucial process step to enhance the volumetric energy density as well as to influence the particle-pore-structure and simultaneously the mechanical and electrochemical properties of the electrode coating. A further way to improve the volumetric energy density is the usage of other materials with higher specific capacity, such as silicon instead of graphite as the active material for anodes. In this study, both opportunities, calendering and using silicon-containing composites, are combined to investigate the relations between material, process and performance. The applied line loads for the compaction are correlated with the silicon mass fraction and lead to a silicon-dependent mathematical model to estimate further line loads for silicon-graphite-composite electrodes. On the basis of established analyzing methods for adhesion strength and deformation behavior, it is shown that with increasing silicon content, the elastic deformation of the electrode coating rises. In addition, the overall porosity of the electrodes is less affected by silicon than the pore size distribution compared to graphite electrodes. Furthermore, the electrical conductivity decreases at higher silicon contents independent of coating density. Moreover, the long-term electrochemical stability deteriorates with increasing silicon content and coating density.
1. Introduction
With rising demand for portable electric devices (e.g., smartphones, laptops) and electric cars and, therefore, mobile energy storage [1,2], the development of rechargeable battery systems with high volumetric and gravimetric energy densities is of high importance. The comparison between different battery systems shows that lithium-ion batteries (LIBs) unite these two requirements best [3]. However, even this battery technology can be improved by using active materials with higher specific capacity or an optimized production process. As active material for anodes with a significantly higher specific capacity than commonly used graphite (372 mAh/g [4]), silicon comes into the focus of research and development. Silicon has a maximal specific capacity of 3579 mAh/g [5], which is around 10 times higher than graphite. Due to this high specific capacity of silicon, a very huge volume expansion of up to around 300% takes place during lithiation [6,7,8,9]. As a result of this huge volume expansion, particle breakage and increased altering of the electrodes take place during long-time cycling [8]. Referring to Pinson and Bazant, a continuous SEI-building is a consequence of the silicon particle breakage due to the newly created surface of the active material and, therefore, continuous reactions with the electrolyte. As a result, capacity fading takes place [10]. However, according to Dhillon et al. [11] and Dose et al. [12], particle breakage was not the main reason for the capacity fade of silicon-containing electrodes. The reduction of ionic diffusion coefficient by the silicon particles should be much more responsible for the cell aging and the continuous SEI-formation caused by cracks of the silicon particles and, therefore, new SEI building [11,12].
The calendering process is a crucial step in electrode manufacturing to increase the energy density of batteries as well as their electrical conductivity. The relationship between electrode parameters and the calendering process was investigated in several publications [13,14,15,16,17]. In addition to the investigations between the calendering of battery electrodes and their resulting mechanical and electrochemical properties, Meyer et al. [18] established a model to describe the relations between applied line load qL and resulting coating density ρC by using a so-called compaction resistance γC as well as initial coating density ρC,0 and maximal achievable coating density ρC,max shown in Equation (1).
ρC = ρC,max − (ρC,max − ρC,0) × exp(−qL/γC)
In further publications, this factor was described in more detail [19,20]. The authors show that the compaction resistance is a function of active material, particle size, mass loading, calender roll temperature and carbon-binder-domain. Meyer et al. [19] defined a specific product parameter μ to calculate the compaction resistance γC for different mass loadings MC after showing a linear correlation between compaction resistance and mass loading.
γC = μ × MC
In order to reduce the influence of different mass loadings on the calendering process and electrode mechanics, it is indispensable to produce electrodes both for comparable mechanical and electrochemical investigations.
2. Material and Methods
This study consisted of 3 development anode active materials from SGL Carbon with different silicon content (silicon content: 0 wt%, 3.4 wt%, 10.2 wt%). The silicon-free material was artificial graphite with a mean particle size (x50) of 14.86 µm. On the other hand, the active material with silicon were composites, where silicon particles (x50 < 150 nm) were embedded in a carbon matrix. The particle structure of the resulting Si-composite was comparable but not identical to Müller et al. [21]. The Si-composite with a Si-content of 3.4 wt% led to 490 mAh/g as well as the particle size of 12.57 µm (x50). The Si-composite with 10.2 wt% Si showed a capacity of 650 mAh/g and particle size of x50 = 10.52 µm. Next to active materials, the anodes consisted of carboxymethyl cellulose from Thermo Scientific (Mw = 700.000 g/mol; DS = 0.9), carbon black from Imerys (Super C65, x50 = 13.9 µm) and styrene-butadiene-rubber from ARLANXEO Deutschland GmbH (solid content of emulsion = 41.98 wt%). Regarding cathode, the active material (NMC622, x50 = 10.2 µm) was purchased from BASF, polyvinylidene fluoride (PVDF; Solef 5130) from Solvey and conductive graphite (SFG 6L) from Imerys.
2.1. Electrode Preparation and Composition
Electrode preparation takes place in a wet processing route. Regarding anode, the powder components (all materials except SBR) were premixed with a 3D shake mixer (Turbula® T2F from Willy A. Bachofen AG Maschinenfabrik, Muttenz, Switzerland) to a homogeneous powder mixture. Afterward, the powder was dispersed into deionized water as a liquid solvent with a Dispermat AE04 dissolver (VMA Getzmann GmbH, Reichshof, Germany). The dissolver was equipped with a temperature control unit that cools the suspension to 20 °C. After full wetting of the powder particles, the tangential speed of 50 mm dissolver disks was set to 9 m/s for 60 min. The styrene-butadiene rubber (SBR) emulsion was added to the slurry, and the tangential speed was set to 3 m/s for another 30 min. This production step was performed under a vacuum to prevent gas bubbles in the slurry. On the other hand, the cathode slurry was produced with a planetary mixer PMH10 (NETZSCH-Feinmahltechnik GmbH, Selb, Germany). The planetary mixer was equipped with a cross beam low-speed stirrer (LSS), a high-speed stirrer (HSS) with a double butterfly setup and a baffle. In the first step, the powder components (NMC622, C65, SFG6L and PVDF) were mixed for 15 min with low intensities (LSS = 20 rpm; HSS = 250 rpm) to achieve a homogeneous powder mixture. Considering a solid content of 70%, a calculated NMP mass was added and stirred (LSS = 50 rpm; HSS = 500 rpm) until all materials were wetted. Then, the dispersing process was performed for 60 min with tip speeds of 100 rpm (LSS) and 2500 rpm (HSS) as well as with constant cooling and degassing.
The final electrode slurries were coated on one-sided continuously on copper foil (10 µm electrolytic foil from Furukawa, Tokyo, Japan) or aluminum foil (20 µm AA 1085 H18 rolled foil from Hydro Aluminium Rolled Products GmbH, Grevenbroich, Germany), respectively, using a comma bar reverse roll coating system in the coating device LabCo® from Kroenert GmbH & Co. KG (Hamburg, Germany). The coating and drying device was divided in 3 separate adjustable segments of 2 m each. For the different anodes coated at 1 m/min substrate velocity, the drying temperature was set to 50/60/70 °C with a diffuse ventilation profile. The cathode was coated on the aluminum foil with a substrate velocity of 2 m/min, and the segment settings regarding the temperature were 80/100/120 °C with a diffuse/diffuse/direct ventilation profile. The aim was to produce 2 variations of anodes. On the one hand, electrodes with a comparable areal coating weight of 12 mg/cm2 and on the other hand, electrodes with a comparable areal capacity of 4 mAh/cm2 were produced. For the anodes with graphite as active material, the 12 mg/cm2 was synonymous with 4 mAh/cm2. In respect to full cell tests, the cathode had an areal capacity of 3.6 mAh/cm2. To investigate the influence of the silicon amount in the active material, 2 silicon-composites were used besides graphite as reference material. The specified mass fractions of silicon in the active materials were calculated from the specific charge capacities given by the manufacturer. The coating composition and selected measured properties of the non-calendered electrodes are shown in Table 1 and Table 2. The resulting dry electrodes were cut into electrode sheets with a length of 35 cm each.

Table 1.
Composition of the electrode coatings in wt%.

Table 2.
Electrode parameters of the non-calendered electrodes.
2.2. Calendering
The electrodes were calendered in a discontinuous process with a pilot-scale 2 roll compactor line GKL 400 (Saueressig GmbH Co KG, Vreden, Germany). The calender rolls diameter was 450 mm and the roll width was 470 mm. They can apply a maximal line load qL of 1500 N/mm to the electrode, whereby the line load was calculated from the rolling force FN and the coating width of 160 mm. The temperature set for all compaction processes was 20 °C, and 6 electrode sheets for each electrode and each degree of compaction were calendered. The rolling force FN was received from the forces of the main cylinders and the roll bending cylinders. For more detailed information on rolling force calculation see Meyer et al. [18].
The electrodes were compacted to similar densities. They were defined to be 1.00, 1.25 and 1.50 g/cm3 in advance. Besides the non-calendered electrode and with maximum density achieved with a calender gap of 25 µm, each electrode type was compressed to 3 or 4 different densities, depending on the maximum achievable coating density.
2.3. Electrode Analysis
The electrodes’ thickness and density were analyzed as equivalent to the electrodes shown by Meyer et al. [18]. The porosity and pore structure was analyzed with mercury intrusion adapted to battery electrodes by Froboese et al. [22] using a mercury intrusion porosimeter PoreMaster 60 (Quantachrome Instruments, Boynton Beach, FL, USA). This method was based on a sample piece (40 cm2) of the produced electrodes. After evacuating the sample chamber, mercury was pressed into the pores of the electrodes and pressure as well as the volume of mercury was measured. For a detailed explanation of the test method, see Froboese et al. [22].
In addition, the electrodes were investigated by a pull-off test developed by Haselrieder et al. [23,24]. For this test, 10 samples with a diameter of 12 mm were punched out from the electrodes. The samples were fixed between 2 coplanar sample holders using double-sided tape. On the upper sample holder, the electrodes were stuck on the tape, and on the lower sample holder, the tape was empty. After preparation, the samples were pressed together with a defined normal force of 68 N using a uniaxial material testing machine (Z020, Zwick GmbH & Co. KG, Ulm, Germany) [23]. Furthermore, the electrodes were characterized with the RM2610 (HIOKI E.E. Corporation, Ueda, Japan) for the electrical resistances of the pure coating.
The elastic and plastic deformation behavior of the calendered electrodes was investigated using a flat punch at a high precision nanoindenter (UNAT, Asmec Advanced Surface Mechanics GmbH, Dresden, Germany) with the so-called energy method developed by Bartali et al. [25]. A huge advantage of the energy method is that measuring data of coatings higher than 10 µm is not affected by the current collector [26].
For electrochemical characterization, the produced and calendered anodes were paired with a 3.6 mAh/cm2 reference cathode (composition see Table 1) in a full cell setup as 126/97 mAh pouch cell. The used separator was Celgard® 2500 (Celgard LLC., Charlotte, NC, USA), and the electrolyte was an LP57 (1 M LiPF6 in EC:EMC 3:7 v:v) with 10 % FEC (Gotion Inc., Fremont, CA, USA). After a 24-hour rest step, the cells were cycled between 3.0 and 4.3 V with the cell tester Maccor Series 4000 (Maccor Inc., Tulsa, OK, USA) at a temperature of 20 °C. For the formation, the first 3 cycles were running at 0.1 C. After these formation cycles, the real cell capacities were measured, and the following cycles were adjusted to the real cell capacities. Next, a C-rate-test was run through at 0.5/1.0/2.0/3.0 C with 3 cycles for each rate. After the C-rate-test, 2 0.1 C cycles were performed for the comparison of the electrode capacity before and after the C-rate test.
3. Results and Discussion
The calendering process step is a crucial step in influencing different electrode parameters as well as LIB-cell parameters. Besides the obvious increase in energy density, calendering influences the mechanical and electrochemical properties of the electrode itself.
3.1. Characterization of the Calendering Process
The applied line loads to the electrodes with comparable mass loading led to an increase in the overall coating density. Since the non-calendered anodes had nearly the same initial coating densities as displayed in Table 3, the aims of the coating densities after calendering were set to 1.00, 1.25, 1.50 g/cm3 as well as the maximum coating density. The resulting densities for a constant mass loading of 12 mg/cm2 are shown in Figure 1a. Using the model from Meyer [18], the material-specific compaction resistance for the different active materials was determined. The compaction resistances are plotted against the silicon mass fraction in Figure 1b. It is noticeable that the compaction resistance grows with an increasing amount of silicon. Figure 1b shows that the compaction resistance can be described with an allometric correlation with γC as compaction resistance, γC,G as compaction resistance of pure graphite electrode, γC,wSi = 1 as the assumed compaction resistance of an electrode with an active material with a silicon amount of 1 wt% and wSi as silicon mass fraction:
γC = γC,G + (γC,wSi = 1 − γC,G) × wSi0.4

Table 3.
Approximation parameters for the electrodes with different silicon mass content.
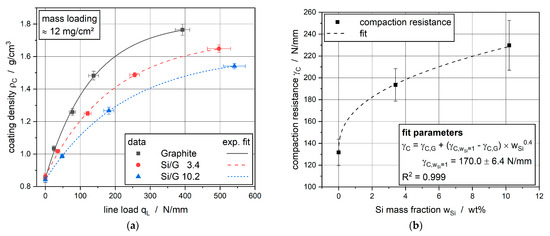
Figure 1.
(a) Increased coating density of Si/G anodes at different line loads; (b) rising compaction resistance with higher silicon mass fractions.
Attention has to be paid to the range of silicon mass fractions close to zero. According to Figure 1b, the compaction resistance is going to reach zero at very low silicon mass fractions.
The increase of the compaction resistance with higher silicon mass fractions is equivalent to a higher required line load to achieve the same coating density. Especially for the coating density of 1.5 g/cm3, these higher line loads can be seen very clearly. This phenomenon can be explained by a higher hardness of the silicon particles (Young’s modulus of 165 GPa [27]) compared to the comparatively weak graphite particles (Young’s modulus of 32.47 GPa [28]). Therefore, a much higher force was needed to cause a rearrangement of the particle structure or deformation of the silicon particles within the Si/G composite coatings.
3.2. Active Material Dependent Pore Structures
In order to compare different active materials in a porous system in terms of their microstructural properties, the distribution of these pores was of very high interest. The pores do not only provide information about the inner structure of the coatings; rather, they give information about the ionic conductivity, which is the main impact factor on electrochemical cycling performance [18].
The electrode porosities were analyzed by mercury intrusion, see Froboese et al. [22]. Figure 2 shows the sum distribution of the specific pore volume in the direction from larger to smaller pores for the electrodes with graphite (Figure 2a), Si/G-composite with 3.4 wt% silicon (Figure 2b), Si/G-composite with 10.2 wt% silicon (Figure 2c) plotted against the pore diameter. Moreover, the absolute coating porosity was displayed as a function of the coating density after calendering (Figure 2d).
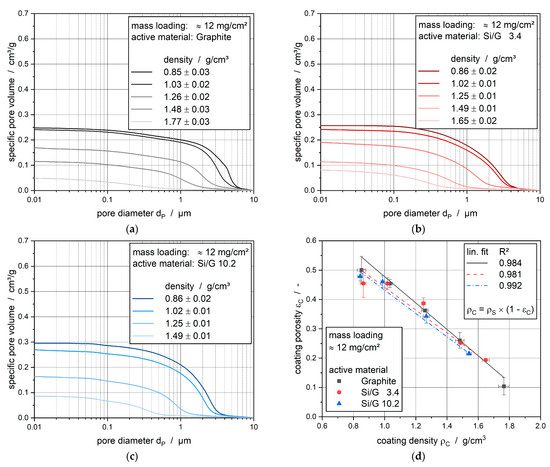
Figure 2.
Specific pore volume of the (a) graphite electrode; (b) Si/G 3.4 electrode; (c) Si/G 10.2 electrode; (d) calculated coating porosity.
The pores appeared in a range between 10 nm and 10 µm, with the main rise of the specific pore volume at pore diameters higher than 1 µm for the non-calendered electrodes. This rise represents the pores between active material particles, whereas a discrete second rise, representing the carbon black pores, was not existing. The pore diameter distribution of graphite anodes with 5 wt% carbon black, as investigated by Meyer et al. [18], would lead to a second rise of the specific pore volume in a pore diameter range between 0.1 and 1 µm. Here, this rise was nearly not present because only 1.4 wt% carbon black was used and, moreover, in parallel on much higher binder content of 5.6 wt% closing the few pores present within carbon black. Thus, the pores which were modified easiest during calendering were the active material pores.
The pore diameter distribution of the non-calendered pure graphite anode showed a typical rise at 4 to 5 µm, which was shifted to smaller pores and strongly decreased with increasing calendering. At a density of 1.48 g/cm3, the bulk of the pores lies between 0.2 and 2 µm. By adding silicon to the system, the course of the specific pore volume stays mainly the same. Indeed, the first rise of the specific pore volume of the non-calendered electrodes widened to a range of 0.1 to 5 µm, which means that the pore structure was more non-uniform. This can lead to a more inhomogeneous ionic diffusion during cycling, and assuming a correlation between diffusion rate and pore size, it would lead to slower diffusion of the lithium ions on average. This change in the porous network can have different reasons. On the one hand, the silicon particles may cover the surface of the graphite particles and, therefore, clog the inner active material pores. On the other hand, it is possible that the silicon particles partly fill the pores between the graphite particles. Both opportunities will lead to smaller pores as measured from the mercury intrusion. A closer look at the pore diameter range of 0.05 and 0.09 µm showed a clear second discrete rise of the sum distribution of the specific pore volume only for the electrode with the Si/G 10.2 active material. For the Si/G 3.4 electrode, this rise can be seen as rudimentary, which means that this additional range of pores can be declared as silicon pores within the electrode system. Therefore, there is a second area of smaller pores due to the existence of silicon, which can lead to different ionic transport properties during cycling.
The overall porosities of the electrodes at comparable densities are quite identical (see Figure 2d). This results from a change within the particle–particle interactions and does not suggest a change in the particles themselves during the production of composites with different mass fractions of silicon.
3.3. Mechanical Analysis
The adhesion strength between the current collector and coating is an important electrode property to evaluate the processability. If the adhesion strength is too low, the coating will detach from the current collector, which would lead to production scrap.
The measured and averaged adhesion strengths of the electrodes are plotted against the coating density in Figure 3.
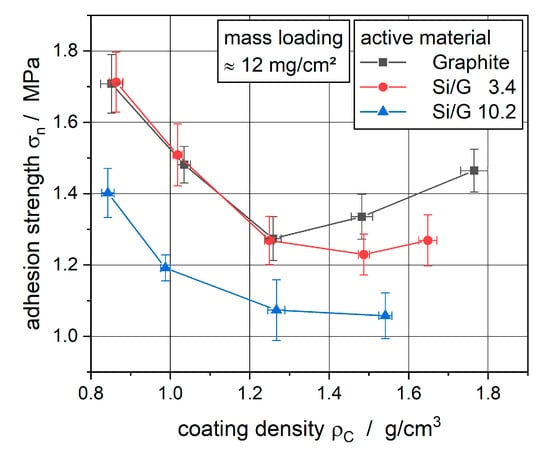
Figure 3.
The adhesion strength between coating and current collector at different coating densities.
Similar to the results from Meyer [20] for NCM-cathodes and Haselrieder [23] for MCMB-anodes as well as NCM-cathodes, the adhesion strength of the silicon-graphite composite anodes decreased at first with increasing line load during calendering. This can be explained by the shear forces between foil and coating because of their different mechanical behaviors, especially elongation. This led to irreversible particle detachment. At higher applied line loads, the particles were pressed towards the current collector, which resulted in the building of new particle–particle interlocking as well as interlocking between collector and active material particles. This interlocking led to an increased adhesion strength at very high line loads for the graphite anode and the anode with 3.4 wt% silicon content.
Compared to the results from Meyer, this typical trend can only be seen fully for the graphite reference electrode. With increasing silicon content, this trend starts to disappear more and more. For the electrode with the highest amount of silicon, a rise in the adhesion strength does not exist anymore. It seems that the harder silicon particles, with their more elastic deformation behavior, prohibit the building of new particle–particle interlocking due to their strong springback after applying the forces during calendering. As investigated by Diener et al. [29], the springback of electrodes after calendering can be in the order of 4% to 37%, depending on the applied line load. Concerning the processability of the electrodes, the calendering of silicon-containing anodes leads to lower adhesion strength and, therefore, the coating can delaminate from the copper foil more easily.
Nanoindentation or micromanipulation, respectively, is a method used to determine the deformation behavior of materials such as battery electrode coatings [24,30,31,32,33]. Using this method, not only the total deformation work can be measured, the plastic and elastic deformation work can be measured as well. Thus, it is possible to lead back the different required line loads of the electrodes during calendering to the deformation behavior of the coating.
For good comparability, the electrodes with a mass loading of about 12 mg/cm2 and a density of about 1.00 g/cm3 are shown in Figure 4. The total distribution Q0 of 80 single measurements of the total deformation work Wtot. is depicted in Figure 4a, the plastic deformation work Wpl. is shown in Figure 4b, and the elastic deformation work Wel. is displayed in Figure 4c. Furthermore, the quotients between the plastic and the elastic deformation works Wpl./Wel. of the single measurements being a measure for the quasi-static restitution coefficient, see Paulick et al. [34], are shown in Figure 4d.
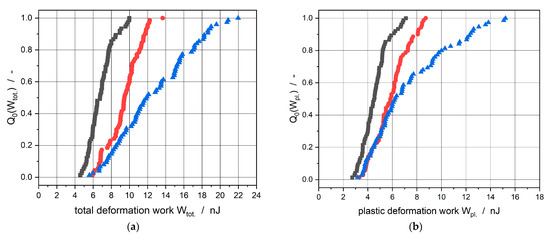
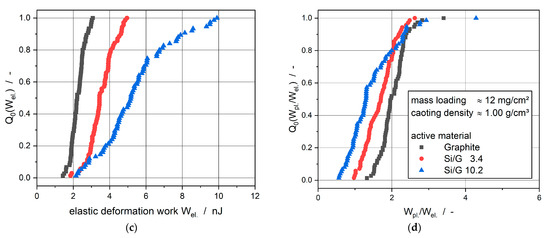
Figure 4.
Electrodes with different active materials, mass loading ≈12 mg/cm2, coating density ≈1.00 g/cm3. (a) Total distribution of total deformation work; (b) total distribution of plastic deformation work; (c) total distribution of elastic deformation work; (d) total distribution of the ratio between plastic and elastic deformation work.
The required work to deform the electrodes increased with an increased silicon mass content due to the fact that the total distributions of the total deformation works were shifted to the right on the abscissa. Considering the distribution curves of the plastic and elastic deformation works and especially the ratio between the plastic and elastic deformation work, it was obvious that silicon in the coating led to a more elastic deformation behavior. The shift to the left on the Wpl./Wel. abscissa with increasing silicon mass content was synonymous with a higher dominance of the elasticity of the particles. These results supported the assumption of a higher elastic deformation and, therefore, of a higher springback of the electrodes during the calendering process. This higher springback was also responsible for the lower adhesion strength between coating and copper foil due to the prohibition of new particle–particle interlockings. Furthermore, the deformation behavior of the electrodes showed that higher works were applied with increasing silicon mass content to reach the same degree of plastic deformation; as a consequence, higher line loads were required to achieve the same coating density as presented in Figure 1a. This trend in the results from silicon-graphite-blend electrodes was equivalent to the mechanical behavior of pure graphite and silicon from nanoindentation measurements [35,36,37].
Figure 5a shows a typical normal force over probe displacement course from nanoindentation measurements. In addition, the maximal displacement hmax after elastoplastic displacement as well as the resulting displacement hend after elastic redisplacement are noted. Thus, hend is the irreversible plastic deformation of the measured sample. For further consideration, the factor fNI is defined as the ratio of elastic deformation and total deformation of the electrodes:
fel = (hmax − hend)/hmax
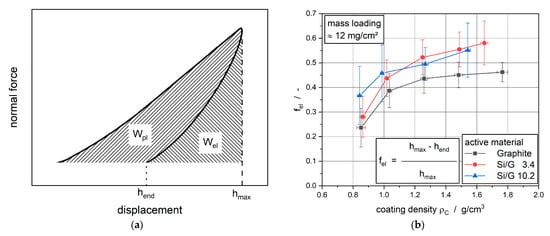
Figure 5.
(a) Typical normal force and displacement behavior during a nanoindentation measurement; (b) factor fel of electrode with different active materials for different coating densities.
From definition, the factor fel has to be in the range of 0 ≤ fel ≤ 1 whereby 0 would be equivalent to ideal plastic material, and 1 would represent an ideal elastic material. This factor was calculated and averaged from the 80 single measurements and is shown in Figure 5b.
The factor fel always lies in the range from 0.15 to 0.7, which means that the investigated electrode samples act elastoplastic. In the case of the non-calendered electrodes with rising silicon content, the factor fel increased. Thus, the higher silicon content was responsible for a more elastic deformation behavior. With increasing coating density and, therefore, higher applied line loads during calendering, the electrode coating underwent more and more plastic deformation. Thus, with increased coating density, the electrodes showed a more elastic deformation behavior, which led to higher springback during calendering. Furthermore, the higher fel-values for the silicon-containing electrodes represented stronger springback due to the elasticity of the coating for the whole investigated area of coating density. In general, the values of fel for the silicon-containing electrodes were higher than comparable fel values of the graphite electrode at the same coating densities. This may lead back to the mechanical influence of silicon on the electrode system. Though, comparing the two silicon-containing anodes the trend as well as the fel values, including standard deviation, can be declared as nearly identical.
3.4. Electric and Electrochemical Analysis
For the electrical analysis by a resistance measurement, a 40 cm2 piece of the electrodes was cut out and measured 10 times at different positions. The results of the composite volume resistivity of the 10 measurements were averaged and displayed in Figure 6.
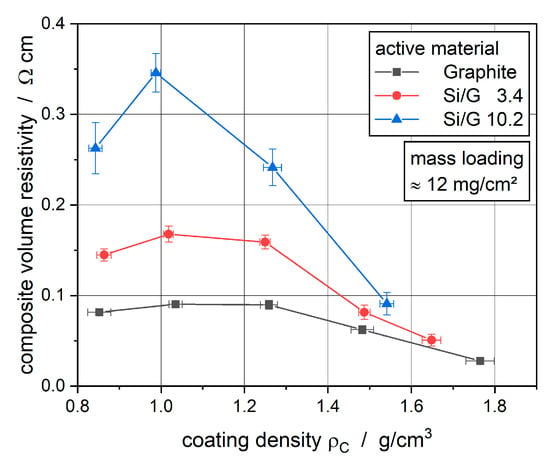
Figure 6.
Composite volume resistivity of the electrodes with different coating densities.
In Figure 6, the composite volume resistivity of the electrodes with different active materials is displayed for different coating densities. With comparatively small applied line loads the resistivity was increasing due to the breaking of the first bonds between the active material particles. As a result of further compaction and, therefore, a lower porosity of the electrode coatings, new electrical particle–particle contacts were created, which led to lower resistivity. Particularly, the lower porosity and, therefore, the new particle–particle contacts led to more direct electrical pathways through the coating, which means that less particle–particle contact resistances occured in a defined area of the coating. These two aspects explain the general course of the curves with increasing coating density. It has to be noticed that the resistivity of the silicon-containing electrodes is 1.5 to 4 times higher than the resistivity of the graphite electrode, especially at coating densities lower than 1.2 g/cm3. Müller et al. [21] show an increased electrical resistance of active material powder when adding silicon nanoparticles to graphite particles and lead this effect back to the electric semiconducting properties of silicon itself. Considering this electric property of silicon, it seems that the existence of silicon particles in the electrode coating is responsible for a higher resistivity. Furthermore, the increased amount of silicon in the active materials of the electrodes leads to an increased resistivity, which supports the assumption of Müller et al. that silicon is mainly responsible for a lower conductivity of a particular battery electrode system.
In Figure 7, the volumetric energy densities of the C-rate test of full cells in a pouch cell setup with an area capacity of 4 mAh/cm2 are shown. For each electrode with different active material and different densities, three cells were built and averaged.
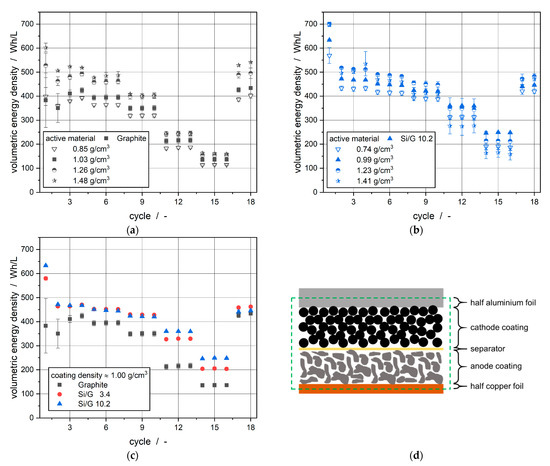
Figure 7.
Volumetric energy densities at C-rate-tests of full cells in pouch cell setup of the (a) graphite electrode at different coating densities; (b) Si/G 10.2 electrode at different coating densities; (c) electrodes with a coating density of ≈1.00 g/cm3; (d) included parts for calculation of volumetric energy density of a battery compartment.
In this study, the produced electrodes were calendered to influence their physical structure and, therefore, their electrical and electrochemical behavior. Thus, the compaction combined with the usage of active materials with different specific capacities should lead to a highly influenced volumetric energy density of the cell stack. The volume of a single cell stack consisting of an anode, separator and cathode was calculated for each electrode-density variation using the averaged thicknesses of the three components and their according areas, as displayed in Figure 7d. The area and the measured heights of the components for cell assembly are listed in Table 4. The height of the electrodes also includes half of the thickness of the collector foils.

Table 4.
Area and height of the used components for full cells in a pouch cell setup.
Figure 7 shows the averaged volume energy densities of three pouch cells each in full cell setup for different densities during C-rate testing. As expected, with rising electrode density and, therefore, decreasing electrode height, the volumetric energy density during the formation cycles rises. This phenomenon occurs for the graphite electrodes as well as for the Si/G 10.2 electrodes. During the C-rate test, the electrodes run through charge and discharge processes, including electric transport processes and in parallel ionic diffusion within the electrolyte of the electrode pores. Thus, porosity and pore structure as well as electrode thickness, have a significant influence on the electrochemical performance of the electrodes. As seen in Figure 7a the volumetric energy density of the graphite electrodes decreases at higher C-rates. This can be explained by a limitation due to one of the two transport processes. Regarding the very good electric conductivity of active materials for anodes compared with active materials for cathodes, it can be assumed that the decreased volumetric energy density is caused by ionic limitation. A limitation of the diffusion of lithium-ions into the graphite active material particles could be a further reason for the decreasing volumetric energy density at higher C-rates [38]. Not only is the porosity decreased, but also the tortuosity will be increased by the calendering resulting in a distinctly decreased effective diffusion coefficient. [22,39,40] For the graphite electrode, a higher volumetric density can be observed for the stronger calendered electrodes. This effect can be explained by the smaller electrode thickness as a result of the compaction process and, therefore, a smaller volume, which was taken into account during the calculation of the volumetric energy densities. After the C-rate test, a full recovered behavior of the graphite electrodes independent of calendering status takes place.
Figure 7b shows the performance during C-rate testing of the electrodes with Si/G 10.2 as active material. Congruent to the behavior of the graphite electrode, the volumetric energy density of the Si/G 10.2 electrode decreases at higher C-rates. Compared to the graphite electrode, the volumetric energy density of the Si/G 10.2 does not increase with stronger calendering for all investigated C-rates. Especially at 2C and 3C the volumetric energy density of the electrode with a coating density of 0.99 g/cm3 surpasses the anodes with higher coating densities and, therefore, lower coating thicknesses. This can be lead back to a combination of ionic diffusion limitation caused by the low porosity of the electrode and the higher mechanical damage of the coating structure due to calendering resulting in disadvantageous volumetric energy densities. In addition, the irreversible loss of capacity between the first cycle during formation and the first cycle after C-rate test of the strongly calendered electrodes with silicon in the active material increases. This increase of irreversible capacity loss can be explained by the mechanical forces due to the lithiation mechanism in combination with the low porosity of the coating resulting in damage of the electrode coating. The comparison between the different produced electrodes with different active materials is displayed in Figure 7c. The density compared was set to around 1.00 g/cm3 according to the worse electrochemical performance of the Si/G 10.2 electrode at higher coating densities. As expected, the initial volumetric energy density was rising with larger amounts of silicon in the active material and, therefore, smaller electrode thicknesses. Further, the electrochemical performance of the Si/G 3.4 electrode shows the same behavior as the other electrodes during C-rate testing. Furthermore, as expected, the volumetric energy density of the Si/G 3.4 electrode lies between the graphite electrode and the Si/G 10.2 electrode. The irreversible capacity loss of the Si/G 3.4 electrode is also smaller compared to the Si/G 10.2 electrode due to lower mechanical forces during lithiation and de-lithiation.
For a deeper look into the charge and discharge behavior of the pouch cells, see Figure S1 in the supplementary part. There, the voltage is plotted against the specific capacity of the NMC622 cathode for all cells at the different C-rates of the C-rate test. As for each rate, three cycles were performed, and the middle one was always chosen for depiction.
4. Conclusions
The effect of applied line loads during calendering and of silicon content of anodes based on silicon-graphite composites on physical and electrochemical anode properties was investigated. Further, electrode properties such as adhesion strength, deformation behavior and electrical and electrochemical performance following the impact of the calendering process were presented. The trend of a rising elastic deformation behavior with increasing silicon mass contents leads to a higher springback and, therefore, stronger damages to the particle system of the electrode resulting in decreased adhesion strength. Furthermore, the electric conductivity of the anodes decreases with rising silicon content due to the semi-conductivity of silicon itself. In addition, the effect of calendering on silicon-containing electrodes does not have to be beneficial for the electrochemical performance at C-rates higher than 1C. The combination of low porosity and mechanical forces during cycling leads to decreased volumetric energy densities.
In further work, anodes based on silicon-graphite composites with more different silicon mass contents and production routes should be investigated to improve the mathematical description of the calendering behavior. In addition, a potential correlation between process route, particle structure and deformation behavior could be determined. The effect of the mass fraction of silicon nanoparticles on the compaction resistance could be described by a potential equation. Furthermore, a special design of silicon-graphite composites such as carbon-coated silicon-graphite particles should be investigated during calendering and the influence of mechanical compaction on the electrochemical performance of these modified active materials.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/batteries8050046/s1, Figure S1: voltage curves at different C-rates for the (a) graphite electrode at 0.85 g/cm3; (b) graphite electrode at 1.03 g/cm3; (c) graphite electrode at 1.26 g/cm3; (d) graphite electrode at 1.48 g/cm3; (e) graphite electrode at 1.76 g/cm3; (f) Si/G 3.4 electrode at 0.98 g/cm3; (g) Si/G 10.2 electrode at 0.74 g/cm3; (h) Si/G 10.2 electrode at 0.99 g/cm3; (i) Si/G 10.2 electrode at 1.23 g/cm3; (j) Si/G 10.2 electrode at 1.41 g/cm3.
Author Contributions
Conceptualization, S.S. and R.J.; formal analysis, S.S. and N.M.; investigation, S.S., N.M. and A.D.; writing—original draft preparation, S.S.; writing—review and editing, A.K. and R.J.; visualization, S.S.; supervision, A.K.; project administration, R.J.; funding acquisition, A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research work was funded by the German Federal Ministry of Education and Research and the Project Management Jülich within the project HEMkoop (Reference No. 03XP0117B). We acknowledge support by the Open Access Publication Funds of Technische Universität Braunschweig.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in this manuscript and the accompanying Supplemental Material.
Acknowledgments
The authors would like to thank the project partner SGL Carbon and ARLANXEO for providing material as well as Stoyan Ivanov, Jan-Michael Kröhnke and Alexander Neuberger from the Institute for Particle Technology for their technical support in electrode production.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Zubi, G.; Dufo-López, R.; Carvalho, M.; Pasaoglu, G. The lithium-ion battery: State of the art and future perspectives. Renew. Sustain. Energy Rev. 2018, 89, 292–308. [Google Scholar] [CrossRef]
- Bryntesen, S.N.; Strømman, A.H.; Tolstorebrov, I.; Shearing, P.R.; Lamb, J.J.; Stokke Burheim, O. Opportunities for the State-of-the-Art Production of LIB Electrodes—A Review. Energies 2021, 14, 1406. [Google Scholar] [CrossRef]
- Diouf, B.; Pode, R. Potential of lithium-ion batteries in renewable energy. Renew. Energy 2015, 76, 375–380. [Google Scholar] [CrossRef]
- Betz, J.; Bieker, G.; Meister, P.; Placke, T.; Winter, M.; Schmuch, R. Theoretical versus Practical Energy: A Plea for More Transparency in the Energy Calculation of Different Rechargeable Battery Systems. Adv. Energy Mater. 2019, 9, 1803170. [Google Scholar] [CrossRef]
- Obrovac, M.N.; Christensen, L. Structural Changes in Silicon Anodes during Lithium Insertion/Extraction. J. Solid State Chem. 2004, 7, A93. [Google Scholar] [CrossRef]
- Beaulieu, L.Y.; Eberman, K.W.; Turner, R.L.; Krause, L.J.; Dahn, J.R. Colossal Reversible Volume Changes in Lithium Alloys. Electrochem. Solid-State Lett. 2001, 4, A137. [Google Scholar] [CrossRef]
- Beaulieu, L.Y.; Hatchard, T.D.; Bonakdarpour, A.; Fleischauer, M.D.; Dahn, J.R. Reaction of Li with Alloy Thin Films Studied by In Situ AFM. J. Electrochem. Soc. 2003, 150, A1457. [Google Scholar] [CrossRef]
- Liu, X.H.; Zhong, L.; Huang, S.; Mao, S.X.; Zhu, T.; Huang, J.Y. Size-dependent fracture of silicon nanoparticles during lithiation. ACS Nano 2012, 6, 1522–1531. [Google Scholar] [CrossRef]
- Obrovac, M.N.; Krause, L.J. Reversible Cycling of Crystalline Silicon Powder. J. Electrochem. Soc. 2007, 154, A103. [Google Scholar] [CrossRef]
- Pinson, M.B.; Bazant, M.Z. Theory of SEI Formation in Rechargeable Batteries: Capacity Fade, Accelerated Aging and Lifetime Prediction. J. Electrochem. Soc. 2013, 160, A243–A250. [Google Scholar] [CrossRef]
- Dhillon, S.; Hernández, G.; Wagner, N.P.; Svensson, A.M.; Brandell, D. Modelling capacity fade in silicon-graphite composite electrodes for lithium-ion batteries. Electrochim. Acta 2021, 377, 138067. [Google Scholar] [CrossRef]
- Dose, W.M.; Piernas-Muñoz, M.J.; Maroni, V.A.; Trask, S.E.; Bloom, I.; Johnson, C.S. Capacity fade in high energy silicon-graphite electrodes for lithium-ion batteries. Chem. Commun. 2018, 54, 3586–3589. [Google Scholar] [CrossRef] [PubMed]
- Haselrieder, W.; Ivanov, S.; Christen, D.K.; Bockholt, H.; Kwade, A. Impact of the Calendering Process on the Interfacial Structure and the Related Electrochemical Performance of Secondary Lithium-Ion Batteries. ECS Trans. 2013, 50, 59–70. [Google Scholar] [CrossRef]
- Karkar, Z.; Jaouhari, T.; Tranchot, A.; Mazouzi, D.; Guyomard, D.; Lestriez, B.; Roué, L. How silicon electrodes can be calendered without altering their mechanical strength and cycle life. J. Power Sources 2017, 371, 136–147. [Google Scholar] [CrossRef]
- Du, Z.; Dunlap, R.A.; Obrovac, M.N. High Energy Density Calendered Si Alloy/Graphite Anodes. J. Electrochem. Soc. 2014, 161, A1698–A1705. [Google Scholar] [CrossRef]
- Indrikova, M.; Grunwald, S.; Golks, F.; Netz, A.; Westphal, B.; Kwade, A. The Morphology of Battery Electrodes with the Focus of the Conductive Additives Paths. J. Electrochem. Soc. 2015, 162, A2021–A2025. [Google Scholar] [CrossRef]
- Kwade, A.; Haselrieder, W.; Leithoff, R.; Modlinger, A.; Dietrich, F.; Droeder, K. Current status and challenges for automotive battery production technologies. Nat. Energy 2018, 3, 290–300. [Google Scholar] [CrossRef]
- Meyer, C.; Bockholt, H.; Haselrieder, W.; Kwade, A. Characterization of the calendering process for compaction of electrodes for lithium-ion batteries. J. Mater. Process. Technol. 2017, 249, 172–178. [Google Scholar] [CrossRef]
- Meyer, C.; Kosfeld, M.; Haselrieder, W.; Kwade, A. Process modeling of the electrode calendering of lithium-ion batteries regarding variation of cathode active materials and mass loadings. J. Energy Storage 2018, 18, 371–379. [Google Scholar] [CrossRef]
- Meyer, C.; Weyhe, M.; Haselrieder, W.; Kwade, A. Heated Calendering of Cathodes for Lithium-Ion Batteries with Varied Carbon Black and Binder Contents. Energy Technol. 2020, 8, 1900175. [Google Scholar] [CrossRef]
- Müller, J.; Abdollahifar, M.; Vinograd, A.; Nöske, M.; Nowak, C.; Chang, S.-J.; Placke, T.; Haselrieder, W.; Winter, M.; Kwade, A.; et al. Si-on-Graphite fabricated by fluidized bed process for high-capacity anodes of Li-ion batteries. Chem. Eng. J. 2021, 407, 126603. [Google Scholar] [CrossRef]
- Froboese, L.; Titscher, P.; Westphal, B.; Haselrieder, W.; Kwade, A. Mercury intrusion for ion- and conversion-based battery electrodes–Structure and diffusion coefficient determination. Mater. Charact. 2017, 133, 102–111. [Google Scholar] [CrossRef]
- Haselrieder, W.; Westphal, B.; Bockholt, H.; Diener, A.; Höft, S.; Kwade, A. Measuring the coating adhesion strength of electrodes for lithium-ion batteries. Int. J. Adhes. Adhes. 2015, 60, 1–8. [Google Scholar] [CrossRef]
- Westphal, B.; Bockholt, H.; Günther, T.; Haselrieder, W.; Kwade, A. Influence of Convective Drying Parameters on Electrode Performance and Physical Electrode Properties. ECS Trans. 2015, 64, 57–68. [Google Scholar] [CrossRef]
- Bartali, R.; Micheli, V.; Gottardi, G.; Vaccari, A.; Laidani, N. Nanoindentation: Unload-to-load work ratio analysis in amorphous carbon films for mechanical properties. Surf. Coat. Technol. 2010, 204, 2073–2076. [Google Scholar] [CrossRef]
- Barth, N.; Schilde, C.; Kwade, A. Einfluss von Prozessparametern auf die mechanischen Eigenschaften von nanopartikulären Beschichtungen. Chem. Ing. Tech. 2012, 84, 328–334. [Google Scholar] [CrossRef]
- Dolbow, J.; Gosz, M. Effect of out-of-plane properties of a polyimide film on the stress fields in microelectronic structures. Mech. Mater. 1996, 23, 311–321. [Google Scholar] [CrossRef]
- Qi, Y.; Guo, H.; Hector, L.G.; Timmons, A. Threefold Increase in the Young’s Modulus of Graphite Negative Electrode during Lithium Intercalation. J. Electrochem. Soc. 2010, 157, A558. [Google Scholar] [CrossRef]
- Diener, A.; Ivanov, S.; Haselrieder, W.; Kwade, A. Evaluation of Deformation Behavior and Fast Elastic Recovery of Lithium-Ion Battery Cathodes via Direct Roll-Gap Detection During Calendering. Energy Technol. 2022, 10, 2101033. [Google Scholar] [CrossRef]
- Sangrós Giménez, C.; Finke, B.; Nowak, C.; Schilde, C.; Kwade, A. Structural and mechanical characterization of lithium-ion battery electrodes via DEM simulations. Adv. Powder Technol. 2018, 29, 2312–2321. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Q.; Li, D.; Hu, J.; Xu, J.; Dang, D.; Xiao, X.; Cheng, Y.-T. Mechanical Property Evolution of Silicon Composite Electrodes Studied by Environmental Nanoindentation. Adv. Energy Mater. 2018, 8, 1702578. [Google Scholar] [CrossRef]
- de Vasconcelos, L.S.; Sharma, N.; Xu, R.; Zhao, K. In-Situ Nanoindentation Measurement of Local Mechanical Behavior of a Li-Ion Battery Cathode in Liquid Electrolyte. Exp. Mech. 2019, 59, 337–347. [Google Scholar] [CrossRef]
- Primo, E.N.; Chouchane, M.; Touzin, M.; Vazquez, P.; Franco, A.A. Understanding the calendering processability of Li(Ni0.33Mn0.33Co0.33)O2-based cathodes. J. Power Sources 2021, 488, 229361. [Google Scholar] [CrossRef]
- Paulick, M.; Morgeneyer, M.; Kwade, A. A new method for the determination of particle contact stiffness. Granul. Matter 2015, 17, 83–93. [Google Scholar] [CrossRef]
- Domnich, V.; Gogotsi, Y.; Dub, S. Effect of phase transformations on the shape of the unloading curve in the nanoindentation of silicon. Appl. Phys. Lett. 2000, 76, 2214–2216. [Google Scholar] [CrossRef]
- Chang, L.; Zhang, L. Mechanical behaviour characterisation of silicon and effect of loading rate on pop-in: A nanoindentation study under ultra-low loads. Mater. Sci. Eng. A 2009, 506, 125–129. [Google Scholar] [CrossRef]
- Pradhan, S.K.; Nayak, B.B.; Sahay, S.S.; Mishra, B.K. Mechanical properties of graphite flakes and spherulites measured by nanoindentation. Carbon 2009, 47, 2290–2292. [Google Scholar] [CrossRef]
- Zhang, S.S.; Xu, K.; Jow, T.R. Study of the charging process of a LiCoO2-based Li-ion battery. J. Power Sources 2006, 160, 1349–1354. [Google Scholar] [CrossRef]
- Adam, A.; Knobbe, E.; Wandt, J.; Kwade, A. Application of the differential charging voltage analysis to determine the onset of lithium-plating during fast charging of lithium-ion cells. J. Power Sources 2021, 495, 229794. [Google Scholar] [CrossRef]
- Grießl, D.; Adam, A.; Huber, K.; Kwade, A. Effect of the Slurry Mixing Process on the Structural Properties of the Anode and the Resulting Fast-Charging Performance of the Lithium-Ion Battery Cell. J. Electrochem. Soc. 2022, 169, 20531. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).