Abstract
The electrolyte is an important component of lithium-ion batteries, especially when it comes to cycling high-voltage cathode materials. In this paper, we propose an algorithm for estimating both the oxidising and reducing potential of electrolytes using molecular dynamics and quantum chemistry techniques. This algorithm can help to determine the composition and structure of the solvate complexes formed when a salt is dissolved in a mixture of solvents. To develop and confirm the efficiency of the algorithm, LiBF4 solutions in binary mixtures of ethylene carbonate (EC)/dimethyl carbonate (DMC) and sulfolane (SL)/dimethyl carbonate (DMC) were studied. The structure and composition of the complexes formed in these systems were determined according to molecular dynamics. Quantum chemical estimation of the thermodynamic and oxidative stability of solvate complexes made it possible to establish which complexes make the most significant contribution to the electrochemical stability of the electrolyte system. This method can also be used to determine the additive value of the oxidation and reduction potentials of the electrolyte, along with the contribution of each complex to the overall stability of the electrolyte. Theoretical calculations were confirmed experimentally in the course of studying electrolytes by step-by-step polarisation using inert electrodes. Thus, the main aim of the study is to demonstrate the possibility of using the developed algorithm to select the optimal composition and solvent ratio to achieve predicted redox stability.
1. Introduction
The almost threefold increase in the energy density of lithium-ion batteries (LIBs) in recent years has been mainly achieved due to increased electrode capacity. The primary factor that limit further increases the energy intensity of cathode materials is the insufficient electrochemical stability of electrolytes. To increase the energy density in the LIB, high-voltage cathode materials with a discharge voltage of ≥4.5 V can be used. These include layered nickel-rich and lithium- and manganese-rich cathode materials [1,2,3,4], LiF-MO nanocomposites (M = Mn, Fe, Co) [4,5], LiCoPO4 [6,7] and others.
The electrolytes used in the production of LIBs typically consist of a 1–1.5 M solution of LiPF6 in baseline mixtures of linear and cyclic carbonates, to which functional additives are additionally introduced [8,9,10]. However, commercial electrolytes, which are stable only to ≤4.3 V, consequently cannot ensure the operability of high-voltage cathode materials [11]. In this regard, electrolytes resistant to anodic oxidation at potentials above 5 V are being developed all around the world [12].
Ethylene carbonate (EC), which provides the formation of a stable solid electrolyte layer (SEI) on the surface of the carbon electrode, remains an indispensable component of commercial lithium-conductive electrolytes. EC, like with other components of the electrolyte solution, affects the properties of the cathode–electrolyte interface (CEI), which forms on the surface of cathodes. Under conditions of anodic polarisation of the positive electrode during the charge cycle, molecules of solvent and lithium salt ions undergo electrochemical oxidation at increased potentials. Insoluble products of these poorly studied processes are part of CEI, affecting the stability of cycling and cell performance. Alkyl carbonates still constitute the main components of the electrolyte solution due to their suitable physicochemical properties. Therefore, one of the possible strategies for increasing the electrochemical stability to ≥5 V by modifying the composition of the electrolyte involves the partial replacement of carbonate solvents with more electrochemically stable compounds (whose complete replacement creates problems with the formation of high-quality SEI) [13]. To replace carbonate solvents, several electrolytes have been proposed such as fluorinated [14,15,16], nitrile-based [17,18,19], ionic liquids [20] and sulfone-based [21,22,23] electrolytes. Among them, of particular interest are cheap and affordable sulfones representing a group of by-products of oil and chemical industries, whose most widely used member is sulfolane (SL) [23].
LiPF6 is used as the main lithium salt in commercial electrolytes for LIBs. Despite its many advantages (commercial availability, high conductivity of solutions, the ability to reliably passivate Al foil [10]), the main disadvantage of lithium hexafluorophosphate is its rather low resistance to anodic oxidation [10]. In high-voltage electrolytes, more electrochemically stable salts can be used instead of LiPF6: LiBF4 [24], LiBOB [25], LiDFOB [26], LiTFSI [27]. In addition, it is known that boron-containing salts improve the electrochemical characteristics of high-voltage cathodes [12]. The ancestor of the listed boron-containing salts is lithium tetrafluoroborate LiBF4. The anion BF4− is characterised by a wider range of electrochemical stability (up to 5.2 V) [28] compared to LiPF6− and therefore can serve as an alternative or additional salt in electrolytes for high-voltage LIBs [29]. The decomposition product of lithium tetrafluoroborate BF3 can affect the composition of the protective layers on the electrodes; having the properties of a Lewis acid, it contributes to the dissolution of poorly conductive LiF [30]. Electrochemical cells with an electrolyte containing LiBF4 demonstrate improved electrochemical characteristics [31,32,33,34,35]. This makes LiBF4 promising for use in electrolyte solutions for high-voltage lithium-ion batteries. It should be noted that the electrochemical stability of LiBF solutions depends on the composition of the solvents. It has been shown that a 1 M solution of LiBF4 in an EC/EMC mixture (3:7) is stable to 6 V [25] and in a mixture of SL/DMC (1:1)—up to 5.5 V [23,34,35,36,37,38,39,40,41].
Thus, the electrochemical stability of electrolyte solutions is determined not only by the combination of solvents, but also by the nature and concentration of the lithium salt; the need to vary all these parameters in order to obtain the best result makes experimental studies very laborious. In this regard, it seems relevant to develop adequate approaches to the theoretical selection of the optimal composition of an electrolyte solution undergoing redox reactions on the surfaces of both electrodes and forming lithium-conductive passivating layers [42].
The theoretical methods of molecular modelling and quantum chemical calculations widely used to describe electrochemical systems [43,44,45,46,47] are certainly useful for searching for compositions with high electrochemical stability. However, when using computational chemistry methods, the obtained results depend on the construction of an adequate calculation model. Ideally, such a model should take into account all the features of the LIB: the surface of the electrode, the composition and stability of the electrolyte, the introduction and extraction of lithium into/from the surface of the electrodes, the peculiarity of the chemical reactions, etc. In reality, the creation of such a model is limited by the possibilities of computational resources and the available level of prediction accuracy. For this reason, the authors of most works use the methods of computational chemistry to solve local problems. For example, classical molecular dynamics methods are used to obtain information about near-order structures in electrolyte solutions, to estimate ionic conductivity, and so on. The obvious advantage of the methods of classical molecular dynamics is the ability to study large atomic–molecular systems, while their main disadvantage is the atomistic level of their description, without taking into account the electronic interaction. On the contrary, quantum chemistry methods can be used to evaluate the electronic parameters of the system, including its thermodynamic and electrochemical stability, as well as the surface profile of the potential energy of chemical reactions. Unfortunately, despite the high accuracy of quantum chemical calculations, this method cannot be used to solve all the necessary problems due to the limited size of the atomic–molecular system under study and the impossibility of assessing the obtained parameters in terms of their dynamics.
For evaluating redox potentials or describing the mechanisms of reactions of electrochemical oxidation of solvents (e.g., sulfolane, propylene carbonate, etc., [48]), quantum chemical calculations are most often used. At the same time, modelling of the studied electrochemical system is typically reduced to a separate consideration of the components that make up this system: isolated solvent molecules, their associates, anionic and cationic solvate complexes and solvated ionic pairs. As a result, a fairly wide range of oxidation (reduction) potential values is obtained, covering all the particles studied. An alternative approach with increased predictive value is to calculate additive values of oxidation (reduction) potentials, taking into account the relative contribution of each particle class [10]. Unfortunately, such studies are extremely scarce in the literature.
In quantum chemical calculations, the redox potential assessment is reduced to optimising the geometric parameters of ionic and molecular particles of various grades with the solution of the oscillatory problem. There are two important points here: firstly, the choice of the optimal calculation method and, secondly, the method of accounting for the solvent. In both cases, the adequacy of the choice is tested by correlation with the experiment. Calculations are carried out either using powerful composite methods (G4MP2) [10,49,50,51,52] or according to approaches based on density functional theory [10,42,49,50,51,52,53,54,55]. As a result, the values of the free Gibbs energies of the initial complex and those of the oxidised (reduced) complex are obtained. Calculations are carried out in the approximation of the gas phase and/or by taking into account the solvent using polarised continuum methods. At the same time, Borodin proposes to use acetone as an implicit solvent, the dielectric constant of which is close to the value of most mixtures of carbonate solvents for commercial electrolytes in LIBs [48]. Redox potential values are calculated from the Born–Haber thermodynamic cycle [56]. As a rule, adiabatic values are evaluated. If it is impossible to optimise a particular oxidised (reduced) complex, vertical values are evaluated.
Thus, the [30,57,58,59] solvent molecules ( EC, SL, DMC) and their complexes fall into a range from 5.73 V to 7.42 V, while the experimental data for electrolyte solutions, which appear in a range from 5.3 to 6.7 V [48,57,58], depend on the nature and concentration of the salt, as well as the material of the working electrode. The range of experimental values depends on the type and concentration of salt. Here, the variation in the calculated OP values is obviously related to the calculation and solvent accounting methods. The values of [48] closest to the experimental data are those calculated using composite methods, for example, G4MP2 [59]. Calculations in the approximation of the gas phase or in a solvent medium with a low dielectric constant give inflated values of OP [48,60,61].
Quantum chemical calculations of reduction potentials, as well as their experimental measurements, are much less common in the literature. Thus, for EC, the calculated value is [58,62,63], and experimental values are from 0.11 to 1.9 V [64].
According to experiment [64], the heteromolecular SL-DMC associate is reduced at 0.10–1.38 V against 0.67 V—the value estimated by quantum chemistry methods.
Anionic solvate complexes are the most “capricious” in terms of optimising the geometric parameters of oxidised and reduced forms. However, for such particles, OP values are often found in the literature. For an unsolvated anion, the BF4− value is estimated to be between 8.00 and 8.57 [48], depending on the calculation method; for the anionic complexes of various compositions formed by it, however, the oxidation potential is significantly lower, ranging from 5.79 to 6.39 V. It is important to note that the authors consider anionic complexes only in individual solvents; RP values for anionic complexes with mixed solvate shell have not been found in the scientific literature.
Although features of the structure of cationic complexes have been well described in the scientific literature [27,49,60,61,65,66], these studies typically refer to individual solvents. Reduction potentials are estimated for cationic solvate complexes Li+(EC)1 and Li+(DMC)1 [27,49,60,61,66]. In the first case, the RP values obtained by different authors fit into the range of 0.45–0.61 V, which is quite consistent with the experimental value of 0.54 V. In the second case, the calculated values range from 0.22 to 0.60 V.
For the solvated ion pairs of the composition {Li+BF4−} (EC)1 and {Li+BF4−} (EC)2, calculated values on the acidity potential fall into the range of 6.60–8.74 V [48]. These neutral particles can undergo both electrochemical oxidation and electrochemical reduction. However, no work has been found in the literature on RP calculations.
As can be seen from the above examples, the redox potential values estimated by the methods of quantum chemistry for various complexes (near-order structures) generally correlate with experimental data. This indicates the adequacy of the quantum chemical methods and methods used to take into account the solvent medium. However, the data available in the scientific literature mainly relate to systems based on a single solvent, whereas, in practice, mixtures of two, three or more solvents are typically used. To predict the electrochemical stability of such solutions, it is necessary to additionally investigate heteromolecular associates and complexes with a mixed solvate shell. In addition, it is noteworthy that the most studied are isolated solvent molecules, their associates and cationic solvate complexes, while solvated ionic pairs are described in less detail, and anionic solvate complexes are practically not considered. At the same time, in order to obtain correctly calculated data on redox potential, it is necessary to consider all local structures existing in the studied electrolyte solution. In addition, in order to increase the predictive value of the calculations, it seems expedient to evaluate the additive values of ORP, taking into account the relative contribution of each of the possible complexes. In this regard, the need to develop a generalised algorithm for theoretical studies of the electrochemical stability of an electrolyte solution becomes obvious, which would allow the analysing of systems of any complexity without restrictions on the component composition, and at the same time reduce the number of particles under study to a reasonable minimum, excluding the unlikely ones from consideration.
In this paper, we investigate a 1 m solution of LiBF4 in two binary solvent mixtures: EC/DMC (1:1) and SL/DMC (1:1). Earlier [67], we proposed an algorithm for the theoretical evaluation of the electrochemical stability of lithium-conducting electrolytes based on a mixed solvent. In this paper, this algorithm is used to analyse the effect of the nature of solvents on the redox potential of the electrolyte. At the first stage, the dominant types of local structures were determined by the methods of molecular dynamics and their relative contribution was estimated; a molecular model of the electrolyte solution was created. Furthermore, quantum chemical calculations of the structure, thermodynamic parameters and electrochemical stability were performed for all isolated particles; special attention was paid to complexes with a mixed solvate shell. The oxidation and reduction potentials were calculated as additive values. Verification of the adequacy of the constructed models of electrolyte solutions and the correctness of the algorithm of complex theoretical studies was carried out through comparison with experimental data regarding the density and window of the electrochemical stability of electrolyte solutions and chemical shift in NMR spectra. The experimental results obtained for both studied solutions are consistent with the theoretically calculated values, which makes it possible to recommend the approach used in this work for predictive optimisation of the composition of electrolyte solutions.
2. Materials and Methods
2.1. Theoretical Part
2.1.1. Molecular Dynamic Simulations
Molecular dynamic modelling was carried out using the Schrodinger Suite Release 2021-2 software package and the Desmond [68] OPLS3/OPLS4 [69,70]. To simulate the selected systems, a model was built where the space is limited by a cubic lattice, taking into account periodic conditions. The number of particles in the design systems corresponded to the composition of the test solution (1 m LiBF4 in EC/DMC (1:1, vol.) and 1 M LiBF4 in SL/DMC (1:1, vol.)). The protocol for preparing the system for simulation included pre-minimisation (conjugate gradient method) and the balancing of components in the NPT ensemble for 2 ns at 298 K and at 400 K, sequentially. The period of the recorded simulation was 50 ns in the ensemble NVT at 298 K. To maintain the constancy of the temperature of the systems, the Nosé–Hoover thermostat was used [71,72].
The study of the structural features of substances, in particular to describe the composition and structure of complexes, was evaluated through the radial distribution function (RDF) and its integral component N (R) [73]. Analysis of the results of molecular dynamics made it possible to estimate the frequency of occurrence of complexes of cationic structure and solvated ion pairs. The geometric parameters of the most frequently occurring complexes were used for the subsequent evaluation of their thermodynamic and electrochemical stability by the methods of quantum chemistry.
2.1.2. Quantum Chemical Calculations
All quantum chemical calculations were carried out using GAUSSIAN 16 rev B.01 software [74]. Optimisation of the geometric parameters of atomic–molecular systems with the frequency task was carried out at the DFT level using the functionality M052x [75] and the basic set TZVP [76]. The empirical dispersion D3 [77] was taken into account. Thermodynamic parameters were calculated in the approximation of the gas phase at 298 K and atmospheric pressure, as well as taking into account the implicit salvation [78]. Acetone with a ε = 20.5 was considered as a solvent, which is close to the value of the dielectric constant of most electrolyte mixtures [79].
To assess the thermodynamic stability of the studied complexes of solvated ionic particles, incremental (stepwise) values of the formation energies (ΔfGoinc) were considered as the Gibbs energy of the reaction of the sequential attachment of the solvent molecule to complexes [67], based on the second consequence of Hess’s law.
The adiabatic oxidation potential (AOP) ΔEoxabs and the adiabatic reduction potential (ARP) ΔEredabs for each class of complexes were evaluated according to the Born–Haber cycle [56].
The value of the oxidative potential can be expressed by the formula:
The value of the reduction potential can be expressed by the formula:
—free ionisation energy in the gas phase at T = 298.15 K, are the free solvation energy of the oxidised and initial complex, respectively; F is Faraday’s constant. The free ionisation energy has the contribution of the ionisation potential, which includes the energy of adiabatic ionisation and zero point vibration correction or entropic contribution of −TΔS [48].
The additive value of the oxidative potential characterising the system as a whole was estimated using Maxwell–Boltzmann statistics using the formula E°additive):
where N is the Maxwell–Boltzmann distribution according to the values of the incremental energies of the formation of the i-complex—adiabatic oxidative potential of the i-complex.
2.2. Experimental
The electrolytes were prepared and stored in a dry argon box. For the preparation of electrolytes, ethylene carbonate (battery grade, Sigma-Aldrich, Saint Louis, MO, USA), sulfolane (anhydrous, ≥99%, Sigma-Aldrich) and dimethyl carbonate (anhydrous, ≥99%, Sigma-Aldrich), as well as LiBF4 (≥98%, Sigma-Aldrich), were used. To remove traces of water from ethylene carbonate (battery grade, Sigma-Aldrich) and dimethyl carbonate (anhydrous, ≥99%, Sigma-Aldrich), the solvent mixture was kept over molecular sieves 3A for 1 week. LiBF4 (≥98%, Sigma-Aldrich) was dried in a vacuum drying oven at 140 °C for 4 days. Salt concentration in the tested solutions was 1 m.
The electrochemical stability window of the electrolyte was determined by step-by-step polarisation according to the procedure described in work [67]. For measurements, three-electrode electrochemical cells with an inert working electrode of platinum, a reversible lithium counter electrode and a lithium comparison electrode were used. During the experiment, a phased polarisation of the cell was carried out with a constant potential difference specified in the range of interest, with stationary current measurement (Iss). The working electrode was gradually polarised for each given potential value, and the dependence of the current on the time to reach a stationary value was recorded. To determine the value of Eox, the dependences of the stationary current on the potential were constructed.
To determine the oxidation potential, the experiment was conducted in a range from 2.5 V (open circuit voltage) to 5.99 V, relative to Li0/Li+. For measurements, potentiostat P-20 × 8 (Elins LLC, Chernogolovka, Russia) was used.
The density of the electrolyte solution was determined using the power of pycnometers with a nominal volume of 5 mL, pre-calibrated with distilled water at a temperature of 25 °C; measurements were performed in three parallels.
The compositions were confirmed using high-resolution NMR. The spectra on the cores 1H, 7Li, 11B, 13C, 17O and 19F were captured on the Bruker Avance III 500 MHz NMR spectrometer. The spectra were recorded at room temperature (24 °C), at frequencies 500, 194, 160, 126, 68 and 471 MHz for 1H, 7Li, 11B, 13C, 17O and 19F, respectively. Liquid samples were placed in standard 5 mm ampoules without the addition of deuteron solvent. To calibrate the chemical shift scale, an additional magnetic field was set from the DMSO-d6 signal as an external standard (2.50 ppm for 1H).
3. Results
3.1. Theoretical Studies
3.1.1. Molecular Dynamics
To determine the density of electrolyte solutions by molecular dynamics, molecular dynamic simulations of the systems under study were carried out within 50 ns. Electrolyte solution density 1 m {Li+BF4−} EC/DMC (1:1, vol.) equal to 1.238 ± 0.04 g/cm3 (Figure S3); for solution 1 m {Li+BF4−} SL/DMC (1:1, vol.) equal to 1.213 ± 0.04 g/cm3 (Figure S4). It has been shown that perturbations in terms of cohesion energy remain within the range of 0.2–0.4 kcal/mol (Figures S1 and S2). Insignificant perturbations of the cohesion energy and a slight standard deviation in the values of the solutions’ density indicate the stay of the dynamic equilibrium of the system and the adequacy of subsequent measurements of physical values. The density values of the systems under study generally correlate with the values estimated as a result of the experiment.
Analysis of the results of the molecular dynamic simulation of the salt solution in solvents also allows us to estimate the frequency and probability of the formation of various solvated complexes. In the case of the systems studied in this work, when using a mixture of solvents, the formation of complexes with a mixed solvate sphere is probable. In both systems, the lithium cation primarily coordinates the anions BF4− around itself via a Li+-F-B 3− bond at a distance of about 2 Å. This is evidenced by the heights of the first peaks on the curve for Li+-F-B-F3− and the function of the radial distribution of particles g(R) in Figure 1a and Figure 2a.

Figure 1.
Radial distribution function g(R) (a,c) and statistical structural —factor N(R) (b,d) for a system modelling a 1 m {Li+BF4−} in (EC)1(DMC)1 (1:1, vol.).
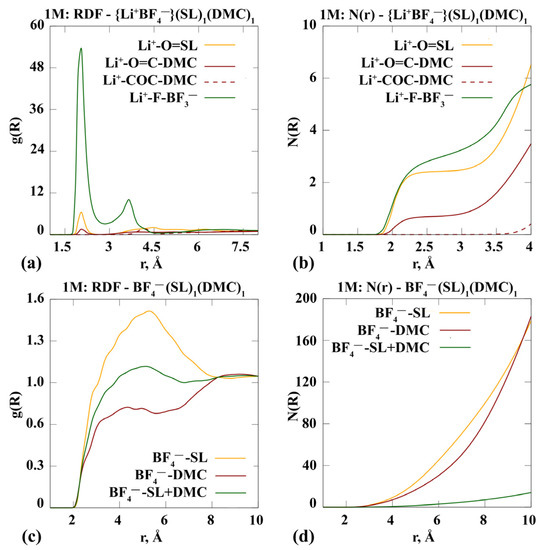
Figure 2.
Radial distribution function g(R) (a,c) and statistical structural factor N(R) (b,d) for a system modelling a 1 m {Li+BF4−} in (SL)1(DMC)1 (1:1, vol.).
Analysing the curves in Figure 1a,b corresponding to the {Li+BF4−} (EC)1(DMC)1 system, it can be noted that the first solvate shell of the lithium cation is likely to include a DMC molecule coordinated to Li+ through an oxygen atom of a carbonyl group. EC coordination with respect to the lithium cation seems unlikely, but in this case the cation also tends to be the carbonyl oxygen atom. The total coordination number of the lithium cation tends to be six: up to three anions, two DMC molecules and no more than one EC. The formation of anionic solvate complexes, if any, is at a distance of 4–6 Å from the anion (Figure 1c). The oscillation of RDF is weakly expressed; the function N(R) is exponential (Figure 1d). All this leads to a conclusion about the weak interaction of the components. At the same time, the coordination of both solvent molecules with respect to the anion is equally likely.
In the {Li+BF4−}(SL)1(DMC)1 system, the coordination of sulfolane with respect to the cation is more pronounced than in the case of the DMC environment. The DMC molecule, just like in a mixture of (EC)1(DMC)1, is coordinated with the cation via carbonyl oxygen. The total value of the coordination number of the cation tends to be six: the coordination of more than three molecules of the anion, two SL and not more than one DMC is likely (Figure 2a,b).
The behaviour of anionic complexes is generally similar to the {Li+BF4−}(EC)1(DMC)1 system: a practical absence of the oscillating nature of g(R) and exponential appearance of N(R) (Figure 2c,d).
Thus, on the basis of data from molecular dynamic simulations, it was shown that in a mixture of EC solvents with DMC, the most likely is the formation of lithium cation complexes, mainly surrounded by DMC molecules (cationic complexes of Li+(DMC)n and solvated pairs {Li+BF4−}(EC)n(DMC)n with a predominance of DMC molecules). The most probable complexes in the SL-DMC mixture are cationic complexes of type Li+(SL)n and solvated pairs of type {Li+BF4−}(SL)n(DMC)n with a predominance of SL molecules.
In addition, anionic complexes are formed in the systems under study. It is logical to consider the composition of possible solvate shells of anions separately from the cation. The near order for the anion BF4− is realised at a distance of 4–5 Å from the centre of the mass of the particle. Such an observation seems quite reasonable, since the radius of the anion is much larger than the radius of the lithium cation.
Analysis of the results of the molecular dynamic simulation allows us to estimate the composition and probability of the formation of various solvate complexes in the system under study. Methods of quantum chemistry are used in this work to assess the thermodynamic and electrochemical stability of complexes.
3.1.2. Quantum Chemical Calculations
In this section, we consider the geometric structure of solvents and a number of solvate complexes, and also estimate the incremental energy of the formation of these complexes.
We have divided all the complexes under consideration into:
- ✓ Cationic, in which solvent molecules are coordinated around a lithium cation;
- ✓ Anionic, where BF4− is also surrounded by solvent molecules and solvated ionic pairs, and where the LiBF4 salt is surrounded by EC, DMC or SL molecules.
Structure and Thermodynamic Stability of Complexes
Solvent associates and anionic complexes
Solvents are prone to forming associates of type (EC)2, (SL)2, (EC)1(DMC)1 and (SL)1(DMC)1. The molecules of many dipolar solvents are prone to self-association and often form dimers or more complex complexes [62]. Possible configurations of EC, DMC and SL molecules, as well as their dimers and heteromolecular associates, are given in Section SI (Figure S5).
According to the analysis of molecular dynamic simulations, the formation of negatively charged anionic complexes is possible in the systems under study. Such complexes are interesting from the point of view of the oxidative stability of the entire system as a whole. Such structures are characterised by a low ionisation potential (IP) value and a low electron affinity (Table S1). Theoretically, anionic complexes can make a significant contribution to the electrochemical stability of the system as a whole.
In molecular dynamic simulations, we observe the formation of mixed-type anionic complexes (Figure 3). Such structures are less common in the scientific literature. Geometric parameters of complexes of composition BF4−(X)n, where X = EC, DMC, SL, are represented in SM (Figure S6).
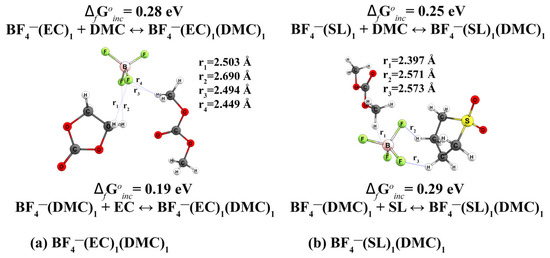
Figure 3.
Geometric structures of anionic complexes BF4− with (EC)1, (DMC)1, (a) (SL)1 and (DMC)1 (b).
In the BF4−(EC)1(DMC)1 complex, the solvents are coordinated on one side of the anion at a distance of about 2.5 Å, with the DMC molecule slightly closer than the EC (Figure 3a). A similar description can be given to the complex of type BF4−(SL)1(DMC)1 (Figure 3b).
The formation of complexes of type BF4−(EC)n, BF4−(DMC)n and BF4−(SL)n (n = 1.2) (Figure S6) is characterised by positive values of the energy of formation (Table A1 #10–13 and Table A2 #10–13). Interestingly, the addition of a second solvent molecule (Table A1 and Table A2 #14) requires less energy than the formation of anionic complexes with pure solvents.
Anionic complexes are unstable structures from the point of view of thermodynamics. Most likely, these are short-lived transition forms of ionic particles. Due to such systems remaining poorly understood, the question of choosing an adequate algorithm for the theoretical study of complexes of this kind becomes an urgent task.
Cation complexes
Cationic complexes, in which molecules of only one type of solvent are coordinated around Li+, are well described in the literature [27,49,60,61,65,66]. The structures we obtained are similar to those published earlier by other researchers. Typically, the arrangement of molecules is quite symmetrical; thus, with an increase in the size of solvent molecules, the distance from the cation to the solvent atom with which the bond is formed increases proportionally. These patterns are observed for the studied cationic complexes (Figures S7–S9). Most cationic complexes are characterised by negative values of the energy of formation (ΔGf°inc) (Table A1 #15–21, 23, 24, 26; Table A2 #15–17, 19–28).
- Complexes of the 1 m {Li+BF4−} в EC/DMC (1:1)
When the DMC and EC molecules are coordinated, the distance from the oxygen atoms to the cation is almost the same (Figure 4). When a mixed complex of Li+(EC)2(DMC)2 is formed, a structure with cross-symmetry of solvents is formed, with the lengths of the bonds differing slightly from each other (Figure 4d).
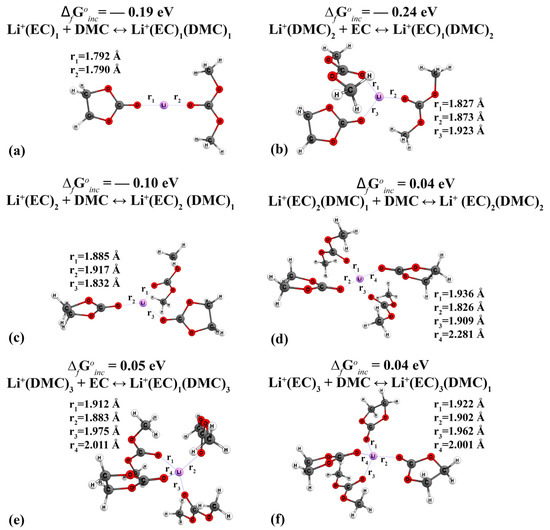
Figure 4.
Geometric structure of mixed-type cationic complexes Li+(EC)n(DMC)n: (a) Li+(EC)1(DMC)1, (b) Li+(EC)1(DMC)2, (c) Li+(EC)2(DMC)1, (d) Li+(EC)2(DMC)2, (e) Li+(EC)1(DMC)3, (f) Li+(EC)3(DMC)1.
From the point of view of their combinatorics, complexes of mixed composition can be formed along various reaction pathways. Here, the free Gibbs energy of the reaction may vary depending on the sequence of attachment of the electrolyte. In Figure 4, we give the lowest values of the incremental energy of the formation of complexes. For more information, see Table A1 and Table A2.
- Complexes of the 1 m {Li+BF4−} в SL/DMC (1:1)
When SLs are coordinated, the distance from oxygen atoms to the cation exceeds that of DMC and EC molecules when comparing the coordination of a single solvent molecule. In the complex Li+(SL)1(DMC)1, the distance from the cation to the SL is 1.832 Å; with the addition of DMC molecules, this distance increases (Figure 5).
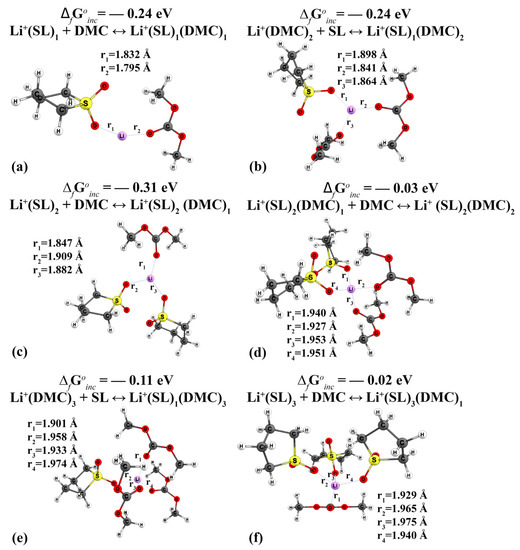
Figure 5.
Geometric structure of mixed-type cationic complexes Li+(SL)n(DMC)n: (a) Li+(SL)1(DMC)1, (b) Li+(SL)1(DMC)2, (c) Li+(SL)2(DMC)1, (d) Li+(SL)2(DMC)2, (e) Li+(SL)1(DMC)3, (f) Li+(SL)3(DMC)1.
All mixed complexes of type Li+(SL)n(DMC)n (Figure 5) are characterised by negative values of free energy (ΔGfoinc). Thus, analysing Figure 4 and Figure 5, as well as the data of Table A1 and Table A2, it logically follows that the formation of lithium cation complexes with molecules (SL)1(DMC)1 proceeds with a greater energy gain than with molecules (EC)1(DMC)1.
Solvated ionic pairs
Negatively charged particles tend to coordinate with a positively charged cation. Given the conformational mobility of anions, the lithium cation coordinates anions around itself in addition to solvent molecules. Here, too, the most interesting complexes are of mixed type (Figure 6). Geometric parameters of the remaining complexes of the type {Li+BF4−}(X)n, where X = EC, DMC, SL, are represented in SM (Figure S10).
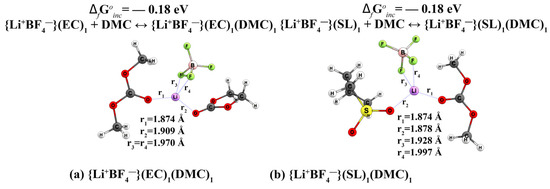
Figure 6.
Geometric structure of mixed-type complexes {Li+BF4−} for system (EC)1(DMC)1 (a) and system (SL)1(DMC)1 (b).
In the {Li+BF4−}(EC)1(DMC)1 complex (Figure 6a), the lithium cation is located closer to the DMC than to the anion or to the EC. The bond length between the oxygen DMC and the cation is 1.874 Å, while the bond length between the boron and Li+ is 1.970 Å and between oxygen EC and cation is 1.909 Å. In the case of {Li+BF4−} (SL)1(DMC)1 (Figure 6b), the cation is also closer to DMC than to SL, but this difference is very small. In other words, the coordination of solvent molecules in relation to the ionic pair is unchanged. The formation energy of −0.18 eV is the same for both these complexes.
Unlike with the associations of solvent molecules and anionic solvate complexes, the formation of solvated and unsolvated ionic pairs always proceeds with an energy gain. The values of the incremental energy of the formation of the complex in all cases considered are negative (Table A1 and Table A2 #30–34).
According to the analysis of NMR signals of the systems under consideration, the ratio of proton signal intensity for EC:DMC solvents is 1.47:1, and SL:DMC = 1:1.1 in the mole ratio. In the considered concentration of salt in solution, one ionic pair accounts for up to 6–7 solvent molecules. Given the structure of solvated complexes, it can be assumed that such a number of molecules makes up the sphere of near and far order. In this paper, we considered near-order complexes and estimated chemical shifts using quantum chemistry methods for systems {Li+BF4−}(EC)1(DMC)1 and {Li+BF4−}(SL)1(DMC)1. There is a correlation between the values of chemical shifts obtained by NMR and those estimated by QM methods (Figure 7).
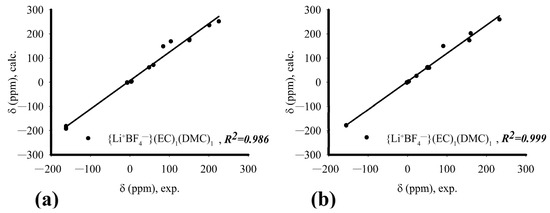
Figure 7.
Dependence of experimental and calculated values of chemical shifts: (a) {Li+BF4−}(EC)1(DMC)1; (b) {Li+BF4−}(SL)1(DMC)1.
Since the approximation of QM-calculated chemical shifts relative to the experimentally obtained values on the nuclei 1H, 7Li, 11B, 13C, 17O and 19F is a straight line at an angle of 45°, there is reason to believe in the correctness of the chosen structure of associates for quantum chemical calculation. Thus, the totality of methods of molecular mechanics, quantum chemistry and experimental NMR data unequivocally confirms the existence of mixed composition complexes.
Electrochemical Stability
The electrochemical stability of the electrolyte solution is determined by the set of formed complexes. The resistance of the electrolyte to oxidation, which can be considered as an additive value, consists of the thermodynamic and electrochemical stability of individual components: isolated solvent molecules, their associates, anionic solvent complexes and unsolvated anions, as well as solvated and unsolvated ionic pairs.
Solvents and their associates
For solvents and their associates, oxidative stability is estimated in the range of 5.73–7.42 V. Thus, evaluated using the methods of quantum chemistry [30,48,62,79,80,81], values of OP (ΔEoxabs) for solvent molecules (EC, SL, DMC) and their associates fall in a range from 5.58 V to 8.50 V [30,48,62,79,80,81]. The experimental data fall in a range from 4.6 to 6.7 V [57,58,64,82,83,84]. RPs (ΔEredabs) for almost all solvents are negative values except SL (Table A1 #3), (SL)1(DMC)1-1 (Table A1 #7) and (SL)1(DMC)1-1 (Table A1 #8). From the literature, it is known that the RP of EC < 1 [30], for SL is 0.4 V [85]. There are two different RPs of (SL)1 (DMC)1-1: 0.102 V and 1.386 V [64]. According to the incremental Gibbs energy values of these complexes, ΔfGoinc, (Table A1 #1–8 and Table A2 #1–8), the formation of such associates is unlikely. ΔfGoinc values are positive.
Anionic complexes
- Oxidation potentials
Negatively charged complexes are characterised by a low IP value (Table S1), as well as a lower value of the OP (Table A1 #10–14 and Table A2 #10–14). The ΔfGoinc values indicate that the formation of such systems in a salt solution requires energy. However, anionic complexes can contribute to the additive value of the OP salt {Li+BF4−} in studied electrolyte solutions.
The formation of solvate complexes of the anion BF4− with molecules EC and/or DMC, and/or SL (Table A1 #10–14, Table A2 #10–14), is also thermodynamically unlikely, despite which of the solvents is coordinated close to the anion first. The fairly high values (ΔEoxabs) of all anionic solvate complexes correspond to a range from 5.43 to 6.16 V. A high value of ΔEoxabs is also characteristic of the unsolvated anion BF4− (8.54 V). All calculated values correlate with the literature data.
- Reduction potentials
The RPs for anionic complexes cannot be calculated. It commonly occurs that the optimising procedure of geometric parameters of the N-1 system (electron removal) ends unsuccessfully with a decomposition of the negatively charged anion–solvent complex. Many [27,48] authors bypass this problematic issue by calculating the vertical values of the OP. However, the calculation of vertical values does not imply a complete optimisation of the geometric parameters of the N-1 system, but represents a single (Single Point) calculation, which does not fully take into account the processes occurring in the system.
Cation complexes
- Oxidation potentials
Oxidising potentials for cationic complexes have not been evaluated. Obviously, the removal of the second electron from a positively charged system would require a large quantity of energy and is therefore unlikely.
- Reduction potentials
The RP values range from −1.02 to 0.52 V, depending on the structure of the complex. The highest RP value is characteristic of the cationic complex of mixed type Li+(EC)1(DMC)1. The RP values of cationic complexes for the system (EC)1(DMC)1 can be arranged in the following series: Li+(DMC)3 < Li+(DMC)2 < Li+(DMC)1 < Li+(EC)1 < Li+(EC)4 < Li+-(DMC)4 < Li+(EC)1(DMC)3 < Li+(EC)3(DMC)1 < Li+(EC)2(DMC)1 < Li+(EC)3 < Li+(EC)2(DMC)2 < Li+(EC)2 < Li+(EC)1(DMC)2 < Li+(EC)1(DMC)1. The values of Li+(EC)1 and Li+(DMC)1 are almost the same. The energy of the Li+ (EC)1 (DMC)1 complex formation does not depend on the type of reaction (Table A1 #23). The sequence addition of one and more molecules (DMC or EC) to the complex reduces the RP values (Table A2 #24).
The values of the potentials of cation complexes for the system (SL)1 (DMC)1 can be arranged in the following series: Li+(SL)4 < Li+(SL)3 < Li+(SL)1(DMC)2 < Li+(DMC)3 < Li+-(SL)1(DMC)1 < Li+(DMC)2 < Li+(SL)2 < Li+(DMC)1 < Li+(SL)1 < Li+(SL)1(DMC)3 < Li+(SL)2(DMC)2 < Li+(SL)2(DMC)1 < Li+(SL)3(DMC)1 < Li+-(DMC)4. In this case, there is a slight difference in the RP values of Li+(SL)1 and Li+(DMC)1 (Table A2 #15, #23). The energy of the Li+(SL)1 (DMC)1 complex formation does not depend on the type of reaction (Table A2 #23). The addition of the first molecule (DMC) to the complex reduces the RP values (Table A2 #24), while the second increases it (Table A2 #25). Conversely, the addition of the first and second molecules (SL) increases the RP value (Table A2 #26, 28).
Solvated ionic pairs
- Oxidation potentials
Regardless of the solvent structure (DMC, EC or SL), uncharged ion pairs are characterised by their high ionisation potential (Table S1) and oxidative stability (Table A1 #29–34, Table A2 #29–34). However, the contribution to the overall electrochemical stability of complexes of the type {Li+BF4−}(DMC)1 is more than {Li+BF4−}(EC)1. The formation energy (ΔfGoinc) of the first complex is less. The addition of the second DMC molecule into the first solvate sphere of the Li+ (complex {Li+BF4−}(DMC)2) insignificantly increases the value of the ionisation potential and oxidative stability.
In the case of (SL)1(DMC)1, the contribution to the overall electrochemical stability of complexes of type {Li+BF4−}(DMC)1 will be approximately equal to that made by complexes of type {Li+BF4−}(SL)1. The addition of the second SL molecule into the first solvate sphere of the Li+ (complex {Li+BF4−}(SL)2) increases the value of the ionisation potential and oxidative stability (Table S1, Table A1 #29–34, Table A2 #29–34).
The OP values of the studied complexes for the system (EC)1 (DMC)1 are located in a range from 6.36 to 9.32 V (Table A1 #29–34), and for the system (SL)1 (DMC)1 from 6.69 to 9.32 V (Table A2 #29–34). All obtained values are in accordance with the experimental values given. The highest value of the AOP equal to 9.32 V was obtained for the unsolvated ion pair {Li+BF4−} (Table A1 #29). However, since the ionic pair quite easily dissociates into ions or forms its solvates, its contribution to the additive value of the oxidative potential cannot be considered. The highest value of OP is characteristic of the mixed complex, such as with {Li+BF4−}(SL)2. The OP of the solvated ion pairs for the EC/DMC system can be arranged in the following series: {Li+BF4−}(EC)2 < {Li+BF4−}(EC)1 < {Li+BF4−}(DMC)1 < {Li+BF4−}(DMC)2 < {Li+BF4−}(EC)1(DMC)1; and for the SL/DMC system: {Li+BF4−}(DMC)1 < {Li+BF4−}(DMC)2 < {Li+BF4−}(SL)1 < {Li+BF4−}(SL)1(DMC)1 < {Li+BF4−}(SL)2.
- Reduction potentials
The values of the reductive stability of the studied complexes for the system (EC)1(DMC)1 are in a range from −0.92 to 0.39 V (Table A1 #30–34), while for the system (SL)1(DMC) 1 the corresponding figures are from −1.04 to 0.04 V (Table A2 #30–34). The lowest RPs have systems demonstrating the highest AOP, namely {Li+BF4−}(EC)1(DMC)1 and {Li+BF4−}(SL)2. The ARP values of the solvated ion pairs for the system (EC)1(DMC)1 can be arranged in the following series: {Li+BF4−}(EC)1(DMC)1 < {Li+BF4−}(DMC)1 < {Li+BF4−}(DMC)2 < {Li+BF4−}(EC)2 < {Li+BF4−}(EC)1. ARP values for the SL/DMC system are as follows: {Li+BF4−}(SL)2 < {Li+BF4−}(SL)1(DMC)1 < {Li+BF4−}(DMC)1 < {Li+BF4−}(SL)1 < {Li+BF4−}(DMC)2.
3.2. Experimental Results
The oxidation potentials of electrolyte solutions of the compositions 1 m {Li+BF4−} in the EC/DMC solvent mixture (1:1) and 1 m {Li+BF4−} in the SL/DMC solvent mixture (1:1) were measured under standard conditions (25 °C, atmospheric pressure).
Figure 8 shows the dependence of the stationary current on the applied potential E in a range from 2.50 to 5.99 V. Based on the shape of the curve, the stability of the solution can be concluded to be based on ethylene carbonate. For a sample of composition 1 m {Li+BF4−} in a mixture of EC/DMC (1:1), a sharp increase in current is observed at 5.5 V; for a sample of 1 m {Li+BF4−} in a mixture of SL/DMC (1:1), a corresponding increase occurs at 5.75 V. The maximum current for the 1 m {Li+BF4−} sample in the EC/DMC mixture (1:1) was 27 µA, while for the 1 m {Li+BF4−} sample in the SL/DMC mixture (1:1) it was 17 µA.
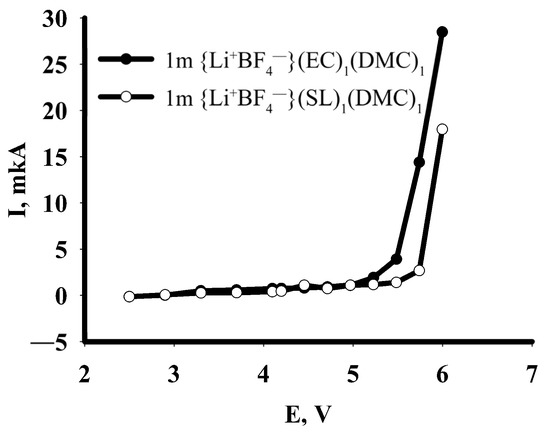
Figure 8.
Dependence of stationary current on applied potential for 1 m solutions of {Li+BF4−} in EC/DMC (1:1, vol.) and SL/DMC (1:1, vol.); evaluation of oxidative stability.
The density of the studied electrolyte solutions was 1.2733 g/cm3 for 1 m {Li+BF4−} EC/DMC (1:1, vol.) and 1.2188 g/cm3 for 1 m {Li+BF4−} SL/DMC (1:1, vol.).
4. Discussion
Based on the thermodynamic parameters of each of the possible complexes and considering their electrochemical stability, we estimated the additive values of the redox potentials of 1 m LiBF4 in mixtures of EC/DMC (1:1) and SL/DMC (1:1) solvents.
Each geometric structure that is part of the electrolyte system is an important component of the electrolyte. Due to the fact that the electrolyte is a multicomponent system, we can state that oxidation and reduction in it occurs gradually. So during theoretical study, the contribution of each component to this process was evaluated.
In the case of {Li+BF4−}(EC)1(DMC)1, the additive redox potentials are 6.19 and −0.02 V, respectively (Figure 9). These values are a window of electrochemical stability. When the AOP value of 6.19 V is reached, all complexes are subject to electrochemical oxidation reactions. As a result, significant rearrangements of their components occur up to the breaking of bonds and the formation of a free HF molecule. Here, the first occurrence at 5.43 V will be oxidised: complex BF4−(EC)1(DMC)1 (Figure 9A). The ionic pair of mixed composition {Li+BF4−}(EC)1(DMC)1 is characterised by the highest resistance to oxidation. Analysis of the NMR spectrum with QC calculations of NMR shifts confirms the existence of such a complex in the system under consideration.
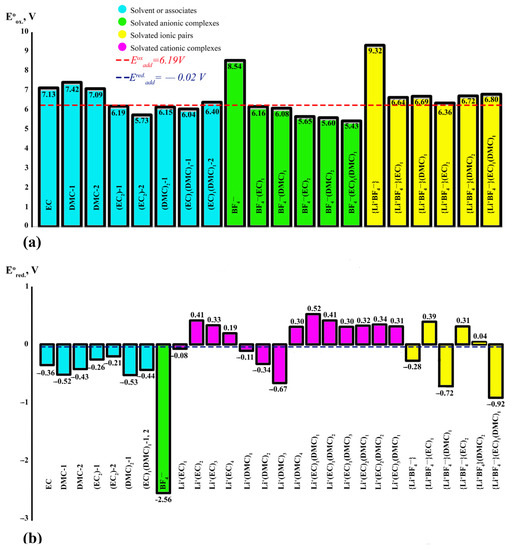
Figure 9.
Oxidation (a) and redox (b) potentials of all possible complexes of 1 m LiBF4 (EC/DMC).
The ARP is measured at −0.02 V, where the cationic complex of the mixed composition Li+(DMC)1(EC)1 is characterised by the highest reduction potential value of 0.98 V. Here, the tendency to acquire an electron increase depending on the volume of the complex should be noted. At the same time, cationic complexes containing only EC molecules are more prone to reduction than those containing only DMC molecules. Cation complexes of mixed composition are characterised by positive ARP values. Among the solvated ionic pairs, the highest RP values are characteristic of complexes containing pure EC. The lowest RP is characteristic of the mixed system {Li+BF4−}(EC)1(DMC)1. In general, the analysis of thermodynamic and electrochemical values for the system {Li+BF4−}(EC)1(DMC)1 indicates that the presence of the DMC molecule in all the complexes under consideration leads to an increase in the thermodynamic stability of the system and an increase in redox potentials.
The additive redox potentials of the {Li+BF4−}(SL)1(DMC)1 system are 6.41 and −0.39 V, respectively (Figure 10). Here, the anionic complex BF4−(DMC)1 will be oxidised first at 5.60 V. Replacing the EC with SL leads to an increase in AOP for a mixed composition complex. A similar phenomenon is observed for solvated ion pairs; as confirmed experimentally, the addition of SL increases the AOP complexes to make the system more stable to oxidation.
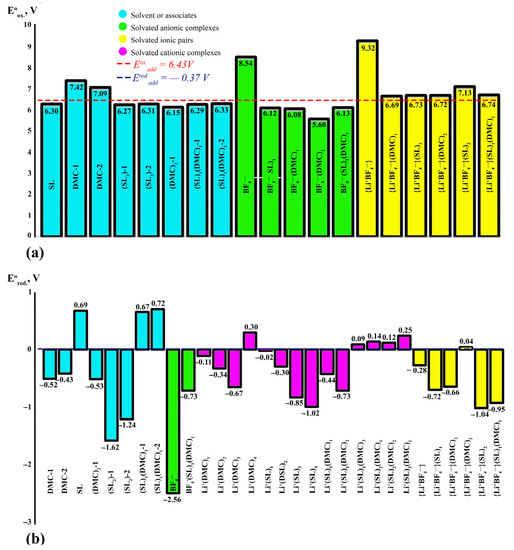
Figure 10.
Oxidation (a) and redox (b) potentials of all possible complexes of 1 m LiBF4 (SL/DMC).
For all complexes containing SL surrounded by Li+, the RP is characterised by negative values. The lowest value of the RP is characteristic of the cationic complex Li + (SL)4. The tendency to accept an electron in cationic complexes of mixed composition increases with an increase in the number of solvent molecules in the solvate sphere of the cation. For solvated ion pairs, all systems containing SL in the coordinate sphere are characterised by negative values of RP, as also confirmed by literature data. SL does not participate in the formation of SEI because of its low potential of reduction [34]. It is one of the problems of using electrolytes based on SL in cells with carbon anodes. Electrolytes containing ethylene carbonate are often reduced at potentials below 0.8 V on the surface of various anode materials [9,27,86] including graphite [87], carbon nanostructures [88], silicon [89] and metal oxides [90], leading to the formation of SEI layers.
Thus, replacing the EC with the SL molecule increases the electrochemical stability window of the system. This is logical, since the stronger electron acceptor group in sulfones compared with carbonates increases resistance to oxidation. When replacing ethylene carbonate with sulfolane in the electrolyte, it was shown experimentally that the beginning of the oxidation processes shifts by 0.25 V from 5.5 V, in the case of a composition of 1 m {Li+BF4−} EC/DMC (1:1), to 5.75 V, for a composition of 1 m {Li+BF4−} SL/DMC (1:1).
5. Conclusions
The main purpose of the work was to develop and test an algorithm for assessing the stability of electrolytes, using a set of methods derived from quantum chemistry and molecular dynamics. The combination of these methods is the main novelty of our work. Using the approach described in this paper, it is possible to predict the value of the oxidation and reduction potential depending on the solvent ratio. In this work, a complex of theoretical and experimental methods was used to evaluate the window of electrochemical stability of electrolytes of compositions 1 m {Li+BF4−} in a mixture of EC/DMC (1:1) and 1 m {Li+BF4−} in a mixture of SL/DMC (1:1). The composition and structures of all the complexes that can form in these electrolytes have been described. A number of mixed-composition complexes are characterised for the first time. Additive redox potentials were evaluated as a result of a large-scale theoretical study. This new algorithm can be used for different electrochemical systems including salts, solvents and additives.
It was experimentally shown that the processes of reducing the ethylene carbonate- based electrolyte begin at higher potentials than the sulfolane-based sample. Oxidative processes in a sulfolane-based solution begin at higher potential values than in an ethylene carbonate-based solution. A similar conclusion can be drawn by analysing the results of theoretical calculations. In other words, the obvious correlation observed between experimental and theoretical data confirms the possibility of using computational chemistry methods to select the optimal composition and ratio of a solvent in order to predict redox stability.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/batteries8120292/s1. Figure S1: Fluctuations in cohesive energy of 1 m LiBF4 (EC/DMC); Figure S2: Fluctuations in cohesive energy of 1 m LiBF4 (SL/DMC); Figure S3: Fluctuation in density value of 1 m LiBF4 (EC/DMC); Figure S4: Fluctuation in density value of 1 m LiBF4 (SL/DMC); Table S1: Ionisation potential (IP) and electron affinity (EA) values for all systems, eV; Figure S5: Geometric structure of EC, DMC, SL solvents and their associates; Figure S6: Geometric structure of anionic complexes of the type BF4−(X)n, where X = EC, DMC, SL; Figure S7: Geometric structure of complexes of the type Li+SLn; Figure S8: Geometric structure of complexes of the type Li+ECn; Figure S9: Geometric structure of complexes of the type Li+DMCn; Figure S10: Geometric structure of complexes of the type {Li+BF4}(X)n, where X = EC, DMC, SL.
Author Contributions
Conceptualisation, Y.A.D. and S.S.B.; methodology, E.Y.E., A.V.S. and O.V.B.; software, T.I.M., E.M.K. and S.S.B.; validation, E.Y.E.; formal analysis, M.G.I., E.M.K. and A.V.C.; investigation, S.S.B.; resources, T.I.M.; writing—original draft preparation, M.G.I.; writing—review and editing, Y.A.D. and O.V.B.; supervision, S.S.B.; project administration, E.Y.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Russian Science Foundation, grant number 22-23-00846 “Prediction of the stability of lithium-conducting electrolytes”.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical reasons.
Acknowledgments
The authors are grateful to the Centre for Bio- and Chemoinformatics of the Institute of Biodesign and Modelling of Complex Systems of the First Moscow State Medical University and thank I. M. Sechenov for the possibility of performing quantum chemical calculations on a computer server.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript or in the decision to publish the results.
Nomenclature
| ΔfGoin | incremental (stepped) Gibbs energy of formation (eV) |
| N | Maxwell–Boltzmann energy distribution |
| ΔEoxabs | adiabatic oxidation potential estimated in this work (M052X/TZVP) |
| ΔEox*abs-calc | adiabatic oxidation potential, published earlier, estimated based on quantum chemical calculations |
| ΔEox | experimentally measured value of the oxidation potential |
| ΔEredabs | adiabatic reduction potential estimated in this work |
| ΔEred*abs-calc | adiabatic reduction potential published earlier, which was estimated based on quantum chemical calculations |
| ΔEred | experimentally measured value of the reduction potential |
Abbreviations
| EC | ethylene carbonate |
| DMC | dimethyl carbonate |
| SL | sulfolane |
| LIB | lithium-ion battery |
| SEI | solid electrolyte layer |
| CEI | cathode–electrolyte interface |
| AOP | adiabatic oxidation potential |
| ARP | adiabatic reduction potential |
| OP | oxidation potential |
| RP | reduction potential |
Appendix A

Table A1.
Thermodynamic and oxidative parameters of solvent molecules and various complexes existing in the system 1 m LiBF4 EC/DMC: ΔfGoinc—incremental (stepped) Gibbs energy of formation (eV); N—Maxwell–Boltzmann energy distribution; ΔEoxabs—adiabatic oxidation potential estimated in this work (M052X/TZVP); ΔEoxabs-calc—adiabatic oxidation potential, published earlier, estimated on the basis of quantum chemical calculations; ΔEoxabs-exp—experimentally measured value of the oxidation potential; ΔEredabs—adiabatic reduction potential estimated in this work (M052X/TZVP); ΔEred*abs-calc—adiabatic reduction potential published earlier, which was estimated on the basis of quantum chemical calculations; ΔEred*abs-exp—experimentally measured value of the reduction potential.
Table A1.
Thermodynamic and oxidative parameters of solvent molecules and various complexes existing in the system 1 m LiBF4 EC/DMC: ΔfGoinc—incremental (stepped) Gibbs energy of formation (eV); N—Maxwell–Boltzmann energy distribution; ΔEoxabs—adiabatic oxidation potential estimated in this work (M052X/TZVP); ΔEoxabs-calc—adiabatic oxidation potential, published earlier, estimated on the basis of quantum chemical calculations; ΔEoxabs-exp—experimentally measured value of the oxidation potential; ΔEredabs—adiabatic reduction potential estimated in this work (M052X/TZVP); ΔEred*abs-calc—adiabatic reduction potential published earlier, which was estimated on the basis of quantum chemical calculations; ΔEred*abs-exp—experimentally measured value of the reduction potential.
| № | Solvent or Complex | ΔfGoinc, eV | N, % | ΔEoxabs, V | ΔEoxabs-calc 1, V | ΔEoxabs-exp 2, V | N, % | ΔEredabs, V | ΔEredabs-calc 1, V | ΔEredabs-exp 2, V |
|---|---|---|---|---|---|---|---|---|---|---|
| Solvent or associates | ||||||||||
| 1 | EC | - | - | 7.13 | 5.58–8.50 [30,48,62,79,80] | 4.60–6.70 [57,64,82,83] | - | −0.36 | −0.32–0.90 [58,62,63] | <1 [30] 0.21 [65] 0.11, 1.94 [64] |
| 2 | DMC-1 | - | - | 7.42 | 5.62–7.60 [48,80] | 5.3–6.7 [57,58,64,82] | - | −0.52 | n/d 3 | n/d |
| 3 | DMC-2 | - | - | 7.09 | 5.62–7.13 [48,80] | n/d | - | −0.43 | n/d | n/d |
| 4 | (EC)2-1 | 0.33 | 6.5 | 6.19 | 5.94–6.00 [81] | n/d | 3.4 | −0.26 | n/d | n/d |
| 5 | (EC)2-2 | 0.25 | 6.7 | 5.73 | 5.91–5.90 [48] | 6.00–6.20 [58] | 3.5 | −0.21 | n/d | n/d |
| 6 | (DMC)2 | 0.13 | 7.0 | 6.15 | 5.84–6.13 [48] | n/d | 3.6 | −0.53 | n/d | n/d |
| 7 | (EC)1(DMC)1-1 | 0.16 | 3.5 | 6.04 | 5.95–7.70 [48] | 6.69 [84] | 2.0 | −0.44 | n/d | n/d |
| 8 | (EC)1(DMC)1-2 | 0.25 | 3.5 | 6.40 | n/d | n/d | 1.6 | −0.44 | n/d | n/d |
| Solvated anionic complexes | ||||||||||
| 9 | Non-solvent anion BF4− | - | - | 8.54 | 8.00–8.57 [48] | n/d | - | −2.56 | n/d | n/d |
| 10 | BF4− (EC)1 | 0.24 | 6.7 | 6.16 | 6.07–6.39 [48,60,79] | n/d | - | Non-optimised | n/d | n/d |
| 11 | BF4−(DMC)1 | 0.33 | 6.5 | 6.08 | 5.79–6.29 [48,79] | n/d | - | n/d | n/d | |
| 12 | BF4− (EC)2 | 0.24 | 6.7 | 5.65 | 6.30–6.46 [48] | n/d | - | n/d | n/d | |
| 13 | BF4−(DMC)2 | 0.33 | 6.5 | 5.60 | n/d | n/d | - | n/d | n/d | |
| 14 | BF4−(EC)1(DMC)1 (Reaction BF4−(EC)1 + DMC ↔ BF4−(EC)1(DMC)1) (Reaction BF4−(DMC)1 + EC ↔ BF4−(EC)1(DMC)1) | 0.28 0.19 | 6.7 | 5.43 | n/d | n/d | - | n/d | n/d | |
| Solvated cationic complexes | ||||||||||
| 15 | Li+(EC)1 | −0.39 | - | - | n/d | n/d | 4.5 | −0.08 | 0.45–0.61 [27,49,60] | 0.54 [65] |
| 16 | Li+(EC)2 (Reaction Li+(EC)1 + EC ↔ Li+(EC)2) | −0.27 | - | - | n/d | n/d | 4.3 | 0.41 | n/d | n/d |
| 17 | Li+(EC)3 (Reaction Li+(EC)2 + EC ↔ Li+(EC)3) | −0.11 | - | - | n/d | n/d | 4.0 | 0.33 | n/d | n/d |
| 18 | Li+(EC)4 (Reaction Li+(EC)3 + EC ↔ Li+(EC)4) | −0.07 | - | - | n/d | n/d | 4.0 | 0.19 | n/d | 0.49 [65] |
| 19 | Li+(DMC)1 | −0.38 | - | - | n/d | n/d | 4.5 | −0.11 | 0.22–0.60 [27,60,61,66] | n/d |
| 20 | Li+(DMC)2 (Reaction Li+(DMC)1 + DMC ↔ Li+(DMC)2) | −0.13 | - | - | n/d | n/d | 4.0 | −0.34 | n/d | n/d |
| 21 | Li+(DMC)3 (Reaction Li+(DMC)2 + DMC ↔ Li+(DMC)3) | −0.21 | - | - | n/d | n/d | 4.2 | −0.67 | n/d | n/d |
| 22 | Li+(DMC)4 (Reaction Li+(DMC)3 + DMC ↔ Li+(DMC)4) | 0.07 | - | - | n/d | n/d | 3.7 | 0.30 | n/d | n/d |
| 23 | Li+(EC)1(DMC)1 (Reaction Li+(EC)1 + DMC ↔ Li+(EC)1(DMC)1) (Reaction Li+(DMC)1 + EC ↔ Li+(EC)1(DMC)1) | −0.19 −0.20 | - | - | n/d | n/d | 4.2 | 0.52 | n/d | n/d |
| 24 | Li+(EC)1(DMC)2 (Reaction Li+(DMC)2 + EC ↔ Li+(EC)1(DMC)2) (Reaction Li+(EC)1(DMC)1 + DMC ↔ Li+(EC)1(DMC)2) | −0.24 −0.17 | - | - | n/d | n/d | 4.2 | 0.41 | n/d | n/d |
| 25 | Li+(EC)1(DMC)3 (Reaction Li+(DMC)3 + EC ↔ Li+(EC)1(DMC)3) (Reaction Li+(EC)1(DMC)2 + DMC ↔ Li+(EC)1(DMC)3) | 0.05 0.07 | - | - | n/d | n/d | 3.7 | 0.30 | n/d | n/d |
| 26 | Li+(EC)2(DMC)1 (Reaction Li+(EC)2 + DMC ↔ Li+(EC)2 (DMC)1) (Reaction Li+(EC)1(DMC)1 + EC ↔ Li+(EC)2 (DMC)1) | −0.10 −0.18 | - | - | n/d | n/d | 4.1 | 0.32 | n/d | n/d |
| 27 | Li+(EC)2(DMC)2 (Reaction Li+(EC)2(DMC)1 + DMC ↔ Li+ (EC)2(DMC)2) (Reaction Li+ (EC)1(DMC)2 + EC ↔ Li+ (EC)2(DMC)2) | 0.04 0.03 | - | - | n/d | n/d | 3.8 | 0.34 | n/d | n/d |
| 28 | Li+(EC)3(DMC)1 (Reaction Li+(EC)3 + DMC ↔ Li+(EC)3(DMC)1) (Reaction Li+(EC)2DMC + EC ↔ Li+(EC)3(DMC)) | 0.04 0.03 | - | - | n/d | n/d | 3.8 | 0.31 | n/d | n/d |
| Solvated ionic pairs | ||||||||||
| 29 | Non-solvent ion pair {Li+BF4−} | −0.51 | - | 9.32 | - | 5.80 [91] | - | −0.28 | n/d | n/d |
| 30 | {Li+BF4−}(EC)1 | −0.19 | 8.0 | 6.64 | 6.64–8.74 [48] | n/d | 4.4 | 0.39 | n/d | n/d |
| 31 | {Li+BF4−}(DMC)1 | −0.26 | 8.2 | 6.69 | - | n/d | 4.5 | −0.72 | n/d | n/d |
| 32 | {Li+BF4−}(EC)2 (Reaction {Li+BF4−}(EC)1 + EC ↔ {Li+BF4−}(EC)2) | −0.06 | 7.6 | 6.36 | 6.60–6.72 [48] | n/d | 4.1 | 0.31 | n/d | n/d |
| 33 | {Li+BF4−}(DMC)2 (Reaction {Li+BF4−}(DMC)1 +DMC ↔ {Li+BF4−}(DMC)2) | −0.12 | 7.8 | 6.72 | n/d | n/d | 4.2 | 0.04 | n/d | n/d |
| 34 | {Li+BF4−}(EC)1(DMC)1 (Reaction {Li+BF4−}(EC)1+DMC ↔ {Li+BF4−}(EC)1(DMC)1) (Reaction {Li+BF4−}(DMC)1 +EC ↔ {Li+BF4−}(EC)1(DMC)1) | −0.18 −0.11 | 7.9 | 6.80 | n/d | n/d | 4.3 | −0.92 | n/d | n/d |
| All system | ||||||||||
| Eox additive (calculation) = 6.19 V | Ered additive (calculation) = −0.02 V | |||||||||
1 Values obtained on quantum chemical calculation and published in articles; 2 values obtained from experimental data and published in articles; 3 relevant data were not found in the literature.

Table A2.
Thermodynamic and oxidative parameters of solvent molecules and various complexes existing in the system 1 m LiBF4 SL/DMC: ΔfGoinc—incremental (stepped) Gibbs energy of formation (eV); N—Maxwell–Boltzmann energy distribution; ΔEoxabs—adiabatic oxidation potential estimated in this work (M052X/TZVP); ΔEoxabs-calc—adiabatic oxidation potential, published earlier, estimated on the basis of quantum chemical calculations; ΔEoxabs-exp—experimentally measured value of the oxidation potential; ΔEredabs—adiabatic reduction potential estimated in this work (M052X/TZVP); ΔEredabs-calc—adiabatic reduction potential published earlier, which was estimated on the basis of quantum chemical calculations; ΔEredabs-exp—experimentally measured value of the reduction potential.
Table A2.
Thermodynamic and oxidative parameters of solvent molecules and various complexes existing in the system 1 m LiBF4 SL/DMC: ΔfGoinc—incremental (stepped) Gibbs energy of formation (eV); N—Maxwell–Boltzmann energy distribution; ΔEoxabs—adiabatic oxidation potential estimated in this work (M052X/TZVP); ΔEoxabs-calc—adiabatic oxidation potential, published earlier, estimated on the basis of quantum chemical calculations; ΔEoxabs-exp—experimentally measured value of the oxidation potential; ΔEredabs—adiabatic reduction potential estimated in this work (M052X/TZVP); ΔEredabs-calc—adiabatic reduction potential published earlier, which was estimated on the basis of quantum chemical calculations; ΔEredabs-exp—experimentally measured value of the reduction potential.
| № | Solvent or Complex | ΔfGoinc, eV | N, % | ΔEoxabs, V | ΔEoxabs-calc, V | ΔEoxabs-exp, V | N, % | ΔEredabs, V | ΔEredabs-calc, V | ΔEredabs-exp, V |
|---|---|---|---|---|---|---|---|---|---|---|
| Solvent or associates | ||||||||||
| 1 | DMC-1 | - | - | 7.42 | 5.62–7.60 [48,80] | 5.3–6.7 [57,58,64,82] | - | −0.52 | n/d | n/d |
| 2 | DMC-2 | - | - | 7.09 | 5.62–7.13 [48,80] | n/d | - | −0.43 | n/d | n/d |
| 3 | SL | - | - | 6.30 | 6.64–6.74 [48] | 4.81 [91] 5.80 [83] | - | 0.69 | n/d | 0.40 [85] |
| 4 | (DMC)2 | 0.13 | 6.2 | 6.15 | 5.84–6.13 [48] | n/d | 3.5 | −0.53 | n/d | n/d |
| 5 | (SL)2-1 | 0.29 | 5.8 | 6.27 | n/d | n/d | 3.3 | −1.62 | n/d | n/d |
| 6 | (SL)2-2 | 0.29 | 5.8 | 6.31 | n/d | n/d | 3.3 | −1.24 | n/d | n/d |
| 7 | (SL)1(DMC)1-1 | 0.28 | 5.9 | 6.29 | n/d | 6.56 [64,84] 4.50 [64] | 3.3 | 0.67 | n/d | 0.10, 1.39 [64] |
| 8 | (SL)1(DMC)1-2 | 0.32 | 5.8 | 6.33 | n/d | n/d | 3.3 | 0.72 | n/d | n/d |
| Solvated anionic complexes | ||||||||||
| 9 | Non-solvent anion BF4− | - | - | 8.54 | 8.00–8.57 [48] | n/d | - | −2.56 | n/d | n/d |
| 10 | BF4−(DMC)1 | 0.33 | 5.7 | 6.08 | 5.79–6.29 [48,79] | n/d | - | Non-optimised | n/d | n/d |
| 11 | BF4− (SL)1 | 0.37 | 5.6 | 6.12 | 6.49, 5.68 [48,91] | 5.80 [92] | - | n/d | n/d | |
| 12 | BF4−(DMC)2 | 0.33 | 5.7 | 5.60 | n/d | n/d | - | n/d | n/d | |
| 13 | BF4− (SL)2 | 0.56 | 5.2 | 6.38 | n/d | n/d | - | n/d | n/d | |
| 14 | BF4−(SL)1(DMC)1 (Reaction BF4−(SL)1 + DMC ↔ BF4−(SL)1(DMC)1) (Reaction BF4−(DMC)1 + SL ↔ BF4−(SL)1(DMC)1) | 0.25 0.29 | 5.9 | 6.13 | n/d | n/d | - | −0.73 | n/d | n/d |
| Solvated cationic complexes | ||||||||||
| 15 | Li+(DMC)1 | −0.38 | - | - | n/d | n/d | 4.3 | −0.11 | n/d | n/d |
| 16 | Li+(DMC)2 (Reaction Li+(DMC)1 + DMC ↔ Li+(DMC)2) | −0.13 | - | - | n/d | n/d | 3.9 | −0.34 | n/d | n/d |
| 17 | Li+(DMC)3 (Reaction Li+(DMC)2 + DMC ↔ Li+(DMC)3) | −0.21 | - | - | n/d | n/d | 4.0 | −0.67 | n/d | n/d |
| 18 | Li+(DMC)4 (Reaction Li+(DMC)3 + DMC ↔ Li+(DMC)4) | 0.07 | - | - | n/d | n/d | 3.6 | 0.30 | n/d | n/d |
| 19 | Li+(SL)1 | −0.38 | - | - | n/d | n/d | 4.3 | −0.02 | n/d | n/d |
| 20 | Li+(SL)2 (Reaction Li+(SL)1 + SL ↔ Li+(SL)2) | −0.20 | - | - | n/d | n/d | 4.0 | −0.30 | n/d | n/d |
| 21 | Li+(SL)3 (Reaction Li+(SL)2 + SL ↔ Li+(SL)3) | −0.26 | - | - | n/d | n/d | 4.1 | −0.85 | n/d | n/d |
| 22 | Li+(SL)4 (Reaction Li+(SL)3 + SL ↔ Li+(SL)4) | −0.14 | - | - | n/d | n/d | 3.9 | −1.02 | n/d | n/d |
| 23 | Li+(SL)1(DMC)1 (Reaction Li+(SL)1 + DMC ↔ Li+(SL)1(DMC)1) Reaction Li+(DMC)1 + SL ↔ Li+(SL)1(DMC)1) | −0.24 −0.24 | - | - | n/d | n/d | 4.1 | −0.44 | n/d | n/d |
| 24 | Li+(SL)1(DMC)2 (Reaction Li+(DMC)2 + SL ↔ Li+(SL)1(DMC)2) (Reaction Li+(SL)1(DMC)1 + DMC ↔ Li+(SL)1(DMC)2 | −0.24 −0.14 | - | - | n/d | n/d | 4.0 | −0.73 | n/d | n/d |
| 25 | Li+(SL)1(DMC)3 (Reaction Li+(DMC)3 + SL ↔ Li+(SL)1(DMC)3) (Reaction Li+ (SL)1(DMC)2 + DMC ↔ Li+(SL)1(DMC)3) | −0.11 −0.08 | - | - | n/d | n/d | 0.09 | 0.09 | n/d | n/d |
| 26 | Li+(SL)2(DMC)1 (Reaction Li+(SL)2 + DMC ↔ Li+(SL)2(DMC)1) (Reaction Li+(SL)(DMC)1 + SL ↔ Li+(SL)2(DMC)1) | −0.31 −0.26 | - | - | n/d | n/d | 0.14 | 0.14 | n/d | n/d |
| 27 | Li+(SL)2(DMC)2 (Reaction Li+(SL)2(DMC) + DMC ↔ Li+(SL)2(DMC)2) (Reaction Li+(SL)(DMC)2 + SL ↔ Li+(SL)2(DMC)2) | −0.03 −0.16 | - | - | n/d | n/d | 0.12 | 0.12 | n/d | n/d |
| 28 | Li+(SL)3(DMC)1 (Reaction Li+(SL)3 + DMC ↔ Li+(SL)3(DMC)1) (Reaction Li+(SL)2(DMC)1 + SL ↔ Li+(SL)3(DMC)1) | −0.02 0.04 | - | - | n/d | n/d | 0.25 | 0.25 | n/d | n/d |
| Solvated ionic pairs | ||||||||||
| 29 | Non-solvent ion pair {Li+BF4−} | - | - | 9.32 | n/d | 5.80 [92] | - | −0.28 | n/d | n/d |
| 30 | {Li+BF4−}(DMC)1 | −0.26 | 7.3 | 6.69 | n/d | n/d | 4.1 | −0.72 | n/d | n/d |
| 31 | {Li+BF4−}(SL)1 | −0.25 | 7.3 | 6.73 | n/d | n/d | 4.1 | −0.66 | n/d | n/d |
| 32 | {Li+BF4−}(DMC)2 (Reaction {Li+BF4−}(DMC)1 +DMC ↔ {Li+BF4−}(DMC)2) | −0.12 | 6.9 | 6.72 | n/d | n/d | 3.9 | 0.04 | n/d | n/d |
| 33 | {Li+BF4−}(SL)2 (Reaction {Li+BF4−}(SL)1 + EC ↔ {Li+BF4−}(SL)2 | −0.22 | 7.2 | 7.13 | n/d | n/d | 4.1 | −1.04 | n/d | n/d |
| 34 | {Li+BF4−}(SL)1(DMC)1 (Reaction {Li+BF4−}(SL)1+DMC ↔ {Li+BF4−}(SL)1(DMC)1 (Reaction {Li+BF4−}(DMC)1 +SL ↔ {Li+BF4−}(SL)1(DMC)1 | −0.18 −0.16 | 7.0 | 6.74 | n/d | n/d | 4.0 | −0.95 | n/d | n/d |
| All system | ||||||||||
| Eox °additive (calculation) = 6.43 V | Ered°additive (calculation) = −0.37 V | |||||||||
References
- Choi, J.; Aurbach, D. Promise and Reality of Post-Lithium-Ion Batteries with High Energy Densities. Nat. Rev. Mater. 2016, 1, 16013. [Google Scholar] [CrossRef]
- Guo, K.; Qi, S.; Wang, H.; Huang, J.; Wu, M.; Yang, Y.; Li, X.; Ren, Y.; Ma, J. High-Voltage Electrolyte Chemistry for Lithium Batteries. Small Sci. 2022, 2. [Google Scholar] [CrossRef]
- Xiang, J.; Wei, Y.; Zhong, Y.; Yang, Y.; Cheng, H.; Yuan, L.; Xu, H.; Huang, Y. Building Practical High-voltage Cathode Materials for Lithium-ion Batteries. Adv. Mater. 2022, 2200912. [Google Scholar] [CrossRef]
- Lee, W.; Muhammad, S.; Sergey, C.; Lee, H.; Yoon, J.; Kang, Y.-M.; Yoon, W.-S. Advances in the Cathode Materials for Making a Breakthrough in the Li Rechargeable Batteries. Angew. Chem. 2019, 132. [Google Scholar] [CrossRef]
- Jung, S.K.; Kim, H.; Cho, M.G.; Cho, S.P.; Lee, B.; Kim, H.; Park, Y.U.; Hong, J.; Park, K.Y.; Yoon, G.; et al. Lithium-free transition metal monoxides for positive electrodes in lithium-ion batteries. Nat. Energy 2017, 2, 16208. [Google Scholar] [CrossRef]
- Wu, J.; Tsai, C.-J. Qualitative modeling of the electrolyte oxidation in long-term cycling of LiCoPO4 for high-voltage lithium-ion batteries. Electrochim. Acta 2021, 368, 137585. [Google Scholar] [CrossRef]
- Sreedeep, S.; Natarajan, S.; Aravindan, V. Recent advancements in LiCoPO4 cathodes using electrolyte additives. Curr. Opin. Electrochem. 2022, 31, 100868. [Google Scholar] [CrossRef]
- Han, J.-G.; Kim, K.; Lee, Y.; Choi, N.-S. Scavenging Materials to Stabilize LiPF6 -Containing Carbonate-Based Electrolytes for Li-Ion Batteries. Adv. Mater. 2019, 31, 1804822. [Google Scholar] [CrossRef]
- Xu, K. Nonaqueous liquid electrolytes for lithium-based rechargeable batteries. Chem. Rev. 2004, 104, 4303–4417. [Google Scholar] [CrossRef]
- Xu, K. Electrolytes and Interphases in Li-Ion Batteries and Beyond. Chem. Rev. 2014, 114, 11503–11618. [Google Scholar] [CrossRef]
- Aurbach, D.; Markovsky, B.; Salitra, G.; Markevich, E.; Talyossef, Y.; Koltypin, M.; Nazar, L.F.; Ellis, B.L.; Kovacheva, D.A. Review on electrode–electrolyte solution interactions, related to cathode materials for Li-ion batteries. J. Power Sources 2007, 165, 491–499. [Google Scholar] [CrossRef]
- Fan, X.; Wang, C. High-voltage liquid electrolytes for Li batteries: Progress and perspectives. Chem. Soc. Rev. 2021, 50, 10486–10566. [Google Scholar] [CrossRef] [PubMed]
- Xia, J.; Petibon, R.; Xiong, D.; Ma, L.; Dahn, J. Enabling linear alkyl carbonate electrolytes for high voltage Li-ion cells. J. Power Sources 2016, 328, 124–135. [Google Scholar] [CrossRef]
- Nagasubramanian, G.; Orendorff, C.J. Hydrofluoroether electrolytes for lithium-ion batteries: Reduced gas decomposition and nonflammable. J. Power Sources 2011, 196, 8604–8609. [Google Scholar] [CrossRef]
- Achiha, T.; Nakajima, T.; Ohzawa, Y.; Koh, M.; Yamauchi, A.; Kagawa, M.; Aoyama, H. Thermal Stability and Electrochemical Properties of Fluorine Compounds as Nonflammable Solvents for Lithium-Ion Batteries. J. Electrochem. Soc. 2010, 157, A707. [Google Scholar] [CrossRef]
- Nanbu, N.; Takimoto, K.; Takehara, M.; Ue, M.; Sasaki, Y. Electrochemical properties of fluoropropylene carbonate and its application to lithium-ion batteries. Electrochem. Commun. 2008, 10, 783–786. [Google Scholar] [CrossRef]
- Lee, S.H.; Hwang, J.-Y.; Park, S.-J.; Park, G.-T.; Sun, Y.-K. Adiponitrile (C6H8N2): A New Bi-Functional Additive for High-Performance Li-Metal Batteries. Adv. Funct. Mater. 2019, 29, 1902496. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, K.; Ding, F.; Li, W.; Liu, X.; Zhang, J. Safety-Reinforced Succinonitrile-Based Electrolyte with Interfacial Stability for High-Performance Lithium Batteries. ACS Appl. Mater. Interfaces 2017, 9, 29820–29828. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, K.; Ding, F.; Li, W.; Liu, X.; Zhang, J. Enhancing the high voltage interface compatibility of LiNi0.5Co0.2Mn0.3O2 in the succinonitrile-based electrolyte. Electrochim. Acta 2019, 298, 818–826. [Google Scholar] [CrossRef]
- Hofmann, A.; Schulz, M.; Indris, S.; Heinzmann, R.; Hanemann, T. Mixtures of Ionic Liquid and Sulfolane as Electrolytes for Li-Ion Batteries. Electrochim. Acta 2014, 147, 704–711. [Google Scholar] [CrossRef]
- Xue, L.; Ueno, K.; Lee, S.-Y.; Angell, C.A. Enhanced performance of sulfone-based electrolytes at lithium ion battery electrodes, including the LiNi0.5Mn1.5O4 high voltage cathode. J. Power Sources 2014, 262, 123–128. [Google Scholar] [CrossRef]
- Sun, X.; Angell, C.A. Doped sulfone electrolytes for high voltage Li-ion cell applications. Electrochem. Commun. 2009, 11, 1418–1421. [Google Scholar] [CrossRef]
- Zhang, T.; Paillard, E. Recent advances toward high voltage, EC-free electrolytes for graphite-based Li-ion battery. Front. Chem. Sci. Eng. 2018, 12, 577–591. [Google Scholar] [CrossRef]
- Zuo, X.; Fan, C.; Liu, J.; Xiao, X.; Wu, J.; Nan, J. Lithium Tetrafluoroborate as an Electrolyte Additive to Improve the High Voltage Performance of Lithium-Ion Battery. J. Electrochem. Soc. 2013, 160, A1199–A1204. [Google Scholar] [CrossRef]
- Xu, K.; Zhang, S.; Jow, T.R.; Xu, W.; Angell, C.A. LiBOB as Salt for Lithium-Ion Batteries: A Possible Solution for High Temperature Operation. Electrochem. Solid-State Lett. 2002, 5, A26. [Google Scholar] [CrossRef]
- Schedlbauer, T.; Krüger, S.; Schmitz, R.; Schmitz, R.W.; Schreiner, C.; Gores, H.J.; Passerini, S.; Winter, M. Lithium difluoro(oxalato)borate: A promising salt for lithium metal based secondary batteries? Electrochim. Acta 2013, 92, 102–107. [Google Scholar] [CrossRef]
- Delp, S.A.; Borodin, O.; Olguin, M.; Eisner, C.G.; Allen, J.L.; Jow, T.R. Importance of Reduction and Oxidation Stability of High Voltage Electrolytes and Additives. Electrochim. Acta 2016, 209, 498–510. [Google Scholar] [CrossRef]
- Ravdel, B.; Abraham, K.M.; Gitzendanner, R.; DiCarlo, J.; Lucht, B.; Campion, C. Thermal stability of lithium-ion battery electrolytes. J. Power Sources 2003, 119–121, 805–810. [Google Scholar] [CrossRef]
- Ellis, L.; Hill, I.; Gering, K.; Dahn, J. Synergistic Effect of LiPF6 and LiBF4 as Electrolyte Salts in Lithium-Ion Cells. J. Electrochem. Soc. 2017, 164, A2426–A2433. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, J.; Yang, L.; Lu, H.; Liu, H.; Zheng, B. Exploring the redox decomposition of ethylene carbonate–propylene carbonate in Li-ion batteries. Mater. Adv. 2021, 2, 1747–1751. [Google Scholar] [CrossRef]
- Doi, T.; Shimizu, Y.; Hashinokuchi, M.; Inaba, M. LiBF4 -Based Concentrated Electrolyte Solutions for Suppression of Electrolyte Decomposition and Rapid Lithium-Ion Transfer at LiNi0.5Mn1.5O4 /Electrolyte Interface. J. Electrochem. Soc. 2016, 163, A2211–A2215. [Google Scholar] [CrossRef]
- Doi, T.; Shimizu, Y.; Hashinokuchi, M.; Inaba, M. Dilution of Highly Concentrated LiBF4 /Propylene Carbonate Electrolyte Solution with Fluoroalkyl Ethers for 5-V LiNi0.5Mn1.5O4 Positive Electrodes. J. Electrochem. Soc. 2017, 164, A6412–A6416. [Google Scholar] [CrossRef]
- Ma, T.; Xu, G.-L.; Li, Y.; Wang, L.; He, X.; Zheng, J.; Liu, J.; Engelhard, M.H.; Zapol, P.; Curtiss, L.A.; et al. Revisiting the Corrosion of the Aluminum Current Collector in Lithium-Ion Batteries. J. Phys. Chem. Lett. 2017, 8, 1072–1077. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Porcher, W.; Paillard, E. Towards practical sulfolane based electrolytes: Choice of Li salt for graphite electrode operation. J. Power Sources 2018, 395, 212–220. [Google Scholar] [CrossRef]
- Liu, T.; Han, X.; Zhang, Z.; Chen, Z.; Wang, P.; Han, P.; Ding, N.; Cui, G. A high concentration electrolyte enables superior cycleability and rate capability for high voltage dual graphite battery. J. Power Sources 2019, 437, 226942. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, J.; Yang, Q.; Wang, S.; Wang, W.; Li, B. Stable Cycling of High-Voltage Lithium-Metal Batteries Enabled by High-Concentration FEC-Based Electrolyte. ACS Appl. Mater. Interfaces 2020, 12, 22901–22909. [Google Scholar] [CrossRef]
- Yamada, Y.; Wang, J.; Ko, S.; Watanabe, E.; Yamada, A. Advances and issues in developing salt-concentrated battery electrolytes. Nat. Energy 2019, 4, 269–280. [Google Scholar] [CrossRef]
- Sheina, L.V.; Kuz’mina, E.V.; Karaseva, E.V.; Gallyamov, A.G.; Prosochkina, T.R.; Kolosnitsyn, V.S. Thermochemical and Electrochemical Stability of Electrolyte Systems based on Sulfolane. Russ. J. Appl. Chem. 2018, 91, 1427–1433. [Google Scholar] [CrossRef]
- Etacheri, V.; Marom, R.; Elazari, R.; Salitra, G.; Aurbach, D. Challenges in the development of advanced Li-ion batteries: A review. Energy Environ. Sci. 2011, 4, 3243–3262. [Google Scholar] [CrossRef]
- Yamada, Y.; Yamada, A. Review—Superconcentrated Electrolytes for Lithium Batteries. J. Electrochem. Soc. 2015, 162, A2406–A2423. [Google Scholar] [CrossRef]
- Xing, L.; Tu, W.; Vatamanu, J.; Liu, Q.; Huang, W.; Wang, Y.; Zhou, H.; Zeng, R.-H.; Li, W. On anodic stability and decomposition mechanism of sulfolane in high-voltage lithium ion battery. Electrochim. Acta 2014, 133, 117–122. [Google Scholar] [CrossRef]
- Wang, X.; Xue, W.; Hu, K.; Li, Y.; Li, Y.; Huang, R. Adiponitrile as Lithium-Ion Battery Electrolyte Additive: A Positive and Peculiar Effect on High-Voltage Systems. ACS Appl. Energy Mater. 2018, 1, 5347–5354. [Google Scholar] [CrossRef]
- Raberg, J.; Vatamanu, J.; Harris, S.; van Oversteeg, C.; Ramos, A.; Borodin, O.; Cuk, T. Probing Electric Double Layer Composition via in-Situ Vibrational Spectroscopy and Molecular Simulations. J. Phys. Chem. Lett. 2019, 10. [Google Scholar] [CrossRef] [PubMed]
- Nakanishi, A.; Ueno, K.; Watanabe, D.; Ugata, Y.; Matsumae, Y.; Liu, J.; Thomas, M.L.; Dokko, K.; Watanabe, M. Sulfolane-Based Highly Concentrated Electrolytes of Lithium Bis(trifluoromethanesulfonyl)amide: Ionic Transport, Li-Ion Coordination, and Li–S Battery Performance. J. Phys. Chem. C 2019, 123, 14229–14238. [Google Scholar] [CrossRef]
- Lin, F.-W.; Tran, N.T.T.; Hsu, W.-D. Effect of 1,3-Propane Sultone on the Formation of Solid Electrolyte Interphase at Li-Ion Battery Anode Surface: A First-Principles Study. ACS Omega 2020, 5, 13541–13547. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, J.; Liu, Z.; Zheng, B. Interaction Mechanisms between Lithium Polysulfides/Sulfide and Small Organic Molecules. ACS Omega 2021, 6, 4995–5000. [Google Scholar] [CrossRef]
- Jiang, Z.; Rappe, A.M. Structure, Diffusion, and Stability of Lithium Salts in Aprotic Dimethyl Sulfoxide and Acetonitrile Electrolytes. J. Phys. Chem. C 2022, 126, 10266–10272. [Google Scholar] [CrossRef]
- Borodin, O.; Behl, W.; Jow, T.R. Oxidative Stability and Initial Decomposition Reactions of Carbonate, Sulfone, and Alkyl Phosphate-Based Electrolytes. J. Phys. Chem. C 2013, 117, 8661–8682. [Google Scholar] [CrossRef]
- Borodin, O. Challenges with Prediction of Battery Electrolyte Electrochemical Stability Window and Guiding the Electrode—Electrolyte Stabilization. Curr. Opin. Electrochem. 2018, 13. [Google Scholar] [CrossRef]
- Xu, K.; Zhuang, G.V.; Allen, J.L.; Lee, U.; Zhang, S.S.; Ross, P.N.; Jow, T.R. Syntheses and Characterization of Lithium Alkyl Mono- and Dicarbonates as Components of Surface Films in Li-Ion Batteries. J. Phys. Chem. B 2006, 110, 7708–7719. [Google Scholar] [CrossRef]
- Watanabe, Y.; Kinoshita, S.-i.; Wada, S.; Hoshino, K.; Morimoto, H.; Tobishima, S.-I. Electrochemical properties and lithium ion solvation behavior of sulfone--ester mixed electrolytes for high-voltage rechargeable lithium cells. J. Power Sources 2008, 179, 770–779. [Google Scholar] [CrossRef]
- Nazri, M. Liquid electrolytes: Some theoretical and practical aspects. In Lithium Batteries; Springer: Boston, MA, USA, 2003; pp. 509–529. [Google Scholar] [CrossRef]
- Abouimrane, A.; Belharouak, I.; Amine, K. Sulfone-based electrolytes for high-voltage Li-ion batteries. Electrochem. Commun. 2009, 11, 1073–1076. [Google Scholar] [CrossRef]
- Li, S.; Zhao, D.; Wang, P.; Cui, X.; Tang, F. Electrochemical effect and mechanism of adiponitrile additive for high-voltage electrolyte. Electrochim. Acta 2016, 222, 668–677. [Google Scholar] [CrossRef]
- Lu, Y.; Xu, S.; Shu, J.B.; Aladat, W.I.A.; Archer, L.A. High voltage LIB cathodes enabled by salt-reinforced liquid electrolytes. Electrochem. Commun. 2015, 51, 23–26. [Google Scholar] [CrossRef]
- Cramer, C.J. Essentials of Computational Chemistry: Theories and Models; John Wiley and Sons: West Sussex, UK; New York, NY, USA, 2002. [Google Scholar] [CrossRef]
- Abe, K.; Ushigoe, Y.; Yoshitake, H.; Yoshio, M. Functional electrolytes: Novel type additives for cathode materials, providing high cycleability performance. J. Power Sources 2006, 153, 328–335. [Google Scholar] [CrossRef]
- Abe, K.; Hattori, T.; Kawabe, K.; Ushigoe, Y.; Yoshitake, H. Functional Electrolytes Triple-Bonded Compound as an Additive for Negative Electrode. J. Electrochem. Soc. 2007, 154. [Google Scholar] [CrossRef]
- Curtiss, L.; Redfern, P.; Raghavachari, K. Gaussian-4 theory using reduced order perturbation theory. J. Chem. Phys. 2007, 127, 124105. [Google Scholar] [CrossRef]
- Borodin, O.; Olguin, M.; Spear, C.; Leiter, K.W.; Knap, J. Towards high throughput screening of electrochemical stability of battery electrolytes. Nanotechnology 2015, 26. [Google Scholar] [CrossRef]
- Borodin, O.; Ren, X.; Vatamanu, J.; von Wald Cresce, A.; Knap, J.; Xu, K. Modeling Insight into Battery Electrolyte Electrochemical Stability and Interfacial Structure. Acc. Chem. Res. 2017, 50, 2886–2894. [Google Scholar] [CrossRef]
- Han, Y.-K.; Lee, K.; Yoo, J.; Huh, Y.S. Virtual screening of borate derivatives as high-performance additives in lithium-ion batteries. Theor. Chem. Acc. 2014, 133. [Google Scholar] [CrossRef]
- Han, Y.-K.; Yoo, J.; Yim, T. Computational screening of phosphite derivatives as high-performance additives in high-voltage Li-ion batteries. RSC Adv. 2017, 7, 20049–20056. [Google Scholar] [CrossRef]
- Xu, K.; Ding, S.P.; Jow, T.R. Toward Reliable Values of Electrochemical Stability Limits for Electrolytes. J. Electrochem. Soc. 1999, 146, 4172–4178. [Google Scholar] [CrossRef]
- Hou, T.; Yang, G.; Rajput, N.N.; Self, J.; Park, S.-W.; Nanda, J.; Persson, K.A. The influence of FEC on the solvation structure and reduction reaction of LiPF6/EC electrolytes and its implication for solid electrolyte interphase formation. Nano Energy 2019, 64, 103881. [Google Scholar] [CrossRef]
- Borodin, O.; Olguin, M.; Spear, C.; Leiter, K.; Knap, J.; Yushin, G.; Childs, A.; Xu, K. (Invited) Challenges with Quantum Chemistry-Based Screening of Electrochemical Stability of Lithium Battery Electrolytes. ECS Trans. 2015, 69, 113–123. [Google Scholar] [CrossRef]
- Sanginov, E.A.; Borisevich, S.S.; Kayumov, R.R.; Istomina, A.S.; Evshchik, E.Y.; Reznitskikh, O.G.; Yaroslavtseva, T.V.; Melnikova, T.I.; Dobrovolsky, Y.A.; Bushkova, O.V. Lithiated Nafion plasticised by a mixture of ethylene carbonate and sulfolane. Electrochim. Acta 2021, 373, 137914. [Google Scholar] [CrossRef]
- Shaw, D.E. Schrödinger: Desmond Molecular Dynamics System: 2021-4; DE Shaw Research: New York, NY, USA; Maestro-Desmond Interoperability Tools Schrödinger: New York, NY, USA, 2021. [Google Scholar]
- Harder, E.; Damm, W.; Maple, J.; Wu, C.; Reboul, M.; Xiang, J.Y.; Wang, L.; Lupyan, D.; Dahlgren, M.K.; Knight, J.L.; et al. OPLS3: A Force Field Providing Broad Coverage of Drug-like Small Molecules and Proteins. J. Chem. Theory Comput. 2016, 12, 281–296. [Google Scholar] [CrossRef]
- Lu, C.; Wu, C.; Ghoreishi, D.; Chen, W.; Wang, L.; Damm, W.; Ross, G.A.; Dahlgren, M.K.; Russell, E.; Von Bargen, C.D.; et al. OPLS4: Improving Force Field Accuracy on Challenging Regimes of Chemical Space. J. Chem. Theory Comput. 2021, 17, 4291–4300. [Google Scholar] [CrossRef] [PubMed]
- Ikeguchi, M. Partial rigid-body dynamics in NPT, NPAT and NPγT ensembles for proteins and membranes. J. Comput. Chem. 2004, 25, 529–541. [Google Scholar] [CrossRef]
- Tildesley, D.; Allen, M. Computer Simulation of Liquids; Clarendon Press: Oxford, UK, 1987. [Google Scholar] [CrossRef]
- March, N.H.; Tosi, M.P. Atomic Dynamics in Liquids; Courier Corporation: North Chelmsford, MA, USA, 1991. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Zhao, Y.; Schultz, N.E.; Truhlar, D.G. Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2006, 2, 364–382. [Google Scholar] [CrossRef]
- Schäfer, A.; Huber, C.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef] [PubMed]
- Borodin, O.; Jow, T.R. Quantum Chemistry Study of the Oxidation-Induced Decomposition of Tetramethylene Sulfone (TMS) Dimer and TMS/BF4-. ECS Trans. 2013, 50, 391–398. [Google Scholar] [CrossRef]
- Zhang, X.; Pugh, J.K.; Ross, P.N.J. Computation of Thermodynamic Oxidation Potentials of Organic Solvents Using Density Functional Theory. J. Electrochem. Soc. 2001, 148. [Google Scholar] [CrossRef]
- Xing, L.; Borodin, O. Oxidation induced decomposition of ethylene carbonate from DFT calculations—Importance of explicitly treating surrounding solvent. Phys. Chem. Chem. Phys. 2012, 14, 12838–12843. [Google Scholar] [CrossRef] [PubMed]
- Azcarate, I.; Yin, W.; Méthivier, C.; Ribot, F.; Laberty-Robert, C.; Grimaud, A. Assessing the Oxidation Behavior of EC:DMC Based Electrolyte on Non- Catalytically Active Surface. J. Electrochem. Soc. 2020, 167, 080530. [Google Scholar] [CrossRef]
- Abe, K.; Miyoshi, K.; Hattori, T.; Ushigoe, Y.; Yoshitake, H. Functional electrolytes: Synergetic effect of electrolyte additives for lithium-ion battery. J. Power Sources 2008, 184, 449–455. [Google Scholar] [CrossRef]
- Ue, M.; Takeda, M.; Takehara, M.; Mori, S. Electrochemical Properties of Quaternary Ammonium Salts for Electrochemical Capacitors. J. Electrochem. Soc. 1997, 144, 2684–2688. [Google Scholar] [CrossRef]
- Alvarado, J.; Schroeder, M.; Zhang, M.; Borodin, O.; Gobrogge, E.; Olguin, M.; Ding, M.; Gobet, M.; Greenbaum, S.; Meng, Y.; et al. A carbonate-free, sulfone-based electrolyte for high-voltage Li-ion batteries. Mater. Today 2018, 21, 341–353. [Google Scholar] [CrossRef]
- Nie, M.; Lucht, B.L. Role of Lithium Salt on Solid Electrolyte Interface (SEI) Formation and Structure in Lithium Ion Batteries. J. Electrochem. Soc. 2014, 161, A1001. [Google Scholar] [CrossRef]
- Agubra, V.A.; Fergus, J.W. The formation and stability of the solid electrolyte interface on the graphite anode. J. Power Sources 2014, 268, 153–162. [Google Scholar] [CrossRef]
- Li, R.; Kamali, A.R. Molten salt assisted conversion of corn lignocellulosic waste into carbon nanostructures with enhanced Li-ion storage performance. Chem. Eng. Sci. 2023, 265, 118222. [Google Scholar] [CrossRef]
- Kamali, A.R.; Haghighat-Shishavan, S.; Nazarian-Samani, M.; Rezaei, A.; Kim, K.-B. Ultra-fast shock-wave combustion synthesis of nanostructured silicon from sand with excellent Li storage performance. Sustain. Energy Fuels 2019, 3, 1396–1405. [Google Scholar] [CrossRef]
- Zhu, W.; Kamali, A.R. Green preparation of nanostructured β-MoO3/hexagonal-shaped MoS2/graphene with enhanced lithium-ion storage performance. J. Alloys Compd. 2023, 932, 167724. [Google Scholar] [CrossRef]
- Kolosnitsyn, V.S.; Sheina, L.V.; Mochalov, S.E. Physicochemical and electrochemical properties of sulfolane solutions of lithium salts. Russ. J. Electrochem. 2008, 44, 575–578. [Google Scholar] [CrossRef]
- Borodin, O.; Jow, T.R. Quantum Chemistry Studies of the Oxidative Stability of Carbonate, Sulfone and Sulfonate-Based Electrolytes Doped with BF4-, PF6- Anions. ECS Trans. 2011, 33, 77–84. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).