Parametric Evaluation of Thermal Behavior for Different Li-Ion Battery Chemistries
Abstract
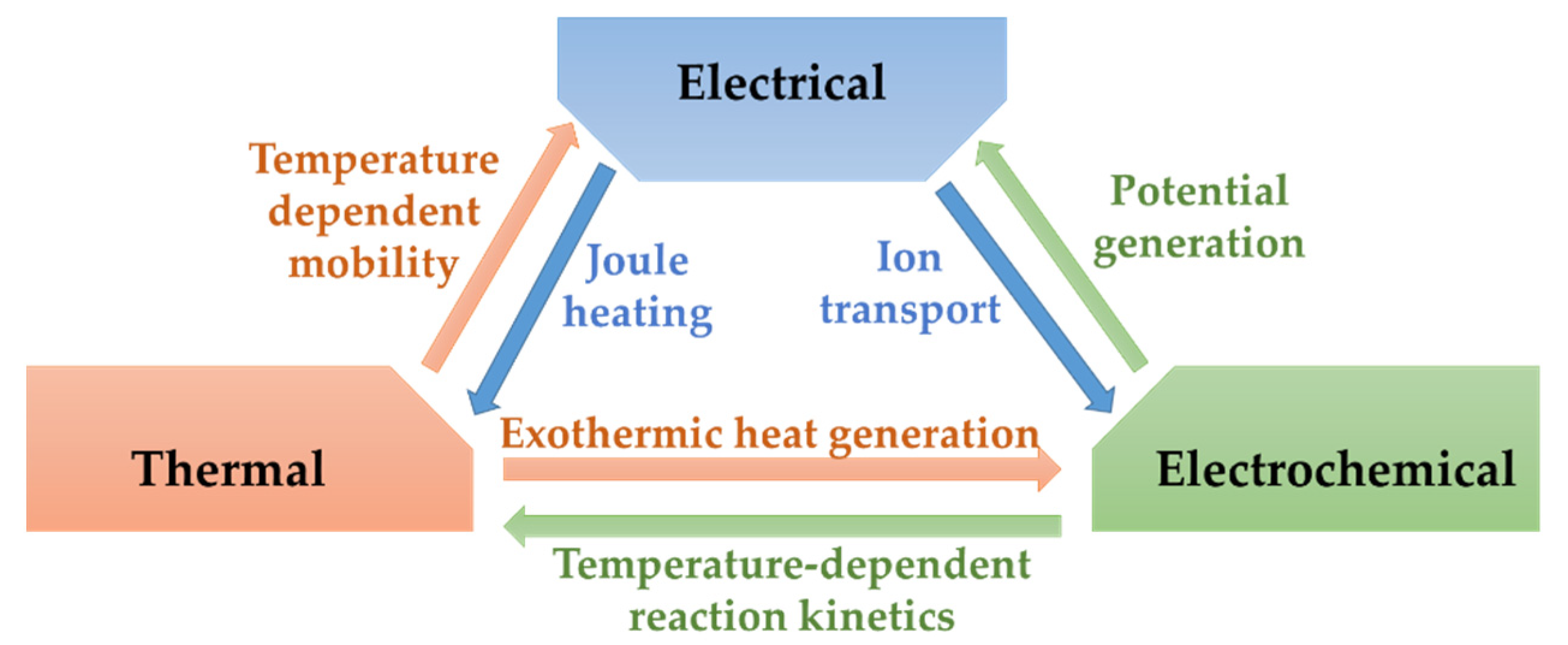
1. Introduction
2. Materials and Methods
Experimental Procedure
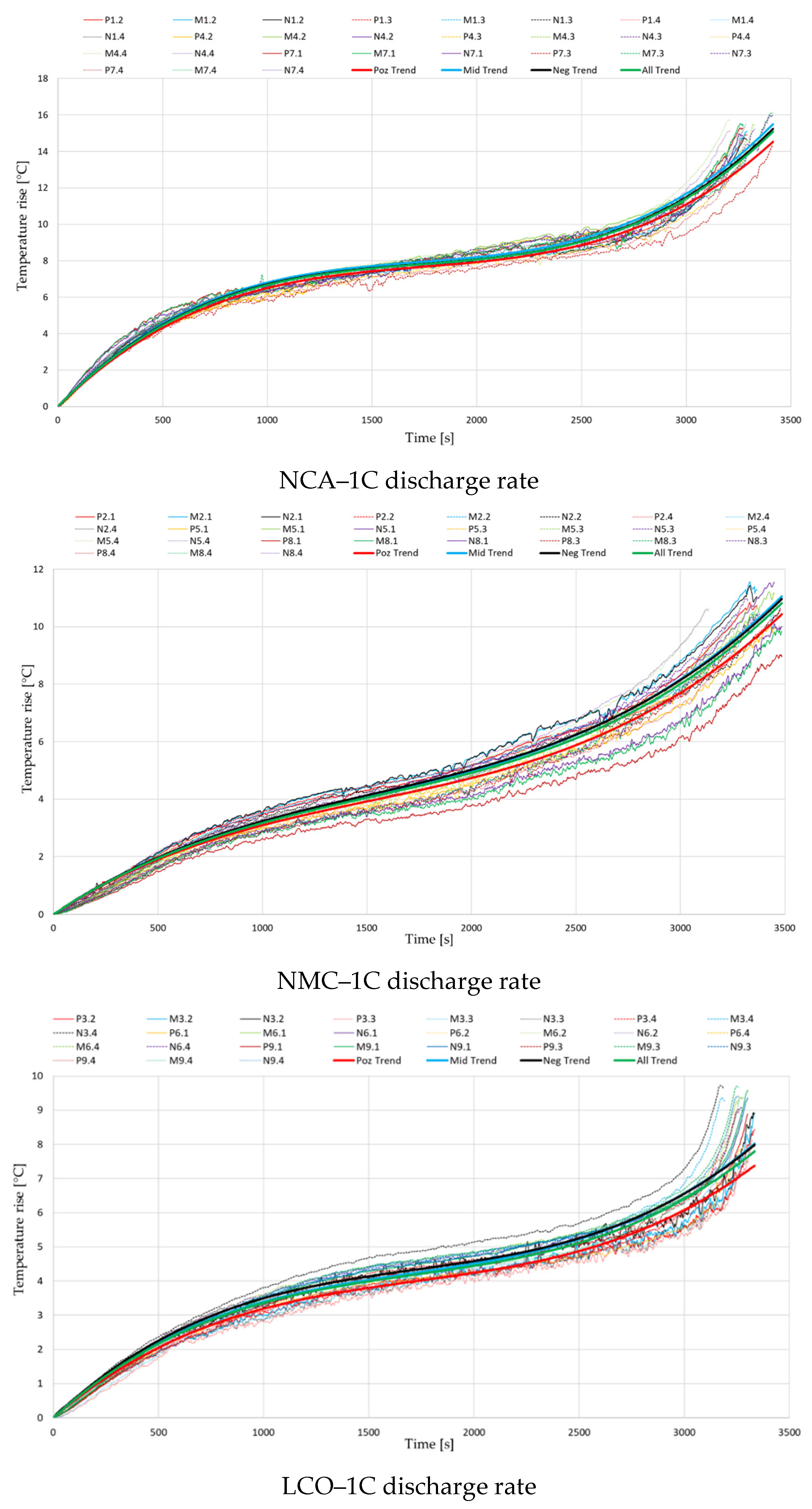
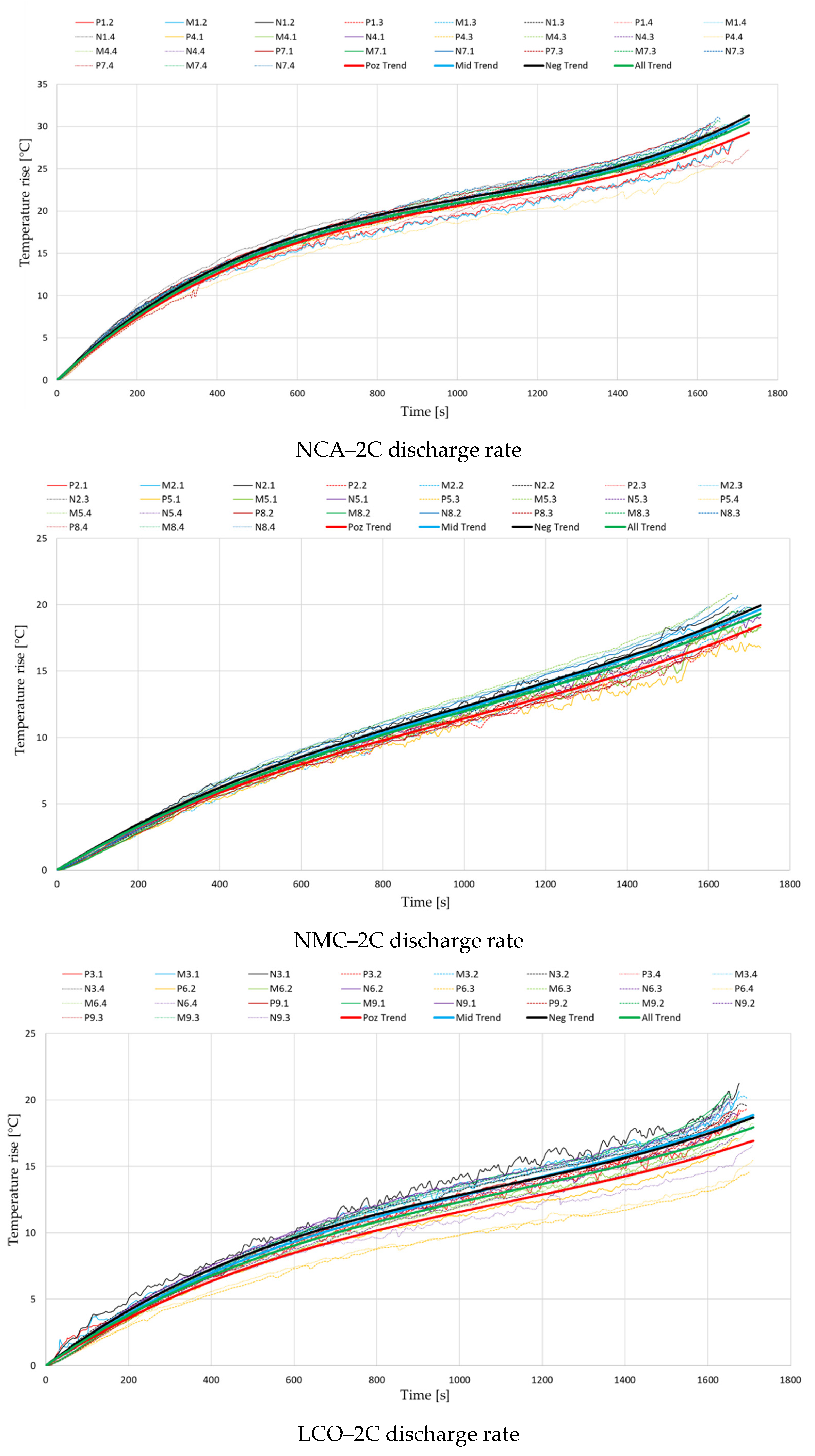
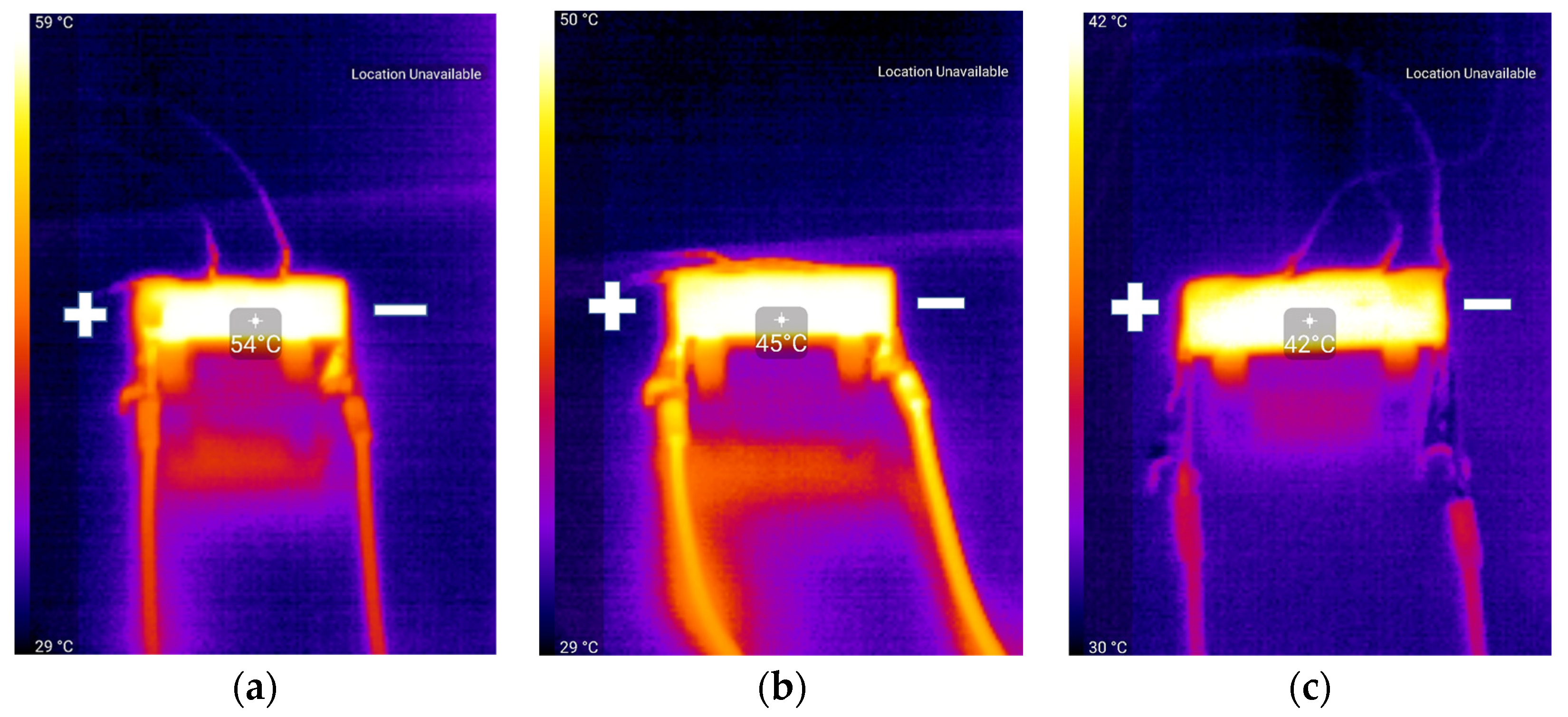
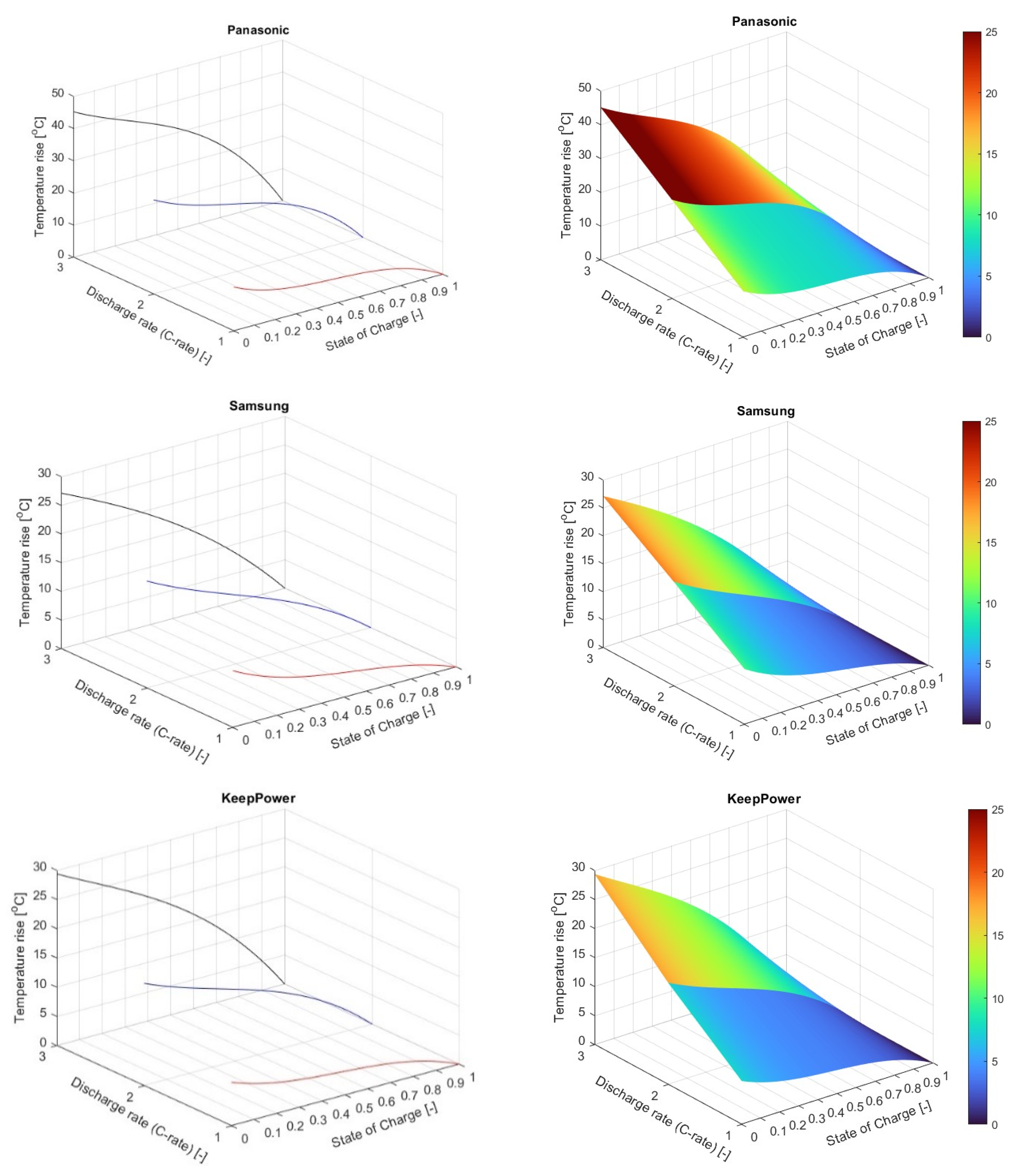
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- New Registrations of Electric Cars, EU-27 2022. Available online: https://www.eea.europa.eu/data-and-maps/daviz/new-electric-vehicles-in-eu-2#tab-chart_3 (accessed on 2 December 2022).
- Bukhari, S.M.A.S.; Maqsood, J.; Baig, M.Q.; Ashraf, S.; Khan, T.A. Comparison of Characteristics—Lead Acid, Nickel Based, Lead Crystal and Lithium Based Batteries. In Proceedings of the 2015 17th UKSim-AMSS International Conference on Modelling and Simulation (UKSim), Cambridge, UK, 25–27 March 2016; pp. 444–450. [Google Scholar] [CrossRef]
- Spitthoff, L.; Shearing, P.; Burheim, O. Temperature, Ageing and Thermal Management of Lithium-Ion Batteries. Energies 2021, 14, 1248. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, H.; Xu, X. A study on the transient heat generation rate of lithium-ion battery based on full matrix orthogonal experimental design with mixed levels. J. Energy Storage 2021, 36, 102446. [Google Scholar] [CrossRef]
- Drake, S.; Martin, M.; Wetz, D.; Ostanek, J.; Miller, S.; Heinzel, J.; Jain, A. Heat generation rate measurement in a Li-ion cell at large C-rates through temperature and heat flux measurements. J. Power Sources 2015, 285, 266–273. [Google Scholar] [CrossRef]
- Liu, P.; Wang, J.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Aging Mechanisms of LiFePO[sub 4] Batteries Deduced by Electrochemical and Structural Analyses. J. Electrochem. Soc. 2010, 157, A499–A507. [Google Scholar] [CrossRef]
- Amine, K.; Liu, J.; Belharouak, I. High-temperature storage and cycling of C-LiFePO4/graphite Li-ion cells. Electrochem. Commun. 2005, 7, 669–673. [Google Scholar] [CrossRef]
- Ramadass, P.; Haran, B.; White, R.; Popov, B.N. Capacity fade of Sony 18650 cells cycled at elevated temperatures: Part I. Cycling performance. J. Power Sources 2002, 112, 606–613. [Google Scholar] [CrossRef]
- Maleki, H.; Deng, G.; Anani, A.; Howard, J. Thermal Stability Studies of Li-Ion Cells and Components. J. Electrochem. Soc. 1999, 146, 3224–3229. [Google Scholar] [CrossRef]
- Drake, S.; Wetz, D.; Ostanek, J.; Miller, S.; Heinzel, J.; Jain, A. Measurement of anisotropic thermophysical properties of cylindrical Li-ion cells. J. Power Sources 2014, 252, 298–304. [Google Scholar] [CrossRef]
- Zhang, G.; Cao, L.; Ge, S.; Wang, C.-Y.; Shaffer, C.E.; Rahn, C.D. In Situ Measurement of Radial Temperature Distributions in Cylindrical Li-Ion Cells. J. Electrochem. Soc. 2014, 161, A1499–A1507. [Google Scholar] [CrossRef]
- Shah, K.; Vishwakarma, V.; Jain, A. Measurement of Multiscale Thermal Transport Phenomena in Li-Ion Cells: A Review. J. Electrochem. Energy Convers. Storage 2016, 13. [Google Scholar] [CrossRef]
- Nazari, A.; Farhad, S. Heat generation in lithium-ion batteries with different nominal capacities and chemistries. Appl. Therm. Eng. 2017, 125, 1501–1517. [Google Scholar] [CrossRef]
- Miao, Y.; Hynan, P.; von Jouanne, A.; Yokochi, A. Current Li-Ion Battery Technologies in Electric Vehicles and Opportunities for Advancements. Energies 2019, 12, 1074. [Google Scholar] [CrossRef]
- Jindal, P.; Katiyar, R.; Bhattacharya, J. Evaluation of accuracy for Bernardi equation in estimating heat generation rate for continuous and pulse-discharge protocols in LFP and NMC based Li-ion batteries. Appl. Therm. Eng. 2021, 201, 117794. [Google Scholar] [CrossRef]
- Xie, Y.; Shi, S.; Tang, J.; Wu, H.; Yu, J. Experimental and analytical study on heat generation characteristics of a lithium-ion power battery. Int. J. Heat Mass Transf. 2018, 122, 884–894. [Google Scholar] [CrossRef]
- Christen, R.; Martin, B.; Rizzo, G. New Experimental Approach for the Determination of the Heat Generation in a Li-Ion Battery Cell. Energies 2021, 14, 6972. [Google Scholar] [CrossRef]
- Arora, S.; Kapoor, A. Experimental Study of Heat Generation Rate during Discharge of LiFePO4 Pouch Cells of Different Nominal Capacities and Thickness. Batteries 2019, 5, 70. [Google Scholar] [CrossRef]
- Huang, Y.; Lu, Y.; Huang, R.; Chen, J.; Chen, F.; Liu, Z.; Yu, X.; Roskilly, A.P. Study on the thermal interaction and heat dissipation of cylindrical Lithium-Ion Battery cells. Energy Procedia 2017, 142, 4029–4036. [Google Scholar] [CrossRef]
- Bandhauer, T.M.; Garimella, S.; Fuller, T.F. A Critical Review of Thermal Issues in Lithium-Ion Batteries. J. Electrochem. Soc. 2011, 158, R1. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, J.; Li, Z.; Wu, B.; Nie, Z.; Sun, Y.; An, F.; Wu, N. Comparison and validation of methods for estimating heat generation rate of large-format lithium-ion batteries. J. Therm. Anal. 2014, 117, 447–461. [Google Scholar] [CrossRef]
- Liu, F.; Lan, F.; Chen, J. Dynamic thermal characteristics of heat pipe via segmented thermal resistance model for electric vehicle battery cooling. J. Power Sources 2016, 321, 57–70. [Google Scholar] [CrossRef]
- Kleiner, J.; Singh, R.; Schmid, M.; Komsiyska, L.; Elger, G.; Endisch, C. Influence of heat pipe assisted terminal cooling on the thermal behavior of a large prismatic lithium-ion cell during fast charging in electric vehicles. Appl. Therm. Eng. 2020, 188, 116328. [Google Scholar] [CrossRef]
- Hosseinzadeh, E.; Marco, J.; Jennings, P. The impact of multi-layered porosity distribution on the performance of a lithium ion battery. Appl. Math. Model. 2018, 61, 107–123. [Google Scholar] [CrossRef]
- Mahfoudi, N.; Boutaous, M.; Xin, S.; Buathier, S. Thermal Analysis of LMO/Graphite Batteries Using Equivalent Circuit Models. Batteries 2021, 7, 58. [Google Scholar] [CrossRef]
- Surya, S.; Marcis, V.; Williamson, S. Core Temperature Estimation for a Lithium Ion 18650 Cell. Energies 2020, 14, 87. [Google Scholar] [CrossRef]
- Thakur, A.K.; Prabakaran, R.; Elkadeem, M.; Sharshir, S.W.; Arıcı, M.; Wang, C.; Zhao, W.; Hwang, J.-Y.; Saidur, R. A state of art review and future viewpoint on advance cooling techniques for Lithium–ion battery system of electric vehicles. J. Energy Storage 2020, 32, 101771. [Google Scholar] [CrossRef]
- Lin, C.; Xu, S.; Liu, J. Measurement of heat generation in a 40 Ah LiFePO4 prismatic battery using accelerating rate calorimetry. Int. J. Hydrogen Energy 2018, 43, 8375–8384. [Google Scholar] [CrossRef]
- Hu, Y.; Choe, S.-Y.; Garrick, T.R. Measurement of heat generation rate and heat sources of pouch type Li-ion cells. Appl. Therm. Eng. 2021, 189, 116709. [Google Scholar] [CrossRef]
- Yin, Y.; Zheng, Z.; Choe, S.-Y. Design of a Calorimeter for Measurement of Heat Generation Rate of Lithium Ion Battery Using Thermoelectric Device. SAE Int. J. Altern. Powertrains 2017, 6, 252–260. [Google Scholar] [CrossRef]
- Diaz, L.B.; Hales, A.; Marzook, M.W.; Patel, Y.; Offer, G. Measuring Irreversible Heat Generation in Lithium-Ion Batteries: An Experimental Methodology. J. Electrochem. Soc. 2022, 169, 030523. [Google Scholar] [CrossRef]
- Chen, S.; Wan, C.; Wang, Y. Thermal analysis of lithium-ion batteries. J. Power Sources 2005, 140, 111–124. [Google Scholar] [CrossRef]
- Chen, S.C.; Wang, Y.-Y.; Wan, C.-C. Thermal Analysis of Spirally Wound Lithium Batteries. J. Electrochem. Soc. 2006, 153, A637–A648. [Google Scholar] [CrossRef]
- Buidin, T.; Mariasiu, F. Battery Thermal Management Systems: Current Status and Design Approach of Cooling Technologies. Energies 2021, 14, 4879. [Google Scholar] [CrossRef]
- Becker, J.A.; Green, C.B.; Pearson, G.L. Properties and Uses of Thermistors—Thermally Sensitive Resistors. Trans. Am. Inst. Electr. Eng. 1946, 65, 711–725. [Google Scholar] [CrossRef]
- Childs, P.R.N.; Greenwood, J.R.; Long, C.A. Review of temperature measurement. Rev. Sci. Instrum. 2000, 71, 2959–2978. [Google Scholar] [CrossRef]
- Raijmakers, L.; Danilov, D.; Eichel, R.-A.; Notten, P. A review on various temperature-indication methods for Li-ion batteries. Appl. Energy 2019, 240, 918–945. [Google Scholar] [CrossRef]
- Duff, M.; Towey, J. Two Ways to Measure Temperature Using Thermocouples Feature Simplicity, Accuracy, and Flexibility. Analog Dialogue 2010, 44, 1–6. [Google Scholar]
- Lv, Y.; Zhou, D.; Yang, X.; Liu, X.; Li, X.; Zhang, G. Experimental investigation on a novel liquid-cooling strategy by coupling with graphene-modified silica gel for the thermal management of cylindrical battery. Appl. Therm. Eng. 2019, 159, 113885. [Google Scholar] [CrossRef]
- Weng, J.; Yang, X.; Zhang, G.; Ouyang, D.; Chen, M.; Wang, J. Optimization of the detailed factors in a phase-change-material module for battery thermal management. Int. J. Heat Mass Transf. 2019, 138, 126–134. [Google Scholar] [CrossRef]
- Yan, J.; Li, K.; Chen, H.; Wang, Q.; Sun, J. Experimental study on the application of phase change material in the dynamic cycling of battery pack system. Energy Convers. Manag. 2016, 128, 12–19. [Google Scholar] [CrossRef]
- Lv, Y.; Situ, W.; Yang, X.; Zhang, G.; Wang, Z. A novel nanosilica-enhanced phase change material with anti-leakage and anti-volume-changes properties for battery thermal management. Energy Convers. Manag. 2018, 163, 250–259. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.; Zhang, G.; Wang, Y.; Guo, J.; Wang, Y.; Huang, Q.; Xiao, C.; Zhong, Z. Characterization and experimental investigation of aluminum nitride-based composite phase change materials for battery thermal management. Energy Convers. Manag. 2019, 204, 112319. [Google Scholar] [CrossRef]
- Ling, Z.; Wen, X.; Zhang, Z.; Fang, X.; Gao, X. Thermal management performance of phase change materials with different thermal conductivities for Li-ion battery packs operated at low temperatures. Energy 2017, 144, 977–983. [Google Scholar] [CrossRef]
- Zhong, G.; Zhang, G.; Yang, X.; Li, X.; Wang, Z.; Yang, C.; Yang, C.; Gao, G. Researches of composite phase change material cooling/resistance wire preheating coupling system of a designed 18650-type battery module. Appl. Therm. Eng. 2017, 127, 176–183. [Google Scholar] [CrossRef]
- Lyu, Y.; Siddique, A.; Majid, S.; Biglarbegian, M.; Gadsden, S.; Mahmud, S. Electric vehicle battery thermal management system with thermoelectric cooling. Energy Rep. 2019, 5, 822–827. [Google Scholar] [CrossRef]
- Li, X.; Zhong, Z.; Luo, J.; Wang, Z.; Yuan, W.; Zhang, G.; Yang, C.; Yang, C. Experimental Investigation on a Thermoelectric Cooler for Thermal Management of a Lithium-Ion Battery Module. Int. J. Photoenergy 2019, 2019, 3725364. [Google Scholar] [CrossRef]
- Behi, H.; Karimi, D.; Behi, M.; Jaguemont, J.; Ghanbarpour, M.; Behnia, M.; Berecibar, M.; Van Mierlo, J. Thermal management analysis using heat pipe in the high current discharging of lithium-ion battery in electric vehicles. J. Energy Storage 2020, 32, 101893. [Google Scholar] [CrossRef]
- Löbberding, H.; Wessel, S.; Offermanns, C.; Kehrer, M.; Rother, J.; Heimes, H.; Kampker, A. From Cell to Battery System in BEVs: Analysis of System Packing Efficiency and Cell Types. World Electr. Veh. J. 2020, 11, 77. [Google Scholar] [CrossRef]
- Liang, J.; Gan, Y.; Li, Y.; Tan, M.; Wang, J. Thermal and electrochemical performance of a serially connected battery module using a heat pipe-based thermal management system under different coolant temperatures. Energy 2019, 189, 116233. [Google Scholar] [CrossRef]
- Barkholtz, H.M.; Preger, Y.; Ivanov, S.; Langendorf, J.; Torres-Castro, L.; Lamb, J.; Chalamala, B.; Ferreira, S.R. Multi-scale thermal stability study of commercial lithium-ion batteries as a function of cathode chemistry and state-of-charge. J. Power Sources 2019, 435, 226777. [Google Scholar] [CrossRef]
- Huang, Y.; Lin, Y.-C.; Jenkins, D.M.; Chernova, N.A.; Chung, Y.; Radhakrishnan, B.; Chu, I.-H.; Fang, J.; Wang, Q.; Omenya, F.; et al. Thermal Stability and Reactivity of Cathode Materials for Li-Ion Batteries. ACS Appl. Mater. Interfaces 2016, 8, 7013–7021. [Google Scholar] [CrossRef]
- Mevawalla, A.; Panchal, S.; Tran, M.-K.; Fowler, M.; Fraser, R. Mathematical Heat Transfer Modeling and Experimental Validation of Lithium-Ion Battery Considering: Tab and Surface Temperature, Separator, Electrolyte Resistance, Anode-Cathode Irreversible and Reversible Heat. Batteries 2020, 6, 61. [Google Scholar] [CrossRef]
- Houache, M.S.E.; Yim, C.-H.; Karkar, Z.; Abu-Lebdeh, Y. On the Current and Future Outlook of Battery Chemistries for Electric Vehicles—Mini Review. Batteries 2022, 8, 70. [Google Scholar] [CrossRef]
- Mirsalehian, M.; Beykirch, R. Thermal Investigation and Physical Modeling of Lithium-ion Batteries. ATZ Worldw. 2020, 122, 36–41. [Google Scholar] [CrossRef]




| Parameters | KeepPower | Panasonic | Samsung |
|---|---|---|---|
| Chemistry | LCO | NCA | NMC |
| Size | 18650 | 18650 | 21700 |
| Anode active material | Graphite | Graphite | Graphite |
| Cathode active material | LiMn2O4 | LiNi0.8Co0.15Al0.05O2 | Li(NiMnCo)O2 |
| Anode electrode thickness | 126 μm | 126 μm | 126 μm |
| Cathode electrode thickness | 125 μm | 125 μm | 125 μm |
| Anode current collector foil thicknesses (copper) | 10 μm | 10 μm | 10 μm |
| Cathode current collector foil thicknesses (aluminum) | 20 μm | 20 μm | 20 μm |
| Electrolyte | Lithium Hexafluorophosphate (LiPF6) | ||
| Separator (polypropylene (PP)) | 20 μm | 20 μm | 22 μm |
| Nominal voltage [V] | 3.7 | 3.6 | 3.6 |
| Nominal capacity [Ah] | 2.6 | 3.1 | 4 |
| Maximum discharge current [A] | 15 | 10 | 45 |
| Discharge Rate | Battery’s Chemistry | Location of Measurement | Polynomial Equations’ Coefficients | R-Square | ||
|---|---|---|---|---|---|---|
| a | b | c | ||||
| 1C | NCA | Positive terminal | 1.14 × 10−9 | 5.95 × 10−6 | 1.13 × 10−2 | 0.9714 |
| Middle | 1.25 × 10−9 | 6.46 × 10−6 | 1.20 × 10−2 | 0.9828 | ||
| Negative terminal | 1.23 × 10−9 | 6.37 × 10−6 | 1.18 × 10−2 | 0.9854 | ||
| All data | 1.21 × 10−9 | 6.26 × 10−6 | 1.17 × 10−2 | 0.9774 | ||
| NMC | Positive terminal | 4.60 × 10−10 | 2.10 × 10−6 | 4.73 × 10−3 | 0.9626 | |
| Middle | 4.68 × 10−10 | 2.11 × 10−6 | 4.84 × 10−3 | 0.9686 | ||
| Negative terminal | 4.62 × 10−10 | 2.11 × 10−6 | 4.88 × 10−3 | 0.97 | ||
| All data | 4.63 × 10−10 | 2.11 × 10−6 | 4.82 × 10−3 | 0.9644 | ||
| LCO | Positive terminal | 4.90 × 10−10 | 2.54 × 10−6 | 5.24 × 10−3 | 0.9763 | |
| Middle | 5.37 × 10−10 | 2.75 × 10−6 | 5.61 × 10−3 | 0.9625 | ||
| Negative terminal | 5.50 × 10−10 | 2.86 × 10−6 | 5.80 × 10−3 | 0.959 | ||
| All data | 5.26 × 10−10 | 2.72 × 10−6 | 5.55 × 10−3 | 0.9581 | ||
| 2C | NCA | Positive terminal | 9.86 × 10−9 | 3.19 × 10−5 | 4.26 × 10−2 | 0.9786 |
| Middle | 1.10 × 10−8 | 3.42 × 10−5 | 4.42 × 10−2 | 0.9915 | ||
| Negative terminal | 1.15 × 10−8 | 3.60 × 10−5 | 4.58 × 10−2 | 0.996 | ||
| All data | 1.08 × 10−8 | 3.40 × 10−5 | 4.42 × 10−2 | 0.9863 | ||
| NMC | Positive terminal | 3.17 × 10−9 | 9.68 × 10−6 | 1.80 × 10−2 | 0.9901 | |
| Middle | 2.68 × 10−9 | 8.44 × 10−6 | 1.79 × 10−2 | 0.9864 | ||
| Negative terminal | 3.23 × 10−9 | 9.90 × 10−6 | 1.90 × 10−2 | 0.9926 | ||
| All data | 3.02 × 10−9 | 9.33 × 10−6 | 1.83 × 10−2 | 0.9841 | ||
| LCO | Positive terminal | 3.68 × 10−9 | 1.23 × 10−5 | 2.02 × 10−2 | 0.934 | |
| Middle | 4.08 × 10−9 | 1.35 × 10−5 | 2.22 × 10−2 | 0.98 | ||
| Negative terminal | 4.73 × 10−9 | 1.55 × 10−5 | 2.36 × 10−2 | 0.9638 | ||
| All data | 3.91 × 10−9 | 1.31 × 10−5 | 2.15 × 10−2 | 0.9481 | ||
| 3C | NCA | Positive terminal | 3.43 × 10−8 | 8.40 × 10−5 | 9.11 × 10−2 | 0.9838 |
| Middle | 3.80 × 10−8 | 9.14 × 10−5 | 9.71 × 10−2 | 0.9977 | ||
| Negative terminal | 4.27 × 10−8 | 9.91 × 10−5 | 0.1 | 0.9971 | ||
| All data | 3.83 × 10−8 | 9.15 × 10−5 | 9.61 × 10−2 | 0.9887 | ||
| NMC | Positive terminal | 6.03 × 10−9 | 2.17 × 10−5 | 4.02 × 10−2 | 0.9885 | |
| Middle | 3.68 × 10−9 | 1.66 × 10−5 | 3.98 × 10−2 | 0.9938 | ||
| Negative terminal | 8.40 × 10−9 | 2.39 × 10−5 | 4.26 × 10−2 | 0.9948 | ||
| All data | 6.04 × 10−9 | 2.07 × 10−5 | 4.08 × 10−2 | 0.9858 | ||
| LCO | Positive terminal | 9.28 × 10−9 | 2.80 × 10−5 | 4.51 × 10−2 | 0.9959 | |
| Middle | 9.47 × 10−9 | 2.86 × 10−5 | 4.63 × 10−2 | 0.9953 | ||
| Negative terminal | 1.46 × 10−8 | 3.91 × ·10−5 | 5.20 × 10−2 | 0.9924 | ||
| All data | 1.11 × 10−8 | 3.19 × 10−5 | 4.78 × 10−2 | 0.9911 | ||
| Parameters | Panasonic NCA | Samsung NMC | KeepPower LCO |
|---|---|---|---|
| B coefficient | 4.697 | 1.26 | 2.786 |
| R-square | 0.993 | 0.991 | 0.993 |
| RMSE | 1.04 | 0.662 | 0.632 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buidin, T.I.C.; Mariasiu, F. Parametric Evaluation of Thermal Behavior for Different Li-Ion Battery Chemistries. Batteries 2022, 8, 291. https://doi.org/10.3390/batteries8120291
Buidin TIC, Mariasiu F. Parametric Evaluation of Thermal Behavior for Different Li-Ion Battery Chemistries. Batteries. 2022; 8(12):291. https://doi.org/10.3390/batteries8120291
Chicago/Turabian StyleBuidin, Thomas Imre Cyrille, and Florin Mariasiu. 2022. "Parametric Evaluation of Thermal Behavior for Different Li-Ion Battery Chemistries" Batteries 8, no. 12: 291. https://doi.org/10.3390/batteries8120291
APA StyleBuidin, T. I. C., & Mariasiu, F. (2022). Parametric Evaluation of Thermal Behavior for Different Li-Ion Battery Chemistries. Batteries, 8(12), 291. https://doi.org/10.3390/batteries8120291







