Investigation of the Temperature Dependence of Parameters in the Generalized Peukert Equation Used to Estimate the Residual Capacity of Traction Lithium-Ion Batteries

Abstract

The Peukert equation is widely used in various analytical models of lithium-ion batteries. However, the classical Peukert equation is applicable to lithium-ion batteries only in a limited range of discharge currents. Additionally, it does not take into account the temperature impact on a battery’s released capacity. In this paper, the applicability of the generalized Peukert equation C = C_m/(1 + (i/i₀)ⁿ) is investigated for the residual capacity determination of lithium-ion batteries based on the Hausmann model. It is proved that all the parameters (C_m, i₀, and n) of this equation depend on a battery’s temperature. That is why, for a battery-released capacity calculation, it is necessary to take into account the battery’s temperature. The equations are found to describe the temperature dependence of all the parameters of the generalized Peukert equation. The physical meaning of all the parameters is established and it is shown that the generalized Peukert equation obtained with temperature consideration is applicable to any current and temperature of a battery.

1. Introduction

Batteries are components of various machine items. That is why, for efficient operation of those technical objects, reliable battery models are needed. For example, during the operation of any device containing batteries, it is necessary to know a battery’s residual capacity, its remaining service time, etc. However, these battery parameters can only be calculated based on very reliable battery models. The most accurate battery models are those based on the physical and chemical fundamental laws [1,2,3,4,5]. However, in practice, fundamental battery models are used very rarely. There are many reasons for this. Firstly, the fundamental models of batteries are so complex that they cannot be calculated by the onboard computers of electric vehicles, airplanes, etc. Secondly, the fundamental models contain a lot of parameters describing internal electrochemical processes running in batteries that can only be found as a result of a very complex electrochemical examination of the battery’s internal processes. Notably, this examination requires a battery’s disassembly, which is prohibited very often as it is inconvenient for companies needing the models. Thirdly, after a battery’s replacement, the fundamental models are hardly applicable as the new batteries require a new very complex calibration. This is so even for batteries of the same electrochemical system and format because any previously measured internal parameters depend to a large extent on a new battery’s internal structure, various additives present in both the active mass and the electrolyte of batteries, etc. Fourthly, the fundamental models cannot describe such poorly studied processes in batteries as thermal runaway [6,7], hydrogen accumulation, aging [8,9], etc. Therefore, the battery models applicable in practice should be simple enough [10] so that they can be calculated by the onboard computers of electric vehicles and airplanes. In addition, it is necessary that the parameters of these models can be found without disassembling the batteries, and after a battery’s replacement, the calibration of the new batteries should be easy. The only models able to satisfy such requirements are analytical models based on empirical equations [11,12,13,14] or nonlinear structural models [15,16,17]. Currently, for the determination of a battery’s remaining capacity or its state of charge (SoC), there are many analytical models and methods. Firstly, the SoC assessment can be done by an open circuit voltage [18]. However, this method is not applicable for lithium iron phosphate batteries distinguished by a flat discharging curve. Moreover, with dynamic battery operation, this method gives an error of up to 20% [19]. Secondly, the Kalman Filter can be used in analytical battery models [20,21,22] but in the battery operation dynamic mode, this method often gives an error of up to 10%. Thirdly, it is possible to calculate the ampere hours spent while a battery is discharging, etc. Further, for battery SoC estimating, there are a lot of analytical models using the Peukert equation. The most promising of them is the Hausmann model [10]. In this group of models, it is very important to have a correct empirical Peukert equation applicable to any lithium-ion battery at any discharge current and any battery temperature.

In [23,24,25], it was experimentally proven that for lithium-ion batteries, the classical Peukert equation is applicable only in the discharge current range from around 0.2 C_n to 2 C_n (C_n is the rated battery capacity). At currents less than 0.2 C_n, the capacity in the Peukert equation tends to infinity, which is impossible for any battery. In experiments [24] at currents more than 2 C_n, the curve C(i) of capacity versus the discharge current becomes convex, while in the Peukert equation, it is always concave (when n > 0).

Therefore, the classical Peukert equation used in the Hausmann model [10] is applicable for lithium-ion batteries only in a very narrow range of temperatures and discharge currents.

Nevertheless, many analytical models of batteries use the classical Peukert equation for calculation [19,26,27,28]. This study, therefore, is aimed at finding a generalized Peukert equation for lithium-ion batteries which would be correct at any discharge current and battery temperature.

2. Theory

For a battery’s residual capacity determination in an electric vehicle, the Hausmann model [10] is used in the following form:

$$C_t=C_{m0}-{\displaystyle \sum _{i=0}^t{I}_{eff}(i_i,T_i)}\Delta t, I_{eff}(i_t,T_t)=f_1(i_t)f_2(T_t)=\gamma {\left(i_t\right)}^{\alpha }{\left(\frac{T_{ref}}{T_t}\right)}^{{\beta }_0}$$

(1)

In Equation (1), for determining the battery residual capacity C_t at the point of time t (from the battery discharge beginning), the entire discharge time interval is divided into small time spans ∆t = 1 s. Then, for every small time span ∆t, the effective currents I_eff(i,T) are summed and subtracted from the maximum battery capacity, C_m0 (1), found at any discharge current and temperature of the battery. T_ref = 298 K is the reference temperature used in the experiments and α, β₀, and γ are the empirical constants.

The relationship between the effective current I_eff(i,T) and the battery capacity C(i,T) [23] is described by the equation:

$$C(i,T)=\frac{C_{m0}}{I_{eff}(i,T)/\left(i\gamma \right)}$$

(2)

From Equations (1) and (2) for C(i,T), we obtain the equation:

$$C\left(i,T\right)=\frac{C_{m0}}{i^n}{\left(\frac{T}{T_{ref}}\right)}^{{\beta }_0},n=\alpha -1$$

(3)

Equation (3) is the Peukert equation taking temperature into account.

Indeed, Equation (3) is the product of two following factors:

$$C(i)=\frac{A}{i^n} \mathrm{and}$$

(4)

$$C\left(T\right)=C_{mref}{\left(\frac{T}{T_{ref}}\right)}^{{\beta }_0},C_{m0}=C_{mref}A$$

(5)

Equation (4) is the classical Peukert equation, which is often written in this form [10,23]. Equation (5) describes the dependence of the battery capacity on its temperature. In Equation (5), C_mref is the maximum battery capacity at the reference temperature T_ref = 298 K, and A is an empirical constant.

It should be noted that the empirical Equations (4) and (5) were obtained experimentally at various constant values of current and temperature, and in the Hausmann model (1), these equations are used in the dynamic mode of battery discharge, when the discharge currents change dramatically during the operation of the electric vehicles. However, at every small time span, ∆t = 1 s, the discharge current and the temperature can be considered to be constant. That is why the Hausmann model (1) gives very good estimates for the battery residual capacity.

In [23,25], it was proved that the generalized Peukert equation:

$$C(i)=\frac{C_m}{1+{\left(\frac{i}{i_0}\right)}^n}$$

(6)

corresponds well to the experimental data obtained for lithium-ion batteries at any discharge current. Notably, C(i₀) = C_m/2. In addition,

$$\underset{i\to i_0}{\lim }\frac{d(C(i)/C_m)}{d(i/i_0)}=-\frac{n}{4} (\mathrm{for} \mathrm{Equation} (6))$$

(7)

Thus, all the parameters of the generalized Peukert Equation (6) have their clear physical meaning: C_m is for the battery top capacity, found at any discharge current and a certain (under study) battery temperature; i₀ is for the current, at which the capacity released by the battery is equal to half of the battery’s top capacity; and n/4 is the tilt angle of the function C(i) in the point i = i₀ in the standardized coordinates (C(i)/C_m, i/i₀). Meanwhile, in the classical Peukert (4) Equation, parameter A is just an empirical constant.

Furthermore, in [23,25], it was shown that Equation (5) is applicable only in a small temperature range close to the temperature value T_ref. In Equation (5), the temperature can vary from zero to infinity; meanwhile, the released capacity will also vary from zero to infinity, which is impossible for any type of battery. In any battery, the released capacity varies from zero (at a temperature close to the freezing point of the electrolyte) to the maximum possible value determined by the battery’s electrochemical system. While in Equation (5), C(T) = 0 only at T = 0, which is impossible for any type of battery. In the same papers, it was shown that the function C(T) corresponding well to the experimental data appears as follows.

$$C(T)=C_{mref}K\frac{{\left(\frac{T-T_k}{T_{ref}-T_k}\right)}^{\beta }}{(K-1)+{\left(\frac{T-T_k}{T_{ref}-T_k}\right)}^{\beta }}$$

(8)

As C(T_k) = 0, T_k is the temperature at which all electrochemical processes stop in the battery, i.e., this temperature is close to the electrolyte freezing temperature. In addition, $\underset{T\to \infty }{\lim }C(T)=C_{mref}K$. Therefore, the parameter K shows how many times (theoretically) the battery capacity can increase compared to its capacity at temperature T_ref, and β is an empirical constant.

In [23], in the Hausmann model (1), instead of the Peukert equation taking temperature into account (3), the generalized Peukert equation was used to consider the temperature in the following form:

$$C(i,T)=\frac{C_{mref}}{\left(1+{\left(\frac{i}{i_0}\right)}^n\right)}K\frac{{\left(\frac{T-T_k}{T_{ref}-T_k}\right)}^{\beta }}{(K-1)+{\left(\frac{T-T_k}{T_{ref}-T_k}\right)}^{\beta }}$$

(9)

Equation (9), when used in the Hausmann model (1), significantly improves the estimation accuracy of the residual battery capacity [23] as compared to the use of Equation (3). This is because Equations (6) and (8) correspond well to the experimental data at any discharge current and battery temperature value. In contrast, Equations (4) and (5) correspond to the experimental data only in the limited ranges of current discharge and temperature.

A comparison between Equation (9) and the generalized Peukert Equation (6) shows that in [23], the authors believed that only one parameter depends on the temperature in Equation (6), namely C_m, while the other two parameters of this Equation (i₀ and n) do not depend on the temperature.

In this paper, we will check the temperature dependence of all the parameters (C_m, i₀, and n) in the generalized Peukert Equation (6).

3. Experimental Methodology

In order to test the temperature dependence of the parameters of the generalized Peukert Equation (6), the following lithium-ion batteries were used: HR3781162227 NMC Pouch (Guangdong, China), voltage 3.7V. The rated capacity of these batteries is C_n =40 Ah.

For battery charging, the workstation ZENNIUM (with a potentiostat PP242) was used in the mode (CC/CV), i.e., constant current/constant voltage. The following values were used: the constant current 0.5 C_n charge to 4.2 V and the constant voltage 4.2 V charge to 0.02 C_n cut-off.

For battery discharging, the electronic load ITECH IT8945-150-2500 was used in the DC mode (CC). The discharge was performed at currents in the range from 0.33 C_n to 10 C_n up to the discharge cut-off voltage of 3 V.

The experimental values of the studied batteries were found at the following temperatures: −18 °C, −10 °C, 0 °C, 10 °C, 25 °C, and 40 °C. The climate chamber Binder MK240 was used for maintaining these battery temperatures. For the purpose of cooling down the batteries when they were discharged with large currents, heat sinks were attached to the batteries from all sides (they were the heat sinks used in computers for cooling down processors). The heat sinks were attached by a heat-conducting paste and special clamps. Moreover, four LM35 temperature sensors were attached to different battery surface points. Due to the LM35 temperature sensors, at any discharge current, the climate chamber maintained the battery temperature close to the specific temperature under examination.

At the same time, we carried out experimental measurements with five batteries at certain discharge currents and temperatures. This procedure enabled us to determine the battery capacity more accurately at certain values of the discharge current and the temperature. Each time, we calculated the average value of the capacity for the five measurements, but the average value is less dependent on any inevitable insignificant random process related to either the battery manufacturing process or the battery capacity measurement process. In addition, this allows for using statistical methods to more accurately estimate the error of each measurement. Because each experimental point is measured multiple times, the error will reflect not only the accuracy of the measuring tools used but also the above-noted inevitable minor random processes.

Before our measurements started, for the parameter stabilization of our new batteries (which comes due to the SEI layer formation [25]), we performed seven training cycles of charge/discharge. In compliance with the battery operation instructions, in our training cycles, the battery’s charge was performed in the standard way (as described above), and the discharge was done by the current 0.5 Cn up to the voltage 3 V.

In order to avoid the influence of charge-discharge cycles on each other (through all possible residual processes), we conducted three training cycles before each change of temperature or discharge current. This guaranteed that each measurement was carried out under the same initial conditions.

We carried out each measurement for five batteries at a certain discharge current and temperature. However, if the obtained battery capacity values differed by more than 5%, we conducted additional training cycles or replaced one or two unstable batteries with new more stable ones. Then we repeated the experiment from the beginning.

4. Results

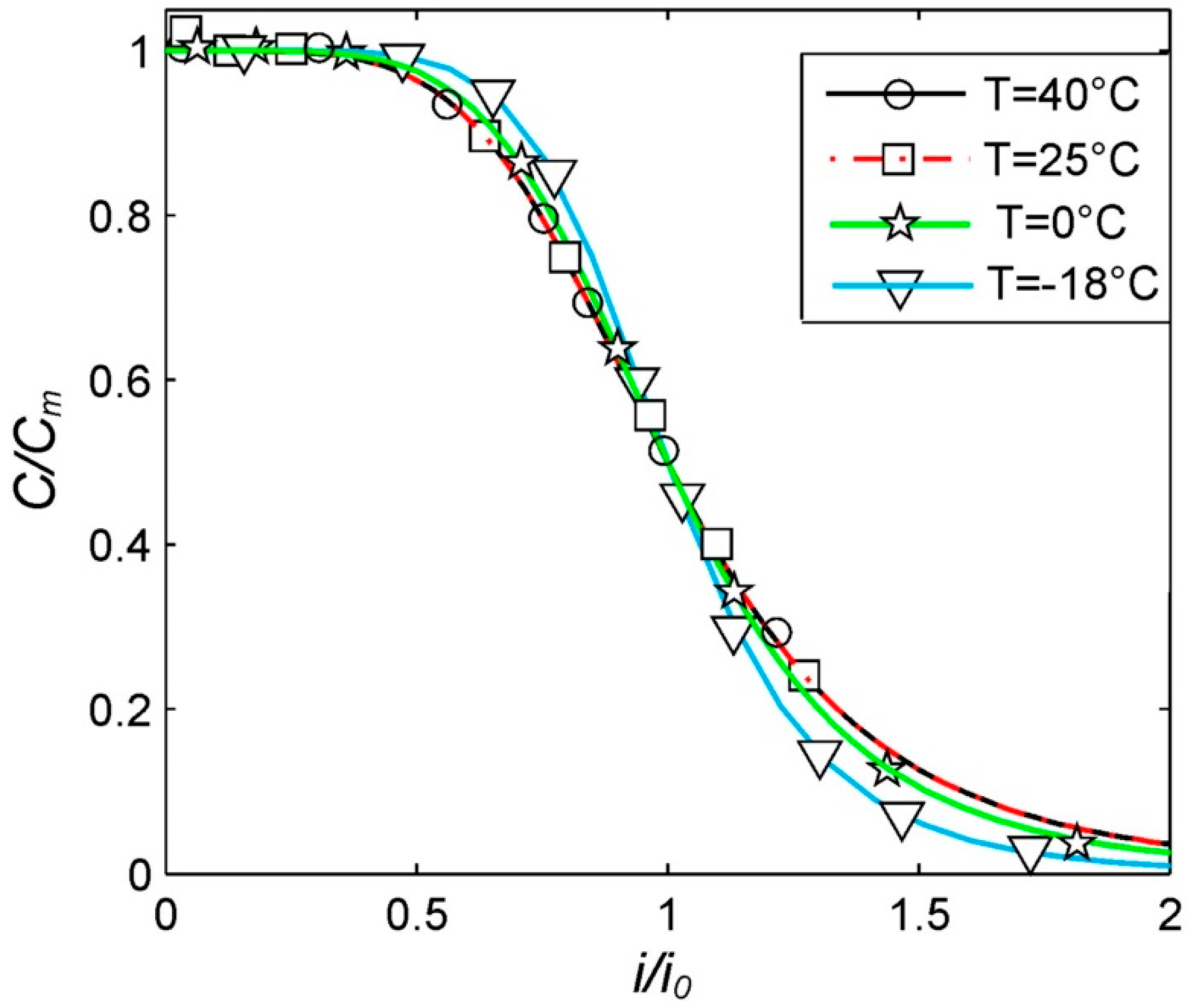
Figure 1 represents the experimental data obtained. We show the experimental data in the standardized coordinates (C/C_m, i/i₀) as this is a more convenient way of data presentation. This method makes it possible to eliminate to a high extent the inevitable small random factors related to both the battery manufacturing process and the measurement of experimental values. This is due to the fact that the parameters (C_m and i₀) are also found experimentally for each specific battery and the same random factors act on them. That is why in the ratios (C/C_m and i/i₀), any random factors related to the battery manufacturing process are compensated completely and random factors related to the measurement of the experimental value are compensated partially. This is why the experimental curves obtained in the standardized coordinates are considered to be more reliable.

The optimal parameters for the Peukert Equation (6) at different temperatures were obtained using the least square method and the Levenberg–Marquardt optimization procedure. For this, the experimental data presented in Figure 1 were used. The obtained parameters are shown in

Table 1. Optimal values for Equation (6) parameters at different temperature values.

Temperature (°C)	−18	−10	0	10	+25	+40
Cm (Ah)	30.097	34.052	36.204	38.485	39.990	39.993
i0 (A)	84.802	157.616	219.657	278.664	314.340	314.345
n	6.703	5.618	5.033	4.926	4.751	4.754
δ (%) 1	0.9	1.7	2.9	1.4	1.0	1.2

¹ Relative error of experimental data approximation by Equation (6) in Figure 1.

.

The experimental data obtained (Table 1) show that the parameters dependent on the battery’s temperature are all the parameters (C_m, i₀, and n) of the Peukert generalized Equation (6) instead of only parameter C_m as believed in the papers [10,23]. Hence, in the Hausmann model (1), it is necessary to take into account the temperature dependence of all the parameters of Equation (6).

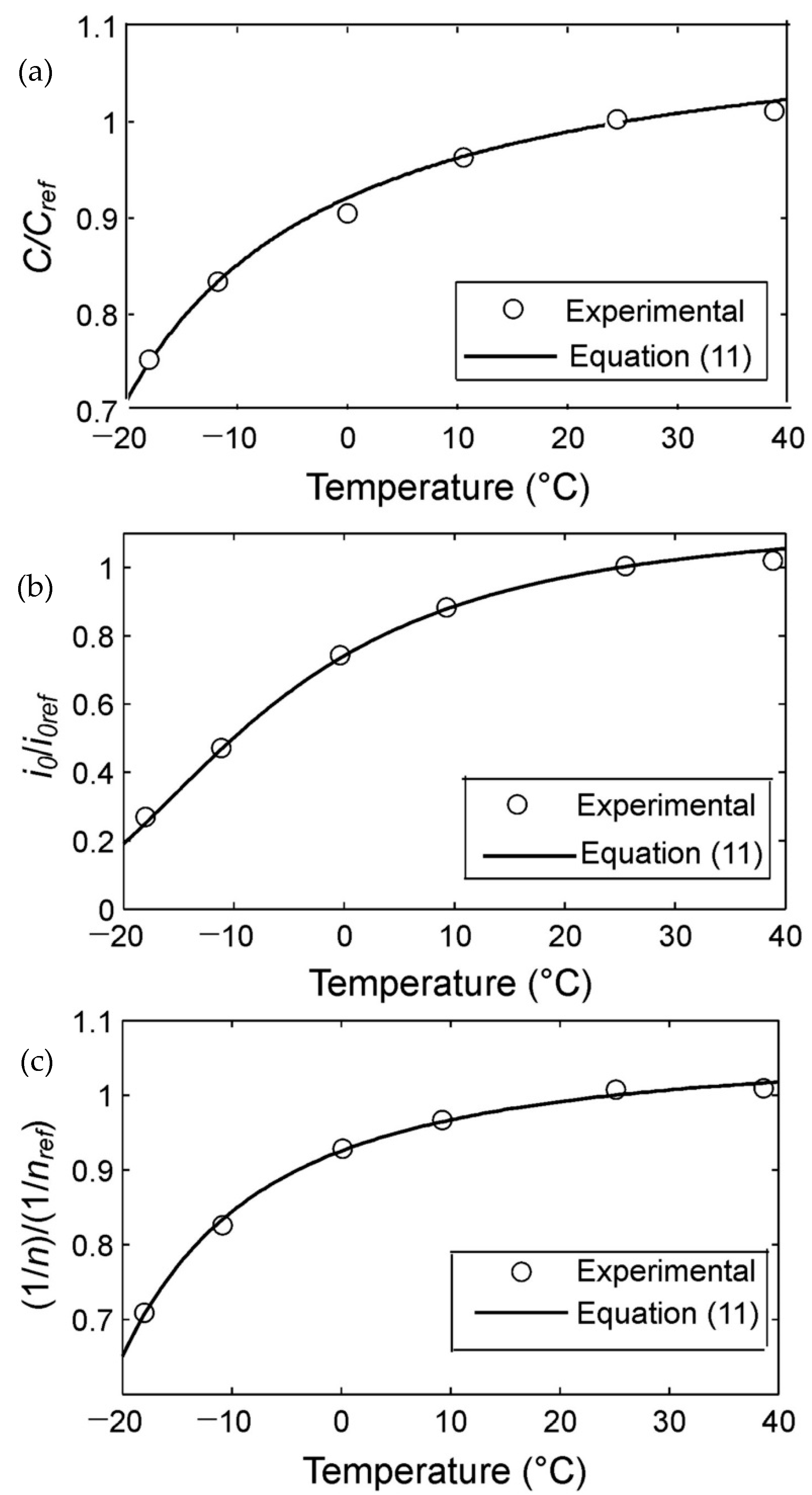
The temperature dependence of the parameters (C_m, i₀, and 1/n) of Equation (6) (from Table 1) is shown in Figure 2. In order to simplify the comparison, the parameters are presented in the standardized coordinates, where C_mref, i_0ref, and 1/n_ref are values of the same parameters at the temperature T_ref = 298 K.

Figure 2 shows clearly that the temperature dependence of the parameters C_m, i₀, and 1/n looks qualitatively the same and is similar to Equation (8).

Here, we introduce the vector of the parameters:

P = (C_m, i₀, 1/n)

(10)

Now the temperature dependences of all the parameters of Equation (6) can be written as a common Equation:

$$P_i(T)={(P_{ref})}_i{K}_i\frac{{\left(\frac{T-{(T_k)}_i}{T_{ref}-{(T_k)}_i}\right)}^{{\beta }_i}}{(K_i-1)+{\left(\frac{T-{(T_k)}_i}{T_{ref}-{(T_k)}_i}\right)}^{{\beta }_i}}, P_{ref}=(C_{mref},i_{kref},n_{ref}),$$

(11)

In Equation (11), the vector P_ref is equal to the vector P at the temperature T_ref = 298 K.

Now, using the experimental data (Table 1), we will check the correspondence of Equation (11) to the experimental data. The optimal parameters of Equation (11) were found with the use of the least square method and the Levenberg–Marquardt optimization procedure.

The values found are presented in

Table 2. Optimal values of the Equation (11) parameters.

Parameters	Cm	i0	1/n
Tk (°C)	−33	−32.9	−32.24
$\beta$	1.054	2.387	1.492
K	1.118	1.14	1.063
δ (%) 1	2.0	1.9	0.9

¹ Relative error of experimental data approximation by Equation (11) in Figure 1.

.

Equation (11) approximates well the experimental data from Table 1 (the relative approximation error is less than 2% (Table 2)). Hence, Equation (11) describes well the dependence of the Equation (6) parameters on temperature.

5. Discussion

Equation (6) (taking into account Equation (11)) has a number of advantages over the classical Peukert Equation (3) when considering the effect of temperature.

Firstly, the classical Peukert Equation (3) is applicable to lithium-ion batteries only in a limited range of discharge currents, from approximately 0.2 C_n to 2 C_n [24]. At lower discharge currents, the classical Peukert Equation (3) tends to infinity, which is impossible for any battery. At higher discharge currents, the experimental function C(i) for lithium-ion batteries is convex (Figure 1), whereas, in the case of the classical Peukert Equation (3), it always has a concave curve (at n > 0). Meanwhile, the generalized Peukert Equation (6) is applicable for any discharge currents.

Secondly, the Peukert Equation (3) is applicable only in the limited temperature range close to the temperature T_ref. In Equation (3), C(i,T) = 0 can only be at the temperature T = 0. However, in the batteries, C(i,T) = 0 is only reached near the freezing point of the electrolyte. Consequently, Equation (3) is not applicable at low temperatures. With the temperature growth in Equation (3), C(i,T) grows indefinitely, too. However, the capacity is always limited at any temperature in batteries; it cannot be larger than the capacity received by the battery from the charger. Meanwhile, the generalized Peukert Equation (6) updated with Equation (11) is applicable at any temperature.

Thirdly, all the parameters (C_m, i₀, and n) of Equation (6) have a clear physical meaning, while the parameters of the classical Peukert Equation (4) are just empirical constants.

Thus, in the Hausmann model (1), instead of the too-limited classical Peukert Equation (3), the more accurate generalized Peukert equation should be used:

$$C(i,T)=\frac{C_m(T)}{1+{\left(\frac{i}{i_0(T)}\right)}^{n(T)}}$$

(12)

Now, using Equations (2) and (12), we can find the following equation for the effective current I_eff(i,T) in the Hausmann model (1)

$$I_{eff}\left(i,T\right)=i\gamma \frac{C_{m0}\left(1+{\left(\frac{i}{i_0(T)}\right)}^{n(T)}\right)}{C_m(T)}$$

(13)

In Equations (12) and (13), the temperature dependence of parameters C_m(T), i₀(T), and n(T) is determined by Equation (11).

The preliminary estimates have shown that during the normal operation of electric vehicles, the use of Equations (12) and (13) plus Equation (11) instead of the Peukert Equation (3) increases the accuracy of the battery’s residual capacity estimation by 10–15% as compared to estimates based on the Hausmann model [10,23]. During extreme driving, when the currents are very small or very high and the temperature of the batteries is low, the use of Equation (13) in the Hausmann model (1) increases the accuracy of estimating the residual battery capacity by several times; thus, this is a subject for further research.

6. Conclusions

Every year the number of lithium-ion batteries of any format steadily grows. Therefore, the need for reliable models of these batteries grows, too. Basically, reliable models of batteries are necessary for the assessment of their residual capacity because the operation of all systems containing the batteries depends on the residual capacity in those batteries.

In this paper, the following is established.

Firstly, the classical Peukert Equation (4) can be used for lithium-ion batteries in a very limited range of discharge currents. An equation usable for any discharge current is the generalized Peukert Equation (6).

Secondly, the capacity of lithium-ion batteries is influenced to a large extent by the battery’s temperature. However, in many models, the battery’s temperature is either not taken into account at all [2,20,29] or is taken into account but in a very limited temperature range [10,23]. This results in significant errors in the estimation of various battery parameters.

In this paper, it is proved experimentally that in the generalized Peukert Equation (6), all the parameters depend strongly on the temperature (in accordance with Equation (11)). Therefore, Equation (6) (taking into account Equation (11)) is true at any battery temperature.

Finding equations that most accurately reflect the processes in batteries, i.e., when the batteries are charged and discharged, enables a correct understanding of these processes. Consequently, these studies are of great theoretical and practical importance.