Online Identification of VLRA Battery Model Parameters Using Electrochemical Impedance Spectroscopy
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Setup and Battery Testing Protocol
2.2. Battery Characterization and EEC Selection
3. Design Methodology
3.1. Zview Algorithm
3.2. Neural Network Algorithm
3.3. PSO Algorithm
3.4. Neural Network with Nelder-Mead Algorithm
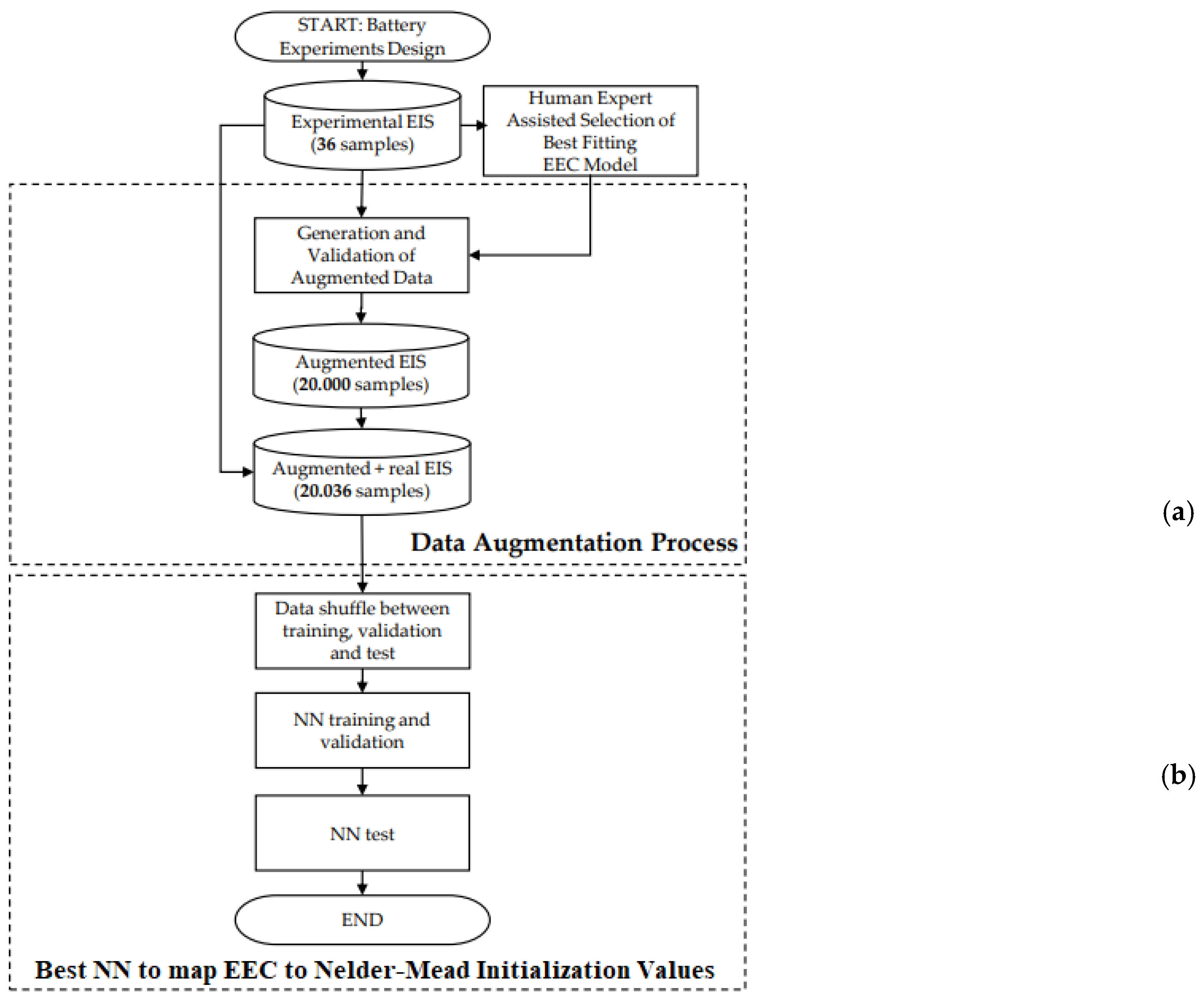
3.4.1. Experiment-Based Data Augmentation
3.4.2. Training, Validation and Testing of the Neural Network Trained with Augmented Data
4. Results and Discussion
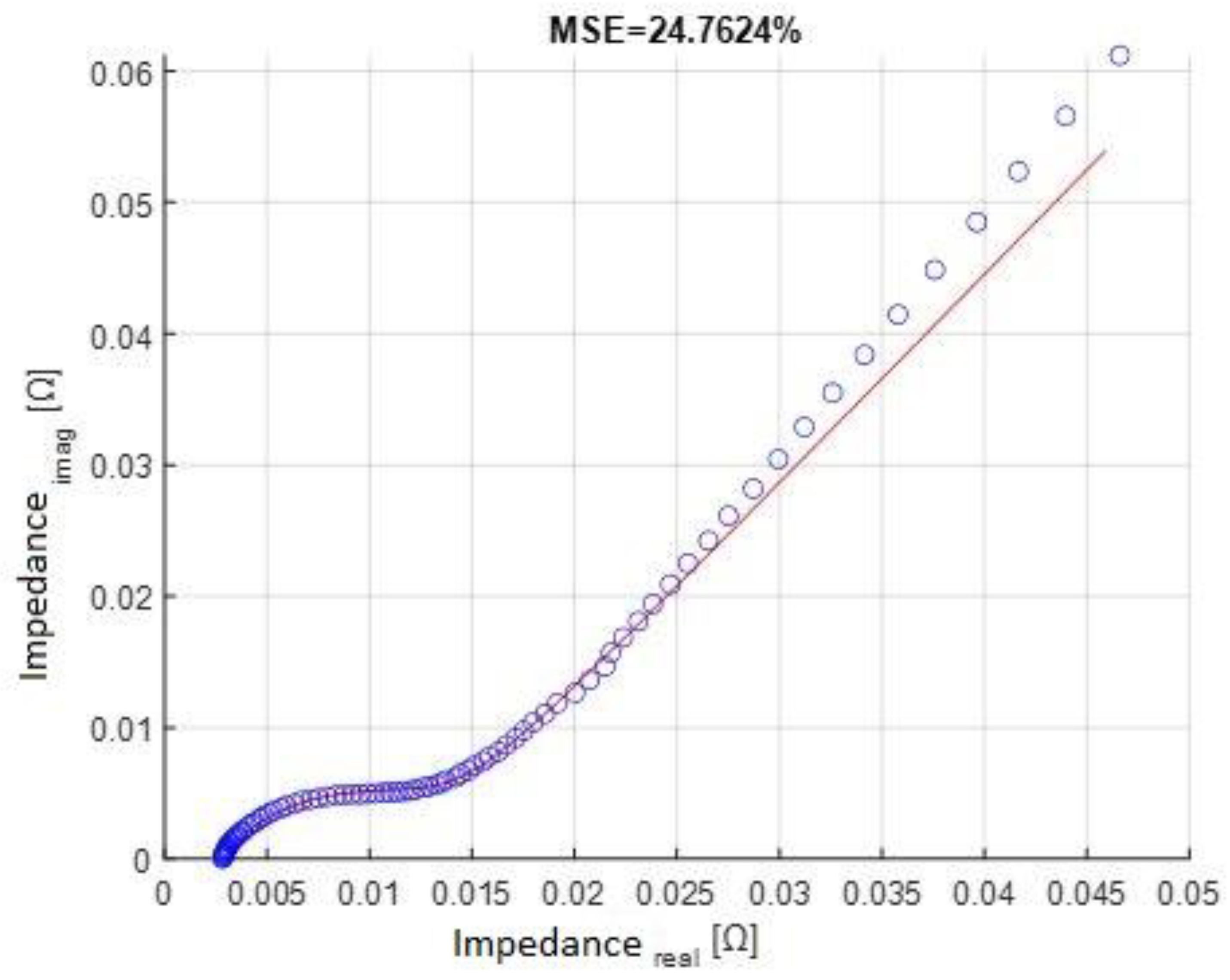
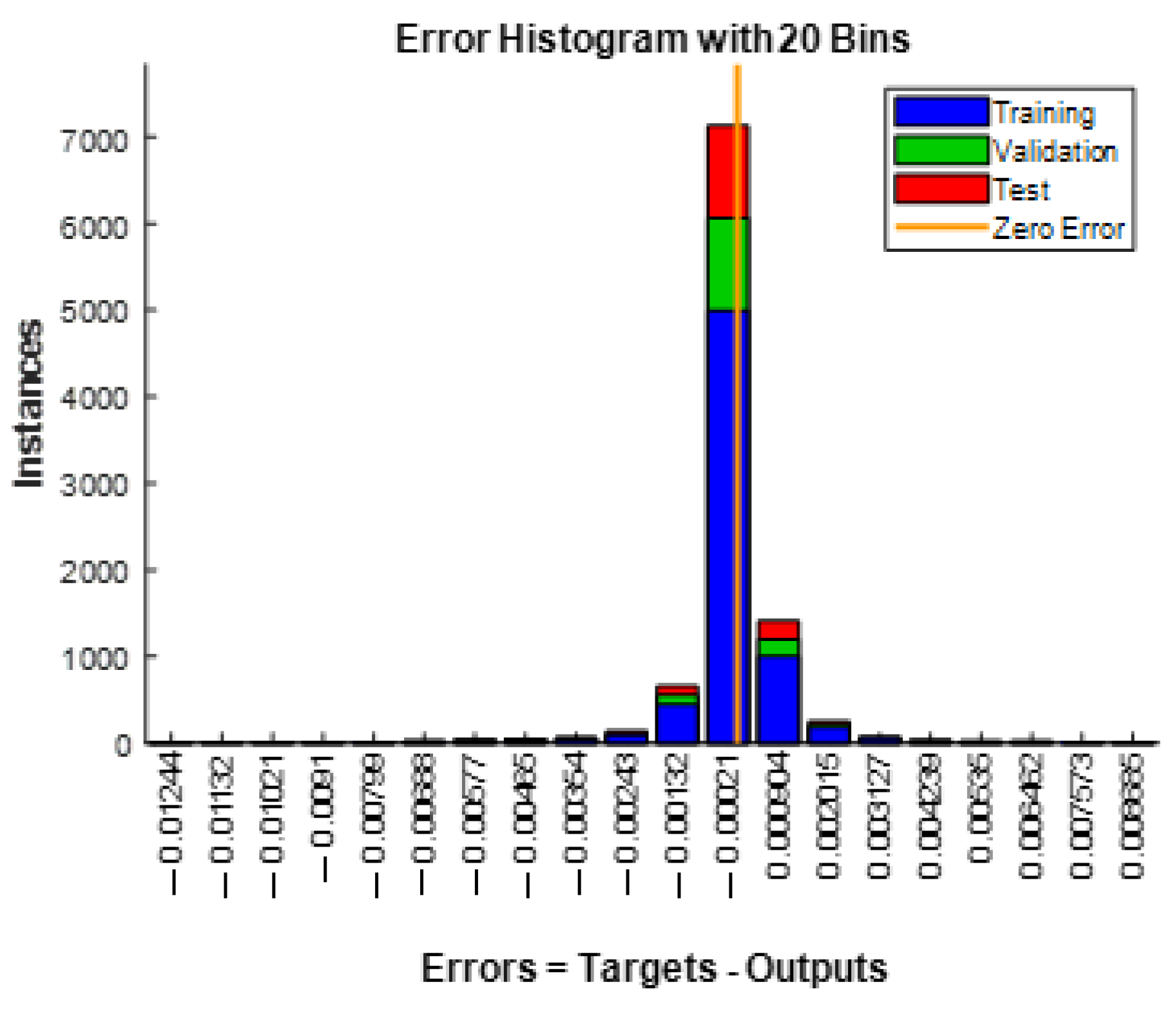
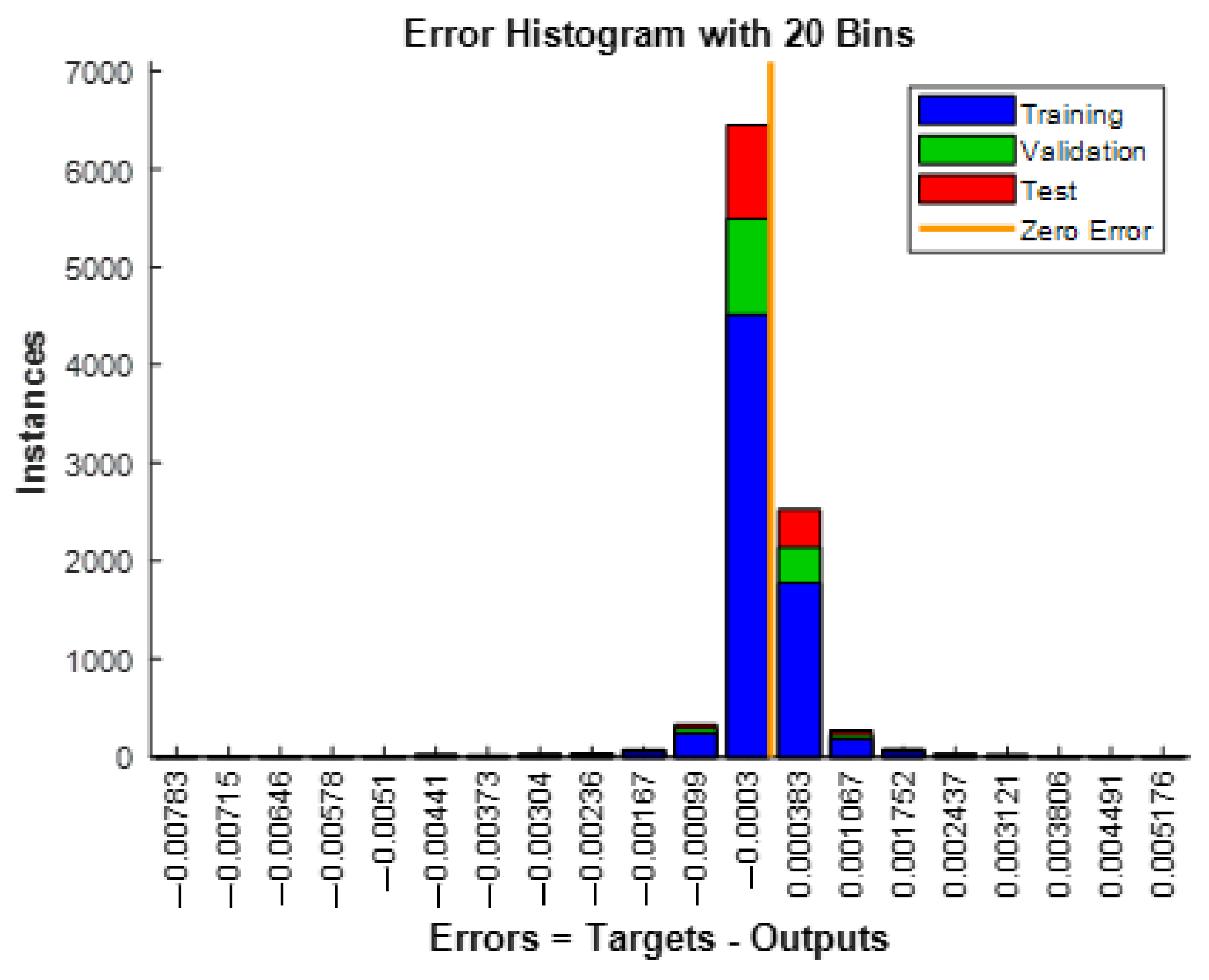
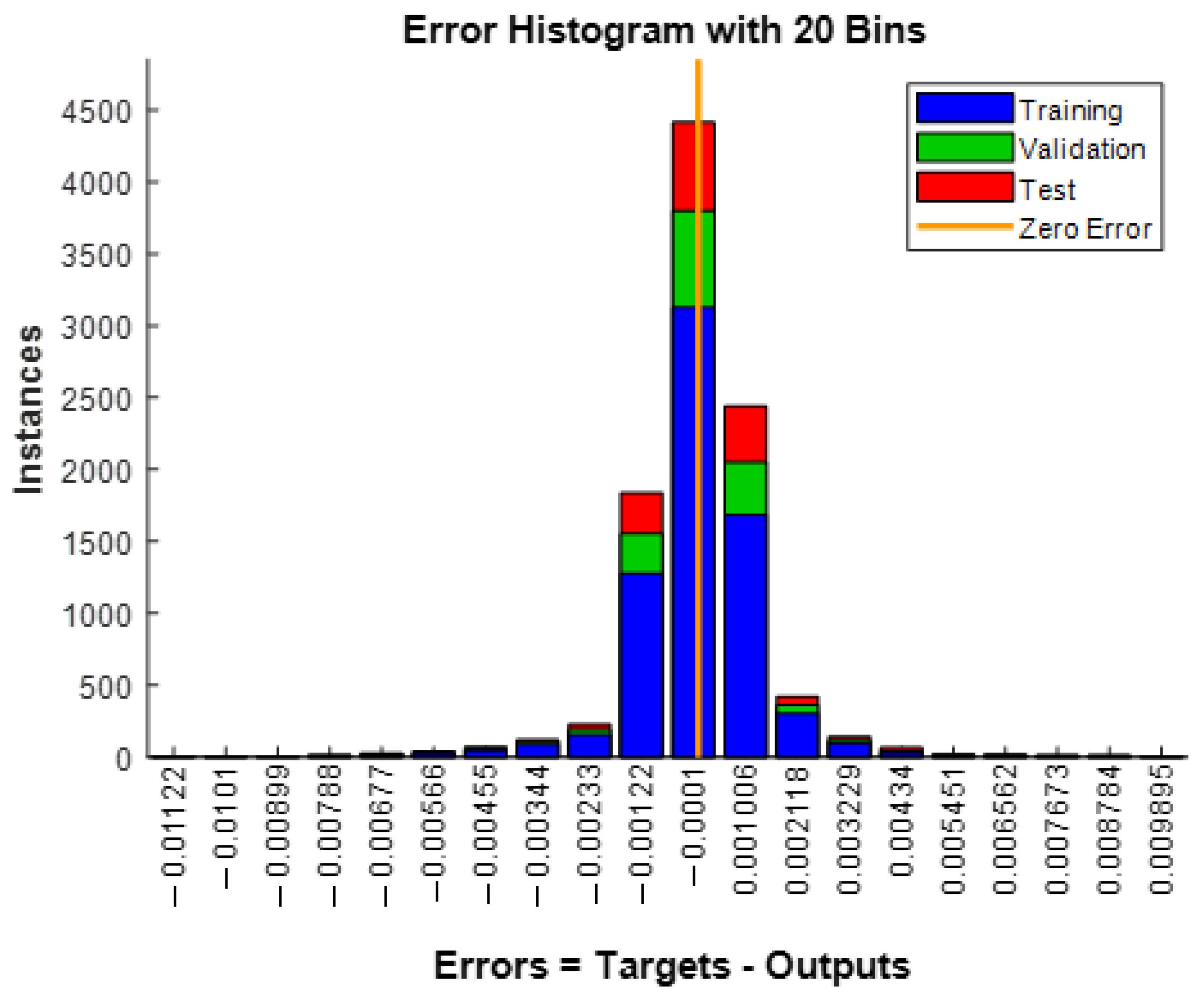
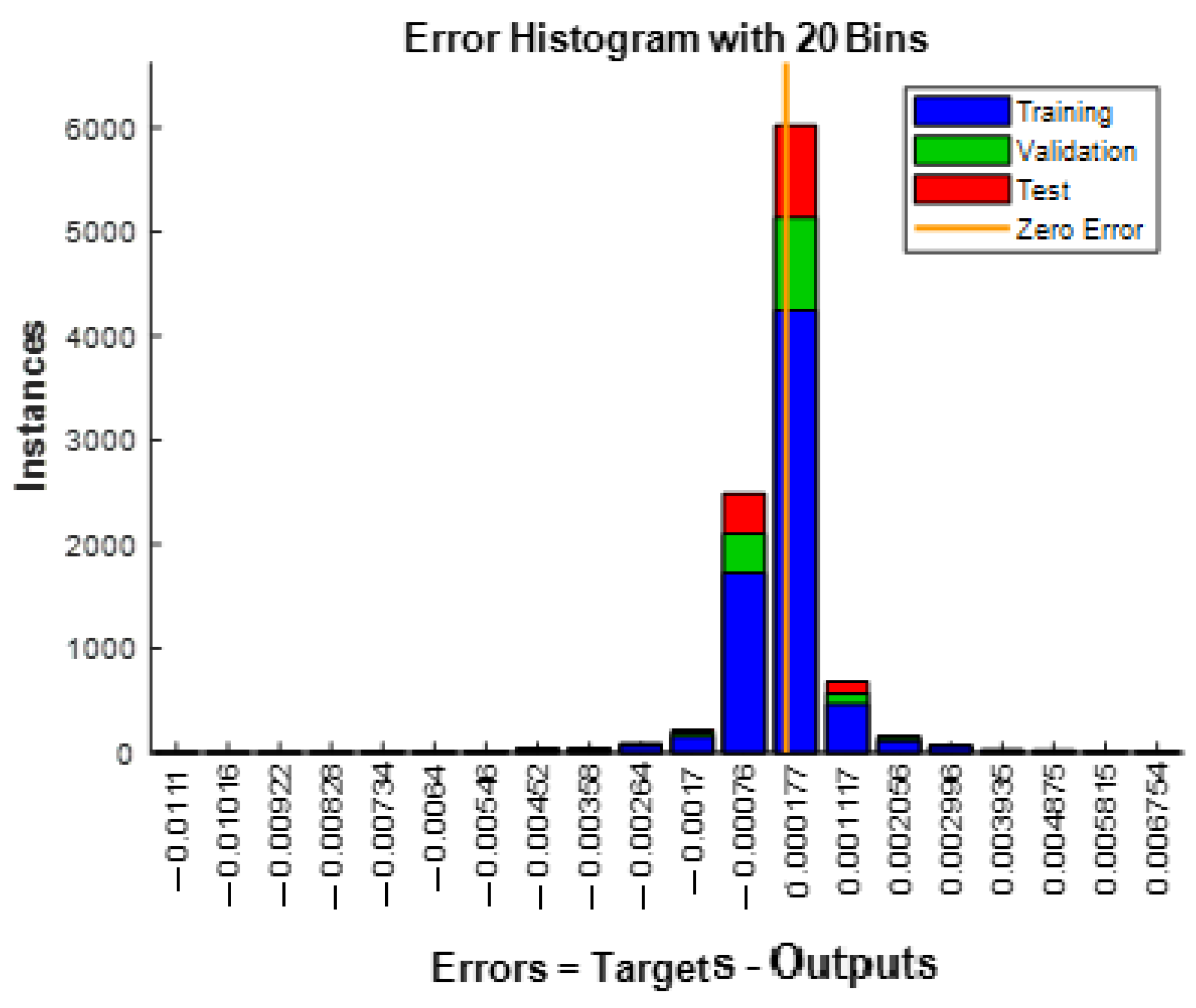
4.1. Neural Network Training and Validation
4.2. Algorithm’s Performance Comparison
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bose, C.S.C.; Laman, F.C. Battery state of health estimation through coup de fouet. In Proceedings of the INTELEC. Twenty-Second International Telecommunications Energy Conference (Cat. No.00CH37131), Phoenix, AZ, USA, 10–14 September 2000; pp. 597–601. [Google Scholar] [CrossRef]
- Ng, K.-S.; Moo, C.-S.; Chen, Y.-P.; Hsieh, Y.-C. State-of-Charge Estimation for Lead-Acid Batteries Based on Dynamic Open-Circuit Voltage. In Proceedings of the 2008 IEEE 2nd International Power and Energy Conference, Johor Bahru, Malaysia, 1–3 December 2008; p. 5. [Google Scholar] [CrossRef]
- Li, A.; Pelissier, S.; Venet, P.; Gyan, P. Fast Characterization Method for Modeling Battery Relaxation Voltage. Batteries 2016, 2, 7. [Google Scholar] [CrossRef]
- Olarte, J.; de Ilarduya, J.M.; Zulueta, E.; Ferret, R.; Kurt, E.; Lopez-Guede, J.M. Estimating State of Charge and State of Health of Vented NiCd Batteries with Evolution of Electrochemical Parameters. JOM 2021, 73, 4085–4090. [Google Scholar] [CrossRef]
- Calborean, A.; Bruj, O.; Murariu, T.; Morari, C. Resonance frequency analysis of lead-acid cells: An EIS approach to predict the state-of-health. J. Energy Storage 2020, 27, 101143. [Google Scholar] [CrossRef]
- Badeda, J.; Kwiecien, M.; Schulte, D.; Sauer, D. Battery State Estimation for Lead-Acid Batteries under Float Charge Conditions by Impedance: Benchmark of Common Detection Methods. Appl. Sci. 2018, 8, 1308. [Google Scholar] [CrossRef]
- Pascoe, P.E.; Anbuky, A.H. Standby Power System VRLA Battery Reserve Life Estimation Scheme. IEEE Trans. Energy Convers. 2005, 20, 887–895. [Google Scholar] [CrossRef]
- Gopikanth, M.L.; Sathyanarayana, S. Impedance parameters and the state-of-charge. II. Lead-acid battery. J. Appl. Electrochem. 1979, 9, 369–379. [Google Scholar] [CrossRef]
- Huet, F. A review of impedance measurements for determination of the state-of-charge or state-of-health of secondary batteries. J. Power Sources 1998, 70, 59–69. [Google Scholar] [CrossRef]
- Lukács, Z.; Kristóf, T. A generalized model of the equivalent circuits in the electrochemical impedance spectroscopy. Electrochim. Acta 2020, 363, 137199. [Google Scholar] [CrossRef]
- Murariu, T.; Morari, C. Time-dependent analysis of the state-of-health for lead-acid batteries: An EIS study. J. Energy Storage 2019, 21, 87–93. [Google Scholar] [CrossRef]
- Harting, N.; Wolff, N.; Krewer, U. Identification of Lithium Plating in Lithium-Ion Batteries Using Nonlinear Frequency Response Analysis (NFRA). Electrochim. Acta 2018, 281, 378–385. [Google Scholar] [CrossRef]
- Kim, W.; Jang, D.; Kim, H.J. Understanding Electronic and Li-Ion Transport of LiNi0.5Co0.2Mn0.3O2 Electrodes Affected by Porosity and Electrolytes Using Electrochemical Impedance Spectroscopy. J. Power Sources 2021, 510, 230338. [Google Scholar] [CrossRef]
- Pastor-Fernández, C.; Uddin, K.; Chouchelamane, G.H.; Widanage, W.D.; Marco, J. A Comparison between Electrochemical Impedance Spectroscopy and Incremental Capacity-Differential Voltage as Li-Ion Diagnostic Techniques to Identify and Quantify the Effects of Degradation Modes within Battery Management Systems. J. Power Sources 2017, 360, 301–318. [Google Scholar] [CrossRef]
- Wang, X.; Wei, X.; Dai, H. Estimation of state of health of lithium-ion batteries based on charge transfer resistance considering different temperature and state of charge. J. Energy Storage 2019, 21, 618–631. [Google Scholar] [CrossRef]
- Olarte, J.; de Ilarduya, J.M.; Zulueta, E.; Ferret, R.; Fernández-Gámiz, U.; Lopez-Guede, J.M. A Battery Management System with EIS Monitoring of Life Expectancy for Lead–Acid Batteries. Electronics 2021, 10, 1228. [Google Scholar] [CrossRef]
- Lombardo, T.; Duquesnoy, M.; El-Bouysidy, H.; Årén, F.; Gallo-Bueno, A.; Jørgensen, P.B.; Bhowmik, A.; Demortière, A.; Ayerbe, E.; Alcaide, F.; et al. Artificial Intelligence Applied to Battery Research: Hype or Reality? Chem. Rev. 2022, 122, 10899–10960. [Google Scholar] [CrossRef]
- Kwiecien, M.; Badeda, J.; Huck, M.; Komut, K.; Duman, D.; Sauer, D. Determination of SoH of Lead-Acid Batteries by Electrochemical Impedance Spectroscopy. Appl. Sci. 2018, 8, 873. [Google Scholar] [CrossRef]
- Densmore, A.; Hanif, M. Determining Battery SoC Using Electrochemical Impedance Spectroscopy and the Extreme Learning Machine. In Proceedings of the 2015 IEEE 2nd International Future Energy Electronics Conference (IFEEC), Taipei, Taiwan, 1–4 November 2015. [Google Scholar]
- Kiel, M.; Sauer, D.U.; Turpin, P.; Naveed, M.; Favre, E. Validation of single frequency Z measurement for standby battery state of health determination. In Proceedings of the INTELEC 2008—2008 IEEE 30th International Telecommunications Energy Conference, San Diego, CA, USA, 14 September 2008; pp. 1–7. [Google Scholar] [CrossRef]
- Raijmakers, L.H.J.; Danilov, D.L.; van Lammeren, J.P.M.; Lammers, M.J.G.; Notten, P.H.L. Sensorless battery temperature measurements based on electrochemical impedance spectroscopy. J. Power Sources 2014, 247, 539–544. [Google Scholar] [CrossRef]
- Karden, E.; Buller, S.; de Doncker, R.W. A method for measurement and interpretation of impedance spectra for industrial batteries. J. Power Sources 2000, 85, 72–78. [Google Scholar] [CrossRef]
- Csomós, B.; Fodor, D. Identification of the material properties of an 18650 Li-ion battery for improving the electrochemical model used in cell testing. Hung. J. Ind. Chem. 2020, 48, 33–41. [Google Scholar] [CrossRef]
- Wang, X.; Wei, X.; Zhu, J.; Dai, H.; Zheng, Y.; Xu, X.; Chen, Q. A review of modeling, acquisition, and application of lithium-ion battery impedance for onboard battery management. eTransportation 2021, 7, 100093. [Google Scholar] [CrossRef]
- Chun, H.; Kim, J.; Han, S. Parameter identification of an electrochemical lithium-ion battery model with convolutional neural network. IFAC-PapersOnLine 2019, 52, 129–134. [Google Scholar] [CrossRef]
- Jiménez-Bermejo, D.; Fraile-Ardanuy, J.; Castaño-Solis, S.; Merino, J.; Álvaro-Hermana, R. Using Dynamic Neural Networks for Battery State of Charge Estimation in Electric Vehicles. Procedia Comput. Sci. 2018, 130, 533–540. [Google Scholar] [CrossRef]
- Yang, D.; Wang, Y.; Pan, R.; Chen, R.; Chen, Z. A Neural Network Based State-of-Health Estimation of Lithium-ion Battery in Electric Vehicles. Energy Procedia 2017, 105, 2059–2064. [Google Scholar] [CrossRef]
- Capizzi, G.; Bonanno, F.; Tina, G.M. Recurrent Neural Network-Based Modeling and Simulation of Lead-Acid Batteries Charge-Discharge. IEEE Trans. Energy Convers. 2011, 26, 435–443. [Google Scholar] [CrossRef]
- Young, R.E.; Li, X.; Perone, S.P. Prediction of individual cell performance in a long-string lead/acid peak-shaving battery: Application of artificial neural networks. J. Power Sources 1996, 62, 121–134. [Google Scholar] [CrossRef]
- Morita, Y.; Yamamoto, S.; Lee, S.H.; Mizuno, N. On-line detection of state-of-charge in lead acid battery using both neural network and on-line identification. In Proceedings of the Iecon 2006—32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 6–10 November 2006; Volume 1–11, pp. 3379–3384. [Google Scholar]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder—Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef]
- Olarte, J.; de Ilarduya, J.M.; Zulueta, E.; Ferret, R.; Fernández-Gámiz, U.; Lopez-Guede, J.M. Automatic Identification Algorithm of Equivalent Electrochemical Circuit Based on Electroscopic Impedance Data for a Lead Acid Battery. Electronics 2021, 10, 1353. [Google Scholar] [CrossRef]
- Komsiyska, L.; Buchberger, T.; Diehl, S.; Ehrensberger, M.; Hanzl, C.; Hartmann, C.; Hölzle, M.; Kleiner, J.; Lewerenz, M.; Liebhart, B.; et al. Critical Review of Intelligent Battery Systems: Challenges, Implementation, and Potential for Electric Vehicles. Energies 2021, 14, 5989. [Google Scholar] [CrossRef]
- Hornik, K. Approximation capabilities of multilayer feedforward networks. Neural Netw. 1991, 4, 251–257. [Google Scholar] [CrossRef]
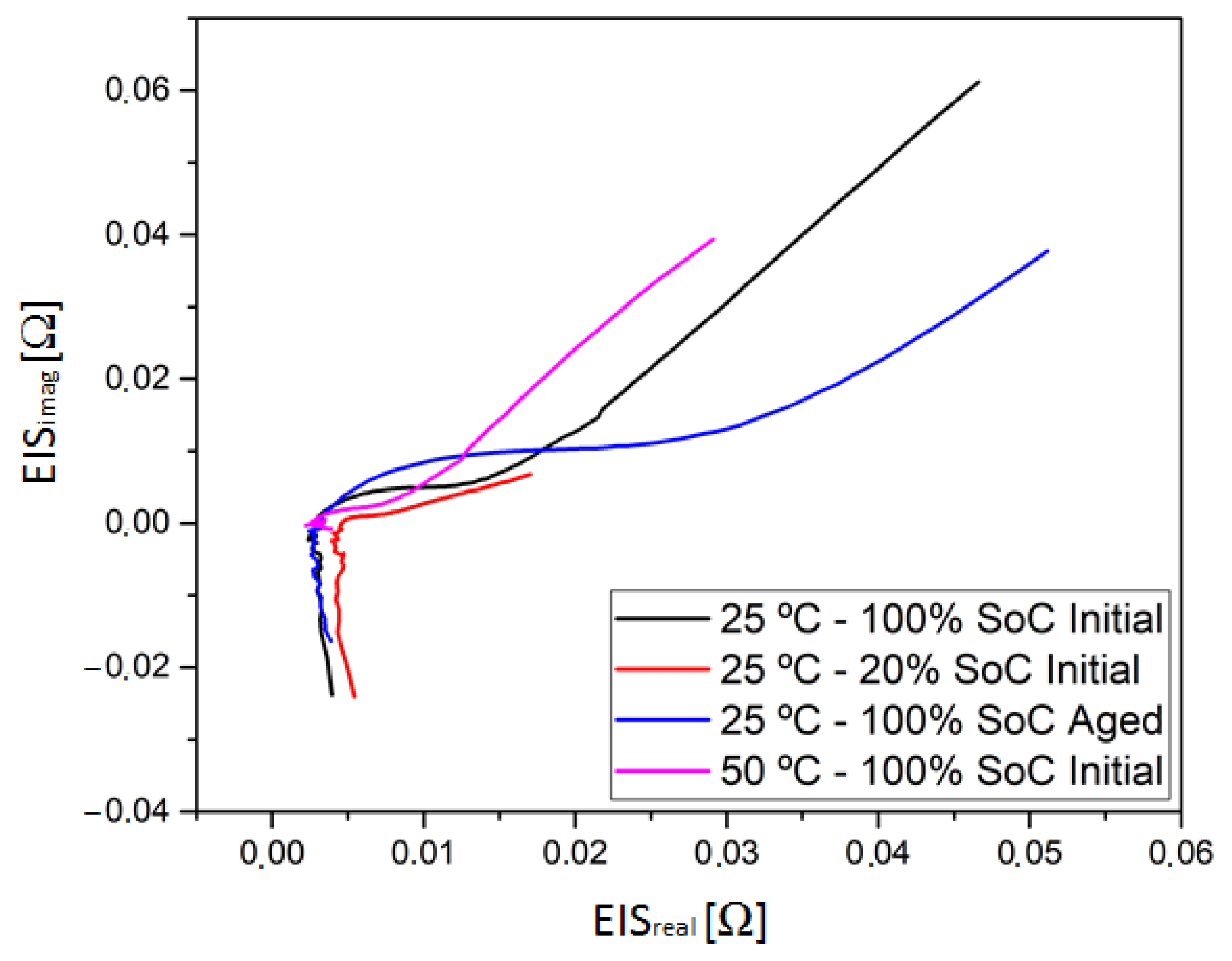
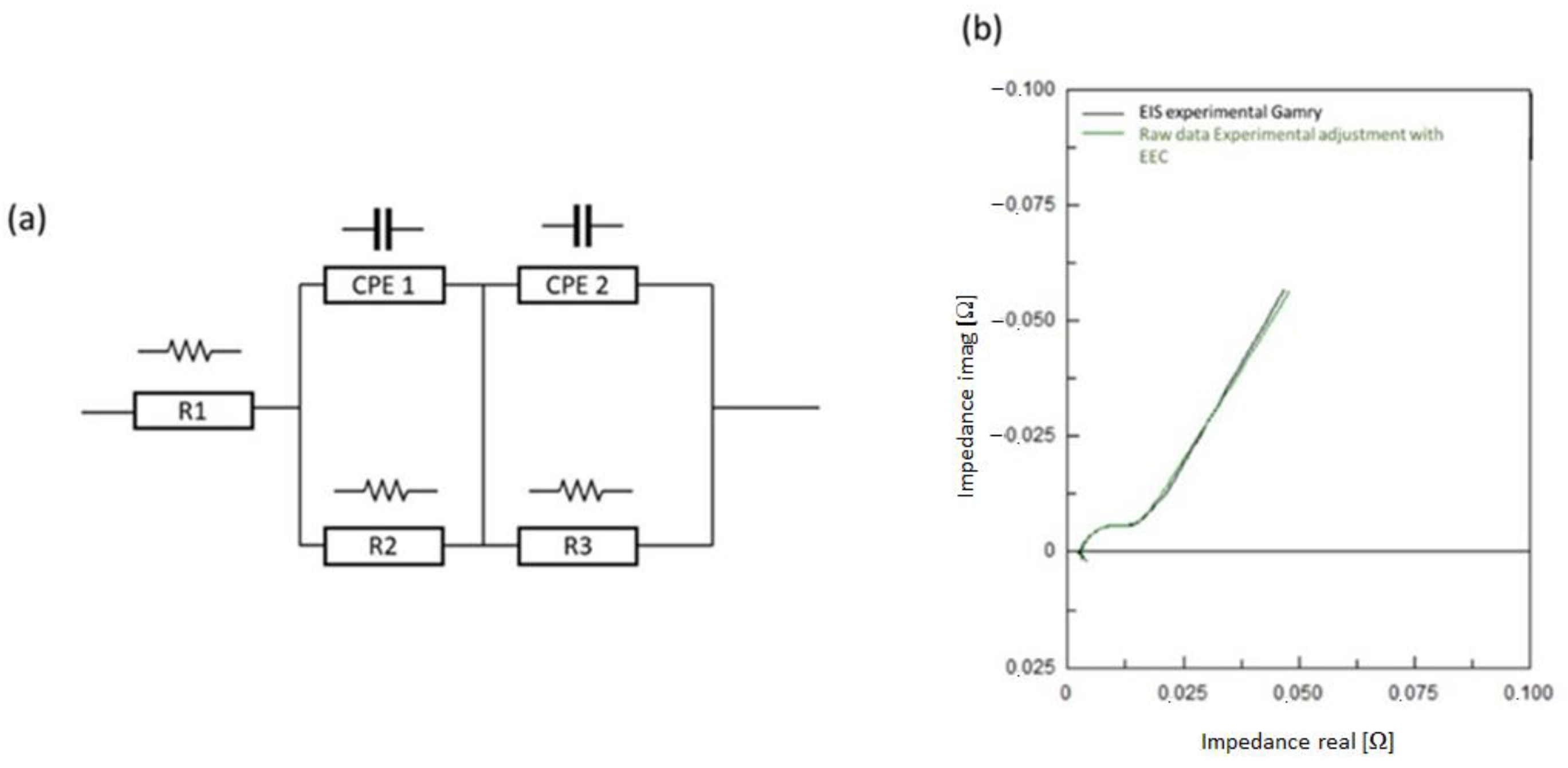

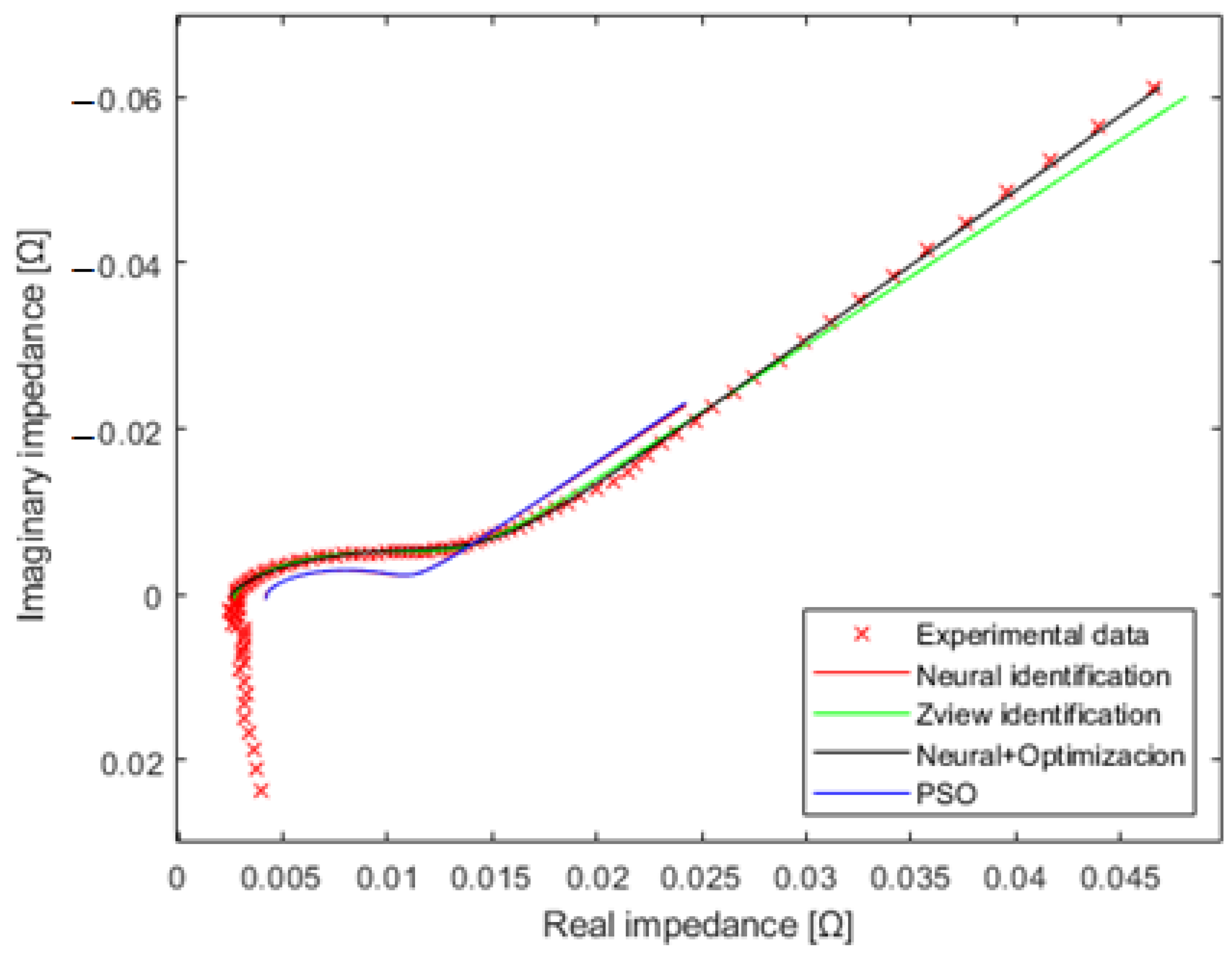
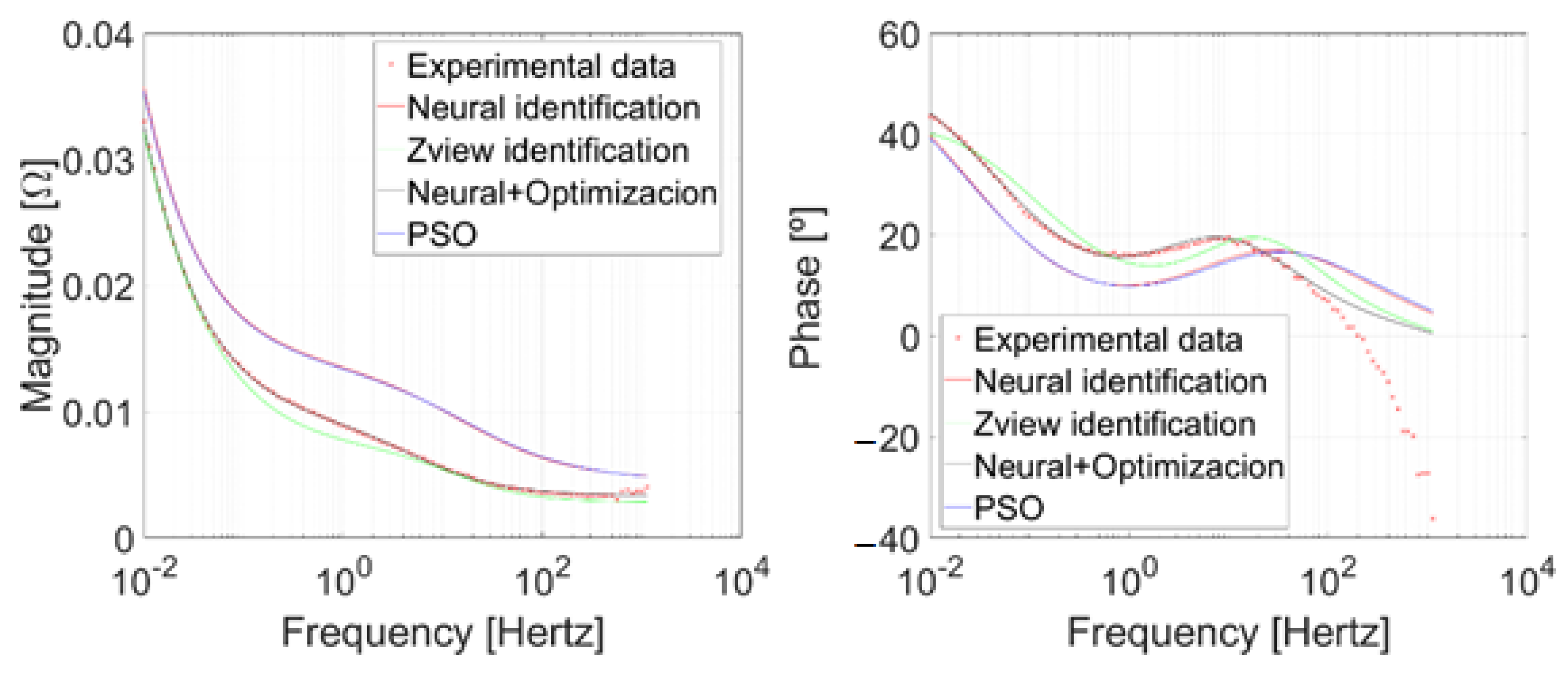

| SoH | R1 | CPE1-T | CPE1-P | R2 | CPE2-T | CPE2-P | R3 |
|---|---|---|---|---|---|---|---|
| 100% | 0.0027176 | 7.17 | 0.85729 | 0.0092174 | 87.18 | 0.65421 | - |
| 80% | 0.0027953 | 9.21 | 0.77865 | 0.0039696 | 184.13 | 0.61221 | 0.21606 |
| 60% | 0.0031349 | 11.21 | 0.75909 | 0.0021683 | 218.80 | 0.56847 | 0.08871 |
| 40% | 0.0033452 | 18.01 | 0.62091 | 0.0020905 | 229.50 | 0.50060 | 0.066692 |
| 20% | 0.0039584 | 14.92 | 0.65745 | 0.0020599 | 199.40 | 0.38122 | 0.12304 |
| 0% | 0.0046775 | 10.12 | 0.70804 | 0.0025044 | 152.20 | 0.29418 | - |
| Neurons | Epochs | Min Error | Max Error | Gradient | MSE Loss Function |
|---|---|---|---|---|---|
| 10 | 100 | −0.00021 | 0.000904 | 1.4505 × 10−4 | 1.2121 × 10−6 |
| 10 | 200 | −0.0003 | 0.000383 | 5.8395 × 10−4 | 3.3363 × 10−7 |
| 5 | 100 | −0.00122 | 0.001006 | 9.2107 × 10−6 | 1.9786 × 10−6 |
| 20 | 100 | −0.00076 | 0.000177 | 3.7085 × 10−4 | 8.3897 × 10−7 |
| Benchmarked Method | Average Error |
|---|---|
| MeanErrorNeural | 6.29% |
| MeanErrorZview | 2.01% |
| MeanErrorNeuralOpt | 0.49% |
| MeanErrorPso | 5.92% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olarte, J.; Martinez de Ilarduya, J.; Zulueta, E.; Ferret, R.; Garcia-Ortega, J.; Lopez-Guede, J.M. Online Identification of VLRA Battery Model Parameters Using Electrochemical Impedance Spectroscopy. Batteries 2022, 8, 238. https://doi.org/10.3390/batteries8110238
Olarte J, Martinez de Ilarduya J, Zulueta E, Ferret R, Garcia-Ortega J, Lopez-Guede JM. Online Identification of VLRA Battery Model Parameters Using Electrochemical Impedance Spectroscopy. Batteries. 2022; 8(11):238. https://doi.org/10.3390/batteries8110238
Chicago/Turabian StyleOlarte, Javier, Jaione Martinez de Ilarduya, Ekaitz Zulueta, Raquel Ferret, Joseba Garcia-Ortega, and Jose Manuel Lopez-Guede. 2022. "Online Identification of VLRA Battery Model Parameters Using Electrochemical Impedance Spectroscopy" Batteries 8, no. 11: 238. https://doi.org/10.3390/batteries8110238
APA StyleOlarte, J., Martinez de Ilarduya, J., Zulueta, E., Ferret, R., Garcia-Ortega, J., & Lopez-Guede, J. M. (2022). Online Identification of VLRA Battery Model Parameters Using Electrochemical Impedance Spectroscopy. Batteries, 8(11), 238. https://doi.org/10.3390/batteries8110238









