Reliable Online Internal Short Circuit Diagnosis on Lithium-Ion Battery Packs via Voltage Anomaly Detection Based on the Mean-Difference Model and the Adaptive Prediction Algorithm
Abstract
:1. Introduction
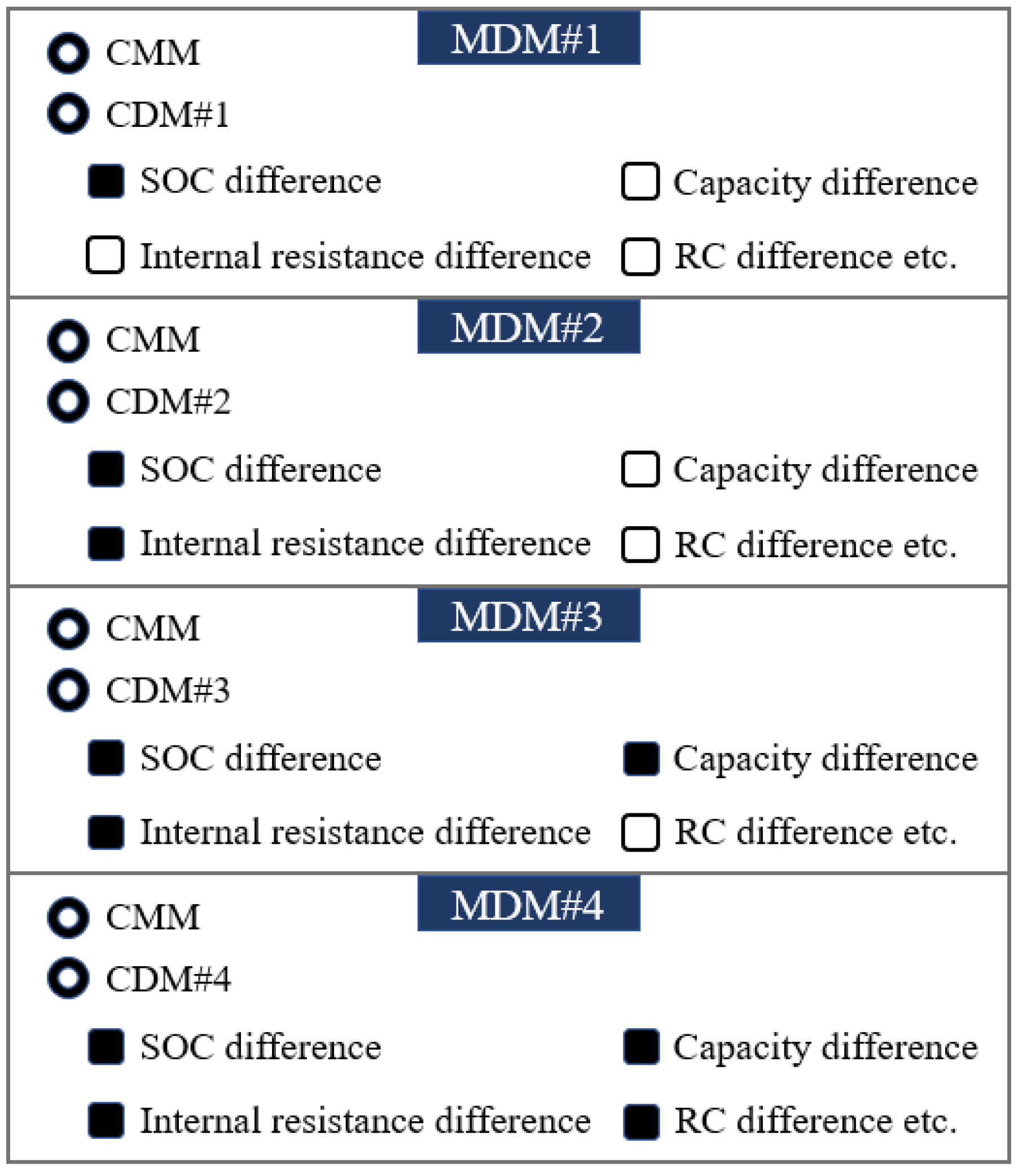
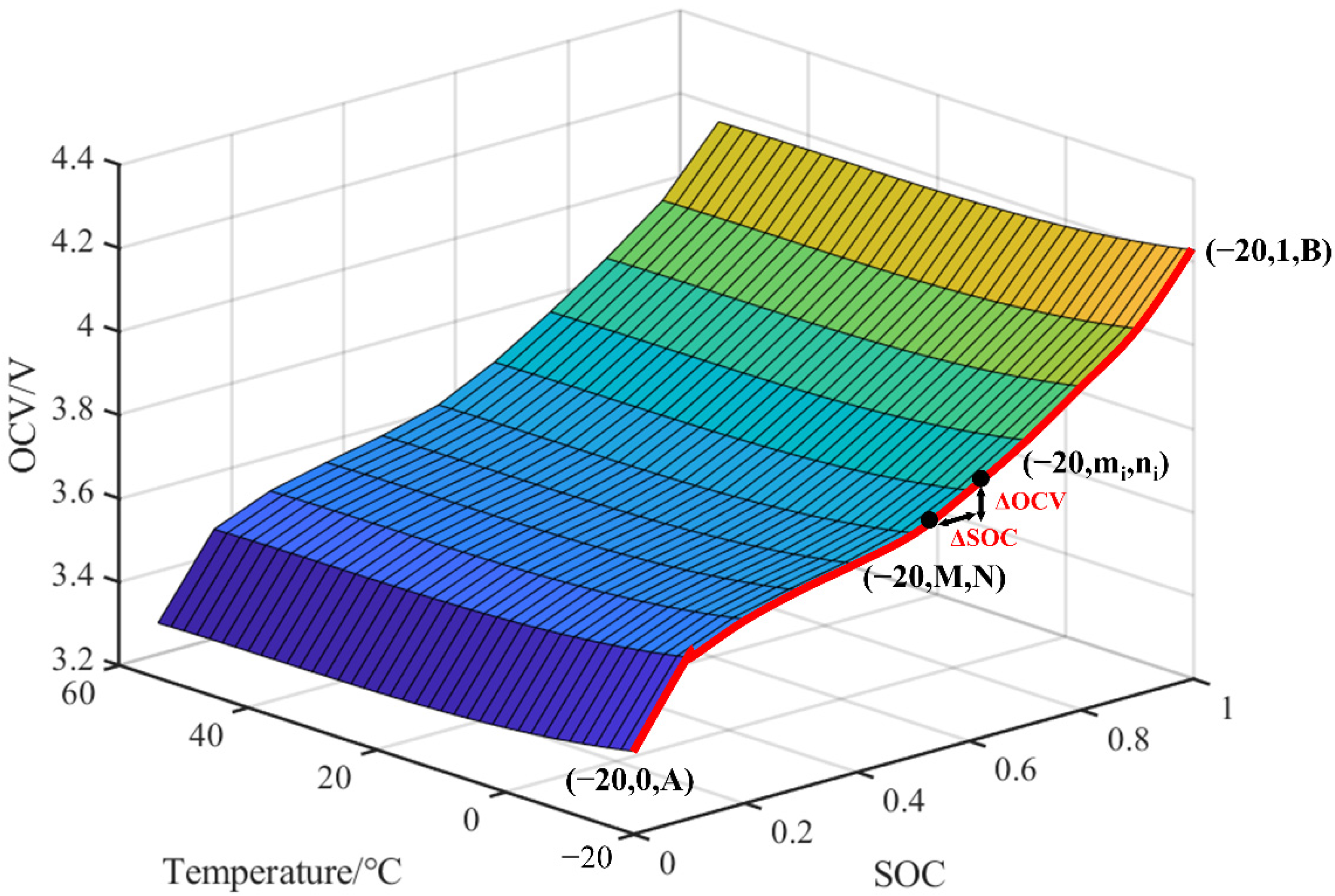
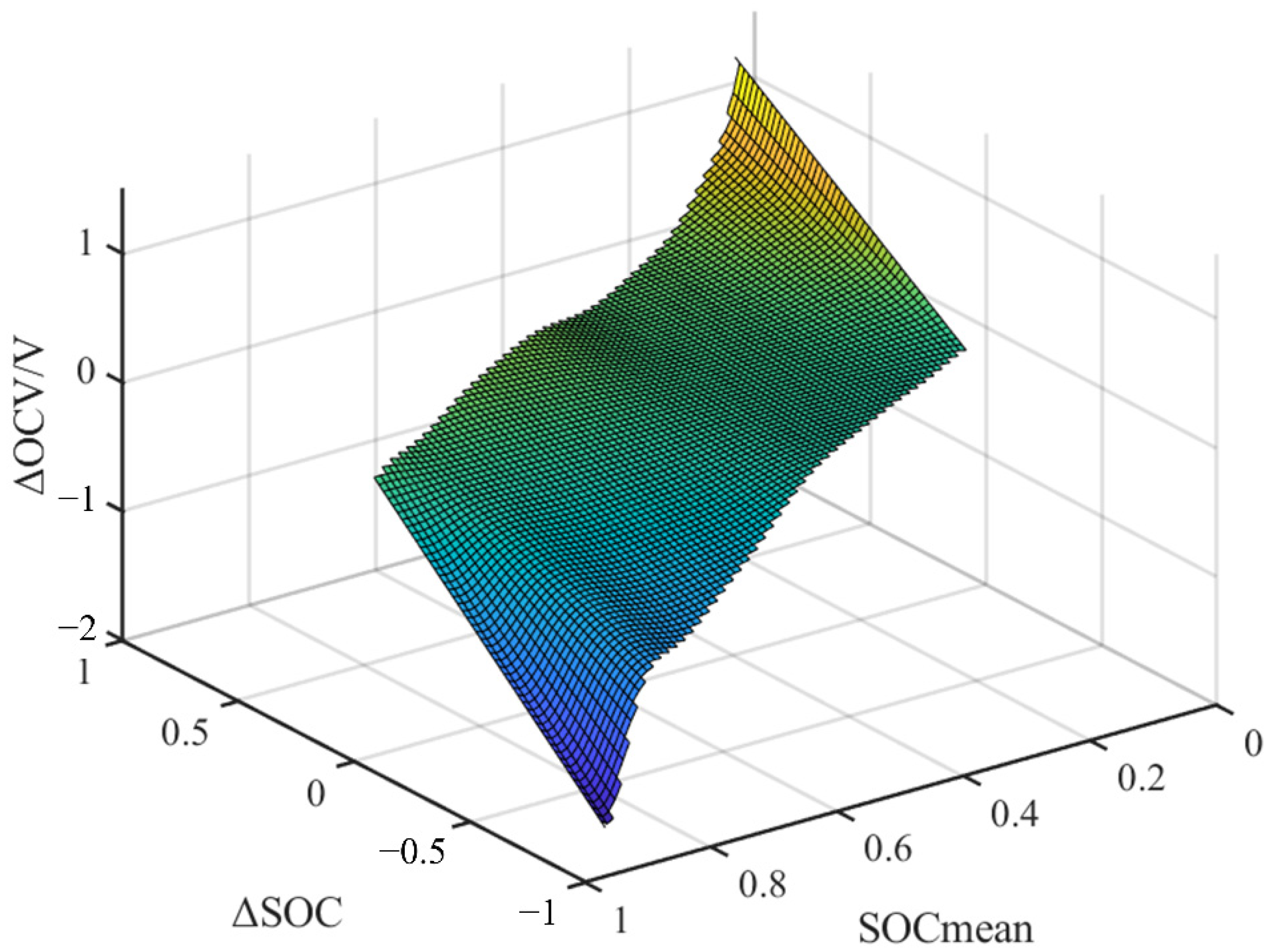
2. Battery Pack Modeling Based on the MDM
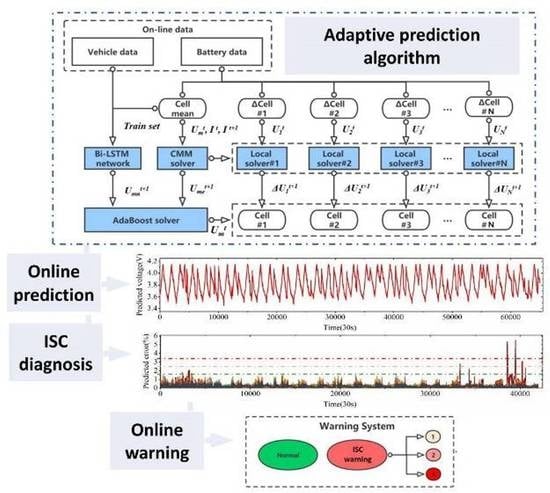
3. Voltage Prediction Framework
3.1. Voltage Prediction via Bi-LSTM on CMM
3.1.1. Schematic of BI-LSTM
3.1.2. Discussion on Input Dataset for Neutral Network
3.2. Cell Voltage Prediction Based on the MDM
3.3. Cell Voltage Prediction Correction Via Adaboost Solver
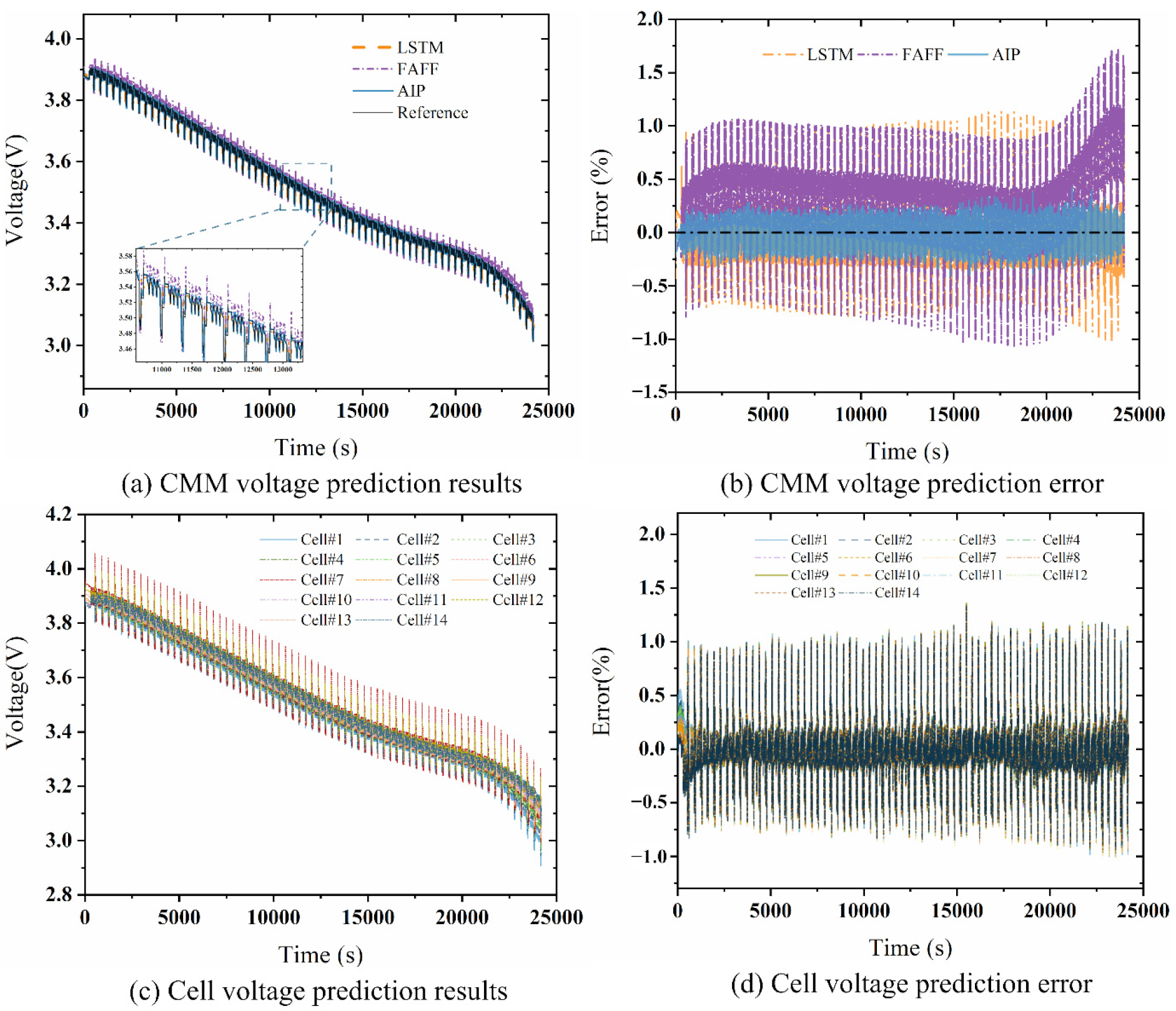
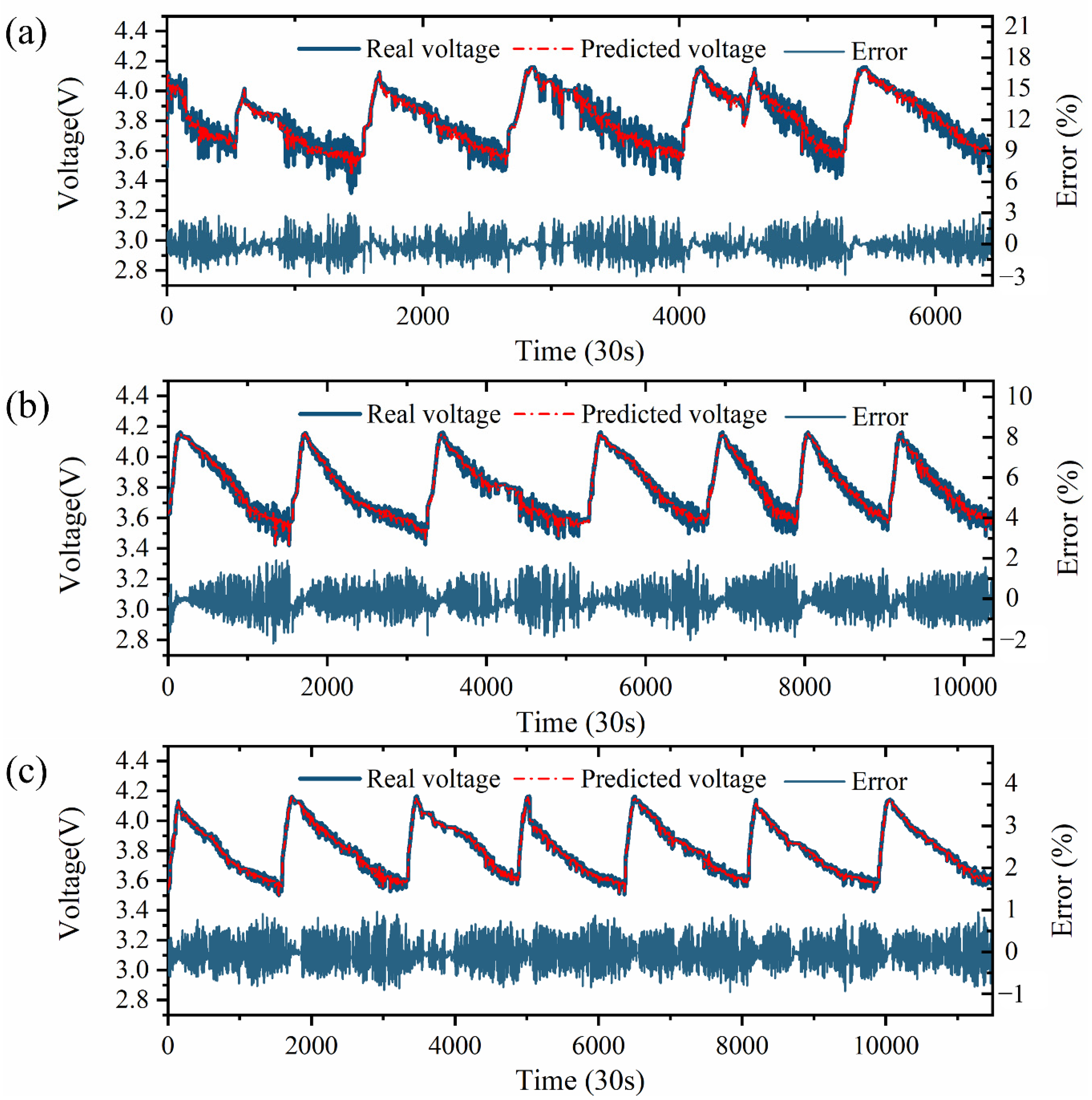
3.4. Prediction Results Based on DST Conditions
4. Results and Discussions
4.1. Data Sources
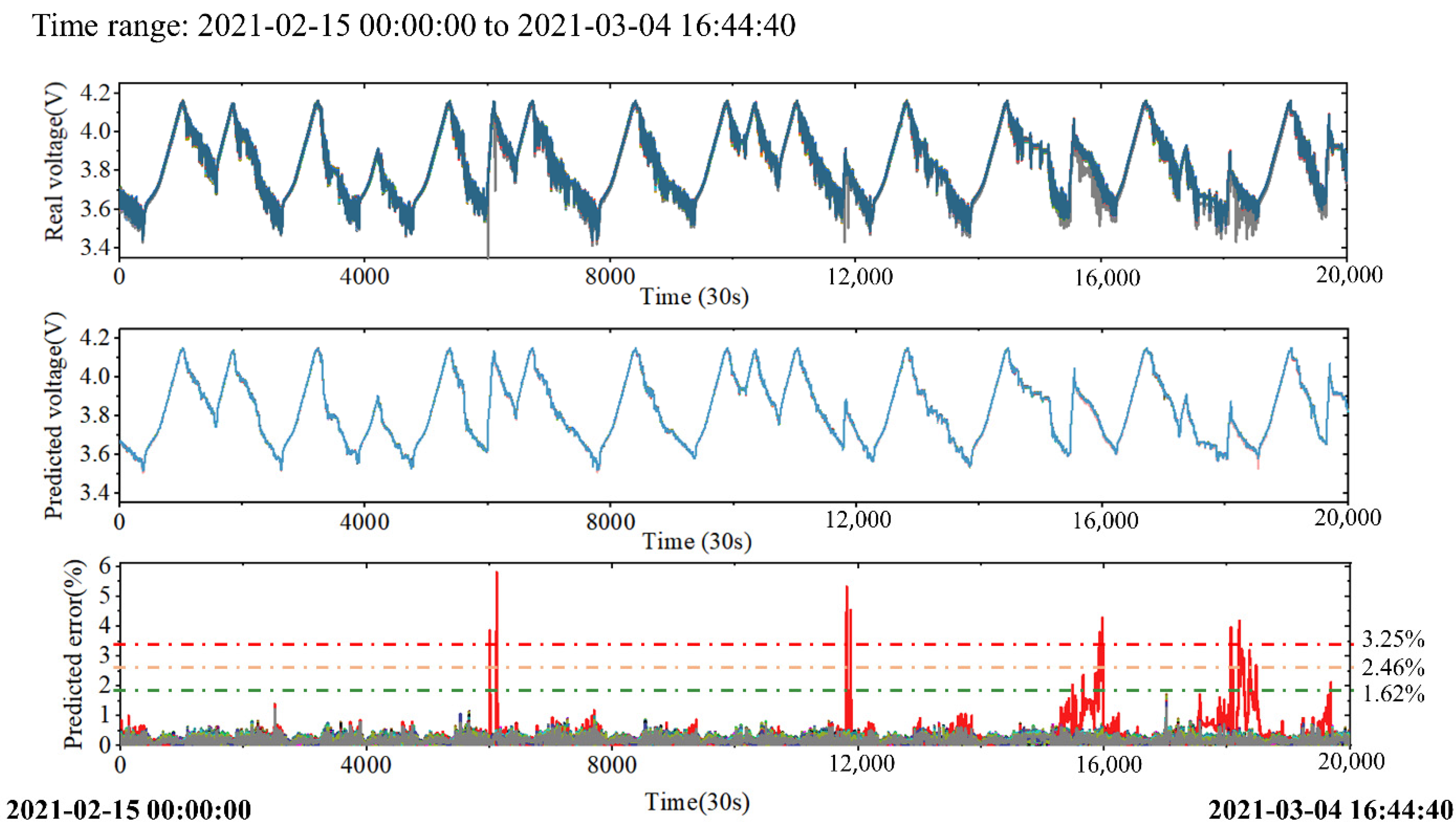
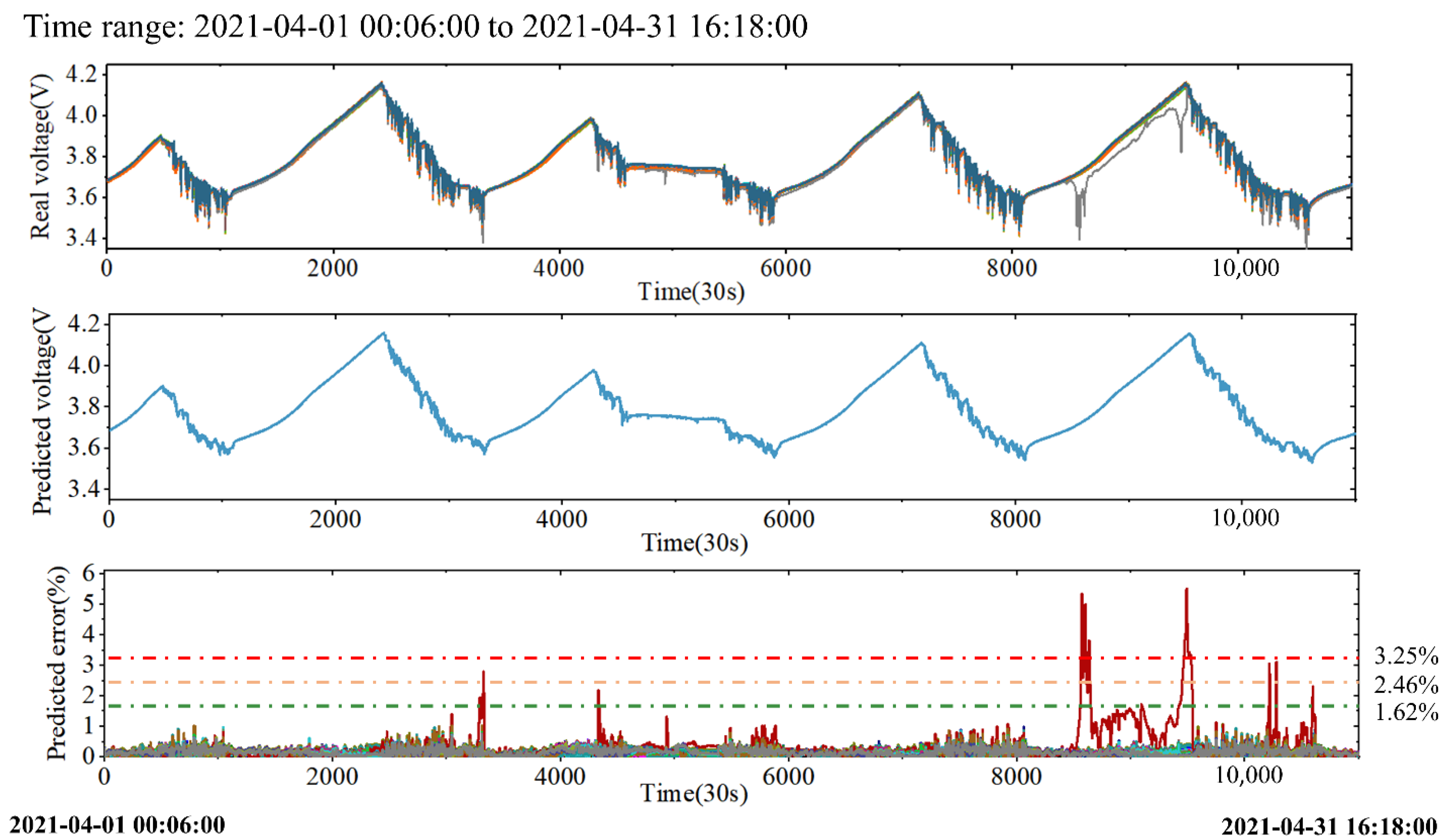
4.2. Diagnosis Results on Real Vehicle Data
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hu, J.; Wei, Z.; He, H. An Online Adaptive Internal Short Circuit Detection Method of Lithium - Ion Battery. Automot. Innov. 2021, 4, 93–102. [Google Scholar] [CrossRef]
- Wang, J.; Deng, Z.; Yu, T.; Yoshida, A.; Xu, L.; Guan, G.; Abudula, A. State of health estimation based on modified Gaussian process regression for lithium-ion batteries. J. Energy Storage 2022, 51, 104512. [Google Scholar] [CrossRef]
- Liang, H.J.; Gu, Z.Y.; Zhao, X.X.; Guo, J.Z.; Yang, J.L.; Li, W.H.; Li, B.; Liu, Z.M.; Sun, Z.H.; Zhang, J.P.; et al. Advanced flame-retardant electrolyte for highly stabilized K-ion storage in graphite anode. Sci. Bull. 2022, 67, 1581–1588. [Google Scholar] [CrossRef]
- Wan, H.; Zhang, J.; Xia, J.; Ji, X.; He, X.; Liu, S.; Wang, C. F and N Rich Solid Electrolyte for Stable All-Solid-State Battery. Adv. Funct. Mater. 2022, 32, 2110876. [Google Scholar] [CrossRef]
- Zhu, X.; Chang, Z.; Yang, H.; He, P.; Zhou, H. Highly safe and stable lithium-metal batteries based on a quasi-solid-state electrolyte. J. Mater. Chem. A 2022, 10, 651–663. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, Y.; Zhi, J.; Huang, R.; Li, W.; Huang, X.; Yan, G.; Ji, Z.; Mai, W. All-inorganic lead-free NiOx/Cs3Bi2Br9 perovskite heterojunction photodetectors for ultraviolet multispectral imaging. Nano Res. 2022, 15, 1094–1101. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, L.; Wang, L.; Liao, C. Joint State-of-Charge and State-of-Available-Power Estimation Based on the Online Parameter Identification of Lithium-Ion Battery Model. IEEE Trans. Ind. Electron. 2022, 69, 3677–3688. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, Y.; Liu, Y.; Xiang, X. Highly Efficient Lithium Extraction from Brine with a High Sodium Content by Adsorption-Coupled Electrochemical Technology. ACS Sustain. Chem. Eng. 2021, 9, 11022–11031. [Google Scholar] [CrossRef]
- Zhao, J.; Burke, A.F. Electric Vehicle Batteries: Status and Perspectives of Data-Driven Diagnosis and Prognosis. Batteries 2022, 8, 142. [Google Scholar] [CrossRef]
- Feng, X.; Ouyang, M.; Liu, X.; Lu, L.; Xia, Y.; He, X. Thermal runaway mechanism of lithium ion battery for electric vehicles: A review. Energy Storage Mater. 2018, 10, 246–267. [Google Scholar] [CrossRef]
- Maleki, H.; Howard, J.N. Internal short circuit in Li-ion cells. J. Power Sources 2009, 191, 568–574. [Google Scholar] [CrossRef]
- Gao, W.; Zheng, Y.; Ouyang, M.; Li, J.; Lai, X.; Hu, X. Micro-short-circuit diagnosis for series-connected lithium-ion battery packs using mean-difference model. IEEE Trans. Ind. Electron. 2019, 66, 2132–2142. [Google Scholar] [CrossRef]
- Huang, L.; Liu, L.; Lu, L.; Feng, X.; Han, X.; Li, W.; Zhang, M.; Li, D.; Liu, X.; Sauer, D.U.; et al. A review of the internal short circuit mechanism in lithium-ion batteries: Inducement, detection and prevention. Int. J. Energy Res. 2021, 45, 15797–15831. [Google Scholar] [CrossRef]
- Gandoman, F.H.; El-shahat, A.; Alaas, Z.M.; Ali, Z.M.; Berecibar, M.; Aleem, S.H.E.A. Understanding Voltage Behavior of Lithium-Ion Batteries in Electric Vehicles Applications. Batteries 2022, 8, 130. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, H.; Wang, Y.; Sha, Z. Review on the electrochemical extraction of lithium from seawater/brine. J. Electroanal. Chem. 2019, 850, 113389. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Mohamed, A. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: Challenges and recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar] [CrossRef]
- Duan, B.; Li, Z.; Gu, P.; Zhou, Z.; Zhang, C. Evaluation of battery inconsistency based on information entropy. J. Energy Storage 2018, 16, 160–166. [Google Scholar] [CrossRef]
- Shang, Y.; Lu, G.; Kang, Y.; Zhou, Z.; Duan, B.; Zhang, C. A multi-fault diagnosis method based on modified Sample Entropy for lithium-ion battery strings. J. Power Sources 2020, 446, 227275. [Google Scholar] [CrossRef]
- Zheng, Y.; Han, X.; Lu, L.; Li, J.; Ouyang, M. Lithium ion battery pack power fade fault identification based on Shannon entropy in electric vehicles. J. Power Sources 2013, 223, 136–146. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, J.; Chen, Z.; Liu, X. Model based insulation fault diagnosis for lithium-ion battery pack in electric vehicles. Meas. J. Int. Meas. Confed. 2019, 131, 443–451. [Google Scholar] [CrossRef]
- Schmid, M.; Gebauer, E.; Hanzl, C.; Endisch, C. Active Model-Based Fault Diagnosis in Reconfigurable Battery Systems. IEEE Trans. Power Electron. 2021, 36, 2584–2597. [Google Scholar] [CrossRef]
- Li, D.; Zhang, Z.; Liu, P.; Wang, Z.; Zhang, L. Battery Fault Diagnosis for Electric Vehicles Based on Voltage Abnormality by Combining the Long Short-Term Memory Neural Network and the Equivalent Circuit Model. IEEE Trans. Power Electron. 2021, 36, 1303–1315. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, P.; Wang, Z.; Zhang, L.; Hong, J. Fault and defect diagnosis of battery for electric vehicles based on big data analysis methods. Appl. Energy 2017, 207, 354–362. [Google Scholar] [CrossRef]
- Yang, S.; He, R.; Zhang, Z.; Cao, Y.; Gao, X.; Liu, X. CHAIN: Cyber Hierarchy and Interactional Network Enabling Digital Solution for Battery Full-Lifespan Management. Matter 2020, 3, 27–41. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, Z.; Cao, R.; Wang, M.; Cheng, H.; Zhang, L.; Jiang, Y.; Li, Y.; Chen, B.; Ling, H.; et al. Implementation for a cloud battery management system based on the CHAIN framework. Energy AI 2021, 5, 100088. [Google Scholar] [CrossRef]
- Zheng, Y.; Ouyang, M.; Lu, L.; Li, J.; Han, X.; Xu, L.; Ma, H.; Dollmeyer, T.A.; Freyermuth, V. Cell state-of-charge inconsistency estimation for LiFePO4 battery pack in hybrid electric vehicles using mean-difference model. Appl. Energy 2013, 111, 571–580. [Google Scholar] [CrossRef]
- Feng, F.; Hu, X.; Liu, K.; Che, Y.; Lin, X.; Jin, G.; Liu, B. A Practical and Comprehensive Evaluation Method for Series-Connected Battery Pack Models. IEEE Trans. Transp. Electrif. 2020, 6, 391–416. [Google Scholar] [CrossRef]
- Fan, S. Fault Diagnosis Method based on Method based based on Stacked Stacked. IFAC Pap. 2020, 53, 790–795. [Google Scholar] [CrossRef]
- Liu, K.; Shang, Y.; Ouyang, Q. A Data-Driven Approach With Uncertainty Quantification for Predicting Future Capacities and Remaining Useful Life of Lithium-ion Battery. IEEE Trans. Ind. Electron. 2021, 68, 3170–3180. [Google Scholar] [CrossRef]
- Carkhuff, B.G.; Demirev, P.A.; Srinivasan, R. Impedance-Based Battery Management System for Safety Monitoring of Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2018, 65, 6497–6504. [Google Scholar] [CrossRef]
- Chemali, E.; Member, S.; Kollmeyer, P.J.; Preindl, M.; Ahmed, R.; Emadi, A. Long Short-Term Memory Networks for Accurate State-of-Charge Estimation of Li-ion Batteries. IEEE Trans. Ind. Electron. 2018, 65, 6730–6739. [Google Scholar] [CrossRef]
- Wang, G.; Gao, Q.; Yan, Y.; Wang, Y. Thermal Management Optimization of a Lithium - Ion Battery Module with Graphite Sheet Fins and Liquid Cold Plates. Automot. Innov. 2020, 3, 336–346. [Google Scholar] [CrossRef]
- Wang, W.; Sun, D. The improved AdaBoost algorithms for imbalanced data classification. Inf. Sci. 2021, 563, 358–374. [Google Scholar] [CrossRef]


| State Equations | |
|---|---|
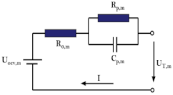 | where represents the mean terminal voltage of the battery pack, and are the polarization internal resistance and polarization capacitance, respectively, is the polarization voltage, represents the ohm internal resistance, and is the instantaneous current. represents the OCV. |
 | where , , , and represent difference of corresponding parameters between the cell i and mean battery model and is the instantaneous current. |
|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, R.; Zhang, Z.; Lin, J.; Lu, J.; Zhang, L.; Xiao, L.; Liu, X.; Yang, S. Reliable Online Internal Short Circuit Diagnosis on Lithium-Ion Battery Packs via Voltage Anomaly Detection Based on the Mean-Difference Model and the Adaptive Prediction Algorithm. Batteries 2022, 8, 224. https://doi.org/10.3390/batteries8110224
Cao R, Zhang Z, Lin J, Lu J, Zhang L, Xiao L, Liu X, Yang S. Reliable Online Internal Short Circuit Diagnosis on Lithium-Ion Battery Packs via Voltage Anomaly Detection Based on the Mean-Difference Model and the Adaptive Prediction Algorithm. Batteries. 2022; 8(11):224. https://doi.org/10.3390/batteries8110224
Chicago/Turabian StyleCao, Rui, Zhengjie Zhang, Jiayuan Lin, Jiayi Lu, Lisheng Zhang, Lingyun Xiao, Xinhua Liu, and Shichun Yang. 2022. "Reliable Online Internal Short Circuit Diagnosis on Lithium-Ion Battery Packs via Voltage Anomaly Detection Based on the Mean-Difference Model and the Adaptive Prediction Algorithm" Batteries 8, no. 11: 224. https://doi.org/10.3390/batteries8110224
APA StyleCao, R., Zhang, Z., Lin, J., Lu, J., Zhang, L., Xiao, L., Liu, X., & Yang, S. (2022). Reliable Online Internal Short Circuit Diagnosis on Lithium-Ion Battery Packs via Voltage Anomaly Detection Based on the Mean-Difference Model and the Adaptive Prediction Algorithm. Batteries, 8(11), 224. https://doi.org/10.3390/batteries8110224