Abstract
Accurate state of health (SoH) estimation is crucial to optimize the lifetime of Li-ion cells while ensuring safety during operations. This work introduces a methodology to track Li-ion cells degradation and estimate SoH based on electrochemical impedance spectroscopy (EIS) measurements. Distribution of relaxation times (DRT) were exploited to derive indicators linked to the so-called degradation modes (DMs), which group the different aging mechanisms. The combination of these indicators was used to model the aging progression over the whole lifetime (both in the “pre-knee” and “after-knee” regions), enabling a physics-based SoH estimation. The methodology was applied to commercial cylindrical cells (NMC811|Graphite SiOx). The results showed that loss of lithium inventory (LLI) is the main driving factor for cell degradation, followed by loss of cathode active material (LAMC). SoH estimation was achievable with a mean absolute error lower than 0.75% for SoH values higher than 85% and lower than 3.70% SoH values between 85% and 80% (end of life). The analyses of the results will allow for guidelines to be defined to replicate the presented methodology, characterize new Li-ion cell types, and perform onboard SoH estimation in battery management system (BMS) solutions.
1. Introduction
Li-ion cells are considered a promising and mature technology to guide the ecological transition to renewable energy sources for mobile devices, the transportation sector and also for stationary storage [1,2,3]. This success is based on high energy and power density, long cycle life, relatively high safety and continuously decreasing costs [4,5,6]. Smooth and safe operations of Li-ion cells are ensured by the battery management systems (BMSs). BMSs include several features to monitor the battery cells, to ensure safe operations, and to optimize battery lifetime [7,8]. As regard the latter point, the tracking of battery health evolution is crucial but challenging because power and capacity fade are caused by various interdependent degradation mechanisms that affect the components inside the cells [9,10]. Those mechanisms can be clustered depending on their main effects into the so-called degradation modes (DMs): (i) loss of lithium inventory (), which accounts consumption of lithium ions for decomposition reactions, solid electrolyte interface (SEI) layer growth and lithium plating; (ii) loss of cathode active material (), which accounts for electrode structural disordering, particle cracking and loss of electric contact; and (iii) loss of anode active material () which accounts for the same mechanisms of but on the anode side, including also graphite exfoliation and blocking of active sites by passivation surface layers [9,11,12].
Next-generation BMSs will exploit non-invasive characterization techniques to provide indication of the occurring DMs and ultimately estimate the state of health (SoH) [13,14,15]. Among the different techniques presented in the literature, the most suitable measurements to achieve the objective are: (i) pseudo-open circuit voltage (pOCV), i.e., full charge or discharge profile at low constant current and (ii) electrochemical impedance spectroscopy (EIS), that maps cells’ impedance over different galvanostatic or potentiostatic excitation frequencies [16,17].
pOCV-based techniques allow users to identify and quantify DMs with high accuracy, but they require a low current rate and long test duration to obtain a quasi-equilibrium condition (i.e., no-load condition). However, it is difficult to achieve these conditions during battery operation [17]. pOCV curves of the two electrodes at beginning of life (BoL) are directly used in the so-called “pOCV methods” to assess degradation in a backward basis [9,11,18]. Even though parametric models have been introduced to estimate and , the main drawback is that the DMs may not be estimated uniquely [18]. Other pOCV-based methods are the incremental capacity (IC) and differential voltage (DV) analyses, based on the evaluation of specific features from the OCV profiles. and indicators are obtained in [19] respectively by IC and DV curves and in [20] by IC curves highlighting the longer incubation time of at anode and cathode sides with respect to . IC profiles are also exploited for SoH estimation, as shown by Schaltz et al. in [21] and by Lin et al. in [22]. However, the main disadvantage for practical implementation of IC/DV method is the need for smooth and high resolution OCV profiles, which demand for additional computational effort from the BMS hardware in on-board applications [17].
EIS-based techniques allow for a shorter diagnosis and provide valuable information to understand the processes and degradation mechanisms occurring inside the cell [23,24,25,26]. In general, electric circuit models (ECM) are exploited to extract the features of interest and develop degradation indicators. For instance, Pastor-Fernández et al. identified from the mid-frequency region (semiarch) and from the low-frequency region (diffusive tail) in [19]. However, the authors explained that the accuracy is highly dependent on measurement quality and the chosen ECM. A way to overcome the model dependency is to apply distribution of relaxation times (DRT), which help in highlighting the processes that are usually overlapped in the frequency domain (impedance Nyquist plot) [27,28,29]. Zhou et al. proposed in [30] and later in [31] a technique to evaluate the growth of resistance related to contact, SEI, charge transfer and diffusion polarization processes. The authors demonstrated the utility in monitoring battery aging and the advantage of using DRT to separate electrolyte- and solid-phase diffusion. However, the analyses were limited to the model parameters and not to the different DMs and SoH estimation. Carthy et al. performed a detailed review about SoH estimation with EIS, showing that ECM fitting methods are widely applied [32]. Those methods showed a maximum estimation error between 3.7% and 15%, depending on the cell chemistry and on the testing conditions [33,34,35,36]. However, in most cases, even if EIS provides valuable information about the physical processes occurring in the cell, the resulting SoH estimation is not directly related to the physical processes and degradation mechanisms occurring inside the cell. Zhang et al. instead proposed a SoH estimation method based on DRT while applying data-driven methods, showing a maximum RMSE of 1.65% [17]. However, the work did not include a specific quantification of DMs but only the evolution of the parameters linked to SoH estimation. For practical implementation of the EIS-based methods described above, different approaches have been presented in literature to perform EIS measurements: use of an AC signal generator which can apply current with specific frequency to battery packs [37,38]; signal processing methods [39] and smart sensing management systems that allow for direct measurement of cell impedance [40]. Moreover, there are products already available on the market, such as the evaluation boards and management systems described in [41,42].
In summary, the main limitations from the literature are twofold: (i) the need for long and complex measurements, as for instance the pOCV and its IC/DV derivation, which make them unexploitable in BMS applications; and (ii) the challenge in fitting EIS from ECM, and its utilization for SoH estimation, being aware of the degradation occurring in the cell. This work aimed to overcome these two limitations by:
- Defining a suitable EIS-based SoH estimation model which uses degradation indicators directly linked to DMs, allowing principled modelling of the physical phenomena (i.e., physics-based SoH estimation);
- Defining a simple and robust framework that could be exploited for online-SoH estimation by next generation smart BMSs based on (i) an appropriate testing campaign to initialize the SoH estimation model for a new Li-ion chemistry/model and (ii) the capability to run onboard EIS measurement.
The work is organized as follows: Section 2 presents materials and methods. The inputs of this work (i.e., material) are the results of cycling aging tests, including EIS measurements, and the DRT calculation algorithm with peaks attribution, as presented in authors’ previous works [43,44]. This work exploits the findings of the previous ones extending the use of DRT to obtain quantitative information about cell degradation with specific indicators and performing SoH estimation from those indicators. The methodology is applied on the experimental dataset in Section 3, where the results about degradation indicators and SoH estimation are showed. Section 4 presents the output of this work: (i) discussion of the obtained results; and (ii) the guidelines to perform online degradation tracking and SoH estimation in BMSs. Final remarks are given in the conclusions.
2. Materials and Methods
2.1. Inputs: Experimental Dataset and DRT Characterization
The experimental dataset used in this work includes cycling aging tests performed on the commercial cylindrical cells presented in Table 1, with lithium Nickel Manganese Cobalt oxide (NMC 811) as cathode material and graphite with silica particles (graphite-SiOx) as anode material. The testing campaign has been performed at the CSEM’s Sustainable Energy Center, Neuchâtel (Switzerland) with testing set-up composed of: (i) a cell tester Biologic BCS815 equipped with 32 parallel, 9V−15A channels (±0.01% FSD accuracy on the voltage and ±0.015% FSD accuracy on current, for each available range) with EIS spectroscope multiplexed and able to range from 10 kHz to 10 mHz (Figure 1a) [45]; and (ii) a thermostatic chamber ATT-DM1200T with −45 °C–180 °C temperature range (Figure 1b) [46]. Ten different cycling conditions have been studied and their details together with the corresponding cell’s IDs are given in Table 2. The tests have been performed in the thermostatic chamber at a constant temperature of 20 °C (Figure 1c).

Table 1.
Main characteristics of the cylindrical commercial cell under investigation. Current-rate (C-rate) values are calculated with respect to the nominal capacity.

Figure 1.
Overview of equipment and cells in Sustainable Energy Center laboratory at CSEM: (a) Biologic BCS815 Battery tester; (b) ATT-DM1200T Thermostatic chamber and; (c) NMC 811 cells under investigation inside the thermostatic chamber.

Table 2.
Overview of cycling aging testing protocols applied to commercial Li-ion cells. The cycling test type is compared to the reference case (1st row).
The reference case (ID:REF) has been set following the details given by the cell manufacturer. Then, in the other cases the depth of discharge (DoD), charging rate or discharging rate were tuned to obtain different degradation paths.
The cells were cycled until end of life (EoL) or end of tests (EoT). In the first case, the tests were stopped as soon as they reached SoH = 80%. In the second case, the tests were stopped whenever the cell reached 1000 equivalent cycles (EqC) regardless of the SoH level, where the EqC was defined as the ratio between the cumulated cycled capacity and two times the initial capacity.
At beginning of life (BoL) and every 50 EqC a diagnosis phase was run to measure the cell capacity ( being the one at BoL) and EIS spectra at different SoCs. The capacity measurements have been used to calculate the SoH as the standard ratio .
The SoH progressions for the different testing protocols are shown in Figure 2. The cells cycled at reduced DoD have been all stopped due to EoT rather than EoL, with SoH higher than 90% in all cases. High discharging rate tests and specifically cells ID:FD05 and FD1 showed a SoH evolution curve similar to cell ID:REF, with SoH higher than 85% at 1000 EqC. Highly fast-charged cells (ID:FC1 and ID:FC2) showed a steep capacity fade, reaching EoL with a number of cycles lower than 100. The remaining cells (ID:REF_w/oCV and FC05) instead showed the so-called “knee” (inflection-point) where degradation accelerates leading to larger capacity fade. The “knee” can be caused by different pathways (or failure modes) that are driven by a complex combination of parameters, such as cell geometry, testing condition and degradation status of the cell components [47]. Generally, this inflection point is attributed to the onset of irreversible lithium plating on the anode surface and is unrelated to the linear aging behavior before this point [48,49]. Therefore, it is relevant to separate these two degradation regions and model them separately. In the following sections, the cells’ degradation will be described as “pre-knee” or “after-knee” based on the characteristics described above.
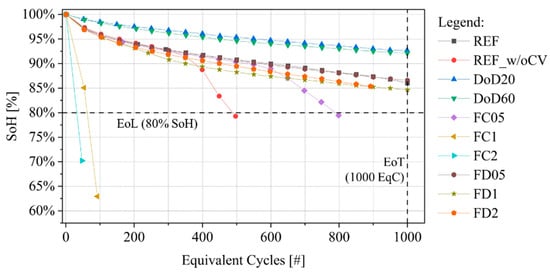
Figure 2.
SoH evolution curves over EqC for the cells under investigation.
EIS spectra were validated via the Kramers–Kronig (KK) test to verify quality and time invariance and used to compute DRT profiles [50,51]. The DRT calculation assumes that an impedance spectrum can be represented as the sum of a resistor that represent ohmic resistance () and an infinite series of RC elements, as shown in the following equation:
where is the function that represents the time relaxation characteristics of the electrochemical system under evaluation and that satisfies the conditions of non-negativity (total and partial polarization resistances are positive for most of the electrochemical systems). The DRT function, i.e., is discretized and solved applying Tikhonov regularization method [52,53]. Details about the mathematical formulation and the algorithm exploited for DRT computation from EIS of Li-ion cells are given in [43]. The peak-based representation of allows to discriminate between different processes occurring at different time constant values. The contribution of those processes is quantified with the resistance values which are found by computing the area under the peaks, when knowing the time constant range [; ]:
The DRT peaks attribution is crucial to determine which are the main processes and degradation mechanisms occurring in the cells. As mentioned above, this work exploits the peak attribution performed in [44], where previous works, such as the analyses of Wildfeuer et al. in [54] and Zhou et al. in [31], have been analyzed and extended with experimental investigations on the same cell type selected in this work. Commercial cells and half-cells DRT profiles were compared to understand the impact of the two electrodes and were validated applying post-mortem analyses with imaging techniques. Those information are used in the next Section to define proxy indicators to track cell degradation.
2.2. Methodology
Figure 3 represents the typical DRT profile of the cells under investigations. The results of DRT peaks attribution were exploited to define which peaks need to be tracked to quantify specific DMs:
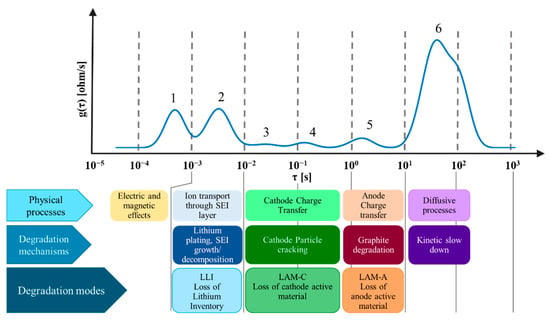
Figure 3.
Typical DRT profile of the cylindrical commercial cells under investigation. Attribution of physical processes, degradation mechanisms and degradation modes. The readers are addressed to [44] and the literature cited therein for more details, specifically [31,54] for similar methodologies and [9,55,56] for details on the degradation mechanisms.
- Peak 2 is attributed to the growth and decomposition of SEI layer and presence of lithium plating on the anode side; it will be used to account for Loss of Lithium Inventory ();
- Peak 3 and peak 4 are attributed to cathode degradation (specifically particle cracking for NMC811) and they are therefore used to account for Loss of Cathode Active Material ();
- Peak 5 is attributed to graphite degradation and it is hence used to account for Loss of Anode Active Material ().
The resistance values of the peaks describing the DMs are combined to quantify the total impedance :
where is the resistance of peak 2, the resistance of peaks 3 and 4 and the resistance of peak 5. is used as proxy in the following Sections deriving indicators to evaluate cell degradation and to estimate SoH.
2.2.1. Degradation Indicators
Three indicators are defined to track the DMs occurring in Li-ion cells as percentage increase of at diagnosis step with respect to the initial state , where . The generic indicator is normalized with the initial total impedance and computed as follows:
The computed values of those indicators could show deviations that are due to the DRT calculation (solving an optimization problem with regularization methods [43]) but that could also come from noisy measurements, especially thinking about onboard implementation in BMS [17,19]. Therefore, a method to filter the indicators is necessary to better appreciate the evolution of DMs and to understand which one is prevailing. The indicators’ filtering process is based on a linear fitting model applied on a defined number of prior measured points with a sliding window. The process is composed by 3 steps, as shown in Figure 4:
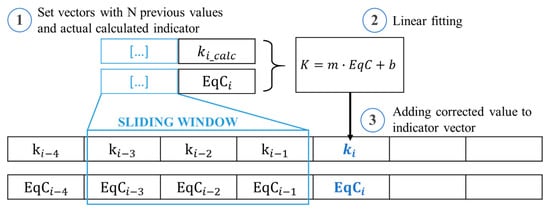
Figure 4.
Three-step procedure to correct the degradation indicators applying a linear fitting model.
- A set of prior points is selected based on a sliding window of size W and is concatenated with the indicator computed at diagnosis step ;
- A linear fitting model is applied to the selected vectors;
- The linear model is used to compute the corrected value of
The sliding window is applied to smooth the indicator small fluctuations and to highlight the large variations due to sudden increase of degradation (e.g., reaching “knee” point). Knowing the maximum variation of DM indicators, corresponding at EoL condition, it is possible to fix limit thresholds to identify outliers and improve even more the filtering process. When is considered outlier, the value of is computed with the linear model obtained only with prior diagnosis points.
Once the degradation indicators are filtered, they are used to compute the total degradation modes parameter as follows:
2.2.2. SoH Estimation
The parameter was used as indicator to perform SoH estimation. The relationship between SoH and is shown in Figure 5a for the experimental dataset presented in Section 2.1: it is possible to distinguish two main regions that are related to the “pre-knee” and the “after-knee” progressions of the SoH trend (Figure 2). Having as an objective SoH estimation in both the two regions, a piecewise model is adopted to build two SoH functions that represents “pre-knee” and “after-knee” degradations. In this way, the SoH model maintains a simple structure yet robust in the “after-knee” trend, crucial to avoid safety issues related to severely aged Li-ion cells.
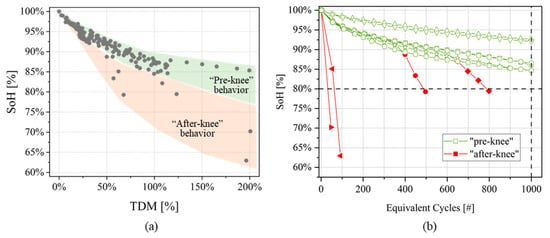
Figure 5.
(a) SoH evolution over values for the cells under investigation. Two regions are depicted, corresponding to “pre-knee” and “after-knee” behaviors; and (b) validation of threshold equal to 1%, identifying all the points with “after-knee” behavior.
Moreover, an additional indicator must be used to distinguish the two regions of Figure 5a. All the parameters extracted by DRT together with the ohmic resistance have been compared to find the most effective one. The analyses showed that the ohmic resistance variation between two consecutives measurements () was providing the most accurate results in differentiating between “pre-knee” and “after-knee” behavior.
Sensitivity analysis was performed to define the threshold value that better discriminate the two regions. A graphical validation of the threshold is obtained checking if the selected value allows to identify all the “after-knee” points on SoH progression curves. For the cells under investigation, the optimal result was found at = 1%; the graphical validation is showed in Figure 5b.
Once threshold is set, SoH can be estimated via logarithmic decay functions. This type of function allows to model the initial steep decay and the consequent slower decay for larger values (Figure 5a). Approaching the inflection point, i.e., the knee, a second function is used to represent the subsequent steep decay. The SoH piecewise model is described as follows:
When the cells show “pre-knee” behavior, i.e., , the coefficients (A1, B1) are found by fitting the available measurement of SoH. When the cells show “after-knee” behavior instead (), the SoH function includes two additional parameters: the value of SoH () and the value of the total degradation indicator () before the knee. As described in Section 2.1, “after-knee” behavior shows an acceleration in capacity fade unrelated to the previous aging behavior. The two additional parameters are introduced to normalize the function because the “knee” does not occur always at the same conditions (i.e., SoH and ) for each cell. Once these parameters are fixed with the last previous point computed in “pre-knee” condition, the coefficients (A2, B2) are found by fitting the available measurements of SoH.
Finally, a validation flow was conceived to evaluate the accuracy of the resulting SoH estimation. Training and validation subsets are shown in Figure 6. Given a specific number of tested cells n (n = 10 in this case), the two subsets are defined as follows:
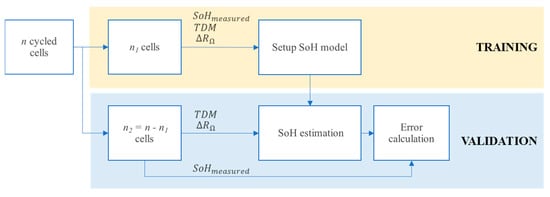
Figure 6.
Algorithm to evaluate the developed SoH model with training and validation phases.
- Training subset: n1 cells are selected and their EIS measurements are used to compute degradation indicators and ohmic indicator. SoH values are fitted to find the parameters of the model described in Equation (6).
- Validation subset: n2 cells (i.e., n2 = 10 − n1) are used to compute the indicator and the SoH is estimated with the SoH model checking the value of . Finally, the estimated value is compared with the one computed by capacity measurement.
The error between estimated () and measured () SoH is defined as:
Therefore, a positive error means overestimation and a negative error means underestimation. The estimation error is evaluated for all the measured SoH values (every 50 eqC). Box plots are exploited to interpret the quality of the estimation. Two additional performance indicators are used to quantify reliability on the estimation: the Mean Bias Error (MBE) and the Mean Absolute Error (MAE). The first one captures the average bias in the estimation and is computed as follows:
where n is the total number of diagnosis points. General underestimation of SoH could be a disadvantage on economic point of view, because the battery could not be exploited in the best way, but it could be an advantage in terms of safety, especially in “after-knee” conditions when the capacity fade is very fast. In this way, it could be possible to avoid cell dangerous conditions. The second performance indicator takes the absolute values of the individual estimation errors and gives more direct information on correctness of the estimation. It is computed as follows (given n number of points):
3. Results
This chapter presents the results obtained by applying the above methodology on the experimental dataset presented in Section 2.1. Specifically, Section 3.1 will give a quantification to the degradations indicators, and Section 3.2 will present the SoH estimation results obtained by using the same.
3.1. Degradation Indicators
The degradation indicators have been computed selecting the EIS spectra measured at 50% SoC on the cells listed in Figure 2. On average, the KK test returned maximum residuals lower than 1.1% from BoL to EoL/EoT, which allows for a reliable DRT calculation. The equations presented in Section 2 have been then used to compute the DMs and the degradation indicators. An example of the indicators is given in Figure 7a–c for cell ID:REF. The plots show both the calculated values of , and and the filtered values (sliding window size equal to 7 prior points) that are highlighted with dashed lines. The three DMs show different evolutions over the cell lifetime (i.e., at increasing EqC):
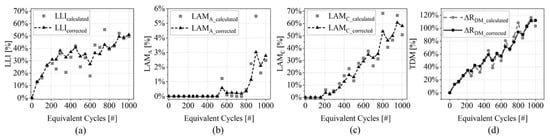
Figure 7.
Example of degradation indicators computed for cell ID:REF (cycling in reference condition, C/3 symmetric with Constant Voltage-phase during charge). The plots show both the not corrected and corrected values of: (a) , (b) , (c) and (d) .
- (Figure 7a): a monotonic growth is observed until around 400 EqC when the indicator decreases its growth and starts to oscillate;
- (Figure 7c): cell’s cathode is not impacted by degradation until 200 EqC; after this point it shows a constant growth up to 60% at 1000 EqC;
- (Figure 7b): this DM is not affecting cell performances until about 800 EqC. Moreover, its magnitude is one order of magnitude lower than the other two indicators.
Those trends suggest that cell aging is mainly driven by SEI-related degradation and lithium plating up to 400 EqC and then by cathode degradation (particle cracking), growing with a faster rate than related mechanisms until EoT. Graphite degradation is negligible and not influencing battery performances.
The total degradation indicator is showed in Figure 7d, where the corrected trend (i.e., sum of corrected DMs) shows a more stable evolution compared with the calculated one.
Figure 8 presents an overview of all the degradation indicators of all the tested cells (reference to cell IDs in Table 2). Each DM is represented with a different color and their cumulated area represents the indicator as function of EqC. In general, has a big influence on cell degradation and it is the main DM for reduced DoD protocols (Figure 8c,d), but it is also true that the same cells (ID:DOD20, ID:DOD60) recorded the smallest , with values lower than 30% at EoT (at 1000 EqC). In other, more stressing conditions, also the other DMs appeared. In cell ID:REF, cell ID:FC05 and the high discharging rate cells, has also a large impact on degradation (Figure 8a,e,h–j). In the cases of high discharging rate at 0.5C (cell ID:FD05) and at 2C (cell ID:FD2), growth up to 100% and 140%, being the most impacting DM and suggesting that cathode particle cracking is driving cell degradation. High charging rate conditions at 1C and 2C instead brought large and fast degradation, with an increase of up to 200% in less than 100 EqC (Figure 8f,g). In both cases the degradation is driven by and in similar quantities: the lithium plating generated inside those cells was reducing the available surface, therefore inhibiting graphite use [44,57]. The other two cells that showed “after-knee” behavior, i.e., cell ID:REF_w/oCV and cell ID:FC05 presented a small amount of (5–12%) at late cycles corresponding to the “after-knee” region (Figure 8b,e). In those cases, EoL was reached mainly due to lithium plating without significant inhibition of graphite surface as in high charging rate cells (ID:FC1 and ID:FC2).
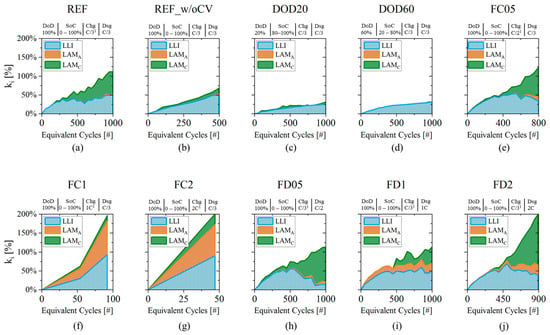
Figure 8.
(a–j) Evolution of the three DMs indicators (, and ) for the cells under investigations. Details about testing protocols are given in plot titles: (i) DoD: Depth of Discharge; (ii) SoC: SoC interval, (iii) Chg: charging rate (1 including Constant Voltage phase with cut-off current at C/50); (iv) Dsg: discharging rate.
3.2. SoH Estimation
The piecewise model presented in Section 2.2.2 was used to perform SoH estimation on the experimental dataset under investigation. The training subset was chosen to include different variety of testing conditions: high charging rate, high discharging rate and reduced DoD (Table 3). It is paramount to include cells with after-knee SoH behavior in the training group to properly initialize and set the SoH model. The two found SoH functions are showed in Figure 9a both for “pre-knee” and “after-knee” conditions. The values of fitted coefficients are given in the table of Figure 9b.

Table 3.
Training subset for SoH estimation. The presence of “pre-knee” and “after-knee” SoH behavior is highlighted in the last two columns. Details about the testing protocols can be found in Table 2.
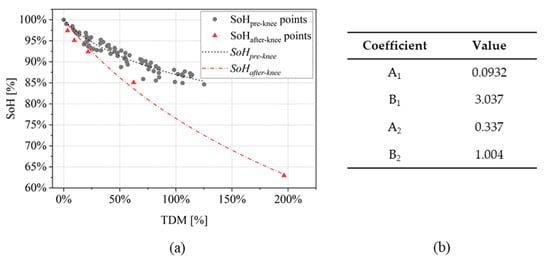
Figure 9.
(a) SoH functions found with the training cells in Table 3; and (b) fitting coefficients (SoH model described in Equation (6)).
The application of the SoH model to the validation subset is shown for each cell in the charts of Figure 10a–e. The list of validation set cells and the results of MBE and MAE are listed in Table 4.
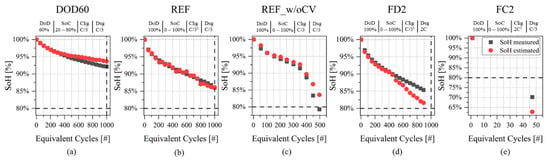
Figure 10.
SoH model validation applying the model of Figure 9. (a–e) Results of application of SoH model to the validation cells of Table 4. Details about testing protocols are given in plot titles: (i) DoD: Depth of Discharge; (ii) SoC: SoC interval, (iii) Chg: charging rate (1 including Constant Voltage phase with cut-off current at C/50); (iv) Dsg: discharging rate.

Table 4.
Validation subset with results of MBE and MAE. Details about the testing protocols in Table 2.
Cell ID:REF shows accurate estimation results in Figure 10b, with MAE = 0.38% and MBE = −0.11%. Reduced DoD protocol with cell ID:DOD60 shows similar values of MAE and MBE, with a tendency in overestimating SoH when EqC > 400, as shown in Figure 10a. Cell ID:REF_w/oCV (Figure 10c) shows a good estimation both in the “pre-knee” and “after-knee” regions, even though the SoH tends to be overestimated in the second region, with MAE = 1.28% at EoL. In the case of fast discharge at 2C (Cell ID:FD2), the SoH underestimation happens in the range between 400 and 900 EqC, as shown in Figure 10d, accounting for a MAE of 1.56%.Lastly, cell ID:FC2 (Figure 10e) with fast charge at 2C shows the largest MBE and MAE, with the same magnitudes (−7.46% and 7.46%). The source of this large error is twofold: on the one side the availability of only one measurement to perform the estimation and (ii) on the other side the deeply aged condition, with measured SoH equal to 70.2%.
Additional analyses were run to understand the error distribution of the SOH estimation in different aging intervals and to understand the stability of the results when testing all the possible combinations of training and validation subsets. The definition of the training group was always based on a key prerequisite: a minimum number of one cell with “after-knee” behavior has been always included to encompass the highly aged condition. The results are shown in Table 5 and in Figure 11. Looking at the MBE, the model tends to overestimation for SoH < 95%. Looking at the MAE, the error increases as the SoH decreases, particularly with SoH < 85%. The result is also influenced by the small quantity of available measured points for SoH < 85%: only 8 points are available over more than 150 points for the cells under investigations. This effect is also observed in the box plot of Figure 11: both the error and absolute error presents large variations for SoH ranges under 85% SoH. Moreover, for SoH < 80% the distribution of the absolute error is asymmetric, with higher number of points at higher magnitudes.

Table 5.
MBE and MAE in different SoH ranges for all the combinations of 5 training cells and 5 validation cells.
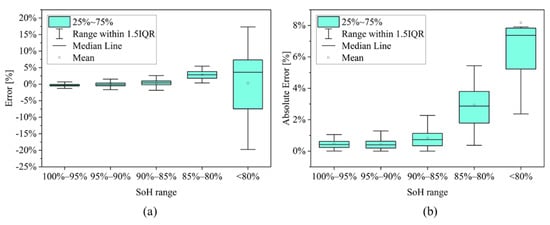
Figure 11.
Box plot representation of the (a) error; and (b) the absolute error for the different SoH ranges introduced in Table 5 with 5 cells in the training set.
4. Discussion
The results presented in Section 3 and obtained applying the methodology described in Section 2 can be analyzed and discussed on different levels: validity, replicability and applicability.
Validity: for the selected case study (NMC811|Graphite SiOx), the defined proxies allowed to quantify the contributions of different DMs during cells’ aging. DMs were distinguished by analyzing the DRT profiles of the cells as explained in [44] on the same cell type investigated in the present work. Indicator filtering (linear and based on a sliding window) was essential to regularize the aging trend and to reduce noise and outliers while preserving information related to steep variations caused by abrupt increase of degradation. The selection of a proper sliding window size was found crucial to encompass cell degradation in a comprehensive way and it depends not only on the type of data but also on the available number of diagnosis points. In this work, the optimal number of prior points to be used for the sliding window was found equal to 7. Looking at SoH estimation, the piecewise model showed good performances for SoH > 85%, while larger errors for SoH < 85%. These larger errors were mainly linked to the small number of available points (i.e., measurements) all belonging to “after-knee” behavior. Therefore, for SoH < 85% only accelerated degradation was available. Two possible solutions can be adopted to mitigate the problem: (i) increase the number of diagnosis points when the cells reach a certain capacity (e.g., SoH < 85%) and (ii) prolong test duration (EoT > 1000 EqC) for those cells that ended the testing campaign with SoH > 85% (i.e., with less severe testing conditions).
Replicability: the calculation of degradation indicators can be extended to other cell types with the same cell chemistry (e.g., pouch cells), given that it is based on DRT peaks attribution performed for NMC cells. Additional investigations will be needed if one wants to apply this methodology to other cell chemistries, in order to obtain the link between DRT peaks and the DMs The setup of degradation indicators filtering and of the piecewise model require to follow specific steps, suggesting the need for clear guidelines to replicate the methodology presented in this work.
Applicability: the methodology presented in Section 2.2 allowed for the development of a simple piecewise SoH model based on total degradation indicator () with reduced degrees of freedom: four fitting coefficients (2 for each SoH function) and 2 parameters (for normalization in “after-knee” function). The model is data-efficient, and does not require large datasets to be trained and its application may be more convenient for on-board applications in BMSs than data-driven approaches, which usually require larger amount of data and more complex hardware [58,59]. The number of training cells was set choosing five different testing conditions that lead to different aging paths. However, the data-efficiency of the SoH model should be checked while varying the number of cells in the training set. All possible combinations of training cells have been simulated in a range between 2 and 8 cells out of the total number of 10 (Table 2). As expected, the training with 2 cells brough to very large errors compared to the other cases, and it is not represented in Figure 12a (MBE = −2.7% and MAE = 3.5%). In all the other cases, the MBE is around 0.1% and the MAE is around 1% (Figure 12a). More in detail, the value of 5 training cells shows the best combination of errors, with MBE = 0.11% and MAE = 0.94%. This result is also confirmed by the box plot representation given in Figure 12b: increasing the number of training cells, the error rises due to data overfitting. Overall, these results confirm that a reduced but relevant number of tests could be sufficient to train the SoH model.
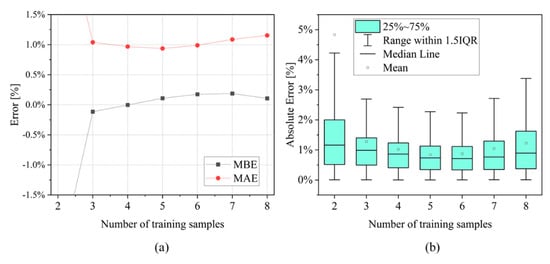
Figure 12.
Analysis of all the possible combinations of training sets with a number of cells between 2 and 8: (a) MBE and MAE results over the whole SoH range; and (b) box plot results in the SoH range 90–85%.
Based on this paper’s findings, it is possible to define guidelines which may help when applying the proposed methodology in real-use cases.
Guidelines: a two-phases procedure will be required: (i) an offline-phase, mainly in laboratory, to set up the degradation tracking and the SoH model and (ii) an online-phase, mainly onboard in BMS, to perform SoH estimation.
As regards the first phase (offline, in the lab), the main steps to develop the degradation indicators and the SoH model are the following:
- Plan relevant aging tests that cover different aging behaviors and allow to train the SoH model both for “pre-knee” and “after-knee” conditions. The selected protocols should include: (i) reduced DoD condition to appreciate slow degradation (i.e., capacity fade); (ii) nominal conditions, to verify the specifications from the manufacturer; (iii) moderate charging or discharging conditions that accelerates degradation with respect to nominal conditions and that could guarantee both “pre-knee” and “after-knee behavior” (such as cell ID:FC05) and (iv) high charging or discharging rate that guarantee fast degradation and “after-knee” conditions (such as cell ID:FC2);
- Perform diagnosis phase (capacity + EIS measurements) at a fixed number of EqC down to a certain value of SoH (e.g., 85%) and then intensify the number of checks by lowering the number of cycles in each repetition. In this way, more measurements will be available in the region where is mainly occurring the “knee” and accelerated capacity fade, reducing the SoH estimation error;
- Run sensitivity analysis on the ohmic resistance variation parameter to discriminate between “pre-knee” and “after-knee” conditions with a suitable threshold. Validation can be performed graphically on SoH evolution curves as done in Figure 5.
As regards the second phase (online, on the BMS) the main requirement is the capability to run EIS measurements and related algorithms on the BMS, as discussed in Section 1 and already available on existing products or prototypes [40,41,42]. Once this is available, the main practical steps for the SoH estimation model are the following:
- Run “diagnosis” based on long-EIS measurements (10 kHz–10 mHz). Select an appropriate criterion on when to acquire two consecutives full-EIS measurements. Depending on battery application, this variable could be set based on cycles number, a fixed period of time, or randomly (e.g., exploiting resting periods during application);
- Run “check-up” based on short-EIS measurements only at high frequency (10 kHz–1 kHz) to frequently update , which is crucial to activate additional “diagnosis” measurements whenever the “after-knee” behavior is reached based on the computation (Section 2.2.2). Additional “diagnosis” can also be activated under a certain estimated value of SoH (e.g., 85%);
- Compute the degradation indicators whenever possible to understand if unexpected behaviors are happening inside the cell. This can be done by updating DMs values and by analyzing them over time and/or over cycle number.
5. Conclusions
This work investigated the use of EIS via DRT to track degradation of Li-ion cells and to perform SoH estimation based on physics-based insights.
An experimental dataset of cycling tests in different aging conditions and an already published algorithm to attribute DRT peaks to degradation mechanisms have been used as inputs. The whole methodology is based on defining how to track the overarching degradation modes (DMs), that are , and . Relevant indicators were presented in Section 2.2.1, which includes filtering method to discard outlier and reduce noise. A piecewise model was developed to estimate SoH from degradation indicators, including two logarithmic functions to encompass the “pre-knee” and “after-knee” behaviors of aging cells. In this way, SoH estimation is directly related to the physical processes and degradation mechanisms occurring inside the cell. Finally, a straightforward procedure to train and validate the model was also presented, which is based on a sensitivity analysis to minimize the dimension of the training subset (i.e., the a-priori knowledge based on testing campaign).
The results showed that is the main DM affecting cell degradation during the whole lifetime while becomes relevant after 400 EqC. SoH estimation showed MAE lower than 0.75% in the SoH range 100%−85% and lower than 3.70% in the range 85%−80%. At SoH < 85% model estimation was negatively influenced by the low number of available measured points with high variability. Tuning the number of training cells in the range 2–8 showed stable error values, proving the data-efficiency of the proposed model, and an optimal training subset of 5 cells (i.e., 5 different testing protocols to comprehensively describe battery degradation).
Finally, user-oriented guidelines have been presented in Section 4 to allow both scientists and BMS engineers to replicate the methodology with their own testing and BMS setups. These guidelines are divided into an offline phase (laboratory phase), to set up the degradation tracking and the SoH model, and an online phase (BMS phase), to diagnose degradation and to perform the actual SoH estimation onboard.
Limits of the presented methodology are twofold: (i) the need to generalize the model to deal with EIS measurements done at different SoCs and temperatures; and (ii) the need of precise and accurate EIS measurements embedded into BMS slave boards. If the first can be solved by extending the a-priori offline phase in the laboratory, the second needs a necessary upgrade of current BMS to include more sensing capabilities at the cell level.
Author Contributions
Conceptualization, P.I., C.B. and R.E.C.; methodology, P.I., C.B. and R.E.C.; validation, P.I.; investigation, P.I.; writing—original draft preparation, P.I.; writing—review and editing, P.I., C.B., R.E.C. and V.W.; visualization, P.I.; supervision, C.B. and V.W.; funding acquisition, C.B. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been partially funded by the HIDDEN project that receives funding from the European Union’s Horizon 2020 research and innovation programme under Grant Agreement No. 957202.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Armand, M.; Tarascon, J.-M. Building Better Batteries. Nature 2008, 451, 652–657. [Google Scholar] [CrossRef] [PubMed]
- Bresser, D.; Moretti, A.; Varzi, A.; Passerini, S. The Role of Batteries for the Successful Transition to Renewable Energy Sources. In Encyclopedia of Electrochemistry; John Wiley & Sons, Ltd.: New York, NY, USA, 2020; pp. 1–9. ISBN 978-3-527-61042-6. [Google Scholar]
- Armand, M.; Axmann, P.; Bresser, D.; Copley, M.; Edström, K.; Ekberg, C.; Guyomard, D.; Lestriez, B.; Novák, P.; Petranikova, M.; et al. Lithium-Ion Batteries—Current State of the Art and Anticipated Developments. J. Power Source 2020, 479, 228708. [Google Scholar] [CrossRef]
- Berckmans, G.; Messagie, M.; Smekens, J.; Omar, N.; Vanhaverbeke, L.; Van Mierlo, J. Cost Projection of State of the Art Lithium-Ion Batteries for Electric Vehicles Up to 2030. Energies 2017, 10, 1314. [Google Scholar] [CrossRef]
- Marinaro, M.; Bresser, D.; Beyer, E.; Faguy, P.; Hosoi, K.; Li, H.; Sakovica, J.; Amine, K.; Wohlfahrt-Mehrens, M.; Passerini, S. Bringing Forward the Development of Battery Cells for Automotive Applications: Perspective of R&D Activities in China, Japan, the EU and the USA. J. Power Source 2020, 459, 228073. [Google Scholar] [CrossRef]
- Tsujikawa, T.; Yabuta, K.; Arakawa, M.; Hayashi, K. Safety of Large-Capacity Lithium-Ion Battery and Evaluation of Battery System for Telecommunications. J. Power Source 2013, 244, 11–16. [Google Scholar] [CrossRef]
- Hu, Y.; Yurkovich, S.; Guezennec, Y.; Yurkovich, B.J. Electro-Thermal Battery Model Identification for Automotive Applications. J. Power Source 2011, 196, 449–457. [Google Scholar] [CrossRef]
- Rahimi-Eichi, H.; Ojha, U.; Baronti, F.; Chow, M.-Y. Battery Management System: An Overview of Its Application in the Smart Grid and Electric Vehicles. IEEE Ind. Electron. Mag. 2013, 7, 4–16. [Google Scholar] [CrossRef]
- Birkl, C.R.; Roberts, M.R.; McTurk, E.; Bruce, P.G.; Howey, D.A. Degradation Diagnostics for Lithium Ion Cells. J. Power Source 2017, 341, 373–386. [Google Scholar] [CrossRef]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A Review on Lithium-Ion Battery Ageing Mechanisms and Estimations for Automotive Applications. J. Power Source 2013, 241, 680–689. [Google Scholar] [CrossRef]
- Dubarry, M.; Truchot, C.; Liaw, B.Y. Synthesize Battery Degradation Modes via a Diagnostic and Prognostic Model. J. Power Source 2012, 219, 204–216. [Google Scholar] [CrossRef]
- Pop, V.; Bergveld, H.J.; Regtien, P.P.L.; Veld, J.H.G.O.H.; Danilov, D.; Notten, P.H.L. Battery Aging and Its Influence on the Electromotive Force. J. Electrochem. Soc. 2007, 154, A744. [Google Scholar] [CrossRef]
- Waag, W.; Fleischer, C.; Sauer, D. Critical Review of the Methods for Monitoring of Lithium-Ion Batteries in Electric and Hybrid Vehicles. J. Power Source 2014, 258, 321–339. [Google Scholar] [CrossRef]
- Brivio, C.; Carrillo, R.E.; Alet, P.-J.; Hutter, A. BestimatorTM: A Novel Model-Based Algorithm for Robust Estimation of Battery SoC. In Proceedings of the 2020 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Sorrento, Italy, 24–26 June 2020; pp. 184–188. [Google Scholar]
- Dai, H.; Jiang, B.; Hu, X.; Lin, X.; Wei, X.; Pecht, M. Advanced Battery Management Strategies for a Sustainable Energy Future: Multilayer Design Concepts and Research Trends. Renew. Sustain. Energy Rev. 2021, 138, 110480. [Google Scholar] [CrossRef]
- Pastor-Fernández, C.; Yu, T.F.; Widanage, W.D.; Marco, J. Critical Review of Non-Invasive Diagnosis Techniques for Quantification of Degradation Modes in Lithium-Ion Batteries. Renew. Sustain. Energy Rev. 2019, 109, 138–159. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, D.; Schaltz, E.; Stroe, D.-I.; Gismero, A.; Yang, B. Degradation Mechanism Analysis and State-of-Health Estimation for Lithium-Ion Batteries Based on Distribution of Relaxation Times. J. Energy Storage 2022, 55, 105386. [Google Scholar] [CrossRef]
- Marongiu, A.; Nlandi, N.; Rong, Y.; Sauer, D.U. On-Board Capacity Estimation of Lithium Iron Phosphate Batteries by Means of Half-Cell Curves. J. Power Source 2016, 324, 158–169. [Google Scholar] [CrossRef]
- Pastor-Fernández, C.; Uddin, K.; Chouchelamane, G.H.; Widanage, W.D.; Marco, J. A Comparison between Electrochemical Impedance Spectroscopy and Incremental Capacity-Differential Voltage as Li-Ion Diagnostic Techniques to Identify and Quantify the Effects of Degradation Modes within Battery Management Systems. J. Power Source 2017, 360, 301–318. [Google Scholar] [CrossRef]
- Anseán, D.; Baure, G.; González, M.; Cameán, I.; García, A.B.; Dubarry, M. Mechanistic Investigation of Silicon-Graphite/LiNi0.8Mn0.1Co0.1O2 Commercial Cells for Non-Intrusive Diagnosis and Prognosis. J. Power Source 2020, 459, 227882. [Google Scholar] [CrossRef]
- Schaltz, E.; Stroe, D.-I.; Nørregaard, K.; Ingvardsen, L.S.; Christensen, A. Incremental Capacity Analysis Applied on Electric Vehicles for Battery State-of-Health Estimation. IEEE Trans. Ind. Appl. 2021, 57, 1810–1817. [Google Scholar] [CrossRef]
- Lin, C.P.; Cabrera, J.; Yu, D.Y.W.; Yang, F.; Tsui, K.L. SOH Estimation and SOC Recalibration of Lithium-Ion Battery with Incremental Capacity Analysis & Cubic Smoothing Spline. J. Electrochem. Soc. 2020, 167, 090537. [Google Scholar] [CrossRef]
- Brivio, C.; Musolino, V.; Merlo, M.; Ballif, C. A Physically-Based Electrical Model for Lithium-Ion Cells. IEEE Trans. Energy Convers. 2019, 34, 594–603. [Google Scholar] [CrossRef]
- Illig, J.; Schmidt, J.P.; Weiss, M.; Weber, A.; Ivers-Tiffée, E. Understanding the Impedance Spectrum of 18650 LiFePO4-Cells. J. Power Source 2013, 239, 670–679. [Google Scholar] [CrossRef]
- Meddings, N.; Heinrich, M.; Overney, F.; Lee, J.-S.; Ruiz, V.; Napolitano, E.; Seitz, S.; Hinds, G.; Raccichini, R.; Gaberšček, M.; et al. Application of Electrochemical Impedance Spectroscopy to Commercial Li-Ion Cells: A Review. J. Power Source 2020, 480, 228742. [Google Scholar] [CrossRef]
- Iurilli, P.; Brivio, C.; Wood, V. On the Use of Electrochemical Impedance Spectroscopy to Characterize and Model the Aging Phenomena of Lithium-Ion Batteries: A Critical Review. J. Power Source 2021, 505, 229860. [Google Scholar] [CrossRef]
- Boukamp, B.A. Distribution (Function) of Relaxation Times, Successor to Complex Nonlinear Least Squares Analysis of Electrochemical Impedance Spectroscopy? J. Phys. Energy 2020, 2, 042001. [Google Scholar] [CrossRef]
- Bartoszek, J.; Liu, Y.-X.; Karczewski, J.; Wang, S.-F.; Mrozinski, A.; Jasinski, P. Distribution of Relaxation Times as a Method of Separation and Identification of Complex Processes Measured by Impedance Spectroscopy. In Proceedings of the 2017 21st European Microelectronics and Packaging Conference (EMPC) & Exhibition, Warsaw, Poland, 10–13 September 2017; pp. 1–5. [Google Scholar]
- Schichlein, H.; Ller, A.C.M.; Voigts, M. Deconvolution of Electrochemical Impedance Spectra for the Identification of Electrode Reaction Mechanisms in Solid Oxide Fuel Cells. J. Appl. Electrochem. 2002, 32, 875–882. [Google Scholar] [CrossRef]
- Zhou, X.; Pan, Z.; Han, X.; Lu, L.; Ouyang, M. An Easy-to-Implement Multi-Point Impedance Technique for Monitoring Aging of Lithium Ion Batteries. J. Power Source 2019, 417, 188–192. [Google Scholar] [CrossRef]
- Zhou, X.; Huang, J.; Pan, Z.; Ouyang, M. Impedance Characterization of Lithium-Ion Batteries Aging under High-Temperature Cycling: Importance of Electrolyte-Phase Diffusion. J. Power Source 2019, 426, 216–222. [Google Scholar] [CrossRef]
- Carthy, K.M.; Gullapalli, H.; Ryan, K.M.; Kennedy, T. Review—Use of Impedance Spectroscopy for the Estimation of Li-Ion Battery State of Charge, State of Health and Internal Temperature. J. Electrochem. Soc. 2021, 168, 080517. [Google Scholar] [CrossRef]
- Jiang, S.; Song, Z. Estimating the State of Health of Lithium-Ion Batteries with a High Discharge Rate through Impedance. Energies 2021, 14, 4833. [Google Scholar] [CrossRef]
- Mingant, R.; Bernard, J.; Sauvant Moynot, V.; Delaille, A.; Mailley, S.; Hognon, J.-L.; Huet, F. EIS Measurements for Determining the SoC and SoH of Li-Ion Batteries. ECS Trans. 2019, 33, 41–53. [Google Scholar] [CrossRef]
- Galeotti, M.; Cinà, L.; Giammanco, C.; Cordiner, S.; Di Carlo, A. Performance Analysis and SOH (State of Health) Evaluation of Lithium Polymer Batteries through Electrochemical Impedance Spectroscopy. Energy 2015, 89, 678–686. [Google Scholar] [CrossRef]
- Chen, L.; Lü, Z.; Lin, W.; Li, J.; Pan, H. A New State-of-Health Estimation Method for Lithium-Ion Batteries through the Intrinsic Relationship between Ohmic Internal Resistance and Capacity. Measurement 2018, 116, 586–595. [Google Scholar] [CrossRef]
- Dam, S.K.; John, V. High-Resolution Converter for Battery Impedance Spectroscopy. IEEE Trans. Ind. Appl. 2018, 54, 1502–1512. [Google Scholar] [CrossRef]
- Wang, X.; Wei, X.; Chen, Q.; Dai, H. A Novel System for Measuring Alternating Current Impedance Spectra of Series-Connected Lithium-Ion Batteries With a High-Power Dual Active Bridge Converter and Distributed Sampling Units. IEEE Trans. Ind. Electron. 2021, 68, 7380–7390. [Google Scholar] [CrossRef]
- Hoshi, Y.; Yakabe, N.; Isobe, K.; Saito, T.; Shitanda, I.; Itagaki, M. Wavelet Transformation to Determine Impedance Spectra of Lithium-Ion Rechargeable Battery. J. Power Source 2016, 315, 351–358. [Google Scholar] [CrossRef]
- Namor, E.; Brivio, C.; Le Roux, E. Battery System and Battery Management Method. European Patent WO 2022/200476 A1, 29 September 2022. [Google Scholar]
- Infineon Technologies Evaluation Board—Infineon Technologies. Available online: https://www.infineon.com/cms/en/design-support/finder-selection-tools/product-finder/evaluation-board/ (accessed on 22 September 2022).
- Infineon Technologies TLE9012DQU|Li-Ion Battery Monitoring and Balancing IC—Infineon Technologies. Available online: https://www.infineon.com/cms/en/product/battery-management-ics/tle9012dqu/ (accessed on 22 September 2022).
- Iurilli, P.; Brivio, C.; Carrillo, R.E.; Wood, V. EIS2MOD: A DRT-Based Modeling Framework for Li-Ion Cells. IEEE Trans. Ind. Appl. 2022, 58, 1429–1439. [Google Scholar] [CrossRef]
- Iurilli, P.; Brivio, C.; Wood, V. Detection of Lithium-Ion Cells’ Degradation through Deconvolution of Electrochemical Impedance Spectroscopy with Distribution of Relaxation Time. Energy Technol. 2022, 10, 2200547. [Google Scholar] [CrossRef]
- Product Specifications—Battery Tester BCS-800 Series. Available online: https://www.biologic.net/documents/hight-throughput-battery-tester-bcs-8xx-series/ (accessed on 16 April 2021).
- Angelantoni Test Technologies Discovery Climatic Chambers. Available online: https://www.acstestchambers.com/en/environmental-test-chambers/discovery-my-climatic-chambers-for-stress-screening/ (accessed on 16 April 2021).
- Attia, P.M.; Bills, A.; Planella, F.B.; Dechent, P.; dos Reis, G.; Dubarry, M.; Gasper, P.; Gilchrist, R.; Greenbank, S.; Howey, D.; et al. Review—“Knees” in Lithium-Ion Battery Aging Trajectories. J. Electrochem. Soc. 2022, 169, 060517. [Google Scholar] [CrossRef]
- Schuster, S.F.; Bach, T.; Fleder, E.; Müller, J.; Brand, M.; Sextl, G.; Jossen, A. Nonlinear Aging Characteristics of Lithium-Ion Cells under Different Operational Conditions. J. Energy Storage 2015, 1, 44–53. [Google Scholar] [CrossRef]
- Diao, W.; Saxena, S.; Han, B.; Pecht, M. Algorithm to Determine the Knee Point on Capacity Fade Curves of Lithium-Ion Cells. Energies 2019, 12, 2910. [Google Scholar] [CrossRef]
- Boukamp, B.A. A Linear Kronig-Kramers Transform Test for Immittance Data Validation. J. Electrochem. Soc. 1995, 142, 1885. [Google Scholar] [CrossRef]
- Hahn, M.; Schindler, S.; Triebs, L.-C.; Danzer, M.A. Optimized Process Parameters for a Reproducible Distribution of Relaxation Times Analysis of Electrochemical Systems. Batteries 2019, 5, 43. [Google Scholar] [CrossRef]
- Wan, T.H.; Saccoccio, M.; Chen, C.; Ciucci, F. Influence of the Discretization Methods on the Distribution of Relaxation Times Deconvolution: Implementing Radial Basis Functions with DRTtools. Electrochim. Acta 2015, 184, 483–499. [Google Scholar] [CrossRef]
- Gavrilyuk, A.L.; Osinkin, D.A.; Bronin, D.I. The Use of Tikhonov Regularization Method for Calculating the Distribution Function of Relaxation Times in Impedance Spectroscopy. Russ. J. Electrochem. 2017, 53, 575–588. [Google Scholar] [CrossRef]
- Wildfeuer, L.; Wassiliadis, N.; Karger, A.; Bauer, F.; Lienkamp, M. Teardown Analysis and Characterization of a Commercial Lithium-Ion Battery for Advanced Algorithms in Battery Electric Vehicles. J. Energy Storage 2022, 48, 103909. [Google Scholar] [CrossRef]
- Yang, X.-G.; Leng, Y.; Zhang, G.; Ge, S.; Wang, C.-Y. Modeling of Lithium Plating Induced Aging of Lithium-Ion Batteries: Transition from Linear to Nonlinear Aging. J. Power Source 2017, 360, 28–40. [Google Scholar] [CrossRef]
- Capron, O.; Gopalakrishnan, R.; Jaguemont, J.; Van den Bossche, P.; Omar, N.; Van Mierlo, J. On the Ageing of High Energy Lithium-Ion Batteries—Comprehensive Electrochemical Diffusivity Studies of Harvested Nickel Manganese Cobalt Electrodes. Materials 2018, 11, 176. [Google Scholar] [CrossRef]
- Yi, M.; Jiang, F.; Zhao, G.; Guo, D.; Ren, D.; Lu, L.; Ouyang, M. Detection of Lithium Plating Based on the Distribution of Relaxation Times. In Proceedings of the 2021 IEEE 4th International Electrical and Energy Conference (CIEEC), Wuhan, China, 28–30 May 2021; pp. 1–5. [Google Scholar]
- Zhang, Y.; Tang, Q.; Zhang, Y.; Wang, J.; Stimming, U.; Lee, A.A. Identifying Degradation Patterns of Lithium Ion Batteries from Impedance Spectroscopy Using Machine Learning. Nat. Commun. 2020, 11, 1706. [Google Scholar] [CrossRef]
- Tian, H.; Qin, P.; Li, K.; Zhao, Z. A Review of the State of Health for Lithium-Ion Batteries: Research Status and Suggestions. J. Clean. Prod. 2020, 261, 120813. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).