1. Introduction
Earth’s sustainability is, nowadays, one of the biggest problems discussed worldwide. Climate change, mainly due to the improper and excessive use of fossil fuels, is no longer just a concern but a strong reality that needs to be addressed [
1]. To counter the harmful effects of climate change and achieve carbon-neutrality targets, energy generation, distribution, consumption, and rationalization techniques must be changed. Among other measures, it is important to increase the efficiency of power electronics systems, invest in clean energy, and change the power grid paradigm [
2].
Nevertheless, renewable energy sources (RES), as is the case of solar photovoltaic (PV), despite the unnumbered environmental advantages, present an intermittent profile, i.e., consumption and production periods are non-coincident [
3]. For this reason, energy storage systems (ESS), such as battery ESS (BESS), are used to balance these periods, contributing directly to the sustainability, stability, and robustness of the power grid [
4]. In addition to RES and ESS, the inclusion of emerging technologies, e.g., electric vehicles (EV), forces the power grid to face new challenges [
5,
6,
7]. Within this context, dc grids have been receiving special prominence, since power quality problems are almost nonexistent and the number of power converters is lower, thus increasing efficiency [
8,
9].
Considering the growing proliferation of domestic electrical appliances, natively operating in dc, and according to the future perspectives for dc grids, it is expectable that self-consumption production units will take a preponderant role in the global energy plan [
10,
11]. In this respect, the consumer will also be a producer, thus decentralizing generation and becoming a prosumer [
12]. Consequently, microgrids with hybrid (or solely dc) architectures can be developed, operating alongside a large set of ancillary services, such as bidirectional power flow, mitigation of power quality problems, fault tolerance, commutation between grid-connected and islanded modes, etc. [
13,
14,
15,
16,
17]. This change would allow a constant supply of energy to all the consumers, even in places located far away from the large urban centers and in the case of grid failure [
18,
19].
In [
20], an analysis and experimental validation of an off-board three-port integrated topology used to interface EV and solar PV panels with the ac power grid is presented. Although the solar PV panels and the EV (instead of stationary BESS) are connected to the same dc-link, the considered topology is non-isolated and the power grid does not present a dc configuration. Furthermore, in [
21,
22], two power electronics architectures that interface ESS and solar PV panels with the ac power grid are presented. Whilst in [
21], galvanic isolation between the ESS and the rest of the system is guaranteed through a dual active bridge (DAB) power converter, the same is no longer the case in [
22]. In the latter, non-isolated buck and boost converters are used, as well as a full bridge dc–ac power converter to interface the ac grid. However, in neither case is the purpose of this paper achieved: the development of a unified power converter that allows, in an isolated way and through a single connection point to a dc grid, the interface of solar PV panels and a BESS. Such application is partly suggested in [
23], where two non-isolated conversion stages interface with the solar PV panels and the BESS. However, the connection to the dc grid, despite being performed using an isolated topology, employs a dual half-bridge power converter, which, compared to a DAB, has lower switching losses, but, in contrast, has fewer degrees of freedom, resulting in lower energy efficiency [
24].
In [
25], to ensure a bidirectional power flow in the DAB converter, three modulations are analyzed and compared: single phase shift (SPS), extended phase shift (EPS), and dual phase shift (DPS). However, to achieve the same objective, but with higher energy efficiency, in [
26], triple phase shift (TPS) modulation is considered. In [
27], duty-cycle modulation, SPS, EPS, DPS, and TPS are analyzed and compared. It was concluded that only DPS and SPS are considered adequate for the proposed topology since duty-cycle modulation presents low-rate power transfer, EPS is more suitable for medium/high power application scenarios, and lastly, TPS, despite being considered the most flexible modulation among the five, presents higher implementation difficulty and costs. In [
28], a review of multiport converters for solar PV and BESS integration is presented, evaluating the performance of each one. On the other hand, in [
29], an isolated microinverter topology is proposed, capable of extracting power from a solar PV module and, subsequently, injecting it into the power grid at the same time that a BESS is charged. However, the presented solution is dedicated to application in a single solar PV module. Moreover, the topology is based on a high-frequency push–pull power converter, used to interface an ac grid instead of a dc grid, as is the case for the solution proposed in this work. In [
30], an energy management and control system for microgrids based on wind-PV-BESS is analyzed, thus meeting the goal of integrating various renewable energy sources.
The proposed unified power converter is presented in
Figure 1. As can be seen, the system consists of a DAB converter and two non-isolated dc–dc power converters, namely a unidirectional boost and a bidirectional buck–boost, responsible to interface solar PV panels and the BESS, respectively. The DAB converter is used to ensure galvanic isolation and adjust the voltages on each side of this conversion stage. In this regard, the main contributions of the proposed unified power converter are: (i) galvanic isolation, achieved through a DAB converter; (ii) reduced number of conversion stages, since the solar PV panels and the BESS are connected to the dc grid through a single connection point; (iii) inexistence of power quality problems, justified by employing a dc architecture; (iv) adoption of distinct operation modes, capable of complying with the energy needs of the consumer. However, it is also important to ensure bidirectional power flow between consumers and producers, increase energy efficiency (applying suitable power converter topologies and control algorithms), guarantee the safety of the equipment, and reduce costs.
This paper is organized as follows:
Section 2 introduces the proposed unified power converter topology. Hardware and correspondent control algorithms are shown in
Section 3.
Section 4 refers to the experimental validation. Conclusions are given in
Section 5.
3. Hardware Architecture and Control Algorithms
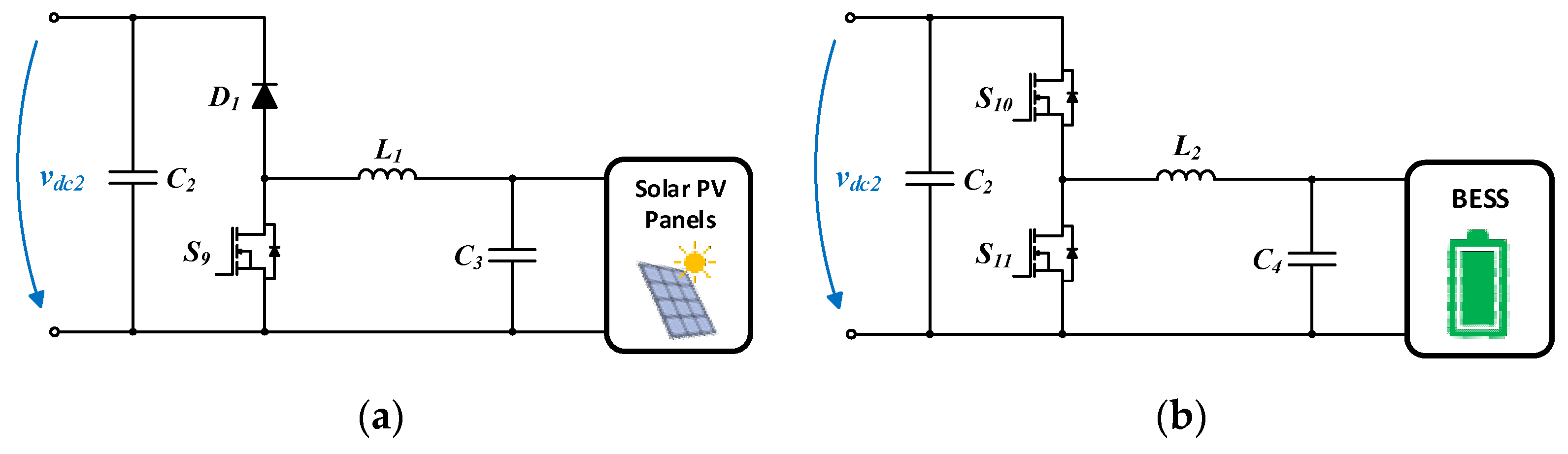
In the smart-grid context, the adopted topology for the unified power converter must provide galvanic isolation and bidirectional power flow between the solar PV panels, BESS, and dc microgrid. Considering the above-mentioned constraints, a non-isolated unidirectional boost dc–dc power converter was selected to interface solar PV panels, as
Figure 3a shows. To continuously extract the maximum instantaneous power of the solar PV panels, a perturb-and-observe maximum-power point-tracking algorithm is used.
On the other hand, to accomplish the interface with the BESS, a non-isolated bidirectional buck–boost dc–dc power converter was adopted, as seen in
Figure 3b. The selection of both topologies is justified based on the functionalities inherent to all operation modes. Simultaneously, both dc–dc boost and dc–dc buck–boost are considered extremely appreciated due to presenting satisfactory results related to power efficiency in view of the ease of its implementation.
As aforementioned, the charge and discharge of a BESS must be controlled following its state of charge (
SoC), calculated using (1). In this equation,
Ibat represents the current that flows through the battery and
Q is the battery equivalent charge.
To increase the lifetime and efficiency of the BESS, certain current and voltage limits must be respected. In this sense, to achieve constant current and voltage values, a proportional-integral (PI) controller is often used, both for the BESS charge and discharge. Despite not having the forecasting ability existing in other control techniques, the PI controller requires lower computational resources. If during PV2B and G2B operation modes the buck–boost dc–dc power converter operates as a buck-type converter, when in mode B2G, it will be employed as a boost-type converter. Since the power flows towards the dc microgrid and the voltage on the battery terminals (vbat) is lower than on the secondary dc-link (vdc2), the latter must be elevated using this back-end converter.
As previously mentioned, it is essential to allow the bidirectional power flow between the dc microgrid, the solar PV panels, and the BESS, but also to ensure galvanic isolation. Thus, a DAB converter has been widely used in the most diverse types of power electronics applications, as is the case of solid-state transformers and medium/high voltage power grids. This isolated topology consists of a full bridge ac–dc converter on each side of a high-frequency transformer, as shown in
Figure 4. The purpose of the high-frequency transformer is to provide galvanic isolation to the power system and, according to its turn ratio (
N =
N1/
N2), adjust the voltage on the primary (
v1) and secondary (
v2) sides to the desired values. Compared to the most distinct isolated topologies, a DAB converter has greater advantages concerning flexibility and efficiency under nominal conditions. For instance, a dual half-bridge topology, despite presenting lower switching losses and costs, has, on the other hand, fewer degrees of freedom, thus decreasing its efficiency.
To fulfill all the previously explained requirements, a phase shift algorithm is applied to the DAB converter. Regardless of the power flow direction, gate signals with a 50% duty cycle ratio are applied to each of the eight semiconductors that constitute this topology, generating square waveforms in
v1 and
v2. However, the phenomenon that allows energy bidirectionality is the phase lag (
φ) between
v1 and
v2, which, when phase-shifted, generates a voltage (
vLlk) in the transformer’s leakage inductance (
Llk) and, consequently, a certain current (
iLlk) will flow through it. Depending on whether
φ is considered positive or negative, the direction of
iLlk will be changed, and the power will flow accordingly. That is, if
v1 is in advance of
v2, as
Figure 5a shows, power will flow from the primary side to the secondary one. If the opposite happens, i.e., if
v2 is in advance of
v1, as
Figure 5b shows, the power flow direction changes. The presented results were obtained using PSIM simulation software. By observing
Figure 5, it is possible to conclude that the maximum values of
v1 and
v2 are, respectively, 400 V and 200 V. These values, considering the voltage ratio of the transformer (2:1) and the adopted modulation technique, are also representative of the nominal voltages on the primary (
vdc1) and secondary (
vdc2) dc-links.
As previously mentioned, there are several modulations that may be applied to the DAB converter: SPS, DPS, EPS, and TPS are the most referenced techniques in the literature. Each one has different advantages over the others, but for the proposed work, the DPS was adopted. Comparing with the SPS, this modulation technique adds a new degree of freedom, i.e., besides considering the mismatch between the two full-bridges (D0, outer-phase-shift angle), the DPS algorithm considers a new phase shift angle, existent between the legs of each full-bridge (D1, inner-phase-shift angle). In this regard, it is possible to obtain a three-level square waveform in the windings of the high-frequency transformer, thus providing higher efficiency. Nonetheless, both D0 and D1 must have limit values, calculated so that the reactive power and the circulating current in the converter are reduced. Moreover, this control technique is usually applied in situations in which the ratio between the voltage values on each side of the DAB converter is very far apart from N.
It is the adjustment of
φ that controls the average transferred power between the two sides of the converter (
Po): the higher its value, the greater the power transferred. For this reason, and to regulate the nominal value of
vdc2 (or
vdc1), it is essential that the values assigned to
D0 and
D1 are calculated dynamically. In this sense, the value of
Po is expressed in (2), result of the multiplication of the constant
Pb, presented in (3), by the expressions dependent on the values assigned to
D0 and
D1.
Thus, to obtain the value of
D0, a PI controller is applied to operate according to the measured value of
vdc2, whereas, to calculate
D1, a proper calculation has to be implemented.
D1 will vary according to the existing relation between
v1 and
v2, with
D1 being higher the lower the value of the
v1/
v2 ratio. Therefore, an exponential equation, capable of calculating the value of
D1, was developed. Knowing that the absolute error is considered the difference between
N and the ratio
v1/
v2, as represented in (4), the value of
D1 is given by (5). In this way, the values of
D1 and
D0 vary dynamically and under the system’s operating conditions, allowing the regulation of
φ (positive or negative) and of the consequent power flow to and from each side of the high-frequency transformer.
The design of the control and power systems represent a key role in the efficiency presented by the unified power converter. However, there will always exist a tradeoff between compaction and performance, since the propagation of electromagnetic noise could have a higher impact on a greater number of elements. Besides the issues related to electromagnetic compatibility, the total system losses (
Ptot) must be as low as possible, using suitable control algorithms, topologies, and components, as well as a heatsink with reduced thermal resistance. In addition, the design of
Llk is also a process that directly influences the energy efficiency of the DAB converter. For the same operating frequency, the greater the value of
Llk, the greater
Ptot. As (6) confirms,
Ptot is considered the result of the sum of the semiconductor conduction (
Pcond) and switching (
Psw) losses, losses in the high-frequency transformer (
Ptr) and losses in the leakage inductance (
PLlk).
The losses on the high-frequency transformer must be as reduced as possible. However, this objective will only be achieved if this magnetic element is projected after a detailed study concerning the conditions thar are capable of influencing those same losses. In this sense,
Table 2 indicates the designations for each of the variables considered in the design of the high-frequency transformer, as well as their value for this specific application. Some of the values are indicated in [
32], while others are a direct consequence of the chosen architecture for the high-frequency transformer core (ETD 59/31/22), as is the case of
MLT,
Ae,
lm, and
WA.
A greater performance of the high-frequency transformer is directly associated with the number and section of its windings (copper losses,
Pcu, given by (7)), as well as to the core material of this element (core losses,
Pcore, represented in (8)). The sum of
Pcu and
Pcore, as (9) suggests, is representative of
Ptr.
In turn, if the number of windings is high, the greater
Pcu and the lesser
Pcore (there is higher winding resistance and a reduced variation in magnetic flux, ∆
B). Logically, if the number of windings drops, the opposite will happen. In this respect, to ensure the lowest possible value to
Ptr, it is essential to find an optimal value for ∆
B, thus reaching a balance between the two types of losses. The optimal value of ∆
B is given by (10).
In this specific case, considering that the values of λ1 and Itot are given, correspondingly, in (11) and (12), it is possible to calculate a value of 0.0906 T for ∆B, of 3.957 W for Pcore and of 5.144 W for Pcu, thus making a value of 9.101 W for Ptr.
To conclude the design of the high-frequency transformer, it is necessary to define the number of windings on each of its sides, as well as their cross-section. Thus, considering a value of 100 kHz for the semiconductors’
fs, an AWG 25 conductor was chosen. With a cross-section of 0.159 mm
2, this conductor, ideally, does not allow the manifestation of skin effect and supports a maximum current of 2.7 A, which justifies the paralleling of a considerable number of conductors. Given that the number of turns for the primary side is provided by (13), the values of 30 and 15 turns were obtained for the primary and secondary side, respectively.
4. Experimental Validation
The primordial objective of the proposed unified power converter development is the power density increase. In part, such a target was obtained based on the assignment of a 100 kHz fs to the power semiconductors, which has a direct consequence on the reduction of the volume and weight of the magnetic elements, as is the case of the DAB high-frequency transformer and the inductors of the back-end dc–dc converters.
Figure 6 presents a photography of the developed unified power converter, in which is possible to verify that a compact strategy was adopted throughout the entire prototype. In order to reduce the electromagnetic noise propagation, it was given special attention to the positioning of each of the solution elements.
During the experimental validation, the individual operation of each power converter was initially corroborated, i.e., DAB, buck–boost, and boost topologies. Thus, the power and control circuits and the corresponding modulation techniques were legitimized, thereby providing greater reliability to the prototype. Subsequently, it was necessary to validate the power electronics system as a whole, as well as the defined operation modes. Moreover, it was also fundamental to fulfill the main premise of this unified power converter: power bidirectionality between dc grid, BESS, and solar PV panels.
For the execution of laboratory tests, the connection of BESS and solar PV panels was relegated to background. Therefore, to authenticate the power flow direction in each of the four operation modes and to emulate the elements that consume and provide/generate energy, resistive loads and dc voltage sources were utilized. Moreover, the digital control of the system was realized using a Texas Instruments TMDSCNCD28335 development board and the experimental results were captured with a Tektronix TPS2024B digital oscilloscope.
4.1. Solar PV Panels to Batteries (PV2B)
In this operation mode, a dc voltage source was used to emulate solar PV panels power generation, whereas a 13 Ω resistive load was connected to the BESS terminals, thus simulating its charge through power consumption. In this regard,
Figure 7 shows the obtained experimental results for this operation mode.
Two PI algorithms were adopted to control
vdc2 and the current that flows through the resistive load (
ibat), the outputs being applicable, correspondingly, to the back-end boost- and buck–boost-type dc–dc power converters. Thus, a 2 A reference for
ibat and a 60 V reference for
vdc2 were defined. As
Figure 7a shows, the measured values (CH4 and CH2, respectively) converge to the established references. It should also be noted that the voltage on the dc source that simulates the PV panels (
vPV, CH1) is 20 V and the voltage on the resistive load (
vbat, CH3) is 27.4 V, very close to the theoretical value.
On the other hand,
Figure 7b shows the gate source voltage in each of the semiconductors that make up the buck–boost bidirectional back-end converter (
vgs_BB1 and
vgs_BB2), validating the applied active rectification technique.
4.2. Solar PV Panels to dc Grid (PV2G)
As with the PV2B operation mode, a dc voltage source was responsible for emulating the solar PV panel power generation. On the other hand, to simulate the dc grid, another dc voltage source was connected in parallel with a 26 Ω resistive load and with the primary dc-link. Moreover, a PI algorithm was implemented to regulate the current that flows through the inductor of the unidirectional boost dc–dc converter, i.e., the current that would be extracted from the solar PV panels (iPV). To regulate the value of vdc2, as in the case of the PV2B operation mode, another PI algorithm was implemented. However, in this case, its output is considered the value of φ between the waveforms of v1 and v2.
In this regard, a 2.5 A reference for
iPV and a 30 V reference for
vdc2 were defined. As
Figure 8a shows, the obtained values are in line with those previously stipulated (CH4 and CH2, respectively), occurring when
vdc1 (CH1) is 60.7 V and the voltage on the dc source (
vPV, CH3) is 19.6 V. To validate the DPS modulation, it is vital to assess the waveforms of
v1 and
v2. As expected, after holding computational simulations and by contemplating
Figure 8b, it is verified that
v1 is delayed concerning
v2, thus proving the direction of the power flow. The negative value of
φ is observed in detail in
Figure 8c.
4.3. Batteries to dc Grid (B2G)
During B2G mode, the BESS should be discharged at a constant current (
ibat) and, as in all operation modes, the value of
vdc2 is regulated in accordance with its reference value. For both cases, a PI control technique was used, in which the output of each one was applied, correspondingly, to the generation of PWM signals for the buck–boost dc–dc converter and in the implementation of the DPS algorithm (providing
φ). In this sense,
Figure 9 shows the obtained experimental results for this operation mode.
During experimental tests, two dc voltage sources were used, one replacing the BESS and the other emulating the dc grid, connected in parallel with a resistive load of 56 Ω and with the primary dc-link. Thus, this solution was optimized for the injection of a constant current of 1 A into the dc grid during the moment that
vbat is 25 V (discharge power of 25 W). By observing
Figure 9, it is verified that
vbat and
ibat (CH3 and CH4, correspondingly) converge to their references. Furthermore,
vdc2 (CH2) is referenced to 40 V and presents a mean value of 41.6 V, which, considering the
N of the high-frequency transformer, is reflected in the existence of a voltage of 79.3 V on the dc grid (
vdc1, CH1).
4.4. Dc Grid to Batteries (G2B)
During the G2B operation mode, the power flows from the dc grid (simulated with a dc voltage source) to the BESS (emulated with a 13 Ω resistive load, as in PV2B mode), thus representing their charging process. In this case, the variables to be controlled are, once again,
vdc2 and the current at the resistive load (
ibat), both of which must present constant values and follow the references defined in the PI algorithms. As shown in
Figure 10a, the reference value for
vdc2 (CH2) is 40 V, which, respecting the
N of the high-frequency transformer, increases
vdc1 (CH1) to 80 V. Based on the operating conditions,
vdc2 assumes the value of 38.9 V and
ibat (CH4) of 1.01 A, very close to its reference of 1 A. Moreover, the voltage on the BESS (
vbat, CH3) has a value of 14 V.
On the other hand, the influence of the DPS algorithm in the control of the power flow from the dc grid to the BESS must be verified. The value of
φ between
v1 and
v2 is automatically adjusted by the above-mentioned PI algorithm, which, consequently, allows the regulation of
vdc2. Analyzing
Figure 10b, it is possible to prove that the power flows from the dc grid to the BESS, since
φ is positive, i.e., the gate source voltage waveform of the semiconductor
S1 (
vgs_S1, CH1) is in advance to the signal measured in the same terminals of the semiconductor
S5 (
vgs_S5, CH2).
Figure 10 shows an unbalanced situation, in which the ratio
v1/
v2 is different from
N, even though
vdc2 converges to its reference. In this extreme case, in which
φ is maximum and assumes the value of 30⁰, the robustness of the DPS algorithm in the face of variations in the nominal operating conditions is proven. This effect can also be seen in
Figure 11a, wherein the waveforms of
v1 and
v2 (CH1 and CH2, respectively) are presented in the same unbalanced situation. Nevertheless, in
Figure 11b, the same waveforms are presented in a situation of equilibrium about the ratio
v1/
v2, and as can be seen, the value of
φ is almost zero. It should also be noted that the results obtained
Figure 11a,b are related to an experimental test carried out when the reference for
vdc2 was 30 V.
5. Conclusions
In this paper, given the expected paradigm shift in electric power grids, the development of a unified power electronics solution capable of interfacing solar photovoltaic (PV) panels and a battery energy storage system (BESS) with a dc microgrid is proposed. In this regard, the developed unified power converter was designed to operate in four operation modes: (i) solar PV panels to batteries (PV2B); (ii) solar PV panels to dc grid (PV2G); (iii) batteries to dc grid (B2G); (iv) dc grid to batteries (G2B).
Dual phase shift (DPS) modulation was applied to a dual active bridge (DAB) converter, the latter being responsible for providing galvanic isolation and for regulating the voltage values on each dc-link. The DPS, besides controlling the direction of the power flow, is also responsible for defining the value of transferred power to and from each side of the DAB. The DPS, when compared to similar modulation techniques, e.g., single phase shift (SPS), by adding a new degree of freedom, produces a three-level square waveform in the windings of the high-frequency transformer. Consequently, the reactive power and circulating current are reduced, thus increasing the efficiency.
The adoption of a high switching frequency (fs, 100 kHz) in the developed unified power converter allowed a reduction in the size of the passive elements, as is the case for the inductors, capacitors, and high-frequency transformer. The development of the high-frequency transformer was detailed throughout the paper, giving special emphasis to the calculation of total losses (Ptot). To this end, the number of windings was obtained as a function of the core physical features, the variation of the optimum magnetic flux (∆B), and the magnitude of power for which the DAB will operate.
The main objective of this paper, which relies on an isolated unified power converter for interfacing RES and BESS with a dc microgrid, was completely validated experimentally with the developed prototype for all the operating modes.