DFT Modelling of Li6SiO4Cl2 Electrolyte Material for Li-Ion Batteries
Abstract
:1. Introduction
2. Computational Methods
3. Results and Discussion
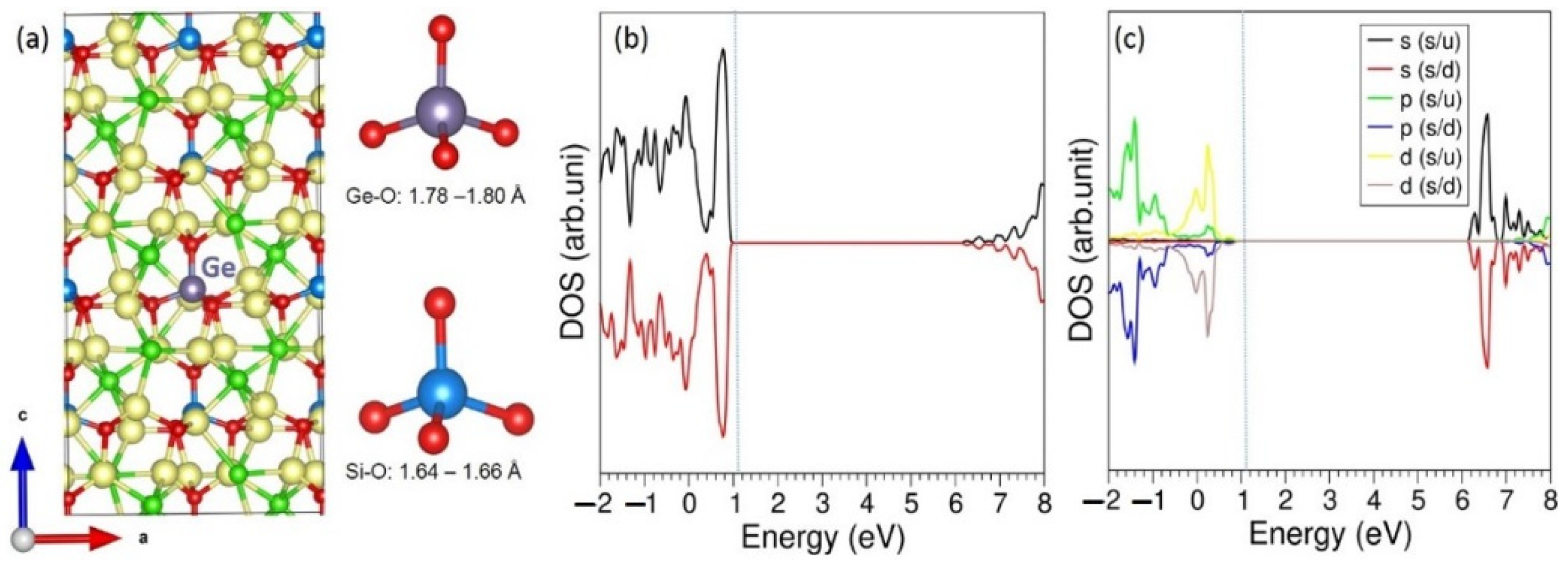
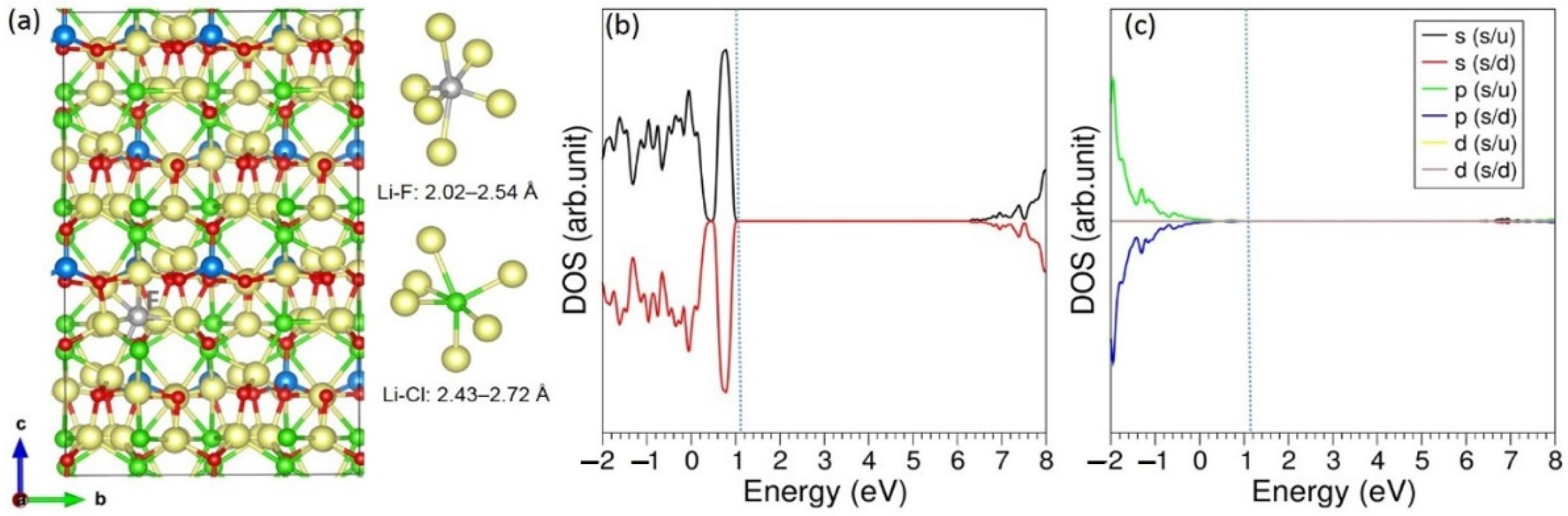
3.1. Bulk Structure of Li6SiO4Cl2
3.2. Intrinsic Defect Properties
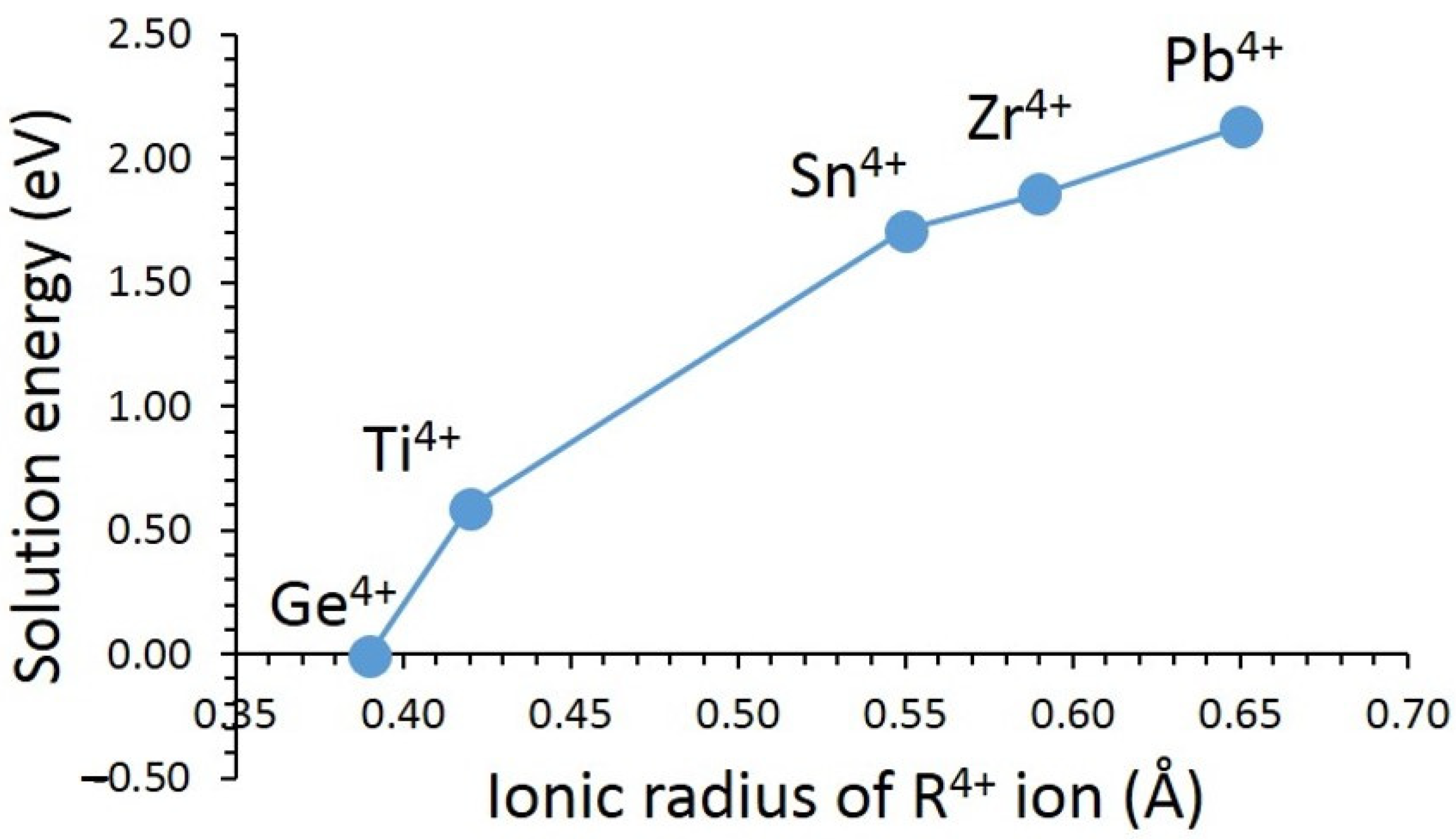
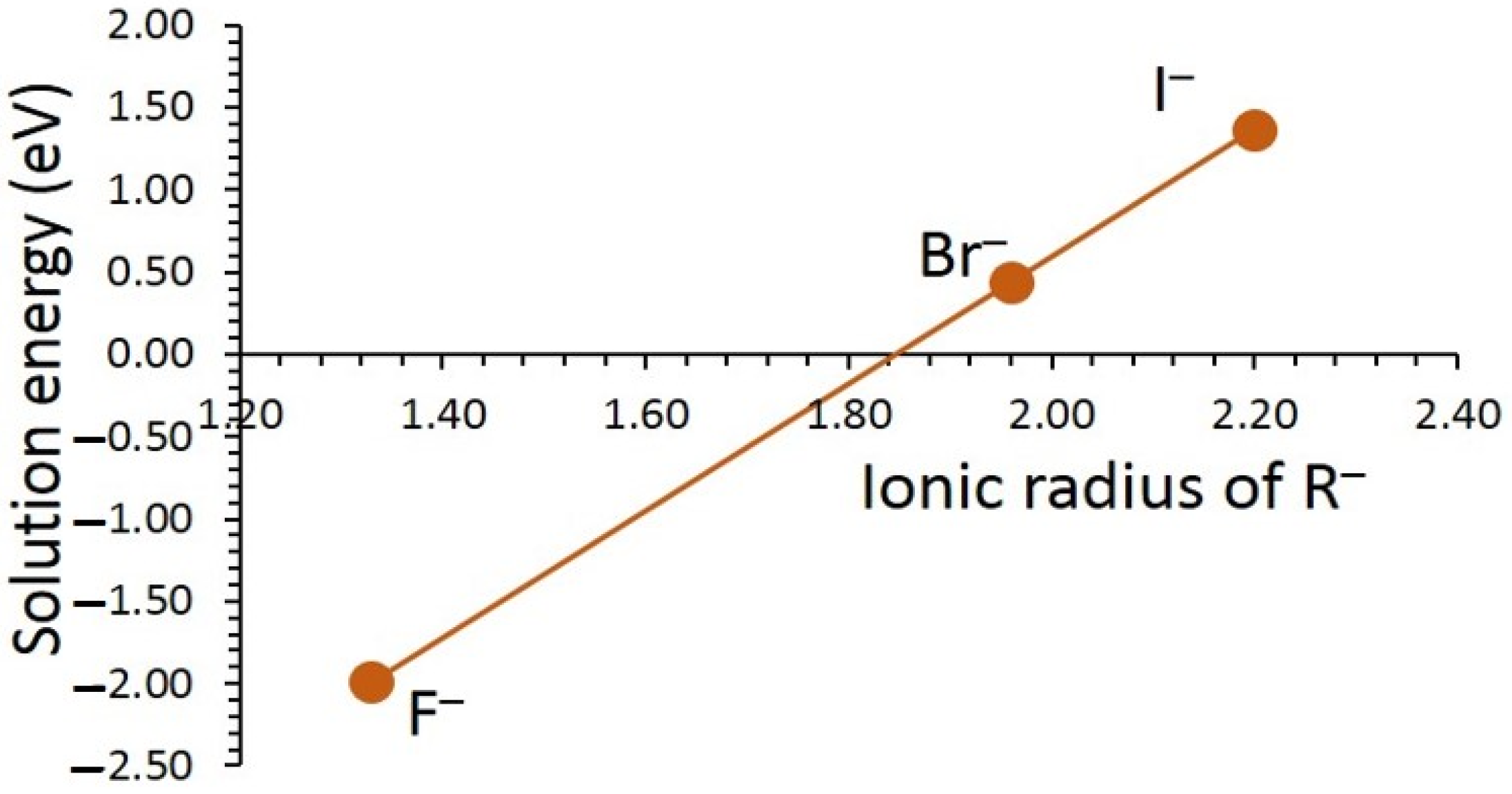
3.3. Solution of Dopants
3.4. Formation of Li6SiO4Cl2
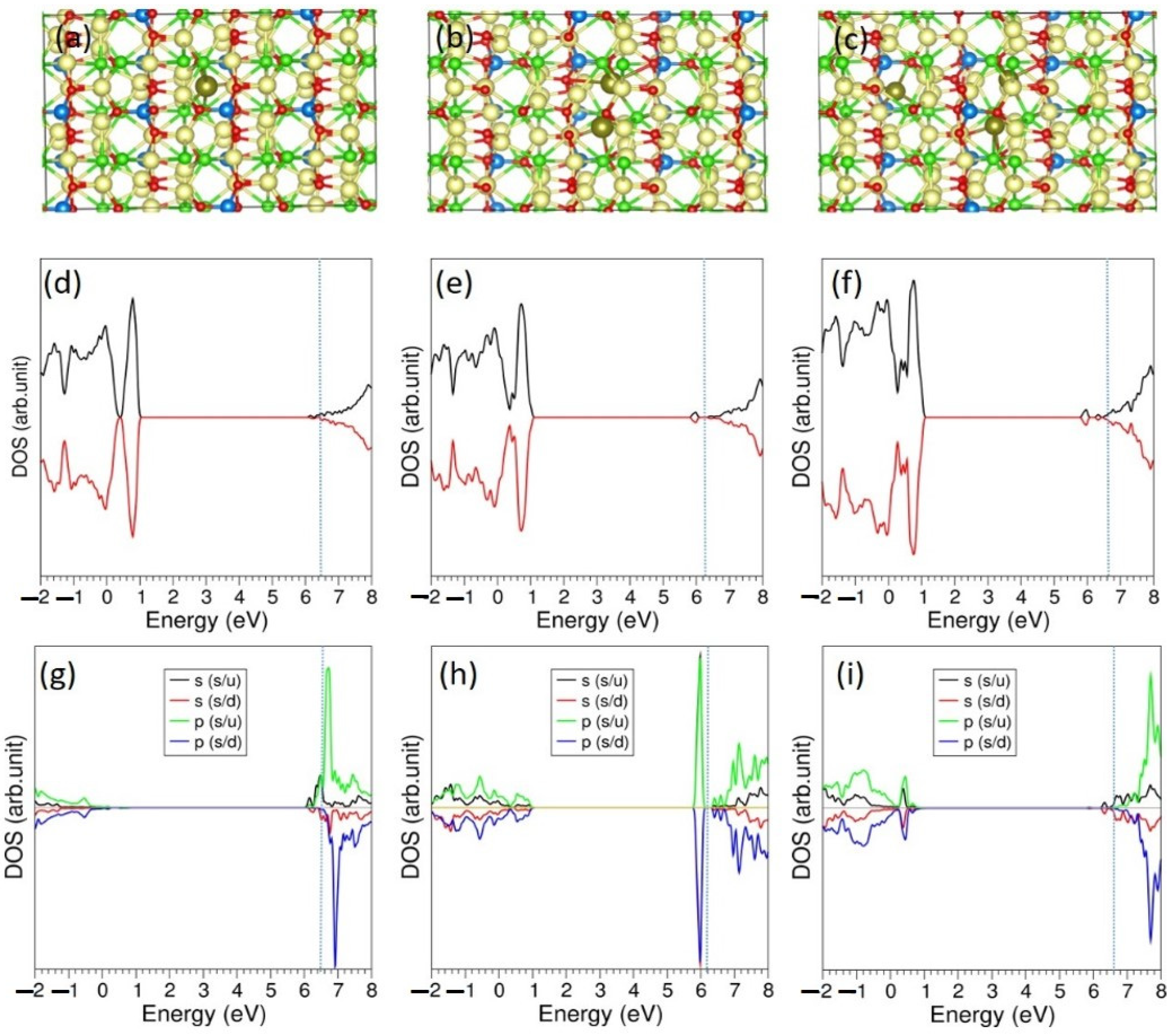
3.5. Li-Incorporation
4. Conclusions
Supplementary Materials
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Weiss, M.; Ruess, R.; Kasnatscheew, J.; Levartovsky, Y.; Levy, N.R.; Minnmann, P.; Stolz, L.; Waldmann, T.; Wohlfahrt-Mehrens, M.; Aurbach, D.; et al. Fast Charging of Lithium-Ion Batteries: A Review of Materials Aspects. Adv. Energy Mater. 2021, 11, 2101126. [Google Scholar] [CrossRef]
- Kim, T.; Song, W.; Son, D.-Y.; Ono, L.K.; Qi, Y. Lithium-ion batteries: Outlook on present, future, and hybridized technologies. J. Mater. Chem. A 2019, 7, 2942–2964. [Google Scholar] [CrossRef]
- Li, M.; Lu, J.; Chen, Z.; Amine, K. 30 Years of Lithium-Ion Batteries. Adv. Mater. 2018, 30, 1800561. [Google Scholar] [CrossRef] [PubMed]
- Cherkashinin, G.; Hausbrand, R.; Jaegermann, W. Performance of Li-Ion Batteries: Contribution of Electronic Factors to the Battery Voltage. J. Electrochem. Soc. 2019, 166, A5308–A5312. [Google Scholar] [CrossRef]
- Blomgren, G.E. The Development and Future of Lithium Ion Batteries. J. Electrochem. Soc. 2016, 164, A5019–A5025. [Google Scholar] [CrossRef]
- Agostini, M.; Brutti, S.; Navarra, M.A.; Panero, S.; Reale, P.; Matic, A.; Scrosati, B. A high-power and fast charging Li-ion battery with outstanding cycle-life. Sci. Rep. 2017, 7, 1104. [Google Scholar] [CrossRef]
- Deng, D. Li-ion batteries: Basics, progress, and challenges. Energy Sci. Eng. 2015, 3, 385–418. [Google Scholar] [CrossRef]
- Tang, W.; Zhu, Y.; Hou, Y.; Liu, L.; Wu, Y.; Loh, K.P.; Zhang, H.; Zhu, K. Aqueous rechargeable lithium batteries as an energy storage system of superfast charging. Energy Environ. Sci. 2013, 6, 2093–2104. [Google Scholar] [CrossRef]
- Xu, K. Electrolytes and Interphases in Li-Ion Batteries and Beyond. Chem. Rev. 2014, 114, 11503–11618. [Google Scholar] [CrossRef]
- Han, L.; Lehmann, M.L.; Zhu, J.; Liu, T.; Zhou, Z.; Tang, X.; Heish, C.-T.; Sokolov, A.P.; Cao, P.; Chen, X.C.; et al. Recent Developments and Challenges in Hybrid Solid Electrolytes for Lithium-Ion Batteries. Front. Energy Res. 2020, 8, 202. [Google Scholar] [CrossRef]
- Sauter, C.; Zahn, R.; Wood, V. Understanding Electrolyte Infilling of Lithium Ion Batteries. J. Electrochem. Soc. 2020, 167, 100546. [Google Scholar] [CrossRef]
- Kwon, W.J.; Kim, H.; Jung, K.-N.; Cho, W.; Kim, S.H.; Lee, J.-W.; Park, M.-S. Enhanced Li+ conduction in perovskite Li3xLa2/3−x□1/3−2xTiO3 solid-electrolytes via microstructural engineering. J. Mater. Chem. A 2017, 5, 6257–6262. [Google Scholar] [CrossRef]
- Heenen, H.H.; Voss, J.; Scheurer, C.; Reuter, K.; Luntz, A.C. Multi-ion Conduction in Li3OCl Glass Electrolytes. J. Phys. Chem. Lett. 2019, 10, 2264–2269. [Google Scholar] [CrossRef] [PubMed]
- El-Shinawi, H.; Greaves, C.; Janek, J. Sol–gel synthesis and room-temperature properties of α-LiZr2(PO4)3. RSC Adv. 2015, 5. [Google Scholar] [CrossRef]
- Shao, C.; Liu, H.; Yu, Z.; Zheng, Z.; Sun, N.; Diao, C. Structure and ionic conductivity of cubic Li7La3Zr2O12 solid electrolyte prepared by chemical co-precipitation method. Solid State Ion. 2016, 287, 13–16. [Google Scholar] [CrossRef]
- Yu, G.; Wang, Y.; Li, K.; Chen, D.; Qin, L.; Xu, H.; Chen, J.; Zhang, W.; Zhang, P.; Sun, Z. Solution-processable Li10GeP2S12 solid electrolyte for a composite electrode in all-solid-state lithium batteries. Sustain. Energy Fuels 2021, 5, 1211–1221. [Google Scholar] [CrossRef]
- López-Aranguren, P.; Reynaud, M.; Głuchowski, P.; Bustinza, A.; Galceran, M.; del Amo, J.M.L.; Armand, M.; Casas-Cabanas, M. Crystalline LiPON as a Bulk-Type Solid Electrolyte. ACS Energy Lett. 2021, 6, 445–450. [Google Scholar] [CrossRef]
- Kuganathan, N.; Chroneos, A. Defects, dopants and lithium incorporation in LiPON electrolyte. Comput. Mater. Sci. 2021, 202, 111000. [Google Scholar] [CrossRef]
- Shin, D.O.; Oh, K.; Kim, K.M.; Park, K.-Y.; Lee, B.; Lee, Y.-G.; Kang, K. Synergistic multi-doping effects on the Li7La3Zr2O12 solid electrolyte for fast lithium ion conduction. Sci. Rep. 2015, 5, 18053. [Google Scholar] [CrossRef]
- Morscher, A.; Dyer, M.S.; Duff, B.B.; Han, G.; Gamon, J.; Daniels, L.M.; Dang, Y.; Surta, W.; Robertson, C.M.; Blanc, F.; et al. Li6SiO4Cl2: A Hexagonal Argyrodite Based on Antiperovskite Layer Stacking. Chem. Mater. 2021, 33, 2206–2217. [Google Scholar]
- Spotte-Smith, E.W.C.; Blau, S.M.; Xie, X.; Patel, H.D.; Wen, M.; Wood, B.; Dwaraknath, S.; Persson, K.A. Quantum chemical calculations of lithium-ion battery electrolyte and interphase species. Sci. Data 2021, 8, 203. [Google Scholar] [CrossRef] [PubMed]
- Urban, A.; Seo, D.-H.; Ceder, G. Computational understanding of Li-ion batteries. npj Comput. Mater. 2016, 2, 16002. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C, 2nd ed.; The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Bader, R.F.W. The zero-flux surface and the topological and quantum definitions of an atom in a molecule. Theor. Chim. Acta 2001, 105, 276–283. [Google Scholar] [CrossRef]
- Kröger, F.A.; Vink, H.J. Relations between the Concentrations of Imperfections in Crystalline Solids. In Solid State Physics; Seitz, F., Turnbull, D., Eds.; Academic Press: Cambridge, MA, USA, 1956; Volume 3, pp. 307–435. [Google Scholar]
- Vineyard, G.H.; Dienes, G.J. The Theory of Defect Concentration in Crystals. Phys. Rev. 1954, 93, 265–268. [Google Scholar] [CrossRef]
- Lee, J.S.; Adams, S.; Maier, J. Defect chemistry and transport characteristics of β-AgI. J. Phys. Chem. Solids 2000, 61, 1607–1622. [Google Scholar] [CrossRef]
- Kuganathan, N.; Chroneos, A. Formation, doping, and lithium incorporation in LiFePO4. AIP Adv. 2022, 12, 045225. [Google Scholar] [CrossRef]
- Kim, Y. Theoretical investigation of the cation antisite defect in layer-structured cathode materials for Li-ion batteries. Phys. Chem. Chem. Phys. 2019, 21, 24139–24146. [Google Scholar] [CrossRef] [PubMed]
- Werner, J.; Neef, C.; Koo, C.; Zvyagin, S.; Ponomaryov, A.; Klingeler, R. Antisite disorder in the battery material LiFePO4. Phys. Rev. Mater. 2020, 4, 115403. [Google Scholar] [CrossRef]
- Raj, H.; Rani, S.; Sil, A. Antisite Defects in Sol-Gel-Synthesized LiFePO4at Higher Temperature: Effect on Lithium-Ion Diffusion. ChemElectroChem 2018, 5, 3525–3532. [Google Scholar] [CrossRef]
- Tang, Z.; Wang, S.; Liao, J.; Wang, S.; He, X.; Pan, B.; He, H.; Chen, C. Facilitating Lithium-Ion Diffusion in Layered Cathode Materials by Introducing Li+/Ni2+ Antisite Defects for High-Rate Li-Ion Batteries. Research 2019, 2019, 2198906. [Google Scholar] [CrossRef]
- Kuganathan, N.; Tsoukalas, L.; Chroneos, A. Defects, dopants and Li-ion diffusion in Li2SiO3. Solid State Ion. 2019, 335, 61–66. [Google Scholar] [CrossRef]
- Liu, H.; Choe, M.-J.; Enrique, R.A.; Orvañanos, B.; Zhou, L.; Liu, T.; Thornton, K.; Grey, C.P. Effects of Antisite Defects on Li Diffusion in LiFePO4 Revealed by Li Isotope Exchange. J. Phys. Chem. C 2017, 121, 12025–12036. [Google Scholar] [CrossRef]
- Devaraju, M.K.; Truong, Q.D.; Hyodo, H.; Sasaki, Y.; Honma, I. Synthesis, characterization and observation of antisite defects in LiNiPO4 nanomaterials. Sci. Rep. 2015, 5, 11041. [Google Scholar] [CrossRef]
- Milović, M.D.; Anicijevic, D.V.; Jugovic, D.; Anićijević, V.J.; Veselinović, L.; Mitrić, M.; Uskoković, D. On the presence of antisite defect in monoclinic Li2FeSiO4—A combined X-Ray diffraction and DFT study. Solid State Sci. 2018, 87, 81–86. [Google Scholar] [CrossRef]
- Armstrong, A.R.; Kuganathan, N.; Islam, M.S.; Bruce, P.G. ChemInform Abstract: Structure and Lithium Transport Pathways in Li2FeSiO4 Cathodes for Lithium Batteries. ChemInform 2011, 42, 13031–13035. [Google Scholar] [CrossRef]
- Kuganathan, N.; Kordatos, A.; Chroneos, A. Defect Chemistry and Li-ion Diffusion in Li2RuO3. Sci. Rep. 2019, 9, 550. [Google Scholar] [CrossRef]
- Kuganathan, N.; Kordatos, A.; Fitzpatrick, M.; Vovk, R.; Chroneos, A. Defect process and lithium diffusion in Li2TiO3. Solid State Ion. 2018, 327, 93–98. [Google Scholar] [CrossRef]
- Yang, X.; Zhang, H.; Xu, W.; Yu, B.; Liu, Y.; Wu, Z. A doping element improving the properties of catalysis: In situ Raman spectroscopy insights into Mn-doped NiMn layered double hydroxide for the urea oxidation reaction. Catal. Sci. Technol. 2022, 12, 4471–4485. [Google Scholar] [CrossRef]
- Wu, X.-W.; Kai, Z.; Sheng, H.; Fu, L.; Liu, Z.; Zhou, C.; Holze, R.; Wu, Y. Improving electrochemical properties by sodium doping for lithium-rich layered oxides. ACS Appl. Energy Mater. 2020, 3, 8953–8959. [Google Scholar] [CrossRef]
- Park, J.S.; Kim, Y.-B.; An, J.; Prinz, F.B. Oxygen diffusion across the grain boundary in bicrystal yttria stabilized zirconia. Solid State Commun. 2012, 152, 2169–2171. [Google Scholar] [CrossRef]
- Gao, Y.; Xiong, K.; Zhang, H.; Zhu, B. Effect of Ru Doping on the Properties of LiFePO4/C Cathode Materials for Lithium-Ion Batteries. ACS Omega 2021, 6, 14122–14129. [Google Scholar] [CrossRef]
- Xue, Z.; Qi, X.; Li, L.; Li, W.; Xu, L.; Xie, Y.; Lai, X.; Hu, G.; Peng, Z.; Cao, Y.; et al. Sodium Doping to Enhance Electrochemical Performance of Overlithiated Oxide Cathode Materials for Li-Ion Batteries via Li/Na Ion-Exchange Method. ACS Appl. Mater. Interfaces 2018, 10, 27141–27149. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, Z.; Jing, Q.; Guo, H.; Li, X.; Yang, Z. Investigation on the effect of Na doping on structure and Li-ion kinetics of layered LiNi0.6Co0.2Mn0.2O2 cathode material. Electrochim. Acta 2016, 192, 120–126. [Google Scholar] [CrossRef]
- Gao, Y.; Yuan, W.; Dou, X. Improvement of the High-Performance Al-Doped LiNi1/3Co1/3Mn1/3O2 Cathode Material for New Electro-Optical Conversion Devices. Front. Phys. 2021, 9, 731851. [Google Scholar] [CrossRef]
- Du, H.; Zhang, X.; Chen, Z.; Wu, D.; Zhang, Z.; Li, J. Carbon coating and Al-doping to improve the electrochemistry of Li2CoSiO4 polymorphs as cathode materials for lithium-ion batteries. RSC Adv. 2018, 8, 22813–22822. [Google Scholar] [CrossRef]
- Zhao, W.; Zou, L.; Jia, H.; Zheng, J.; Wang, D.; Song, J.; Hong, C.; Liu, R.; Xu, W.; Yang, Y.; et al. Optimized Al Doping Improves Both Interphase Stability and Bulk Structural Integrity of Ni-Rich NMC Cathode Materials. ACS Appl. Energy Mater. 2020, 3, 3369–3377. [Google Scholar] [CrossRef]
- Kuganathan, N.; Islam, M.S. Li2MnSiO4 Lithium Battery Material: Atomic-Scale Study of Defects, Lithium Mobility, and Trivalent Dopants. Chem. Mater. 2009, 21, 5196–5202. [Google Scholar] [CrossRef]
- Duncan, H.; Aboud, D.; Maiocco, C.; Abu-Lebdeh, Y.; Davidson, I.J. Improvement of the Battery Performance of Li2MnSiO4 by Aliovalent (Al3+) Doping. ECS Meet. Abstr. 2010, MA2010-03, 483. [Google Scholar] [CrossRef]
- Kuganathan, N. Intrinsic Defects, Diffusion and Dopants in AVSi2O6 (A = Li and Na) Electrode Materials. Batteries 2022, 8, 20. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, W.; Xin, S.; Li, S.; Zhu, J.; Lü, X.; Cui, Z.; Jia, Q.; Zhou, J.; Zhou, Y.; et al. Fluorine-Doped Antiperovskite Electrolyte for All-Solid-State Lithium-Ion Batteries. Angew. Chem. Int. Ed. 2016, 55, 9965–9968. [Google Scholar] [CrossRef] [PubMed]
- Song, Q.-W.; He, L.-N. Atom Economy. In Encyclopedia of Sustainability Science and Technology; Meyers, R.A., Ed.; Springer: New York, NY, USA, 2018; pp. 1–21. [Google Scholar]
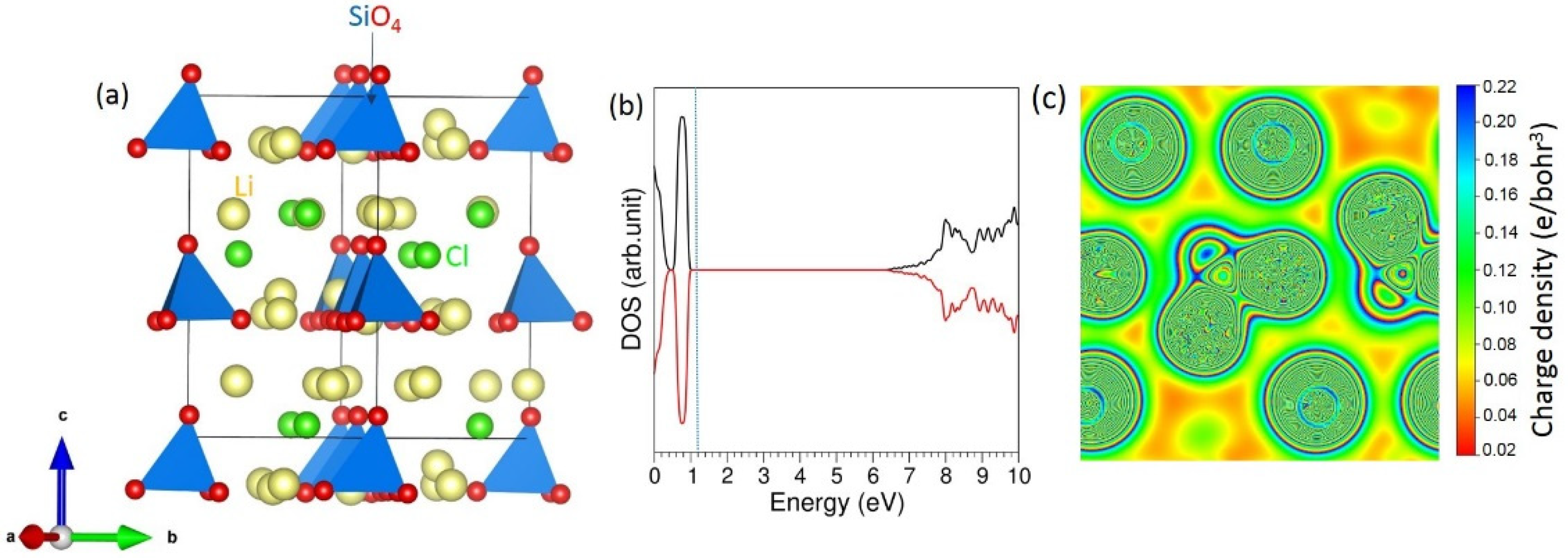

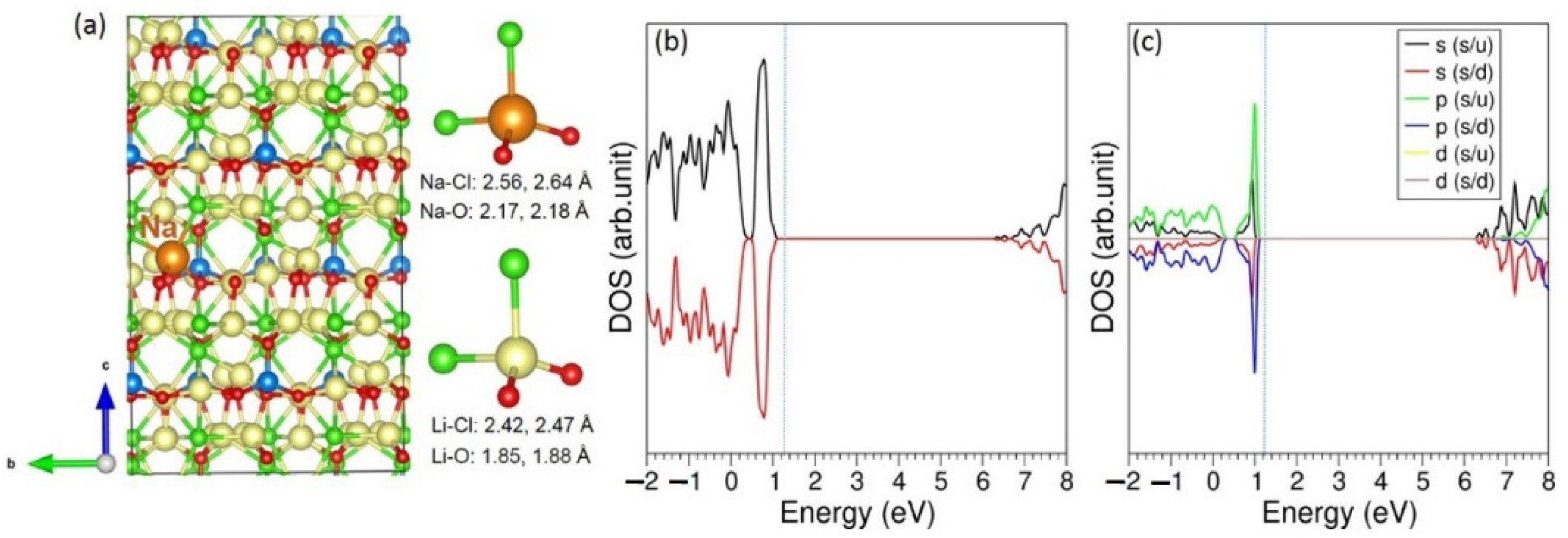
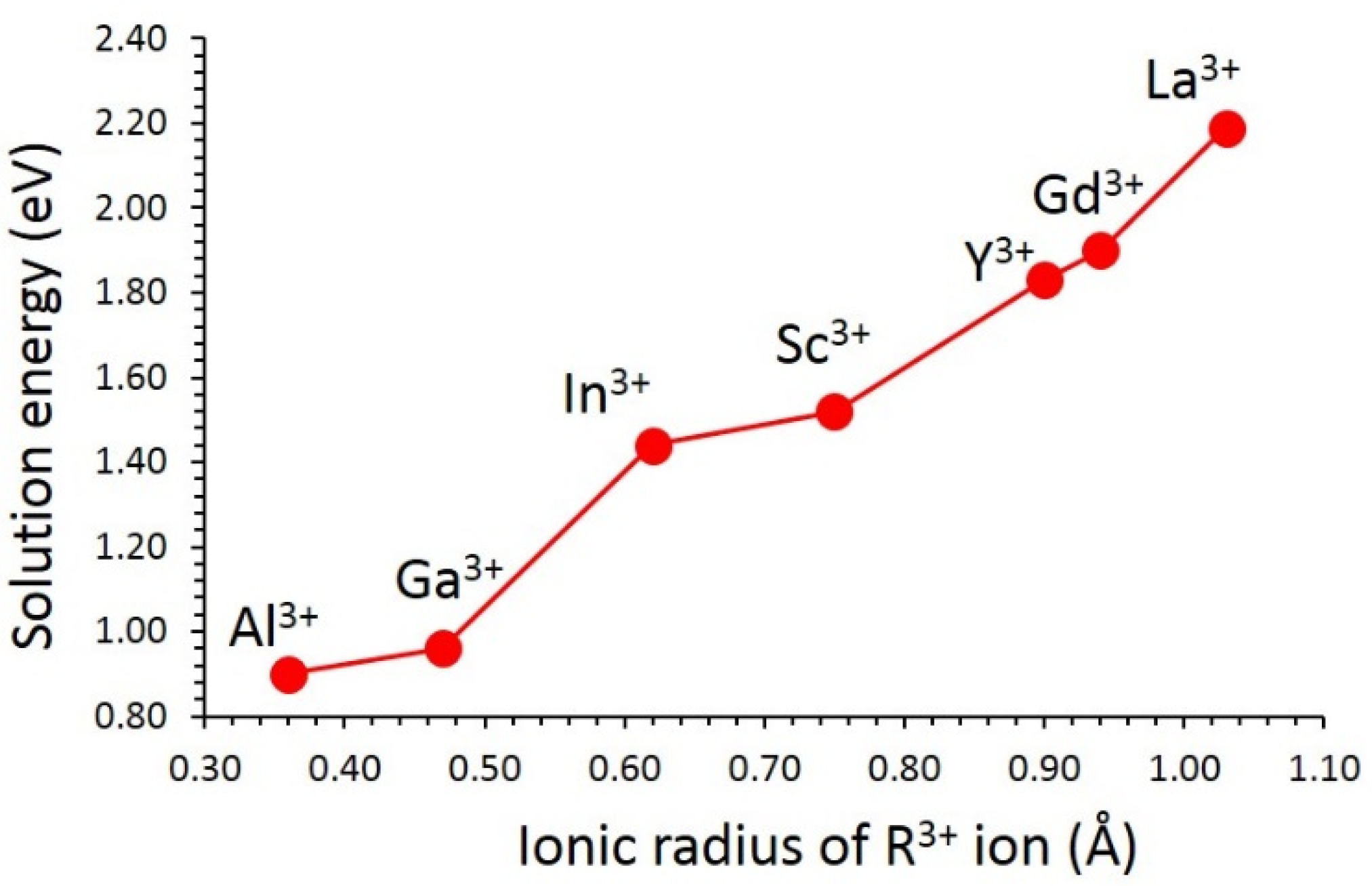
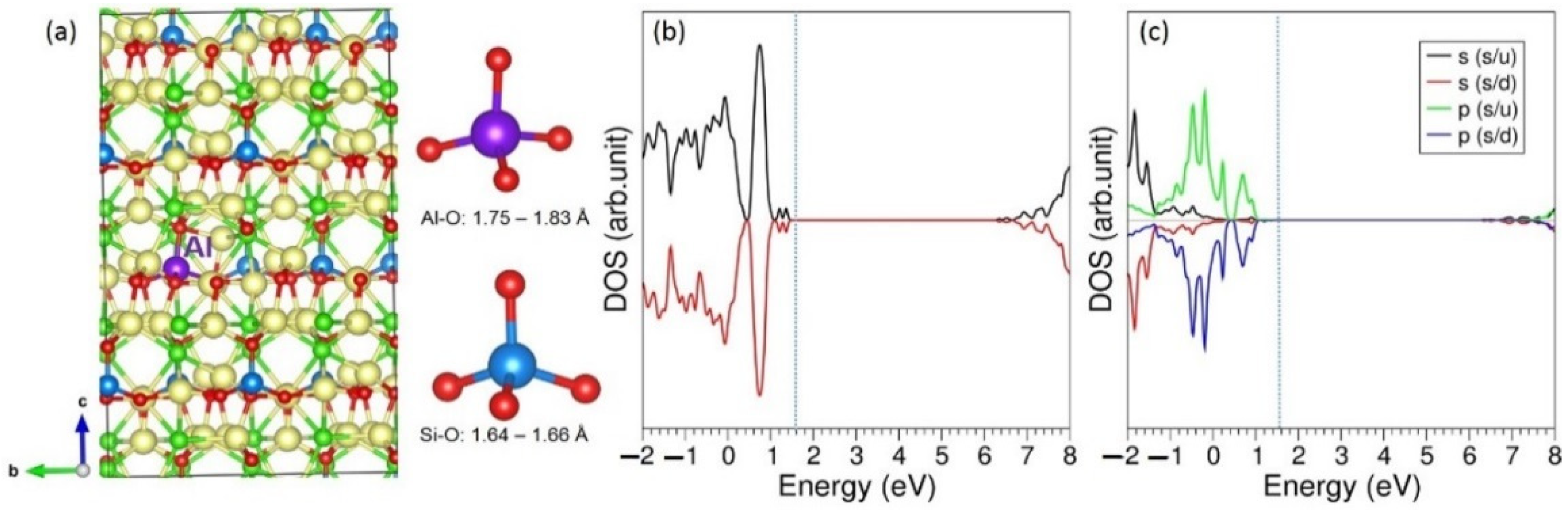
| Parameter | Calculated | Experiment [20] | |∆| (%) |
|---|---|---|---|
| a (Å) | 10.479 | 10.524 | 0.43 |
| b (Å) | 6.036 | 6.076 | 0.66 |
| c (Å) | 9.918 | 9.953 | 0.35 |
| α = β = γ (°) | 90.0 | 90.0 | 0.00 |
| V (Å3) | 627.34 | 636.17 | 0.16 |
| Atom | Bader Charge |
|---|---|
| Li | +1.00 |
| Si | +4.00 |
| O | −1.99, −2.01 |
| Cl | −0.99 |
| Defect Process | Reaction Equation | Reaction Energy/Defect (eV) |
|---|---|---|
| Li Frenkel | (1) | 2.94 |
| Si Frenkel | (2) | 10.39 |
| O Frenkel | (3) | 5.96 |
| Cl Frenkel | (4) | 3.07 |
| Schottky | (5) | 3.72 |
| Li2O Schottky | (6) | 3.22 |
| LiCl Schottky | (7) | 2.88 |
| SiO2 Schottky | (8) | 6.52 |
| O/Cl anti-site (isolated) | (9) | 3.71 |
| O/Cl anti-site (cluster) | (10) | 0.07 |
| Reaction Number | Reaction | Reaction Energy (eV) |
|---|---|---|
| 1 | Li4SiO4 + 2 LiCl → Li6SiO4Cl2 | −0.12 |
| 2 | Li2O + Li2SiO3 + 2 LiCl → Li6SiO4Cl2 | −0.68 |
| 3 | 2 Li2O + SiO2 + 2 LiCl → Li6SiO4Cl2 | −1.98 |
| 4 | Li2O + Li3OCl + SiO2 + LiCl → Li6SiO4Cl2 | −2.09 |
| 5 | 2 Li3OCl + SiO2 → Li6SiO4Cl2 | −2.20 |
| 6 | 6 Li + Si + 2 O2 + Cl2 → Li6SiO4Cl2 | −30.54 |
| Reaction | Incorporation Energy (eV)/Li | Bader Charge (|e|) | ||
|---|---|---|---|---|
| Ref: Li Atom | Ref: Li Bulk | |||
| Li + Li6SiO4Cl2 → Li•Li6SiO4Cl2 | 0.47 | 2.08 | +1.00 | 0.92 |
| 2 Li + Li6SiO4Cl2 → 2 Li•Li6SiO4Cl2 | 0.30 | 1.91 | +1.00 (2) | 1.34 |
| 3 Li + Li6SiO4Cl2 → 3 Li•Li6SiO4Cl2 | 0.28 | 1.89 | +1.00 (3) | 1.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuganathan, N. DFT Modelling of Li6SiO4Cl2 Electrolyte Material for Li-Ion Batteries. Batteries 2022, 8, 137. https://doi.org/10.3390/batteries8100137
Kuganathan N. DFT Modelling of Li6SiO4Cl2 Electrolyte Material for Li-Ion Batteries. Batteries. 2022; 8(10):137. https://doi.org/10.3390/batteries8100137
Chicago/Turabian StyleKuganathan, Navaratnarajah. 2022. "DFT Modelling of Li6SiO4Cl2 Electrolyte Material for Li-Ion Batteries" Batteries 8, no. 10: 137. https://doi.org/10.3390/batteries8100137
APA StyleKuganathan, N. (2022). DFT Modelling of Li6SiO4Cl2 Electrolyte Material for Li-Ion Batteries. Batteries, 8(10), 137. https://doi.org/10.3390/batteries8100137






