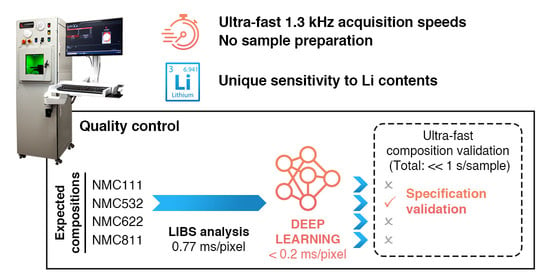
Deep Learning Classification of Li-Ion Battery Materials Targeting Accurate Composition Classification from Laser-Induced Breakdown Spectroscopy High-Speed Analyses
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation and Materials
2.2. Laser-Induced Breakdown Spectroscopy Instrumentation
2.3. Machine Learning Methods
2.3.1. Training, Testing, and Validation Sets
2.3.2. Normalization on Single Transition Lines
2.3.3. Normalization on Full Spectra
2.3.4. Angle Mapper (AM)
2.3.5. Support Vector Machine (SVM)
2.3.6. Random Forest (RF)
2.3.7. Deep Learning Architectures
2.3.8. Training and Testing Times
3. Results and Discussion
3.1. LIBS Spectra of Different Battery Materials
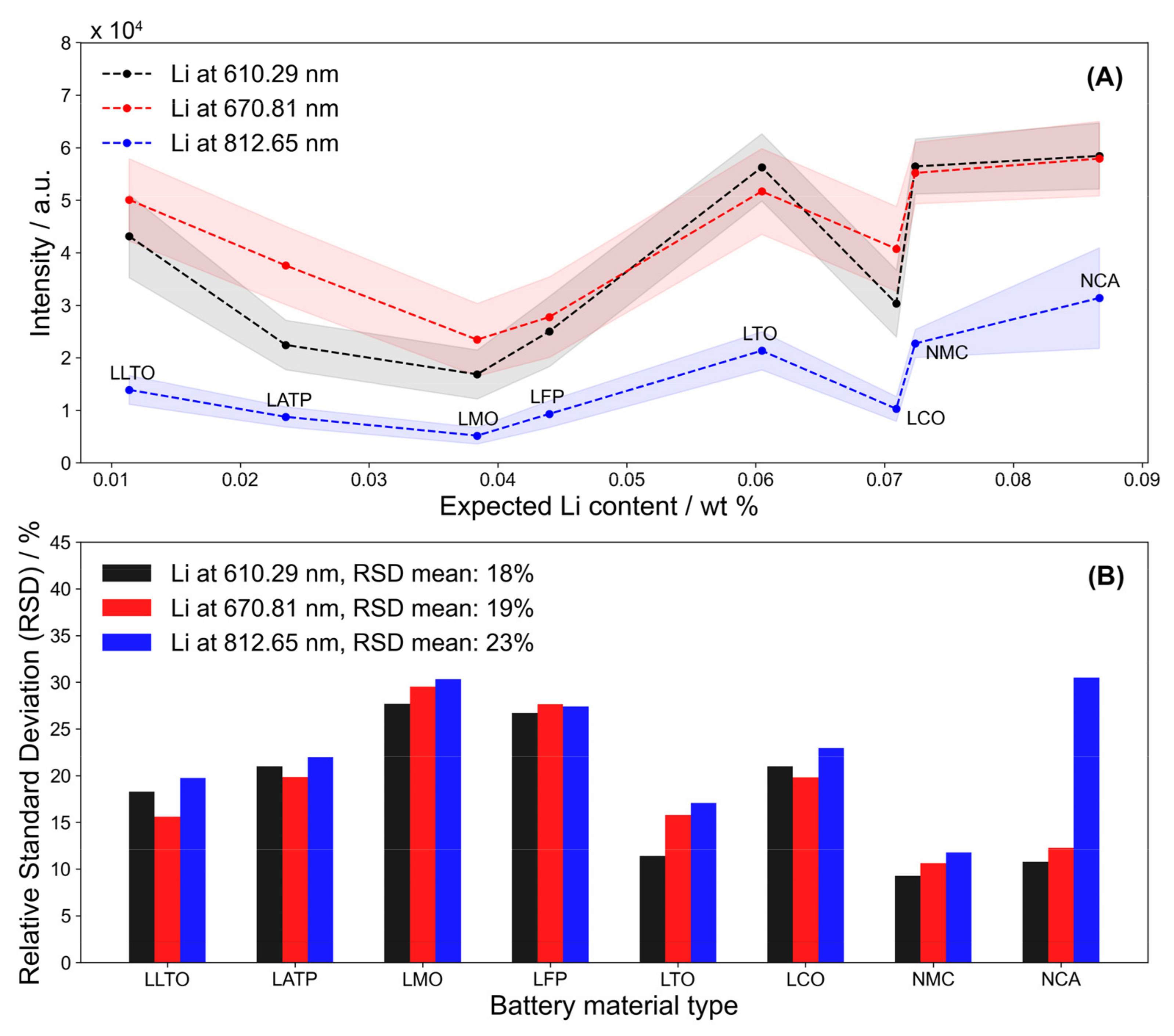
3.2. Li Transition Lines in Active Material Pellets
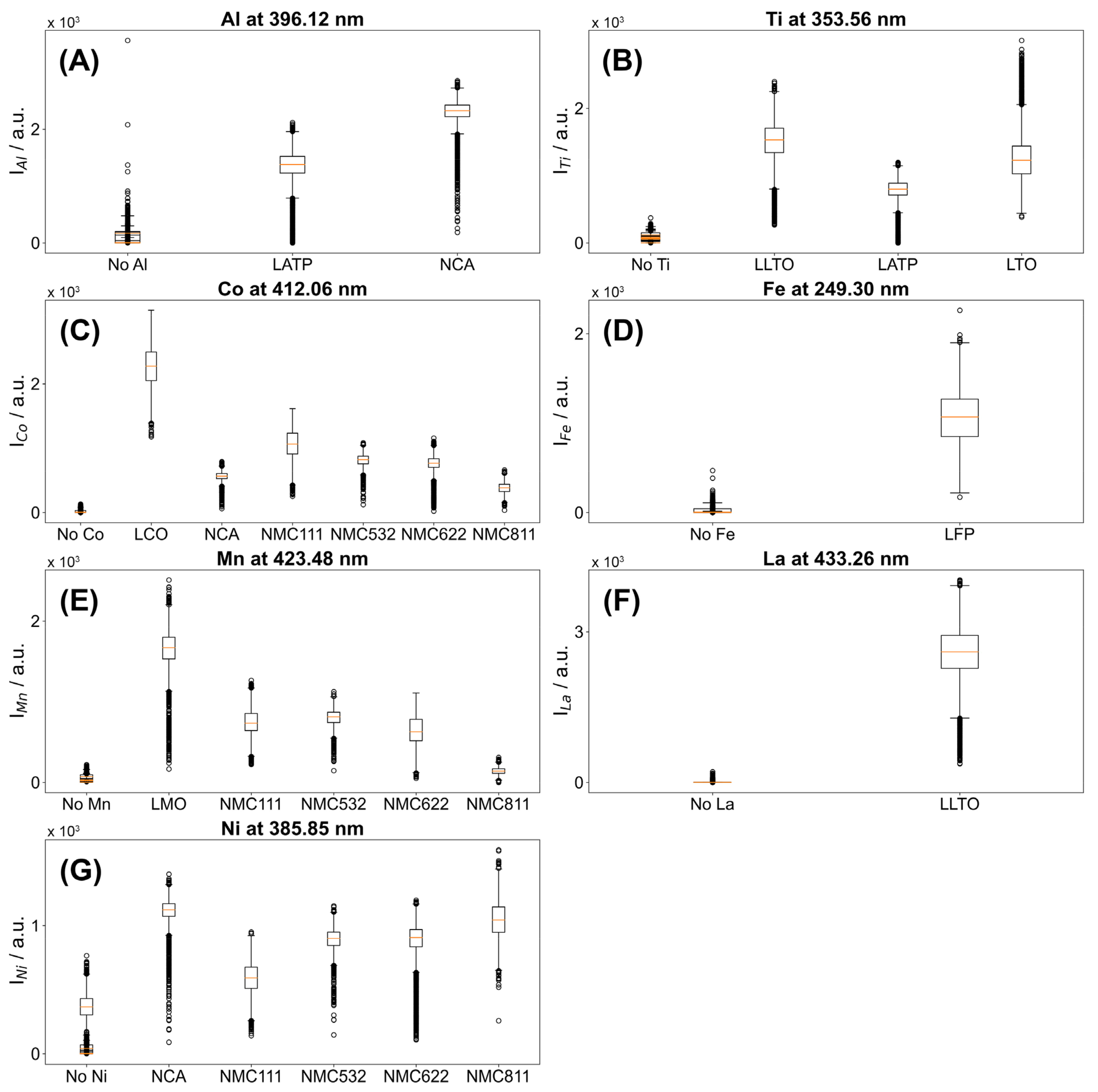
3.3. Specificity of Different Transition Lines
3.4. Linearity of Ni, Mn, and Co Transition Lines
3.5. Dimension Reduction at the Risk of Crucial Information Loss
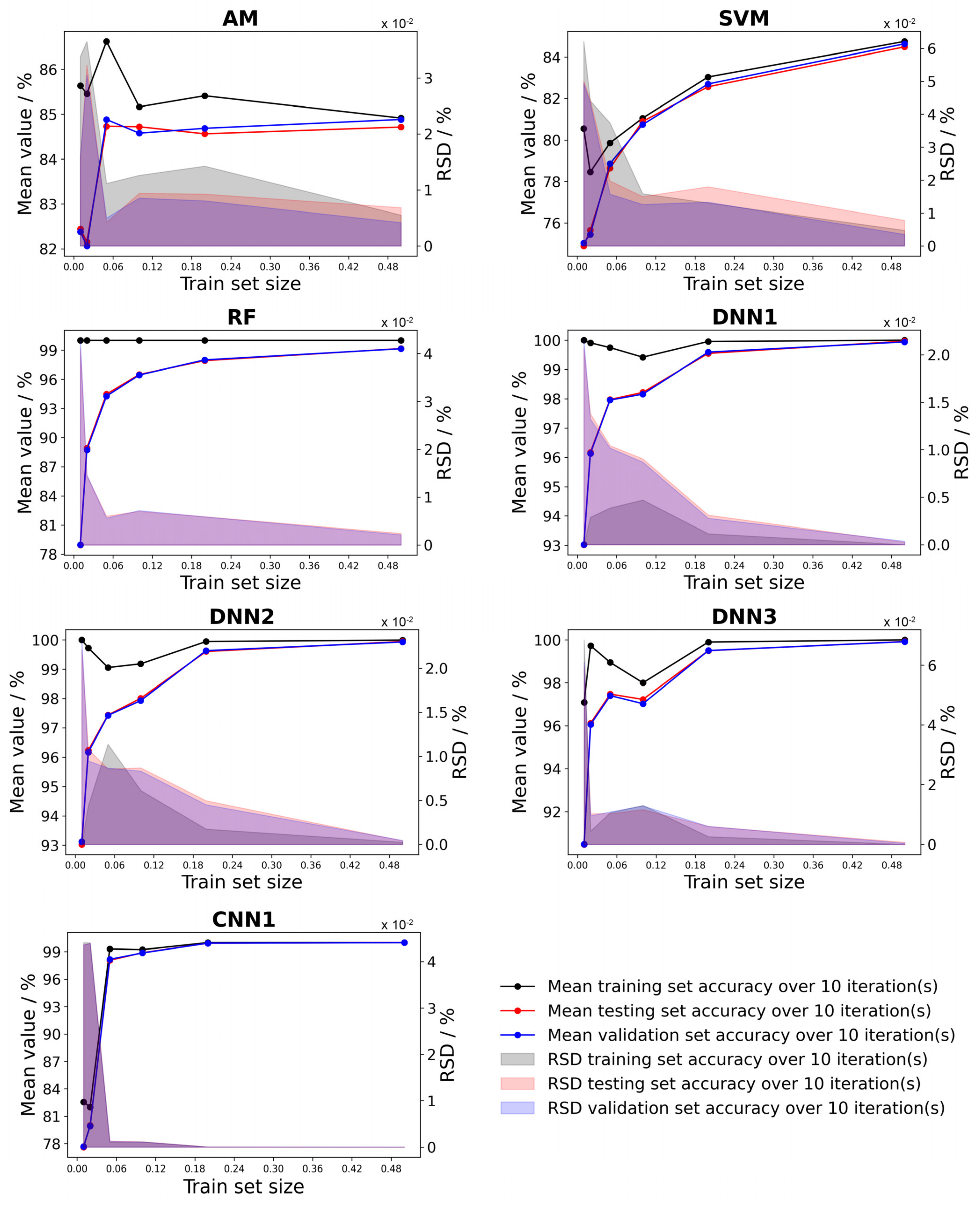
3.6. Deep Neural Network Classification
3.7. Training and Testing Times
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhu, Z.; Jiang, T.; Ali, M.; Meng, Y.; Jin, Y.; Cui, Y.; Chen, W. Rechargeable Batteries for Grid Scale Energy Storage. Chem. Rev. 2022. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Garg, A.; Zheng, J.; Gao, L.; Oh, K.Y. Battery pack recycling challenges for the year 2030: Recommended solutions based on intelligent robotics for safe and efficient disassembly, residual energy detection, and secondary utilization. Energy Storage 2020, 3, e190. [Google Scholar] [CrossRef]
- Lu, Y.; Han, X.; Li, Z. Enabling Intelligent Recovery of Critical Materials from Li-Ion Battery through Direct Recycling Process with Internet-of-Things. Materials 2021, 14, 7153. [Google Scholar] [CrossRef] [PubMed]
- Paradis, M.-C.M.; Doucet, F.R.; Rifai, K.; Özcan, L.Ç.; Azami, N.; Vidal, F. ECORE: A New Fast Automated Quantitative Mineral and Elemental Core Scanner. Minerals 2021, 11, 859. [Google Scholar] [CrossRef]
- Rifai, K.; Michaud Paradis, M.-C.; Swierczek, Z.; Doucet, F.; Özcan, L.; Fayad, A.; Li, J.; Vidal, F. Emergences of New Technology for Ultrafast Automated Mineral Phase Identification and Quantitative Analysis Using the CORIOSITY Laser-Induced Breakdown Spectroscopy (LIBS) System. Minerals 2020, 10, 918. [Google Scholar] [CrossRef]
- Rifai, K.; Constantin, M.; Yilmaz, A.; Özcan, L.Ç.; Doucet, F.R.; Azami, N. Quantification of Lithium and Mineralogical Mapping in Crushed Ore Samples Using Laser Induced Breakdown Spectroscopy. Minerals 2022, 12, 253. [Google Scholar] [CrossRef]
- Pamu, R.; Davari, S.A.; Darbar, D.; Self, E.C.; Nanda, J.; Mukherjee, D. Calibration-Free Quantitative Analysis of Lithium-Ion Battery (LiB) Electrode Materials Using Laser-Induced Breakdown Spectroscopy (LIBS). ACS Appl. Energy Mater. 2021, 4, 7259–7267. [Google Scholar] [CrossRef]
- Imashuku, S.; Taguchi, H.; Kawamata, T.; Fujieda, S.; Kashiwakura, S.; Suzuki, S.; Wagatsuma, K. Quantitative lithium mapping of lithium-ion battery cathode using laser-induced breakdown spectroscopy. J. Power Sources 2018, 399, 186–191. [Google Scholar] [CrossRef]
- Smyrek, P.; Zheng, Y.; Rakebrandt, J.-H.; Seifert, H.J.; Pfleging, W. Investigation of Micro-Structured Li(Ni1/3Mn1/3Co1/3)O2 Cathodes by Laser-Induced Breakdown Spectroscopy. In Proceedings of the SPIE LASE, San Francisco, CA, USA, 17 February 2017. [Google Scholar] [CrossRef]
- Smyrek, P.; Bergfeldt, T.; Seifert, H.J.; Pfleging, W. Laser-induced breakdown spectroscopy for the quantitative measurement of lithium concentration profiles in structured and unstructured electrodes. J. Mater. Chem. A 2019, 7, 5656–5665. [Google Scholar] [CrossRef]
- Smyrek, P.; Pröll, J.; Seifert, H.J.; Pfleging, W. Laser-Induced Breakdown Spectroscopy of Laser-Structured Li(NiMnCo)O2Electrodes for Lithium-Ion Batteries. J. Electrochem. Soc. 2015, 163, A19–A26. [Google Scholar] [CrossRef]
- Smyrek, P.; Zheng, Y.; Seifert, H.J.; Pfleging, W. Post-mortem characterization of fs laser-generated micro-pillars in Li(Ni1/3Mn1/3Co1/3)O2 electrodes by laser-induced breakdown spectroscopy. In Proceedings of the SPIE LASE, San Francisco, CA, USA, 18 March 2016. [Google Scholar] [CrossRef]
- Zorba, V.; Syzdek, J.; Mao, X.; Russo, R.E.; Kostecki, R. Ultrafast laser induced breakdown spectroscopy of electrode/electrolyte interfaces. Appl. Phys. Lett. 2012, 100, 234101. [Google Scholar] [CrossRef]
- Zheng, Y.; Pfäffl, L.; Seifert, H.J.; Pfleging, W. Lithium Distribution in Structured Graphite Anodes Investigated by Laser-Induced Breakdown Spectroscopy. Appl. Sci. 2019, 9, 4218. [Google Scholar] [CrossRef]
- Imashuku, S.; Taguchi, H.; Fujieda, S.; Suzuki, S.; Wagatsuma, K. Three-dimensional lithium mapping of graphite anode using laser-induced breakdown spectroscopy. Electrochim. Acta 2019, 293, 78–83. [Google Scholar] [CrossRef]
- Hou, H.; Cheng, L.; Richardson, T.; Chen, G.; Doeff, M.; Zheng, R.; Russo, R.; Zorba, V. Three-dimensional elemental imaging of Li-ion solid-state electrolytes using fs-laser induced breakdown spectroscopy (LIBS). J. Anal. At. Spectrom. 2015, 30, 2295–2302. [Google Scholar] [CrossRef]
- Peng, L.; Sun, D.; Su, M.; Han, J.; Dong, C. Rapid analysis on the heavy metal content of spent zinc–manganese batteries by laser-induced breakdown spectroscopy. Opt. Laser Technol. 2012, 44, 2469–2475. [Google Scholar] [CrossRef]
- Costa, V.C.; de Mello, M.L.; Babos, D.V.; Castro, J.P.; Pereira-Filho, E.R. Calibration strategies for determination of Pb content in recycled polypropylene from car batteries using laser-induced breakdown spectroscopy (LIBS). Microchem. J. 2020, 159, 105558. [Google Scholar] [CrossRef]
- Meima, J.A.; Rammlmair, D. Investigation of compositional variations in chromitite ore with imaging Laser Induced Breakdown Spectroscopy and Spectral Angle Mapper classification algorithm. Chem. Geol. 2020, 532, 119376. [Google Scholar] [CrossRef]
- Han, L.; Liu, F.; Zhang, L. An Improved Sub-Model PLSR Quantitative Analysis Method Based on SVM Classifier for ChemCam Laser-Induced Breakdown Spectroscopy. Symmetry 2021, 13, 319. [Google Scholar] [CrossRef]
- Yang, H.-X.; Fu, H.-B.; Wang, H.-D.; Jia, J.-W.; Sigrist, M.W.; Dong, F.-Z. Laser-induced breakdown spectroscopy applied to the characterization of rock by support vector machine combined with principal component analysis. Chin. Phys. B 2016, 25, 065201. [Google Scholar] [CrossRef]
- Janovszky, P.; Jancsek, K.; Palásti, D.J.; Kopniczky, J.; Hopp, B.; Tóth, T.M.; Galbács, G. Classification of minerals and the assessment of lithium and beryllium content in granitoid rocks by laser-induced breakdown spectroscopy. J. Anal. At. Spectrom. 2021, 36, 813–823. [Google Scholar] [CrossRef]
- Koujelev, A.; Sabsabi, M.; Motto-Ros, V.; Laville, S.; Lui, S.L. Laser-induced breakdown spectroscopy with artificial neural network processing for material identification. Planet. Space Sci. 2010, 58, 682–690. [Google Scholar] [CrossRef]
- Yang, Y.; Li, C.; Liu, S.; Min, H.; Yan, C.; Yang, M.; Yu, J. Classification and identification of brands of iron ores using laser-induced breakdown spectroscopy combined with principal component analysis and artificial neural networks. Anal. Methods 2020, 12, 1316–1323. [Google Scholar] [CrossRef]
- Chen, J.; Pisonero, J.; Chen, S.; Wang, X.; Fan, Q.; Duan, Y. Convolutional neural network as a novel classification approach for laser-induced breakdown spectroscopy applications in lithological recognition. Spectrochim. Acta Part B At. Spectrosc. 2020, 166, 105801. [Google Scholar] [CrossRef]
- Chen, T.; Sun, L.; Yu, H.; Wang, W.; Qi, L.; Zhang, P.; Zeng, P. Deep learning with laser-induced breakdown spectroscopy (LIBS) for the classification of rocks based on elemental imaging. Appl. Geochem. 2022, 136, 105135. [Google Scholar] [CrossRef]
- Li, L.-N.; Liu, X.-F.; Xu, W.-M.; Wang, J.-Y.; Shu, R. A laser-induced breakdown spectroscopy multi-component quantitative analytical method based on a deep convolutional neural network. Spectrochim. Acta Part B At. Spectrosc. 2020, 169, 105850. [Google Scholar] [CrossRef]
- Castorena, J.; Oyen, D.; Ollila, A.; Legget, C.; Lanza, N. Deep spectral CNN for laser induced breakdown spectroscopy. Spectrochim. Acta Part B At. Spectrosc. 2021, 178, 106125. [Google Scholar] [CrossRef]
- Zhao, W.; Li, C.; Yan, C.; Min, H.; An, Y.; Liu, S. Interpretable deep learning-assisted laser-induced breakdown spectroscopy for brand classification of iron ores. Anal. Chim. Acta 2021, 1166, 338574. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J. NIST Atomic Spectra Database (ver. 5.9); NIST: Gaithersburg, MD, USA, 2021. [Google Scholar] [CrossRef]




| Material Acronym | Empirical Formula | Use | Provenance |
|---|---|---|---|
| LATP | Li1.3Al0.3Ti1.7(PO4)3 | Solid-state electrolytes | Commercial manufacturer |
| LLTO | La0.57Li0.29TiO3 | Commercial manufacturer | |
| LFP | LiFePO4 | Cathode active material | Commercial manufacturer |
| LTO | Li4Ti5O12 | Commercial manufacturer | |
| LCO | LiCoO2 | Commercial manufacturer | |
| LMO | LiMn2O4 | Commercial manufacturer | |
| NCA | LiNiCoAlO2 | Commercial manufacturer | |
| NMC111-M1 | LiNi0.33Mn0.33Co0.33O2 | Commercial manufacturer 1 | |
| NMC111-M2 | LiNi0.33Mn0.33Co0.33O2 | Commercial manufacturer 2 | |
| NMC111-M3 | LiNi0.33Mn0.33Co0.33O2 | Commercial manufacturer 3 | |
| NMC532-M1 | LiNi0.5Mn0.3Co0.2O2 | Commercial manufacturer 1 | |
| NMC532-M2 | LiNi0.5Mn0.3Co0.2O2 | Commercial manufacturer 2 | |
| NMC622-M1 | LiNi0.6Mn0.2Co0.2O2 | Commercial manufacturer 1 | |
| NMC622-M2 | LiNi0.6Mn0.2Co0.2O2 | Commercial manufacturer 2 | |
| NMC811 + Nb coating | LiNi0.8Mn0.1Co0.1O2 + Nb | Commercial manufacturer |
| Laser energy | 1 mJ/pulse |
| Laser source wavelength | 1064 nm |
| Acquisition rate | 1300 Hz |
| Spatial resolution | 50 µm |
| Rayleigh zone (depth of field) | 6 mm |
| Working distance (optical window-sample surface) | 250 mm |
| Dwell time | 770 µs |
| Step size | 50 µm |
| Surface analyzed | 0.5 cm2 |
| Scanning speed in real time | 0.77 ms/pixel |
| Train Set Size | Samples in the Train Set | Samples in the Test Set | Samples in the Validation Set |
|---|---|---|---|
| 0.01 | 5 | 495 | 500 |
| 0.02 | 10 | 490 | 500 |
| 0.05 | 25 | 475 | 500 |
| 0.10 | 50 | 450 | 500 |
| 0.20 | 100 | 400 | 500 |
| 0.50 | 250 | 250 | 500 |
| Angle Mapper (AM) |
|
| Support Vector Machine (SVM) |
|
| Random Forest (RF) |
|
| Deep Neural Networks 1 (DNN1) |
|
| Deep Neural Networks 2 (DNN2) |
|
| Deep Neural Networks 3 (DNN3) |
|
| Convolutional Neural Networks (CNN1) |
|
| Element | Transition/nm |
|---|---|
| Li | 610.29 |
| Al | 396.12 |
| Ti | 353.56 |
| Co | 412.06 |
| Fe | 249.30 |
| Mn | 423.48 |
| La | 433.26 |
| Ni | 385.85 |
| Algorithm | Train Set: 1% Test Set: 99% | Train Set: 5% Test Set: 95% | Train Set: 20% Test Set: 80% | Train Set: 50% Test Set: 50% | |||||
|---|---|---|---|---|---|---|---|---|---|
| Train Set | Validation Set | Train Set | Validation Set | Train Set | Validation Set | Train Set | Validation Set | ||
| AM | Mean accuracy/% | 9.09 | 9.09 | 9.16 | 9.09 | 9.09 | 9.09 | 9.09 | 9.09 |
| RSD/% | <0.01 | <0.01 | 0.02 | <0.01 | <0.01 | <0.01 | <0.01 | <0.01 | |
| SVM | Mean accuracy/% | 75.82 | 66.87 | 61.75 | 61.25 | 59.69 | 58.65 | 59.69 | 58.65 |
| RSD/% | 0.06 | 0.11 | 0.09 | 0.08 | 0.03 | 0.06 | 0.04 | 0.05 | |
| RF | Mean accuracy/% | 100.00 | 87.77 | 100.00 | 94.57 | 100.00 | 96.26 | 100.00 | 96.81 |
| RSD/% | <0.01 | 0.02 | <0.01 | 0.01 | <0.01 | <0.01 | <0.01 | <0.01 | |
| DNN1 | Mean accuracy/% | 97.09 | 94.96 | 96.07 | 95.46 | 96.38 | 95.81 | 96.16 | 96.03 |
| RSD/% | 0.02 | <0.01 | 0.01 | <0.01 | 0.01 | <0.01 | 0.01 | <0.01 | |
| Algorithm | Train Set: 1% Test Set: 99% | Train Set: 5% Test Set: 95% | Train Set: 20% Test Set: 80% | Train Set: 50% Test Set: 50% | |||||
|---|---|---|---|---|---|---|---|---|---|
| Train Set | Validation Set | Train Set | Validation Set | Train Set | Validation Set | Train Set | Validation Set | ||
| AM | Mean accuracy/% | 85.64 | 82.38 | 86.62 | 84.88 | 85.41 | 84.68 | 84.91 | 84.88 |
| RSD/% | 0.03 | 0.02 | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | <0.01 | |
| SVM | Mean accuracy/% | 80.55 | 75.04 | 79.85 | 78.86 | 83.04 | 82.70 | 84.75 | 84.63 |
| RSD/% | 0.06 | 0.05 | 0.04 | 0.02 | 0.01 | 0.01 | <0.01 | <0.01 | |
| RF | Mean accuracy/% | 100.00 | 78.97 | 100.00 | 94.27 | 100.00 | 97.99 | 100.00 | 99.14 |
| RSD/% | <0.01 | 0.04 | <0.01 | 0.01 | <0.01 | 0.01 | <0.01 | <0.01 | |
| DNN1 | Mean accuracy/% | 100.00 | 93.03 | 99.75 | 97.95 | 99.95 | 99.59 | 100.00 | 99.94 |
| RSD/% | <0.01 | 0.02 | <0.01 | 0.01 | <0.01 | <0.01 | <0.01 | <0.01 | |
| DNN2 | Mean accuracy/% | 100.00 | 93.12 | 99.05 | 97.42 | 99.95 | 99.63 | 99.99 | 99.63 |
| RSD/% | <0.01 | 0.02 | 0.01 | 0.01 | <0.01 | <0.01 | <0.01 | <0.01 | |
| DNN3 | Mean accuracy/% | 97.09 | 90.49 | 98.95 | 97.41 | 99.90 | 99.50 | 100.00 | 99.92 |
| RSD/% | 0.07 | 0.06 | 0.01 | 0.01 | <0.01 | 0.01 | <0.01 | <0.01 | |
| CNN1 | Mean accuracy/% | 82.55 | 77.68 | 99.31 | 98.18 | 100.00 | 99.94 | 100.00 | 99.99 |
| RSD/% | 0.44 | 0.44 | 0.01 | 0.01 | <0.01 | <0.01 | <0.01 | <0.01 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michaud Paradis, M.-C.; Doucet, F.R.; Rousselot, S.; Hernández-García, A.; Rifai, K.; Touag, O.; Özcan, L.Ç.; Azami, N.; Dollé, M. Deep Learning Classification of Li-Ion Battery Materials Targeting Accurate Composition Classification from Laser-Induced Breakdown Spectroscopy High-Speed Analyses. Batteries 2022, 8, 231. https://doi.org/10.3390/batteries8110231
Michaud Paradis M-C, Doucet FR, Rousselot S, Hernández-García A, Rifai K, Touag O, Özcan LÇ, Azami N, Dollé M. Deep Learning Classification of Li-Ion Battery Materials Targeting Accurate Composition Classification from Laser-Induced Breakdown Spectroscopy High-Speed Analyses. Batteries. 2022; 8(11):231. https://doi.org/10.3390/batteries8110231
Chicago/Turabian StyleMichaud Paradis, Marie-Chloé, François R. Doucet, Steeve Rousselot, Alex Hernández-García, Kheireddine Rifai, Ouardia Touag, Lütfü Ç. Özcan, Nawfal Azami, and Mickaël Dollé. 2022. "Deep Learning Classification of Li-Ion Battery Materials Targeting Accurate Composition Classification from Laser-Induced Breakdown Spectroscopy High-Speed Analyses" Batteries 8, no. 11: 231. https://doi.org/10.3390/batteries8110231
APA StyleMichaud Paradis, M.-C., Doucet, F. R., Rousselot, S., Hernández-García, A., Rifai, K., Touag, O., Özcan, L. Ç., Azami, N., & Dollé, M. (2022). Deep Learning Classification of Li-Ion Battery Materials Targeting Accurate Composition Classification from Laser-Induced Breakdown Spectroscopy High-Speed Analyses. Batteries, 8(11), 231. https://doi.org/10.3390/batteries8110231