Calendar Aging of Li-Ion Cells—Experimental Investigation and Empirical Correlation
Abstract
1. Introduction
2. Experimental Setup
2.1. Boundary Conditions and Testing Procedure
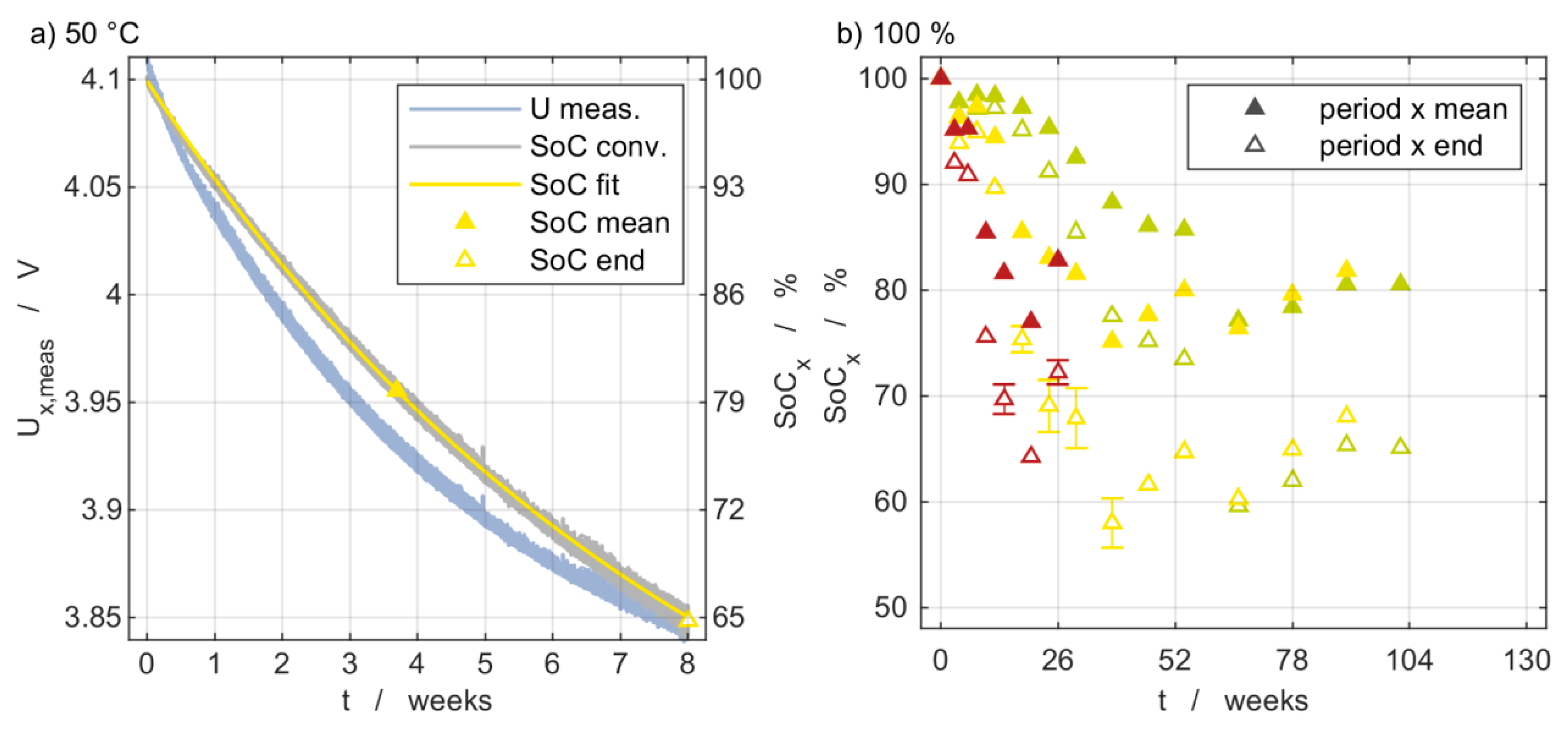
2.2. Self-Discharge during Storage
- Transferring the voltage progression into an SoC progression. Based on the OCV from the previous intermediate characterization x − 1, an SoC value is assigned to each voltage value according to Equation (2). The approach is comparable to the long-time model equations for self-discharge presented by Deutschen et al. [35].
- Fitting of the SoC decline over time according to Equation (3) This approach is in accordance with the exponential decay model describing leakage current during self-discharge presented by Redondo et al. [27].
- Calculating an equivalent mean storage SoC via integration over time.
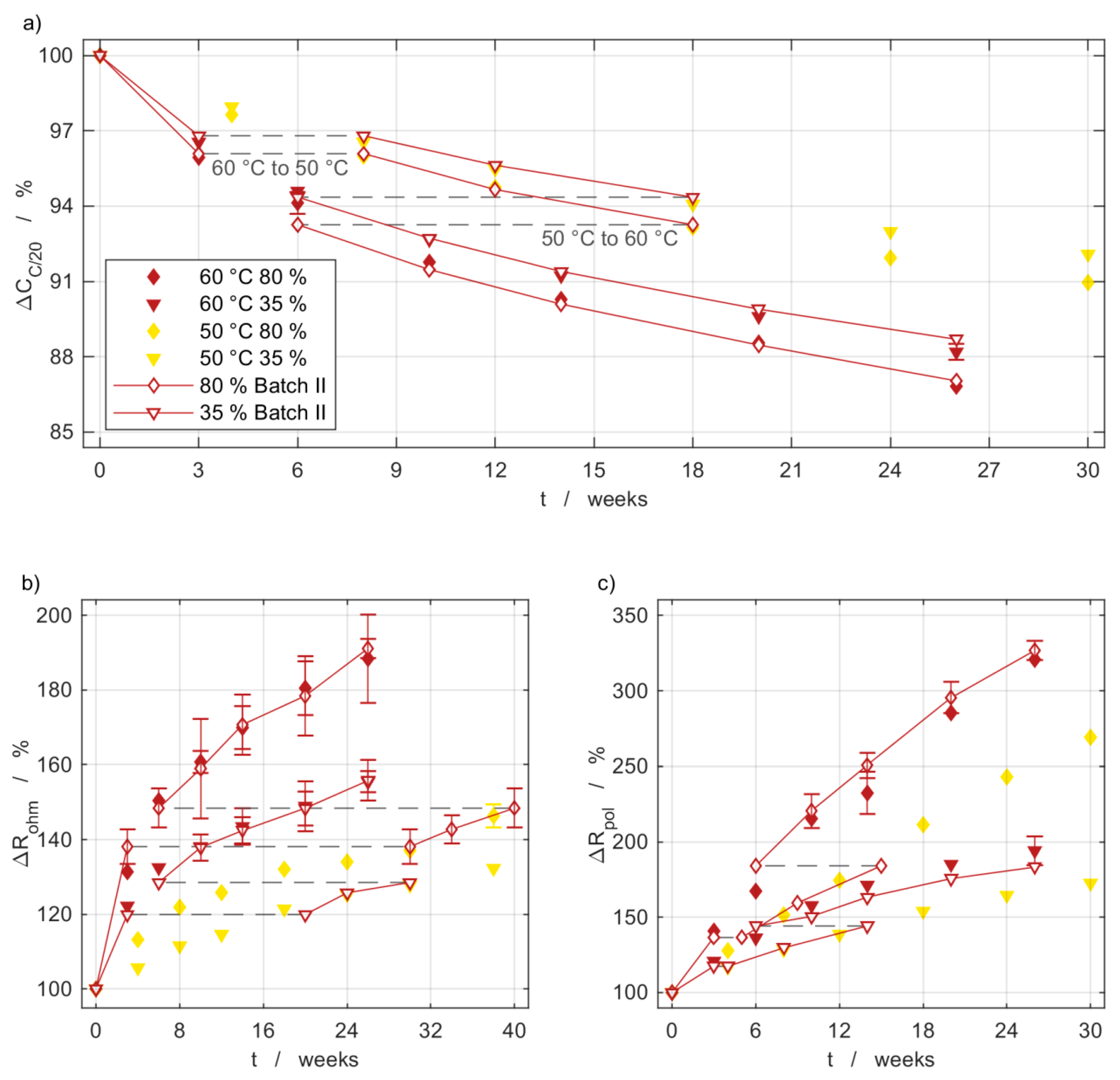
2.3. Path Dependency of Temperature Changes
3. Results and Discussion
3.1. Initial State
3.2. Self-Discharge Evaluation
3.3. Path Dependency and Reproducibility
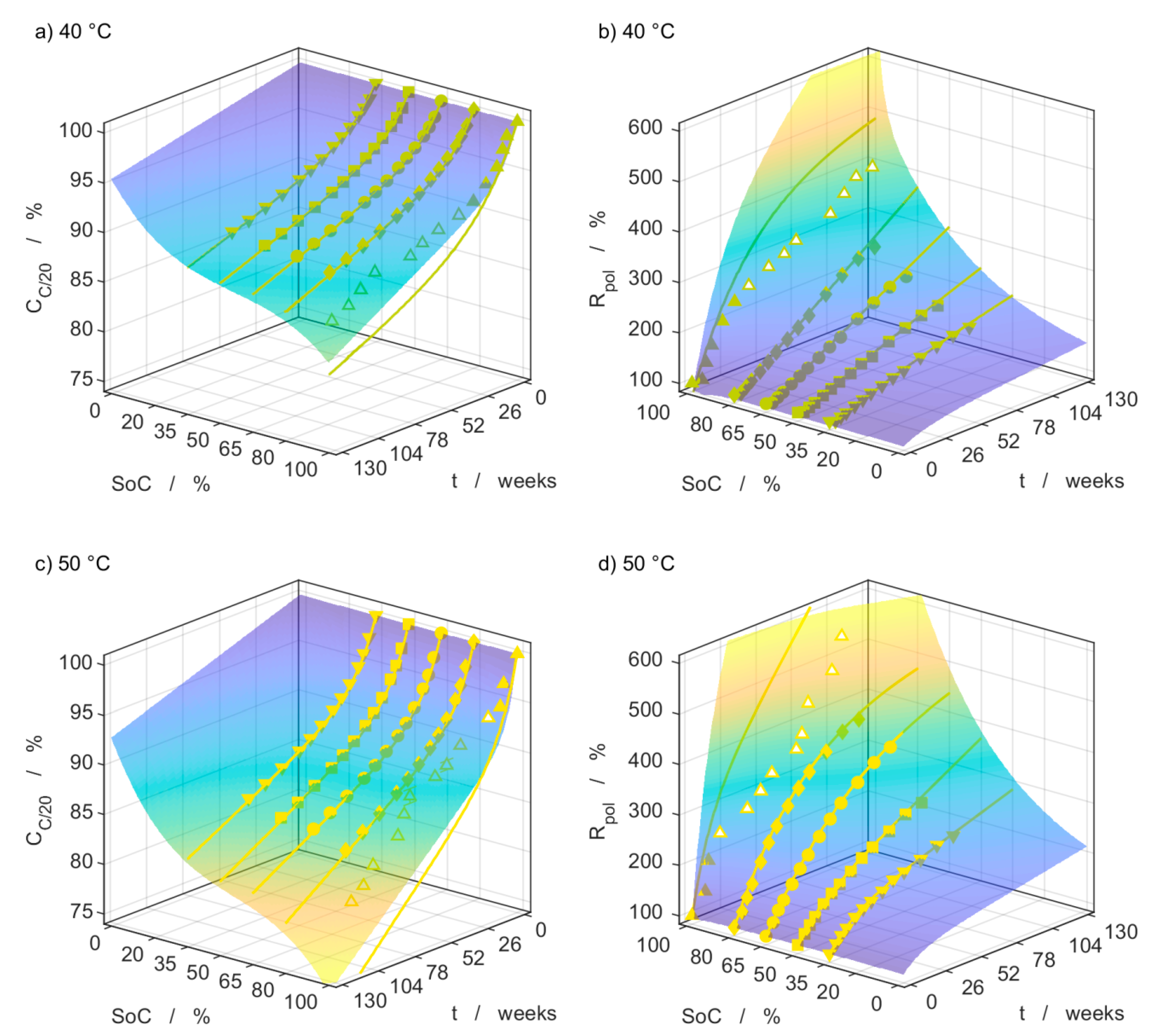
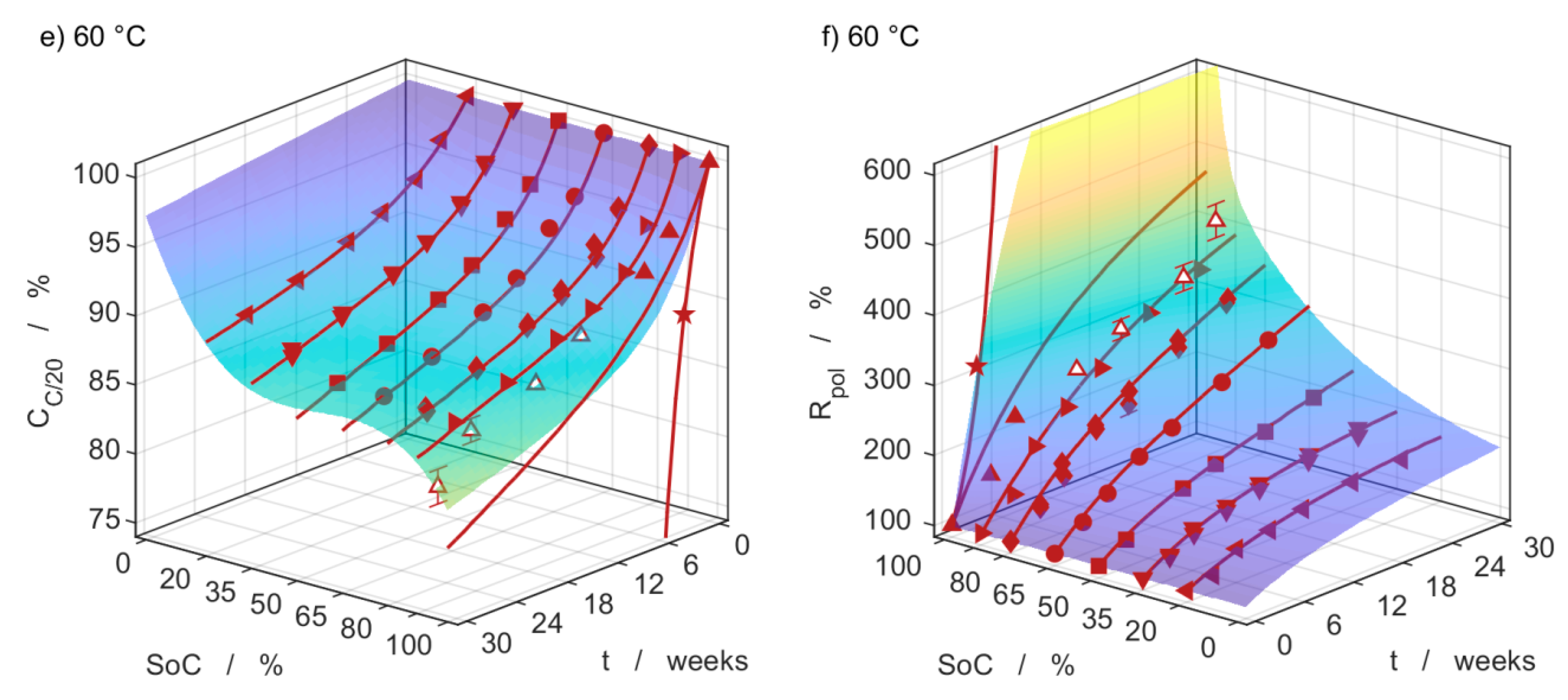
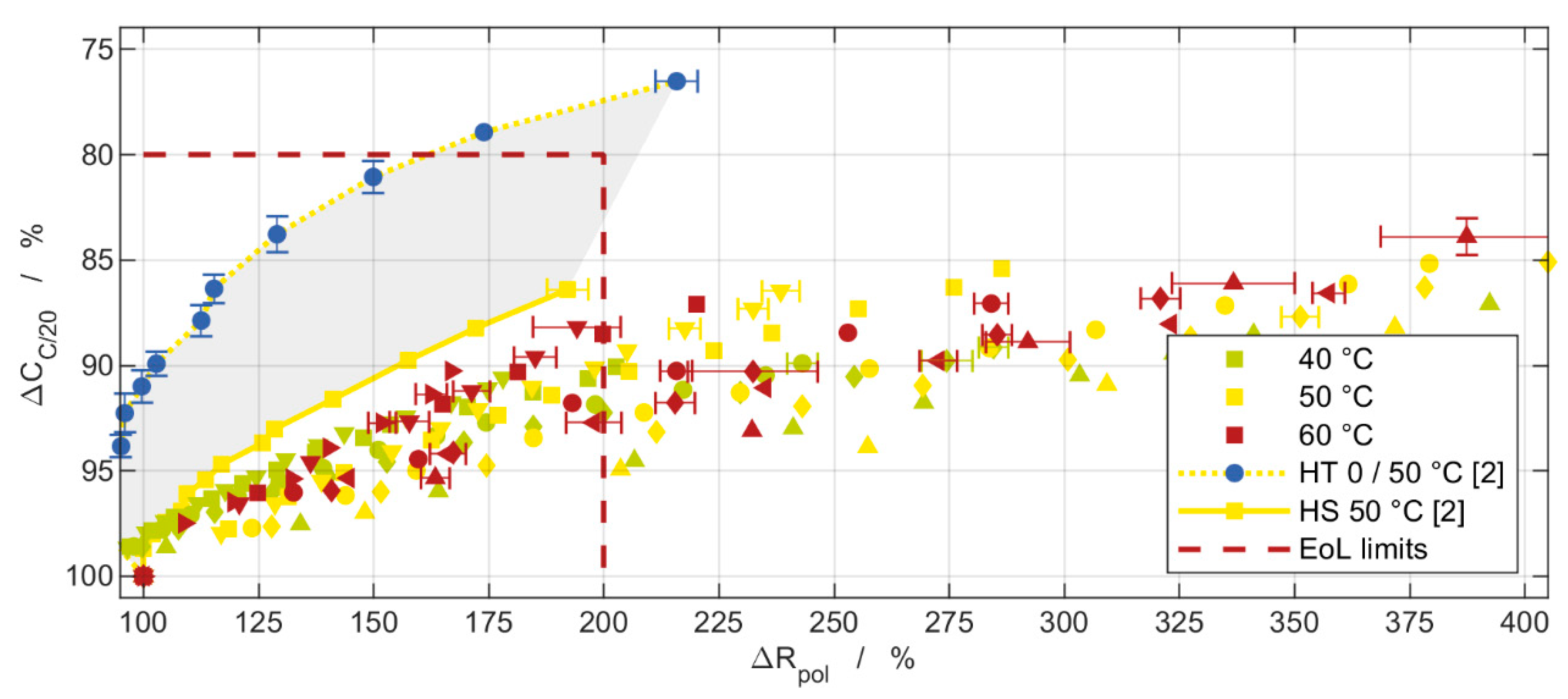
3.4. Capacity Measurements
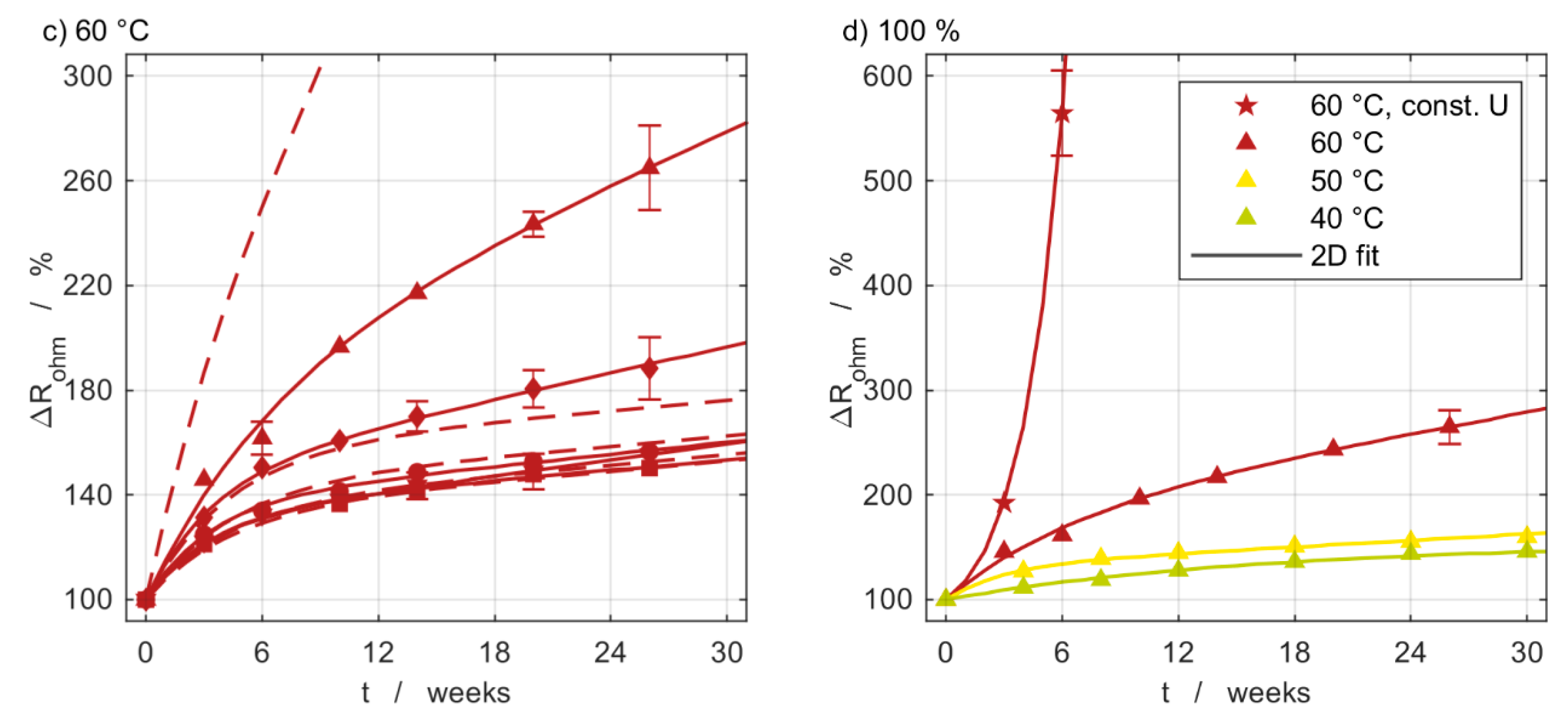
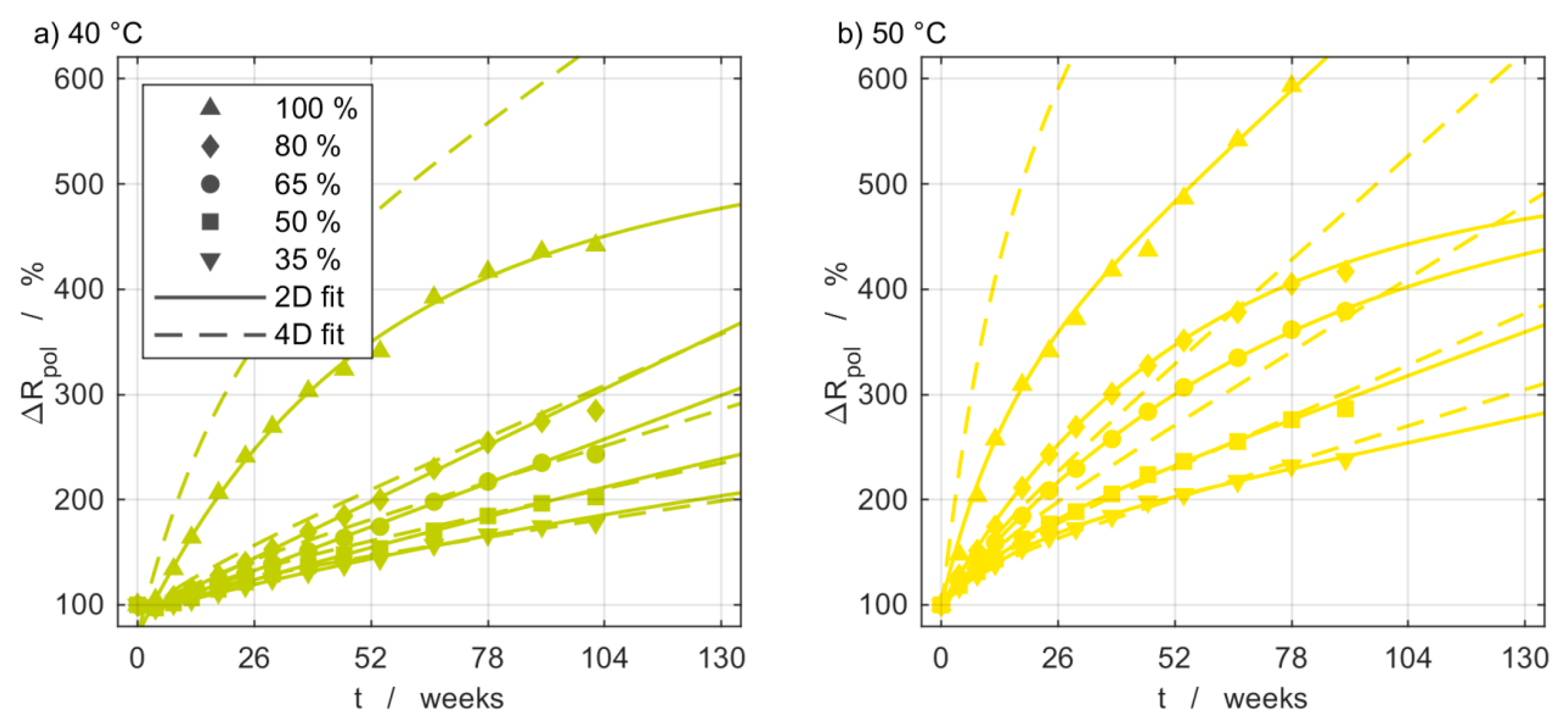
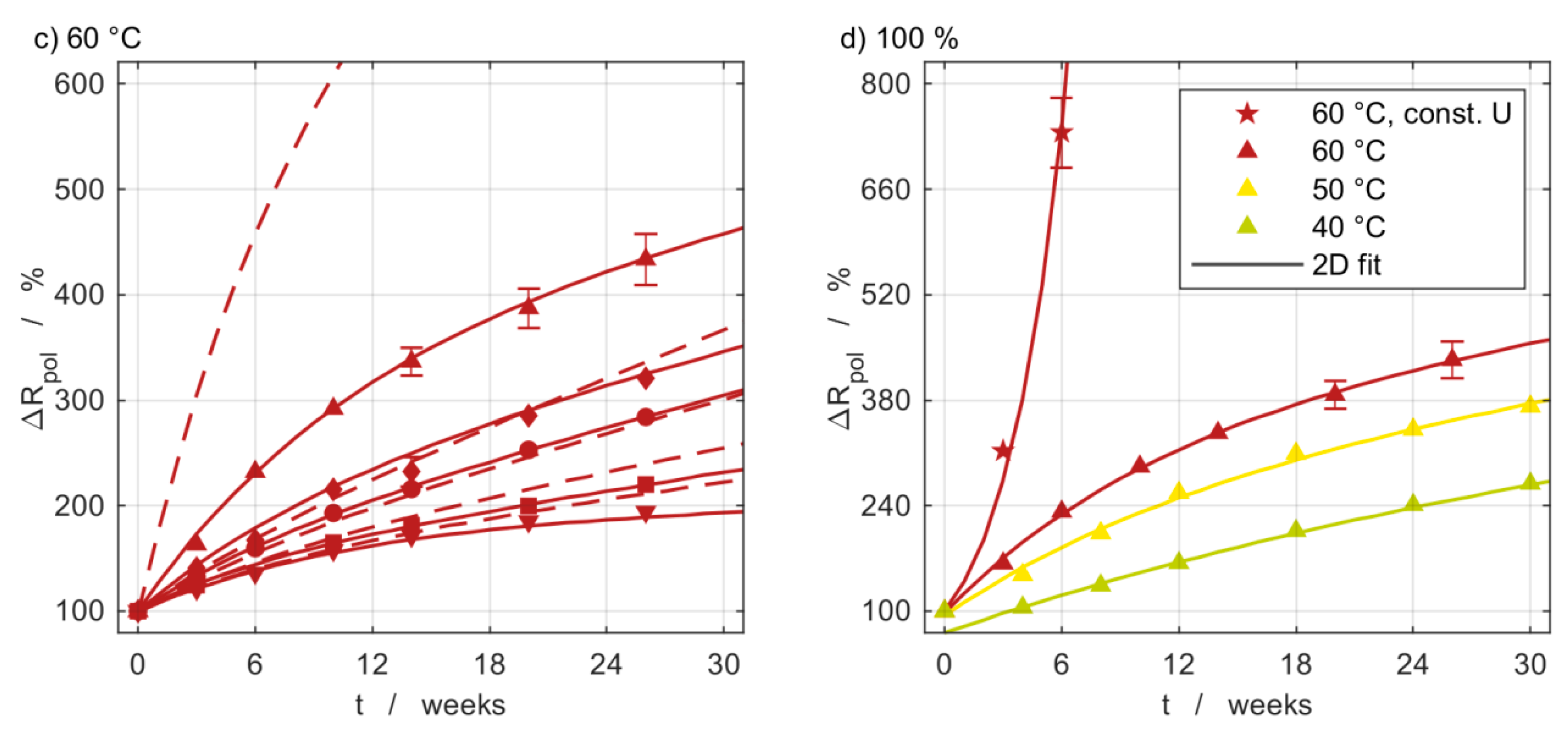
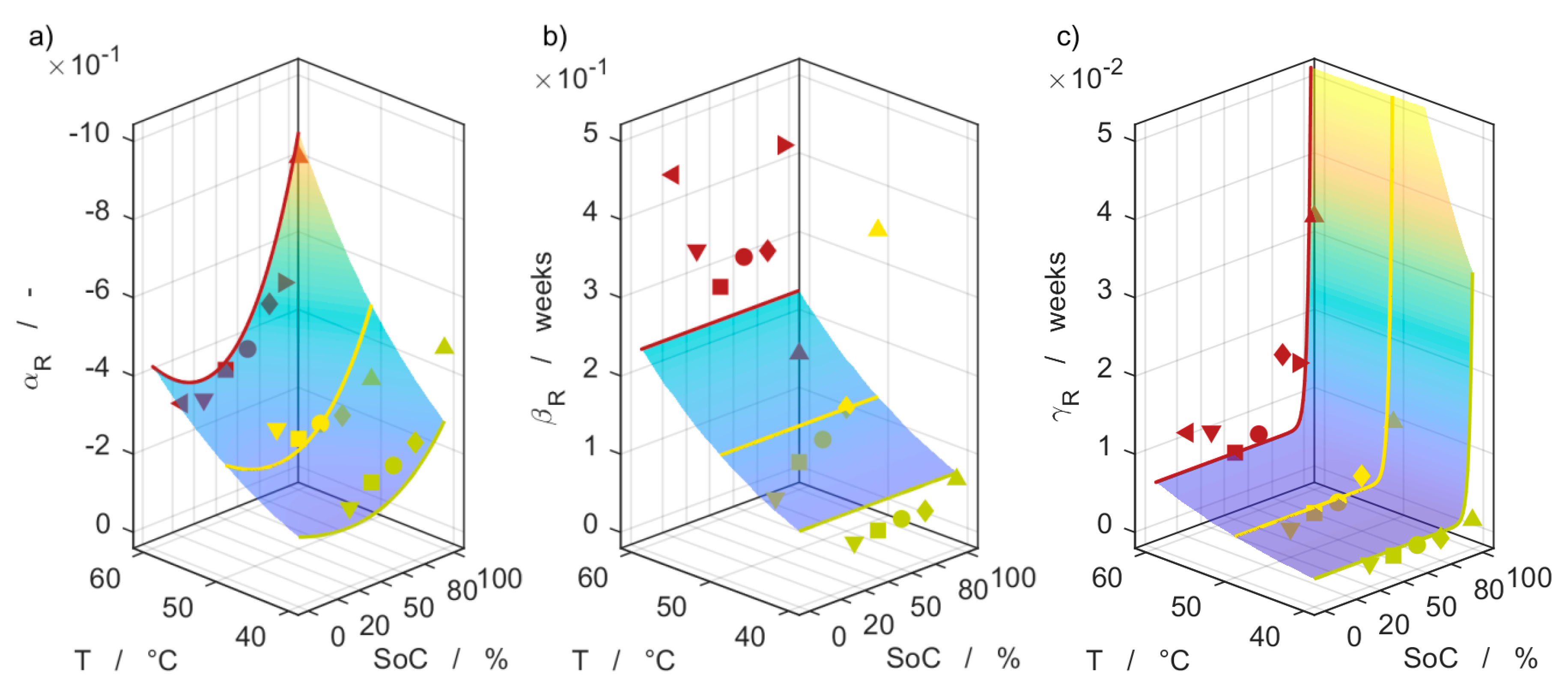
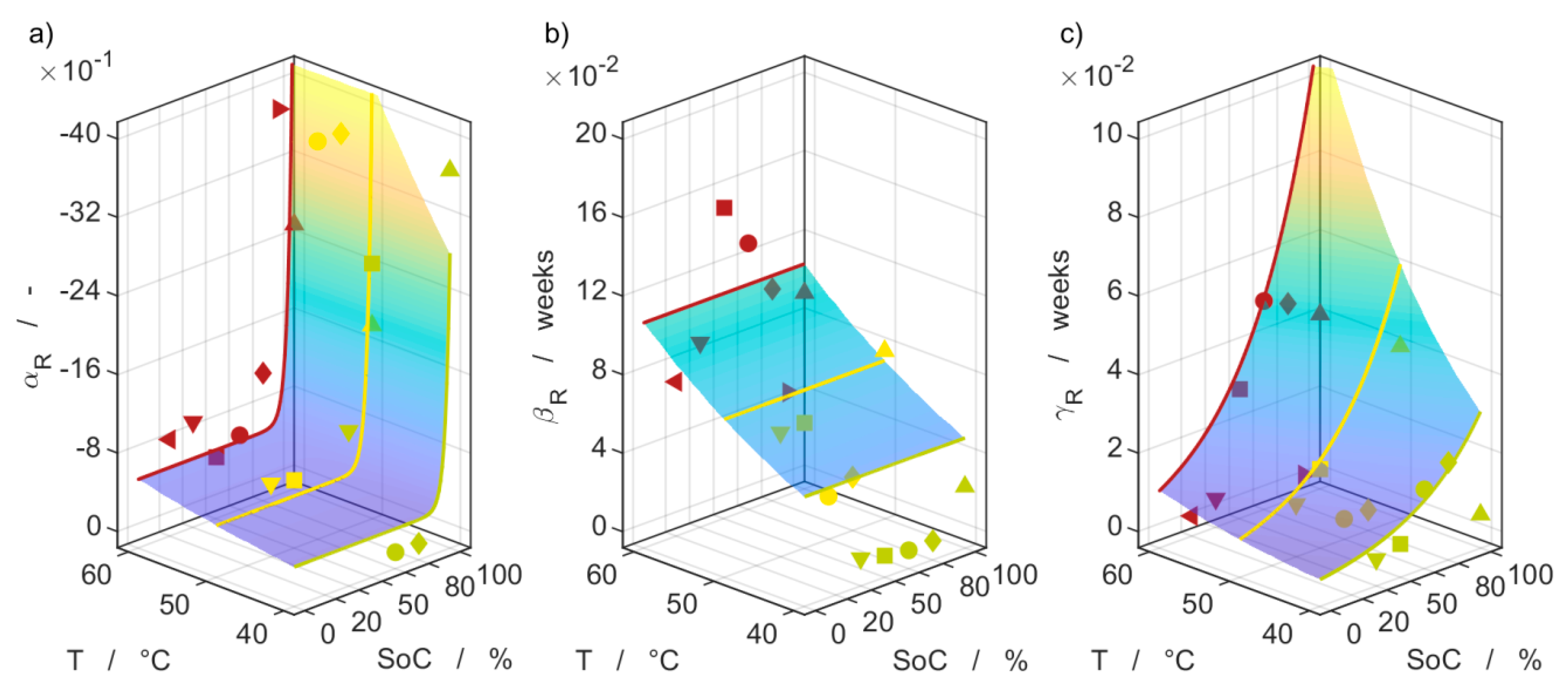
3.5. Impedance Measurements
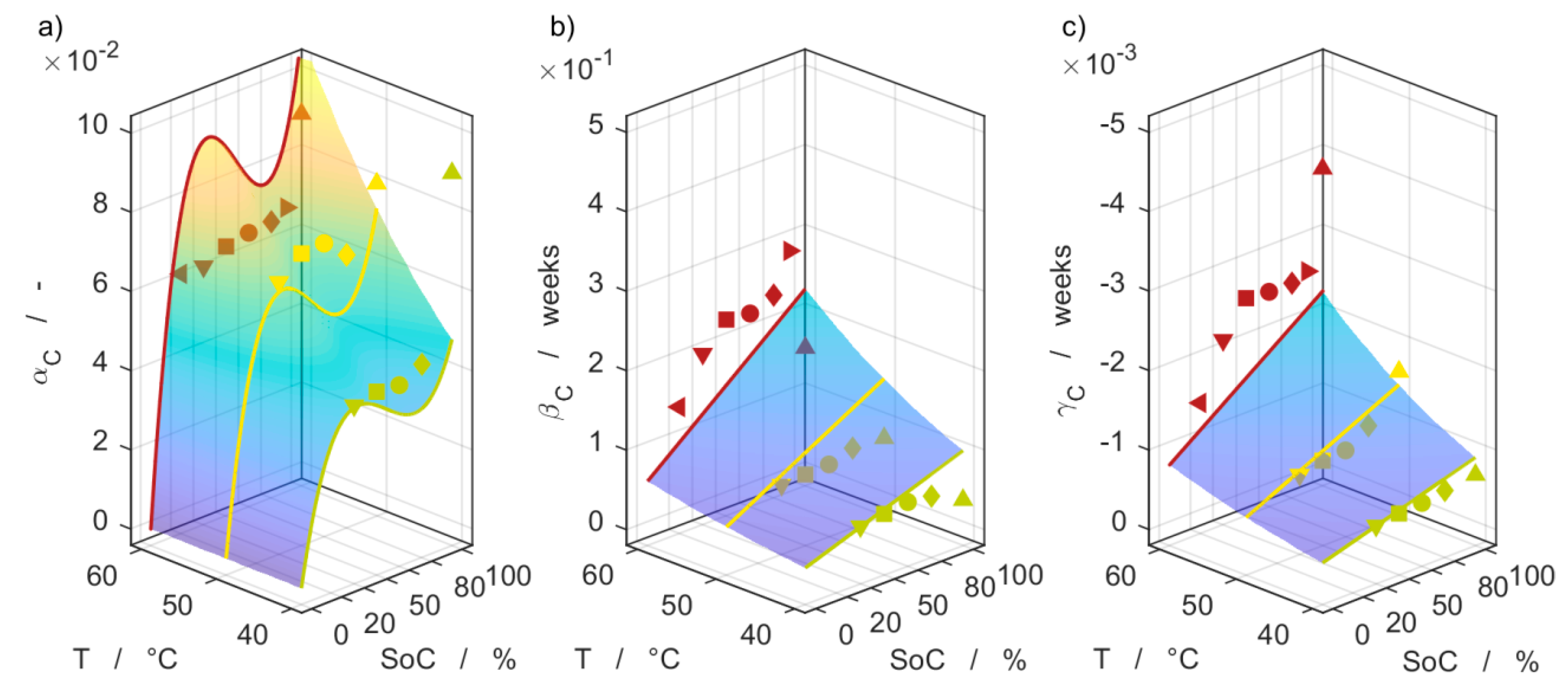
3.6. Model Comparison
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Werner, D.; Paarmann, S.; Wiebelt, A.; Wetzel, T. Inhomogeneous Temperature Distribution Affecting the Cyclic Aging of Li-Ion Cells. Part I: Experimental Investigation. Batteries 2020, 6, 13. [Google Scholar] [CrossRef]
- Werner, D.; Paarmann, S.; Wiebelt, A.; Wetzel, T. Inhomogeneous Temperature Distribution Affecting the Cyclic Aging of Li-Ion Cells. Part II: Analysis and Correlation. Batteries 2020, 6, 12. [Google Scholar] [CrossRef]
- Ecker, M.; Gerschler, J.B.; Vogel, J.; Käbitz, S.; Hust, F.; Dechent, P.; Sauer, D.U. Development of a lifetime prediction model for lithium-ion batteries based on extended accelerated aging test data. J. Power Sources 2012, 215, 248–257. [Google Scholar] [CrossRef]
- Käbitz, S.; Gerschler, J.B.; Ecker, M.; Yurdagel, Y.; Emmermacher, B.; André, D.; Mitsch, T.; Sauer, D.U. Cycle and calendar life study of a graphite|LiNi1/3Mn1/3Co1/3O2 Li-ion high energy system. Part A: Full cell characterization. J. Power Sources 2013, 239, 572–583. [Google Scholar] [CrossRef]
- Schmalstieg, J.; Käbitz, S.; Ecker, M.; Sauer, D.U. A holistic aging model for Li(NiMnCo)O2 based 18650 lithium-ion batteries. J. Power Sources 2014, 257, 325–334. [Google Scholar] [CrossRef]
- Ecker, M.; Nieto, N.; Käbitz, S.; Schmalstieg, J.; Blanke, H.; Warnecke, A.; Sauer, D.U. Calendar and cycle life study of Li(NiMnCo)O2-based 18650 lithium-ion batteries. J. Power Sources 2014, 248, 839–851. [Google Scholar] [CrossRef]
- Baghdadi, I.; Briat, O.; Delétage, J.-Y.; Gyan, P.; Vinassa, J.-M. Lithium battery aging model based on Dakin’s degradation approach. J. Power Sources 2016, 325, 273–285. [Google Scholar] [CrossRef]
- Keil, P.; Schuster, S.F.; Wilhelm, J.; Travi, J.; Hauser, A.; Karl, R.C.; Jossen, A. Calendar Aging of Lithium-Ion Batteries. J. Electrochem. Soc. 2016, 163, A1872–A1880. [Google Scholar] [CrossRef]
- de Hoog, J.; Timmermans, J.M.; Ioan-Stroe, D.; Swierczynski, M.; Jaguemont, J.; Goutam, S.; Omar, N.; Van Mierlo, J.; Van Den Bossche, P. Combined cycling and calendar capacity fade modeling of a Nickel-Manganese-Cobalt Oxide Cell with real-life profile validation. Appl. Energy 2017, 200, 47–61. [Google Scholar] [CrossRef]
- Redondo-Iglesias, E.; Venet, P.; Pelissier, S. Eyring acceleration model for predicting calendar ageing of lithium-ion batteries. J. Energy Storage 2017, 13, 176–183. [Google Scholar] [CrossRef]
- Keil, P.; Jossen, A. Calendar Aging of NCA Lithium-Ion Batteries Investigated by Differential Voltage Analysis and Coulomb Tracking. J. Electrochem. Soc. 2017, 164, A6066–A6074. [Google Scholar] [CrossRef]
- Hahn, S.L.; Storch, M.; Swaminathan, R.; Obry, B.; Bandlow, J.; Birke, K.P. Quantitative validation of calendar aging models for lithium-ion batteries. J. Power Sources 2018, 400, 402–414. [Google Scholar] [CrossRef]
- Broussely, M.; Herreyre, S.; Biensan, P.; Kasztejna, P.; Nechev, K.; Staniewicz, R.J. Aging mechanism in Li ion cells and calendar life predictions. J. Power Sources 2001, 97–98, 13–21. [Google Scholar] [CrossRef]
- Broussely, M.; Biensan, P.; Bonhomme, F.; Blanchard, P.; Herreyre, S.; Nechev, K.; Staniewicz, R.J. Main aging mechanisms in Li ion batteries. J. Power Sources 2005, 146, 90–96. [Google Scholar] [CrossRef]
- Vetter, J.; Novák, P.; Wagner, M.R.; Veit, C.; Möller, K.-C.; Besenhard, J.O.; Winter, M.; Wohlfahrt-Mehrens, M.; Vogler, C.; Hammouche, A. Ageing mechanisms in lithium-ion batteries. J. Power Sources 2005, 147, 269–281. [Google Scholar] [CrossRef]
- Scrosati, B.; Garche, J.; Tillmetz, W. Advances in Battery Technologies for Electric Vehicles; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Dubarry, M.; Qin, N.; Brooker, P. Calendar aging of commercial Li-ion cells of different chemistries—A review. Curr. Opin. Electrochem. 2018, 9, 106–113. [Google Scholar] [CrossRef]
- Kasnatscheew, J.; Evertz, M.; Kloepsch, R.; Streipert, B.; Wagner, R.; Cekic Laskovic, I.; Winter, M. Learning from Electrochemical Data: Simple Evaluation and Classification of LiMO2-type-based Positive Electrodes for Li-Ion Batteries. Energy Technol. 2017, 5, 1670–1679. [Google Scholar] [CrossRef]
- Kasnatscheew, J.; Evertz, M.; Streipert, B.; Wagner, R.; Nowak, S.; Cekic Laskovic, I.; Winter, M. Improving cycle life of layered lithium transition metal oxide (LiMO2) based positive electrodes for Li ion batteries by smart selection of the electrochemical charge conditions. J. Power Sources 2017, 359, 458–467. [Google Scholar] [CrossRef]
- Kasnatscheew, J.; Röser, S.; Börner, M.; Winter, M. Do Increased Ni Contents in LiNixMnyCozO2 (NMC) Electrodes Decrease Structural and Thermal Stability of Li Ion Batteries? A Thorough Look by Consideration of the Li + Extraction Ratio. ACS Appl. Energy Mater. 2019, 2, 7733–7737. [Google Scholar] [CrossRef]
- Xu, G.; Liu, X.; Daali, A.; Amine, R.; Chen, Z.; Amine, K. Challenges and Strategies to Advance High-Energy Nickel-Rich Layered Lithium Transition Metal Oxide Cathodes for Harsh Operation. Adv. Funct. Mater. 2020, 30, 2004748. [Google Scholar] [CrossRef]
- Peled, E.; Yamin, H. The Passivating Layer on Lithium in Lithium Tetrachloroalumnate-SOCl2 Solutions. In Proceedings of the 28th Power Sources Symposium, Atlantic City, NJ, USA, 12–15 June 1978; p. 237. [Google Scholar]
- Peled, E. The Electrochemical Behavior of Alkali and Alkaline Earth Metals in Nonaqueous Battery Systems-The Solid Electrolyte Interphase Model. J. Electrochem. Soc. 1979, 126, 2047–2051. [Google Scholar] [CrossRef]
- Schmitt, J.; Maheshwari, A.; Heck, M.; Lux, S.; Vetter, M. Impedance change and capacity fade of lithium nickel manganese cobalt oxide-based batteries during calendar aging. J. Power Sources 2017, 353, 183–194. [Google Scholar] [CrossRef]
- Attia, P.M.; Chueh, W.C.; Harris, S.J. Revisiting the t 0.5 Dependence of SEI Growth. J. Electrochem. Soc. 2020, 167, 090535. [Google Scholar] [CrossRef]
- Pinson, M.B.; Bazant, M.Z. Theory of SEI Formation in Rechargeable Batteries: Capacity Fade, Accelerated Aging and Lifetime Prediction. J. Electrochem. Soc. 2012, 160, A243–A250. [Google Scholar] [CrossRef]
- Redondo-Iglesias, E.; Venet, P.; Pelissier, S. Global Model for Self-Discharge and Capacity Fade in Lithium-Ion Batteries Based on the Generalized Eyring Relationship. IEEE Trans. Veh. Technol. 2018, 67, 104–113. [Google Scholar] [CrossRef]
- Redondo-Iglesias, E.; Venet, P.; Pelissier, S. Modelling Lithium-Ion Battery Ageing in Electric Vehicle Applications—Calendar and Cycling Ageing Combination Effects. Batteries 2020, 6, 14. [Google Scholar] [CrossRef]
- Cuervo-Reyes, E.; Flückiger, R. One Law to Rule Them All: Stretched Exponential Master Curve of Capacity Fade for Li-Ion Batteries. J. Electrochem. Soc. 2019, 166, A1463–A1470. [Google Scholar] [CrossRef]
- Wang, J.; Purewal, J.; Liu, P.; Hicks-Garner, J.; Soukazian, S.; Sherman, E.; Sorenson, A.; Vu, L.; Tataria, H.; Verbrugge, M.W. Degradation of lithium ion batteries employing graphite negatives and nickel-cobalt-manganese oxide + spinel manganese oxide positives: Part 1, aging mechanisms and life estimation. J. Power Sources 2014, 269, 937–948. [Google Scholar] [CrossRef]
- Lewerenz, M.; Käbitz, S.; Knips, M.; Münnix, J.; Schmalstieg, J.; Warnecke, A.; Sauer, D.U. New method evaluating currents keeping the voltage constant for fast and highly resolved measurement of Arrhenius relation and capacity fade. J. Power Sources 2017, 353, 144–151. [Google Scholar] [CrossRef]
- Schimpe, M.; von Kuepach, M.E.; Naumann, M.; Hesse, H.C.; Smith, K.; Jossen, A. Comprehensive Modeling of Temperature-Dependent Degradation Mechanisms in Lithium Iron Phosphate Batteries. J. Electrochem. Soc. 2018, 165, A181–A193. [Google Scholar] [CrossRef]
- Arrhenius, S. Über die Reaktionsgeschwindigkeit bei der Inversion von Rohrzucker durch Säuren. Z. für Phys. Chem. 1889, 4, 226–248. [Google Scholar] [CrossRef]
- Su, L.; Zhang, J.; Huang, J.; Ge, H.; Li, Z.; Xie, F.; Liaw, B.Y.B.Y. Path dependence of lithium ion cells aging under storage conditions. J. Power Sources 2016, 315, 35–46. [Google Scholar] [CrossRef]
- Deutschen, T.; Gasser, S.; Schaller, M.; Siehr, J. Modeling the self-discharge by voltage decay of a NMC/graphite lithium-ion cell. J. Energy Storage 2018, 19, 113–119. [Google Scholar] [CrossRef]
- Redondo-Iglesias, E.; Venet, P.; Pelissier, S. Influence of the non-conservation of SoC value during calendar ageing tests on modelling the capacity loss of batteries. In Proceedings of the 2015 Tenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 31 March–2 April 2015; pp. 1–5. [Google Scholar]
- Lewerenz, M.; Fuchs, G.; Becker, L.; Sauer, D.U. Irreversible calendar aging and quantification of the reversible capacity loss caused by anode overhang. J. Energy Storage 2018, 18, 149–159. [Google Scholar] [CrossRef]
- Lewerenz, M.; Sauer, D.U. Evaluation of cyclic aging tests of prismatic automotive LiNiMnCoO2-Graphite cells considering influence of homogeneity and anode overhang. J. Energy Storage 2018, 18, 421–434. [Google Scholar] [CrossRef]
- Lewerenz, M.; Dechent, P.; Sauer, D.U. Investigation of capacity recovery during rest period at different states-of-charge after cycle life test for prismatic Li(Ni1/3Mn1/3Co1/3)O2-graphite cells. J. Energy Storage 2019, 21, 680–690. [Google Scholar] [CrossRef]
- Fath, J.P.; Alsheimer, L.; Storch, M.; Stadler, J.; Bandlow, J.; Hahn, S.; Riedel, R.; Wetzel, T. The influence of the anode overhang effect on the capacity of lithium-ion cells–a 0D-modeling approach. J. Energy Storage 2020, 29, 101344. [Google Scholar] [CrossRef]
- Schuster, S.F.; Brand, M.J.; Campestrini, C.; Gleissenberger, M.; Jossen, A. Correlation between capacity and impedance of lithium-ion cells during calendar and cycle life. J. Power Sources 2016, 305, 191–199. [Google Scholar] [CrossRef]
- Farmann, A.; Sauer, D.U. A study on the dependency of the open-circuit voltage on temperature and actual aging state of lithium-ion batteries. J. Power Sources 2017, 347, 1–13. [Google Scholar] [CrossRef]
- Wilhelm, J.; Seidlmayer, S.; Keil, P.; Schuster, J.; Kriele, A.; Gilles, R.; Jossen, A. Cycling capacity recovery effect: A coulombic efficiency and post-mortem study. J. Power Sources 2017, 365, 327–338. [Google Scholar] [CrossRef]




| Parameter | Batch I | Batch II |
|---|---|---|
| CC/20 | (3.033 ± 0.017) Ah | (3.021 ± 0.011) Ah |
| Rohm | (1.528 ± 0.059) mΩ | (1.542 ± 0.082) mΩ |
| Rpol | (5.992 ± 0.300) mΩ | (6.038 ± 0.215) mΩ |
| SoC | 40 °C Max./Avg. | 50 °C Max./Avg. | 60 °C Max./Avg. |
|---|---|---|---|
| 100% | −40%/−20% | −42%/−28% | −36%/−23% |
| 90% | not measured | not measured | −5.0%/−3.6% |
| 80% | −1.4%/−1.1% | −2.4%/−1.6% | −3.4%/−2.4% |
| 65% | −1.1%/−0.83% | −1.7%/−1.3% | −2.5%/−1.7% |
| 50% | −1.0%/−0.69% | −1.3%/−1.1% | −1.9%/−1.5% |
| 35% | −0.84%/+0.59% | −1.1%/−0.88% | −1.6%/−1.2% |
| 20% | not measured | not measured | −1.1%/−0.89% |
| Parameter | αC,1 103%−1 | αC,2 %−2 | αC,3 %−3 | βC,0 103 | βC,1 %−1 | γC,0 10−3 | γC,1 %−1 | Ea,αβ kJ mol−1 | Ea,γ kJ mol−1 |
|---|---|---|---|---|---|---|---|---|---|
| CC/20 | 2.635 | −52.16 | 0.3072 | 27.20 | 749.5 | −1.225 | −21.61 | 36.04 | 39.40 |
| Parameter | αR,0 103 | αR,1 103%−1 | αR,2 - | αR,3 10−3%−1 | βR,0 103 | γR,0 103 | γR,2 - | γR,3 10−3%−1 | Ea,αβ kJ mol−1 | Ea,γ kJ mol−1 |
|---|---|---|---|---|---|---|---|---|---|---|
| Rohm | 0 | 476.8 | −1.818 × 107 | 15.45 | 10,050 | 39,790 | −2.220 × 10−14 | 519.8 | 48.68 | 62.46 |
| Rpol | −151.3 | 0 | −8.351 × 10−10 | 352.2 | 30.18 | 116.9 | 1.114 × 107 | 24.12 | 34.78 | 57.61 |
| Parameter | CC/20 | Rohm | Rpol |
|---|---|---|---|
| 2D fit | 3 | 3 | 3 |
| 4D fit | 9 | 9 | 9 |
| Ecker et al. [3] | 7 + 1 per SoC | 7 + 1 per SoC | 7 + 1 per SoC |
| cα | −0.004479 | 0.07920 | 0.4558 |
| cV | 1.072 | 8.244 | 1.290 |
| cT | 1.755 | 2.029 | 1.869 |
| V0 = 3.5 V * | 3.501 V | 3.777 V | 4.086 V |
| T0 = 25 °C * | 28.34 °C | 56.04 °C | 55.37 °C |
| ∆V = 0.1 V * | 0.09940 V | 0.8563 V | 0.09853 V |
| ∆T = 10 °C * | 12.27 °C | 10.03 °C | 13.08 °C |
| Schmalstieg et al. [5] | 3 + 1 per SoC | 3 + 1 per SoC | 3 + 1 per SoC |
| V0 | 6.581 | 2.147 × 108 | 2.406 × 103 |
| αV | 2.434 V−1 | 6.377 × 107 V−1 | 6.728 × 102 V−1 |
| αT | 6445 K | 10,500 K | 6214 K |
| Parameter | CC/20 | Rohm | Rpol |
|---|---|---|---|
| Ea,αβ | 36.04 kJ mol−1 | 48.68 kJ mol−1 | 34.78 kJ mol−1 |
| Ea,γ | 39.40 kJ mol−1 | 62.46 kJ mol−1 | 57.61 kJ mol−1 |
| αT∙ * | 53.59 kJ mol−1 | 87.34 kJ mol−1 | 51.67 kJ mol−1 |
| Ea [5] | 58.0 kJ mol−1 (C1C) | 49.8 kJ mol−1 (R10s) | |
| Ea [4] | 43.60 kJ mol−1 (C1C) | 36.85 kJ mol−1 (R10s) | |
| Ea [6] | ≈55 kJ mol−1 (C1C) | ≈55 kJ mol−1 (R17s) | |
| Ea [10] | ≈69.6 kJ mol−1 (C1C) | - | - |
| Ea [12] | >28 kJ mol−1 (C1C) | - | - |
| Ea [30] | 24.5 kJ mol−1 (CC/2) | - | - |
| Ea [31] | ≈86 kJ mol−1 (C1C) | - | - |
| Ea [32] | 20.6 kJ mol−1 (C1C) | - | - |
| Parameter | CC/20 | Rohm | Rpol |
|---|---|---|---|
| 2D fit | (0.155 ± 0.121)% | (1.31 ± 0.840)% | (3.50 ± 2.43)% |
| 4D fit | 0.437% | 3.08% | 12.1% |
| Ecker et al. [3] | 0.575% | 4.66% | 27.2% |
| Schmalstieg et al. [5] | 1.17% | 10.1% | 17.8% |
| Parameter 60 °C/50 °C/40 °C | CC/20 tEoL/Weeks | Rohm tEoL/Weeks | Rpol tEoL/Weeks |
|---|---|---|---|
| 2D fit | 274/151/54 | 1059/310/103 | 93/35/20 |
| 4D fit | 261/142/72 | 582/248/100 | 92/37/16 |
| Ecker et al. [3] | 452/181/72 | 1515/369/90 | 108/35/14 |
| Schmalstieg et al. [5] | 262/112/50 | 686/172/47 | 93/37/17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Werner, D.; Paarmann, S.; Wetzel, T. Calendar Aging of Li-Ion Cells—Experimental Investigation and Empirical Correlation. Batteries 2021, 7, 28. https://doi.org/10.3390/batteries7020028
Werner D, Paarmann S, Wetzel T. Calendar Aging of Li-Ion Cells—Experimental Investigation and Empirical Correlation. Batteries. 2021; 7(2):28. https://doi.org/10.3390/batteries7020028
Chicago/Turabian StyleWerner, Daniel, Sabine Paarmann, and Thomas Wetzel. 2021. "Calendar Aging of Li-Ion Cells—Experimental Investigation and Empirical Correlation" Batteries 7, no. 2: 28. https://doi.org/10.3390/batteries7020028
APA StyleWerner, D., Paarmann, S., & Wetzel, T. (2021). Calendar Aging of Li-Ion Cells—Experimental Investigation and Empirical Correlation. Batteries, 7(2), 28. https://doi.org/10.3390/batteries7020028







