Abstract
Temperature heavily affects the behavior of any energy storage chemistries. In particular, lithium-ion batteries (LIBs) play a significant role in almost all storage application fields, including Electric Vehicles (EVs). Therefore, a full comprehension of the influence of the temperature on the key cell components and their governing equations is mandatory for the effective integration of LIBs into the application. If the battery is exposed to extreme thermal environments or the desired temperature cannot be maintained, the rates of chemical reactions and/or the mobility of the active species may change drastically. The alteration of properties of LIBs with temperature may create at best a performance problem and at worst a safety problem. Despite the presence of many reports on LIBs in the literature, their industrial realization has still been difficult, as the technologies developed in different labs have not been standardized yet. Thus, the field requires a systematic analysis of the effect of temperature on the critical properties of LIBs. In this paper, we report a comprehensive review of the effect of temperature on the properties of LIBs such as performance, cycle life, and safety. In addition, we focus on the alterations in resistances, energy losses, physicochemical properties, and aging mechanism when the temperature of LIBs are not under control.
1. Introduction
Lithium-ion batteries (LIBs) as rechargeable devices play a key role in electrochemical energy storage systems [1]. With the steady improvements in the performances in terms of energy and power densities, the application areas for LIB technology are increasing. Particularly in electrical vehicles (EVs), their widespread applications attract much attention [2,3]. Despite their advantages and widespread applications, the LIBs suffer from safety problems, high cost, and thermal issues [4,5,6,7,8,9].
Battery degradation rates, which affect lifetime, are influenced by many external factors such as battery operating temperature, charge/discharge current rate, depth of discharge (DOD), and time intervals between full charge cycles [10,11,12,13,14]. Among these factors, the temperature is the major parameter affecting the battery performance such as power output, capacity, safety, and cycle life [6,15]. For example, at higher operating temperatures, active material and electrolyte decomposition, changes in the solid electrolyte interface and side reaction rates increase resulting in capacity fading, power fading, and thermal runaway [5,16,17]. Similarly, at lower operation temperatures, reduced ionic conductivity of electrolytes, increased charge transfer resistance, high polarization of graphite anode (lithium plating), and limited diffusivity of lithium ions in electrodes result in low energy and power output [17,18,19]. A significant example of the influence of temperature is, for instance, reported by Nagasubramanian [20] who showed that when the ambient temperature is changed from 25 into −40 °C, the power and energy density of the 18,650 Panasonic cells are dropped by 98.7% and 95%, respectively. Similarly, Gong and Mi [21] studied the collected data from 7375 distinctive individual trips of one major commercial EV national wide in the United States, and showed that the average EV available range decreased from 120 miles at 20 °C to 60 miles at −20 °C.
The physical laws and mathematical functions that link material parameters with temperature are essential to simplify the evaluation of new materials by providing, through an inductive process, the scale-up of performance at the cell level. Moreover, with these functions properly parameterized, the sizing and integration of the thermal conditioning system to the battery pack is greatly facilitated, as simulation tools based on these equations can be then adopted. This engineering process is key, as the parameters influencing the battery lifetime are highly temperature-dependent. For example, Motloch et al. [22] reported that each grade of increase in temperature in a range of 30–40 °C results in approximately two months decrease in the battery cycle-life. Therefore, in order to comply with the life and safety requirements, the cells of a pack must remain within a well-defined temperature range, this range for the most common type of LIBs is between 10–50 °C [10,13,23]. In this work, a comprehensive and systematic review of a wide range of relevant studies on the temperature-dependent properties of LIBs and their effects on battery performance and degradation are investigated and summarized. Therefore, this work provides a hands-on overview of all the most relevant phenomena affected by the temperature within a lithium–ion cell, so that material developers as well as engineers in the battery design could use it for simulations, cell performance estimations, battery pack integrations, and thermal management developments.
2. Energy Conservation and Energy Losses
There have been published numerous studies on the modeling of the thermal behavior of Li-ion cells. The general energy balance for LIBs is derived from principles of nonequilibrium thermodynamics and is given by Equation (1) [24]
where the temperature T can change spatially and temporally, and is the volumetric heat generation source. The primary source of heat generation in the Li-ion cells are the charge transfer reactions, which result in an irreversible reaction heat and a reversible entropy heat component. The rate of the irreversible reaction heat is given as a product of the reaction flux, the electrode surface area per unit volume, and the overpotential as below [25,26]
where n represents cathode (c) or anode (a). Regardless of charging or discharging the cell, the irreversible heat generation is an exothermic quantity. On the other hand, the reversible heat, which is generated due to entropy changes during intercalation or deintercalation, is given as below [25,26]
Based on the rate of the reaction, the reversible heat can be either exothermic or endothermic. The secondary source of volumetric heat generation in the battery cell is ohmic heat, which is due to electronic current conduction in the solid phase and ionic current conduction in the electrolyte phase. The ohmic heat generation is given as the product of current density in the solid or electrolyte phase and the corresponding potential gradient. Thus, in the electrode region, it is given as [25,26]
and in the electrolyte region, it is given by
In addition to heat generation originating from charge transfer processes (Butler–Volmer reaction) and ohmic heat, in some cells, a heat source due to phase transitions in the electrodes is also considered. This quantity, the phase transition heat is given as a product of the difference in the enthalpies of two phases (, and the rate of phase transition at the interface [24].
Therefore, the overall energy conservation for a Li-ion cell can be rewritten as
The maximum amount of electric energy derived by the electrochemical oxidation and reduction in the electrodes is proportional to the change in the standard free energy of the electrochemical couples, as stated in Equation (8) [27].
However, chemical energy cannot be fully converted to useful electric energy because of the polarization loss and the cell internal impedance during discharge [28,29,30]. The sources of polarization during charge/discharge are activation polarization, concentration polarization, and ohmic polarization, which will be discussed in this section. Therefore, the cell potential E is derived as shown in Equation (9) [30]
where: ± is + during charge and during discharge.
Activation polarization (charge transfer polarization) is the voltage loss associated with overcoming the energy barrier to the electrochemical reactions. It usually happens when the rate of oxidation or reduction reactions on the electrodes are not enough to yield a desired current. To reduce the activation polarization, the electrode materials need to be highly porous to have maximum reaction rates. Activation polarization is a function of the operating temperature, of the state of charge (SOC), and of the electrode properties, and can be expressed as in Equation (10) [30]
The activation polarization can also be expressed as the Tafel Equation [31]
where and [32].
Concentration polarization is the mass transfer resistance associated with the concentration difference between the electrode surface and the bulk of the electrolyte. To have a minimum concentration polarization, electrolyte diffusivity should be maximum to lower the mass transport limitations. The concentration polarization is given in Equation (12) [30,33]
The other source of energy loss is ohmic polarization that causes the voltage (IR) drop which is proportional to the current drown from the cell. The total cell internal impedance is originated from the ionic electrolyte resistance and the electronic resistance of the electrode active material, current collectors, positive and negative tabs, and contact resistance between the current collectors and electrodes. Therefore, ionic conductivity of the electrolyte in conjunction with the electronic conductivity of the electrodes and current collectors should be high enough to lower the ohmic drop [33].
Therefore, Equation (9) could be rewritten as
Equation (14) shows that part of the useful potential is lost as a result of the aforementioned polarizations (Figure 1). The open circuit potential (OCP) of the cathode and the anode can be approximated by Taylor’s expansion as a function of the temperature and concentrations as in Equation (15) [34]
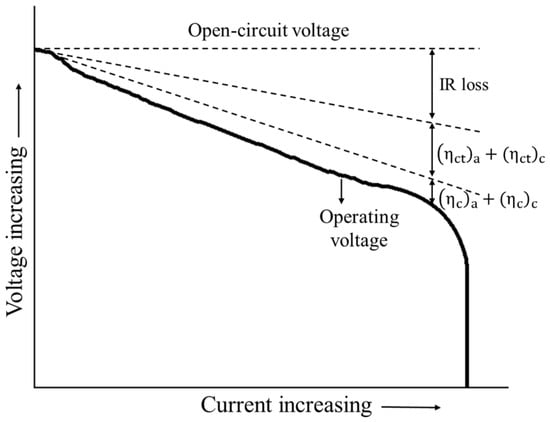
Figure 1.
Typical polarization of a cell (re-elaborated from [30]).
3. Temperature Effects on Electrochemical Resistances
Battery resistances are strongly temperature-dependent parameters [35,36]. In the literature, three major resistances are considered for the LIBs, which are the bulk resistance, the surface film resistance, and the charge transfer resistance [37,38]. The temperature dependency of these resistances is reviewed in the following section.
3.1. Ohmic Resistance
The ohmic resistance of the cell includes ionic resistance of the electrolyte and electronic resistance of the other cell components such as the electrode materials, the separator, the current collectors, and the cell terminals. In general, it specifies the capability of the cell to handle a certain current [39]. The instantaneous voltage drop at the beginning of the discharge process is due to the ohmic resistance.
The operating temperature of an LIB has opposite effects on the electrolyte ionic resistance and the electronic resistance of other electronic conductors. The ionic resistance of the electrolyte increases as the operating temperature decreases. This can be explained by the fact that the increase in the number of free ions due to the dissociation of molecules exceeds the growth of ion scattering during collisions with solvent molecules. On the other hand, the electronic resistivity of the conductors increases with increasing temperature [40].
Andre et al. [41] used electrochemical impedance spectroscopy to investigate the effect of operating condition, such as temperature and SOC, on the electrochemical performance of commercial high-power batteries. They showed that the ohmic resistance is almost unaffected by the SOC. However, it is strongly influenced by the operating temperature of the cell due to the high sensitivity of the electrolyte diffusion rate on the temperature. These results were confirmed by many researchers, such as Zhange et al. [42] (Figure 2) and other researchers [43,44], however, Yang et al. [45] showed that the ohmic resistance increases rapidly when the SOC is between 0 and 0.2, and it becomes stable when SOC is larger than 0.2.
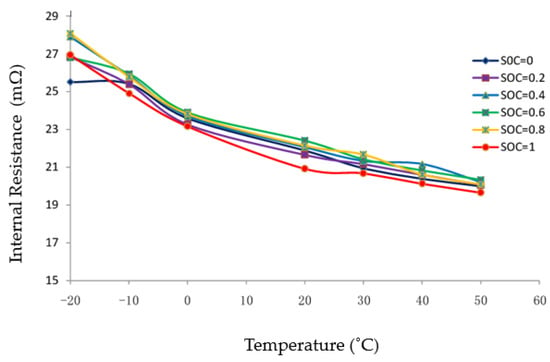
Figure 2.
Temperature dependency of internal resistance [42].
3.2. Surface Film Resistance
The common electrolytes used in LIBs are thermodynamically unstable at the LIBs’ operating potential range, and they are reduced/oxidized and get chemically decomposed at the electrode/electrolyte interface [46,47]. The decomposed products are not soluble in the electrolyte solution, and they precipitate and form a protective film on the surface of electrodes. This protective layer is called solid electrolyte interphase (SEI) which protects the electrolyte components from being further reduced on the anode surface [16,48]. In addition, the SEI layer is not thermally and mechanically stable and in the case of abuse conditions such as an internal short circuit, overvoltage, and high temperatures’ exposure, the cells can undergo failure or safety issues such as thermal runaway. It is well-known that the SEI decomposition is the first process that leads to exothermic reactions under thermal abuse conditions.
The resistance associated with the SEI layer is expressed as the surface film resistance (RSEI). Mogi et al. [49] evaluated the effect of temperature on surface film formation on nickel-based electrode at a temperature range of from 40 to 80 °C. According to their study, even though at higher temperatures the film on the anode surface gets thicker, the resistance associated with the SEI layer decreases with the increasing temperature. Suresh et al. [40] reported that the RSEI is nearly unaltered with SOC, while there is a significant variance with the temperature (Figure 3). They showed that variation in the RSEI with the temperature obeys Arrhenius’ law, and its magnitude decreases as temperature increases.
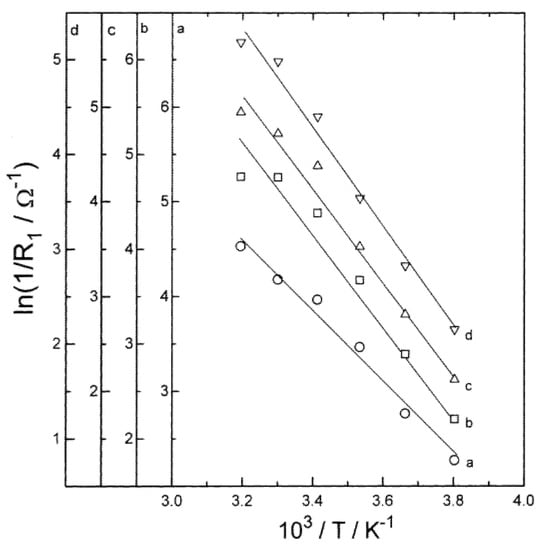
Figure 3.
Variation of ln (1/R1) versus inverse of temperature (T) for SOC values (a) 1, (b) 0.8, (c) 0.5 and (d) 0.2 [40].
3.3. Charge Transfer Resistance
The charge transfer process is expressed as transforming a solvated Li+ in the electrolyte into Li in the positive or negative electrode by accepting an electron. Generally, it includes three main steps: de-solvation of Li+ at the SEI/electrolyte interface, Li+ transfer through SEI layer or bulk of active material, and intercalation in the electrode). Normally, the last step is fast and the other two steps can be rate-limiting processes depending on the operating temperature, and electrode or electrolyte material [50]. For example, Wang et al. [51], who studied the low-temperature performance of graphite and mesocarbon microbeads (MCMB) electrode, found that the stage transformation (diffusion in the bulk electrode) is a rate-limiting step at room temperature, while transfer through SEI layer is a rate-determining step at −30 °C.
The resistance associated with the charge transfer process on the electrode–electrolyte interface is defined as the charge transfer resistance (Rct). It is identified with the reaction kinetics from the Butler–Volmer Equation for charge-transfer-controlled electrochemical reactions [52].
The exchange current density, , has a nonlinear relationship with the Lithium ion concentration in the solid phase as given below
the solid phase concentration can be given as
therefore, in Equation (18) can be written as
Thus, combining Equations (18)–(20), Equation (17) can be written as
The reaction standard rate constant is obtained from the Arrhenius Equation as a function of temperature
then, Equation (21) can be rewritten as
where k () is a constant. The charge transfer resistance () dependence on SOC and temperature can be obtained separately. For this purpose, Equation (23) can be written as follows
and then, on differentiation, we obtain
By differentiation and rewriting Equation (24) in the form of Equations (25) and (26), Suresh et al. [40] evaluated the activation energy () and the transfer coefficient ( by plotting the variation of with , and variation in with .
Zheng et al. [53] and Kumar et al. [54] found that the charge transfer resistance at the electrolyte/electrode interface is the most temperature-dependent resistance source of Li-ion cells. This is also confirmed by Liao et al. [55], who studied the low-temperature performance of a LiFePO4 cathode and showed that, compared to and , the is most significantly increased resistance, especially at subzero temperatures. This is because the is controlled by the kinetics of the reactions, while the and are mainly controlled by the electrolyte ionic conductivity, which is less temperature-dependent than the reaction kinetics. Kumar et al. [54] showed that the of a LiCoO2 cell drops from 4 to nearly 0 Ω in a temperature range of −20 to 60 °C.
4. Temperature-Dependent Chemical–Thermal–Physical Properties of LIBs
The parameters used in the electrochemical–thermal models such as the kinetic reaction parameters, electrolyte conductivity, electrolyte and solid phase diffusivities, and open circuit voltage of the anode and cathode are mainly functions of the material type, the cell operating temperature, and the concentration. The most temperature-dependent physiochemical properties of the Li ion cell are the electrolyte density, the dynamic viscosity of the electrolyte, the solid-phase diffusion coefficient, the exchange current density, the electrolyte diffusion coefficient, the electrode electronic conductivity, the electrolyte ionic conductivity, and the chemical reaction rate, which will be discussed separately in the following sections.
4.1. Electrolytes
Generally, four types of electrolytes are used in LIBs: liquid electrolytes (solutions of lithium salt in aprotic solvents), solid/gel systems, solid-state electrolytes and ionic liquids [56]. In the following section, the effects of the operating temperature on the thermal, physical, and chemical properties of these electrolytes are reviewed.
4.1.1. Liquid Electrolytes (Standard)
The selection of solvents for liquid electrolytes is constrained since it must be mechanically, thermally, and chemically stable at the low potential of the anode and the high potential of the cathode [57]. Furthermore, the ideal liquid electrolyte should benefit from a wide operating temperature window, meaning that it should have a low melting point and a high boiling point. Xu et al. [58] reported the operating temperature range for a list of organic carbonates, esters, and ethers as an electrolyte solution. The cyclic organic carbonates are found to be the most desired solvents because of their high dielectric constants and formation of low energy complexes with lithium cations. However, these solvents suffer from the high viscosity and a high melting point. For instance, the ethylene carbonate (EC) is solid at room temperature. In the commercial cells, the acyclic alkyl carbonates are commonly added to benefit from their low viscosity and low melting point [56,59]. For example, Logan et al. [60] studied the effect of adding methyl acetate (MA) as an ester co-solvent on the low-temperature performance and rate capability of cells. They found that adding MA significantly decreases the viscosity of EC, while its’ effect on overall electrolyte conductivity is negligible. Generally, the LiPF6 as salt and EC as solvent are two indispensable components used in the present liquid electrolyte. Despite their many advantages for use as a salt and solvent, both are highly sensitive to the operating temperature. Simply, the LiPF6 contributes to a higher temperature failure due to its reactivity with solvents, and the EC contributes to a lower temperature instability due to its higher melting point and lower conductivity, especially at subzero temperatures [58].
The operating temperature range for the liquid electrolytes is defined based on a liquidus temperature, at which point one of the electrolyte components begins to crystallize and a bubble temperature, at which point one of its components begins to vaporize. Tarascon et al. [61] and Ding et al. [62] studied the temperature range for nonaqueous electrolytes used in Li-ion cells and found that the upper temperature limit (bubble temperature) in a binary or ternary electrolyte system is dominated by the lower boiling temperature. This is different from the operating temperature range defined for the Li-ion cell, since other factors are playing a role when an overall cell system is considered. For instance, the upper temperature limit is approximately 90 °C for dimethyl carbonate (DMC-), 110 °C for ethyl methyl carbonate (EMC-), and 120 °C for diethyl carbonate (DEC-) based electrolytes, while it is 70 °C for the LiPF6 salt. On the other hand, a lower boundary of the electrolyte range contributes to the low-temperature instability of a liquid electrolyte. Tarascon and Guyomard showed that the low-temperature limit for a binary EC/DMC (3:7) electrolyte is −25 °C [61]. Nonflammability of the electrolytes is also important if safety issues are considered [63]. Hu et al. [64] reported a dual-anion deep eutectic solution (combination of nitrile and lithium salts) as a nonflammable electrolyte with superior interphase stability and ionic conductivity.
Ion conductivity is one of the main characteristic properties of the electrolyte, which determines how fast the energy stored in the electrodes can be delivered. It mainly consists of two steps: (1) the solvation/dissociation of ionic compounds and (2) the migration of the solvated ions through the solvent. The ionic conductivity of liquid electrolytes is highly temperature-dependent and normally it increases monotonically with temperature. However, at very high temperatures, the ionic conductivity is more dominantly affected by the dielectric constants of the solvent mixture. One of the most common equations used for fitting the temperature dependence of conductivity data is the Vogel–Tamman–Fulcher (VTF) Equation [65,66]:
The potential drop in the electrolyte and the absolute ionic current, without considering diffusion and convection, is directly proportional to the ionic conductivity. However, the binary diffusion coefficient is a proportionality factor between the ion flux and the concentration gradient [67]. In other words, the driving force for migration is the electric potential gradient, while the diffusion is due to the concentration gradient. Landesfeind and Gasteiger studied the binary diffusion coefficient over a large concentration and temperature range and for three different electrolyte mixtures. They reported that at 0.1 M LiPF6, the diffusion coefficients range from ≈2.3–7.4 × 10−6 cm2/s for EC:DMC (1:1 w:w) and EC:EMC (3:7 w:w) as well as from ≈2.7–8.0 × 10−6 cm2/s for EMC:FEC (19:1 w:w), as the temperature increases from −7.5 °C to +50 °C, respectively; at 3.0 M LiPF6, the diffusion coefficients values range from ≈0.2–2.4 × 10−6 cm2/s (EC:DMC (1:1 w:w)), ≈0.2–1.6 × 10−6 cm2/s (EC:EMC (3:7 w:w)), and ≈0.2–2.0 × 10−6 cm2/s (EMC:FEC (19:1 w:w)) for the same temperature increase [67]. Xu et al. [26] reported the temperature-dependence of the Li ion diffusion coefficient in the electrolyte phase () as
4.1.2. Solid/Gel Polymer Electrolytes
Polymer electrolytes (PEs) are generally a membrane that consists of a polymer host and a lithium salt. They possess good transport properties and compared to liquid electrolytes have some advantages such as non-flammability, no-internal shorting, non-volatility, no electrolyte leakage, improved safety, and lower decomposition at the electrodes’ surface [68,69,70]. The most commonly studied PEs are based on poly(oxa alkanes), poly(aza alkanes) or poly(thia alkanes) [71]. The materials used in polymer electrolytes (PEs) are required to be mechanically and thermally stable over a wide range of temperatures, to be electrochemically stable at high and low electrode potentials, to have low activation energy for conduction, and to be not reactive at the electrolyte-electrode interface. More importantly, they are required to have a low glass transition temperature (Tg) since the ionic conductivity becomes lower at the highly polymer crystalline structure [72]. Mindemark et al. [73] synthesized an electrolyte based on the copolymers of trimethylene carbonate and ε-caprolactone and reported that increasing the ester content improves the ionic conductivity and lowers the Tg. The polyether–lithium salt complexes are the most studied PEs for which the ionic conductivity is in the order of 10−7 to 10−8 S.cm−1. Their low ionic conductivity is due to their highly crystalline structure at ambient temperatures which limits their applications [56]. Sun et al. [74] reported that plots of the ionic conductivity versus temperature for poly(trimethylene carbonate)-based polymer electrolytes demonstrate Vogel–Tammann–Fulcher (VTF) behavior in a temperature range of 294 to 357 K. Aside from the restricted ionic conductivity, there is additionally a high interfacial obstruction brought about by the poor contact and wetting of polymer electrolytes on regular composite cathodes/anodes. Sun et al. [75] reported improved electrode/electrolyte interphase properties by adding poly(trimethylene carbonate) oligomer as an interfacial mediator. The PEs also suffer from the low thermal conductivity together with the low lithium transference number, which varies between 0.1–0.2 [56]. For better mechanical and thermal stability, the PEs are crosslinked using a crosslinking agent such as isocyanates. Sukeshini et al. [76] studied the temperature dependence of the ionic conductivity for a ternary polymer electrolyte containing poly(vinyl chloride) as a solvent, lithium bis(trimethyl sulfonyl)imide as a salt, and dibutyl phthalate as a plasticizer. Nest et al. [77] developed a relationship between the glass transition temperature (Tg) and the crosslinking agent molarity (C) as below
where is the glass transition temperature at C = 0.
4.1.3. Solid-State Electrolytes
Solid-state electrolytes are thermally more stable and non-flammable with higher melting points compared to the commercially used liquid- and polymer-based electrolytes [78,79,80]. The functional solid-state electrolytes are required to have high room-temperature ionic conductivity and fast interfacial charge transport to be applicable in solid-state batteries [81,82,83]. They can be classified into three main types: garnet-type, sulfide-based, and phosphate-based electrolytes.
Garnet-type Li7-xLa3Zr2-xTaxO12 (LLZT) is considered as a good alternative for solid electrolytes because of its’ sensibly high conductivity around 1 mS cm−1 at room temperature and stability against lithium metal [78]. Its conductivity follows an Arrhenius-like behavior and reaches 16 mS cm−1 at 100 °C [84].
Sulfide-based solid electrolytes (SE) are very alluring for application in all-solid-state batteries (ASSB) due to their high ionic conductivities and low grain boundary resistance. However, restricted chemical and electrochemical stability necessitates protection on both the cathode and anode side [85]. The initial challenge of poor ionic conductivity at ambient temperature has been met with sulfide-based materials like Li10GeP2S12 (LGPS) or Li2S·P2S5. Their conductivities is as high as 25 mS cm−1, surpassing that of current liquid electrolytes [86,87]. In addition, their softness allows for good contacting, hence giving lower grain-boundary and interfacial resistance contrasted with oxide-based solid-state electrolytes [85]. A significant issue for sulfide-based SEs is their chemical instability in contact with air and moisture, as well as with Li metal and the cathode materials [88].
Solid-state electrolytes made of phosphate-based ion conducting glass-ceramics with a NASICON structure have rather lower conductivity and poor plasticity compared with sulfide-based materials. However, they have different focal points, for example, their chemical stability and ease of handling [89]. They additionally have great mechanical stability, which could stop the dendrite growth, which causes significant issues in some liquid electrolyte-based batteries [90]. A promising material system is LAGP (Li1+xAlxGe2−x(PO4)3 with x = 0.3–0.7. The measured values of the ionic conductivities were in the range of 0.1 to 1 mS cm−1 at room temperature, but exhibited an increasing behavior as a function of temperature, reaching a level of the order of 10 mS cm−1 above 200 °C [91]. In addition, it has been shown by Cui et al. and Mahmoud et al. that the ionic conductivity can be influenced by the microstructure using different sintering methods [92,93]. Figure 4 shows, e.g., that microwave-assisted sintering can enhance the ionic conductivity of LAGP in comparison to melt-quenching [92]. Only recently, Rohde et al. have reported that the thermal conductivity of LAGP varies only slowly as a function of temperature, but its level depends on the composition. The apparent specific heat relies likewise upon the composition and exhibits enthalpy changes because of phase transitions at higher temperatures for LAGP samples with x > 0.5 [61].
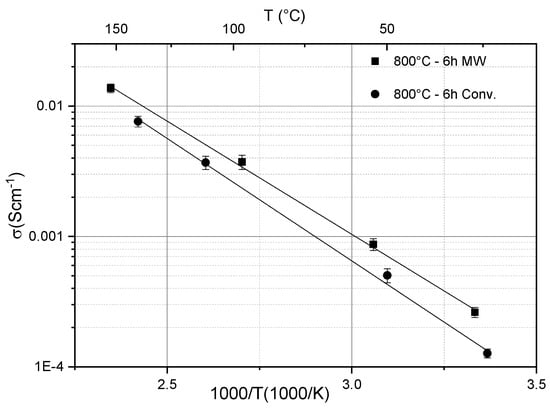
Figure 4.
Ionic conductivity of LAGP glass-ceramics samples heat-treated at 800 °C for 6 h using 30 GHz microwave and conventional heating [92].
4.1.4. Ionic Liquids
Unlike the standard electrolytes that are obtained by dissolution of salts in molecular solvents, the ionic liquids (ILs) are obtained by the melting down or liquefaction of a salt by providing a heat to counterbalance the salt lattice energy. The ionic liquids benefit from excellent properties, for example, non-volatility, non-combustibility, thermal and chemical stability, high ionic conductivity, and wide potential range, which makes them an ideal alternative to be used as electrolyte in batteries [94].
Zheng et al. [53] reported the effect of temperature on the physiochemical properties of an ionic liquid comprising of Trimethylhexylammonium (TMHA) cation and bis (trifluoromethane) sulfonylimide (TFSI) anion containing various concentrations of LiTFSI salt. They fitted the experimental density and viscosity data of the TMHA-TFSI ionic liquid to the linear model presented in Equation (30) and to the Arrhenius model in Equation (31), respectively. Figure 5a shows a linear decrease in the solution density with the temperature, and Figure 5b shows the decrease in the solution viscosity with the temperature for the TMHA-TFSI ionic liquid containing different concentrations of LiTFSI salt.
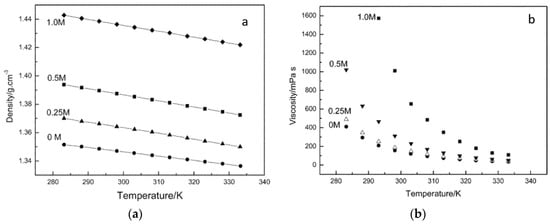
Figure 5.
(a) Variation in solution density, and (b) solution viscosity with temperature for TMHA-TFSI ionic liquid containing different concentrations of LiTFSI salt [53].
Shobukawa et al. [95] studied the temperature-dependent molar conductivity and ionic conductivity for novel lithium salts of borates having two electron-withdrawing groups (either 1,1,1,3,3,3-hexafluoro-2-propoxy or pentafluorophenoxy group) and two methoxy-oligo (ethylene oxide) groups (number of repeating unit: n = 3, 4, 7.2). They used the Nernst–Einstein Equation to correlate the molar conductivity of the ionic liquids with the diffusion coefficients of the cation and anion as below
They also exhibited the Arrhenius plots of the ionic conductivity for the ionic liquids as in Equation (33).
They measured the ionic conductivity of the developed ionic liquids as 10−5 to 10−4 S cm−1 at 30 °C, which is lower than that of typical ionic liquids by two orders of magnitude. They explained the increase in the ionic conductivity of the solution with increasing temperatures by the inverse proportion of the solution viscosity with temperature based on the Vogel–Fulcher–Tammann–Hesse law
where A, B and T0 are constants, and T is the absolute temperature.
4.2. Electrode Materials
Temperature can strongly affect the mass transfer, reaction kinetics, and charge transfer rates in the electrodes. The most temperature-dependent parameters in the solid phases are the current density, the diffusion rates, the conductivity, and the reaction rate constant. The local current density due the electrochemical reactions per active material area is governed by the Butler–Volmer Equation and is given by
where is the temperature-dependent exchange current density, and it is expressed as [96]
Kumar et al. [54] calculated the value of as a function of the temperature and showed that it changes from 5.5 to 730 mA/cm2 when the temperature changes from −20 to 60 °C. Therefore, they reported that the low discharge capacity of the cell can be related to very low values of the at subzero temperatures.
The temperature-dependent behavior of the Li ion diffusion coefficient in the solid phase () [34,97,98,99], the solid phase electronic conductivity () [100], and the reaction constant () [26], follows an Arrhenius law as stated in Equations (37)–(40). The constant diffusion coefficient at the reference temperature is a function of SOC as presented in Equation (38).
Xu et al. [26] reported the values to be 20 kJ/mol for the LFP (LiFePO4) cathode and 4 kJ/mol for the anode. They also reported the as below
The coefficients for different Lithium metal oxide cathodes in the temperature range −198 to 27 °C are reported by Heikes and Johnston [100].
The values for and are reported as 3 × 10−11 m2.5 mol−0.5/s and 20 kJ/mol for the LFP cathode, and similarly, they are reported as 1.2 × 10−14 m2.5 mol−0.5/s and 30 kJ/mol for the anode [99].
5. Temperature Effects on LIB’s Aging Mechanisms
5.1. Temperature-Dependent Aging Mechanisms
Identifying the exact aging mechanisms of LIBs has been one of the main challenges for the researchers. There are numerous factors that influence battery capacity loss and resistance growth which makes understanding of the aging mechanisms more complicated [101,102,103,104,105]. The main factors known to influence the degradation rate of the LIBs are the temperature [16,106], the low or high SOC [107,108], and the current [109]. The degradation process mainly takes place in the electrodes, and there are significant differences between the aging mechanisms of positive and negative electrodes. The main aging mechanisms have been known for a long time [16] and can be summarized as: [110]
- Structural changes in the insertion electrode;
- Electrolyte decomposition;
- Active material dissolution;
- Phase change in the insertion electrode;
- Passive film formation over electrodes and current collector surface.
By developing an electrochemical based electrical (ECBE) model and linking the model parameters to specific ageing mechanisms, Leng et al. [111] have shown recently on a graphite/LCO coin cell that the LIB degradation is a hierarchical process that returns, as indicated by a progression of associated forms. These procedures are: (i) solid electrolyte interphase (SEI) growth on the anode surfaces; (ii) cathode phase change from active hexagonal to less active spinel phases; (iii) Joule heating because of the raised cell resistance resulting in the cracking and re-growth of SEI along with surface spallation at the cathode, as well as degradation of the separator; (iv) active Li losses as a result of metal plating on the electrodes during overcharge and over discharge; (v) exfoliation of the negative electrode and the degradation of positive electrode; and (vi) intergranular contact detachment inside electrodes. These procedures results in overall decay in the capacity limit and the LIB working potential in an unexpected way.
The operating temperature of the LIBs greatly influences the electrochemical performance, the cycle life, and the safety of the batteries [5,7,110,111,112]. It is also one of the main factors affecting the aging rate of the batteries. In recent years, many researchers have studied the effects of operating temperature on the aging mechanisms. Markevich et al. [113] studied the behavior of graphite electrode at elevated temperatures (up to 80 °C); Ramadass et al. [114] studied the capacity fade of Sony 18,650 Li-ion cells at room temperature, 45, 50, and 55 °C; Handel et al. [115] studied the thermal decomposition of the electrolyte, and Bodenes et al. [116] investigated the high-temperature influences on the degradation process of positive electrode’s binder, SEI, and positive active material. Uddin et al. [117] summarized the effects of high operating temperature on negative and positive electrodes, respectively. The effects of temperature on the degradation rate of electrodes will be discussed separately in the following sections. The electrolyte aging mechanisms can be regarded as a part of electrode aging and will not be discussed separately.
5.1.1. Temperature Effect on Aging of the Negative Electrode
The most common materials chosen as the negative electrode for LIBs are graphite, carbon, silicone or Lithium titanate Li4Ti5O12 (LTO) [101,118]. Graphite anodes have some advantages over the other anode electrodes such as high capacity, low cost, long cycle life, low volume expansion, and safety [101,119,120]. Despite these advantages, as an anode material, its aging is significantly depending on the operating temperature, which limits the LIBs’ application on subzero and high ambient temperatures. The temperature dependent aging mechanisms of the anode material are reviewed below, and they are summarized in Figure 6.
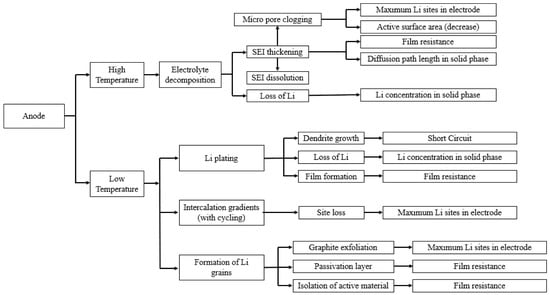
Figure 6.
Schematic of the temperature effect on aging of the negative electrode (re-elaborated from Uddin et al. [117]).
High Temperature
The common electrolytes used in Li-ion cells are not electrochemically stable at the voltage range that battery anodes are operating. Therefore, the main aging mechanism of a graphite electrode is believed to be the formation and growth of the solid electrolyte interphase (SEI) on the electrode surface with time [105]. The SEI layer is developed through the reduction in electrolyte components and the formation of a passive film at zero potential on the graphite surface [16,102,121]. Since the SEI layer is not fully permeable for the lithium ions, the amount of recyclable lithium ions decreases as the thickness of the SEI layer increases with the number of cycles, which leads to capacity fading [122]. Another possible graphite aging mechanism can be solvent co-intercalation into the carbon and exfoliation of the carbon particles. This process results in the formation of carbon intercalation compounds (CIC), which in turn lead to irreversible capacity fading [12,123,124].
The developed SEI layer is not thermally stable, and increased temperature results in an increased degradation rate of the SEI layer [125]. The collapsed SEI layer must be replaced by a new one. Thus, more Lithium ions are consumed in the new SEI layer replacement process. Moreover, the old broken layer fills the empty volumes, resulting in decreased available surface area on the active material [126]. A high temperature also accelerates the formation of CIC. Leng et al. [110] used an electrochemistry-based model to investigate the effect of temperature on the aging behavior of a cycled LIB within the temperature range from 25 to 55 °C. They have studied the impact of temperature on the aging rate of LCO electrode (cathode), graphite electrode (anode), and electrolyte separately. Based on their study, both of the aging mechanisms of graphite electrode (SEI and CIC growth) lead to more degradation at higher operating temperatures. Another negative impact is that at high temperatures, metastable organic SEI components are converted into more stable inorganic components. Since these inorganic components are more stable, their growth may decrease the conductivity of the SEI layer [127].
Low Temperature
On the other hand, the cold operating temperature, in conjunction with the high charging rate and non-uniform current distribution result in lithium plating on the negative electrode [128]. Lithium plating is defined as precipitation of the lithium ions on the electrode surface when the potential of the electrode is very close to that of the lithium deposition potential. The main reason is the reduced rate of Li ion diffusion into the anode particles and accumulation of the ions as inactive metallic Li on the particles surface at the low potential of the anode. Therefore, lithium plating at lower temperatures decreases the amount of cyclable lithium ions and results in capacity fading [129,130]. Uddin et al. [117] summarized the effects of low operating temperature on a negative electrode.
Another effect of low temperature on the anode is the intercalation gradient with cycling which accelerates the electrode aging. At low temperatures, when the cell is charged at higher current rates, a mechanical strain is applied on the anode due to a sharp ion gradient which results in crack formation and splits in the graphite particles [127,131,132].
5.1.2. Temperature Effect on Aging of the Positive Electrode
A large number of previous studies have been focused on the degradation mechanisms of the lithium metal oxide cathodes [104,133,134,135]. Briefly, the changes that have been observed on the lithium oxide metals are: [16,103,105,136,137]
- Degradation of active material;
- Degradation of cathode components such as conductive agents, binder, corrosion of current collectors;
- Electrolyte oxidation and SEI formation;
- Interaction between the aging products of a positive electrode (dissolved within the electrolyte) with a negative electrode.
The thermal stability of a cathode material has been one of the most important safety-related concerns of cell manufacturers and researchers [138]. The LiMPO4 cathodes, where M stands for transition metals such as Fe, Mn and Co, have attracted much attention due to their better stability at elevated temperatures and good safety features [139]. However, the transition metal oxide cathodes suffer from the dissolution of the transition metals into the electrolyte at high temperatures and high SOC. This process not only affects the cathode morphology, but also changes the SEI layer composition on the anode surface. After the dissolution in the electrolyte, the transition metals migrate through the electrolyte and subsequently deposit on the anode side where they can from dendrites on the anode surface or react with the SEI layer to form new compositions [140]. According to many researchers [141,142,143], Ni is the most stable transition metal in terms of dissolution in electrolytes and, in comparison with the other common transition metals, the following decreasing order has been observed: Mn > Co > Ni. The low Ni dissolution can be explained by the stable NiO-like rocksalt phase generated at high potential via loss of oxygen [140].
The other high-temperature degradation mechanism at the cathode side is related to the oxidation of the electrolyte at the cathode electrolyte interface (CEI) and the instability of the CEI itself [144]. These processes are irreversible and result in a passivation film formation on the cathode surface, which is called a surface layer or passivation film. The electrolyte oxidation occurs when the Fermi level of the cathode material is located below the electrolyte HOMO (highest occupied molecular orbital) level [145]. Edstrom et al. [146] studied the temperature effect on the cathode-electrolyte interface for different cathode chemistries: LiMn2O4, LiCoO2/LiNi0.8Co0.2O2, and carbon-coated LiFePO4. They reported that the composition of the SEI layer on the cathode surface is dependent on the chemistry of the cathode material. However, in all of the cases, the thickness of the SEI layer on the cathode side is increased with the increasing temperature indicating the higher electrolyte oxidation at higher temperatures. Leng et al. [110] studied the effect of temperature on the degradation of a LCO (LiCoO2) cathode. They found that degradation of an LCO electrode could be related to two main mechanisms: formation of SEI layer and structural/phase change of the electrode. Both of these two mechanisms reduce the reaction rate of the Li ion insertion/de-intercalation and the charge transfer rates. Furthermore, the influence of these mechanisms on degradation of the LCO electrode increases with temperature. This impact is more evident for a larger number of cycles [147,148]. The temperature dependence of the cathode material is summarized in Figure 7.
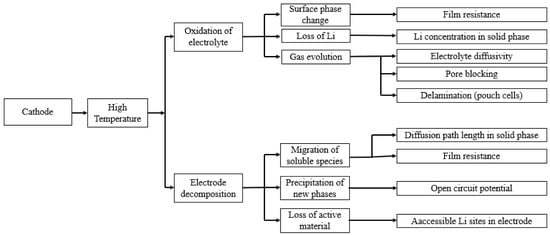
Figure 7.
Schematic of the temperature effect on aging of the positive electrode (re-elaborated from Uddin et al. [117]).
Unlike the high-temperature effects on the cathode aging, there are limited studies on the low- temperature effects. Many researchers such as Gandoman et al. [149] and Uddin et al. [117] have neglected the low-temperature effects on the cathode aging. However, Wu et al. [150], who applied non-destructive aging detection methods on LIBs, reported that the vulnerability to low-temperature (10 °C) primarily originates from cathode. They explained this phenomena by the increased charge-transfer resistance in the electrode–electrolyte interface due to the passive layer growth and phase transitions on the cathode surface.
5.1.3. Temperature Effect on the Electrolyte Decomposition
The concerns over aging of electrolytes necessitates to study the thermal stability of the electrolyte at elevated and low operating temperatures. Contrary to electrode material, thermal stability of the electrolytes has not been studied so much. The electrolytes which tolerates both elevated and very low temperatures are especially important in military and space-related applications [151]. The main reason of electrolyte decomposition at elevated temperature is reported to be the decomposition or hydrolysis of LiPF6 by trace moisture which results in the formation of Lewis acid, HF, PF5, or POxFy. These formed components later interact with the cyclic or linear carbonates of the solvent and causes the electrolyte to be decomposed [58]. Botte et al. [152] used a differential scanning calorimeter to study thermal stability of the LiPF6–EC:EMC electrolyte, and they reported that it is highly dependent on the salt concentration, the solvent concentration, and the heating rates. Eshetu et al. [153] reported that cyclic solvents such as EC and PC, are more thermally stable than linear solvents such as DMC and DEC. Especially for LiNi1-x-yMnxCoyO2 (NMC) cathodes with high Ni content, such as LiNi0.8Mn0.1Co0.1O2 (NMC811), even at room temperature, the electrolyte decomposition plays a major role at elevated operating voltage [154].
5.2. Modeling of Temperature-Dependent Aging Mechanisms
Modeling of the aging mechanisms and degradation rate is necessary for lifetime prognosis of LIBs [155] and reducing the time and the cost needed for the experimental aging tests [23,156,157,158]. There are a number of aging models in the literature such as models based on neural networks (machine learning) [159,160,161,162,163,164], physiochemical models [165,166,167], and empirical models [108,168,169,170]. The temperature effect on the aging of LIBs has been well studied and formulated. The proposed models for both calendar and cycle aging are reviewed below.
5.2.1. Calendar Aging Model
Calendar aging is described as the capacity loss due to progress in time that occurs independent of charge/discharge cycling. The calendar capacity loss is described with a square-root dependence on time, which accounts for the diffusion-limited capacity loss. Most studies done on calendar aging mechanism suggest that the rate of calendar aging of the battery strongly depends on the temperature and the SOC (potential that the battery is kept) [171,172,173,174]. A high temperature accelerates the rate of chemical side reactions, which in turn results in increasing the SEI layer thickness and irreversible Li ion loss [175,176,177].
Schimpe et al. [178] reported a model predicting the cyclic aging with time in which the capacity loss is proportional to the square root of time.
where is a stress factor and is a function of time and SOC, as shown in Equation (42)
where is defined as the calendar reference stress factor at and , is the open circuit potential at SOC = 50%, and is a constant.
Xu et al. [179] also modeled the calendar aging as time, temperature, and SOC dependent stress factors as the following equations. However, they proposed that the time stress factor changes linearly with time.
where the stress model for temperature and SOC is derived from Arrhenius law, and the stress model for time is obtained as:
Wang et al. [175] proposed that calendar aging is mostly affected by temperature and time, but they ignored the SOC effect.
5.2.2. Cyclic Aging Model
Cyclic aging includes all the degradation processes when the battery is cycled using any kind of load profile [180,181,182]. Cyclic aging mechanisms are different and depend on several factors. Schimpe et al. [178] proposed a model for the temperature and SOC-dependent cyclic aging and investigated the dominant cyclic aging mechanism separately. The main cyclic aging mechanisms are: [103,178,183,184]
- High Temperature ;
- Low Temperature ;
- Low Temperature, High SOC .
Thus, the temperature-dependent cycling aging models are different at low and high temperatures. At high temperature levels, the cyclic aging is proportional to the total charge throughput during both charging and discharging (), as shown in Equation (45).
The cyclic aging stress factor is a function of the temperature, which is expressed as
At low temperatures, the cyclic aging depends on both temperature and current rate, and it is proportional to the square root of charging aging, .
The cyclic stress factor at low temperature as a function of the temperature and charging current is given as follows
where is a constant.
The last cyclic aging mechanism is associated with the mechanism at low temperature and high SOC which is expressed as
For the mentioned mechanism, the cyclic aging stress factor is a function of the temperature, the charging current, and the SOC, and is expressed as follows
The parameters obtained from fitting the data for cyclic aging can be found in the work of Schimpe et al [178]. Overall, the combined calendar and cyclic aging can be expressed as follows: [178]
Wang et al. proposed two main aging mechanism for the LIB with composite cathode material which are high current rates at low temperature (cycle aging) and Li ion loss at high temperature due to increased side reactions and SEI layer thickness increase (cycle and calendar aging) [138]. Their proposed model for total aging (cycle and calendar) is as below
Xu et al. [179] proposed a semi-empirical aging model based on the stress models as in Equation (53). They ignored the C-rate effects in their model and linked it to the battery operating temperature.
6. Temperature Effects on LIB’s Performance and Safety
The temperature effect on battery resistances, physiochemical-thermal properties, and aging mechanisms have been reviewed in the previous sections. Variations in the aforementioned properties with temperature affect LIB’s electrochemical performance, safety, and the cycle life of the battery. Table 1 and Table 2 are summarizing the thermal effects on LIB’s performance and safety, respectively.

Table 1.
Review of thermal effects on lithium-ion batteries (LIB)’s performance and safety.

Table 2.
Review of thermal effects on LIB’s safety.
Besides the absolute temperature of a battery, non-uniform temperature distribution between the cells inside a battery pack and within each cell causes electric unbalances, poor battery performance, and capacity and power fading [207,208,209,210,211]. Temperature non-uniformity along single cell layers causes non-uniform current density along the cell and, consequently, localized aging [15,193,212,213]. Chiu et al. [214] developed an aging model to simulate and analyze the capacity fade of ten series connected cells operated at different temperatures. According to their study, by setting each cell with a different temperature, the whole battery pack’s capacity is limited by the highest temperature cell. Troxler et al. [215] applied a controlled temperature gradient between the cells of a battery pack with one hundred cells and proposed a model for the effect of the temperature gradient on the cell resistances. In this approach, they computed the equivalent resistance of sets of resistors that are connected in parallel, and each resistor is a function of temperature
where is the effective resistor of a pack with a temperature gradient between the cells, and R is a temperature-dependent resistance parameter. They used an Arrhenius Equation to describe the SEI resistance and the charge transfer resistance as a function of temperature, as in Equation (55)
Klein et al. [216] studied the effects of a temperature gradient on the nominal capacity of a 10Ah Li ion pouch cell. They used a PID temperature controller to apply controlled non-uniform temperature conditions and performed hybrid pulse power characterization (HPPC) tests to figure out the instantaneous power capability effects. They found that the overpotential values increase as the temperature gradient (∆T) increases. Moreover, they reported that the overpotential sensitivity to ∆T is more distinguished at lower temperature levels, and the temperature gradient influences the maximum capacity as the SOC decreases with increasing ∆T.
7. Conclusions
After a comprehensive analysis of the literature, this paper reports a consensus on the massive influence of the temperature on the key cell components and parameters. Among these, the open-circuit voltage, solid-state kinetics in the electrodes, electrolyte conductivity, and growth phenomena of the SEI layer play the main role.
Consequently, the temperature also affects the macroscopic behaviour of the cell, thus the available capacity and power capability are enhanced or massively reduced by temperatures outside of the favourable operating range between 10 and 35 °C for almost any lithium-ion cell. Outside of this range, the cycle or calendar life suffers from reduction. The predominant ageing mechanism caused by the low temperature is the plating of metallic lithium on the anode, while the elevated temperatures accelerate the degradation of the cathode and SEI layer growth on the anode, leading to capacity fade and internal resistance increase. In the worst case, the temperature triggers reactions which could give rise to critical hazardous conditions like a thermal runaway. In this work, the main thermal–chemical–physical governing equations and their dependency from temperature have been summarized. These are essential for overcoming the thermal issues of the LIBs. The work proposes an organically organized collection of the most relevant temperature-dependant cell-governing equations. Moreover, for these relationships, initial parameter sets have been provided which help the reader to select and implement the specific equation in his own investigations. Examples of typical application problems are the physicochemical simulation of new cells as well as the development of the battery management system, which usually aims to maintain the battery within the optimum temperature and voltage windows for maximal performance and cycle life achievement.
Author Contributions
Conceptualization, M.A., F.V.C. and R.K.; writing—original draft preparation, M.A.; writing—review and editing, F.V.C. and C.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This work was supported by the Koc University, and the Koc University Tupras Energy Center (KUTEM).
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| A0 | Preexponential factor | SDOD | DOD dependent stress factor |
| Aio | Cell exchange current density multiplier | SSOC | SOC dependent stress factor |
| as | Electrode specific surface area (m−1) | St(t) | Time dependent stress factor |
| C0 | Nominal capacity (mAh) | ST(T) | Temperature dependent stress factor |
| CB | Bulk concentration of electroactive species (mol/m3) | t | Time (s) |
| ce | Lithium concentration in electrolyte (mol/m3) | T | Absolute temperature (K) |
| CE | Concentration in an electrode (mol/m3) | Tg | Glass transition temperature (K) |
| Cp | Specific heat (J/kg.K) | Tref | Reference temperature (K) |
| cs | Solid phase concentration (mol/m3) | x | Coordinate |
| cs,max | Maximum concentration that can be taken from the electrode (mol/m3) | t+ | Transferring number of Li+ |
| De | Diffusion coefficient of Li ion in electrolyte (m2/s) | Greek Letters | |
| Ds | Diffusion coefficient of Li ion in solid (m2/s) | α | Transfer coefficient |
| E0 | Open circuit potential (V) | Li poor phase | |
| Ea | Reaction activation energy (J/mol) | Li rich phase | |
| EaD | Diffusion activation energy (J/mol) | ∆G | The change in the cell’s standard free energy (J/mol) |
| Eσ | Energy barrier against conductivity (J/mol) | ∆H | Enthalpy change (J/mol) |
| Eμ | Energy barrier hindering the ions to move (J/mol) | ∆H0 | Enthalpy change of activation for the Li-Li+ reaction (J/mol) |
| F | Faraday’s constant (96,487 C/mol) | ∆S | Entropy change (J/mol) |
| i | Current (A) | η | Overpotential (V) |
| i0 | Exchange current density (A/m2) | ηco | Concentration overpotential (V) |
| iloc | Local current density (A/m2) | ηct | Charge transfer overpotential (V) |
| k | Thermal conductivity (W/m.K) | ηΩ | Ohmic overpotential (V) |
| KCal | Calendar stress factor | Λ | Molar conductivity (S/m) |
| KCyc | Cyclic factor | μ | Dynamic viscosity (m2/s) |
| ks | Reaction rate constant (m2.5/mol0.5.s) | Density (kg/m3) | |
| n | Number of transferred ions | σs | Electronic conductivity of the solid phase (S/m) |
| p | Pressure (Pa) | σe | Ionic conductivity of electrolyte (S/m) |
| QCal | Calendric capacity loss (mAh) | Potential (V) | |
| QCyc | Cyclic capacity loss (mAh) | Subscripts, Superscripts and Acronyms | |
| QCh | Charging aging | 0 | Initial value |
| QV | Volumetric heat (W/m3) | a | Anode |
| Qirr,V | Irreversible heat (W/m3) | c | Cathode |
| Qohm,V | Ohmic heat (W/m3) | Cal | Calendar |
| Qpt,V | Phase transition heat (W/m3) | Ch | Charging |
| Qrev,V | Reversible heat generation (W/m3) | Cyc | Cyclic |
| R | Universal gas coefficient (8.314 J/mol.K) | eff | Efficient |
| Rct | Contact resistance (Ω) | e | Electrolyte |
| Reff | Effective resistance (Ω) | n | Indicator |
| Ri | Internal impedance (Ω) | max | Maximum |
| RSEI | Surface film resistance (Ω) | ref | Reference |
| s | Solid | ||
References
- Zubi, G.; Dufo-López, R.; Carvalho, M.; Pasaoglu, G. The lithium-ion battery: State of the art and future perspectives. Renew. Sustain. Energy Rev. 2018, 89, 292–308. [Google Scholar] [CrossRef]
- Ding, Y.; Cano, Z.P.; Yu, A.; Lu, J.; Chen, Z. Automotive Li-ion batteries: Current status and future perspectives. Electrochem. Energy Rev. 2019, 2, 1–28. [Google Scholar] [CrossRef]
- Goodenough, J.B.; Park, K.-S. The Li-ion rechargeable battery: A perspective. J. Am. Chem. Soc. 2013, 135, 1167–1176. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Source 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Bandhauer, T.M.; Garimella, S.; Fuller, T.F. A critical review of thermal issues in lithium-ion batteries. J. Electrochem. Soc. 2011, 158, R1–R25. [Google Scholar] [CrossRef]
- Tarascon, J.-M.; Armand, M. Issues and challenges facing rechargeable lithium batteries. In Materials for Sustainable Energy: A Collection of Peer-Reviewed Research and Review Articles from Nature Publishing Group; World Scientific: Singapore, 2011; pp. 171–179. [Google Scholar]
- Wen, J.; Yu, Y.; Chen, C. A review on lithium-ion batteries safety issues: Existing problems and possible solutions. Mater. Express 2012, 2, 197–212. [Google Scholar] [CrossRef]
- Rao, Z.; Wang, S. A review of power battery thermal Energy management. Renew. Sustain. Energy Rev. 2011, 15, 4554–4571. [Google Scholar] [CrossRef]
- Alipour, M.; Esen, E.; Varzeghani, A.R.; Kizilel, R. Performance of high capacity Li-ion pouch cells over wide range of operating temperatures and discharge rates. J. Electroanal. Chem. 2020, 860, 113903. [Google Scholar] [CrossRef]
- Rezvanizaniani, S.M.; Liu, Z.; Chen, Y.; Lee, J. Review and recent advances in battery health monitoring and prognostics technologies for electric vehicle (EV) safety and mobility. J. Power Source 2014, 256, 110–124. [Google Scholar] [CrossRef]
- Wenzl, H.; Baring-Gould, I.; Kaiser, R.; Liaw, B.Y.; Lundsager, P.; Manwell, J.; Ruddell, A.; Svoboda, V. Life prediction of batteries for selecting the technically most suitable and cost effective battery. J. Power Source 2005, 144, 373–384. [Google Scholar] [CrossRef]
- Ning, G.; Haran, B.; Popov, B.N. Capacity fade study of lithium-ion batteries cycled at high discharge rates. J. Power Source 2003, 117, 160–169. [Google Scholar] [CrossRef]
- Qian, K.; Zhou, C.; Yuan, Y.; Allan, M. Temperature effect on electric vehicle battery cycle life in vehicle-to-grid applications. In Proceedings of the 2010 China International Conference on Electricity Distribution, Nanjing, China, 13–16 September 2010; pp. 1–6. [Google Scholar]
- Dubarry, M.; Svoboda, V.; Hwu, R.; Liaw, B.Y. Capacity loss in rechargeable lithium cells during cycle life testing: The importance of determining state-of-charge. J. Power Source 2007, 174, 1121–1125. [Google Scholar] [CrossRef]
- Song, W.; Chen, M.; Bai, F.; Lin, S.; Chen, Y.; Feng, Z. Non-uniform effect on the thermal/aging performance of Lithium-ion pouch battery. Appl. Therm. Eng. 2018, 128, 1165–1174. [Google Scholar] [CrossRef]
- Vetter, J.; Novák, P.; Wagner, M.R.; Veit, C.; Möller, K.-C.; Besenhard, J.; Winter, M.; Wohlfahrt-Mehrens, M.; Vogler, C.; Hammouche, A. Ageing mechanisms in lithium-ion batteries. J. Power Source 2005, 147, 269–281. [Google Scholar] [CrossRef]
- Zhang, S.S.; Xu, K.; Jow, T.R. A new approach toward improved low temperature performance of Li-ion battery. Electrochem. Commun. 2002, 4, 928–932. [Google Scholar] [CrossRef]
- Zhang, S.S.; Xu, K.; Jow, T.R. The low temperature performance of Li-ion batteries. J. Power Source 2003, 115, 137–140. [Google Scholar] [CrossRef]
- Zhang, S.S.; Xu, K.; Jow, T.R. Electrochemical impedance study on the low temperature of Li-ion batteries. Electrochim. Acta 2004, 49, 1057–1061. [Google Scholar] [CrossRef]
- Nagasubramanian, G. Electrical characteristics of 18650 Li-ion cells at low temperatures. J. Appl. Electrochem. 2001, 31, 99–104. [Google Scholar] [CrossRef]
- Gong, X.; Mi, C.C. Temperature-dependent performance of lithium ion batteries in electric vehicles. In Proceedings of the 2015 IEEE Applied Power Electronics Conference and Exposition, Charlotte, NC, USA, 13 March 2015; pp. 1065–1072. [Google Scholar]
- Motloch, C.G.; Christophersen, J.P.; Belt, J.R.; Wright, R.B.; Hunt, G.L.; Sutula, R.A.; Duong, T.; Tartamella, T.J.; Haskins, H.J.; Miller, T.J. High-Power Battery Testing Procedures and Analytical Methodologies for HEV’s. SAE Trans. 2002, 111, 797–802. [Google Scholar]
- Ecker, M.; Gerschler, J.B.; Vogel, J.; Käbitz, S.; Hust, F.; Dechent, P.; Sauer, D.U. Development of a lifetime prediction model for lithium-ion batteries based on extended accelerated aging test data. J. Power Source 2012, 215, 248–257. [Google Scholar] [CrossRef]
- Hariharan, K.S.; Tagade, P.; Ramachandran, S. Mathematical Modeling of Lithium Batteries: From Electrochemical Models to State Estimator Algorithms; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Bahiraei, F.; Ghalkhani, M.; Fartaj, A.; Nazri, G.-A. A pseudo 3D electrochemical-thermal modeling and analysis of a lithium-ion battery for electric vehicle thermal management applications. Appl. Therm. Eng. 2017, 125, 904–918. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, Z.; Wang, X.; Jia, L.; Yang, L. A pseudo three-dimensional electrochemical—Thermal model of a prismatic LiFePO4 battery during discharge process. Energy 2015, 80, 303–317. [Google Scholar] [CrossRef]
- David, L.; Thomas, B.R. Handbook of Batteries; McGraw-Hill Professional: New York, NY, USA, 2001. [Google Scholar]
- O’M, B.J.; Reddy, A. Modern Electrochemistry; MacDonald Technical and Scientific: London, UK, 1970; Volume 2. [Google Scholar]
- West, A.C.; Deligianni, H.; Andricacos, P.C. Electrochemical planarization of interconnect metallization. IBM J. Res. Dev. 2005, 49, 37–48. [Google Scholar] [CrossRef]
- Broadhead, J.; Kuo, H.C. Electrochemical principles and reactions. In Handbook of Batteries; McGraw-Hill Professional: New York, NY, USA, 2001. [Google Scholar]
- Butler, J.A.V. Hydrogen overvoltage and the reversible hydrogen electrode. Proc. R. Soc. Lond. A 1936, 157, 423–433. [Google Scholar]
- Bockris, J.O.M.; Reddy, A.K. Modern Electrochemistry 2B: Electrodics in Chemistry, Engineering, Biology and Environmental Science; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2000; Volume 2. [Google Scholar]
- Barsoukov, E.; Macdonald, J.R. Impedance Spectroscopy: Theory, Experiment, and Applications; John Wiley and Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Guo, M.; Sikha, G.; White, R.E. Single-particle model for a lithium-ion cell: Thermal behavior. J. Electrochem. Soc. 2011, 158, A122–A132. [Google Scholar] [CrossRef]
- Gao, L.; Liu, S.; Dougal, R.A. Dynamic lithium-ion battery model for system simulation. IEEE Trans. Compon. Packag. Technol. 2002, 25, 495–505. [Google Scholar]
- Johnson, V.H.; Pesaran, A.A.; Sack, T. Temperature-Dependent Battery Models for High-Power Lithium-Ion Batteries; National Renewable Energy Laboratory City of Golden: Golden, CO, USA, 2001.
- Chang, M.-T.; Lin, Y.-S.; Ling, S.-H.; Liang, S.-H.; Lin, C.-H.; Chen, K.-C. Identification of the Parameters in Equivalent Circuit Model of Lithium-Ion Batteries. ECS Trans. 2014, 61, 125–130. [Google Scholar] [CrossRef]
- Heins, T.P.; Harms, N.; Schramm, L.S.; Schröder, U. Development of a new Electrochemical Impedance Spectroscopy Approach for Monitoring the Solid Electrolyte Interphase Formation. Energy Technol. 2016, 4, 1509–1513. [Google Scholar] [CrossRef]
- Kiehne, H.A. Battery Technology Handbook; CRC Press: Boca Raton, FL, USA, 2003; Volume 118. [Google Scholar]
- Suresh, P.; Shukla, A.; Munichandraiah, N. Temperature dependence studies of ac impedance of lithium-ion cells. J. Appl. Electrochem. 2002, 32, 267–273. [Google Scholar] [CrossRef]
- Andre, D.; Meiler, M.; Steiner, K.; Wimmer, C.; Soczka-Guth, T.; Sauer, D. Characterization of high-power lithium-ion batteries by electrochemical impedance spectroscopy. I. Experimental investigation. J. Power Source 2011, 196, 5334–5341. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, R.; Zhu, C.; Zhao, Y. On-line measurement of internal resistance of lithium ion battery for EV and its application research. Int. J. U E Serv. Sci. Technol. 2014, 7, 301–310. [Google Scholar] [CrossRef]
- Farmann, A.; Waag, W.; Sauer, D.U. Application-specific electrical characterization of high power batteries with lithium titanate anodes for electric vehicles. Energy 2016, 112, 294–306. [Google Scholar] [CrossRef]
- Galeotti, M.; Cinà, L.; Giammanco, C.; Cordiner, S.; Di Carlo, A. Performance analysis and SOH (state of health) evaluation of lithium polymer batteries through electrochemical impedance spectroscopy. Energy 2015, 89, 678–686. [Google Scholar] [CrossRef]
- Yang, S.; Deng, C.; Zhang, Y.; He, Y. State of charge estimation for lithium-ion battery with a temperature-compensated model. Energies 2017, 10, 1560. [Google Scholar] [CrossRef]
- Aurbach, D.; Markovsky, B.; Shechter, A.; Ein-Eli, Y.; Cohen, H. A comparative study of synthetic graphite and Li electrodes in electrolyte solutions based on ethylene carbonate-dimethyl carbonate mixtures. J. Electrochem. Soc. 1996, 143, 3809–3820. [Google Scholar] [CrossRef]
- Aurbach, D. Review of selected electrode–solution interactions which determine the performance of Li and Li ion batteries. J. Power Source 2000, 89, 206–218. [Google Scholar] [CrossRef]
- Peled, E. The electrochemical behavior of alkali and alkaline earth metals in nonaqueous battery systems—The solid electrolyte interphase model. J. Electrochem. Soc. 1979, 126, 2047–2051. [Google Scholar] [CrossRef]
- Mogi, R.; Inaba, M.; Iriyama, Y.; Abe, T.; Ogumi, Z. Surface film formation on nickel electrodes in a propylene carbonate solution at elevated temperatures. J. Power Source 2002, 108, 163–173. [Google Scholar] [CrossRef]
- Jow, T.R.; Delp, S.A.; Allen, J.L.; Jones, J.-P.; Smart, M.C. Factors limiting Li+ charge transfer kinetics in Li-ion batteries. J. Electrochem. Soc. 2018, 165, A361–A367. [Google Scholar] [CrossRef]
- Wang, C.; Appleby, A.J.; Little, F.E. Low-temperature characterization of lithium-ion carbon anodes via microperturbation measurement. J. Electrochem. Soc. 2002, 149, A754–A760. [Google Scholar] [CrossRef]
- Macdonald, R.; Franceschetti, D. The electrical analogs of physical and chemical processes. Impedance Spectrosc. 1987, 1, 27. [Google Scholar]
- Zheng, H.; Zhang, H.; Fu, Y.; Abe, T.; Ogumi, Z. Temperature effects on the electrochemical behavior of spinel LiMn2O4 in quaternary ammonium-based ionic liquid electrolyte. J. Phys. Chem. B 2005, 109, 13676–13684. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.S.; Satyavani, T.; Senthilkumar, M. Effect of temperature and charge stand on performance of lithium-ion polymer pouch cell. J. Energy Storage 2016, 6, 239–247. [Google Scholar] [CrossRef]
- Liao, X.-Z.; Ma, Z.-F.; Gong, Q.; He, Y.-S.; Pei, L.; Zeng, L.-J. Low-temperature performance of LiFePO4/C cathode in a quaternary carbonate-based electrolyte. Electrochem. Commun. 2008, 10, 691–694. [Google Scholar] [CrossRef]
- Marcinek, M.; Syzdek, J.; Marczewski, M.; Piszcz, M.; Niedzicki, L.; Kalita, M.; Plewa-Marczewska, A.; Bitner, A.; Wieczorek, P.; Trzeciak, T. Electrolytes for Li-ion transport—Review. Solid State Ion. 2015, 276, 107–126. [Google Scholar] [CrossRef]
- Xiao, L.; Zeng, Z.; Liu, X.; Fang, Y.; Jiang, X.; Shao, Y.; Zhuang, L.; Ai, X.; Yang, H.; Cao, Y. Stable Li metal anode with “ion-solvent-coordinated” nonflammable electrolyte for safe Li metal batteries. ACS Energy Lett. 2019, 4, 483–488. [Google Scholar] [CrossRef]
- Xu, K. Nonaqueous liquid electrolytes for lithium-based rechargeable batteries. Chem. Rev. 2004, 104, 4303–4418. [Google Scholar] [CrossRef]
- Jow, T.R.; Xu, K.; Borodin, O.; Ue, M. Electrolytes for Lithium and Lithium-Ion Batteries; Springer: Berlin/Heidelberg, Germany, 2014; Volume 58. [Google Scholar]
- Logan, E.; Tonita, E.M.; Gering, K.; Li, J.; Ma, X.; Beaulieu, L.; Dahn, J. A study of the physical properties of Li-Ion battery electrolytes containing esters. J. Electrochem. Soc. 2018, 165, A21. [Google Scholar] [CrossRef]
- Tarascon, J.; Guyomard, D. New electrolyte compositions stable over the 0 to 5 V voltage range and compatible with the Li1+ xMn2O4/carbon Li-ion cells. Solid State Ion. 1994, 69, 293–305. [Google Scholar] [CrossRef]
- Ding, M.S. Liquid phase boundaries, dielectric constant, and viscosity of PC-DEC and PC-EC binary carbonates. J. Electrochem. Soc. 2003, 150, A455–A462. [Google Scholar] [CrossRef]
- Zheng, J.; Zhao, Q.; Tang, T.; Yin, J.; Quilty, C.D.; Renderos, G.D.; Liu, X.; Deng, Y.; Wang, L.; Bock, D.C. Reversible epitaxial electrodeposition of metals in battery anodes. Science 2019, 366, 645–648. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Xian, F.; Guo, Z.; Lu, C.; Du, X.; Cheng, X.; Zhang, S.; Dong, S.; Cui, G.; Chen, L. Nonflammable Nitrile Deep Eutectic Electrolyte Enables High-Voltage Lithium Metal Batteries. Chem. Mater. 2020, 32, 3405–3413. [Google Scholar] [CrossRef]
- Ding, M.; Xu, K.; Zhang, S.; Amine, K.; Henriksen, G.; Jow, T. Change of conductivity with salt content, solvent composition, and temperature for electrolytes of LiPF6 in ethylene carbonate-ethyl methyl carbonate. J. Electrochem. Soc. 2001, 148, A1196–A1204. [Google Scholar] [CrossRef]
- Smedley, S.I. Electrical conductivity in ionic liquids at high temperatures. In The Interpretation of Ionic Conductivity in Liquids; Springer: Berlin/Heidelberg, Germany, 1980; pp. 101–132. [Google Scholar]
- Landesfeind, J.; Gasteiger, H.A. Temperature and Concentration Dependence of the Ionic Transport Properties of Lithium-Ion Battery Electrolytes. J. Electrochem. Soc. 2019, 166, A3079–A3097. [Google Scholar] [CrossRef]
- Stephan, A.M. Review on gel polymer electrolytes for lithium batteries. Eur. Polym. J. 2006, 42, 21–42. [Google Scholar] [CrossRef]
- Mauger, A.; Julien, C.; Paolella, A.; Armand, M.; Zaghib, K. Recent progress on organic electrodes materials for rechargeable batteries and supercapacitors. Materials 2019, 12, 1770. [Google Scholar] [CrossRef] [PubMed]
- Choudhury, S.; Stalin, S.; Vu, D.; Warren, A.; Deng, Y.; Biswal, P.; Archer, L.A. Solid-state polymer electrolytes for high-performance lithium metal batteries. Nat. Commun. 2019, 10, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Gray, F.M. Polymer Electrolytes, RSC Materials Monographs; The Royal Society of Chemistry: Cambridge, UK, 1997. [Google Scholar]
- Mindemark, J.; Lacey, M.J.; Bowden, T.; Brandell, D. Beyond PEO—Alternative host materials for Li+-conducting solid polymer electrolytes. Prog. Polym. Sci. 2018, 81, 114–143. [Google Scholar] [CrossRef]
- Mindemark, J.; Törmä, E.; Sun, B.; Brandell, D. Copolymers of trimethylene carbonate and ε-caprolactone as electrolytes for lithium-ion batteries. Polymer 2015, 63, 91–98. [Google Scholar] [CrossRef]
- Sun, B.; Mindemark, J.; Edström, K.; Brandell, D. Polycarbonate-based solid polymer electrolytes for Li-ion batteries. Solid State Ion. 2014, 262, 738–742. [Google Scholar] [CrossRef]
- Sun, B.; Mindemark, J.; Edström, K.; Brandell, D. Realization of high performance polycarbonate-based Li polymer batteries. Electrochem. Commun. 2015, 52, 71–74. [Google Scholar] [CrossRef]
- Sukeshini, A.M.; Nishimoto, A.; Watanabe, M. Transport and electrochemical characterization of plasticized poly (vinyl chloride) solid electrolytes. Solid State Ion. 1996, 86, 385–393. [Google Scholar] [CrossRef]
- Nest, J.F.L.; Gandini, A.; Cheradame, H. Crosslinked polyethers as media for ionic conduction. Br. Polym. J. 1988, 20, 253–268. [Google Scholar] [CrossRef]
- Maleki, H.; Deng, G.; Kerzhner-Haller, I.; Anani, A.; Howard, J.N. Thermal Stability Studies of Binder Materials in Anodes for Lithium-Ion Batteries. J. Electrochem. Soc. 2000, 147, 4470. [Google Scholar] [CrossRef]
- Wang, Q.; Ping, P.; Zhao, X.; Chu, G.; Sun, J.; Chen, C. Thermal runaway caused fire and explosion of lithium ion battery. J. Power Source 2012, 208, 210–224. [Google Scholar] [CrossRef]
- Liu, L.; Chu, L.; Jiang, B.; Li, M. Li1.4Al0.4Ti1.6 (PO4) 3 nanoparticle-reinforced solid polymer electrolytes for all-solid-state lithium batteries. Solid State Ion. 2019, 331, 89–95. [Google Scholar] [CrossRef]
- Zhao, Q.; Liu, X.; Stalin, S.; Khan, K.; Archer, L.A. Solid-state polymer electrolytes with in-built fast interfacial transport for secondary lithium batteries. Nat. Energy 2019, 4, 365–373. [Google Scholar] [CrossRef]
- Wang, X.; Zhai, H.; Qie, B.; Cheng, Q.; Li, A.; Borovilas, J.; Xu, B.; Shi, C.; Jin, T.; Liao, X. Rechargeable solid-state lithium metal batteries with vertically aligned ceramic nanoparticle/polymer composite electrolyte. Nano Energy 2019, 60, 205–212. [Google Scholar] [CrossRef]
- Paolella, A.; Zhu, W.; Bertoni, G.; Perea, A.; Demers, H.; Savoie, S.; Girard, G.; Delaporte, N.; Guerfi, A.; Rumpel, M. Toward an All-Ceramic Cathode–Electrolyte Interface with Low-Temperature Pressed NASICON Li1. 5Al0. 5Ge1. 5 (PO4) 3 Electrolyte. Adv. Mater. Interfaces 2020. [Google Scholar] [CrossRef]
- Inada, R.; Yasuda, S.; Hosokawa, H.; Saito, M.; Tojo, T.; Sakurai, Y. Formation and stability of interface between garnet-type Ta-doped Li7La3Zr2O12 solid electrolyte and lithium metal electrode. Batteries 2018, 4, 26. [Google Scholar] [CrossRef]
- Riphaus, N.; Stiaszny, B.; Beyer, H.; Indris, S.; Gasteiger, H.A.; Sedlmaier, S.J. Understanding chemical stability issues between different solid electrolytes in all-solid-state batteries. J. Electrochem. Soc. 2019, 166, A975–A983. [Google Scholar] [CrossRef]
- Bron, P.; Johansson, S.; Zick, K.; Schmedt auf der Günne, J.; Dehnen, S.; Roling, B. Li10SnP2S12: An affordable lithium superionic conductor. J. Am. Chem. Soc. 2013, 135, 15694–15697. [Google Scholar] [CrossRef] [PubMed]
- Kato, Y.; Hori, S.; Saito, T.; Suzuki, K.; Hirayama, M.; Mitsui, A.; Yonemura, M.; Iba, H.; Kanno, R. High-power all-solid-state batteries using sulfide superionic conductors. Nat. Energy 2016, 1, 1–7. [Google Scholar] [CrossRef]
- Janek, J.; Zeier, W.G. A solid future for battery development. Nat. Energy 2016, 1, 1–4. [Google Scholar] [CrossRef]
- Knauth, P. Inorganic solid Li ion conductors: An overview. Solid State Ion. 2009, 180, 911–916. [Google Scholar] [CrossRef]
- Mariappan, C.R.; Yada, C.; Rosciano, F.; Roling, B. Correlation between micro-structural properties and ionic conductivity of Li1.5Al0.5Ge1.5 (PO4) 3 ceramics. J. Power Source 2011, 196, 6456–6464. [Google Scholar] [CrossRef]
- Rohde, M.; Cui, Y.; Ziebert, C.; Seifert, H.J. Thermophysical Properties of Lithium Aluminum Germanium Phosphate with Different Compositions. Int. J. Thermophys. 2020, 41, 31. [Google Scholar] [CrossRef]
- Mahmoud, M.M.; Cui, Y.; Rohde, M.; Ziebert, C.; Link, G.; Seifert, H.J. Microwave crystallization of lithium aluminum germanium phosphate solid-state electrolyte. Materials 2016, 9, 506. [Google Scholar] [CrossRef]
- Cui, Y.; Mahmoud, M.M.; Rohde, M.; Ziebert, C.; Seifert, H.J. Thermal and ionic conductivity studies of lithium aluminum germanium phosphate solid-state electrolyte. Solid State Ion. 2016, 289, 125–132. [Google Scholar] [CrossRef]
- Galiński, M.; Lewandowski, A.; Stępniak, I. Ionic liquids as electrolytes. Electrochim. Acta 2006, 51, 5567–5580. [Google Scholar] [CrossRef]
- Shobukawa, H.; Tokuda, H.; Tabata, S.-I.; Watanabe, M. Preparation and transport properties of novel lithium ionic liquids. Electrochim. Acta 2004, 50, 305–309. [Google Scholar] [CrossRef]
- Verbrugge, M.W. Three-dimensionai temperature and current distribution in a battery module. AIChE J. 1995, 41, 1550–1562. [Google Scholar] [CrossRef]
- Bernardi, D.; Pawlikowski, E.; Newman, J. A general Energy balance for battery systems. J. Electrochem. Soc. 1985, 132, 5–12. [Google Scholar] [CrossRef]
- Hellwig, C.; Sörgel, S.; Bessler, W.G. A multi-scale electrochemical and thermal model of a LiFePO4 battery. ECS Trans. 2011, 35, 215–228. [Google Scholar] [CrossRef]
- Alipour, M.; Esen, E.; Kizilel, R. Investigation of 3-D multilayer approach in predicting the thermal behavior of 20 Ah Li-ion cells. Appl. Therm. Eng. 2019, 153, 620–632. [Google Scholar] [CrossRef]
- Heikes, R.; Johnston, W. Mechanism of conduction in Li-substituted transition metal oxides. J. Chem. Phys. 1957, 26, 582–587. [Google Scholar] [CrossRef]
- Antolini, E. LiCoO2: Formation, structure, lithium and oxygen nonstoichiometry, electrochemical behaviour and transport properties. Solid State Ion. 2004, 170, 159–171. [Google Scholar] [CrossRef]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Source 2013, 241, 680–689. [Google Scholar] [CrossRef]
- Broussely, M.; Biensan, P.; Bonhomme, F.; Blanchard, P.; Herreyre, S.; Nechev, K.; Staniewicz, R. Main aging mechanisms in Li ion batteries. J. Power Source 2005, 146, 90–96. [Google Scholar] [CrossRef]
- Wohlfahrt-Mehrens, M.; Vogler, C.; Garche, J. Aging mechanisms of lithium cathode materials. J. Power Source 2004, 127, 58–64. [Google Scholar] [CrossRef]
- Arora, P.; White, R.E.; Doyle, M. Capacity fade mechanisms and side reactions in lithium-ion batteries. J. Electrochem. Soc. 1998, 145, 3647–3667. [Google Scholar] [CrossRef]
- Fleckenstein, M.; Bohlen, O.; Roscher, M.A.; Bäker, B. Current density and state of charge inhomogeneities in Li-ion battery cells with LiFePO4 as cathode material due to temperature gradients. J. Power Source 2011, 196, 4769–4778. [Google Scholar] [CrossRef]
- Fu, R.; Xiao, M.; Choe, S.-Y. Modeling, validation and analysis of mechanical stress generation and dimension changes of a pouch type high power Li-ion battery. J. Power Source 2013, 224, 211–224. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Cycle-life model for graphite-LiFePO4 cells. J. Power Source 2011, 196, 3942–3948. [Google Scholar] [CrossRef]
- Savoye, F.; Venet, P.; Millet, M.; Groot, J. Impact of periodic current pulses on Li-ion battery performance. IEEE Trans. Ind. Electron. 2012, 59, 3481–3488. [Google Scholar] [CrossRef]
- Leng, F.; Tan, C.M.; Pecht, M. Effect of temperature on the aging rate of Li ion battery operating above room temperature. Sci. Rep. 2015, 5, 12967. [Google Scholar] [CrossRef]
- Leng, F.; Wei, Z.; Tan, C.M.; Yazami, R. Hierarchical degradation processes in lithium-ion batteries during ageing. Electrochim. Acta 2017, 256, 52–62. [Google Scholar] [CrossRef]
- Xu, K.; Zhang, S.; Jow, T.R.; Xu, W.; Angell, C.A. LiBOB as salt for lithium-ion batteries: A possible solution for high temperature operation. Electrochem. Solid State Lett. 2002, 5, A26–A29. [Google Scholar] [CrossRef]
- Markevich, E.; Pollak, E.; Salitra, G.; Aurbach, D. On the performance of graphitized meso carbon microbeads (MCMB)—Meso carbon fibers (MCF) and synthetic graphite electrodes at elevated temperatures. J. Power Source 2007, 174, 1263–1269. [Google Scholar] [CrossRef]
- Ramadass, P.; Haran, B.; White, R.; Popov, B.N. Capacity fade of Sony 18650 cells cycled at elevated temperatures: Part I. Cycling performance. J. Power Source 2002, 112, 606–613. [Google Scholar] [CrossRef]
- Handel, P.; Fauler, G.; Kapper, K.; Schmuck, M.; Stangl, C.; Fischer, R.; Uhlig, F.; Koller, S. Thermal aging of electrolytes used in lithium-ion batteries—An investigation of the impact of protic impurities and different housing materials. J. Power Source 2014, 267, 255–259. [Google Scholar] [CrossRef]
- Bodenes, L.; Naturel, R.; Martinez, H.; Dedryvère, R.; Menetrier, M.; Croguennec, L.; Pérès, J.-P.; Tessier, C.; Fischer, F. Lithium secondary batteries working at very high temperature: Capacity fade and understanding of aging mechanisms. J. Power Source 2013, 236, 265–275. [Google Scholar] [CrossRef]
- Uddin, K.; Perera, S.; Widanage, W.D.; Somerville, L.; Marco, J. Characterising lithium-ion battery degradation through the identification and tracking of electrochemical battery model parameters. Batteries 2016, 2, 13. [Google Scholar] [CrossRef]
- Wu, Y.-P.; Rahm, E.; Holze, R. Carbon anode materials for lithium ion batteries. J. Power Source 2003, 114, 228–236. [Google Scholar] [CrossRef]
- Goers, D.; Spahr, M.E.; Leone, A.; Märkle, W.; Novák, P. The influence of the local current density on the electrochemical exfoliation of graphite in lithium-ion battery negative electrodes. Electrochim. Acta 2011, 56, 3799–3808. [Google Scholar] [CrossRef]
- Broussely, M.; Herreyre, S.; Biensan, P.; Kasztejna, P.; Nechev, K.; Staniewicz, R.J. Aging mechanism in Li ion cells and calendar life predictions. J. Power Source 2001, 98, 13–21. [Google Scholar] [CrossRef]
- ME, S.C.N.; ME, B.B.; Babu, S.S.; Rizzoni, G.; Guezennec, Y. Aging Mechanisms in Li-ion Batteries. J. Power Source 2005, 146, 90–96. [Google Scholar]
- Agubra, V.; Fergus, J. Lithium ion battery anode aging mechanisms. Materials 2013, 6, 1310–1325. [Google Scholar] [CrossRef]
- Buqa, H.; Würsig, A.; Vetter, J.; Spahr, M.E.; Krumeich, F.; Novák, P. SEI film formation on highly crystalline graphitic materials in lithium-ion batteries. J. Power Source 2006, 153, 385–390. [Google Scholar] [CrossRef]
- Zhang, S.S. A review on electrolyte additives for lithium-ion batteries. J. Power Source 2006, 162, 1379–1394. [Google Scholar] [CrossRef]
- Richard, M.; Dahn, J. Accelerating rate calorimetry study on the thermal stability of lithium intercalated graphite in electrolyte. I. Experimental. J. Electrochem. Soc. 1999, 146, 2068–2077. [Google Scholar] [CrossRef]
- Maleki, H.; Deng, G.; Anani, A.; Howard, J. Thermal Stability Studies of Li-Ion Cells and Components. J. Electrochem. Soc. 1999, 146, 3224–3229. [Google Scholar] [CrossRef]
- MacNeil, D.; Larcher, D.; Dahn, J. Comparison of the reactivity of various carbon electrode materials with electrolyte at elevated temperature. J. Electrochem. Soc. 1999, 146, 3596. [Google Scholar] [CrossRef]
- Petzl, M.; Kasper, M.; Danzer, M.A. Lithium plating in a commercial lithium-ion battery—A low-temperature aging study. J. Power Source 2015, 275, 799–807. [Google Scholar] [CrossRef]
- Zinth, V.; Von Lüders, C.; Hofmann, M.; Hattendorff, J.; Buchberger, I.; Erhard, S.; Rebelo-Kornmeier, J.; Jossen, A.; Gilles, R. Lithium plating in lithium-ion batteries at sub-ambient temperatures investigated by in situ neutron diffraction. J. Power Source 2014, 271, 152–159. [Google Scholar] [CrossRef]
- Waldmann, T.; Wilka, M.; Kasper, M.; Fleischhammer, M.; Wohlfahrt-Mehrens, M. Temperature dependent ageing mechanisms in Lithium-ion batteries—A Post-Mortem study. J. Power Source 2014, 262, 129–135. [Google Scholar] [CrossRef]
- Yuqin, C.; Hong, L.; Lie, W.; Tianhong, L. Irreversible capacity loss of graphite electrode in lithium-ion batteries. J. Power Source 1997, 68, 187–190. [Google Scholar] [CrossRef]
- Shim, J.; Striebel, K.A. The dependence of natural graphite anode performance on electrode density. J. Power Source 2004, 130, 247–253. [Google Scholar] [CrossRef]
- Jung, S.K.; Gwon, H.; Hong, J.; Park, K.Y.; Seo, D.H.; Kim, H.; Hyun, J.; Yang, W.; Kang, K. Understanding the degradation mechanisms of LiNi0. 5Co0. 2Mn0. 3O2 cathode material in lithium ion batteries. Adv. Energy Mater. 2014, 4, 1300787. [Google Scholar] [CrossRef]
- Hausbrand, R.; Cherkashinin, G.; Ehrenberg, H.; Gröting, M.; Albe, K.; Hess, C.; Jaegermann, W. Fundamental degradation mechanisms of layered oxide Li-ion battery cathode materials: Methodology, insights and novel approaches. Mater. Sci. Eng. B 2015, 192, 3–25. [Google Scholar] [CrossRef]
- Fergus, J.W. Recent developments in cathode materials for lithium ion batteries. J. Power Source 2010, 195, 939–954. [Google Scholar] [CrossRef]
- Zhu, J.; Zeng, K.; Lu, L. Cycling effects on surface morphology, nanomechanical and interfacial reliability of LiMn2O4 cathode in thin film lithium ion batteries. Electrochim. Acta 2012, 68, 52–59. [Google Scholar] [CrossRef]
- Markovsky, B.; Rodkin, A.; Cohen, Y.S.; Palchik, O.; Levi, E.; Aurbach, D.; Kim, H.J.; Schmidt, M. The study of capacity fading processes of Li-ion batteries: Major factors that play a role. J. Power Source 2003, 121, 504–510. [Google Scholar] [CrossRef]
- MacNeil, D.; Lu, Z.; Chen, Z.; Dahn, J.R. A comparison of the electrode/electrolyte reaction at elevated temperatures for various Li-ion battery cathodes. J. Power Source 2002, 108, 8–14. [Google Scholar] [CrossRef]
- Martha, S.K.; Haik, O.; Zinigrad, E.; Exnar, I.; Drezen, T.; Miners, J.H.; Aurbach, D. On the thermal stability of olivine cathode materials for lithium-ion batteries. J. Electrochem. Soc. 2011, 158, A1115. [Google Scholar] [CrossRef]
- Zhan, C.; Wu, T.; Lu, J.; Amine, K. Dissolution, migration, and deposition of transition metal ions in Li-ion batteries exemplified by Mn-based cathodes—A critical review. Energy Environ. Sci. 2018, 11, 243–257. [Google Scholar] [CrossRef]
- Biensan, P.; Simon, B.; Peres, J.; De Guibert, A.; Broussely, M.; Bodet, J.; Perton, F. On safety of lithium-ion cells. J. Power Source 1999, 81, 906–912. [Google Scholar] [CrossRef]
- Ochida, M.; Doi, T.; Domi, Y.; Tsubouchi, S.; Nakagawa, H.; Yamanaka, T.; Abe, T.; Ogumi, Z. Effects of electrolyte additives on the suppression of Mn deposition on edge plane graphite for lithium-ion batteries. J. Electrochem. Soc. 2013, 160, A410–A413. [Google Scholar] [CrossRef]
- Watanabe, S.; Kinoshita, M.; Hosokawa, T.; Morigaki, K.; Nakura, K. Capacity fade of LiAlyNi1-x-yCoxO2 cathode for lithium-ion batteries during accelerated calendar and cycle life tests (surface analysis of LiAlyNi1-x-yCoxO2 cathode after cycle tests in restricted depth of discharge ranges). J. Power Source 2014, 258, 210–217. [Google Scholar] [CrossRef]
- Teichert, P.; Eshetu, G.G.; Jahnke, H.; Figgemeier, E. Degradation and Aging Routes of Ni-rich Cathode Based Li-Ion Batteries. Batteries 2020, 6, 8. [Google Scholar] [CrossRef]
- Goodenough, J.B.; Kim, Y. Challenges for rechargeable Li batteries. Chem. Mater. 2010, 22, 587–603. [Google Scholar] [CrossRef]
- Edström, K.; Gustafsson, T.; Thomas, J.O. The cathode-electrolyte interface in the Li-ion battery. Electrochim. Acta 2004, 50, 397–403. [Google Scholar] [CrossRef]
- Zhang, D.; Haran, B.; Durairajan, A.; White, R.E.; Podrazhansky, Y.; Popov, B.N. Studies on capacity fade of lithium-ion batteries. J. Power Source 2000, 91, 122–129. [Google Scholar] [CrossRef]
- Jow, T.R.; Allen, J.; Marx, M.; Nechev, K.; Deveney, B.; Rickman, S. Electrolytes, SEI and charge discharge kinetics in Li-ion batteries. ECS Trans. 2010, 25, 3–12. [Google Scholar] [CrossRef]
- Gandoman, F.H.; Jaguemont, J.; Goutam, S.; Gopalakrishnan, R.; Firouz, Y.; Kalogiannis, T.; Omar, N.; Van Mierlo, J. Concept of reliability and safety assessment of lithium-ion batteries in electric vehicles: Basics, progress, and challenges. Appl. Energy 2019, 251, 113343. [Google Scholar] [CrossRef]
- Wu, Y.; Keil, P.; Schuster, S.F.; Jossen, A. Impact of temperature and discharge rate on the aging of a LiCoO2/LiNi0.8Co0.15Al0.05O2 lithium-ion pouch cell. J. Electrochem. Soc. 2017, 164, A1438–A1445. [Google Scholar] [CrossRef]
- Jha, A. Next-Generation Batteries and Fuel Cells for Commercial, Military, and Space Applications; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Botte, G.G.; White, R.E.; Zhang, Z. Thermal stability of LiPF6–EC: EMC electrolyte for lithium ion batteries. J. Power Source 2001, 97, 570–575. [Google Scholar] [CrossRef]
- Eshetu, G.G.; Grugeon, S.; Laruelle, S.; Boyanov, S.; Lecocq, A.; Bertrand, J.-P.; Marlair, G. In-depth safety-focused analysis of solvents used in electrolytes for large scale lithium ion batteries. Phys. Chem. Chem. Phys. 2013, 15, 9145–9155. [Google Scholar] [CrossRef]
- Laszczynski, N.; Solchenbach, S.; Gasteiger, H.A.; Lucht, B.L. Understanding electrolyte decomposition of graphite/NCM811 cells at elevated operating voltage. J. Electrochem. Soc. 2019, 166, A1853–A1859. [Google Scholar] [CrossRef]
- Kassem, M.; Bernard, J.; Revel, R.; Pelissier, S.; Duclaud, F.; Delacourt, C. Calendar aging of a graphite/LiFePO4 cell. J. Power Source 2012, 208, 296–305. [Google Scholar] [CrossRef]
- Malek, K.; Franco, A.A. Microstructure-based modeling of aging mechanisms in catalyst layers of polymer electrolyte fuel cells. J. Phys. Chem. B 2011, 115, 8088–8101. [Google Scholar] [CrossRef] [PubMed]
- Millner, A. Modeling lithium ion battery degradation in electric vehicles. In Proceedings of the Innovative Technologies for an Efficient and Reliable Electricity Supply, 2010 IEEE Conference, Cape Town, South Africa, 23–27 May 2010; pp. 349–356. [Google Scholar]
- Ning, G.; Popov, B.N. Cycle life modeling of lithium-ion batteries. J. Electrochem. Soc. 2004, 151, A1584–A1591. [Google Scholar] [CrossRef]
- Jungst, R.G.; Nagasubramanian, G.; Case, H.L.; Liaw, B.Y.; Urbina, A.; Paez, T.L.; Doughty, D.H. Accelerated calendar and pulse life analysis of lithium-ion cells. J. Power Source 2003, 119, 870–873. [Google Scholar] [CrossRef]
- Saha, B.; Goebel, K.; Christophersen, J. Comparison of prognostic algorithms for estimating remaining useful life of batteries. Trans. Inst. Meas. Control 2009, 31, 293–308. [Google Scholar] [CrossRef]
- Bai, G.; Wang, P.; Hu, C.; Pecht, M. A generic model-free approach for lithium-ion battery health management. Appl. Energy 2014, 135, 247–260. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.; Cho, B. Complementary cooperation algorithm based on DEKF combined with pattern recognition for SOC/capacity estimation and SOH prediction. IEEE Trans. Power Electron. 2012, 27, 436–451. [Google Scholar] [CrossRef]
- Eddahech, A.; Briat, O.; Bertrand, N.; Delétage, J.-Y.; Vinassa, J.-M. Behavior and state-of-health monitoring of Li-ion batteries using impedance spectroscopy and recurrent neural networks. Int. J. Electr. Power Energy Syst. 2012, 42, 487–494. [Google Scholar] [CrossRef]
- Widodo, A.; Shim, M.-C.; Caesarendra, W.; Yang, B.-S. Intelligent prognostics for battery health monitoring based on sample entropy. Expert Syst. Appl. 2011, 38, 11763–11769. [Google Scholar] [CrossRef]
- Patsios, C.; Wu, B.; Chatzinikolaou, E.; Rogers, D.J.; Wade, N.; Brandon, N.P.; Taylor, P. An integrated approach for the analysis and control of grid connected Energy storage systems. J. Energy Storage 2016, 5, 48–61. [Google Scholar] [CrossRef]
- Jin, X.; Vora, A.; Hoshing, V.; Saha, T.; Shaver, G.; García, R.E.; Wasynczuk, O.; Varigonda, S. Physically-based reduced-order capacity loss model for graphite anodes in Li-ion battery cells. J. Power Source 2017, 342, 750–761. [Google Scholar] [CrossRef]
- Delacourt, C.; Safari, M. Life simulation of a graphite/LiFePO4 cell under cycling and storage. J. Electrochem. Soc. 2012, 159, A1283–A1291. [Google Scholar] [CrossRef]
- Sarasketa-Zabala, E.; Gandiaga, I.; Rodriguez-Martinez, L.; Villarreal, I. Calendar ageing analysis of a LiFePO4/graphite cell with dynamic model validations: Towards realistic lifetime predictions. J. Power Source 2014, 272, 45–57. [Google Scholar] [CrossRef]
- Grolleau, S.; Delaille, A.; Gualous, H.; Gyan, P.; Revel, R.; Bernard, J.; Redondo-Iglesias, E.; Peter, J.; Network, S. Calendar aging of commercial graphite/LiFePO4 cell—Predicting capacity fade under time dependent storage conditions. J. Power Source 2014, 255, 450–458. [Google Scholar] [CrossRef]
- Sarasketa-Zabala, E.; Gandiaga, I.; Martinez-Laserna, E.; Rodriguez-Martinez, L.; Villarreal, I. Cycle ageing analysis of a LiFePO4/graphite cell with dynamic model validations: Towards realistic lifetime predictions. J. Power Source 2015, 275, 573–587. [Google Scholar] [CrossRef]
- Magnor, D.; Gerschler, J.B.; Ecker, M.; Merk, P.; Sauer, D.U. Concept of a battery aging model for lithium-ion batteries considering the lifetime dependency on the operation strategy. In Proceedings of the European Photovoltaic Solar Energy Conference, Hamburg, Germany, 21–24 September 2009; pp. 21–25. [Google Scholar]
- Keil, P.; Schuster, S.F.; Wilhelm, J.; Travi, J.; Hauser, A.; Karl, R.C.; Jossen, A. Calendar aging of lithium-ion batteries I. Impact of the graphite anode on capacity fade. J. Electrochem. Soc. 2016, 163, A1872–A1880. [Google Scholar] [CrossRef]
- Ecker, M.; Nieto, N.; Käbitz, S.; Schmalstieg, J.; Blanke, H.; Warnecke, A.; Sauer, D.U. Calendar and cycle life study of Li (NiMnCo) O2-based 18650 lithium-ion batteries. J. Power Source 2014, 248, 839–851. [Google Scholar] [CrossRef]
- Belt, J.; Utgikar, V.; Bloom, I. Calendar and PHEV cycle life aging of high-Energy, lithium-ion cells containing blended spinel and layered-oxide cathodes. J. Power Source 2011, 196, 10213–10221. [Google Scholar] [CrossRef]
- Wang, J.; Purewal, J.; Liu, P.; Hicks-Garner, J.; Soukazian, S.; Sherman, E.; Sorenson, A.; Vu, L.; Tataria, H.; Verbrugge, M.W. Degradation of lithium ion batteries employing graphite negatives and nickel-cobalt-manganese oxide+ spinel manganese oxide positives: Part 1, aging mechanisms and life estimation. J. Power Source 2014, 269, 937–948. [Google Scholar] [CrossRef]
- Deshpande, R.; Verbrugge, M.; Cheng, Y.-T.; Wang, J.; Liu, P. Battery cycle life prediction with coupled chemical degradation and fatigue mechanics. J. Electrochem. Soc. 2012, 159, A1730–A1738. [Google Scholar] [CrossRef]
- Markervich, E.; Salitra, G.; Levi, M.; Aurbach, D. Capacity fading of lithiated graphite electrodes studied by a combination of electroanalytical methods, Raman spectroscopy and SEM. J. Power Source 2005, 146, 146–150. [Google Scholar] [CrossRef]
- Schimpe, M.; Von Kuepach, M.; Naumann, M.; Hesse, H.; Smith, K.; Jossen, A. Comprehensive Modeling of Temperature-Dependent Degradation Mechanisms in Lithium Iron Phosphate Batteries. J. Electrochem. Soc. 2018, 165, A181–A193. [Google Scholar] [CrossRef]
- Xu, B.; Oudalov, A.; Ulbig, A.; Andersson, G.; Kirschen, D.S. Modeling of lithium-ion battery degradation for cell life assessment. IEEE Trans. Smart Grid 2016, 9, 1131–1140. [Google Scholar] [CrossRef]
- Zavalis, T.G.; Klett, M.; Kjell, M.H.; Behm, M.; Lindström, R.W.; Lindbergh, G. Aging in lithium-ion batteries: Model and experimental investigation of harvested LiFePO4 and mesocarbon microbead graphite electrodes. Electrochim. Acta 2013, 110, 335–348. [Google Scholar] [CrossRef]
- Othman, A.M. Fracture resistance of rubber-modified asphaltic mixtures exposed to high-temperature cyclic aging. J. Elastom. Plast. 2006, 38, 19–30. [Google Scholar] [CrossRef]
- Narayanrao, R.; Joglekar, M.; Inguva, S. A phenomenological degradation model for cyclic aging of lithium ion cell materials. J. Electrochem. Soc. 2013, 160, A125–A137. [Google Scholar] [CrossRef]
- Laresgoiti, I.; Käbitz, S.; Ecker, M.; Sauer, D.U. Modeling mechanical degradation in lithium ion batteries during cycling: Solid electrolyte interphase fracture. J. Power Source 2015, 300, 112–122. [Google Scholar] [CrossRef]
- Lin, C.; Tang, A.; Mu, H.; Wang, W.; Wang, C. Aging mechanisms of electrode materials in lithium-ion batteries for electric vehicles. J. Chem. 2015. [Google Scholar] [CrossRef]
- Ramadass, P.; Haran, B.; White, R.; Popov, B.N. Capacity fade of Sony 18650 cells cycled at elevated temperatures: Part II. Capacity fade analysis. J. Power Source 2002, 112, 614–620. [Google Scholar] [CrossRef]
- Belt, J.R.; Ho, C.D.; Miller, T.J.; Habib, M.A.; Duong, T.Q. The effect of temperature on capacity and power in cycled lithium ion batteries. J. Power Source 2005, 142, 354–360. [Google Scholar] [CrossRef]
- Stroe, D.-I.; Knap, V.; Swierczynski, M.; Stroe, A.-I.; Teodorescu, R. Operation of a grid-connected lithium-ion battery Energy storage system for primary frequency regulation: A battery lifetime perspective. IEEE Trans. Ind. Appl. 2016, 53, 430–438. [Google Scholar] [CrossRef]
- Cordoba-Arenas, A.; Onori, S.; Guezennec, Y.; Rizzoni, G. Capacity and power fade cycle-life model for plug-in hybrid electric vehicle lithium-ion battery cells containing blended spinel and layered-oxide positive electrodes. J. Power Source 2015, 278, 473–483. [Google Scholar] [CrossRef]
- Utsunomiya, T.; Hatozaki, O.; Yoshimoto, N.; Egashira, M.; Morita, M. Self-discharge behavior and its temperature dependence of carbon electrodes in lithium-ion batteries. J. Power Source 2011, 196, 8598–8603. [Google Scholar] [CrossRef]
- Kurzweil, P.; Shamonin, M. State-of-charge monitoring by impedance spectroscopy during long-term self-discharge of supercapacitors and Lithium-Ion batteries. Batteries 2018, 4, 35. [Google Scholar] [CrossRef]
- Schmidt, J.P.; Weber, A.; Ivers-Tiffée, E. A novel and fast method of characterizing the self-discharge behavior of lithium-ion cells using a pulse-measurement technique. J. Power Source 2015, 274, 1231–1238. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, X.; Shang, B.; Li, G. Unbalanced discharging and aging due to temperature differences among the cells in a lithium-ion battery pack with parallel combination. J. Power Source 2016, 306, 733–741. [Google Scholar] [CrossRef]
- Osswald, P.J.; Erhard, S.V.; Rheinfeld, A.; Rieger, B.; Hoster, H.E.; Jossen, A. Temperature dependency of state of charge inhomogeneities and their equalization in cylindrical lithium-ion cells. J. Power Source 2016, 329, 546–552. [Google Scholar] [CrossRef]
- Sides, C.R.; Martin, C.R. Nanostructured Electrodes and the Low-Temperature Performance of Li-Ion Batteries. Adv. Mater. 2005, 17, 125–128. [Google Scholar] [CrossRef]
- Huang, C.K.; Sakamoto, J.; Wolfenstine, J.; Surampudi, S. The limits of low-temperature performance of Li-ion cells. J. Electrochem. Soc. 2000, 147, 2893–2896. [Google Scholar] [CrossRef]
- Beauregard, G.P. Report of Investigation: Hybrids Plus Plug in Hybrid Electric Vehicle; US Department of Energy, Idaho National Laboratory: Idaho Falls, ID, USA, 2008.
- Bugryniec, P.J.; Davidson, J.N.; Cumming, D.J.; Brown, S.F. Pursuing safer batteries: Thermal abuse of LiFePO4 cells. J. Power Source 2019, 414, 557–568. [Google Scholar] [CrossRef]
- Ohsaki, T.; Kishi, T.; Kuboki, T.; Takami, N.; Shimura, N.; Sato, Y.; Sekino, M.; Satoh, A. Overcharge reaction of lithium-ion batteries. J. Power Source 2005, 146, 97–100. [Google Scholar] [CrossRef]
- Al Hallaj, S.; Maleki, H.; Hong, J.-S.; Selman, J.R. Thermal modeling and design considerations of lithium-ion batteries. J. Power Source 1999, 83, 1–8. [Google Scholar] [CrossRef]
- Lei, B.; Zhao, W.; Ziebert, C.; Uhlmann, N.; Rohde, M.; Seifert, H.J. Experimental analysis of thermal runaway in 18650 cylindrical Li-ion cells using an accelerating rate calorimeter. Batteries 2017, 3, 14. [Google Scholar] [CrossRef]
- Wang, S.; Rafiz, K.; Liu, J.; Jin, Y.; Lin, J.Y. Effects of lithium dendrites on thermal runaway and gassing of LiFePO 4 batteries. Sustain. Energy Fuels 2020, 4, 2342–2351. [Google Scholar] [CrossRef]
- Hofmann, A.; Migeot, M.; Thißen, E.; Schulz, M.; Heinzmann, R.; Indris, S.; Bergfeldt, T.; Lei, B.; Ziebert, C.; Hanemann, T. Electrolyte Mixtures Based on Ethylene Carbonate and Dimethyl Sulfone for Li-Ion Batteries with Improved Safety Characteristics. ChemSusChem 2015, 8, 1892–1900. [Google Scholar] [CrossRef] [PubMed]
- Hofmann, A.; Uhlmann, N.; Ziebert, C.; Wiegand, O.; Schmidt, A.; Hanemann, T. Preventing Li-ion cell explosion during thermal runaway with reduced pressure. Appl. Therm. Eng. 2017, 124, 539–544. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, P.; Xu, M.; Wang, X. Computational identification of the safety regime of Li-ion battery thermal runaway. Appl. Energy 2020, 261, 114440. [Google Scholar] [CrossRef]
- Perea, A.; Paolella, A.; Dubé, J.; Champagne, D.; Mauger, A.; Zaghib, K. State of charge influence on thermal reactions and abuse tests in commercial lithium-ion cells. J. Power Source 2018, 399, 392–397. [Google Scholar] [CrossRef]
- Liu, B.; Jia, Y.; Yuan, C.; Wang, L.; Gao, X.; Yin, S.; Xu, J. Safety issues and mechanisms of lithium-ion battery cell upon mechanical abusive loading: A review. Energy Storage Mater. 2020, 24, 85–112. [Google Scholar] [CrossRef]
- Kim, G.-H.; Pesaran, A.; Spotnitz, R. A three-dimensional thermal abuse model for lithium-ion cells. J. Power Source 2007, 170, 476–489. [Google Scholar] [CrossRef]
- Karimi, G.; Li, X. Thermal management of lithium-ion batteries for electric vehicles. Int. J. Energy Res. 2013, 37, 13–24. [Google Scholar] [CrossRef]
- Kim, U.S.; Shin, C.B.; Kim, C.-S. Effect of electrode configuration on the thermal behavior of a lithium-polymer battery. J. Power Source 2008, 180, 909–916. [Google Scholar] [CrossRef]
- Al Hallaj, S.; Selman, J. A novel thermal management system for electric vehicle batteries using phase-change material. J. Electrochem. Soc. 2000, 147, 3231–3236. [Google Scholar] [CrossRef]
- Chen, D.; Jiang, J.; Kim, G.-H.; Yang, C.; Pesaran, A. Comparison of different cooling methods for lithium ion battery cells. Appl. Therm. Eng. 2016, 94, 846–854. [Google Scholar] [CrossRef]
- Zhang, G.; Shaffer, C.E.; Wang, C.-Y.; Rahn, C.D. In-situ measurement of current distribution in a Li-Ion cell. J. Electrochem. Soc. 2013, 160, A610–A615. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J. A comparative study of commercial lithium ion battery cycle life in electric vehicle: Capacity loss estimation. J. Power Source 2014, 268, 658–669. [Google Scholar] [CrossRef]
- Chiu, K.-C.; Lin, C.-H.; Yeh, S.-F.; Lin, Y.-H.; Huang, C.-S.; Chen, K.-C. Cycle life analysis of series connected lithium-ion batteries with temperature difference. J. Power Source 2014, 263, 75–84. [Google Scholar] [CrossRef]
- Troxler, Y.; Wu, B.; Marinescu, M.; Yufit, V.; Patel, Y.; Marquis, A.J.; Brandon, N.P.; Offer, G.J. The effect of thermal gradients on the performance of lithium-ion batteries. J. Power Source 2014, 247, 1018–1025. [Google Scholar] [CrossRef]
- Klein, M.; Tong, S.; Park, J. In-plane nonuniform temperature effects on the performance of a large-format lithium-ion pouch cell. Appl. Energy 2016, 165, 639–647. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).